1. На главную
  2. Электронные версии
  3. Известия РАН. Физика атмосферы и океана
  4. T. 56, № 4, 2020

Известия РАН. Физика атмосферы и океана, 2020, T. 56, № 4, стр. 433-445

Динамика среднезональных характеристик циркуляции в средней атмосфере

О. С. Зоркальцева a, b, *, В. И. Мордвинов a, А. И. Погорельцев c, d, Н. С. Домбровская a

a Институт солнечно-земной физики СО РАН
664033 Иркутск, ул. Лермонтова, 126а, Россия

b Иркутский Государственный Университет
664033 Иркутск, ул. Лермонтова, 126, Россия

c Российский Государственный Гидрометеорологический Университет
195196 Санкт-Петербург, Малоохтинский проспект, д. 98, Россия

d Санкт-Петербургский государственный университет
198504 Петергоф, Университетский просп., 26, Россия

* E-mail: olgak@mail.iszf.irk.ru

Поступила в редакцию 26.09.2019
После доработки 29.01.2020
Принята к публикации 05.02.2020

Полный текст (PDF)

Аннотация

Для исследования динамических процессов в средней атмосфере использованы данные архива ERA-Interim и расчеты циркуляции с помощью модели средней и верхней атмосферы (МСВА). По данным наблюдений и модельным расчетам выполнен анализ вариаций среднезональных характеристик атмосферы. В средней атмосфере в диапазоне 10–30 сут выделяются синхронные колебания температуры в протяженных по широте и вертикали зонах. Знак вариаций меняется по горизонтали в области струйных течений (и не меняется на экваторе), по вертикали смена знака происходит в областях стратопаузы и мезопаузы. Характер вариаций практически не зависит от фазы квазидвухлетнего цикла в экваториальной стратосфере. Колебания имеют глобальный характер и напоминают колебания в меридиональных ячейках циркуляции.

Ключевые слова: стратосфера, мезосфера, внезапные стратосферные потепления, квазидвухлетнее колебание

1. ВВЕДЕНИЕ

Низкочастотная изменчивость атмосферы в диапазоне 10–30 сут включает изменчивость, обусловленную бегущими волнами Россби и квазистационарными волнами, связанными с орографическими и термическими аномалиями, а также нелинейными взаимодействиями [1, 2]. Одним из наиболее сложных динамических явлений в средней атмосфере являются внезапные стратосферные потепления (ВСП) [3–5], во время которых происходит разрушение полярного вихря. При этом температура в высоких широтах может возрастать на несколько десятков градусов. Практически во всей толще средней атмосферы значительные вариации демонстрируют зонально осредненные метеорологические величины (средняя зональная скорость, средняя зональная температура и т.п.), характеризующие динамику полярного вихря, возрастают термические и барические аномалии вдоль широтных кругов. Морфологически ВСП можно представить, как результат динамического взаимодействия в средней атмосфере полярного циклонического вихря и одного или нескольких антициклонических вихрей [6].

ВСП связывают либо с собственными неустойчивостями струйных течений в средней атмосфере [7–9], либо с “внешними” факторами – распространяющимися из тропосферы стационарными планетарными волнами, блокингами, возмущениями, обусловленными конвективными процессами в тропиках [3, 6, 10]. Неясно, однако, в какой степени соотносятся эти механизмы, являются ли ВСП в большей степени взрывным усилением собственных колебаний в средней атмосфере, либо следствием переноса энергии извне и взаимодействием волн и вихрей со средним потоком.

Удобным диагностическим средством исследования динамических процессов являются зональные осреднения, позволяющие не только выделять “жизненный цикл” возмущений, но и исследовать их связь с внешними факторами и “фоновыми” квазирегулярными колебаниями в средней атмосфере. Известно, что среднезональные характеристики испытывают вариации в широком диапазоне частот – от сезонных до межсуточных [11]. Вариации в диапазоне 40–50 сут обычно связывают с орографическим возбуждением [12] и осцилляцией Маддена–Джулиана [11, 13], интервал 10–30 сут изучен гораздо хуже.

Для исследования колебаний в стратосфере и нижней мезосфере могут быть использованы современные архивы ре-анализа. Для изучения процессов в верхней мезосфере и нижней термосфере необходимо привлечение модельных расчетов. В работе [14] мы использовали для этой цели модель общей циркуляции атмосферы МСВА [15]. Расчеты воспроизвели многие закономерности в распределении и динамике среднезональных характеристик циркуляции во время ВСП при различных фазах КДК и колебания Маддена–Джулиана. Особенную ценность использованию модельных расчетов придает возможность контроля внешних факторов, которые могут генерировать не только квазирегулярные колебания в верхних слоях атмосферы, но и взрывные процессы типа ВСП.

В разделе 2 приводится описание модели МСВА и схема численных экспериментов. Влияние КДК задавалось дополнительным слагаемым в прогностическом уравнении. Результаты расчетов сопоставлялись с данными архива ERA-Interim раздельно для западной и восточной фаз КДК в разных широтных зонах и на разных высотах атмосферы. Тренды и высокочастотные колебания исключались с помощью скользящего осреднения в окнах 10 и 30 сут. Для анализа распространения возмущений по вертикали и вдоль меридиана строились диаграммы широта-время, высота-время и взаимные корреляционные кривые между вариациями средней зональной скорости и средней зональной температуры в разных широтных зонах и на разных уровнях атмосферы. В разделе 3 приводятся результаты расчетов взаимных корреляционных кривых по данным ERA-Interim и модельным расчетам. Анализируется степень согласия наблюдательных данных и модельных расчетов, особенности распределений взаимных корреляционных кривых.

2. ОПИСАНИЕ МОДЕЛЬНЫХ ЭКСПЕРИМЕНТОВ

2.1. Метод моделирования

Для моделирования теплового режима и общей циркуляции атмосферы использовалась трехмерная нелинейная модель циркуляции атмосферы (МСВА) в области высот 0–300 км, реализованная на сетке 5.625° по долготе, 5° по широте, 56 уровней по высоте [15]. Шаг интегрирования по времени составлял 225 с. В последней версии МСВА включена новая параметризация эффектов орографических гравитационных волн [16], а также новые климатические распределения озона [17] и паров воды в тропосфере [18], учитывающие зависимость от долготы. Вертикальной координатой модели является безразмерная log-изобарическая высота x = –ln(p/1000), где р – давление в гПа. Нижние граничные условия на уровне 1000 гПа представляют собой распределения геопотенциальной высоты и температуры в январе, учитывающие средние зональные значения и стационарные планетарные волны с зональными волновыми числами m = 1–5. Для исключения влияния явления Эль Ниньо – Южное Колебание (ЭНЮК) при расчете нижних граничных условий использовались данные японского ре-анализа JRA55 [19] в периоды нейтральной фазы ЭНЮК согласно индексу MEI (Multivariate ENSO Index).

Влияние КДК задавалось дополнительным слагаемым в прогностическом уравнении для зональной компоненты скорости, пропорциональным разности рассчитанных и климатических распределений среднезональных значений зональной скорости ветра для западной и восточной фазы КДК. Дополнительное слагаемое “включалось” в интервале широт 17.5° S–17.5° N на высотах 0–50 км. Характерное время “притяжения” модельного среднего зонального потока к данным ре-анализа MERRA [20] составляло 5 сут.

2.2. Схема численных экспериментов

Численные эксперименты проводились отдельно для восточной и западной фазы КДК. Длительность каждой реализации составляла 400 модельных дней, в течение первых 120 дней учитывался только среднесуточный нагрев атмосферы. Включение суточных вариаций нагрева и постепенное включение дополнительного уравнения для возмущения геопотенциала на нижней границе расчетной области происходило после 120 дня и продолжалось до 330 дня. В период с 331 по 400 день (1 января–11 марта) расчеты проводились с учетом изменения зенитного угла Солнца. Постепенное включение суточных вариаций нагрева и дополнительного уравнения в 121, 122…, 130 день позволило получить ансамбли полей гидродинамических величин, состоящие из 10 реализаций модели, рассчитанных с различными начальными условиями.

2.3. Методика обработки данных

Объектом анализа и сопоставления модельных расчетов и данных наблюдений были среднезональные величины температуры и зональной компоненты ветра. Тренды и высокочастотные колебания исключались с помощью скользящего осреднения в окнах 10 и 30 сут [21]. Для удобства сопоставления вариаций в разных широтных зонах временные ряды нормировались на разность между максимальным и минимальным значением. Обозначим полученные после обработки средние зональные величины температуры и зональной компоненты ветра U* и Т*. Распределения U* и Т* наносились затем на диаграммы широта–время и высота–время. Для анализа распространения возмущений по вертикали и вдоль меридиана строились диаграммы широта–время, высота–время и взаимные корреляционные кривые между вариациями U* и T* в разных широтных зонах и на разных уровнях атмосферы.

3. РЕЗУЛЬТАТЫ РАСЧЕТОВ

3.1. Горизонтальный перенос

На рис. 1 приведен пример изменений со временем распределений U* и Т* на уровне 10 гПа (~30 км) по данным наблюдений зимой 2017 года (справа) и по данным модельных расчетов (слева) для одной из реализаций при западной фазе КДК. На рисунках внизу изображены графики изменений среднезональной температуры в полярной области. Выделяются два эпизода стратосферных потеплений в конце января и конце февраля.

Рис. 1.

Диаграммы широта-время T* и U* по данным МСВА (слева) и по данным ERA-Interim (справа). Внизу графики вариаций среденезональной температуры воздуха в полярной области по данным МСВА (слева) и по данным ERA-Interim (справа).

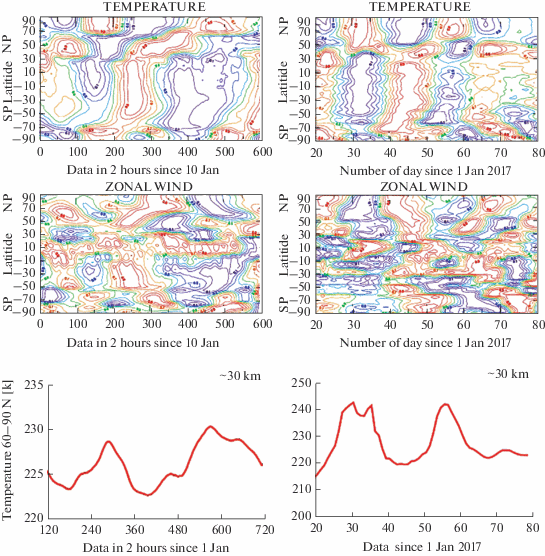
Хорошо видно качественное согласие модельных расчетов и данных наблюдений. В обоих случаях колебания продолжительностью 15–30 сут имеют глобальный характер и не ограничиваются только высокими широтами Северного полушария. В Южном полушарии по данным наблюдений возмущения достигают ~50° ю.ш., а по модельным расчетам – ~70° ю.ш. Частью возмущений являются крутильные колебания, распространяющиеся в меридиональном направлении. Крутильные колебания хорошо видны в данных наблюдений и в модельных расчетах в интервале широт 30–60° с.ш. В вариациях T* переносы между разными широтными зонами выражены в меньшей степени, здесь преобладают синхронные колебания (в фазе или в противофазе), занимающие протяженные широтные полосы. Вариации Т* напоминают колебания температуры в конвективных ячейках с чередующимися во времени восходящими и нисходящими движениями. Линии раздела восходящих и нисходящих движений совпадают со средним климатическим положением струйных течений.

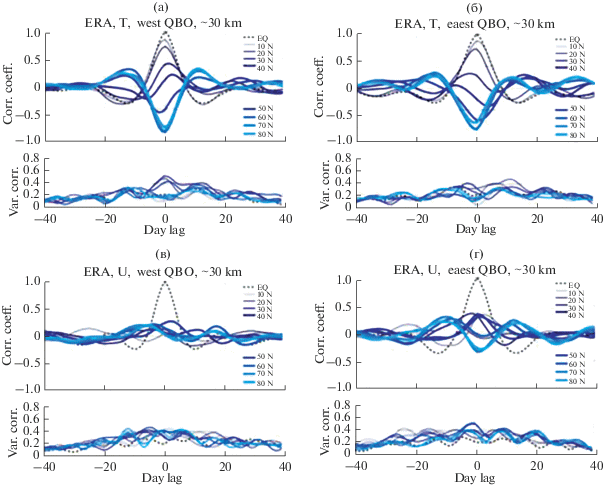
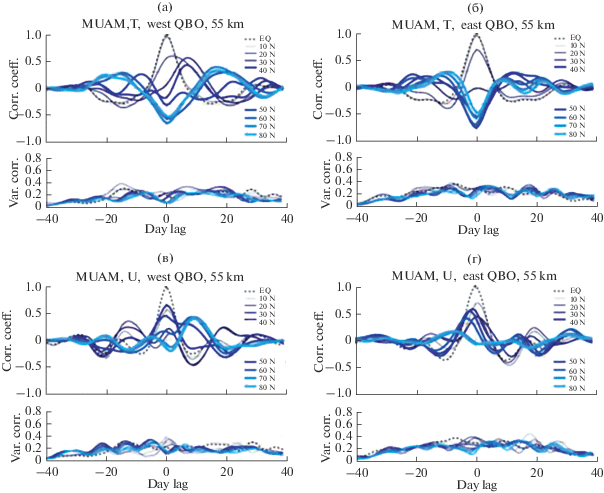
Перечисленные выше особенности характерны для всех реализаций модельных расчетов и для разных лет наблюдений. Это подтверждают приведенные на рис. 2–9 графики коэффициентов корреляции, рассчитанные со сдвигом от –40 дней до +40 дней между изменениями со временем T* и U* в разных широтных зонах на высотах ~30 км (рис. 2–5) и ~55 км (рис. 6–9), усредненные по 10 модельным реализациям и по данным ERA-Interim за годы с разными фазами КДК. Фазы КДК определялись по значениям средней зональной скорости на экваторе на уровне 10 гПа. Годы с западной фазы КДК, отобранные для расчетов, включали 1993, 1995, 1997, 1999, 2002, 2004, 2006, 2008, 2011, 2014, 2017 гг., годы с восточной фазой КДК – 1994, 1998, 2000, 2001, 2003, 2005, 2007, 2010, 2012, 2015 гг.

Рис. 2.

Вверху - коэффициенты корреляции вариаций T* (а, б) и U* (в, г) в разных широтных интервалах, усредненные по 10 модельным реализациям на высоте ~30 км. Графики слева относятся к западной фазе КДК, графики справа – к восточной фазе КДК. Штриховой линией показан график автокорреляции на экваторе, от синего к голубому выделены коэффициенты корреляции между экваториальной зоной (0° с.ш.) и широтными зонами 10° с.ш., 20° с.ш, 30° с.ш, 40° с.ш., 50° с.ш , 60° с.ш , 70° с.ш , 80° с.ш; внизу – среднеквадратичные отклонения коэффициентов корреляции, рассчитанные по 10 модельным реализациям.

Рис. 3.

То же, что и на рис. 2, но по данным ERA-Interim.

Рис. 4.

То же, что и на рис. 2, но на высоте ~55 км.

Рис. 5.

То же, что и на рис. 3, но по данным ERA-Interim.

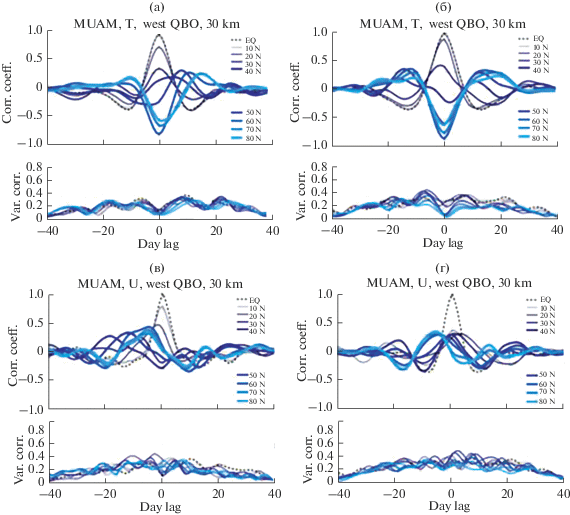
Рис. 6.

Распределения коэффициентов корреляции между вариациями T* на экваторе с вариациями T* в широтных зонах от 80° с.ш. до 80° ю.ш. на высоте ~30 км. Коэффициенты корреляции рассчитывались отдельно за зимне-весенний (справа) и летний (слева) периоды.

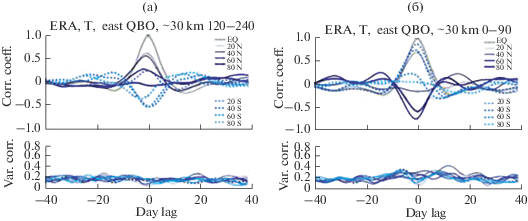
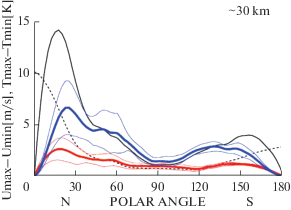
Рис. 7.

Графики зависимости от широты разностей между максимальными и минимальными значениями временных рядов среднезональной температуры (штриховая кривая) и среднезональной скорости (сплошная линия) за 140 сут, начиная с 1 января на уровне 10 гПа. На рисунок нанесены нормированные на длину широтных кругов кривые для среднезональной температуры (красный цвет) и среднезональной скорости (синий цвет), приведенные к широте 40° с.ш.

Рис. 8.

То же, что на рис. 7, но на уровне 500 гПа.

Рис. 9.

Распределения по вертикали T* и U* для западной (слева) и восточной (справа) фазы КДК.

Графики слева относятся к западной фазе КДК, графики справа – к восточной фазе КДК. Во всех реализациях модельных расчетов и по данным ERA-Interim при западной и при восточной фазах КДК вариации T* в умеренных и высоких широтах противоположны по знаку вариациям в низких широтах. Вариации U* на низких и высоких широтах имеют более сложный характер, в высоких широтах вариации смещены по фазе относительно вариаций в низких широтах примерно на 5–10 сут.

В нижней части рисунков приведены графики среднеквадратичных отклонений коэффициентов корреляции. По крайней мере, в интервале сдвигов от –10 до +10 дней значения коэффициентов корреляции превышают величину среднеквадратичного отклонения, а в интервале –5–+5 дней – удвоенные значения среднеквадратичного отклонения. Это говорит о том, что статистический разброс между отдельными реализациями невелик и особенности динамики возмущений, приведенные на диаграммах, характерны для всех реализаций.

Различия между графиками коэффициентов корреляции на высотах 30 и 55 км не очень велики. Основная особенность в вариациях T* – антикорреляция возмущений в низких и высоких широтах одинакова на разных высотах и в модельных расчетах и в данных наблюдений. В промежуточных широтных зонах видны признаки переноса возмущений вдоль меридиана, однако надежность этих выводов не очень велика, так как амплитуда вариаций с увеличением сдвига чаще всего не превышает величины среднеквадратичного отклонения.

Заметим, что корреляции между вариациями в разных широтных зонах не ограничиваются только одним полушарием. Это хорошо видно на диаграммах, приведенных на рис. 1. Это подтверждают и графики коэффициентов корреляции на рис. 6, на котором построены распределения коэффициентов корреляции между T* на экваторе с вариациями T* в широтных зонах от 80° с.ш. до 80° ю.ш. на высоте ~30 км. Коэффициенты корреляции рассчитывались раздельно за зимне-весенний и летний периоды. Зимой северного полушария графики демонстрируют уже знакомую нам антикорреляцию T* на высоких и низких широтах. Однако синхронно с вариациями на экваторе температура меняется в широтной полосе 0–40° ю.ш., т.е. колебания охватывают и северное и южное полушарие.

В летний период колебания столь же глобальны, однако характер связей меняется – синхронные изменения в широтной полосе ~0–40° с.ш. антикоррелируют с вариациями T* в интервале широт 40–80° ю.ш. Если учесть, что в летний период внезапные стратосферные потепления отсутствуют и в северном, и в южном полушариях, можно утверждать, что найденные закономерности вариаций относятся к “фоновым” характеристикам циркуляции в средней атмосфере.

К сожалению, особенности использованного метода фильтрации не позволяют оценить области генерации и области распространения колебаний. Нормировка временных рядов на разности между максимальными и минимальными значениями исключает какую-либо информацию об амплитуде колебаний в разных широтных зонах. Чтобы восполнить этот пробел хотя бы частично, мы проанализировали изменения с широтой разностей между максимальными и минимальными значениями во временных рядах средней зональной температуры и средней зональной скорости. Если ограничить временные ряды сезонными интервалами, то максимальные и минимальные значения рядов будут, скорее всего, соседствовать и соответствовать одному и тому же явлению, хотя некоторая вероятность принадлежности максимумов и минимумов разным событиям остается. При осреднении за разные годы роль этих различий снижается.

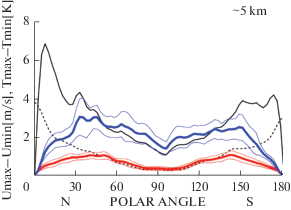
На рис. 7 приведены графики изменений с широтой на уровне 10 гПа разностей между максимальными и минимальными значениями временных рядов средней зональной температуры (штриховая кривая) и средней зональной скорости (сплошная линия) за 140 сут, начиная с 1 января. Графики осреднены за 20 лет с 1997 по 2017 гг. Кривые имеют характерные изломы, которые особенно хорошо выделяются при нормировании на длину широтного круга. Нормированные на длину широтного круга кривые для средней зональной температуры (красный цвет) и средней зональной скорости (синий цвет), приведенные к широте 40° с.ш. нанесены на рис. 7. Можно ожидать, что в тех широтных зонах, где отсутствует накачка и затухание колебаний, графики нормированных величин будут иметь вид прямых линий, а там, где колебания усиливаются (затухают), значения разностей будут возрастать (уменьшаться). Для оценки достоверности вариаций на рисунки нанесены также графики среднеквадратичных отклонений (тонкие линии).

Анализ рисунка показывает, что возможной областью генерации колебаний являются высокие широты с максимумом на широтах примерно 70–80°. Это хорошо видно и на графиках разности максимальных и минимальных значений температуры и на графиках вариаций среднезональной скорости. Вариации в этой области превышают среднеквадратичное отклонение и, следовательно, скорее всего, реальны. На широтах 40–60° с.ш. амплитуды вариаций имеют второй, менее выраженный максимум, небольшое повышение вблизи экватора и максимум на широтах 50–60° ю.ш., но только в среднезональной скорости.

Следует заметить, что в стратосфере, в отличие от тропосферы, вариации среднезональных величин сложнее интерпретировать, так как в зимний период наряду с полярным вихрем, и в стратосфере, и в мезосфере формируется один или несколько антициклонических вихрей. Взаимодействие этих образований определяет динамику циркуляции в средней атмосфере во время внезапных стратосферных потеплений. Диагностировать эту динамику только по зональным средним величинам сложно. Для этого обычно дополнительно привлекают разложения величин вдоль широтных кругов в ряд Фурье. Для сравнения на рис. 8 приведены графики разностей среднезональных величин скорости (сплошная линия, синий цвет) и температуры (штриховая линия, красный цвет), аналогичные графикам на рис. 7, но для уровня 500 гПа. Видно, что амплитуда колебаний среднезональной скорости и температуры на этом уровне меньше, чем в стратоосфере. При этом максимальные вариации температуры и, в меньшей степени, вариации среднезональной скорости смещены по сравнению со стратосферой в область умеренных широт. Максимум генерации колебаний приходится на широту примерно 40°, т.е. попадает в область субтропического струйного течения. В южном полушарии амплитуда вариаций температуры возрастает примерно до 50° ю.ш., а затем падает. Амплитуда вариаций среднезональной скорости до этого широтного круга остается постоянной, а дальше к югу также быстро уменьшается.

Хотя механизм раскачки колебаний неясен, увеличение амплитуды колебаний в зоне субтропического струйного течения в тропосфере и в окрестностях полярного вихря в средней атмосфере представляется вполне естественным. Действительно, именно в этих областях наиболее вероятно развитие бароклинной и баротропной неустойчивостей, именно в этих областях наиболее велики запасы доступной лабильной энергии. Характер колебаний и зональной скорости и среднезональной температуры позволяет предположить, что вариации этих величин отражают скорее собственные глобальные колебания, чем колебания, обусловленные локализованными источниками. В большей степени это предположение относится к циркуляции в средней атмосфере, чем к циркуляции в тропосфере.

3.2. Вертикальный перенос

На основании анализа данных наблюдений считается установленным факт распространения возмущений температуры во время ВСП сверху вниз – из мезосферы в стратосферу, причем знак вариаций температуры в мезосфере и стратосфере чаще всего противоположен [4]. Эту особенность вполне подтверждают модельные расчеты, причем оказывается, что характер вариаций зависит от фазы КДК [14].

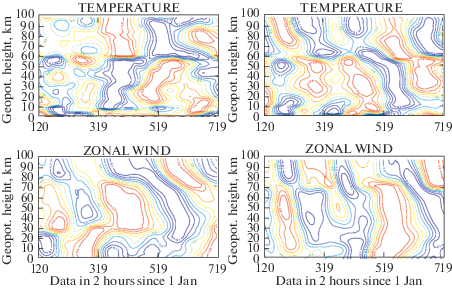
Чтобы проанализировать динамику процессов по вертикали более детально, мы построили распределения T* и U* на диаграммах высота-время в широтной полосе от 60 до 90 с.ш. для западной и восточной фазы КДК. На рис. 9 приведен пример диаграмм для двух произвольно выбранных реализаций модельных расчетов. Диапазон уровней по вертикали охватывает стратосферу, мезосферу и нижнюю часть термосферы.

В мезосфере хорошо виден перенос возмущений сверху вниз и в T*, и в U*. В стратосфере можно видеть движения и сверху вниз и снизу вверх, однако в температуре преобладают все же движения снизу вверх, а в средней зональной скорости – сверху вниз. Характер движений одинаков и при западной и при восточной фазах КДК. Основной особенностью распределений T* является противоположный знак возмущений температуры в стратосфере и мезосфере. Эта особенность прослеживается во всех реализациях модельных расчетов. На рис. 10 приведены распределения коэффициентов корреляции между изменениями со временем T* (вверху) и U* (внизу) в широтной полосе от 60° до 90° с.ш. на разных высотах атмосферы относительно вариаций на высоте 35 км, усредненные по 10 модельным реализациям. Графики слева относятся к западной фазе КДК, графики справа – к восточной фазе КДК.

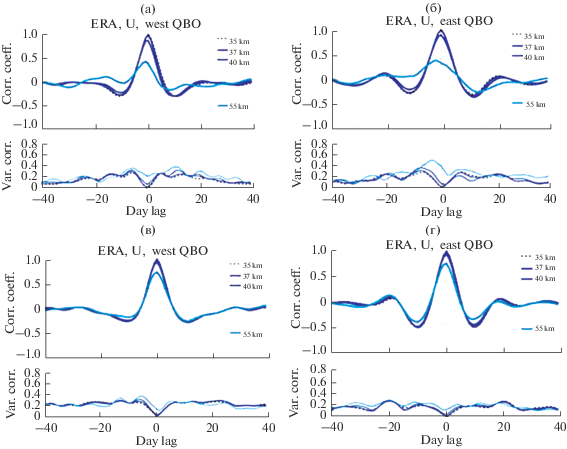
Рис. 10.

Коэффициенты корреляции (вверху), рассчитанные со сдвигом от –40 дней до +40 дней, между изменениями со временем Т* (а, б) и U* (в, г) на разных уровнях атмосферы относительно вариаций на высоте 18 км, усредненные по 10 модельным реализациям. Графики слева относятся к западной фазе КДК (а, в), графики справа – к восточной фазе циркуляции (б, г); внизу – среднеквадратичные отклонения коэффициентов корреляции, рассчитанные по 10 модельным реализациям.

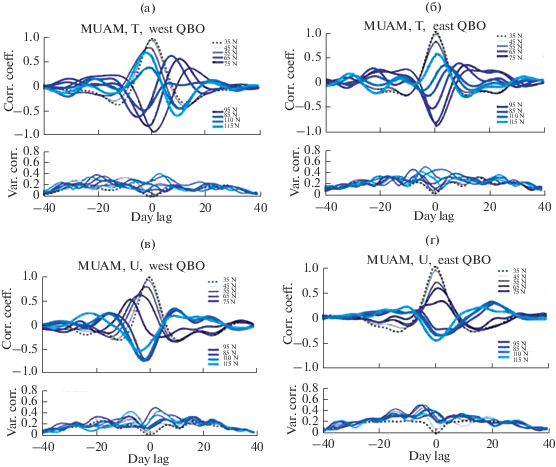
На графиках коэффициентов корреляции хорошо видна основная особенность в распределении вариаций T* – противоположный характер вариаций в мезосфере и стратосфере, причем в мезосфере смещение корреляционных кривых, соответствующих разным высотам, указывает на перенос возмущений сверху вниз, как при западной, так и при восточной фазах КДК. В интервале сдвигов по времени от –10 до +10 дней значения коэффициентов корреляции превышают величину среднеквадратичного отклонения, а в интервале –5–+5 дней – удвоенные значения среднеквадратичного отклонения.

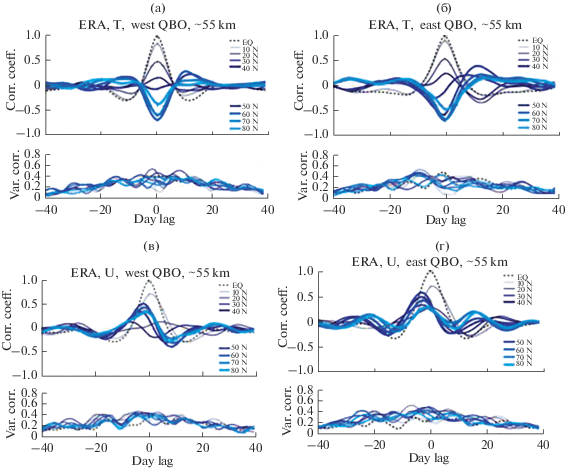
На рис. 11 приведены корреляционные кривые T* и U*, построенные по данным наблюдений. К сожалению, данные архива ERA-Interim ограничены уровнем 0.1 гПа, поэтому характерные для модельных расчетов антикорреляции между вариациями температуры в средней атмосфере на рис. 11 отсутствуют. Хорошо видно, однако, соответствие между корреляциями, построенными по модельным расчетам и данным наблюдений до высоты ~55 км.

Рис. 11.

Корреляционные кривые T* и U*, построенные по данным наблюдений.

4. ОБСУЖДЕНИЕ

Анализ вариаций метеорологических величин в средней атмосфере показал наличие глобальных колебаний среднезональной скорости и среднезональной температуре как в данных Era-Interim, так и в результатах расчетов. Масштабы колебаний вдоль меридиана составляют десятки градусов, колебания развиваются согласованно и в северном, и в южном полушариях. Вертикальный масштаб колебаний составляет десятки километров. Колебания меняют знак в области струйных течений (и не меняет знак на экваторе). По вертикали знак колебаний изменяется в стратопаузе и мезопаузе, период колебаний приблизительно 10–30 сут. Частью возмущений являются крутильные колебания, распространяющиеся в меридиональном направлении. Крутильные колебания хорошо видны в данных наблюдений и в модельных расчетах в интервале широт 30–60° с.ш.

Согласно одной из наиболее распространенных точек зрения колебания в атмосфере является следствием бароклинной и баротропной неустойчивости и, следовательно, могут иметь структуру наиболее неустойчивых собственных колебаний системы. Для выделения таких колебаний Ляпуновым был предложен метод анализа уравнений по линейному приближению [22]. Результатом анализа являются нормальные моды операторов, характеризующих взаимодействие возмущений со средним потоком.

Первые интерпретации колебаний в умеренных широтах сводились к проектированию реальных возмущений на функции Хафа и сферические гармоники, являющиеся нормальными модами зонально симметричных течений [23–28]. Результаты сопоставлений нормальных мод и реальных возмущений оказались, однако, не очень убедительными.

В [26] сопоставлены нормальные моды дифференциальных операторов, ответственных за взаимодействие возмущений с осесимметричной компонентой, аномалиями среднего потока и аномалиями толщины слоя в баротропной квазигеострофической модели. Наименьшие инкременты и большие периоды колебаний имели нормальные моды, обусловленные меридиональными градиентами осесимметричного течения. Аномалии среднего потока и толщины слоя увеличивали инкременты почти на порядок. Характерное время развития неустойчивостей составило несколько суток, периоды колебаний – от 10 до нескольких десятков суток, распространение возмущений могло происходить как на запад, так и на восток. Периоды, инкременты и пространственная структура нормальных мод сильно зависели от структуры аномалий среднего потока и параметризации турбулентной вязкости.

Авторы работы [27] исследовали неустойчивые нормальные моды климатического январского распределения поля скорости на уровне 300 гПа в эволюционной модели с линейным экмановским затуханием и вязкостью четвертого порядка. Расчеты показали, что наиболее быстро растущая мода имела период, равный примерно 45 дням, и характерное время роста 6.8 дней в отсутствии линейного затухания. В течение полупериода развитие моды напоминало попеременное включение с разным знаком центров действия над Тихим океаном и над Атлантикой. При желании можно было увидеть некоторое сходство полученной моды с Арктической осцилляцией, а также распространение знакопеременных возмущений от полюса в направлении Центральной Азии.

Резюмируем результаты исследований собственных колебаний гидродинамических течений. Не было получено прямых подтверждений существования зонально-симметричных колебаний. Установлена сильная зависимость нормальных мод от формы, амплитуды аномалий среднего потока и параметризации вязкости. Однако при этом некоторые нормальные моды демонстрировали особенности динамики, которые при зональном осреднении можно было бы интерпретировать как распространение в меридиональном направлении крутильных колебаний и смену знака аномалий метеовеличин в протяженных широтных зонах. Таким образом, несмотря на отсутствие прямых доказательств существования собственных колебаний крупномасштабных течений на сфере, имеющих зональную симметрию, полностью отказываться от этой гипотезы нельзя.

Более вероятным является, однако, другое предположение – выделенные колебания являются следствием хорошо известных нормальных мод в низкочастотном диапазоне, распространяющихся в зональном направлении на восток или на запад. Взаимодействуя с зональными неоднородностями среднего потока в стратомезосфере или в верней тропосфере, эти моды могут порождать вторичные возмущения, распространяющиеся в меридиональном направлении, и имеющие периоды, соответствующие нормальным модам. На высокую вероятность подобной интерпретации указывает то, что в модель включена параметризация основных нормальных атмосферных мод с периодами 5, 10 и 16 сут через задание локализованных в тропосфере дополнительных источников нагрева, широтная структура которых задается соответствующими функциями Хафа [8].

Важное значение для интерпретации колебаний имеет определение пространственной структуры вариаций метеорологических полей в низкочастотном диапазоне в средней атмосфере. Для решения этой задачи можно использовать разложения на естественные ортогональные функции (ЕОФ), хотя этот метод не вполне корректен из-за формально-математических условий, накладываемых на ЕОФ, или одноточечными корреляциями со сдвигом во времени. Применение этих методов в тропосфере позволило обнаружить т.н. “дальние связи” (teleconnections), интерпретация которых пока еще далека от завершения.

Работа с архивными данными и расчеты проводились в рамках базового финансирования программы II.16.1.1 ФНИ государственных академий на 2013–2020 годы. Моделирование циркуляции средней атмосферы проводилось при поддержке гранта РФФИ № 18-05-01050. Интерпретация результатов расчетов ре-анализа и моделирования выполнена в рамках проекта РНФ № 19-77-00009.

Список литературы

  1. Wallace J.M., Blackmon M.L. Observation of low-frequency atmospheric variability // Large-scale dynamic processes in the atmosphere. Moscow, 1988. P. 66–109.

  2. Branstator G. The maintenance of low-frequency atmospheric anomalies // J. Atmos. Sci. 1992. V. 49. P. 1924–1945.

  3. Matsuno T.A Dynamical model of the Stratosphere sudden warming // J. Atmos. Sci. 1971. V. 28. P. 1479–1494.

  4. Chandran A., Collins R.L., Harvey V.L. Review Stratosphere-mesosphere coupling during stratospheric sudden warming events // Advances in Space Research. 2014. V. 53. P. 1265–1289.

  5. Limpasuvan V., Thompson D.W.J., Hartmann D.L. The Life Cycle of the Northern Hemisphere Sudden Stratospheric Warmings // J. Climate. 2004. V. 17. P. 2584-2595.

  6. Butler A.H., Sjoberg J.P., Seidel D.J., Rosenlof K.H. A sudden stratospheric warming compendium // Earth Syst. Sci. Data. 2017. V. 9. P. 63–76.

  7. Погорельцев А.И. Генерация нормальных атмосферных мод стратосферными васцилляциями // Изв. РАН. Физика атмосферы и океана. 2007. Т. 43. № 4. С. 463–475.

  8. Погорельцев А.И., Савенкова Е.Н., Перцев Н.Н. Внезапные стратосферные потепления: Роль нормальных атмосферных мод // Геомагнетизм и аэрономия. 2014. Т. 54. № 3. С. 387-403.

  9. Liu H.-L., Roble R.G. A study of a self-generated stratospheric sudden warming and its mesospheric-lower thermospheric impacts using the coupled TIME-GCM/CCM3. // J. Geophys. Res. 2002. V. 107. P. 46–95.

  10. Кочеткова О.С., Мордвинов В.И., Руднева М.А. Анализ факторов, влияющих на возникновение стратосферных потеплений // Оптика атмосферы и океана. 2014. Т. 27. № 8. С. 719–727.

  11. Dickey J.O. Ghil M., Marcus S.L. Extratropical Aspects of the 40-50 Day Oscillation in Length- of-Day and Atmospheric Angular Momentum // J. Geophys. Res 1991. V. 96. P. 22,643–22,658.

  12. Lott F., Robertson A.W., Michael G. Mountain Torques and Northern Hemisphere Low-Frequency Variability. Part I: Hemispheric Aspects // J. Atmos. Sci. 2004. V. 61. P. 1259–1271.

  13. Weickmann K., Berry E. The Tropical Madden–Julian Oscillation and the Global Wind Oscillation // Monthly Weather Review 2009. V. 137. P. 1601–1614.

  14. Kandieva K.K., Aniskina O.G., Pogoreltsev A.O., Zorkaltseva O.S., Mordvinov V.I. Effect of Madden–Julian Oscillation and Quasi-Biennial Oscillation on the Dynamics of Extratropical Stratosphere // Geomagnetism and Aeronomy. 2019. V. 59. № 1. P. 105–114.

  15. Pogoreltsev A.I., Vlasov A.A., Frцhlich K., Jacobi Ch. Planetary waves in coupling the lower and upper atmosphere // J. Atmos. Sol.-Terr. Phys. 2007. V. 69. P. 2083–2101.

  16. Гаврилов Н.М., Коваль А.В. Параметризация воздействия мезомасштабных стационарных орографических волн для использования в численных моделях динамики атмосферы // Изв. РАН. Физика атмосферы и океана. 2013. Т. 49. № 3. С. 271–278.

  17. Суворова Е.Н., Дробашевская Е.А., Погорельцев А.И. Климатическая модель трехмерных распределений озона по данным реанализа MERRA // Ученые записки РГГМУ. 2017. № 49. С. 38–46.

  18. Ермакова Т.С., Статная И.А., Федулина И.Н., Суворова Е.В., Погорельцев А.И. Трехмерная полуэмпирическая климатическая модель распределения водяного пара и ее использование в радиационном блоке модели средней и верхней атмосферы // Метеорология и гидрология. 2017. № 9. С. 75–82.

  19. Kobayashi S., Harada Y., Ota Y. et al. The JRA-55 reanalysis: General specifications and basic characteristics // J. Meteor. Soc. Japan. 2015. V. 93. P. 548.

  20. Rienecker M.M., Suarez M.J., Gelaro R. et al. MERRA: NASA’s modern-era retrospective analysis for research and applications // J. Climate. 2011. V. 14. P. 3624–3648.

  21. Zorkaltseva O.S., Mordvinov V.I., Devyatova E.V., Dombrovskaya N.S. Method for calculating torsional oscillations in Earth’s atmosphere from NCEP/NCAR, MERRA-2, ECMWF ERA-40, and ERA-INTERIM // J. Atmos. Sol.-Terr. Phys. 2019. V. 5. Iss. 1. P. 69–76.

  22. Вычислительные процессы и системы: сборник трудов / Под ред. Марчука Г.И., М.: Наука, главная редакция физ.-мат. литературы, 1986. 270 с.

  23. Дымников В.П. Избранные главы теории устойчивости динамики двумерной несжимаемой жидкости. М.: ИВМ РАН, 2004. 140 с.

  24. Madden R. Observations of large-scale traveling Rossby waves // Rev. Geophys. Space Phys. 1979. V. 17. P. 1935–1949.

  25. Salby M. A ubiquitous wavenumber 5 anomaly in the Southern Hemisphere during FGGE // Mon. Wea. Rev. 1982. V.110. P. 1712–1720.

  26. Simmons A.J., Wallace J.M., Branstator G.M. Barotropic Wave Propagation and Instability, and Atmosphere Teleconnection Patterns // J. Atmos. Sci. 1983. V. 40. Iss. 6. P. 1363–1392.

  27. Branststor G.M. A Striking Example of the Amosphere’s Leading Traveling Pattern // J. Atm. Sciences. 1987. V. 44. P. 2310–2323.

  28. Мордвинов В.И., Девятова Е.В., Томозов В.М. Гидродинамические неустойчивости в тахоклине, обусловленные вариациями толщины слоя и неоднородностями среднего потока // Солнечно-земная физика. 2013. № 23. С. 3–12.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Физика атмосферы и океана

Архивы выпусков Информация о журнале Отправить рукопись в журнал