Известия РАН. Физика атмосферы и океана, 2021, T. 57, № 3, стр. 362-371

ВВЕДЕНИЕ

В реальном океане внутренние гравитационные волны (ВГВ) распространяются на фоне фоновых сдвиговых океанических течений. Поэтому в связи с прогрессом в изучении крупномасштабных океанических волновых процессов изучение динамики и распространения ВГВ в океане с учетом наличия течений является актуальной задачей [1–5]. В общей постановке описание динамики ВГВ в океане с фоновыми полями сдвиговых течений является весьма сложной задачей уже в линейном приближении. В этом случае задача сводится к анализу системы уравнений в частных производных [6–9]. При одновременном учете вертикальной и горизонтальной неоднородностей эта система уравнений не допускает разделение переменных. Используя различные приближения, в том числе метод ВКБ, основанный на реалистичном предположении о плавности изменения параметров океанической среды по сравнению длинами ВГВ можно построить аналитические решения для модельных распределений частоты плавучести и сдвиговых течений [1, 10, 11]. Поэтому представляет несомненный интерес изучение ВГВ в океане с произвольным распределением по вертикали как плотности, так и наблюдаемых в морских условиях фоновых сдвиговых течений [12–15]. Тем самым появляется возможность изучения амплитудно-фазовых характеристик волновых полей для реальных океанологических параметров. Можно ожидать, что учет неаналитических зависимостей параметров морской среды позволит исследовать новые качественные эффекты волновой генерации. В настоящей работе численно и аналитически рассматривается генерация ВГВ в океане с произвольным распределением частоты плавучести и сдвигового течения локализованным осциллирующим источником возмущений. В качестве такого механизма возбуждения ВГВ можно рассматривать, например, генерацию волн периодическим течением на склонах поперечных хребтов в проливах [7, 8].

ПОСТАНОВКА ЗАДАЧИ

Рассматривается вертикально стратифицированная среда конечной глубины H. Исходной является линеаризованная система уравнений гидродинамики относительно невозмущенного состояния, которая имеет вид [1, 4, 10]

где $(V(z),U(z))$ – вектор фонового сдвигового течения на горизонте $z$, где (${{U}_{1}}$,${{U}_{2}}$,$W$) – компоненты возмущенной скорости, ($p$,$\rho $) – возмущения давления и плотности, ${{\rho }_{0}}(z)$ – невозмущенная плотность среды. $Q(t,x,y,z)$ – плотность распределения источников массы. Воспользовавшись приближением Буссинеска, можно получить одно уравнение для малых возмущений вертикальной компоненты скорости [1, 6, 10] где ${{N}^{2}}(z)$ – квадрат частоты Брента–Вяйсяля (частоты плавучести), $g$ – ускорение свободного падения. Граничные условия берутся в виде (вертикальная ось $z$ направлена вверх): $W = 0$ при $z = 0, - H$. Далее решение этой задачи ищется в виде: $W(t,x,y,z)$ = $\exp (i\Omega t)w(x,y,z)$, то есть рассматривается гармонический источник возмущений единичной интенсивности. Тогда функция $w(x,y,z)$ определяется из (1), где дифференциальный оператор имеет вид: $\frac{D}{{Dt}} = i\Omega + U(z)\frac{\partial }{{\partial x}}$ + + $V(z)\frac{\partial }{{\partial y}}$. Далее ищется функция Грина уравнения (1), то есть решение задачи где ${{z}_{0}}$ – глубина точечного источника возмущений. Волновые возмущения от произвольного нестационарного нелокального источника возмущений определяются соответствующей сверткой [1, 6, 10, 11].

Для исследования вынужденных ВГВ в океане со сдвиговыми течениями необходимо решать задачу: $LW = S\left( {t,x,y,z,{{z}_{0}}} \right)$ с ненулевой правой частью $S\left( {t,x,y,z,{{z}_{0}}} \right)$, конкретное представление которой определяется видом источника возмущений. Если рассматривать в качестве источника направленную по вертикали силу, то: $S\left( {t,x,y,z,{{z}_{0}}} \right)$ = + + 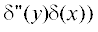. В случае точечного источника массы: $S\left( {t,x,y,z,{{z}_{0}}} \right)$ = . В более общем случае функция $S\left( {t,x,y,z,{{z}_{0}}} \right)$ может определяться из результатов прямого численного моделирования ближнего поля с учетом нелинейных уравнений гидродинамики или из сугубо оценочных (полуэмпирических) соображений, позволяющих аппроксимировать ближнее поле некоторой системой модельных источников. В силу линейности рассматриваемой задачи с помощью функции Грина можно получить представления для полей ВГВ, генерируемых произвольными нелокальными и нестационарными источниками. На больших расстояниях реальные источники возмущений ВГВ в океане допускают физически обоснованную аппроксимацию системой точечных локализованных источников, взятых с определенными весами. Такой подход является общепринятым и обоснованным для решения многих задач моделирования генерации линейных ВГВ в океане с учетом сдвиговых течений, так как на больших расстояниях точная форма источника практически не влияет на основные волновые характеристики, определяемые параметрами среды и законами дисперсии [6, 9].

Так как при наличии фоновых сдвиговых течений ВГВ могут взаимодействовать с этими течениями и обмениваться с ними энергией, то собственные волновые колебания могут быть экспоненциально нарастающими. Поэтому необходимо, чтобы вертикальный градиент фоновых сдвиговых течений был невелик по сравнению с частотой плавучести. Далее предполагается выполненным условие устойчивости Майлса–Ховарда для числа Ричардсона: $Ri(z)$ = ${{{{N}^{2}}(z)} \mathord{\left/ {\vphantom {{{{N}^{2}}(z)} {\left( {\left( {\frac{{d{{V}^{2}}}}{{dz}}} \right) + \left( {\frac{{d{{U}^{2}}}}{{dz}}} \right)} \right)}}} \right. \kern-0em} {\left( {\left( {\frac{{d{{V}^{2}}}}{{dz}}} \right) + \left( {\frac{{d{{U}^{2}}}}{{dz}}} \right)} \right)}}$ > > 1/4 [16–19]. Если выполнено условие Майлса–Ховарда, то соответствующая спектральная задача не имеет комплексных собственных значений [3, 10, 20, 21]. Характерные значения чисел Ричардсона в акваториях Мирового океана при отсутствии динамической неустойчивости фоновых сдвиговых течений могут находиться в интервалах от 2 до 20 [8, 13, 14].

ИНТЕГРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ РЕШЕНИЯ

Решение задачи (2) ищется в виде интегралов Фурье

Функция $G(\mu ,\nu ,z,{{z}_{0}})$ является решением следующей задачи

Пусть далее ${{\varphi }_{1}}(\mu ,\nu ,z)$, ${{\varphi }_{2}}(\mu ,\nu ,z)$ – функции, удовлетворяющие уравнению ${{L}_{0}}{{\varphi }_{{1,2}}}(\mu ,\nu ,z) = 0$ и обращающиеся в ноль при $z = 0$ и $z = - H$ соответственно. Тогда можно получить

где $B = B(\mu ,\nu ,\Omega ) = {{\varphi }_{1}}(\mu ,\nu ,H)\frac{{\partial {{\varphi }_{2}}(\mu ,\nu , - H)}}{{\partial z}}$ – вронскиан функций ${{\varphi }_{1}}(\mu ,\nu ,z)$, ${{\varphi }_{2}}(\mu ,\nu ,z)$. Функция $B = B(\mu ,\nu ,\Omega )$ такова, что уравнение $B(\mu ,\nu ,\omega ) = 0$ является одной из возможных форм записи дисперсионного соотношения для описания ВГВ в стратифицированном океане со средним сдвиговым течением [1, 3, 10, 11]. Разрешая это уравнение относительно переменной $\omega $, можно получить дисперсионное соотношение в виде: $\omega = {{\omega }_{n}}(\mu ,\nu )$. Очевидно, что множество решений уравнения ${{\omega }_{n}}(\mu ,\nu ) = \Omega $ образует дисперсионную кривую ${{L}_{n}}{\kern 1pt} :\mu = {{\mu }_{n}}(\nu ,\Omega )$. Полюса функции $G(\mu ,\nu ,z,{{z}_{0}})$ – это нули вронскиана, то есть нули функции ${{\varphi }_{1}}(\mu ,\nu , - H)$, которые в свою очередь совпадают с собственными числами ${{\mu }_{n}}(\nu ,\Omega )$ вертикальной спектральной задачи

Ясно, что ${{\varphi }_{1}}({{\mu }_{n}}(\nu ),\nu ,z)$ = ${{\varphi }_{2}}({{\mu }_{n}}(\nu ),\nu ,z)$ = = ${{\varphi }_{n}}(z,{{\mu }_{n}}(\nu ),\nu )$, где ${{\varphi }_{n}} = {{\varphi }_{n}}(z,{{\mu }_{n}}(\nu ),\nu )$ – собственная функция спектральной задачи (3). Для определения функции $\Gamma (x,y,z,{{z}_{0}})$ необходимо выполнить обратное преобразование Фурье. Вычеты $\mathop {res}\limits_{\mu = {{\mu }_{m}}(\nu ,\Omega )} G(\mu ,\nu ,z,{{z}_{0}})$ функции $G(\mu ,\nu ,z,{{z}_{0}})$ выражаются через $\frac{{\partial B}}{{\partial \mu }}$. Тогда интегрирование по переменной $\mu $ можно провести, используя теорему о вычетах. Можно показать, что имеет место следующее интегральное представление для функции $\frac{{\partial B}}{{\partial \mu }}$ при $\mu = {{\mu }_{n}}(\nu )$

Следовательно

Тогда замыкая контур интегрирования по переменной $\mu $ в нижней полуплоскости, можно получить

Далее рассмотрим поведение отдельной моды ${{\Gamma }_{n}}$ вдоль некоторого направления ${{S}_{\alpha }}$, составляющего угол $\alpha $ с положительной осью оси X. То есть будем считать, что $x = r\cos \alpha ,$ $y = r\sin \alpha ,$ $r > 0,\,\,0 \leqslant \alpha \leqslant 2\pi $. Тогда очевидно, что интегрирование в (4) следует выполнять не по всей длине дисперсионной кривой ${{L}_{n}}$, а лишь вдоль той ее части ${{l}_{n}}(\alpha )$, на которой выполнено условие $\frac{{\partial \omega }}{{\partial {{S}_{\alpha }}}} > 0$. Это условие означает, что проекция вектора групповой скорости ВГВ на направление ${{S}_{\alpha }}$ положительна, т.е. волновая энергия распространяется наружу от источника. Тогда пределы интегрирования в (4) заменяются в соответствии с выбором соответствующей кривой ${{l}_{n}}(\alpha )$, и можно получить выражение для вклада n-ой моды в суммарное поле в виде

где правая часть представляет собой криволинейный интеграл второго рода по дисперсионной кривой ${{l}_{n}}(\alpha )$, причем из двух возможных направлений обхода этой кривой выбирается то, для которого проекция касательной к дисперсионной кривой на направление ${{S}_{{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2} + \alpha }}}$ должна быть положительной [1, 10, 11].

ЧИСЛЕННЫЙ АЛГОРИТМ

Для произвольных распределений функций $N(z),V(z),U(z)$ спектральную задачу (3) можно решить только численно. Для решения задачи будем использовать следующий алгоритм, позволяющий, в отличие от [6, 22, 23], более точно аппроксимировать основные коэффициенты, входящие в (3). Заменим в дифференциальном операторе $\Pi $ фиксированное значение $\Omega $ на переменную $\omega $ и будем считать $\omega = {{\omega }_{n}}(\mu ,\nu )$ спектральным параметром, требующим определения, и, соответственно, $\mu ,\nu $ – свободными параметрами. Введем новую функцию $F = {{\varphi (z)} \mathord{\left/ {\vphantom {{\varphi (z)} {(\omega - f(z))}}} \right. \kern-0em} {(\omega - f(z))}}$, тогда задачу (3) можно представить в виде

Для численного решения задачи (5) необходимо разбить интервал изменения $ - H < z < 0$ на $J$ отрезков (слоев): ${{I}_{j}} = [{{z}_{{j - 1}}},{{z}_{j}}],$ $j = 1,2, \ldots J,$ где ${{z}_{0}} = 0,\,\,{{z}_{J}} = - H.$ Далее аппроксимируем коэффициент перед функцией $\frac{{\partial F}}{{\partial z}}$ кусочно-линейной, а коэффициент перед функцией $F$ – кусочно-постоянной функцией, то есть будем считать, что при ${{z}_{j}} \in {{I}_{j}}{\kern 1pt} :{{(\omega - f)}^{2}}$ = ${{A}_{j}} + {{B}_{j}}(z - {{z}_{j}})$ = ${{D}_{j}} + {{B}_{j}}{{z}_{j}},$ ${{N}^{2}}(z)$ – ${{(\omega - f)}^{2}}$ = ${{C}_{j}}$, где ${{A}_{j}} = \omega - f({{z}_{{j - 1}}}),$ ${{B}_{j}} = f({{z}_{{j - 1}}})$ – ${{f({{z}_{j}})} \mathord{\left/ {\vphantom {{f({{z}_{j}})} {({{z}_{j}} - {{z}_{{j - 1}}})}}} \right. \kern-0em} {({{z}_{j}} - {{z}_{{j - 1}}})}}$, ${{D}_{j}} = {{A}_{j}}$ – ${{B}_{j}}{{z}_{{j - 1}}}$, ${{C}_{j}}$ = ${{N}^{2}}(0.5({{z}_{j}} + {{z}_{{j - 1}}}))$ – ${{(\omega - f(0.5({{z}_{j}} + {{z}_{{j - 1}}})))}^{2}}$. В результате для каждого отрезка (слоя) получается уравнение Эйлера

Общее решение ${{F}_{j}}(z)$ уравнения (6) в каждом $j$-ом слое определяется соотношениями между коэффициентами ${{D}_{j}},{{C}_{j}},{{B}_{j}}$. Если ${{B}_{j}} \ne 0$ и $B_{j}^{2} > 4{{k}^{2}}{{C}_{j}}$, то ${{F}_{j}}(z)$ = ${{S}_{{1j}}}{{\left| {{{D}_{j}} + {{B}_{j}}z} \right|}^{{{{\lambda }_{j}} - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ + + ${{S}_{{2j}}}{{\left| {{{D}_{j}} + {{B}_{j}}z} \right|}^{{ - {{\lambda }_{j}} - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$, где ${{\lambda }_{j}}$ = ${{0.5\sqrt {B_{j}^{2} - 4{{k}^{2}}{{C}_{j}}} } \mathord{\left/ {\vphantom {{0.5\sqrt {B_{j}^{2} - 4{{k}^{2}}{{C}_{j}}} } {{{B}_{j}}}}} \right. \kern-0em} {{{B}_{j}}}}$. Если ${{B}_{j}} \ne 0$ и $B_{j}^{2} < 4{{k}^{2}}{{C}_{j}}$, то ${{F}_{j}}(z) = {{\left| {{{D}_{j}} + {{B}_{j}}z} \right|}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}$ × × $({{S}_{{1j}}}\cos ({{\Phi }_{j}}(z))$ + ${{S}_{{2j}}}\sin ({{\Phi }_{j}}(z))$, где Φ_j(z) = = ${{\lambda }_{j}}\ln \left| {{{D}_{j}} + {{B}_{j}}z} \right|,$ ${{\lambda }_{j}}$ = $0.5{\kern 1pt} {{\sqrt { - B_{j}^{2} + 4{{k}^{2}}{{C}_{j}}} } \mathord{\left/ {\vphantom {{\sqrt { - B_{j}^{2} + 4{{k}^{2}}{{C}_{j}}} } {{{B}_{j}}}}} \right. \kern-0em} {{{B}_{j}}}}$. Если B_j = = 0, ${{C}_{j}} > 0$, то ${{F}_{j}}(z)$ = $({{S}_{{1j}}}\cos ({{k\sqrt {{{C}_{j}}} } \mathord{\left/ {\vphantom {{k\sqrt {{{C}_{j}}} } {{{A}_{j}}}}} \right. \kern-0em} {{{A}_{j}}}})(z - {{z}_{{j - 1}}}))$ + $ + \,{{S}_{{2j}}}\sin (({{k\sqrt {{{C}_{j}}} } \mathord{\left/ {\vphantom {{k\sqrt {{{C}_{j}}} } {{{A}_{j}}}}} \right. \kern-0em} {{{A}_{j}}}})(z - {{z}_{{j - 1}}}))$. Если ${{B}_{j}} = 0$, ${{C}_{j}} < 0,$ то ${{F}_{j}}(z)$ = $({{Q}_{{1j}}}ch(k{{\sqrt { - {{C}_{j}}} } \mathord{\left/ {\vphantom {{\sqrt { - {{C}_{j}}} } {{{A}_{j}}}}} \right. \kern-0em} {{{A}_{j}}}})(z - {{z}_{{j - 1}}}))$ + + ${{Q}_{{2j}}}sh((k{{\sqrt { - {{C}_{j}}} } \mathord{\left/ {\vphantom {{\sqrt { - {{C}_{j}}} } {{{A}_{j}}}}} \right. \kern-0em} {{{A}_{j}}}})$(z – z_{j – 1})). Постоянные ${{Q}_{{1j}}},{{Q}_{{2j}}}$ определяются из условия непрерывности функций ${{F}_{j}}(z)$ и ее производных

Начальные условия берутся в виде

Так как при решении данной задачи предполагается выполненным условие устойчивости Майлса–Ховарда, то все собственные числа ${{\omega }_{n}} = {{\omega }_{n}}(\mu ,\nu )$ являются вещественными и находятся вне отрезка $[{{f}_{ - }},{{f}_{ + }}]$, где ${{f}_{ \pm }}$ – максимальные (минимальные) значения функции $f$ на интервале изменения переменной $z$ от $ - H$ до $0$ соответственно [1, 3, 6, 10]. На этом свойстве дисперсионных соотношений основан основной алгоритм определения собственного числа ${{\omega }_{n}}$. Выберем какое-либо значение ${{\omega }_{0}}$, такое, что ${{\omega }_{0}} > {{f}_{ + }}$, или ${{\omega }_{0}} < {{f}_{ - }}$. Проинтегрируем (6)–(8), используя выбранное значение ${{\omega }_{0}}$ в качестве начального приближения. Если полученное в результате численного интегрирования решение $F(z)$ имеет на интервале $( - H,0)$ $m < n - 1$ (n – номер волновой моды) нулей, то значение ${{\omega }_{0}}$ надо увеличить. Если функция_{$F(z)$ имеет на интервале $( - H,0)$ $m > n - 1$ нулей, то значение ${{\omega }_{0}}$ надо уменьшить. Подборомзначения${{\omega }_{0}}$ можно добиться того, чтобы полученноерешение$F(z)$ удовлетворяло условию:$F( - H) = 0$, а также имело на интервале$( - H,0)$$n - 1$ перемену знаков, или, соответственно, n экстремумов. Полученное таким образом значение${{\omega }_{n}}$ является собственным числом${{\omega }_{n}}(\mu ,\nu )$ n-ойволновой моды. Тогда дисперсионные зависимости$\mu = {{\mu }_{n}}(\nu )$ вертикальной спектральной задачи (3) могут быть найдены как решения уравнения$\Omega = {{\omega }_{n}}(\mu ,\nu )$ ($\Omega $ – частота осцилляций источника возмущений). Собственные функции ${{\varphi }_{n}} = {{\varphi }_{n}}({{\mu }_{n}}(\nu ),\nu )$ вычисляются по формуле: φn = = $({{\omega }_{n}}(\mu ,\nu )$ – $f(z))F(z)$, где$F(z)$ – полученное численно решение задачи (6)–(8).}

РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ

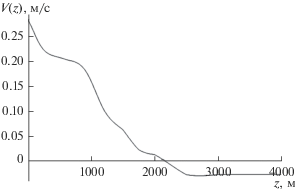
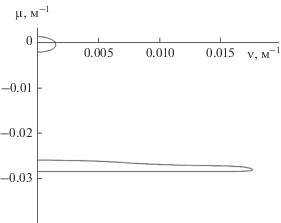
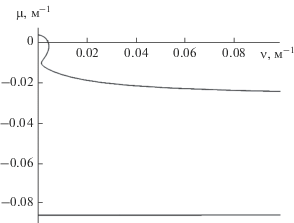
Для численных расчетов были использованы распределения частоты плавучести $N(z)$ и одной компоненты сдвигового течения $V(z)$, приведенные на рис. 1, 2, которые характерны для многих районов Мирового океана, в частности акватории Северной Атлантики (проходы Восточно-Азорского хребта) [8, 12–15]. Компонента сдвигового течения $U(z)$ предполагалась равной нулю: $U(z) = 0$. Далее все расчеты приведены для первой волновой моды. На рис. 3 приведены результаты расчетов дисперсионной поверхности ${{\omega }_{1}}(\mu ,\nu )$. На рис. 4–7 приведены результаты расчетов дисперсионных зависимостей $\mu = {{\mu }_{1}}(\nu )$ для различных значений частоты осцилляции источника возмущений $\Omega $, для рис. 4 значение $\Omega = 0.002\,\,{{{\text{с}}}^{{ - 1}}}$, рис. 5 – $\Omega = 0.00205\,\,{{{\text{с}}}^{{ - 1}}}$, рис. 6 – $\Omega = 0.0038\,\,{{{\text{с}}}^{{ - 1}}}$, рис. 7 – $\Omega = 0.007\,\,{{{\text{с}}}^{{ - 1}}}$. Результаты расчетов показывают сильную изменчивость качественного поведения дисперсионных картин в зависимости от значений $\Omega $. При относительно небольших значениях $\Omega $ дисперсионная зависимость определяется только одной замкнутой ветвью. При увеличении $\Omega $ дисперсионные кривые имеют вид двух замкнутых ветвей. Далее по мере увеличения $\Omega $ происходит качественная перестройка дисперсионных кривых, и при некотором значении $\Omega $ эти ветви могут сливаться. При некоторых значениях частоты осцилляции источника может наблюдаться отчетливая омега-образная структура дисперсионных кривых, что означает многозначность функции ${{\mu }_{1}}(\nu )$ для некоторых интервалов значений $\nu $. По мере увеличении $\Omega $ происходит размыкание нижней ветви дисперсионных зависимостей на две разомкнутые кривые, и дисперсионные кривые $\mu = {{\mu }_{1}}(\nu )$ становятся однозначными функциями переменной $\nu $. Эти две разомкнутые ветви дисперсионных зависимостей при увеличении $\Omega $ все более и более расходятся друг от друга. Причем одна (верхняя) ветвь дисперсионной кривой может пересекать ось $\nu = 0$ и менять знак, а другая (нижняя) ветвь всегда имеет отрицательные значения.

В общем случае решение задачи, описывающее дальние поля ВГВ в океане с фоновыми сдвиговыми течениями, можно представить в виде суммы вертикальных волновых мод, где каждая мода является суперпозицией плоских волн вида (4) [1, 3, 6, 10]. Интегралы этого типа на больших расстояниях (при больших значениях $x,y$) можно вычислить методом стационарной фазы [1, 6, 10, 11, 24]. Стационарные точки фазовой функции ${{\Theta }_{n}}(\nu )$ определяются из решения уравнения: $\Theta _{n}^{'}(\nu ) = {y \mathord{\left/ {\vphantom {y x}} \right. \kern-0em} x}$. Фазовая функция ${{\Theta }_{n}}(\nu )$ может иметь $K$ стационарных (особых) точек на интервале интегрирования, и полное поле отдельной волновой моды вдали от источников возмущений есть сумма по всем $K$ стационарным (особым) точкам [24–26]. Поэтому на больших расстояниях от источников качественное поведение возбуждаемых полей ВГВ определяется наличием или отсутствием на интервалах интегрирования по переменной $\nu $ экстремумов функций ${{\mu }_{n}}(\nu ,\Omega )$, отвечающих соответствующим стационарным (особым) точкам фазовых функций ${{\Theta }_{n}}(\nu )$. Из представленных численных результатов видно, что для произвольных непостоянных распределения частоты плавучести и сдвигового течения может наблюдаться (в зависимости от частоты $\Omega $) дисперсионная картина с одним или несколькими экстремумами функций ${{\mu }_{n}}(\nu ,\Omega )$. Численные расчеты показывают, что качественная картина дисперсионных зависимостей ${{\mu }_{n}}(\nu ,\Omega )$ сильно зависит от частоты $\Omega $. Топология дисперсионных поверхностей ${{\omega }_{n}}(\mu ,\nu )$ имеет достаточно сложную структуру (рис. 3), зависящую как от параметров среды (стратификации и распределения по глубине сдвигового течения), так и от параметров волновой генерации. Расчеты показывают также, что при увеличении номера волновой моды количество локальных экстремумов функций ${{\omega }_{n}}(\mu ,\nu )$, как правило, возрастает. Это означает, что вклад в дальнее поле ВГВ вносят несколько волновых цугов. Кроме того, численные расчеты показывают, что при изменении параметров волновой генерации (увеличение или уменьшение частоты $\Omega $) происходит заметная качественная перестройка фазовых картин возбуждаемых волновых полей.

Линии постоянной фазы $\Phi $ отдельной моды определяются из решения системы уравнений

Решение этой системы для каждой волновой моды определяет линии равной фазы $\Phi $, заданные параметрически (с параметром $\nu $)

На рис. 8, 9 представлены результаты расчетов линии равной фазы $\Phi $ (сплошные линии) для различных параметров волновой генерации. Штриховые линии на рисунках – соответствующие волновые фронты. На рис. 8 значения параметров $\Omega = 0.012\,\,{{{\text{с}}}^{{ - 1}}},$ $t = 3600\,\,{\text{с}}$, угол полураствора волнового клина ${{{{\alpha }}}_{1}} = 12.49^\circ ,$ где ${{\alpha }_{1}} = arctg(\mu _{1}^{'}(\nu *))$, $\nu {\text{*}}$ – корень уравнения . Волны внутри волнового клина распространяются вдоль положительного направления оси $X$ от источника возмущений, значения фазы вдоль гребней волн (справа налево) $\Phi = 4\pi ,6\pi , \ldots ,12\pi $. На рис. 9 значения параметров $\Omega = 0.0045\,\,{{{\text{с}}}^{{ - 1}}},$ $t = 3500{\text{с}}$, угол полураствора внешнего волнового клина ${{{{\alpha }}}_{1}} = 80.72^\circ $ , угол полураствора внутреннего волнового клина ${{{{\alpha }}}_{0}} = 49.63^\circ $. Величина ${{{{\alpha }}}_{0}}$ определяется равенством ${{{{\alpha }}}_{0}} = - {\text{arctg\;}}{{\nu }_{0}}$, где ${{\nu }_{0}}$ – положительный корень уравнения $\mu _{1}^{'}(\nu ) = {{{{\mu }_{1}}(\nu )} \mathord{\left/ {\vphantom {{{{\mu }_{1}}(\nu )} \nu }} \right. \kern-0em} \nu }$. Положение внешнего волнового фронта определяется асимптотикой ${{\mu }_{1}}(\nu )$ при больших значениях $\nu $, с углом полураствора, большим ${{\alpha }_{0}}$. Волны во внутреннем клине (волны первого типа) распространяются в направлении источника, расположенного в начале координат. Волны во внешнем клине (волны второго типа) распространяются в направлении от источника в начале координат. Фаза вдоль гребней волн первого типа (слева направо): $\Phi = 6\pi ,8\pi , \ldots ,14\pi $. Фазы вдоль гребней волн второго типа (справа налево): $\Phi = 0,2\pi ,4\pi .$ В момент времени $t = {\Phi \mathord{\left/ {\vphantom {\Phi \Omega }} \right. \kern-0em} \Omega }$ происходит превращение волны первого типа в волну второго типа. Для волн второго типа увеличение фазы ведет к приближению соответствующей линии равной фазы к началу координат (положению источника возмущений), а для волн первого типа – к удалению от него. Скорость распространения вершины гребня волны первого типа в направлении источника возмущений равна ${\Omega \mathord{\left/ {\vphantom {\Omega {{{\mu }_{1}}(\infty )}}} \right. \kern-0em} {{{\mu }_{1}}(\infty )}} < 0$. Скорость распространения точки пересечения гребня волны второго типа с осью $X$ в сторону от источника возмущений равна ${\Omega \mathord{\left/ {\vphantom {\Omega {{{\mu }_{1}}(0)}}} \right. \kern-0em} {{{\mu }_{1}}(0)}} > 0$. Линия равной фазы $y = - \mu _{1}^{'}(\nu )x$ при значении $\nu = {{\nu }_{0}}$ неподвижна.

Как показывают численные расчеты, учет вертикальной изменчивости частоты плавучести и фоновых сдвиговых океанических течений приводит к заметному усложнение структуры и качественному разнообразию дисперсионных зависимостей. Вариативность и неоднозначность дисперсионных соотношений является причиной генерации различных типов волн. В частности, замкнутые ветви дисперсионных кривых могут при определенных волновых числах приводить к возбуждению кольцевых (поперечных) волн. Разомкнутые ветви дисперсионных зависимостей определяют систему продольных (клиновидных) волн. Как показывают численные расчеты, при малых частотах осцилляций источника $\Omega $ возбуждаются только кольцевые (поперечные) волны. Причем в некоторых случаях одновременно может возбуждаться более двух волновых пакетов таких волн. Число возбуждаемых пакетов определяется общим количеством отдельных ветвей дисперсионных кривых. При больших значениях $\Omega $ возбуждаются только клиновидные (продольные) волны двух типов, причем при увеличении значения частоты осцилляции угол полураствора волновых фронтов уменьшается. Можно также отметить, что существуют такие значения $\Omega $, при которых угол полураствора волнового фронта близок к $90^\circ $. Это означает, что при определенных параметрах волновой генерации существуют такие значения $\nu $, при которых $\mu _{n}^{'}(\nu ) \to \infty $ (рис. 4–6). Поэтому при этих значениях частоты $\Omega $ в силу многозначности дисперсионных соотношений волновая картина возбуждаемых полей представляет собой сложную волновую систему, обладающую одновременно как свойствами продольных, так и поперечных волн.

Можно отметить, что для модельных линейных фоновых сдвиговых течений и постоянного распределения частоты плавучести качественная волновая картина ВГВ определяется только характером течения (безразмерной амплитудой приповерхностного течения и вертикальным градиентом) и не зависит от частоты гармонической волны $\Omega $. В частности, однонаправленное течение порождает как клиновидные (продольные), так и кольцевые (поперечные) волны, а разнонаправленное течение генерирует только кольцевые волны (поперечные) [27, 28].

Численные расчеты показывают также, что при определенных режимах волновой генерации, в частности, может наблюдаться характерная фазовая картина типа “ласточкин хвост”. В фиксированной точке наблюдения также может происходить перестройка одновременно приходящих волновых фронтов. В этом случае полное поле ВГВ может представлять собой сложную картину волновых биений, когда в фиксированную точку пространства одновременно приходит несколько волновых цугов с разными амплитудами и фазами. Сложность топологии дисперсионных зависимостей требует для корректного асимптотического исследования дальних полей ВГВ применения специального математического аппарата. Особые точки фазовых функций могут сближаться с другими особыми точками или с какой-либо особенностью (полюсом, точкой ветвления) подынтегральной функции. В этом случае стандартные методы исследования асимптотик полей ВГВ (с помощью подходящей замены переменных исходный интеграл заменяется на эталонный) становятся неприменимы. Например, при слиянии двух стационарных точек асимптотика интегралов выражается через функцию Эйри, при слиянии стационарных точек и полюса – через интеграл Френеля. Важно отметить, что наиболее интересными с практической точки зрения являются локальные максимумы дисперсионных поверхностей, так как поле ВГВ в окрестности этих максимумов может описываться эталонными интегралами. Случай слияния трех стационарных точек может описываться функцией Пирси, часто применяемой в теории особенностей и катастроф. Если две из трех сливающихся стационарных точек находятся строго симметрично относительно третьей, то асимптотика соответствующего интеграла может выражаться через функцию Ханкеля. Численные расчеты дисперсионных зависимостей показывают, что для реальных стратификаций природных сред (океан, атмосфера) и непостоянных фоновых сдвиговых течений могут возникать физически интересные случаи генерации волновых структур, которые не описываются известными эталонными интегралами [29, 30].

ЗАКЛЮЧЕНИЕ

В работе решена задача о генерации внутренних гравитационных волн, возбуждаемых локализованным гармоническим источником возмущений в океане с произвольными распределениями по глубине частоты плавучести и компонент фонового сдвигового течения. При выполнении условия устойчивости Майлса–Ховарда построены интегральные представления решения. Для решения спектральной задачи предложен эффективный численный алгоритм расчета дисперсионных зависимостей, определяющих фазовую структуру возбуждаемых полей. Приведены результаты численных расчетов дисперсионных кривых и фазовых картин волновых полей для реальных распределений частоты плавучести и фоновых сдвиговых течений, наблюдаемых в океане. Показано, что при изменении параметров волновой генерации происходит заметная качественная перестройка фазовых картин возбуждаемых полей внутренних гравитационных волн.

Работа выполнена по темам государственного задания: В.В. Булатов, Ю.В. Владимиров (№ АААА-А20-120011690131-7), И.Ю. Владимиров (№ 0149-2019-0004), (№ 0128-2021-0002), и при частичной финансовой поддержке РФФИ, проект № 20-01-00111А.