Известия РАН. Физика атмосферы и океана, 2021, T. 57, № 6, стр. 743-752

1. ВВЕДЕНИЕ

Детальное понимание физических механизмов мелкомасштабных процессов обмена, происходящих на границе раздела атмосферы и океана, необходимо для их корректной параметризации в крупномасштабных моделях прогноза погоды и климата. Одним из факторов, влияющих на процессы обмена, является наличие дрейфового течения, развивающегося в приповерхностном слое океана под воздействием ветра [1].

Исследованию ветрового дрейфа посвящено большое количество экспериментальных и теоретических работ, в которых основное внимание уделяется режиму, наблюдаемому при балковой скорости ветра (т.е. скорости на высоте 10 м от поверхности в натурном эксперименте или скорости, экстраполированной по логарифмическому профилю, в лабораторном) свыше 3–4 м/с, характеризуемому присутствием достаточно крутых (обрушающихся и/или микрообрушающихся) поверхностных гравитационных волн (см., напр., [2–7]). При этом течение в приповерхностном водном слое, как правило, является турбулентным и состоит как из дрейфа, вызываемого сдвиговым напряжением ветра, так и течений, индуцированных волнами (вязкого и Стоксова дрейфа, Ленгмюровских циркуляций, а также течений, обусловленных обрушениями) [7]. Все эти вклады практически невозможно исследовать обособленно в лабораторном эксперименте.

С другой стороны, при достаточно слабом ветре (до 2–3 м/с) водная поверхность может рассматриваться как аэродинамически гладкая, поскольку влияние возмущений водной поверхности, вызываемых флуктуациями воздушного потока, незначительно. Этот режим до сих пор остается относительно мало исследованным из-за сложности измерений, связанных с большой относительной погрешностью при определении характеристик воздушного потока при малых скоростях ветра, а также с трудностями измерений индуцированного ветром течения в тонком (толщиной до нескольких мм) приповерхностном водном слое.

Натурные исследования водной поверхности, проводившиеся при скоростях ветра до 2–3 м/с, показали, что в условиях нейтральной стратификации дрейфовое течение в приповерхностном водном слое характеризуется наличием вихревых структур, вытянутых по направлению ветра [8]. В лабораторном исследовании приповерхностного водного слоя при скорости ветра от 1.5 до 2.6 м/с в ветро-волновом лотке наблюдался турбулентный режим, с профилем средней скорости, аналогичным логарифмическому профилю вблизи твердой поверхности [5]. В лабораторном эксперименте и теоретически исследовался также переход к турбулентности в пространственно развивающемся пограничном приповерхностном водном слое при скорости ветра от 3 до 7 м/с [9]. В этой работе наблюдалось развитие турбулентности в виде локализованных трехмерных структур (пятен), сопровождавшееся генерацией капиллярно-гравитационных поверхностных волн. Теоретический анализ в [9] показывает, что нет неустойчивых решений линейной задачи (уравнения Орра–Зоммерфельда), и переход к турбулентности происходит благодаря взрывному росту слабонелинейных решений в виде уединенных волн и сопровождается возбуждением поверхностных капиллярных волн.

Результаты перечисленных исследований не дают однозначного ответа на вопрос о том, какова динамика развивающегося во времени дрейфового течения при слабом ветре, и как скорость дрейфа водной поверхности связана с ее известной параметризацией в терминах скорости трения воздушного погранслоя (см., напр., [3]).

Целью настоящей работы является исследование динамики дрейфового течения, индуцированного в приповерхностном водном слое турбулентным ветром, с помощью прямого численного моделирования (DNS, Direct Numerical Simulation). Рассматриваются относительно небольшие (до 2 × 10⁴) значения числа Рейнольдса воздушного потока, определяемого скоростью ветра, высотой домена и молекулярной вязкостью воздуха. При рассматриваемых параметрах потока в численном эксперименте флуктуации вертикальной компоненты скорости в приповерхностном водном слое остаются пренебрежимо малыми, и поэтому водная поверхность рассматривается как плоская.

2. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Схема численного эксперимента представлена на рис. 1. Рассматривается декартова система координат (x, y, z), где x – координата по направлению ветра, y – поперечная координата и z – вертикальная координата. По вертикали область счета разделена на два слоя: –H < z < 0 – водный слой, и 0 < z < H – воздушный слой, с границей раздела (водной поверхностью) при z = 0. Ставятся условия прилипания на покоящейся нижней границе (z = –H) и верхней граничной плоскости (z = H), движущейся вдоль оси x со скоростью ветра U₀ . Все поля периодичны по горизонтальным координатам x и y. На водной поверхности (z = 0) ставятся условия непрерывности потока импульса и равенства скоростей воды и воздуха [10].

Уравнения Навье–Стокса для воды и воздуха решаются численно в безразмерных переменных в виде:

В уравнениях (1), (2) по повторяющимся индексам проводится суммирование, $U_{i}^{{a,w}}$ и ${{P}_{{a,w}}}$ – скорость и давление в воздухе (a) и воде (w) (i = x, y, z), соответствующие числа Рейнольдса течений воздуха и воды определяются как

где ${{\nu }_{{a,w}}}$ – кинематическая вязкость воды (w) и воздуха (a). В численном моделировании задается число Рейнольдса воздуха, Re_a, автоматически определяющее число Рейнольдса воды, поскольку Re_w = Re_a${{{{\nu }_{a}}} \mathord{\left/ {\vphantom {{{{\nu }_{a}}} {{{\nu }_{w}}}}} \right. \kern-0em} {{{\nu }_{w}}}}$.

Уравнения (1), (2) для воздуха и воды решаются с использованием метода Адамса–Бэшфорта второго порядка точности в области 0 ≤ x/H ≤ 6, 0 ≤ y/H ≤ 4, –1 ≤ z/H ≤ 1 на разнесенной сетке 360 × 240 × 360 с однородным шагом по горизонтальным координатам x, y и сгущением узлов в окрестности водной поверхности и верхней плоскости по вертикальной координате z. Используется метод расщепления, и уравнение Пуассона для давления решается с помощью преобразования Фурье в горизонтальной плоскости и методом Гаусса по вертикальной координате [11, 12].

Граничные условия для полей скорости воды и воздуха на водной поверхности (z = 0) записываются в безразмерном виде:

где ${{{{\rho }_{a}}} \mathord{\left/ {\vphantom {{{{\rho }_{a}}} {{{\rho }_{w}}}}} \right. \kern-0em} {{{\rho }_{w}}}} \approx {{10}^{{ - 3}}}$ – отношение плотностей воздуха и воды.

В исходный момент времени поле скорости воздуха задается в виде линейного профиля ламинарного течения Куэтта с наложенными на него слабыми (с амплитудой порядка 5%) флуктуациями. Исходное поле скорости воды полагается нулевым. Как показывают расчеты, течение в воздушном погранслое становится полностью турбулентным на временах U₀t/H > 200. Статистические характеристики течения определяются осреднением по горизонтальным координатам и, по мере установления стационарного режима, также “оконным” усреднением по времени.

3. РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ

Численное моделирование проводилось для значений Re_a от 8 × 10³ до 2 × 10⁴, как с учетом влияния развивающегося дрейфового течения на воздушный погранслой, так и без учета этого влияния. В последнем случае для воздуха ставилось граничное условие прилипания на покоящейся горизонтальной поверхности при z = 0.

На рис. 2 представлены мгновенные поля модуля завихренности в воздухе и воде. Как видно из рисунков, в рассматриваемый момент времени (tU₀/H = 400) воздушный погранслой является турбулентным и характеризуется наличием подковообразных вихрей, инициированных в вязком подслое и “уходящих” вглубь потока (рис. 2а, 2б, 2д) [13]. При этом в тонком приповерхностном водном слое наблюдаются относительно малые возмущения завихренности в виде ориентированных по среднему потоку полосчатых структур (рис. 2в, 2г, 2е). Необходимо отметить, что значения завихренности в воздухе ω_a почти на два порядка превосходят завихренность в воде ω_w.

Под действием напряжения сдвига ветра на водной поверхности с течением времени в приповерхностном слое развивается дрейфовое течение. На рис. 3 представлены вертикальные профили средней скорости, $\left\langle {{{U}_{w}}} \right\rangle $, и флуктуаций (среднеквадратичных отклонений) трех ее компонент, полученные осреднением по координатам x и y в разные моменты времени. Профили $\left\langle {{{U}_{w}}} \right\rangle $ сравниваются с аналитическим решением для ламинарного течения, описываемого уравнением, получающимся из уравнений Навье–Стокса для случая плоско-параллельного потока:

c граничным условием (4) на поверхности z = 0. Решение задачи (5) аналогичного решению одномерного уравнения теплопроводности с заданным постоянным потоком тепла на границе [14 ] :

где ${\text{erfc}}\left( z \right) = \frac{2}{{\sqrt \pi }}\int_z^\infty {\exp \left( { - {{x}^{2}}} \right)} dx$ – дополнительная функция ошибок, и производная средней дрейфовой скорости на водной поверхности $\left( {\frac{{\partial U_{d}^{l}(0)}}{{\partial z}}} \right)$ определяется по мгновенному, осредненному по x и y профилю. Эта производная связана со скоростью трения в воздушном турбулентном погранслое $u{\text{*}}$ благодаря граничному условию (4):

Следует отметить, что развитие дрейфового течения приводит к уменьшению потока импульса от ветра к воздуху и, соответственно, к изменению величин $\left( {\frac{{\partial U_{d}^{l}(0)}}{{\partial z}}} \right)$ и скорости трения $u{\text{*}}$. Однако, как будет видно из дальнейшего (см. ниже рис. 6), это уменьшение весьма медленное и незначительное, такое, что воздушный погранслой относительно быстро “подстраивается” под развивающееся дрейфовое течение.

Как видно из рис. 3, решение (6) для ламинарного потока хорошо описывает поведение профиля дрейфового течения на временах tU₀/H < < 3 × 10³, когда флуктуации достаточно малы. На больших временах развивающаяся турбулентность модифицирует профиль течения. Рисунок 3г, 3д, 3е показывает, что турбулентность в приповерхностном водном слое анизотропна, причем доминируют флуктуации x-компоненты скорости, и флуктуации вертикальной компоненты пренебрежимо малы, ${{U}_{{w,x}}} \gg {{U}_{{w,y}}} > {{U}_{{w,z}}}$.

Дрейфовая скорость водной поверхности для ламинарного режима определяется из (6) и (7) в виде

и сравнивается на рис. 4 с результатами численных расчетов для различных чисел Рейнольдса Re_a. На рисунке также представлены временные зависимости кинетической энергии флуктуаций скорости в воде E_w.

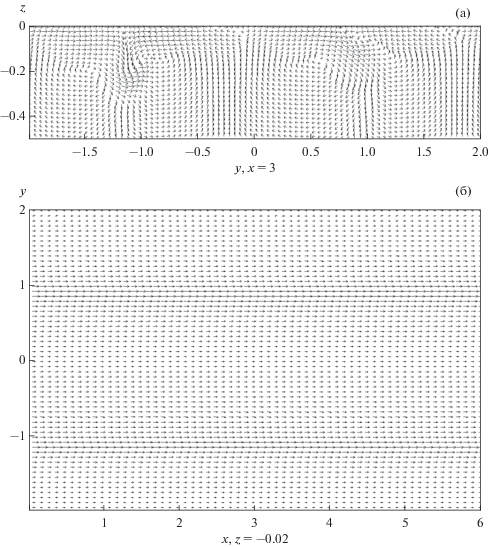
Из рис. 4 видно, что решение (8) для ламинарного режима хорошо описывает рост скорости дрейфа на поверхности U_s на временах, когда энергия флуктуаций достаточно мала (т.е. пока не наблюдается ее экспоненциальный рост), при tU₀/H < 1.5 × 10³ (Re_a = 2 × 10⁴), tU₀/H < 2.5 × 10³ (Re_a = 1.5 × 10⁴), tU₀/H < 4 × 10³ (Re_a = 10⁴) и tU₀/H < < 5 × 10³ (Re_a = 8 × 10³). На больших временах, когда флуктуации растут экспоненциально, наблюдается насыщение роста скорости поверхностного дрейфа. При этом течение в приповерхностном водном слое приобретает турбулентный характер, и происходит развитие вихревых структур, ориентированных вдоль среднего течения (рис. 5). Эта картина течения качественно согласуется с натурными наблюдениями морской поверхности при слабом ветре (2–3 м/с) [8], где наблюдались подобные полосчатые структуры.

Статистически стационарный режим флуктуаций в воде в DNS достичь не удается, поскольку рост флуктуаций приводит к проблемам их разрешения при выбранном шаге сетки. Кроме того, предположение об аэродинамической гладкости поверхности (т.е. об отсутствии волн) при этом также становится необоснованным (см., напр., [9], где в лабораторном эксперименте при слабом ветре наблюдалось развитие турбулентности, сопровождавшееся генерацией капиллярно-гравитационных поверхностных волн).

Характеристики течения в воздушном и водном приповерхностном слоях на стадии насыщения роста дрейфовой скорости на поверхности воды определялись осреднением по горизонтальным координатам x и y и “оконным” усреднением по времени. Профили средней скорости U_{a, w} и турбулентного потока импульса τ_a,w, полученные для числа Рейнольдса воздушного потока Re_a = = 1.5 × 10³ на временном интервале 3.6 × 10³ < < tU₀/H < 3.8 × 10³, представлены на рис. 6. Для сравнения, на рисунке также показаны профили течения в воздушном погранслое в случае фиксированной поверхности z = 0 (с поверхностной скоростью дрейфа U_s = 0).

Как видно из рис. 6a, профили скорости в воздушном погранслое хорошо описываются классическими асимптотиками вязкого подслоя и логарифмического погранслоя [15]:

Развитие дрейфового течения приводит к некоторому (сравнительно медленному и незначительному, порядка 3% к моменту времени tU₀/H = 3.8 × × 10³) уменьшению скорости трения, определяемой турбулентным потоком импульса вдали от водной поверхности, $u* = \sqrt {{{\tau }_{a}}} $ при z/H = 1/2, по сравнению с ветром над фиксированной поверхностью.

Рисунок 6в показывает, что профиль скорости дрейфового течения имеет линейный участок, соответствующий вязкому подслою. Соответствующая асимптотика для скорости на этом участке имеет вид

Турбулентный поток импульса в воде τ_w достигает максимума на глубине –z/H ≈ 0.17 и далее уменьшается, не выходя на плато, что говорит о переходном (“квазитурбулентном”) характере течения на рассматриваемом временном интервале. Расчеты показывают, что дальнейший экспоненциальный рост флуктуаций приводит к генерации интенсивных мелкомасштабных вихрей, разрешение которых требует существенного дробления узлов сетки. Результаты лабораторного эксперимента [9] говорят о том, что развитие турбулентных пульсаций скорости в воде сопровождается ростом флуктуаций уровня водной поверхности и генерацией капиллярных волн. Поскольку все эти эффекты требуют модификации численного метода и учета поверхностных волн, расчеты на временах, когда турбулентность в воде становится развитой, остаются предметом будущих исследований.

4. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Результаты численного моделирования на рис. 3, 4 показывают, что на ранних временах в приповерхностном водном слое, находящегося под действием турбулентного воздушного потока, флуктуации малы, и развивающееся дрейфовое течение является ламинарным и описывается аналитическим решением (6)–(8). Используя это решение, можно оценить число Рейнольдса дрейфового течения:

Как показывают расчеты (рис. 4), на достаточно больших временах в приповерхностном водном слое развивается турбулентность. Подставляя в (12) значения времени [tU₀/H ≈ 1.5 × 10³ (Re_a = 2 × × 10⁴), tU₀/H ≈ 2.5 × 10³ (Re_a = 1.5 × 10⁴), tU₀/H ≈ 4 × × 10³ (Re_a = 10⁴) и tU₀/H ≈ 5 × 10³ (Re_a = 8 × 10³)], соотношение плотностей и кинематических вязкостей воздуха и воды (${{{{\rho }_{a}}} \mathord{\left/ {\vphantom {{{{\rho }_{a}}} {{{\rho }_{w}}}}} \right. \kern-0em} {{{\rho }_{w}}}}$≈ 10^–3 и ${{{{\nu }_{a}}} \mathord{\left/ {\vphantom {{{{\nu }_{a}}} {{{\nu }_{w}}}}} \right. \kern-0em} {{{\nu }_{w}}}}$≈ 15) и значение скорости трения воздушного потока в DNS (${{u{\text{*}}} \mathord{\left/ {\vphantom {{u{\text{*}}} {{{U}_{0}}}}} \right. \kern-0em} {{{U}_{0}}}}$≈ 2.8 × 10^–2), получаем оценку критического значения числа Рейнольдса $\operatorname{Re} _{d}^{c}$, при котором в дрейфовом течении в DNS наблюдается переход от ламинарного режима к турбулентности, оказывающееся примерно одинаковым для рассматриваемых Re_a:

С другой стороны, можно переписать (12) в виде

где время перехода к турбулентности обозначено как t_c. Подставляя (14) в (8), находим критическое значение скорости дрейфа водной поверхности, при котором происходит переход:

Подставляя в (15) ${{{{\rho }_{a}}} \mathord{\left/ {\vphantom {{{{\rho }_{a}}} {{{\rho }_{w}}}}} \right. \kern-0em} {{{\rho }_{w}}}}$≈ 10^–3 и оценку (13) для $\operatorname{Re} _{d}^{c}$, находим:

Выражение (16) дает оценку “сверху” скорости дрейфа на водной поверхности, достигаемой при слабом ветре до развития турбулентности дрейфового течения, на стадии, когда водная поверхность остается аэродинамически гладкой. Для скоростей ветра порядка O(1м/с) и высоты O(1м) по данным DNS и согласно оценке (14) характерное время развития дрейфового течения составляет O(10³ c). Значение (16) превышает широко используемую оценку скорости дрейфа, полученную на основе данных лабораторных экспериментов при сравнительно больших (более 5 м/с) скоростях ветра [3, 4], ${{U}_{s}} \approx 0.53u{\text{*}}$, когда течение в приповерхностном слое является турбулентным и модифицируется развитием поверхностных гравитационно-капиллярных волн.

5. ВЫВОДЫ

Проведено прямое численное моделирование (DNS) динамики дрейфового течения в приповерхностном водном слое, находящегося под воздействием турбулентного ветра. В DNS рассматриваются достаточно большие числа Рейнольдса воздушного потока Re_a (до 2 × 10⁴), такие что воздушный погранслой турбулентный, а пульсации скорости в воде малы, и водная поверхность остается аэродинамически гладкой (т.е. поверхностные гравитационно-капиллярные волны в DNS не учитываются). Такой режим реализуется в лабораторных условиях при скоростях ветра порядка 2–3 м/с.

Показано, что на достаточно малых временах в приповерхностном водном слое развивается дрейфовое течение, профиль которого хорошо описывается аналитическим решением одномерного уравнения теплопроводности. На больших временах, когда балковое число Рейнольдса дрейфового течения Re_d превышает пороговое значение ($\operatorname{Re} _{d}^{c} \approx 500$), в водном слое развиваются вытянутые по потоку вихревые структуры. Это далее приводит к развитию турбулентности и существенному замедлению роста дрейфовой скорости водной поверхности. С использованием ламинарного решения и порогового значения числа Рейнольдса для дрейфового течения в численном эксперименте получена параметризация поверхностной скорости дрейфа. Полученная параметризация представляет собой оценку “сверху” скорости дрейфа на водной поверхности, достигаемой при слабом ветре до развития турбулентности дрейфового течения, на стадии, когда водная поверхность остается аэродинамически гладкой. Моделирование динамики дрейфового течения на больших временах требует учета эффектов, связанных с возбуждением поверхностных волн, и остается предметом будущих исследований.