1. На главную
  2. Электронные версии
  3. Известия РАН. Физика атмосферы и океана
  4. T. 58, № 1, 2022

Известия РАН. Физика атмосферы и океана, 2022, T. 58, № 1, стр. 79-91

Моделирование сезонных изменений интенсивности внутренних гравитационных волн в нижней термосфере

Н. М. Гаврилов a, *, А. А. Попов a

a Санкт-Петербургский государственный университет
199034 Санкт-Петербург, Университетская набережная, 7–9, Россия

* E-mail: n.gavrilov@spbu.ru

Поступила в редакцию 30.08.2021
После доработки 24.09.2021
Принята к публикации 07.10.2021

Полный текст (PDF)

Аннотация

Описана модернизированная численная модель распространения набора спектральных гармоник внутренних гравитационных волн (ВГВ) в неоднородной атмосфере от земной поверхности до нижней термосферы. Учтена диссипация ВГВ из-за турбулентной вязкости и теплопроводности, радиационного теплообмена и ионного трения в нижней ионосфере. Выполнено численное моделирование распространения спектра ВГВ в фоновых полях ветра и температуры, соответствующих координатам станций Звенигород (56° с.ш., 37° в.д.), Маймага (63° с.ш., 130° в.д.) и Торы (52° с.ш., 103° в.д.), на которых проводятся систематические наблюдения ночной эмиссии гидроксила. Рассчитаны сезонные вариации стандартных отклонений возмущений компонент горизонтальной скорости, создаваемых модельным спектром ВГВ. Обнаружено общее сходство сезонных вариаций модельных амплитуд ВГВ и наблюдаемой дисперсии мезомасштабных возмущений вращательной температуры гидроксила в Звенигороде и Торах. Это является свидетельством того, что интенсивность мезомасштабных возмущений температуры вблизи мезопаузы может зависеть от интенсивности ВГВ, распространяющихся из нижней атмосферы, и от профилей фоновых характеристик средней атмосферы на пути распространения волновых пакетов в различные сезоны и в разных географических пунктах.

Ключевые слова: мезосфера, термосфера, ночные эмиссии, внутренние гравитационные волны, сезонные вариации, численное моделирование

1. ВВЕДЕНИЕ

Внутренние гравитационные волны (ВГВ) играют важную роль в динамике средней и верхней атмосферы. Их основные источники расположены в нижней атмосфере. Распространяясь вверх, ВГВ могут обеспечить значительные потоки импульса и энергии и, таким образом, воздействовать на циркуляцию, тепловой режим и состав на всех атмосферных уровнях.

Одним из методов мониторинга мезомасштабной возмущенности в области мезопаузы является наблюдение вариаций параметров свечений ночного неба. В светящихся слоях ВГВ могут изменять температуру и яркость излучения [1]. Были обнаружены и многократно наблюдались волновые структуры в областях различных ночных свечений (О, O2, Na, OH) на высотах 80–100 км [2–4]. Наблюдения [5, 6] обнаружили структуры ВГВ в области свечения гидроксила (ОН), которые имели горизонтальные длины волны 5–l60 км. Типичные значения параметров ВГВ, визуально наблюдаемых на видеосъемках свечения ОН лежат в пределах горизонтальных длин 5–60 км, периодов 5–30 мин. и горизонтальных фазовых скоростей 0–100 m/s [7]. Статистический анализ ВГВ более крупных масштабов показал наличие спектральных составляющих с периодами 0.5–5 h и горизонтальными длинами волны 100–1700 километров в слоях излучения OH и О2 [8].

Ряд исследователей рассматривал долговременные вариации интенсивности ВГВ вблизи мезопаузы. Перминов и др. [9] исследовали сезонную и межгодовую изменчивость температуры по данным спектральных наблюдений излучения ОН в Звенигороде и Иркутске в 2000–2010 гг. В работах [10, 11] исследованы изменения характеристик области мезосферы и нижней термосфры (МНТ) во время внезапных стратосферных потеплений. Авторы [12, 13] с помощью цифровых разностных фильтров исследовали сезонные и межгодовые вариации дисперсий мезомасштабных возмущений вращательной температуры ОН по данным российских станций Звенигород (56° с.ш., 37° в.д.), Маймага (63° с.ш., 130° в.д.) и Торы (52° с.ш., 103° в.д.).

Численное моделирование показало, что сезонные вариации интенсивности ВГВ изменяются с высотой и зависят от сезонных изменений вертикальных профилей фоновых ветра и температуры в средней и верхней атмосфере. В [14] получено достаточно хорошее соответствие моделируемых сезонных вариаций интенсивности ВГВ с наблюдениями в области МНТ с помощью японского МСТ радара.

В данной работе выполнено численное моделирование сезонных вариаций средних характеристик набора волновых гармоник, соответствующих спектру ВГВ, распространяющихся из нижней атмосферы в область МНТ. Исследовано влияние изменений вертикальных профилей фоновых ветра и температуры на моделируемые амплитуды ВГВ для интерпретации сезонных вариаций дисперсий мезомасштабных возмущений вращательной температуры ОН, наблюдаемых оптическими методами на различных российских станциях.

2. ЭНЕРГЕТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ВГВ

При распространении ВГВ в неоднородной дисссипативной атмосфере возникает обмен импульсом между средним потоком и волнами, а также нагрев атмосферы вследствие диссипации энергии ВГВ. Согласно [15], уравнение баланса волновой энергии в случае стационарности и горизонтальной однородности средних за период волны величин можно записать в следующем виде:

(1)
$\begin{gathered} {{\partial {{F}_{E}}} \mathord{\left/ {\vphantom {{\partial {{F}_{E}}} {\partial z}}} \right. \kern-0em} {\partial z}} = {{\rho }_{0}}Q - {{\rho }_{0}}D - {{\rho }_{0}}{{v}_{{0\alpha }}}{{a}_{{w\alpha }}}, \\ {{a}_{{w\alpha }}} = {{ - \rho _{0}^{{ - 1}}\partial {{F}_{{m\alpha }}}} \mathord{\left/ {\vphantom {{ - \rho _{0}^{{ - 1}}\partial {{F}_{{m\alpha }}}} {\partial z}}} \right. \kern-0em} {\partial z}}; \\ {{F}_{E}} = \left\langle {p{\kern 1pt} 'w{\kern 1pt} '} \right\rangle + {{v}_{{0\alpha }}}{{F}_{{m\alpha }}};\,\,\,\,{{F}_{{m\alpha }}} = {{\rho }_{0}}\left\langle {v_{\alpha }^{'}w{\kern 1pt} '} \right\rangle , \\ \end{gathered} $
где p и ρ – атмосферные давление и плотность, соответственно; vα и w – компоненты скорости вдоль горизонтальных осей xα и вертикальной оси z, соответственно; по повторяющимся греческим индексам производится суммирование; Fmα – вертикальные волновые потоки α-компонент горизонтального импульса; ${{F}_{E}}$ – суммарный вертикальный поток волновой энергии, складывающийся из потока волновой энергии в покоящейся среде и ее переноса средним движением; Q – мощность локальных волновых источников; D – скорость диссипации волновой энергии; ${{a}_{{w\alpha }}}$ – компоненты волнового ускорения среднего потока, входящие в уравнение для горизонтальных компонент средней скорости; уголковые скобки $\left\langle {} \right\rangle $ обозначают усреднение по периоду волны, индексами 0 отмечены средние а штрихами – волновые компоненты соответствующих величин. Согласно [15], скорость диссипации волновой энергии с точностью до слагаемых второго порядка малости по амплитудам ВГВ описывается выражением
(2)
$\begin{gathered} {{\rho }_{0}}D = \left\langle {{{v_{\beta }^{'}\partial (\sigma _{{\alpha \beta }}^{'} + \tau _{{\alpha \beta }}^{'})} \mathord{\left/ {\vphantom {{v_{\beta }^{'}\partial (\sigma _{{\alpha \beta }}^{'} + \tau _{{\alpha \beta }}^{'})} {\partial {{x}_{\alpha }}}}} \right. \kern-0em} {\partial {{x}_{\alpha }}}}} \right\rangle - \left\langle {(\rho {{X}_{\alpha }}){\kern 1pt} 'v_{\alpha }^{'}} \right\rangle - \\ {{ - \,\,\left\langle {(\varepsilon _{t}^{'} + \varepsilon _{m}^{'} + \varepsilon _{r}^{'})[p{\kern 1pt} '\,\, + s{\kern 1pt} '(\gamma - 1){{\rho }_{0}}{{{{T}_{0}}} \mathord{\left/ {\vphantom {{{{T}_{0}}} B}} \right. \kern-0em} B}]} \right\rangle } \mathord{\left/ {\vphantom {{ - \,\,\left\langle {(\varepsilon _{t}^{'} + \varepsilon _{m}^{'} + \varepsilon _{r}^{'})[p{\kern 1pt} '\,\, + s{\kern 1pt} '(\gamma - 1){{\rho }_{0}}{{{{T}_{0}}} \mathord{\left/ {\vphantom {{{{T}_{0}}} B}} \right. \kern-0em} B}]} \right\rangle } {c_{s}^{2}}}} \right. \kern-0em} {c_{s}^{2}}}, \\ \end{gathered} $
где ${{\sigma }_{{\alpha \beta }}}$ и ${{\tau }_{{\alpha \beta }}}$ – тензоры молекулярных и турбулентных вязких напряжений; Xα – плотность сторонних сил; $B = {{c_{s}^{2}{{N}^{2}}} \mathord{\left/ {\vphantom {{c_{s}^{2}{{N}^{2}}} {{{g}^{2}}}}} \right. \kern-0em} {{{g}^{2}}}}$ – параметр статической устойчивости атмосферы, cs – скорость звука, N – частота Брента–Вяисяля, g – гравитационное ускорение, $\varepsilon _{t}^{'},\varepsilon _{m}^{'},\varepsilon _{r}^{'}$ – волновые компоненты притоков тепла за счет турбулентной и молекулярной теплопроводности и радиационного теплообмена, соответственно, s' = (p' – $c_{s}^{2}\rho {\kern 1pt} '$)/((γ – 1)ρ0T0 – волновая компонента энтропии, $\gamma = {{{{c}_{p}}} \mathord{\left/ {\vphantom {{{{c}_{p}}} {{{c}_{v}}}}} \right. \kern-0em} {{{c}_{v}}}}$ – отношение теплоемкостей.

Слагаемые в правой части первого уравнения в (1) описывают мощность локальных волновых источников, диссипацию волновой энергии, а также работу нелинейного взаимодействия между волной и средним потоком, которая зависит от скорости среднего потока и волнового ускорения.

3. ПЛОСКИЕ МОНОХРОМАТИЧЕСКИЕ МОДЫ ВГВ

Для стационарной и горизонтально однородной модели можно выполнить преобразования Фурье всех полей ВГВ и рассмотреть спектр монохроматических плоских спектральных волновых мод с различными частотами σ и векторами горизонтальных волновых чисел kh. Для каждой спектральной составляющей удобно выбрать горизонтальную ось χ в направлении kh. В [15] показано, что при наличии вертикального градиента среднего ветра можно получить следущее выражение для FE:

(3)
$\begin{gathered} {{F}_{E}} = c{{F}_{m}} + {{({{{{\rho }_{0}}\partial {{v}_{{0\chi }}}} \mathord{\left/ {\vphantom {{{{\rho }_{0}}\partial {{v}_{{0\chi }}}} {\partial z}}} \right. \kern-0em} {\partial z}})}^{{ - 1}}} \times \\ \times \,\,\left\langle {[p{\kern 1pt} '\,\, - {{\rho }_{0}}v_{\chi }^{'}{{c}_{\chi }}][(\rho {{X}_{\chi }}){\kern 1pt} '\,\, + {{\partial (\sigma _{{\alpha \chi }}^{'} + \tau _{{\alpha \chi }}^{'})} \mathord{\left/ {\vphantom {{\partial (\sigma _{{\alpha \chi }}^{'} + \tau _{{\alpha \chi }}^{'})} {\partial {{x}_{\alpha }}}}} \right. \kern-0em} {\partial {{x}_{\alpha }}}}]} \right\rangle , \\ \end{gathered} $
где с = σ/kh – горизонтальная фазовая скорость; Fm – вертикальный волновой поток горизонтального импульса вдоль направления распространения волны χ; cχ = ω/kh = c – ${{v}_{{0\chi }}}$. Поляризационные соотношения для ВГВ в невращающейся атмосфере [16] показывают, что в (3) [p' – ${{\rho }_{0}}v_{\chi }^{'}{{с}_{\chi }}$] ≈ 0 и подстановка (3) в (1) дает следующее уравнение изменения вертикального потока волнового импульса:

(4)
${{\partial {{F}_{m}}} \mathord{\left/ {\vphantom {{\partial {{F}_{m}}} {\partial z}}} \right. \kern-0em} {\partial z}} = {{{{\rho }_{0}}(Q - D)} \mathord{\left/ {\vphantom {{{{\rho }_{0}}(Q - D)} {{{c}_{\chi }}}}} \right. \kern-0em} {{{c}_{\chi }}}}.$

Подстановка (4) во второе уравнение (1) позволяет определить горизонтальное волновое ускорение вдоль направления распространения волны χ. Важной энергетической характеристикой является тепловое воздействие за счет диссипации и переноса энергии ВГВ [17]. Часто предполагается, что волновой приток тепла определяется дивиргенцией вертикального волнового потока энтальпии. Это справедливо для гидростатических динамических моделей [18]. При учете негидростатичности и сжимаемости необходимо также учесть работу упругих сил сжатия и разрежения [19]. Кроме того, в уравнении притока тепла для среднего течения надо учесть скорость вязкой диссипации механической энергии волн в тепло. В [15, 20] показано, что полный волновой приток тепла, εw, описывается выражением

(5)
$\begin{gathered} {{\varepsilon }_{w}} = - \frac{1}{{{{\rho }_{0}}}}\frac{{\partial {{F}_{T}}}}{{\partial z}};\,\,\,\,{{F}_{T}} = {{\rho }_{0}}{{c}_{p}}\left\langle {T{\kern 1pt} 'w{\kern 1pt} '} \right\rangle + \\ + \,\,{{v}_{{0\chi }}}{{F}_{m}} - \left\langle {(\sigma _{{z\chi }}^{'} + \tau _{{z\chi }}^{'})v_{\chi }^{'}} \right\rangle , \\ \end{gathered} $
где T – температура, а FТ можно рассматривать как полный волновой поток тепла. Учитывая связи волновых потоков энтальпии, энергии, энтропии и импульса, в [15] показано, что

(6)
$\begin{gathered} {{F}_{T}} = c{{F}_{m}} - \left\langle {(\sigma _{{z\chi }}^{'} + \tau _{{z\chi }}^{'})v_{\chi }^{'}} \right\rangle + \\ + \,\,\frac{{(\gamma - 1){{\rho }_{0}}{{T}_{0}}}}{{gB}}\left\langle {(\varepsilon _{t}^{'} + \varepsilon _{m}^{'} + \varepsilon _{r}^{'})s{\kern 1pt} '} \right\rangle . \\ \end{gathered} $

Учет (1) и (3) дает выражение

(7)
$\begin{gathered} {{\varepsilon }_{w}} = c{{a}_{{w\chi }}} + \frac{1}{{{{\rho }_{0}}}}\frac{\partial }{{\partial z}} \times \\ \times \,\,\left[ {\left\langle {(\sigma _{{z\chi }}^{'} + \tau _{{z\chi }}^{'})v_{\chi }^{'}} \right\rangle - \frac{{(\gamma - 1){{\rho }_{0}}{{T}_{0}}}}{{gB}}\left\langle {(\varepsilon _{t}^{'} + \varepsilon _{m}^{'} + \varepsilon _{r}^{'})s{\kern 1pt} '} \right\rangle } \right]. \\ \end{gathered} $

Формулы (2), (4) и (7) показывают, что волновые ускорения и притоки тепла отличны от нуля только при наличии диссипации и неадиабатичности ВГВ. Определить связи величин Fm, D, awχ и εw с параметрами ВГВ можно используя соотношения стандартной теории ВГВ [16]. Для стационарной и горизонтально однородной модели мы можем выполнить преобразования Фурье всех полей ВГВ и волновых источников. Для каждой монохроматической плоской гармоники ВГВ, распространяющейся вдоль оси χ дисперсионное уравнение стандартной теории атмосферных ВГВ в плоской невращающейся атмосфере (см., например, [21]) дает следующее выражение для вертикального волнового числа m:

(8)
${{m}^{2}} = \frac{{{{N}^{2}} - {{\omega }^{2}}}}{{c_{\chi }^{2}}} - \frac{{\omega _{a}^{2} - {{\omega }^{2}}}}{{c_{s}^{2}}},$
где свойственная (внутренняя) частота ВГВ, ω, частота Брента–Вяисяля, N, и граничная акустическая частота, ωa, в неизотермической модели с учетом среднего ветра описыватся приближенными формулами [21]:
(9)
$\begin{gathered} \omega = \sigma - {{k}_{h}}{{v}_{{0\chi }}};\,\,\,\,{{N}^{2}} = \frac{g}{{{{T}_{0}}}}\left( {\frac{{\partial {{T}_{0}}}}{{\partial z}} + {{\gamma }_{a}}} \right); \\ \omega _{a}^{2} = \frac{{c_{s}^{2}}}{{4{{H}^{2}}}}\left( {1 + 2\frac{{\partial H}}{{\partial z}}} \right), \\ \end{gathered} $
где γa = g/cp, Н – высота однородной атмосферы. Для низкочастотных ВГВ с ω2$ \ll $ N2, согласно (8), горизонтальные длины волн обычно значительно превосходят вертикальные длины ВГВ. В этом случае в диссипативных слагаемых (2)–(4) можно ограничиться только молекулярной диффузией по вертикали и использовать выражения (см. [22])
(10)
$\begin{gathered} \sigma _{{z\chi }}^{'} + \tau _{{z\chi }}^{'} = {{\rho }_{0}}{{\nu }_{z}}\frac{{\partial v_{\chi }^{'}}}{{\partial z}}; \\ \varepsilon _{m}^{'} + \varepsilon _{t}^{'} = \frac{1}{{{{\rho }_{0}}}}\frac{\partial }{{\partial z}}\left( {{{\rho }_{0}}{{c}_{p}}{{\kappa }_{z}}\frac{{\partial T{\kern 1pt} '}}{{\partial z}}} \right); \\ \varepsilon _{r}^{'} = - {{c}_{p}}{{N}_{r}}T{\kern 1pt} ', \\ \end{gathered} $
где νz = ν + Kz, κz = κ + Ktz, а ν, Kz и κ, Ktz – вертикальные кинематические коэффициенты молекулярной и турбулентной вязкости и теплопроводности, соответственно; Nr – скорость сглаживания температурных неоднородностей за счет радиационного теплообмена. В ионизированной атмосфере может стать существенным ионное трение, когда в (2)
(11)
$(\rho {{X}_{\chi }}){\kern 1pt} ' = - {{\rho }_{0}}{{N}_{i}}v_{\chi }^{'};\,\,\,\,{{\rho }_{0}}{{N}_{i}} = {{\sigma }_{p}}B_{0}^{2},$
где σp – педерсеновская проводимость, B0 – индукция геомагнитного поля [15]. Поляризационные соотношения для ВГВ дают соотношения между амплитудами волновых вариаций различных гидродинамических величин. В частности, для стандартных отклорений вариаций вертикальной скорости, |w'|, и температуры |T'|, получаем:
(12)
$\begin{gathered} \left| {w{\kern 1pt} '} \right| = {{q}_{w}}{{U}_{w}};\,\,\,\,\left| {T{\kern 1pt} '} \right| = {{q}_{T}}{{U}_{w}}; \\ {{q}_{w}} = \frac{{k\left| {1 - {{c_{\chi }^{2}} \mathord{\left/ {\vphantom {{c_{\chi }^{2}} {c_{s}^{2}}}} \right. \kern-0em} {c_{s}^{2}}}} \right|}}{{\sqrt {{{m}^{2}} + {{\Gamma }^{2}}} }};\,\,\,\,{{q}_{T}} = \frac{{{{T}_{0}}N}}{g}, \\ \end{gathered} $
где Uw – амплитуда колебаний компоненты скорости вдоль горизонтального направления распространения ВГВ, Γ = (2 – γ)/(2γH). Используя (10)–(12) можно получить следующие выражения для волнового потока импульса, волнового ускорения и притока тепла:
(13)
$\begin{gathered} {{F}_{m}} = \frac{{{{\rho }_{0}}{{q}_{m}}U_{w}^{2}}}{2};\,\,\,\,{{q}_{m}} = \frac{{{{k}_{h}}m}}{{{{m}^{2}} + {{\Gamma }^{2}}}}\left( {1 - \frac{{c_{\chi }^{2}}}{{c_{s}^{2}}}} \right); \\ {{a}_{{w\chi }}} = \frac{{D - Q}}{{{{c}_{\chi }}}};\,\,\,\,D = \frac{{{{N}_{d}}U_{w}^{2}}}{2}; \\ {{N}_{k}} = {{\nu }_{z}}\left( {{{m}^{2}} - \frac{1}{{{{U}_{w}}}}\frac{{{{\partial }^{2}}{{U}_{w}}}}{{\partial {{z}^{2}}}}} \right);\,\,\,\,{{N}_{d}} = {{N}_{k}} + {{N}_{i}} + \\ + \,\,\frac{{{{\kappa }_{z}}}}{{(\gamma - 1)}}\left( {{{m}^{2}} - \frac{1}{{{{q}_{T}}{{U}_{w}}}}\frac{{{{\partial }^{2}}{{q}_{T}}{{U}_{w}}}}{{\partial {{z}^{2}}}}} \right) + \frac{{{{N}_{r}}}}{{(\gamma - 1)}}; \\ {{\varepsilon }_{w}} = c{{a}_{{w\chi }}} + \rho _{0}^{{ - 1}}{\partial \mathord{\left/ {\vphantom {\partial {\partial z}}} \right. \kern-0em} {\partial z}}\left[ {{{\rho }_{0}}H\delta ({{a}_{{w\chi }}}{{c}_{\chi }} + Q)} \right]; \\ \delta = {{\gamma {{d}_{T}}} \mathord{\left/ {\vphantom {{\gamma {{d}_{T}}} {[(\gamma - 1){{d}_{V}}]}}} \right. \kern-0em} {[(\gamma - 1){{d}_{V}}]}}; \\ \end{gathered} $
где Nk – скорость диссипации кинетической энергии волны, Nd – суммарная скорость диссипации ВГВ. В формулах (13) положительные значения m соответствуют восходящим волновым потокам импульса и энергии. Последнее уравнение (13) содержит множитель δ, который зависит от отношения коэффициентов диссипации неоднородностей поля температуры, dT, и ветра, dV, введенных в [18]. Согласно [18], в случае dT = dV множитель δ = γ/(γ – 1). Анализ (7) и (2) приводит к значению δ = γ[1 – (Nd – Nk – Ni)/Nd]. Источниками постоянной генерации ВГВ в атмосфере могут быть мезомасштабные неоднородности, возникающие вследствие динамической и конвективной неустойчивости. Для каждой монохроматической плоской спектральной гармоники ВГВ можно использовать параметризацию (см. [20]),
(14)
$Q = s{{U}_{w}},$
где параметр s описывает активность волновых источников и имеет размерность силы, действующей на единицу массы атмосферного газа. Вводя новую переменную Φ = |2Fm|1/2, можно преобразовать (4) к следующему виду:

(15)
$\begin{gathered} \frac{{\partial \Phi }}{{\partial z}} + \frac{\Phi }{h} = f;\,\,\,\,h = \frac{{2{{c}_{\chi }}{{q}_{m}}}}{{{{N}_{d}}}}; \\ f = \frac{s}{{{{c}_{\chi }}}}\sqrt {\frac{{{{\rho }_{0}}}}{{{{q}_{m}}}}} {\kern 1pt} {\text{sign}}{\kern 1pt} ({{F}_{m}}). \\ \end{gathered} $

Это неоднородное уравнение учитывает генерацию ВГВ гидродинамическими источниками импульса, массы, и тепла [20]. После решения (15), амплитуду волны и вертикальный волновой поток импульса можно определить по формулам:

(16)
$U = \frac{\Phi }{{\sqrt {{{\rho }_{0}}{{q}_{m}}} }};\,\,\,\,{{F}_{m}} = \frac{{{{\Phi }^{2}}}}{2}{\text{sign}}{\kern 1pt} ({{F}_{m}}).$

При численном решении, интегрирование начинается с нижней границы модели (с поверхности Земли), причем значение Si + 1 на высотном уровне zi + 1 вычисляется по значениям Si и коэффициентов уравнения (15) на предыдущем высотном уровне по рекуррентной формуле

(17)
${{\Phi }_{{i + 1}}} = ({{\Phi }_{i}} + {{f}_{i}}\Delta z)\exp ({{ - \Delta z} \mathord{\left/ {\vphantom {{ - \Delta z} {{{h}_{i}}}}} \right. \kern-0em} {{{h}_{i}}}}),$
где Δz – шаг интегрирования по высоте. Формула (13) для Nd содержит вторые производные по высоте, для вычисления которых нужны три предыдущих высотных уровня. Поэтому предполагается, что на 3-х нижних уровнях модели отсутствует диссипация и волновые источники и нижние граничные условия для решения уравнения (13) задаются в виде
(18)
${{\Phi }_{0}} = {{\Phi }_{1}} = {{\Phi }_{2}} = \sqrt {2{{F}_{{mb}}}} ,$
где Fmb – значение волнового потока импульса на нижней границе. Вычисления по рекуррентной формуле (17) начинаются с 4-го высотного уровня. При заданном волновом потоке импульса на нижней границе уравнение (15) можно решить методом (17) относительно Φ для заданных высотных профилей ${{v}_{{0\chi }}}$ и T0. Затем по формулам (16) находятся амплитуда ВГВ и волновой поток импульса, а по формулам (13) можно определить волновое ускорение ${{a}_{{w\chi }}}$ вдоль оси χ и полный волновой приток тепла εw, которые нужны для учета динамического и теплового воздействия гравитационных волн в атмосферных динамических моделях.

Рассмотрение выражения для εw в (13) показывает, что первое слагаемое в правой части всегда положительно, в то время, как второе слагаемое может стать отрицательным в областях уменьшения awχ с высотой. Поэтому, волновой приток тепла εw может стать отрицательным, т.е. диссипирующие ВГВ могут приводить к локальному охлаждению атмосферы, что более типично для высот более 100 км [17–19]. Модель также позволяет оценить эффективную скорость вертикального волнового потока массы

(19)
${{w}_{{wm}}} = \frac{{\left\langle {\rho {\kern 1pt} 'w{\kern 1pt} '} \right\rangle }}{{{{\rho }_{0}}}} = \frac{{\omega mU_{w}^{2}}}{{2c_{s}^{2}({{m}^{2}} + {{\Gamma }^{2}})}}\left( {1 - \frac{{c_{\chi }^{2}}}{{c_{s}^{2}}}} \right).$

4. СЛУЧАЙНЫЕ ВОЛНОВЫЕ ИСТОЧНИКИ

Мезомасштабные гидродинамические источники ВГВ можно рассматривать случайно распределенными внутри атмосферы. Можно предположить, что случайные элементарные волновые источники излучают волновые компоненты со случайными частотами σ, горизонтальными фазовыми скоростями c и азимутами φ. Наложение волновых гармоник, распространяющихся от различных источников создает “волновой шум”. Для выбранного статистического ансамбля ВГВ гармоник с σ = σi, c = cj и φ = φk можно рассчитать набор значений любого волнового параметра Ψijk = Ψ(σi, cj, φk), тогда среднее значение этого параметра находится по формуле

(20)
${{\Psi }_{0}} = \sum\limits_{i,j,k} {{{\Psi }_{{ijk}}}P({{\sigma }_{i}},{{c}_{j}},{{\varphi }_{k}}),} $
где P(σi, cj, φk) – вероятность того, что волновая гармоника имеет $\sigma \in \left[ {{{\sigma }_{i}},{{\sigma }_{{i + 1}}}} \right),$ $c \in \left[ {{{c}_{j}},{{c}_{{j + 1}}}} \right)~$ и $~\varphi \in \left[ {{{\varphi }_{k}},{{\varphi }_{{k + 1}}}} \right),$ причем

(21)
$\sum\limits_{i,j,k} {P({{\sigma }_{i}},{{c}_{j}},{{\varphi }_{k}}) = 1.} $

В предположении однородности плотности вероятности распределений σ, c и φ и их статистической независимости можно получить

(22)
$P({{\sigma }_{i}},{{c}_{j}},{{\varphi }_{k}}) = \frac{{d{{\sigma }_{i}}}}{{\Delta \sigma }}\frac{{d{{c}_{j}}}}{{\Delta c}}\frac{{d{{\varphi }_{k}}}}{{\Delta \varphi }},$
где dσi = σi +1– σi; dcj = cj + 1– cj; dφk = φk + 1– φk, а Δσ, Δc и Δφ – полные диапазоны изменения соответствующих параметров. Решая уравнения (4) или (15) для набора значений рассматриваемых параметров и используя (20), можно получить средние значения волновых характеристик, которые создаются моделируемым спектром гармоник ВГВ. Сила волновых источников s в (14) также может зависеть от σ, c и φ. Наиболее простым предположением является разделение спектров ВГВ по указанным переменным, когда
(23)
$\begin{gathered} s(\sigma ,c,\varphi ,{{v}_{{0\chi }}},N) = S({{v}_{{0\chi }}},N){{F}_{\sigma }}(\sigma ){{F}_{c}}(c){{F}_{\varphi }}(\varphi ), \\ {{F}_{\sigma }}(\sigma ) = {1 \mathord{\left/ {\vphantom {1 {[1 + {{{({\sigma \mathord{\left/ {\vphantom {\sigma {{{\sigma }_{0}}}}} \right. \kern-0em} {{{\sigma }_{0}}}})}}^{\eta }}];}}} \right. \kern-0em} {[1 + {{{({\sigma \mathord{\left/ {\vphantom {\sigma {{{\sigma }_{0}}}}} \right. \kern-0em} {{{\sigma }_{0}}}})}}^{\eta }}];}} \\ {{F}_{c}}(c) = {1 \mathord{\left/ {\vphantom {1 {[1 + {{{({c \mathord{\left/ {\vphantom {c {{{c}_{1}}}}} \right. \kern-0em} {{{c}_{1}}}})}}^{\xi }} + {{{({{{{c}_{2}}} \mathord{\left/ {\vphantom {{{{c}_{2}}} c}} \right. \kern-0em} c})}}^{\zeta }}]}}} \right. \kern-0em} {[1 + {{{({c \mathord{\left/ {\vphantom {c {{{c}_{1}}}}} \right. \kern-0em} {{{c}_{1}}}})}}^{\xi }} + {{{({{{{c}_{2}}} \mathord{\left/ {\vphantom {{{{c}_{2}}} c}} \right. \kern-0em} c})}}^{\zeta }}]}}, \\ \end{gathered} $
где σ0, c1, c2 и η, ξ, ζ – константы. Следует отметить, что независимое задание частоты σ и горизонтальной фазовой скорости c не противоречит дисперсионному уравнению теории ВГВ [16], которое содержит также вертикальное волновое число m. Это уравнение используется в виде (8) для определения m для каждой спектральной моды с заданными значениями σ и c. Функция Fσ убывает при больших σ, а функция Fc при малых и больших значениях c. Такое поведение типично для турбулентных [23] и волновых [24] атмосферных течений. Первая формула в (23) содержит азимутальную функцию, для которой можно использовать следующее выражение, зависящее от азимута направления горизонтальной оси χ:
(24)
${{F}_{\varphi }}(\varphi ) = [1 + {{B}_{1}}{{({{{{v}_{{0\chi }}}} \mathord{\left/ {\vphantom {{{{v}_{{0\chi }}}} {{{V}_{0}}}}} \right. \kern-0em} {{{V}_{0}}}})}^{2}}](1 + {{{{B}_{2}}{{v}_{{0\chi }}}} \mathord{\left/ {\vphantom {{{{B}_{2}}{{v}_{{0\chi }}}} {{{V}_{0}}}}} \right. \kern-0em} {{{V}_{0}}}}),$
где V0 – модуль горизонтального среднего ветра, B1 и B2 – константы. Выражение в квадратных скобках (24) соответствует эллипсу с главной осью направленной вдоль вектора среднего ветра. Второй множитель в (24) учитывает возможную асимметрию в амплитудах ВГВ, излучаемых вдоль и навстречу среднему ветру. В соответствии с наблюдениями можно ожидать, что сила гидродинамических волновых источников может зависеть от V0 и от устойчивости температурного профиля, который характеризуется частотой Брента–Вяисяля N. Поэтому в (23) используется простая параметризвция
(25)
$S({{V}_{0}},N) = {{{{S}_{0}}V_{0}^{n}} \mathord{\left/ {\vphantom {{{{S}_{0}}V_{0}^{n}} {{{N}^{l}}}}} \right. \kern-0em} {{{N}^{l}}}},$
где S0, n и l – константы. Описываемая схема позволяет также учитывать ВГВ, входящие через нижнюю границу модели. В этом случае необходимо задать в (18) отличные от нуля граничные значения Fmb для всех спектральных составляющих. При этом распределение Fmb по частотам и горизонтальным фазовым скоростям можно аппроксимировать функциями типа Fσ(σ) и Fc(c) в (23).

Уравнения (15) используют для каждой спектральной гармоники ВГВ свою систему координат с горизонтальной осью χ, направленной по азимуту распространения волны φ, который отсчитывается по часовой стрелке от северного направления. Компонента средней скорости вдоль этого направления

(26)
${{v}_{{0\chi }}} = {{u}_{0}}\sin \varphi + {{v}_{0}}\cos \varphi ,$
где u0 и v0 – компоненты средней скорости вдоль горизонтальных осей x и y, направленных на восток и на север, соответственно. В результате решения (15) получаются значения Fm, awχ и U, направленные вдоль осей χ разных для различных азимутов распространения спектральных составляющих ВГВ. Поэтому, перед осреднением по (20) необходимо вычислить компоненты волновых характеристик вдоль осей x и y:

(27)
$\begin{gathered} {{F}_{{mx}}} = {{F}_{m}}\sin \varphi ,\,\,\,\,{{a}_{{wx}}} = {{a}_{{w\chi }}}\sin \varphi ,\,\,\,\,{{U}_{x}} = U\sin \varphi ; \\ {{F}_{{my}}} = {{F}_{m}}\cos \varphi ,\,\,\,\,{{a}_{{wy}}} = {{a}_{{w\chi }}}\cos \varphi ,\,\,\,\,{{U}_{y}} = U\cos \varphi . \\ \end{gathered} $

5. ФОНОВЫЕ ТЕМПЕРАТУРА И ВЕТЕР

Для интегрирования уравнения (15) методом (17) требуется задание вертикальных профилей средних (фоновых) температуры и ветра. В настоящем исследовании расчеты выполнены для состояний атмосферы над российскими пунктами Звенигород (56° с.ш., 37° в.д.), Торы (52° с.ш., 103° в.д.) и Маймага (63° с.ш., 130° в.д.), где проводятся регулярные наблюдения ночной эмиссии гидроксила OH. Распределения фоновой температуры в различные месяцы для среднего значения потока солнечного радиоизлучения F10.7 = 150 sfu построены с использованием стандартной модели NRLMSISE-00 [25]. Фоновые значения зональной и меридиональной компонент ветра задаются согласно модели горизонтального ветра HWM14 [26]. Примеры вертикальных профилей температуры и ветра для января и июля приведены на рис. 1. Видно, что в различных географических пунктах профили несколько различаются между собой.

Рис. 1.

Вертикальные профили фоновой температуры в K (а), зонального (б) и меридионального (в) ветра в м/с в январе (слева) и в июле (справа) для координат пунктов наблюдений ночных свечений Маймага – 1, Торы – 2 и Звенигород – 3.

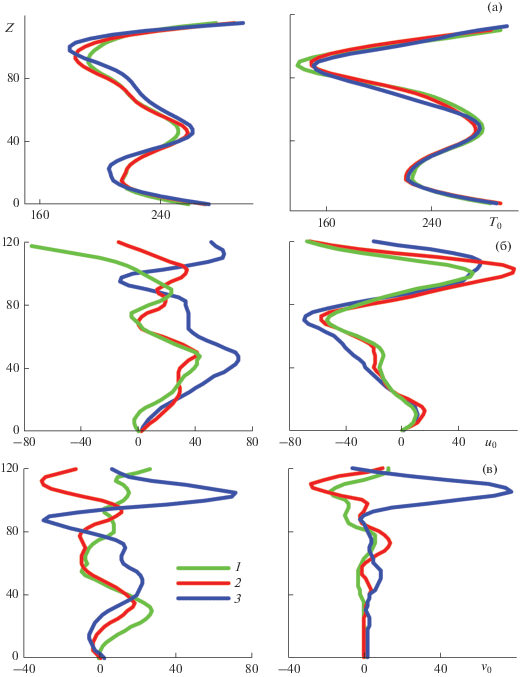
На левом рис. 1б до высот 90–100 км в январе зональный ветер направлен на восток с максимумом до 70 м/с на высотах около 50 км. Скорость этого струйного течения больше на станции Звенигород по сравнению с Торами и Маймагой. На правом рис. 1б на высотах 15–20 км происходит разворот зонального ветра, который до высот около 80 км направлен на запад и достигает максимальных значений (до –70 м/с) на высотах около 70 км. Направление меридиональной компоненты фонового ветра на рис. 1в более изменчиво на разных станциях.

Различия вертикальных профилей на разных станциях в разные месяцы года (см. рис. 1) приводит к различиям сезонных вариаций фоновых полей на фиксированных высотах в разных географических пунктах, которые изображены на рис. 2.

Рис. 2.

Сезонные вариации фоновой температуры в K (слева), зонального (в середине) и меридионального (справа) ветра в м/с на высотах 87, 75, 50, 15 км (а–г) для координат пунктов наблюдений ночных свечений Маймага – 1, Торы – 2 и Звенигород – 3.

На левых графиках рис. 2а средняя температура летом максимальна ниже 50–60 км и минимальна на больших высотах. Средние графики рис. 2б и 2в показывают максимальные значения ветров, направленных на запад в июле и направленных на восток в зимние месяцы. На высоте ночного свечения ОН 87 км в мае – июле происходит разворот зонального ветра с восточного на западный, причем сроки этого разворота в разных географических пунктах могут различаться (см средний график рис. 2а).

Формулы (13) содержат скорость диссипации ВГВ, Nd, из-за турбулентной и молекулярной вязкости и теплопроводности, ионного трения и радиационного теплообмена. Для наших расчетов используются вертикальные профили скорости затухания ВГВ за счет радиационного теплообмена, согласно [15]. Ионное сопротивление рассчитывается с использованием международной модели ионосферы IRI-86 для изучаемых географических пунктов при умеренной солнечной активности [27]. Один из основных механизмов диссипации ВГВ в средней атмосфере – мелкомасштабная турбулентность. Она может генерироваться при разрушении волн из-за динамической и конвективной неустойчивости [28]. Выше уровня разрушения, на котором ВГВ становятся неустойчивыми, коэффициент турбулентной диффузии, генерируемый волной, рассчитывается с использованием полуэмпирической модели [29].

Авторы [30] предположили существование гипотетических неустойчивостей ВГВ, которые могут обеспечивать плавный рост турбулентной вязкости от минимума в стратосфере до больших значений, соответствующих насыщенным ВГВ выше уровня неустойчивости волны. Одним из возможных механизмов такой дополнительной турбулентности может быть нелинейное разрушение первичных ВГВ в спектр нерегулярных вторичных гармоник [31]. На высотах меньших уровня разрушения мы используем формулу для эффективного коэффициента турбулентности, создаваемой спектром нерегулярных вторичных гармоник, полученную в [32].

В нижней атмосфере амплитуды ВГВ и генерация турбулентности волнами могут быть очень малыми. Поэтому предполагается наличие других источников, обеспечивающих некоторый фоновый уровень турбулентной диффузии K0, который имеет максимумы ~10 м2/с в приземном слое и на высотах около 100 км, а также минимум ~0.1 м2/с в стратосфере.

При распространении спектра гармоник ВГВ, некоторые из них (распространяющиеся в направлении среднего ветра с небольшими горизонтальными фазовыми скоростями) могут достигать критических уровней, где ω → 0. В этом случае, в (8) cχ → 0 и m → ∞, что ведет к сильной диссипации волны. С другой стороны, ВГВ, распространяющиеся навстречу среднему ветру, могут достичь высоты, на которой ω → N. Согласно (8), вблизи этого уровня m2 становится отрицательным и можно ожидать сильное отражение энергии волны [33]. В наших расчетах все ВГВ, которые достигают критических уровней и уровней, отражения, удаляются из спектра идущих вверх волновых гармоник выше этих уровней.

Указанные на рис. 1 и 2 различия фоновых полей ветра и температуры могут приводить к различиям условий распространения гармоник ВГВ в средней атмосфере и могут влиять на сезонные вариации интенсивности ВГВ в различных географических пунктах, которые исследуются ниже с помощью численного моделирования.

6. РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ ВГВ

Система уравнений (15)–(17) решается численно для фоновой атмосферы, представляющей различные месяцы года в местах проведения наблюдений ночной эмиссии гидроксила (см. п. 5). Вертикальный шаг интегрирования Δz = 250 м.

Уравнения решаются для набора из 50 × 50 × 12 гармоник, моделирующих спектр ВГВ, где множители обозначают количество волн с различными частотами, горизонтальными фазовыми скоростями и азимутами, соответственно. Параметры ВГВ охватывают диапазоны частот σ = 3 × 10–4–7 × 10–3 рад/с, горизонтальных фазовых скоростей с = 5–100 м/с, и азимутов распространения φ = 0–360°. Шаги изменения этих параметров dσi, dcj и dφk в (22) выбраны постоянными вдоль координат ln(σ), ln(c) и φ. Значения констант, определяющих спектральные распределения источников волн в (23) – (25), приняты следующими: σ0 = = 10–4 рад/с, η = 5/6, с1 = 10 м/с, β = 1, с2 = 4 м/с, γ = 1.5, B1 = 0.04, B2 = 0, n = 2 and l = 0. Авторы [14] показали, что такой набор параметров обеспечивает соответствие рассчитанных сезонных вариаций интенсивности ВГВ с наблюдениями на японским МСТ радаре в средней атмосфере.

Выбор диапазона достаточно больших значений с = 5–100 м/с определяется желанием рассмотреть в данном исследовании моды ВГВ, подвергающиеся слабой диссипации в средней атмосфере и способные распространяться из нижней атмосферы до больших высот. Следует отметить, что вблизи критических уровней, когда ${{v}_{{0\chi }}}$ → с, в (8) cχ → 0 и m2 → ∞. Таким образом, короткими в вертикальном направлении и неустойчивыми могут стать даже рассматриваемые ВГВ со сравнительно большими горизонтальными фазовыми скоростями при их распространении в направлении среднего ветра. Коэффициенты турбулентной диффузии, создаваемые в зонах сдвиговой и конвективной неустойчивости рассматриваемых мод ВГВ вычисляются по схеме, предложенной в [29]. Дополнительная диссипация, вызванная каскадом вторичных нелинейных волн учитывается с применением формул из работы [32].

Рисунок 3 демонстрирует рассчитанные с применением (20) вертикальные профили средних стандартных отклонений вариаций зональной, Ux, меридиональной, Uy, и горизонтальной, Uh = ${{\left( {U_{x}^{2} + U_{y}^{2}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$, скорости, которые создаются рассматриваемым спектром гармоник ВГВ, распространяющихся из нижней атмосферы в верхнюю в фоновых полях температуры и ветра, показанных для января и июля на рис. 1. Изменения указанных величин с высотой зависят от интенсивности динамических источников ВГВ, параметризуемых соотношением (25) и от скорости диссипации волн, учитывающихся в модели (см. пп. 2–4).

Рис. 3.

Вертикальные профили стандартных отклонений горизонтальной скорости (а), и ее зональной (b) и меридиональной (c) компонент в м/с, создаваемых спектром ВГВ в январе (слева) и в июле (справа), для координат пунктов наблюдений ночных свечений Маймага – 1, Торы – 2 и Звенигород – 3.

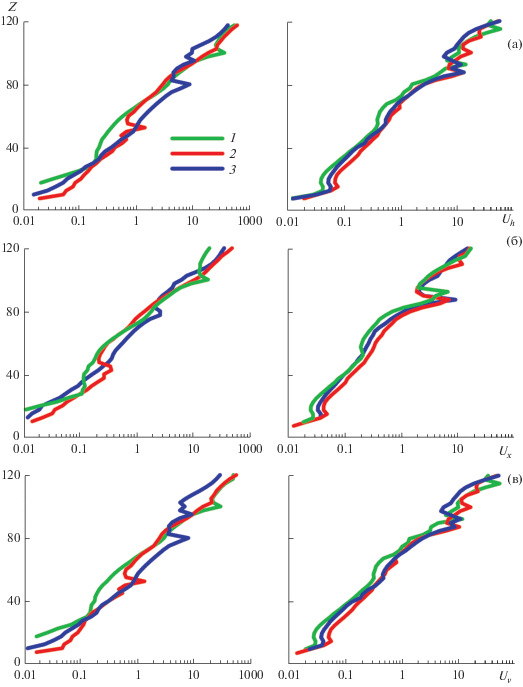
Различия вертикальных профилей фоновых полей на станциях Звенигород, Маймага и Торы на рис. 1 приводят к различиям вертикальных профилей стандартных отклонений волновых вариаций горизонтальной скорости (характеризующих интенсивность ВГВ) на рис. 3. Это приводит к различиям сезонных вариаций интенсивности ВГВ в различных географических пунктах, которые показаны на рис. 4.

Рис. 4.

Сезонные вариации модельных стандартных отклонений горизонтальной скорости (слева), и ее зональной (в середине) и меридиональной (справа) компонент в м/с, создаваемых спектром ВГВ на высотах 87, 75, 50, 15 км (а–г) для координат пунктов наблюдений ночных свечений Маймага – 1, Торы – 2 и Звенигород – 3.

Характер сезонных вариаций на рис. 4 изменяется с увеличением высоты. На высоте слоя ночной эмиссии ОН 87 км (рис. 4а) видна тенденция к формированию максимумов интенсивности ВГВ в весенние, летние и осенние месяцы, причем величины и положение этих максимумов могут различаться в разных географических пунктах. Кроме того, анализ средних и правых графиков на рис. 4 показывает, что относительные величины и сезонные вариации могут различаться для стандартных отклонений волновых возмущений зональной и меридиональной компонент скорости. Это может быть связано с различиями сезонных вариаций зональной и меридиональной компонент фонового ветра на рис. 2.

Авторы [12] исследовали сезонные вариации мезомасштабных возмущений вращательной температуры ОН и оценили амплитуды ВГВ вблизи мезопаузы. Рис. 2 статьи [12] для Звенигорода показывает наличие максимумов интенсивности мезомасштабных возмущений температуры в марте, июне–июле и в ноябре, причем весенний и осенний максимумы более отчетливо проявляются в области наибольших периодов возмущений τ ~ ~ 4–11 ч, которые исследовались в указанной работе. Для станции Торы рис. 2 статьи [12] показывает главные максимумы интенсивности мезомасштабных вариаций температуры в мае и в декабре–январе.

Описанные различия сезонных вариаций мезомасштабных возмущений температуры в Звенигороде и Торах соответствуют рис. 4а для средней высоты слоя ночного свечения ОН 87 км. Сезонные вариации Uh в Звенигороде имеют три выраженных максимума весной, летом и осенью (см. левый график рис. 4). На станции Торы осенний максимум Uh на левом рис. 4 имеет величину меньшую, чем значения Uh в первой половине года. Общее сходство сезонных вариаций модельных амплитуд ВГВ и наблюдаемой интенсивности мезомасштабных возмущений температуры в слое ночного свечения OH в Звенигороде и Торах является дополнительным свидетельством того, что важной причиной возмущений температуры вблизи мезопаузы могут быть ВГВ, распространяющиеся из нижней атмосферы. Анализ сезонных вариаций мезомасштабных возмущений вращательной температуры ОН проводился также на станции Маймага [13]. Однако наличие светлых ночей на широте 63° с.ш. приводит к невозможности наблюдения ночной эмиссии ОН в летние месяцы, что не позволяет получить полную картину сезонных вариаций.

В расчетах, приведенных на рис. 3 и 4 использованы значения n = 2 и l = 0 в параметризации (25) зависимости активности атмосферных волновых источников от среднего ветра и частоты Брента–Вяисяля. Расчеты для значений n = 1 и n = 3 показали, что увеличение n (усиление зависимости волновых источников от фонового ветра) приводит к увеличению модельных амплитуд ВГВ на высоте 87 км в зимние месяцы по сравнению с летним сезоном на всех анализируемых станциях. Расчеты для l = 2 (при усилении зависимости волновых источников от статической устойчивости атмосферы) привели к увеличению летних амплитуд ВГВ по сравнению с зимним сезоном. Следует отметить, что параметризация волновых источников (25) является грубым приближением и способна описать только общие тенденции генерации ВГВ при изменениях среднего ветра и устойчивости атмосферы. Для совершенствования модели распространения спектра гармоник ВГВ требуется разработка более точных параметризаций волновых источников в атмосфере.

Изложенные выше результаты численного моделирования и сравнения с результатами оптических наблюдений в МНТ области показывают, что интенсивность мезомасштабных возмущений вращательной температуры ОН вблизи мезопаузы может быть связана с интенсивностью ВГВ, распространяющихся из нижней атмосферы и зависит от профилей фоновых характеристик средней атмосферы на пути распространения волновых пакетов. Применяемая модель ВГВ использует линеаризованные уравнения гидродинамики, поэтому она может адекватно описывать только волны малой амплитуды. Случаи, когда амплитуды ВГВ становятся сравнимы с их горизонтальными фазовыми скоростями, требуют использования нелинейных волновых моделей.

ЗАКЛЮЧЕНИЕ

В данной статье описана модернизированная численная модель распространения набора спектральных гармоник ВГВ в неоднородной атмосфере от земной поверхности до нижней термосферы. Модель включает простую параметризацию зависимости активности динамических источников ВГВ от скорости ветра в струйных течениях и от статической устойчивости фонового поля температуры. Учтена диссипация ВГВ из-за турбулентной вязкости и теплопроводности, радиационного теплообмена и ионного трения в нижней ионосфере. Выполнено численное моделирование распространения спектра ВГВ в фоновых полях ветра и температуры, соответствующих координатам станций Звенигород (56° с.ш., 37° в.д.), Маймага (63° с.ш., 130° в.д.) и Торы (52° с.ш., 103° в.д.), на которых проводятся систематические наблюдения ночной эмиссии ОН. Рассчитаны сезонные вариации стандартных отклонений возмущений компонент горизонтальной скорости, создаваемых модельным спектром ВГВ.

Показано, что различия вертикальных профилей фоновых полей приводят к различиям сезонных вариаций интенсивности ВГВ в различных географических пунктах. Сезонные вариации модельных амплитуд ВГВ в Звенигороде имеют три выраженных максимума весной, летом и осенью. На станции Торы осенний максимум амплитуд ВГВ имеет величину меньшую, чем значения амплитуд в первой половине года.

Общее сходство сезонных вариаций модельных амплитуд ВГВ и опубликованных наблюдений дисперсии мезомасштабных возмущений вращательной температуры OH в Звенигороде и Торах является дополнительным свидетельством того, что интенсивность мезомасштабных возмущений вращательной температуры ОН вблизи мезопаузы может зависеть от интенсивности ВГВ, распространяющихся из нижней атмосферы, и зависит от профилей фоновых характеристик средней атмосферы на пути распространения волновых пакетов в различные сезоны и в разных географических пунктах.

Список литературы

  1. Шефов Н.Н., Семенов А.И., Хомич В.Ю. Излучение верхней атмосферы– индикатор ее структуры и динамики. М.: ГЕОС, 2006. 741 с.

  2. Krassovski V.I. Infrasonic variations of OH emission in the upper atmosphere // Ann. Géophys. 1972. V. 28. P. 739–746.

  3. Красовский В.И., Потапов Б.П., Семенов А.И., Шефов Н.Н. Внутренние гравитационные волны вблизи мезопаузы. 1. Результаты исследований гидроксильной эмиссии // Полярные сияния и свечение ночного неба / Под ред. Ю.И. Гальперина. М.: Сов. Радио, 1978. № 26. С. 5–29.

  4. Taylor M.J., Hapgood M.A., Rothwell P. Observations of gravity wave propagation in the OI (557.7 nm), Na (589.2 nm) and the near infrared OH nightglow emissions // Planet. Space Sci. 1987. V. 35. № 4. P. 413–427.

  5. Taylor M.J., Hapgood M.A. On the origin of ripple-type wave structure in the OH nightglow emission // Planet. Space Sci. 1990. V. 38. № 11. P. 1421–1430.

  6. Vadas S.L., Taylor M.J., Pautet S.P.-D., Fritts D.C., Liu H.-L. Convection: the likely source of the medium-scale gravity waves observed in the OH airglow layer near Brasilia, Brazil, during the SpreadFEx campaign // Ann. Geophys. 2009. V. 27. P. 231–259.

  7. Nakamura T., Higashikawa A., Tsuda T., Matsushita Y. Seasonal variations of gravity wave structures in OH airglow with a CCD imager at Shigaraki // Earth Planets Space. 1999. V. 51. P. 897–906.

  8. Gavrilov N.M., Shiokawa K., Ogawa T. Seasonal variations of medium-scale gravity wave parameters in the lower thermosphere obtained from SATI observations at Shigaraki, Japan // J. Geophys. Res. 2002. V. 107. № D24. P. 4755. https://doi.org/10.1029/2001JD001469

  9. Перминов В.И., Семенов А.И., Медведева И.В., Перцев Н.Н. Изменчивость температуры в области мезопаузы по наблюдениям гидроксильного излучения на средних широтах // Геомагнетизм и аэрономия. 2014. Т. 54. № 2. С. 246–256.

  10. Медведева И.В., Белецкий А.Б., Перминов В.И., Перцев Н.Н. Вариации температуры атмосферы на высотах мезопаузы и нижней термосферы в периодах стратосферных потеплений по данным наземных и спутниковых измерений в различных долготных секторах // Современные проблемы дистанционного зондирования Земли из космоса. 2011. Т. 8. № 4. С. 127–135.

  11. Перцев Н.Н., Андреев А.Б., Мерзляков Е.Г., Перминов В.И. Мезосферно-термосферные проявления стратосферных потеплений: совместное использование спутниковых и наземных измерений // Современные проблемы дистанционного зондирования Земли из космоса. 2013. Т. 10. № 1. С. 93–100.

  12. Popov A.A., Gavrilov N.M., Perminov V.I., Pertsev N.N., Medvedeva I.V. Multi-year observations of mesoscale variances of hydroxyl nightglow near the mesopause at Tory and Zvenigorod // J. Atmos. Solar-Terr. Phys. 2020. V. 205. P. 105311. https://doi.org/10.1016/j.jastp.2020.105311

  13. Gavrilov N.M., Popov A.A., Perminov V.I., Pertsev N.N., Medvedeva I.V., Ammosov P.P., Gavrilyeva G.A., Koltov-skoi I.I. Mesoscale variations of hydroxyl rotational temperature from observations at Russian sites // Proc. SPIE. 2020. V. 11560. P. 115607W. https://doi.org/10.1117/12.2574795 2020.

  14. Gavrilov N.M., Fukao S. A comparison of seasonal variations of gravity wave intensity observed by the MU radar with a theoretical model // J. Atmos. Sci. 1999. V. 56. P. 3485–3494.

  15. Гаврилов Н.М. Параметризация динамического и теплового воздействия установившихся внутренних гравитационных волн на среднюю атмосферу // Изв. РАН. Физика атмосферы и океана. 1989. Т. 25. № 3. С. 271–278.

  16. Gossard E.E., Hooke W.H. Waves in the atmosphere. Amsterdam-Oxford-New York: Elsevier Sci. Publ. Co. 1975. 456 p.

  17. Yiğit E., Medvedev A.S. Heating and cooling of the thermosphere by internal gravity waves // Geophys. Res. Lett. 2009. V. 36. P. P. L14807. https://doi.org/10.1029/2009GL038507

  18. Medvedev A.S., Klaassen P. Thermal effects of saturating gravity waves in the atmosphere // J. Geophys. Res. 2003. V. 108. № D2, P. 4040. https://doi.org/10.1029/2002JD002504

  19. Akmaev R.A. On the energetics of the mean-flow interactions with thermally dissipating gravity waves // J. Geophys. Res. 2007. V. 112. P. D11125. https://doi.org/10.1029.2006JD007908

  20. Gavrilov N.M. Parameterization of momentum and energy depositions from gravity waves generated by tropospheric hydrodynamic sources // Ann. Geophys. 1997. V. 15 P. 1570–1580.

  21. Gough D. An elementary introduction to the JWKB approximation // Astron Nachr. 2006. V. AN999. № 88. P. 789–801.

  22. Гаврилов Н.М., Швед Г.М. Затухание акустико-гравитацтонных волн в анизотропно турбулизованной излучающей атмосфере // Изв. АН СССР, Физика атмосферы и океана. 1975. Т. 11. № 7. С. 681–689.

  23. Монин А.С., Яглом А.М. Статистическая гидромеханика, М.: Наука. Физматгиз, ч. 2. 1967. 722 с.

  24. Fritts D.C., Alexander M.J. Gravity wave dynamics and effects in the middle atmosphere // Rev. Geophys. 2003. V. 41. № 1. P. 1003. https://doi.org/10.1029/2001RG000106

  25. Picone J.M., Hedin A.E., Drob D.P., Aikin A.C. NRLMSISE-00 empirical model of the atmosphere: Statistical comparisons and scientific issues. // J. Geophys. Res., 2002. V. 107. № A12. P. 1468. https://doi.org/10.1029/2002JA009430

  26. Drob D.P., Emmert J.T., Meriwether J.W. et al. An update to the Horizontal Wind Model (HWM): The quiet time thermosphere // Earth and Space Sci. 2015. V. 2. № 7. P. 301–309. https://doi.org/10.1002/2014EA000089

  27. Bilitza D. IRI 86 and MSIS 86 models updated // EOS. 1987. V. 68. № 25. P. 595–595. https://doi.org/10.1029/EO068i025p00595-02

  28. Lindzen R.S. Turbulence and stress owing to gravity wave and tidal breakdown // J. Geophys. Res. 1981. V. 86. № CI0. P. 9707–9714.

  29. Gavrilov N.M., Yudin V.A. Model for coefficients of turbulence and effective Prandtl number produced by breaking gravity waves in the upper atmosphere // J. Geophys. Res. 1992. V. 97. № D7. P. 7619–7624.

  30. Lindzen R.S., Forbes J. Turbulence originating from convectively stable internal waves // J. Geophys. Res. 1983. V. 88. P. 6549–6553.

  31. Weinstock J. Theoretical relation between momentum deposition and diffusion caused by gravity waves // Geophys. Res. Lett. 1982. V. 9. № 8. P. 863–865. https://doi.org/10.1029/GL009i008p00863

  32. Розенфельд С.Х. О затухании внутренних гравитационных волн в атмосфере из-за генерации вторичных гармоник // Изв. АН СССР, Физика атмосферы и океана. 1983. Т. 19. № 9. С. 1011–1019.

  33. Medvedev A.S., Yi ̆git E. Gravity waves in planetary atmospheres: Their effects and parameterization in global circulation models // Atmosphere. 2019. V. 10. P. 531. https://doi.org/10.3390/atmos10090531

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Физика атмосферы и океана

Архивы выпусков Информация о журнале Отправить рукопись в журнал