Известия РАН. Физика атмосферы и океана, 2022, T. 58, № 3, стр. 344-351

ВВЕДЕНИЕ

Турбулентные образования играют заметную роль в процессах нагрева атмосферы, перераспределении химических составляющих атмосферного воздуха, в разрушении и демпфировании внутренних гравитационных волн (ВГВ), а также в диссипации струйных течений свободной атмосферы. К механизмам, порождающим турбулентность свободной атмосферы, относят два типа неустойчивости воздушных потоков: конвективную и сдвиговую (Кельвина–Гельмгольца). Конвективная неустойчивость является основной причиной образования турбулентности при опрокидывании ВГВ, амплитуда которых растет по мере падения плотности атмосферы с высотой. По достижении некоторого порогового значения [1, 2], волна становится неустойчивой и опрокидывается, образуя “движущиеся” вместе с ней турбулентные области. Сама по себе порожденная волной турбулентность “вморожена” в фоновый атмосферный поток, однако, границы турбулентной зоны следуют за фазой волны, обеспечивающей наиболее благоприятные условия для ее генерации [2, 3]. В этом смысле, можно говорить о “движении” турбулентной области вслед за породившей ее гравитационной волной.

Эффекты, обусловленные “движущейся” турбулентной областью, до настоящего времени не получили должного отражения в научной литературе. Данная работа, вероятно, является первой попыткой промоделировать один из них. В настоящей статье моделируется максимально упрощенная и идеализированная ситуация, когда изолированная турбулентная область движется с постоянной горизонтальной скоростью в горизонтально однородной стационарной атмосфере, без учета породившей ее волны. Т.е. на данном этапе мы рассматриваем “движущуюся” турбулентную область как некоторую данность, не интересуясь ее происхождением. Математическая модель механизма, сопровождающего это движение, представлена в следующем разделе статьи. Третий раздел посвящен обсуждению возможных проявлений результатов действия данного механизма в нижней и средней атмосфере Земли. Выводы представлены в заключительном разделе.

МОДЕЛЬ

Постановка задачи

Пусть турбулентная область толщиной 2h₀ “движется” с горизонтальной скоростью С относительно горизонтально однородного стационарного фонового воздушного потока, чья потенциальная температура линейно растет с высотой. Введем прямоугольную систему координат $(x,z)$, начало которой совпадает с серединой задней границы турбулентной области, так как это показано на рис. 1. В этом случае вертикальный ход потенциальной температуры в фоновом атмосферном потоке будет задан линейной функцией $\bar {\theta }(z) = {{\theta }_{0}} + \beta z$, где $\beta > 0$.

Рис. 1.

Схема, иллюстрирующая положение гипотетической турбулентной области (заштрихованный прямоугольник) и введенной системы координат (x, z) по отношению к набегающему со скоростью C фоновому атмосферному потоку.

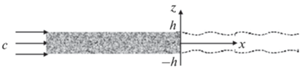
В выбранной системе отсчета фоновый воздушный поток будет набегать на неподвижную турбулентную область с постоянной скоростью С. Для простоты допустим, что она имеет резкие границы, т.е. при пересечении ее передней границы ламинарный фоновый поток превращается в турбулентный, а при выходе из нее (при $x = 0$) вновь становится ламинарным. Принимая во внимание тот факт, что перемешивание воздуха внутри турбулентного слоя устанавливает однородное распределение потенциальной температуры, будем считать, что после прохождения турбулентной зоны устойчиво стратифицированный фоновый атмосферный поток превращается в поток с двумя температурными инверсиями и слоем с почти постоянным значением потенциальной температуры ($\theta (z) \approx {{\theta }_{0}}$) между ними [4]. В этом случае, при выходе воздушного потока из турбулентной зоны (при $x = 0$) отклонение потенциальной температуры от ее фоновых значений будет определяться следующим соотношением:

(1)

$\Delta \theta (z) = {{\theta }_{0}} - \bar {\theta }(z) = \left\{ {\begin{array}{*{20}{c}} { - \beta z,\,\,\,\,{\text{при}}\,\,\,\,\left| z \right| \leqslant {{h}_{0}};} \\ {0,\,\,\,\,\,\,\,{\text{при}}\,\,\,\,\left| z \right| > {{h}_{0}}.} \end{array}} \right.$

Механизм формирования струи

Соотношение (1) показывает, что на воздушный поток, сразу после выхода из турбулентной зоны, действуют встречно направленные силы плавучести: его верхняя часть ($0 < z < {{h}_{0}}$), обладающая отрицательной плавучестью, вдавливается вниз, в то время как его нижняя часть ($ - {{h}_{0}} < z < 0$) выталкивается положительной плавучестью вверх. В результате, в воздушном потоке, прошедшем через турбулентную зону, возникает компенсирующая сила давления, которая и ускоряет воздушный поток в положительном направлении горизонтальной оси x, формируя локальное струйное течение в направлении противоположном движению турбулентной области (см. рис. 2). Тем самым, мы фактически предполагаем, что динамика воздушного потока, прошедшего через турбулентную область определяется двумя факторами: плавучестью $b = g{{\theta {\kern 1pt} '} \mathord{\left/ {\vphantom {{\theta {\kern 1pt} '} {{{\theta }_{0}}}}} \right. \kern-0em} {{{\theta }_{0}}}}$ и компенсирующим давлением $p{\kern 1pt} '$. Величины $\theta {\kern 1pt} '$ и $p{\kern 1pt} '$ определим как отклонения от фоновых значений потенциальной температуры $\theta {\kern 1pt} ' = \theta - \bar {\theta }$ и гидростатического давления $p{\kern 1pt} ' = p - \bar {p}$.

Рис. 2.

Схематическая иллюстрация механизма ускорения атмосферного потока после прохождения им турбулентной области. Вертикальные пунктирные стрелки, помеченные латинской буквой b, обозначают силы плавучести. Фигурная пунктирная стрелка, помеченная латинской буквой p, обозначает компенсирующее давление. Линии тока атмосферного потока изображены толстыми линиями, проходящими через турбулентную область, обозначенную заштрихованным прямоугольником.

Математическая модель

Для того чтобы построить математическую модель описанного выше физического механизма запишем систему гидродинамических уравнений, используя условие гидростатики $g{{\rho }_{0}} = - {{d\bar {p}} \mathord{\left/ {\vphantom {{d\bar {p}} {dz}}} \right. \kern-0em} {dz}}$ и приближение Буссинеска, полагая при этом, что частота Брента-Вяйсяля $N = {{g\beta } \mathord{\left/ {\vphantom {{g\beta } {{{\theta }_{0}}}}} \right. \kern-0em} {{{\theta }_{0}}}}$. Здесь и далее g – ускорение силы тяжести, ${{\rho }_{0}}$и ${{\theta }_{0}}$ – соответственно, плотность воздуха и потенциальная температура фонового потока при $z = 0$, $\bar {p}$ – гидростатическая составляющая давления.

Учитывая то, что мы рассматриваем случай установившегося стационарного движения, частные производные по времени в левых частях уравнений гидродинамики могут быть отброшены. Кроме того, в правые части уравнений баланса импульса и энергии не будем включать диссипативные члены, описывающие влияние молекулярной и турбулентной вязкости и теплопроводности, заменив их линейным диссипативным членом $ - \alpha b$ в правой части уравнения баланса тепла. Здесь $\alpha $‑коэффициент, величина которого пропорциональна скорости их затухания. С учетом вышесказанного система уравнений, описывающих действие рассматриваемого механизма, выглядит следующим образом:

(2)

$u\frac{{\partial b}}{{\partial x}} + {{N}^{2}}w = - \alpha b,$

(3)

$u\frac{{\partial w}}{{\partial x}} + w\frac{{\partial w}}{{\partial z}} = - \frac{1}{{{{\rho }_{0}}}}\frac{{\partial p{\kern 1pt} '}}{{\partial z}} + b,$

(4)

$u\frac{{\partial u}}{{\partial x}} + w\frac{{\partial u}}{{\partial z}} = - \frac{1}{{{{\rho }_{0}}}}\frac{{\partial p{\kern 1pt} '}}{{\partial x}},$

(5)

$\frac{{\partial u}}{{\partial x}} + \frac{{\partial w}}{{\partial z}} = 0.$

Уравнение (2) представляет собой баланс тепла, уравнения (3) и (4) – баланс импульса по z- и х-оси, соответственно, а уравнение (5) – условие неразрывности несжимаемой среды.

Для того чтобы исключить из этой системы уравнений давление $p{\kern 1pt} '$, будем считать, что влияние диссипативных процессов на динамику потока, описываемого данной системой уравнений, невелико. В силу чего воспользуемся приближенной записью интеграла (соотношения) Бернулли:

(6)

$\begin{gathered} \frac{1}{{{{\rho }_{0}}}}(\bar {p} + p{\kern 1pt} ') + \frac{1}{2}{{u}^{2}} + \frac{1}{2}{{w}^{2}} + \\ + \,\,gz\left( {1 + \frac{{\beta {\kern 1pt} z}}{{{{\theta }_{0}} + \beta {\kern 1pt} z}}} \right) \approx {\text{const,}} \\ \end{gathered} $

в котором ${{\left| {\beta z} \right|} \mathord{\left/ {\vphantom {{\left| {\beta z} \right|} {({{\theta }_{0}} + \beta z)}}} \right. \kern-0em} {({{\theta }_{0}} + \beta z)}} \ll 1$ и $g{{\rho }_{0}} = - {{d\bar {p}} \mathord{\left/ {\vphantom {{d\bar {p}} {dz}}} \right. \kern-0em} {dz}}$. В результате, после дифференцирования соотношения (6), можем записать

(7)

$\frac{1}{{{{\rho }_{0}}}}\frac{{\partial p{\kern 1pt} '}}{{\partial x}} + u\frac{{\partial u}}{{\partial x}} + w\frac{{\partial w}}{{\partial x}} \approx 0,$

(8)

$\frac{1}{{{{\rho }_{0}}}}\frac{{\partial p{\kern 1pt} '}}{{\partial z}} + u\frac{{\partial u}}{{\partial z}} + w\frac{{\partial w}}{{\partial z}} \approx 0.$

Полагая, что

(9)

$\left| {\frac{{\partial {{u}^{2}}}}{{\partial x}}} \right| \gg \left| {\frac{{\partial {{w}^{2}}}}{{\partial x}}} \right|,$

соотношение (7) приведем к виду

(10)

$ - \frac{1}{{{{\rho }_{0}}}}\frac{{\partial p{\kern 1pt} '}}{{\partial x}} \approx u\frac{{\partial u}}{{\partial x}}.$

При этом уравнение (4) превратится в

(11)

$w\frac{{\partial u}}{{\partial z}} = 0.$

Из последнего уравнения следует, что горизонтальная скорость потока, прошедшего через турбулентную зону, постоянна в любом его вертикальном сечении. Подставляя (8) в (3), с учетом (11), получим

(12)

$u\frac{{\partial w}}{{\partial x}} = b.$

Таким образом, после исключения из рассматриваемой системы уравнений (2)–(5) компенсирующего давления $p{\kern 1pt} '$, она превращается в систему трех уравнений: баланса тепла (2), неразрывности (5) и уравнения (12).

Исходя из соотношения (1) мы можем записать начальное условие (при х = 0) для плавучести

(13)

$b(0,z) = - {{N}^{2}}z,$

а из условия “вмороженности” турбулентности в фоновый поток следуют начальные условия (при х = 0) для горизонтальной u и вертикальной w скорости:

(14)

$u(0,z) = C,$

(15)

$w(0,z) = 0.$

В ПРИЛОЖЕНИИ показано, что решение системы уравнений (2), (5), (12) с начальными условиями (13)–(15) сводится к решению обыкновенного нелинейного дифференциального уравнения второго порядка (П14) относительно безразмерной горизонтальной скорости $U({x \mathord{\left/ {\vphantom {x C}} \right. \kern-0em} C})$. С помощью обратных замен $U({x \mathord{\left/ {\vphantom {x C}} \right. \kern-0em} C}) = {{u(x)} \mathord{\left/ {\vphantom {{u(x)} С}} \right. \kern-0em} С}$ и $x = C\tau $ уравнение (П14) преобразуем к уравнению

(16)

$u\frac{{{{d}^{2}}u}}{{d{{x}^{2}}}} + \alpha {\kern 1pt} {\kern 1pt} \frac{{du}}{{dx}} + {\kern 1pt} {{N}^{2}}\ln \left( {\frac{u}{{eC}}} \right) = 0,$

с начальными условиями:

(17)

${{\left. u \right|}_{{x = 0}}} = C,$

(18)

${{\left. {\frac{{du}}{{dx}}} \right|}_{{x = 0}}} = 0.$

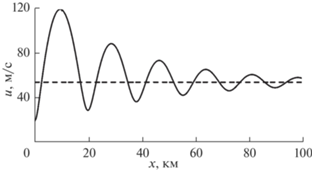
Численное интегрирование задачи Коши (16), (17), (18), с использованием метода Рунге–Кутта 4-го порядка при $N = $ 0.02 с^–1, $\alpha = $ 0.003 с^–1, ${{h}_{0}} = $ = 500 м, было проведено на интервале $0 \leqslant x \leqslant 100$ км для $C = $20 м/с. Результаты, приведенные на рис. 3, показывают, что уравнение (16) описывает поток с нелинейными пульсациями скорости. По мере роста величины х, амплитуда нелинейных пульсаций горизонтальной скорости снижается, и пульсации превращаются в гармонические затухающие колебания, приводящие к формированию плоской струи, с постоянным значением скорости еС. Последний процесс описывается соответствующим линейным дифференциальным уравнением затухающих гармонических колебаний:

(19)

$\frac{{{{d}^{2}}u{\kern 1pt} '}}{{d{{x}^{2}}}} + \frac{\alpha }{{eC}}{\kern 1pt} {\kern 1pt} \frac{{du{\kern 1pt} '}}{{dx}} + \,{\kern 1pt} {{\left( {\frac{N}{{eC}}} \right)}^{2}}u{\kern 1pt} ' = 0,$

Рис. 3.

График зависимости $u(x)$ горизонтальной скорости плоской струи, сформированной атмосферным потоком, набегающим со скоростью С = 20 м/с на турбулентную область. Пунктирная линия соответствует предельному значению скорости плоской струи еС ≈ 54 м/с.

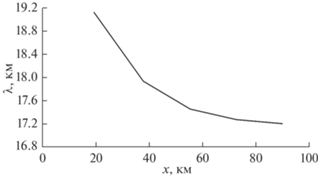
которое следует из уравнения (16) при |u'| = = $\left| {u - eC} \right| \ll eC$. Пространственный период гармонических колебаний ${{\lambda = 2\pi еС} \mathord{\left/ {\vphantom {{\lambda = 2\pi еС} N}} \right. \kern-0em} N}$ является предельным значением для монотонно убывающего пространственного периода нелинейных пульсаций скорости (см. рис. 4). Учитывая то, что уравнение (16) записано в системе отсчета, связанной с турбулентной областью, движущейся со скоростью C относительно фоновой атмосферы, результирующая скорость плоской струи относительно фоновой атмосферы будет равна $(e - 1)C$.

Рис. 4.

График зависимости пространственного периода $\lambda (x)$ нелинейных пульсаций скорости плоской струи, соответствующий зависимости $u(x)$, приведенный на рис. 3.

Воспользовавшись соотношением

(20)

$w(x,z) = - z\frac{{du}}{{dx}},$

которое следует из уравнения (П6), запишем выражение для линий тока в плоской струе

(21)

$z(x) = \frac{C}{{u(x)}}{{z}_{0}},$

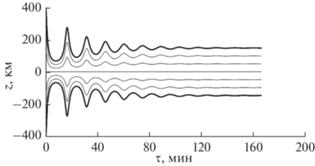
где ${{z}_{0}} = z(x = 0)$ – вертикальная координата точки выхода данной линия тока из турбулентной области. Линии тока, рассчитанные для $C = $ 20 м/с, показаны на рис. 5. Видно, что линии тока симметричны относительно горизонтальной оси симметрии турбулентной области, что объясняется нечетным характером функции $w(x,z)$ по переменной z. Следует также отметить, что из соотношения (21) следует постоянство интегральной величины потока воздуха $2{{\rho }_{0}}C{{h}_{0}}$ (или горизонтального импульса) в любом вертикальном сечении струи. Чем сильнее сжимают струю силы плавучести, тем выше ее скорость.

Рис. 5.

Линии тока в плоской струе, сформированной атмосферным потоком, набегающим со скоростью С = 20 м/с на турбулентную область, толщиной $2h = $ 1000 м. Прерывистые прямые линии обозначают границы плоской струи при $x \to \infty $.

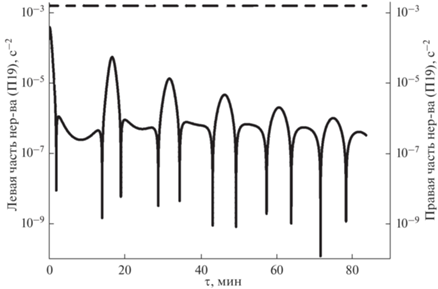
В заключение данного раздела напомним, что условием применимости уравнения (16) является выполнение условия, накладываемого неравенством (9), которое в ПРИЛОЖЕНИИ было преобразовано в неравенство (П19). Результат проверки применимости уравнения (16) для ${{h}_{0}} = $ 500 м и $C = $ 20 м/с приведен на рис. 6, где изображены графики левой и правой частей неравенства (П19). Учитывая, что правая часть неравенства (П19) не зависит ни от C, ни от ${{h}_{0}}$, можно утверждать, что это неравенство будет также справедливо для всех ${{h}_{0}}$ и C, удовлетворяющих условию ${C \mathord{\left/ {\vphantom {C {{{h}_{0}} > }}} \right. \kern-0em} {{{h}_{0}} > }}{{10}^{{ - {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}$ с^–1.

Рис. 6.

Проверка условия применимости (9) уравнения (16) для турбулентной области толщиной $2h = $ 1000 м и скорости фонового атмосферного потока С = 20 м/с. Прерывистая прямая линия соответствует значению левой части неравенства (9). Непрерывная линия соответствует значениям правой части неравенства (9) при всех $0 \leqslant x \leqslant 100$ км.

ОБСУЖДЕНИЕ И СРАВНЕНИЕ С НАБЛЮДЕНИЯМИ

В данной статье затронут относительно новый вопрос – как влияет на характеристики фонового атмосферного потока перемещающаяся относительно него турбулентная область? В качестве ответа был предложен следующий физический механизм: (i) благодаря турбулентному перемешиванию, в воздушном потоке, прошедшем через турбулентную область, устанавливается почти адиабатический профиль температуры; (ii) в результате чего струя получает некоторый запас доступной потенциальной энергии [5], (iii) ее верхняя часть, приобретает отрицательную плавучесть, а нижняя – положительную; (iv) возникающие при этом силы плавучести сдавливают ее, а соответствующее компенсирующее давление ускоряет в горизонтальном направлении, формируяя плоскую пульсирующую струю. Тем самым происходит расслоение фонового ламинарного потока, с образованием слоя, с резко отличающейся от остальной его части скоростью. При этом на фоне циклических взаимопревращений доступной потенциальной и кинетической энергии струи остается неизменным ее горизонтальный импульс (см. формулу (21)). Взаимодействие струи с фоновым атмосферным потоком приводит к возникновению на ее верхней и нижней границе сдвиговой неустойчивости, образованию вихрей, которые по мере их роста приводят к эрозии ее границ и в конечном итоге к ее диссипации. Очевидно, перемещение в фоновой атмосфере подобной динамической структуры должно привести к генерации вторичных мелкомасштабных ВГВ.

Источником движущихся в атмосфере турбулентных областей являются насыщенные ВГВ, т.е. волны, рост амплитуды которых ограничивается за счет генерации ими мелкомасштабной турбулентности. В рамках линейного приближения критерием начала этого процесса принято рассматривать равенство амплитуды волны $\tilde {u}$ значению ее горизонтальной фазовой скорости C относительно фонового потока [6]. Так как амплитуды ВГВ, распространяющихся из нижней атмосферы в верхнюю, растут с высотой, то по мере подъема все большее их число переходит из ненасыщенного в насыщенное состояние. Соответственно, и диапазон значений фазовых скоростей множества насыщенных ВГВ также расширяется. Применительно к рассматриваемому механизму это означает, что величина верхней границы ${{C}_{ * }}$ диапазона возможных значений скорости турбулентных областей C относительно фонового потока в мезосфере будет выше, чем в тропосфере. Действительно, результаты измерений спектров скорости ветра [7] показали, что в нижней стратосфере верхняя граница этого диапазона ${{C}_{ * }}$ ≈ 3 – 5 м/с, а в верхней мезосфере ${{C}_{ * }}$ ≈ 25 – 30 м/с. Так как величина пульсаций горизонтальной скорости в плоской струе прямо пропорциональна величине C, можно утверждать, что в тропосфере величина пульсаций скорости в плоских струях, формируемых насыщенными ВГВ, будут ограничены максимальным значением ${{u}_{{\max }}} \approx $ 30 м/с. В то время как в верхней мезосфере, в струях, образованных насыщенными ВГВ, с максимально возможными фазовыми скоростями $C \approx $ 30 м/с, пульсации скорости могут достигать ${{u}_{{\max }}} \approx $ 180 м/с. Действительно, измерения вертикальных профилей ветра в диапазоне высот 80–110 км с помощью химических трассеров [8, 9], а также инфразвуковое зондирование атмосферы [10–12], указывают на наличие в верхней мезосфере и нижней термосфере слоистых структур с очень большими вертикальными сдвигами ветра и скоростями, достигающими 150–200 м/с.

В качестве еще одного возможного следствия механизма расслоения фонового атмосферного потока можно рассматривать локальные волнистые структуры, с длиной волны, не превышающей 25 км, часто присутствующие на фотографиях гидроксильного слоя и именуемые в англоязычной научной периодике как рябь (ripple) [13, 14]. Действительно, если в верхней мезосфере верхняя граница значений фазовой скорости насыщенных ВГВ ${{C}_{ * }} \approx $ 25–30 м/с, то в таком же диапазоне лежат скорости турбулентных пятен, следующих за породивших их волнами. Соответственно, пространственный период пульсаций плоских струй, генерируемых ими, будет составлять примерно ${{2\pi еС} \mathord{\left/ {\vphantom {{2\pi еС} N}} \right. \kern-0em} N}$ ≈ 21 км.

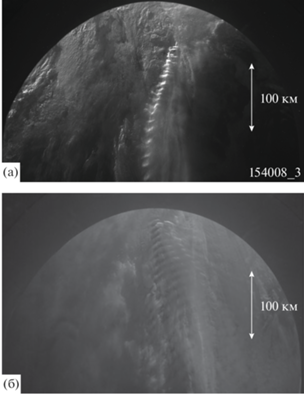
Проведенное сопоставление модельных оценок с результатами натурных измерений свидетельствует о значительно более высокой эффективности данного механизма в мезосфере по сравнению с тропосферой. Однако, на наш взгляд, должно существовать исключение из этого правила. Подтверждением чего являются снимки земной атмосферы, сделанные с борта Международной космической станции (МКС) в ходе проведения космического эксперимента “Терминатор” (см. рис. 7). На снимках присутствуют протяженные (≈250 км) волнистые облачные структуры, происхождение которых можно объяснить с помощью нашей модели следующим образом. В тропосфере источниками турбулентности являются горные волны большой амплитуды, порожденные обтеканием местного рельефа интенсивным ветровым потоком. Эти волны имеют нулевую фазовую скорость относительно земной поверхности. В силу чего турбулентные зоны, порождаемые ими, неподвижны относительно земной поверхности. Набегающий ветровой поток, проходя сквозь них, превращается из ламинарного в турбулентный. По выходе из турбулентной зоны ветровой поток ускоряется за счет действия описанного выше механизма, приводящего к формированию пульсирующих струй, которые, в свою очередь, модулирует облачные структуры, видимые на снимках.

Рис. 7.

Фотографии тропосферной облачности в окрестности солнечного терминатора. (а) – Фотография тропосферной облачности, сделанная с МКС 23.12.2020, в окрестности острова Кергелен (южная часть Индийского океана); (б) – фотография тропосферной облачности, сделанная с МКС 01.05.2021, в окрестности острова Окленд-Айлендс (юго-западная часть Тихого океана).

ЗАКЛЮЧЕНИЕ

Для моделирования основных эффектов, вызванных перемещающейся относительно фонового атмосферного потока турбулентной областью, была разработана максимально упрощенная идеализированная математическая модель, описывающая расслоение движущейся турбулентной областью ламинарного атмосферного потока. Очевидно, что полученные модельные результаты могут лишь весьма грубо воспроизвести реальные эффекты, инициированные насыщенной ВГВ и порожденной ею турбулентностью. А упомянутые в предыдущем разделе наблюдаемые структурные особенности атмосферы можно расценивать лишь как косвенные подтверждения модели. К тому же они допускают и иные механизмы, объясняющие их появление. В силу этого, для того чтобы убедиться в существовании/отсутствии в реальной атмосфере механизма, подобного рассмотренному в настоящей статье, необходимо получить значительно более объемные и точные данные наблюдений.

ПРИЛОЖЕНИЕ

Будем искать решение задачи Коши для системы дифференциальных уравнений (2), (5), (11) с начальными условиями (12)–(14), полагая, что в функциях плавучести $b(x,z)$ и вертикальной скорости $w(x,z)$переменные x и z могут быть разделены следующим образом:

а функция горизонтальной скорости $u(x)$представлена с помощью соотношения подобия

Последнее соотношение следует из совместного рассмотрения уравнений (П2) и (5).Здесь и далее функции $B({x \mathord{\left/ {\vphantom {x C}} \right. \kern-0em} C})$, $W({x \mathord{\left/ {\vphantom {x C}} \right. \kern-0em} C})$и $U({x \mathord{\left/ {\vphantom {x C}} \right. \kern-0em} C})$ являются функциями одной переменной $\tau = {x \mathord{\left/ {\vphantom {x C}} \right. \kern-0em} C}$.

После подстановки соотношений (П1), (П2) и (П3) в систему уравнений (2), (5) и (11) приходим к следующей системе:

с начальными условиями:

Подстановка (П6) в (П5) приводит к следующему соотношению между функциями$B(\tau )$ и $U(\tau )$

С учетом (П10) и (П6), уравнение (П4) преобразуется в обыкновенное нелинейное дифференциальное уравнение третьего порядка

Интегрируя (П11), понижаем порядок этого дифференциального уравнения

Подставив выражение для ${{c}_{1}}$ в (П12), преобразуем это уравнение к окончательному виду

с начальным условием (П9), дополненным условием

Обоснованность уравнения (П14) определяется справедливостью условия (9) для его решений. Для того чтобы преобразовать условие (9) к виду удобному для проведения такой проверки, подставим $U$ и $W$ из (П3) и (П2) в (9):

Используя (П6), перепишем (П16) в виде

В соответствии с законом сохранения потока воздуха через произвольное вертикальное сечение плоской струи, можно записать $z = {{{{z}_{0}}} \mathord{\left/ {\vphantom {{{{z}_{0}}} {U(\tau )}}} \right. \kern-0em} {U(\tau )}}$, где $z = z{}_{0}$ при $\tau = 0$. Тогда уравнение (П17) может быть приведено к виду

А так как $\left| {{{z}_{0}}} \right| \leqslant {{h}_{0}}$, то использование уравнения (П14) будет правомерно, если будет выполнено условие