Известия РАН. Физика атмосферы и океана, 2022, T. 58, № 3, стр. 300-309

Безотражательное распространение внутренних волн в канале переменного сечения при наличии течения

С. М. Чурилов^*

Институт солнечно–земной физики СО РАН
664033 Иркутск, ул. Лермонтова, 126a, Россия

Поступила в редакцию 16.12.2021
После доработки 10.01.2022
Принята к публикации 09.02.2022

EDN: EHSLZF
DOI: 10.31857/S000235152203004X

Аннотация

В линейном приближении рассматривается распространение длинных внутренних волн произвольной формы в стационарном течении двухслойной жидкости в канале переменного сечения под крышкой. Найдены и изучены два вида течений, в которых волны распространяются без отражения. Сравнение с аналогичной задачей для каналов без течения, рассматривавшейся ранее, показало, что присутствие течения существенно сужает возможности безотражательного распространения волн. В частности, при наличии течения нет согласованных каналов, в которых волны могут распространяться без отражения на любые расстояния. Ограничение протяженности безотражательных каналов с течением обусловлено, главным образом, тем, что скорость течения изменяется гораздо быстрее, чем скорость распространения волн, и обязательно есть точка, в которой они становятся равными.

Ключевые слова: двухслойное течение, канал переменного сечения, внутренние волны, распространение без отражения

1. ВВЕДЕНИЕ

Внутренние волны (ВВ) являются непременной составляющей разнообразных процессов в океане и, как правило, играют в них существенную роль (см, например, [1–3]). При определенном сочетании обстоятельств (рельеф дна, характер изменения ширины бухты или пролива и т.д.) оказывается возможным распространение ВВ без отражения и рассеяния на неоднородностях (см., например, [4] и цитированную там литературу). В таких случаях вклад ВВ в динамику процессов заметно возрастает благодаря, в частности, тому, что они могут переносить энергию без потерь на значительные расстояния.

Даже для волн малой амплитуды поиск “безотражательных” конфигураций рельефа – задача довольно трудная, и тут для более глубокого понимания физики явления крайне полезны достаточно простые модели, допускающие полное аналитическое исследование. На сегодня основной подход к построению таких моделей базируется на приведении уравнения для волн к уравнению с не зависящими от координат коэффициентами [5]. В его рамках рассматривались фактически два класса моделей, в зависимости от того, изучается ли распространение монохроматической волны (или спектрально узкого пакета волн), или зависимость возмущения от времени достаточно произвольна. В первом случае предполагается, что рельеф зависит от одной горизонтальной координаты $x$, а частота плавучести и скорость невозмущенного течения (вдоль $x$) – от вертикальной координаты $z$ (см., например, [6, 7]). Во втором случае приходится ограничиться двухслойной средой в приближении мелкой воды без течения. Рельеф при этом по-прежнему считается зависящим только от $x$, а по $y$ может быть либо однородным (см., например, [8]), либо ограниченным каналом ширины $W(x)$ (см. [4, 9, 10]).

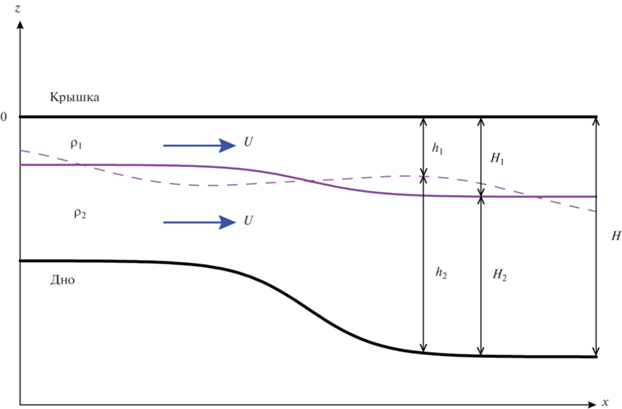
Цель данной работы – изучить возможность распространения линейных ВВ без отражения в каналах с зависящим от $x$ течением двухслойной среды. Для этого применяется несколько иной подход, основанный на факторизации уравнения для волн и недавно апробированный на физически очень похожей задаче о безотражательном распространении поверхностных волн на неоднородном течении мелкой воды [11]. Присутствие течения делает задачу гораздо более трудной, и чтобы не усложнять ее чрезмерно, будем предполагать, что течение ограничено сверху горизонтальной твердой крышкой (рис. 1), под которой следует понимать, прежде всего, ледовое покрытие.

Рис. 1.

Схема течения в канале. Пунктиром показана возмущенная граница раздела.

Исследование свойств волновых движений под ледяным покровом занимает в последние десятилетия заметное место в океанологии. Оно охватывает волны различных частотных диапазонов, от поверхностных гравитационных (точнее, изгибно-гравитационных) и внутренних волн (см., например [12]) до волн Россби [13]. Мы будем изучать безотражательное распространение внутренних волн с частотами, значительно превосходящими параметр Кориолиса ($\omega \gg {{f}_{0}}$), в двухслойном течении в приближении мелкой воды.

В ${{\S}}$ 2 получены основные уравнения, описывающие распространение ВВ, и выведены два альтернативных условия их распространения без отражения. В ${{\S}}$ 3 найдены решения, соответствующие каждому из этих условий, а обсуждению результатов посвящен ${{\S}}$ 4.

2. ОСНОВНЫЕ УРАВНЕНИЯ

Рассмотрим распространение длинных внутренних волн малой амплитуды в двухслойной среде в канале под твердой горизонтальной крышкой. Ширина $W(x)$ и глубина $H(x)$ канала плавно изменяются вдоль направления течения, а жидкости в слоях идеальны, однородны, несжимаемы и не смешиваются. В приближении мелкой воды система уравнений, описывающих течение вдоль оси $x$, имеет вид (см., например, [16, 17])

(1)

$\begin{gathered} \frac{{\partial {{V}_{{1,2}}}}}{{\partial t}} + \frac{\partial }{{\partial x}}\left( {\frac{{V_{{1,2}}^{2}}}{2} + \frac{{{{P}_{{1,2}}}}}{{{{\rho }_{{1,2}}}}}} \right) = 0, \\ \frac{{\partial {{S}_{{1,2}}}}}{{\partial t}} + \frac{\partial }{{\partial x}}\left( {{{S}_{{1,2}}}{{V}_{{1,2}}}} \right) = 0, \\ \end{gathered} $

где индексы 1 и 2 относятся к верхнему и нижнему слою соответственно, ${{V}_{{1,2}}}(x,t)$ – скорости течения, ${{\rho }_{1}} < {{\rho }_{2}}$ – плотности, ${{h}_{{1,2}}}(x,t)$ и S_{1, 2}(x, t) = = $W(x){{h}_{{1,2}}}(x,t)$ – толщины и площади поперечного сечения слоев (см. рис. 1), причем h₁(x, t) + h₂(x, t) = = H(x). Давление в слоях определяется гидростатическими соотношениями

(2)

$\begin{gathered} {{P}_{1}}(x,z,t) = {{P}_{0}}(x,t) - g{{\rho }_{1}}z,\,\,\,\, - {{h}_{1}} \leqslant z \leqslant 0, \\ {{P}_{2}}(x,z,t) = {{P}_{0}}(x,t) + g({{\rho }_{2}} - {{\rho }_{1}}){{h}_{1}}(x,t) - g{{\rho }_{2}}z, \\ - H \leqslant z \leqslant - {{h}_{1}}, \\ \end{gathered} $

где ${{P}_{0}}$ – давление прямо под крышкой (в равновесии – при $z = - 0$), $g$ – ускорение силы тяжести. Относительно невозмущенного течения предполагаем, что оно не имеет сдвига скорости между слоями, т.е. ${{V}_{1}} = {{V}_{2}} = U(x) > 0$. Глубины слоев, ${{h}_{{1,2}}} = {{H}_{{1,2}}}(x)$, связаны со скоростью течения и шириной канала законами сохранения потока

(3)

${{\Phi }_{{1,2}}} = U(x)W(x){{H}_{{1,2}}}(x) = \,\,{\kern 1pt} {\text{const}},$

так что ${{{{H}_{1}}(x)} \mathord{\left/ {\vphantom {{{{H}_{1}}(x)} {{{H}_{2}}(x)}}} \right. \kern-0em} {{{H}_{2}}(x)}} = {\text{const}}{\kern 1pt} $, и можно представить

(4)

$\begin{gathered} {{H}_{1}}(x) = \eta {\kern 1pt} H(x),\,\,\,\,{{H}_{2}}(x) = (1 - \eta )H(x), \\ \eta = \,\,{\kern 1pt} {\text{const}}{\kern 1pt} . \\ \end{gathered} $

Кроме того, из первой пары уравнений (1) следует аналог уравнения Бернулли

(5)

$\frac{{{{U}^{2}}(x)}}{2} - g{{H}_{1}}(x) = {\text{const}}{\kern 1pt} .$

На динамику волн вызванные ими деформация и движение ледового покрова (моделируемого тонкой однородной упругой пластиной толщины $d$) влияют посредством вклада в возмущение ${{p}_{0}}(x,t)$ давления на границе вода–лед (см., например, [12–15]),

(6)

$\begin{gathered} \frac{{{{p}_{0}}}}{{{{\rho }_{1}}g}} = \eta + D{{\Delta }^{2}}\eta + Q\Delta \eta + M\frac{{{{\partial }^{2}}\eta }}{{\partial {{t}^{2}}}}, \\ D = \frac{{E{\kern 1pt} {{d}^{3}}}}{{12(1 - {{\nu }^{2}}){{\rho }_{1}}g}},\,\,\,Q = \frac{{N{\kern 1pt} d}}{{{{\rho }_{1}}g}}, \\ M = \frac{{{{\rho }_{i}}d}}{{{{\rho }_{1}}g}},\,\,\,\Delta = \frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}}, \\ \end{gathered} $

где $\eta $ – смещение границы, ${{\rho }_{i}} \approx 0.9{{\rho }_{1}}$ – плотность льда, $E \approx 5 \times {{10}^{9}}$ Дж/м$^{2}$ – модуль Юнга, $\nu \approx 0.3$ – коэффициент Пуассона, $\left| N \right| \approx {{10}^{6}}$ кг/с$^{2}$ – сжимающее ($N > 0$) или растягивающее ($N < 0$) напряжение в ледяной пластине. Полагая, что глубина канала $H \sim (10{\kern 1pt} - {\kern 1pt} 100)$ м, а перепад плотности ${{\Delta \rho } \mathord{\left/ {\vphantom {{\Delta \rho } {{{\rho }_{2}}}}} \right. \kern-0em} {{{\rho }_{2}}}} = 1 - {{{{\rho }_{1}}} \mathord{\left/ {\vphantom {{{{\rho }_{1}}} {{{\rho }_{2}}}}} \right. \kern-0em} {{{\rho }_{2}}}} \sim {{10}^{{ - 3}}}$, находим, что скорость распространения ВВ порядка 1 м/с и, с учетом принятых приближений ($\omega \gg {{f}_{0}}$ и $kH \ll 1$), характерное волновое число изучаемых возмущений составляет ${{(10}^{{ - 3}}}{\kern 1pt} - {\kern 1pt} {{10}^{{ - 2}}})$ м^–1. Легко видеть, что при таких параметрах все члены в правой части (6), обусловленные ледовым покровом, малы по сравнению с первым и потому не оказывают существенного влияния на свойства ВВ по сравнению со случаем свободной поверхности (см. также [12], ${{\S}}$ 3).

Налагая возмущения,

$\begin{gathered} {{V}_{{1,2}}}(x,t) = U(x) + {{u}_{{1,2}}}(x,t),\,\,\,\,{{P}_{0}}(x,t) = {{P}_{0}}(x) + {{p}_{0}}(x,t), \\ {{h}_{1}}(x,t) = {{H}_{1}}(x) - \zeta (x,t),\,\,\,{{h}_{2}}(x,t) = {{H}_{2}}(x) + \zeta (x,t), \\ \end{gathered} $

и линеаризуя по ним уравнения (1) и (2), получим

(7)

$\begin{gathered} \frac{{\partial {{u}_{1}}}}{{\partial t}} + \frac{\partial }{{\partial x}}\left( {U{{u}_{1}} + \frac{{{{p}_{0}}}}{{{{\rho }_{1}}}}} \right) = 0, \\ \frac{{\partial {{u}_{2}}}}{{\partial t}} + \frac{\partial }{{\partial x}}\left( {U{{u}_{2}} + \frac{{{{p}_{0}}}}{{{{\rho }_{2}}}} + \frac{{\Delta \rho }}{{{{\rho }_{2}}}}{\kern 1pt} g\zeta } \right) = 0, \\ \end{gathered} $

(8)

$\begin{gathered} \frac{{\partial \zeta }}{{\partial t}} + \frac{1}{W}{\kern 1pt} \frac{\partial }{{\partial x}}[W(U\zeta - {{H}_{1}}{{u}_{1}})] = 0, \\ \frac{{\partial \zeta }}{{\partial t}} + \frac{1}{W}{\kern 1pt} \frac{\partial }{{\partial x}}[W(U\zeta + {{H}_{2}}{{u}_{2}})] = 0, \\ \end{gathered} $

откуда, с учетом (4), следует, что ηu₁(x, t) + + $(1 - \eta ){{u}_{2}}(x,t) = 0.$ Исключив из (7) ${{p}_{0}}$ и ${{u}_{1}}$, приходим к уравнению

(9)

$\begin{gathered} \frac{{\partial {{u}_{2}}}}{{\partial t}} + \frac{\partial }{{\partial x}}\left( {U{{u}_{2}} + \frac{{\Delta \rho }}{{{{\rho }_{*}}}}{\kern 1pt} g\zeta } \right) = 0, \\ {{\rho }_{*}} = \frac{{{{H}_{1}}{{\rho }_{2}} + {{H}_{2}}{{\rho }_{1}}}}{{{{H}_{1}}}} = {{\rho }_{2}} + \frac{{1 - \eta }}{\eta }{\kern 1pt} {{\rho }_{1}}. \\ \end{gathered} $

Теперь есть два варианта дальнейших действий. С одной стороны, можно ввести потенциал скорости, положив ${{u}_{2}}(x,t) = {{\partial \varphi (x,t)} \mathord{\left/ {\vphantom {{\partial \varphi (x,t)} {\partial x}}} \right. \kern-0em} {\partial x}}$. Проинтегрировав уравнение (9),

$\frac{{\partial \varphi }}{{\partial t}} + U{\kern 1pt} \frac{{\partial \varphi }}{{\partial x}} + \frac{{\Delta \rho }}{{{{\rho }_{*}}}}{\kern 1pt} g\zeta = 0,$

выразим $\zeta $ через $\varphi $, подставим во второе уравнение (8) и получим

(10)

$\begin{gathered} \left[ {\frac{\partial }{{\partial t}} + U\frac{\partial }{{\partial x}} + \frac{{(UW){\kern 1pt} '}}{W}} \right]\left( {\frac{{\partial \varphi }}{{\partial t}} + U\frac{{\partial \varphi }}{{\partial x}}} \right) = \\ = \,\,\frac{1}{W}\frac{\partial }{{\partial x}}\left( {W{\kern 1pt} {{s}^{2}}{\kern 1pt} \frac{{\partial \varphi }}{{\partial x}}} \right), \\ \end{gathered} $

где штрих обозначает производную по $x$ и

(11)

$\begin{gathered} {{s}^{2}}(x) = \frac{{\Delta \rho }}{{{{\rho }_{*}}}}{\kern 1pt} g{{H}_{2}}(x) \equiv \\ \equiv \frac{{\eta (1 - \eta )\Delta \rho }}{{(1 - \eta ){{\rho }_{1}} + \eta {{\rho }_{2}}}}{\kern 1pt} gH(x) \equiv g{\kern 1pt} 'H(x) \\ \end{gathered} $

– квадрат скорости распространения ВВ вдоль границы раздела, а $g{\kern 1pt} '$ – редуцированное ускорение силы тяжести. Заметим, что уравнение (10) справедливо и в отсутствие среднего течения ($U \equiv 0$), и в этом случае совпадает с изучавшимся ранее (см. [9, 10]).

Выразив с помощью (3) $W(x)$ через $U(x)$ и $s(x)$, положим

(12)

$\varphi (x,t) = a(x)\psi (x,t),\,\,\,\,a(x) > 0,$

и придем к уравнению

(13)

$\begin{gathered} \frac{{{{\partial }^{2}}\psi }}{{\partial {{t}^{2}}}} + ({{U}^{2}} - {{s}^{2}}){\kern 1pt} \frac{{{{\partial }^{2}}\psi }}{{\partial {{x}^{2}}}} + 2U{\kern 1pt} \frac{{{{\partial }^{2}}\psi }}{{\partial t\partial x}} + \\ + 2U\left( {\frac{{a{\kern 1pt} '}}{a} - \frac{{s{\kern 1pt} '}}{s}} \right)\frac{{\partial \psi }}{{\partial t}} + \\ + \,\,\left[ {2({{U}^{2}} - {{s}^{2}}){\kern 1pt} \frac{{a{\kern 1pt} '}}{a} + ({{U}^{2}} + {{s}^{2}}){\kern 1pt} \frac{{U{\kern 1pt} '}}{U} - 2{{U}^{2}}\frac{{s{\kern 1pt} '}}{s}} \right] \times \\ \times \,\,\frac{{\partial \psi }}{{\partial x}} + {{T}_{1}}(x)\psi = 0, \\ \end{gathered} $

где

Наконец, найдем условие, при котором уравнение (13) содержит только производные от $\psi $. Приравнивая ${{T}_{1}}(x)$ нулю, получим уравнение в полных дифференциалах

${\text{d}}(\ln a{\kern 1pt} ') = {\text{d}}\left( {\ln {\kern 1pt} \frac{{{{s}^{2}}U}}{{{{s}^{2}} - {{U}^{2}}}}} \right).$

Его интегрирование дает

(14)

$\frac{{{\text{d}}a}}{{{\text{d}}x}} = \frac{{B{\kern 1pt} {{s}^{2}}U}}{{{{s}^{2}} - {{U}^{2}}}},\,\,\,\,B = {\text{const}}.$

С другой стороны, можно ввести “потенциал смещения границы раздела”, положив W(x)ζ(x, t) = = ${{\partial \phi (x,t)} \mathord{\left/ {\vphantom {{\partial \phi (x,t)} {\partial x}}} \right. \kern-0em} {\partial x}}$. Тогда, проинтегрировав по $x$ второе уравнение (8), выразим ${{u}_{2}}$ через $\phi $ и подставим в (9):

$\left( {\frac{\partial }{{\partial t}} + U\frac{\partial }{{\partial x}} + 2U{\kern 1pt} '} \right)\left( {\frac{{\partial \phi }}{{\partial t}} + U\frac{{\partial \phi }}{{\partial x}}} \right) = {{s}^{2}}W\frac{\partial }{{\partial x}}\left( {\frac{1}{W}{\kern 1pt} \frac{{\partial \phi }}{{\partial x}}} \right).$

Теперь с помощью (3) исключим $W$, представим

(15)

$\phi (x,t) = A(x)\chi (x,t),\,\,\,\,A(x) > 0,$

и получим уравнение

(16)

$\begin{gathered} \frac{{{{\partial }^{2}}\chi }}{{\partial {{t}^{2}}}} + ({{U}^{2}} - {{s}^{2}}){\kern 1pt} \frac{{{{\partial }^{2}}\chi }}{{\partial {{x}^{2}}}} + 2U{\kern 1pt} \frac{{{{\partial }^{2}}\chi }}{{\partial t\partial x}} + 2\left( {U{\kern 1pt} \frac{{A{\kern 1pt} '}}{A} + U{\kern 1pt} '} \right)\frac{{\partial \chi }}{{\partial t}} + \\ + \,\,{\kern 1pt} \left[ {2({{U}^{2}} - {{s}^{2}}){\kern 1pt} \frac{{A{\kern 1pt} '}}{A} - {{s}^{2}}{\kern 1pt} \frac{{U{\kern 1pt} '}}{U} + 3UU{\kern 1pt} '\,\, - 2ss{\kern 1pt} '} \right]\frac{{\partial \chi }}{{\partial x}} + \\ + \,\,{{T}_{2}}(x)\chi = 0, \\ \end{gathered} $

в котором

Легко видеть, что ${{T}_{2}}(x) \equiv 0$, если

(17)

$\frac{{{\text{d}}A}}{{{\text{d}}x}} = \frac{C}{{U(x)[{{U}^{2}}(x) - {{s}^{2}}(x)]}}{\kern 1pt} ,\,\,\,C = {\text{const}}{\kern 1pt} .$

Рассмотрим теперь модельное уравнение

(18)

$\left( {\frac{\partial }{{\partial t}} + {{v}_{1}}(x){\kern 1pt} \frac{\partial }{{\partial x}} + F(x)} \right)\left( {\frac{\partial }{{\partial t}} + {{v}_{2}}(x){\kern 1pt} \frac{\partial }{{\partial x}}} \right)f(x,t) = 0,$

у которого по крайней мере одно из решений имеет вид бегущей волны,

$f(x,t) = {{f}_{1}}\left( {t - \int \frac{{{\text{d}}x}}{{{{v}_{2}}(x)}}} \right),$

где ${{f}_{1}}(z)$ – произвольная функция. Раскроем в (18) скобки,

(19)

$\begin{gathered} \frac{{{{\partial }^{2}}f}}{{\partial {{t}^{2}}}} + {{v}_{1}}(x){{v}_{2}}(x){\kern 1pt} \frac{{{{\partial }^{2}}f}}{{\partial {{x}^{2}}}} + [{{v}_{1}}(x) + {{v}_{2}}(x)]\frac{{{{\partial }^{2}}f}}{{\partial t\partial x}} + \\ + \,\,F(x){\kern 1pt} \frac{{\partial f}}{{\partial t}} + [{{v}_{1}}(x)v_{2}^{'}(x) + F(x){{v}_{2}}(x)]\frac{{\partial f}}{{\partial x}} = 0, \\ \end{gathered} $

и посмотрим сначала, когда это уравнение совпадает с уравнением (13), если условие (14) выполнено и ${{T}_{1}}(x) \equiv 0$. Необходимые для этого соотношения имеют вид

(20)

$\begin{gathered} {{v}_{1}}(x){{v}_{2}}(x) = {{U}^{2}}(x) - {{s}^{2}}(x),\,\,\,\,{{v}_{1}}(x) + {{v}_{2}}(x) = 2U(x), \\ F(x) = 2U(x){\kern 1pt} \left( {\frac{{a{\kern 1pt} '(x)}}{{a(x)}} - \frac{{s{\kern 1pt} '(x)}}{{s(x)}}} \right), \\ \end{gathered} $

(21)

$\begin{gathered} {{v}_{1}}(x)v_{2}^{'}(x) + F(x){{v}_{2}}(x) = 2[{{U}^{2}}(x) - {{s}^{2}}(x)]\frac{{a{\kern 1pt} '(x)}}{{a(x)}} + \\ + \,\,[{{U}^{2}}(x) + {{s}^{2}}(x)]\frac{{U{\kern 1pt} '(x)}}{{U(x)}} - 2{{U}^{2}}(x){\kern 1pt} \frac{{s{\kern 1pt} '(x)}}{{s(x)}}{\kern 1pt} . \\ \end{gathered} $

Первые два уравнения (20) выполняются, если либо ${{v}_{1}} = U - s$, ${{v}_{2}} = U + s$, либо ${{v}_{1}} = U + s$, ${{v}_{2}} = U - s$. Легко видеть, однако, что в обоих случаях уравнение (21) с точностью до несущественного численного множителя дает

(22)

$a(x) = [s(x)U(x{{)]}^{{1/2}}}.$

Подчеркнем, что здесь и далее ${{s}^{{1/2}}}(x)$ и ${{U}^{{1/2}}}(x)$ следует рассматривать как положительные функции. Подставив в (14), находим в явном виде связь между $s(x)$ и $U(x)$,

(23)

$\frac{d}{{dx}}[s(x)U(x)] = \frac{{B{{s}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}(x){{U}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}(x)}}{{{{s}^{2}}(x) - {{U}^{2}}(x)}},$

точно такую же, как и в задаче о поверхностных волнах (см. уравнение (2.19) в [11]).

Итак, при выполнении соотношений (20), (22) и (14) уравнение (13) можно представить в двух эквивалентных видах,

(24)

$\begin{gathered} \left\{ {\frac{\partial }{{\partial t}} + [U(x) - s(x)]{\kern 1pt} \frac{\partial }{{\partial x}} + U(x)\left( {\frac{{U{\kern 1pt} '(x)}}{{U(x)}} - \frac{{s{\kern 1pt} '(x)}}{{s(x)}}} \right)} \right\} \times \\ \times \,\,\left( {\frac{\partial }{{\partial t}} + [U(x) + s(x)]\frac{\partial }{{\partial x}}} \right)\psi \equiv \\ \equiv \left\{ {\frac{\partial }{{\partial t}} + [U(x) + s(x)]{\kern 1pt} \frac{\partial }{{\partial x}} + U(x)\left( {\frac{{U{\kern 1pt} '(x)}}{{U(x)}} - \frac{{s{\kern 1pt} '(x)}}{{s(x)}}} \right)} \right\} \times \\ \times \,\,\left( {\frac{\partial }{{\partial t}} + [U(x) - s(x)]\frac{\partial }{{\partial x}}} \right)\psi = 0. \\ \end{gathered} $

Следовательно, его общее решение представляет собой суперпозицию двух волн произвольной формы, бегущих с разными скоростями,

(25)

$\begin{gathered} \psi (x,t) = {{\psi }_{1}}\left( {t - \int \frac{{{\text{d}}x}}{{U(x) + s(x)}}} \right) + \\ + \,\,{{\psi }_{2}}\left( {t - \int \frac{{{\text{d}}x}}{{U(x) - s(x)}}} \right). \\ \end{gathered} $

Независимое распространение каждой из этих волн в неоднородной среде обеспечивается уравнением (23), задающим такую связь скоростей $U(x)$ и $s(x)$, чтобы течение было безотражательным. Физические переменные ${{u}_{2}}$, ${{u}_{1}}$ и $\zeta $ связаны с $\varphi $ и $\psi $ соотношениями

(26)

$\begin{gathered} {{u}_{2}}(x,t) = \frac{{\partial \varphi }}{{\partial x}} = a(x){\kern 1pt} \frac{{\partial \psi }}{{\partial x}} + a{\kern 1pt} '(x)\psi (x,t), \\ {{u}_{1}}(x,t) = - \frac{{1 - \eta }}{\eta }{\kern 1pt} {{u}_{2}}(x,t), \\ \zeta (x,t) = - \frac{{{{\rho }_{*}}}}{{g\Delta \rho }}\left[ {\frac{{\partial \varphi }}{{\partial t}} + U(x){\kern 1pt} \frac{{\partial \varphi }}{{\partial x}}} \right] = \\ = \,\,\frac{{{{\rho }_{*}}a(x)}}{{g\Delta \rho }}\left[ {\frac{{\partial \psi }}{{\partial t}} + U(x){\kern 1pt} \frac{{\partial \psi }}{{\partial x}} + \frac{{a{\kern 1pt} '(x)}}{{a(x)}}{\kern 1pt} U(x)\psi (x,t)} \right]. \\ \end{gathered} $

Сопоставим теперь уравнения (16) и (19), считая уравнение (17) выполненным. Получим те же два решения для ${{v}_{1}}$ и ${{v}_{2}}$, но другое выражение для $F(x)$ и другое уравнение вместо (21), а именно

$\begin{gathered} F = 2\left( {U{\kern 1pt} \frac{{A{\kern 1pt} '}}{A} + U{\kern 1pt} '} \right),\,\,\,\,{{v}_{1}}v_{2}^{'} + F{\kern 1pt} {{v}_{2}} = \\ = 2({{U}^{2}} - {{s}^{2}}){\kern 1pt} \frac{{A{\kern 1pt} '}}{A} - {{s}^{2}}{\kern 1pt} \frac{{U{\kern 1pt} '}}{U} + 3UU{\kern 1pt} '\,\, - 2ss{\kern 1pt} '. \\ \end{gathered} $

При любом выборе пары ${{v}_{1}}$, ${{v}_{2}}$ эти соотношения дают уравнение ${{{\text{d}}[\ln ({{A}^{2}}Us)]} \mathord{\left/ {\vphantom {{{\text{d}}[\ln ({{A}^{2}}Us)]} {{\text{d}}x}}} \right. \kern-0em} {{\text{d}}x}} = 0$, т.е., с точностью до несущественного числового множителя,

(27)

$A(x) = [s(x)U(x{{)]}^{{ - 1/2}}} \equiv {{a}^{{ - 1}}}(x).$

С учетом этого уравнение (17) можно записать в виде

(28)

$\frac{{\text{d}}}{{{\text{d}}x}}[s(x){\kern 1pt} U(x)]\,\, = \,\,\frac{{C{\kern 1pt} {{s}^{{3/2}}}(x){{U}^{{1/2}}}(x)}}{{{{s}^{2}}(x) - {{U}^{2}}(x)}}{\kern 1pt} .$

При выполнении (28) функция $\chi (x,t)$ удовлетворяет тому же уравнению (24), что и $\psi (x,t)$, и в общем случае тоже равна сумме двух бегущих волн произвольной формы:

$\begin{gathered} \chi (x,t) = {{\chi }_{1}}\left( {t - \int \frac{{{\text{d}}x}}{{U(x) + s(x)}}} \right) + \\ + \,\,{{\chi }_{2}}\left( {t - \int \frac{{{\text{d}}x}}{{U(x) - s(x)}}} \right), \\ \end{gathered} $

только независимое их распространение обеспечивается теперь уравнением (28), которое отличается от уравнения (23). Связь физических переменных ${{u}_{2}}$ и $\zeta $ с $\phi $ и $\chi $ такова:

(29)

$\begin{gathered} {{u}_{2}}(x,t) = - \frac{{U(x)}}{{{{\Phi }_{2}}}}\left[ {\frac{{\partial \phi }}{{\partial t}} + U(x){\kern 1pt} \frac{{\partial \phi }}{{\partial x}}} \right] = \\ = - \frac{{U(x)}}{{{{\Phi }_{2}}a(x)}}\left[ {\frac{{\partial \chi }}{{\partial t}} + U(x){\kern 1pt} \frac{{\partial \chi }}{{\partial x}} - \frac{{a'(x)}}{{a(x)}}{\kern 1pt} U(x)\chi (x,t)} \right], \\ \zeta (x,t) = \frac{1}{{W(x)}}{\kern 1pt} \frac{{\partial \phi }}{{\partial x}} = \frac{1}{{W(x)a(x)}}\left[ {\frac{{\partial \chi }}{{\partial x}} - \frac{{a{\kern 1pt} '(x)}}{{a(x)}}{\kern 1pt} \chi (x,t)} \right]. \\ \end{gathered} $

Итак, ВВ распространяются без отражения в канале с течением, если $s(x)$ и $U(x)$ удовлетворяют уравнению (5), которое, с учетом (11), запишем в виде

(30)

$\begin{gathered} {{s}^{2}}(x) - {{\beta }^{2}}{\kern 1pt} {{U}^{2}}(x) = s_{0}^{2} = \,\,{\kern 1pt} {\text{cons}}t{\kern 1pt} , \\ {{\beta }^{2}} = \frac{{(1 - \eta )\Delta \rho }}{{2[(1 - \eta ){{\rho }_{1}} + \eta {\kern 1pt} {{\rho }_{2}}]}}{\kern 1pt} , \\ \end{gathered} $

и одному из уравнений (23) и (28). Так как в условиях океана $\Delta \rho \ll {{\rho }_{{1,2}}}$, выбираем в (30) положительный знак константы $s_{0}^{2}$.

Уравнения (23) и (28) существенно отличаются друг от друга, но при $B = C = 0$ приводят к одному и тому же соотношению между скоростями

(31)

$s(x)U(x) = \Pi = \,\,{\kern 1pt} {\text{const}}{\kern 1pt} ,$

которое в силу (3) эквивалентно равенству $W(x){\kern 1pt} {{H}^{{1/2}}}(x){\kern 1pt} \,\,{\text{ = }}{\kern 1pt} $ const. Оно характерно для так называемых согласованных каналов (см. [9, 10]) – единственного класса каналов без течения с регулярными профилями $W(x)$ и $H(x)$, в которых ВВ распространяются без отражения вдоль всей оси $x$. К сожалению, в нашей задаче (т.е. при $U(x) \ne 0$) такими свойствами обладают только каналы с не зависящими от $x$ шириной и глубиной и постоянной скоростью течения. Действительно, заданной паре констант $s_{0}^{2}$ и $\Pi $ уравнения (30) и (31) ставят в соответствие единственную пару положительных чисел $s$ и $U$.

3. БЕЗОТРАЖАТЕЛЬНЫЕ ТЕЧЕНИЯ В КАНАЛАХ

Течения, удовлетворяющие уравнению (23) с $B \ne 0$.

Уравнение (23) однородно по скоростям $s$ и $U$, а $B$ имеет размерность обратной длины. С учетом (11) введем безразмерные переменные

(32)

$\begin{gathered} \xi = B{\kern 1pt} x,\,\,\,\,\tilde {U}(\xi ) = {{U(x)} \mathord{\left/ {\vphantom {{U(x)} {{{s}_{0}}}}} \right. \kern-0em} {{{s}_{0}}}}, \\ \tilde {s}(\xi ) = {{s(x)} \mathord{\left/ {\vphantom {{s(x)} {{{s}_{0}}}}} \right. \kern-0em} {{{s}_{0}}}},\,\,\,\,\tilde {H}(\xi ) = {{{\tilde {s}}}^{2}}(\xi ) \\ \end{gathered} $

и, опуская в дальнейшем тильду, запишем уравнения (23) и (30) в виде

$\frac{{\text{d}}}{{{\text{d}}\xi }}[s(\xi ){\kern 1pt} U(\xi )]\,\, = \,\,\frac{{2{\kern 1pt} {{s}^{{5/2}}}(\xi ){\kern 1pt} {{U}^{{3/2}}}(\xi )}}{{{{s}^{2}}(\xi ) - {{U}^{2}}(\xi )}}{\kern 1pt} ,\,\,\,\,{{s}^{2}}(\xi ) = 1 + {{\beta }^{2}}{{U}^{2}}(\xi ).$

Выражая $s(\xi )$ через $U(\xi )$, получим уравнение

$\frac{{{\text{d}}U}}{{{\text{d}}\xi }}\,\, = \,\,\frac{{2{{U}^{{3/2}}}{{{(1 + {{\beta }^{2}}{{U}^{2}})}}^{{7/4}}}}}{{(1 + 2{{\beta }^{2}}{{U}^{2}})[1 - (1 - {{\beta }^{2}}){{U}^{2}}]}}$

и упростим его, положив $u = (1 - {{\beta }^{2}}{{)}^{{1/2}}}U$, ξ₁ = = ${\xi \mathord{\left/ {\vphantom {\xi {{{{(1 - {{\beta }^{2}})}}^{{1/4}}}}}} \right. \kern-0em} {{{{(1 - {{\beta }^{2}})}}^{{1/4}}}}}$, ${{\alpha }^{2}} = {{{{\beta }^{2}}} \mathord{\left/ {\vphantom {{{{\beta }^{2}}} {(1 - {{\beta }^{2}})}}} \right. \kern-0em} {(1 - {{\beta }^{2}})}}$:

(33)

$\frac{1}{u}{\kern 1pt} \frac{{{\text{d}}u}}{{{\text{d}}{{\xi }_{1}}}} = \frac{{2{{u}^{{1/2}}}{{{(1 + {{\alpha }^{2}}{{u}^{2}})}}^{{7/4}}}}}{{(1 + 2{{\alpha }^{2}}{{u}^{2}})(1 - {{u}^{2}})}}{\kern 1pt} .$

Его правая часть сингулярна при $u = 1$,¹ ¹ $u = 0$ и $u \to \infty $. Легко видеть, что первая особенность достигается при конечных значениях ${{\xi }_{1}}$, скажем, при ${{\xi }_{1}} = {{\xi }_{*}}$, а две другие – лишь асимптотически, при ${{\xi }_{1}} \to - \infty $.

В окрестности критической точки ${{\xi }_{1}} = {{\xi }_{*}}$ методом итераций находим, что

(34)

$\begin{gathered} {{u}_{ \pm }}({{\xi }_{1}}) = 1 \pm {{\left( {\frac{{2(1 + {{\alpha }^{2}}{{)}^{{7/4}}}}}{{1 + 2{{\alpha }^{2}}}}{\kern 1pt} ({{\xi }_{*}} - {{\xi }_{1}})} \right)}^{{1/2}}} + \\ + \,\,\frac{{2(1 + {{\alpha }^{2}}{{)}^{{7/4}}}}}{{3(1 + 2{{\alpha }^{2}})}}\left[ {1 - \frac{{{{\alpha }^{2}}(1 - 6{{\alpha }^{2}})}}{{2(1 + {{\alpha }^{2}})(1 + 2{{\alpha }^{2}})}}} \right]({{\xi }_{*}} - {{\xi }_{1}}) + \\ + \,\,{\kern 1pt} O[{{\left| {{{\xi }_{*}} - {{\xi }_{1}}} \right|}^{{3/2}}}]. \\ \end{gathered} $

Таким образом, обе ветви решения, докритическая (${{u}_{ - }}({{\xi }_{1}}) < 1$, соответствующая $U(\xi ) < s(\xi )$) и сверхкритическая (${{u}_{ + }}({{\xi }_{1}}) > 1$, соответствующая $U(\xi ) > s(\xi )$), определены только слева от критической точки, при ${{\xi }_{1}} < {{\xi }_{*}}$.

Используя соотношение (см. [18], формула 1.2.4.3.)

$\int\limits_0^x \frac{{{{x}^{{\lambda - 1}}}{\text{d}}x}}{{{{{(x + a)}}^{\nu }}}} = \frac{{{{x}^{\lambda }}}}{{\lambda {{a}^{\nu }}}}F\left( {\nu ,{\kern 1pt} \lambda ;{\kern 1pt} 1 + \lambda ; - \frac{x}{a}} \right),\,\,\,\,{\text{Re}}{\kern 1pt} \lambda > 0,$

где $F(a,b;c;z)$ – гипергеометрическая функция, проинтегрируем уравнение (33):

(35)

$\begin{gathered} 2{{u}^{{3/2}}}F\left( {\frac{3}{4}{\kern 1pt} ,\frac{3}{4}{\kern 1pt} ;\frac{7}{4}{\kern 1pt} ; - {{\alpha }^{2}}{{u}^{2}}} \right) - \frac{{(1 - 2{{\alpha }^{2}}){{u}^{{3/2}}}}}{{{{{(1 + {{\alpha }^{2}}{{u}^{2}})}}^{{3/4}}}}} + \\ + \,\,\frac{{3{\kern 1pt} {{u}^{{ - 1/2}}}}}{{{{{(1 + {{\alpha }^{2}}{{u}^{2}})}}^{{3/4}}}}} = 3{\kern 1pt} ({{\xi }_{B}} - {{\xi }_{1}}), \\ \end{gathered} $

${{\xi }_{B}}$ – константа интегрирования. Так как $\alpha \ll 1$, приведем (35) и в приближенном виде, справедливом при ${{\alpha }^{2}}{{u}^{2}} \ll 1$:

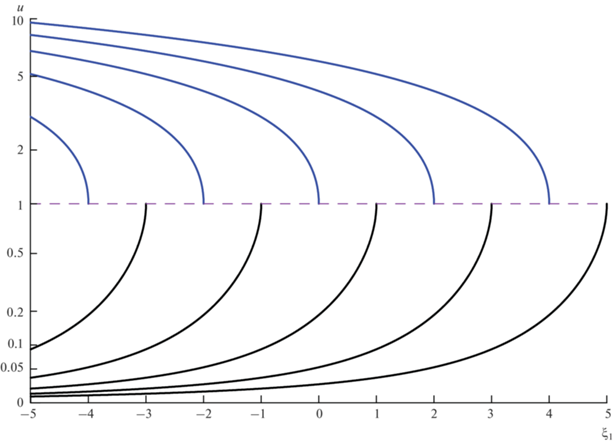
$\begin{gathered} {{u}^{2}} + 3({{\xi }_{1}} - {{\xi }_{B}}){{u}^{{1/2}}} + 3 = \\ = \frac{{{{\alpha }^{2}}}}{4}{\kern 1pt} {{u}^{2}}\left( {1 - \frac{3}{7}{\kern 1pt} {{u}^{2}}} \right) + O({{\alpha }^{4}}{{u}^{4}} + {{\alpha }^{4}}{{u}^{6}}). \\ \end{gathered} $

Легко видеть, что ${{\xi }_{*}} = {{\xi }_{B}} - \frac{4}{3}\left[ {1 - \frac{{{{\alpha }^{2}}}}{{28}} + O({{\alpha }^{4}})} \right]$. Решения уравнения (35) показаны на рис. 2.

Рис. 2.

Решения уравнения (35) при ${{\alpha }^{2}} = 3 \times {{10}^{{ - 3}}}$ и различных значениях ${{\xi }_{B}}$ в докритической ($u < 1$) и сверхкритической ($u > 1$) областях.

Изменение скорости безотражательного течения обеспечивается согласованной вариацией глубины $H$ и ширины $W$ канала, изменяются и амплитуды распространяющихся волн. В безразмерных переменных (32) с учетом (3) и (22) находим

(36)

$\begin{array}{*{20}{l}} \begin{gathered} H = {{s}^{2}} = 1 + {{\beta }^{2}}{{U}^{2}} \equiv 1 + {{\alpha }^{2}}{{u}^{2}}, \hfill \\ W = {{{{W}_{0}}} \mathord{\left/ {\vphantom {{{{W}_{0}}} {[u(1 + {{\alpha }^{2}}{{u}^{2}})]}}} \right. \kern-0em} {[u(1 + {{\alpha }^{2}}{{u}^{2}})]}}, \hfill \\ \end{gathered} \\ \begin{gathered} a = (s{\kern 1pt} U{{)}^{{1/2}}} = {{u}^{{1/2}}}{{[1 - {{\beta }^{2}}(1 - {{u}^{2}})]}^{{1/4}}}; \\ {{\alpha }^{2}} = {{{{\beta }^{2}}} \mathord{\left/ {\vphantom {{{{\beta }^{2}}} {(1 - {{\beta }^{2}})}}} \right. \kern-0em} {(1 - {{\beta }^{2}})}}. \\ \end{gathered} \end{array}$

Параметры ${{\alpha }^{2}} \approx {{\beta }^{2}} \sim {{\Delta \rho } \mathord{\left/ {\vphantom {{\Delta \rho } \rho }} \right. \kern-0em} \rho } \ll 1$, поэтому изменение скорости течения обеспечивается, главным образом, изменением ширины канала $W \approx {{{{W}_{0}}} \mathord{\left/ {\vphantom {{{{W}_{0}}} u}} \right. \kern-0em} u}$, в то время как его глубина медленно увеличивается или уменьшается вместе со скоростью течения. Фактор $a$, определяющий изменение амплитуды потенциала $\varphi $ (см. (12) и (25)), растет и убывает вместе со скоростью так, что приближенно выполняется соотношение $a \sim {{W}^{{ - 1/2}}}$. Возмущения скорости течения в слоях и смещение границы раздела связаны с $\varphi $ уравнениями (26).

Течения, удовлетворяющие уравнению (28) с $C \ne 0$.

Уравнение (28) неоднородно по скоростям $s$ и $U$. Поэтому сначала обезразмерим $s$ и $U$ на ${{s}_{0}}$, а затем введем безразмерную координату ${{\xi }_{2}} = (1 - {{\beta }^{2}}{{)}^{{1/4}}}{{C{\kern 1pt} x} \mathord{\left/ {\vphantom {{C{\kern 1pt} x} {s_{0}^{2}}}} \right. \kern-0em} {s_{0}^{2}}}$ и перейдем к переменной $u$. Получим уравнение (ср. с (33))

(37)

$\frac{1}{u}{\kern 1pt} \frac{{{\text{d}}u}}{{{\text{d}}{{\xi }_{2}}}}\,\, = \,\,\frac{{2(1 + {{\alpha }^{2}}{{u}^{2}}{{)}^{{5/4}}}}}{{{{u}^{{1/2}}}(1 + 2{{\alpha }^{2}}{{u}^{2}})(1 - {{u}^{2}})}}{\kern 1pt} .$

Его правая часть имеет те же особенности, что и в (33), но теперь при конечных значениях ${{\xi }_{2}}$ достигается не только $u = 1$, но и $u = 0$, и лишь $u \to \infty $ асимптотически, при ${{\xi }_{2}} \to - \infty $. Как следствие, обе ветви решения, докритическая (${{u}_{ - }}({{\xi }_{2}}) < 1$) и сверхкритическая (${{u}_{ + }}({{\xi }_{2}}) > 1$), определены только слева от точки ${{\xi }_{2}} = {{\xi }_{*}}$ такой, что $u({{\xi }_{*}}) = 1$, причем докритическая ветвь – лишь на конечном интервале ${{\xi }_{C}} < {{\xi }_{2}} < {{\xi }_{*}}$, так как ${{u}_{ - }} \to 0$ при ${{\xi }_{2}} \to {{\xi }_{C}} + 0$. Легко показать, что при ${{\xi }_{2}} \to {{\xi }_{*}} - 0$ поведение решения очень похоже на (34),

$\begin{gathered} {{u}_{ \pm }}({{\xi }_{2}}) = 1 \pm {{\left( {\frac{{2(1 + {{\alpha }^{2}}{{)}^{{5/4}}}}}{{1 + 2{{\alpha }^{2}}}}{\kern 1pt} ({{\xi }_{*}} - {{\xi }_{2}})} \right)}^{{1/2}}} + \\ + \,\,\frac{{{{\alpha }^{2}}(3 - 2{{\alpha }^{2}})(1 + {{\alpha }^{2}}{{)}^{{1/4}}}}}{{3(1 + 2{{\alpha }^{2}}{{)}^{2}}}}{\kern 1pt} ({{\xi }_{*}} - {{\xi }_{2}}) + O[{{\left| {{{\xi }_{*}} - {{\xi }_{2}}} \right|}^{{3/2}}}], \\ \end{gathered} $

а при ${{\xi }_{2}} \to {{\xi }_{C}} + 0$

(38)

$\begin{gathered} {{u}_{ - }}({{\xi }_{2}}) = ({{\xi }_{2}} - {{\xi }_{C}}{{)}^{2}} + \frac{2}{5}\left( {1 + \frac{3}{4}{\kern 1pt} {{\alpha }^{2}}} \right) \times \\ \times \,\,{{({{\xi }_{2}} - {{\xi }_{C}})}^{6}} + O[({{\xi }_{2}} - {{\xi }_{C}}{{)}^{{10}}}]. \\ \end{gathered} $

Интегрирование (37) дает уравнение

(39)

$\begin{gathered} \frac{{3 + 4{{\alpha }^{2}}}}{{10}}{\kern 1pt} {{u}^{{5/2}}}F\left( {\frac{5}{4}{\kern 1pt} ,\frac{5}{4}{\kern 1pt} ;\frac{9}{4}{\kern 1pt} ; - {{\alpha }^{2}}{{u}^{2}}} \right) + \\ + \,\,\frac{{{{u}^{{1/2}}}(2 - {{u}^{2}})}}{{2(1 + {{\alpha }^{2}}{{u}^{2}}{{)}^{{1/4}}}}} = {{\xi }_{2}} - {{\xi }_{C}}, \\ \end{gathered} $

или в приближенном виде, справедливом при ${{\alpha }^{2}}{{u}^{2}} \ll 1$,

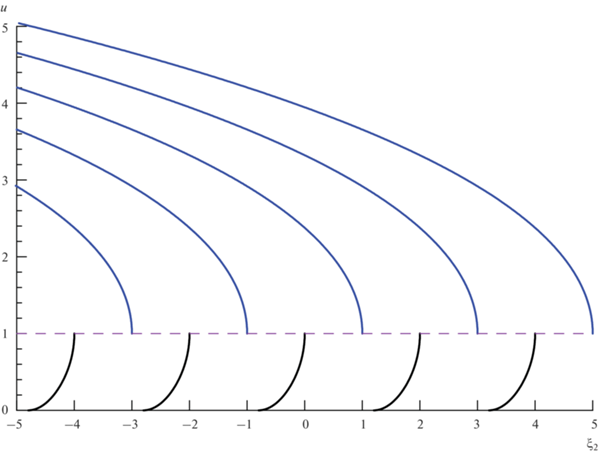
$\begin{gathered} {{u}^{{5/2}}} - 5{{u}^{{1/2}}} + 5({{\xi }_{2}} - {{\xi }_{C}}) = \\ = \frac{{{{\alpha }^{2}}}}{4}{\kern 1pt} {{u}^{{5/2}}}\left[ {3 - \frac{5}{3}{\kern 1pt} {{u}^{2}} + O({{\alpha }^{2}}{{u}^{2}} + {{\alpha }^{2}}{{u}^{4}})} \right]. \\ \end{gathered} $

Легко проверить, что ${{u}_{ - }}({{\xi }_{C}}) = 0$, а ξ* = ξ_C + + $\frac{4}{5}\left[ {1 + \frac{{{{\alpha }^{2}}}}{{12}} + O({{\alpha }^{4}})} \right]$. Решения уравнения (39) показаны на рис. 3.

Рис. 3.

Решения уравнения (39) при ${{\alpha }^{2}} = 3 \times {{10}^{{ - 3}}}$ и различных значениях ${{\xi }_{C}}$ в докритической ($u < 1$) и сверхкритической ($u > 1$) областях.

В течениях этого вида ширина и глубина канала, а также фактор $a$, по-прежнему определяются соотношениями (36), так что увеличение (уменьшение) скорости течения так же обеспечивается, главным образом, сужением (расширением) канала. Но амплитуда волн здесь (см. (15) и (27)) пропорциональна $A({{\xi }_{2}}) = {{a}^{{ - 1}}}({{\xi }_{2}})$ и потому связана с $W$ приближенным соотношением $A({{\xi }_{2}}) \sim {{W}^{{1/2}}}({{\xi }_{2}})$. Возмущение скорости течения и смещение границы раздела описываются уравнениями (29).

4. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Из проведенного нами анализа следует, что наличие стационарного течения в канале сужает возможности распространения ВВ без отражения, отнимая, в некотором смысле, одну степень свободы. Действительно, канал без течения характеризуется не зависящими друг от друга a priori шириной $W(x)$ и глубиной $H(x) = {{H}_{1}} + {{H}_{2}}(x)$ (или, эквивалентно, скоростью распространения ВВ $s(x)$). Их связывает условие безотражательности, и остается одна произвольная функция, которая и дает разнообразие искомых конфигураций (см. [9, 10]). Добавив скорость течения $U(x)$, мы с неизбежностью налагаем еще две связи – законы сохранения потока (3) и энергии (5), и имеем в результате лишь свободу выбора условия безотражательности – (23) или (28). Как следствие, теряется целый класс согласованных каналов, и остаются только два вида ограниченных безотражательных течений, показанные на рис. 2 и 3 .

Чтобы не было отражения, скорость течения должна меняться вдоль канала определенным образом, и меняется она так, что в некоторой точке $x = {{x}_{*}}$ становится равной скорости распространения ВВ, т.е. число Фруда достигает критического значения ${\text{Fr}} = 1$. В геофизических течениях это, как правило, связано с особенностью, и рассмотренный нами класс течений – не исключение. При $x = {{x}_{*}}$ скорости $U(x)$ и $s(x)$ конечны, но их производные бесконечны (см. (34)). В силу сохранения потока (3) течение продолжается и по другую сторону от ${{x}_{*}}$, но безотражательным больше не будет. Вопрос о том, что происходит с волной при переходе через критическую точку, требует отдельного исследования.

Таким образом, в рассмотренной нами задаче перспектива достижения критического числа Фруда ограничивает протяженность каждого безотражательного течения, по крайней мере, с одной стороны. По той же причине течения делятся на докритические, в которых всюду $U(x) < s(x)$, и сверхкритические, где $U(x) > s(x)$ (заметим, что последние обладают рядом интересных свойств, в частности, в них могут распространяться волны отрицательной энергии [19, 20]). Все сверхкритические течения формально ограничены только с одной стороны, критической точкой. Правда, в другую сторону их скорость и глубина должны неограниченно расти, входя в противоречие с приближением мелкой воды, но лишь асимптотически, при $\left| {x - {{x}_{*}}} \right| \to \infty $. А вот докритические течения, удовлетворяющие уравнению (28), резко ограничены с обеих сторон, так как на конечном расстоянии от критической точки $x = {{x}_{*}}$ их скорость стремится к нулю (см. (38) и рис. 3), а ширина канала, соответственно, – к бесконечности. В реальности это, скорее всего, означает что одномерное течение становится двумерным, приобретая $y$-компоненту скорости.

С другой стороны, наличие течения избавляет нас от одной из сингулярностей, присущих каналам без течения и ограничивающих их протяженность. В таких каналах уменьшение глубины может привести к исчезновению нижнего слоя и разрушению ВВ (см., например, [8, 9]). Если же течение есть, сохранение потока в каждом из слоев не позволяет нижнему слою исчезнуть: с уменьшением глубины канала толщины слоев уменьшаются пропорционально, скорость течения замедляется, а канал расширяется (см. (36)).

Заметим, кроме того, что для понимания смысла полученных нами решений нужно иметь в виду еще одно обстоятельство. Уравнения (23) и (28) инвариантны при одновременной замене знака координаты $x$ и константы $B$ или, соответственно, $C$. Следовательно, переход к координатам ${{\xi }_{1}} \sim B{\kern 1pt} x$ и ${{\xi }_{2}} \sim C{\kern 1pt} x$ (и к уравнениям (33) и (37)) в определенной мере стирает различие между понятиями “вверх по течению” и “вниз по течению”: если $s(x)$ и $U(x)$ – решение уравнения (23) (или (28)) при $B = {{B}_{0}}$ (или $C = {{C}_{0}}$), то $s( - x)$ и $U( - x)$ – тоже решение, при $B = - {{B}_{0}}$ (или $C = - {{C}_{0}}$). Поэтому тот факт, что все безотражательные течения определены слева от критической точки ${{\xi }_{*}}$ (см. рис. 2 и 3 ), не означает, что критическая точка $x = {{x}_{*}}$ непременно расположена вниз по течению.

Теперь уместно сравнить полученные выше результаты для ВВ с картиной распространения без отражения поверхностных волн в каналах [11], которая изобилует разнообразием возможных течений, как ограниченных, так и не ограниченных по протяженности. И те, и другие волны распространяются вдоль поверхности раздела, и с физической точки зрения главное различие состоит в величине перепада плотности: ${{\Delta \rho } \mathord{\left/ {\vphantom {{\Delta \rho } \rho }} \right. \kern-0em} \rho } \approx 1$ в случае поверхностных волн и ${{\Delta \rho } \mathord{\left/ {\vphantom {{\Delta \rho } \rho }} \right. \kern-0em} \rho } \ll 1$ в случае ВВ. Как следствие, изменение скорости течения сопровождается практически таким же изменением скорости распространения поверхностных волн и лишь незначительным изменением скорости ВВ (см. (30)). То есть сопоставлять следует картину для ВВ с картиной для поверхностных волн при (практически) постоянной скорости их распространения (т.е. рис. 2 с рис. 3 (a) в статье [11] – согласие хорошее).

И последнее. В данной статье изучено распространение ВВ без отражения в течениях под твердой крышкой. Как отмечалось во Введении, такая модель соответствует некоторым геофизическим течениям, например, течениям под ледовым покровом. Кроме того, полученные с ее помощью результаты приложимы к течениям в подводных туннелях (каналах), соединяющих различные водоемы (резервуары), а также могут оказаться полезными для оценки эффективности и безопасности инженерных сооружений. Но несомненно гораздо больший интерес представляет подобная задача для течений со свободной поверхностью, где приближение твердой крышки используется лишь для фильтрации поверхностных волн. Предварительный анализ показывает, что в такой постановке ее сложность существенно выше, но есть надежда на “восстановление” разнообразия безотражательных течений на новом уровне. Мы планируем рассмотреть ее в ближайшее время.

ИСТОЧНИКИ ФИНАНСИРОВАНИЯ

Работа выполнена при финансовой поддержке Минобрнауки России.

Список литературы

Миропольский Ю.З. Динамика внутренних гравитационных волн в океане. Л.: Гидрометеоиздат, 1981. 302 с.
Морозов Е.Г. Океанские внутренние волны. М.: Наука, 1985. 151 с.
Sutherland B.R. Internal gravity waves. Cambridge: CUP, 2010. 394 p.
Pelinovsky E., Talipova T., Didenkulova I., Didenkulova E. Interfacial long traveling waves in a two-layer fluid with variable depth // Stud. Appl. Math. 2019. V. 142. P. 513–527.
Grimshaw R., Pelinovsky D., Pelinovsky E. Homogenization of variable-speed wave eqation // Wave Motion. 2010. V. 47. P. 496–507.
Талипова Т.Г., Пелиновский Е.Н., Петрухин Н.С. О проникновении длинной внутренней волны в толщу океана // Океанология. 2009. Т. 49. № 5. С. 673–680.
Grimshaw R., Pelinovsky E., Talipova T. Nonreflecting internal wave beam propagation in the deep ocean // J. Phys. Oceanography. 2010. V. 40. P. 802–813.
Талипова Т.Г., Пелиновский Е.Н. Трансформация внутренних волн над неровным дном: аналитические результаты // Океанология. 2011. Т. 51. № 4. С. 621–626.
Талипова Т.Г., Пелиновский Е.Н., Куркина О.Е., Рувинская Е.А., Гиниятуллин А.Р., Наумов А.А. Безотражательное распространение внутренних волн в канале переменного сечения и глубины // Фундам. и прикл. геофиз. 2013. Т. 6. № 3. С. 46–53.
Багаев А.В., Пелиновский Е.Н. Конфигурация канала переменного сечения, допускающая безотражательное распространение внутренних волн в океане // Журн. СВМО. 2016. Т. 18. № 3. С. 127–136.
Churilov S.M., Stepanyants Yu.A. Reflectionless wave propagation on shallow water with variable bathymetry and current // J. Fluid Mech. 2022. V. 931. A15. 25 p.
Музылев С.В. Волны в океане под ледяным покровом: основы теории и модельные задачи // Современные проблемы динамики океана и атмосферы. М.: Триада ЛТД, 2010 г. С. 315–345.
Stepanyants Yu.A., Sturova I.V. Rossby waves in the ocean covered by compressed ice // Geophys. Astrophys. Fluid Dyn. 2020. V. 114. P. 306–316.
Хейсин Д.Е. Динамика ледяного покрова. Л: Гидрометеоиздат, 1967. 215 с.
Букатов А.Е. Влияние продольно сжатой упругой пластинки на неустановившееся волновое движение однородной жидкости // Изв. АН СССР. Механика жидкости и газа. 1980. № 5. С. 68–75.
Baines P.G. A unified description of two-layer flow over topography // J. Fluid Mech. 1984. V. 146. P. 127–167.
Baines P.G. Topographic effects in stratified flows. Cambridge: CUP, 1997. 498 p.
Прудников А.П., Брычков Ю.А., Маричев О.И. Интегралы и ряды. Т. 1. Элементарные функции. М.: Физматлит, 2002. 632 с.
Островский Л.А, Рыбак С.А., Цимринг Л.Ш. Волны отрицательной энергии в гидродинамике // УФН. 1986. Т. 150. № 3. С. 417–437.
Степанянц Ю.А, Фабрикант А.Л. Распространение волн в сдвиговых гидродинамических течениях // УФН. 1989. Т. 159. № 1. С. 83–123.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Физика атмосферы и океана

Архивы выпусков Информация о журнале Отправить рукопись в журнал