1. На главную
  2. Электронные версии
  3. Известия РАН. Физика атмосферы и океана
  4. T. 58, № 3, 2022

Известия РАН. Физика атмосферы и океана, 2022, T. 58, № 3, стр. 263-281

Вихреразрешающее моделирование и исследование параметризаций затухающей турбулентности в вечернем переходе атмосферного пограничного слоя

Е. В. Ткаченко a, *, А. В. Дебольский a, b, Е. В. Мортиков a, c, А. В. Глазунов a, c

a Московский государственный университет им. М.В. Ломоносова, Научно-исследовательский вычислительный центр
119991 Москва, Ленинские горы, 1, стр. 4, Россия

b Институт физики атмосферы им. А.М. Обухова РАН
119017 Москва, Пыжевский пер., 3, Россия

c Институт вычислительной математики им. Г.И. Марчука РАН
119333 Москва, ул. Губкина, 8, Россия

* E-mail: evtkachenko@hotmail.com

Поступила в редакцию 08.10.2021
После доработки 23.01.2022
Принята к публикации 09.02.2022

Полный текст (PDF)

Аннотация

В работе представлены результаты вихреразрешающего моделирования вечернего перехода в атмосферном пограничном слое в случае свободной конвекции и при наличии геострофического ветра. Проведен анализ баланса кинетической энергии турбулентности (КЭТ) и динамики дисперсий компонент скорости, из которого следует существование интервалов быстрого и медленного затухания КЭТ. Показаны различия в характере анизотропии энергии в этих двух режимах. Так, в интервале быстрого затухания значительная часть энергии, находящаяся в вертикальной компоненте на крупных масштабах, разрушается за счет инерционного всплытия термиков после прекращения конвекции. В дальнейшем КЭТ перераспределяется в крупные масштабы горизонтальных компонент, что приводит к квазидвумерному режиму турбулентности, в котором диссипация энергии происходит значительно медленнее, чем в случае изотропной однородной турбулентности. Показано, что одномерная (по вертикали) модель пограничного слоя, в которой турбулентные потоки параметризуются с помощью двухпараметрического замыкания на основе уравнений для КЭТ и скорости ее диссипации, не воспроизводит подобную динамику вечернего перехода. В частности, использование градиентного приближения в одномерной модели приводит к сохранению конвективного распределения потока тепла по вертикали во время переходного периода и дополнительной генерации КЭТ в пограничном слое за счет действия сил плавучести. Привлечение феноменологического уравнения для скорости диссипации может приводить к занижению скорости затухания КЭТ в интервале быстрого затухания и, напротив, к ее завышению в интервале медленного затухания. В работе обсуждаются возможные подходы к модификации RANS (Reynolds-Averaged Navier-Stokes) замыканий для воспроизведения переходных периодов в атмосферном пограничном слое.

Ключевые слова: вихреразрешающее моделирование, вечерний переход, турбулентность, атмосферный пограничный слой

1. ВВЕДЕНИЕ

Планетарный пограничный слой атмосферы (АПС) является нижним слоем атмосферы толщиной от 100 м до 3 км [1], который находится в непосредственном взаимодействии с поверхностью Земли. Он характеризуется турбулентной динамикой, определяющей процессы переноса в воздухе, и наличием суточного хода вследствие нагрева поверхности лучистой энергией Солнца днем и длинноволнового радиационного выхолаживания ночью, что обуславливает чередование устойчивого (УПС) и конвективного (КПС) режимов пограничного слоя (ПС).

Смена одного режима ПС на другой происходит через переходные периоды – утренний переход от устойчивого к конвективному ПС и вечерний – от конвективного к устойчивому. Утренний переход сопровождается нагревом поверхности Земли и передачей тепла в приземный слой атмосферы, и последующим развитием конвективной неустойчивости. Во время вечернего перехода происходит перестройка АПС, формирование более низкого УПС вблизи поверхности и затухание образовавшейся во время дневной конвекции кинетической энергии турбулентности (КЭТ) в располагающемся над УПС остаточном слое.

Существующие параметризации процессов турбулентного обмена, используемые в моделях прогноза погоды и климата, позволяют верно воспроизвести вертикальную структуру первых и вторых моментов гидродинамических полей для горизонтально однородных стратифицированных пограничных слоев, близких к статистически стационарному состоянию [2, 3]. Однако данные замыкания с недостаточной точностью описывают суточный ход [4] и нестационарные процессы в АПС, связанные, в том числе, с резкой сменой крупномасштабных метеорологических полей. Расхождения с данными наблюдений и результатами вихреразрешающего LES (Large-Eddy Simulation) моделирования наблюдаются в оценках температуры и скорости ветра, в особенности в утреннее и вечернее время [5]. Точность описания, например, вечернего переходного периода в свою очередь влияет на воспроизведение моделями формирования струйного течения в УПС и образование радиационных туманов [6], а также на прогноз переноса примесей и химическую реактивность малых газовых составляющих в пограничном слое [7, 8]. Турбулентные замыкания первого и второго порядка, как правило, используют предположения о том, что мелкомасштабные компоненты течения находятся в состояниях близких к стационарным, что позволяет параметризовать статистические моменты более высокого порядка и упростить выражения для турбулентных потоков импульса, тепла и скаляров (см., например, замыкания в работах [9, 10]). В частности, феноменологическое уравнение относительно скорости диссипации КЭТ, используемое в RANS (Reynolds-Averaged Navier-Stokes) моделях [11], аппроксимируется релаксационным соотношением к равновесному состоянию со временем релаксации сопоставимым с турбулентным масштабом времени [3]. Применимость подобных приближений для описания нестационарной динамики турбулентных течений, в особенности при наличии стратификации, и суточного хода АПС на сегодняшний день не установлена и требует детального изучения с помощью данных LES расчетов и прямого DNS (Direct Numerical Simulation) численного моделирования.

В настоящей работе рассматривается возможность привлечения двухпараметрических RANS моделей [11], основанных на решении прогностических уравнений относительно КЭТ и скорости ее диссипации, для параметризации процессов турбулентного обмена во время вечернего перехода в АПС. Замыкания подобного типа применительно к задачам воспроизведения вертикальной структуры АПС исследовались в [3, 12, 13] и используются, например, в негидростатических региональных моделях атмосферы [14, 15] и в трехмерных RANS моделях расчета турбулентного потока в условиях городской застройки [16, 17]. Напротив, в моделях общей циркуляции атмосферы на сегодняшний день, как правило, применяются однопараметрические замыкания, в которых учитывается изменчивость КЭТ, а турбулентный масштаб длины рассчитывается из диагностических соотношений [18]. Вместе с тем в ряде работ (см., например, [13]) отмечается, что достоверное воспроизведение суточного хода в АПС, в том числе при наличии неоднородной подстилающей поверхности, может требовать использования эволюционных уравнений для масштаба длины или связанных величин, скорости диссипации КЭТ или турбулентного масштаба времени, необходимых для задания коэффициентов турбулентного обмена из соотношений подобия. Сравнение параметризаций турбулентного обмена в оперативной модели [15] также показывает возможность уточнения прогноза циклонической активности, скорости ветра в приповерхностном слое и верхней части тропосферы в случае расчета скорости диссипации КЭТ на основе эмпирического эволюционного уравнения.

Для оценки применимости отдельных предположений, используемых в двухпараметрических замыканиях, проведены трехмерные LES эксперименты в идеализированной постановке, где конвективный пограничный слой формируется при предписанном потоке тепла на поверхности, а вечерний переход наступает при его мгновенной смене на нулевой. Эксперименты проводились как для случая свободной конвекции, так и при наличии постоянного геострофического ветра и, соответственно, сдвигово-конвективного режима. Несмотря на очевидные упрощения, данная постановка позволяет напрямую сравнить RANS модель пограничного слоя с результатами LES расчетов.

Интерес представляет возможность воспроизведения затухания КЭТ во время вечернего переходного периода с помощью двухпараметрических моделей, где механизмы генерации, потребления и переноса турбулентной энергии определены замыканием. В частности, верное воспроизведение КЭТ и в общем случае дисперсии поля скорости необходимо для прогнозирования распространения примесей в АПС с помощью лагранжевых стохастических моделей [7]. Вихреразрешающее моделирование вечернего перехода проводилось в работах [19–23], где отмечается, что изменение осредненной по пограничному слою энергии разрешаемых явно турбулентных пульсаций приближенно описывается степенными зависимостями ${{E}_{n}}\left( {{{t}_{n}}} \right) \propto t_{n}^{{ - {{\alpha }}}}$, где параметр ${{\alpha }}$ определяет скорость затухания, ${{E}_{n}}$ и ${{t}_{n}}$ есть КЭТ и время соответственно, обезразмеренные с использованием масштабов конвективного пограничного слоя [24].

Степенные зависимости для скорости затухания КЭТ справедливы для однородной и изотропной турбулентности. В предположении сохранения инварианта Лойцянского в работе А.Н. Колмогорова [25] было показано, что $\alpha = \,\,~{{10} \mathord{\left/ {\vphantom {{10} 7}} \right. \kern-0em} 7}$. Несколько меньшая оценка ${{\alpha }} = \,\,~{6 \mathord{\left/ {\vphantom {6 5}} \right. \kern-0em} 5}$ была получена [26] при рассмотрении интегрального инварианта уравнений Кармана-Ховарта, предложенного в статье [27]. Именно аналитические оценки скорости затухания для однородной нестратифицированной турбулентности, подтверждаемые данными лабораторных и численных DNS экспериментов, используются для калибровки RANS моделей. В то же время согласованный с указанными значениями выбор констант в двухпараметрических замыканиях может приводить к неограниченному росту интегрального турбулентного масштаба длины в режиме затухающей турбулентности [28].

В случае вечернего перехода в работе [20] показано, что ${{\alpha }} = \,\,~2$, при условии, что турбулентный масштаб длины остается постоянным (пропорциональным высоте КПС) во время периода затухания. Однако данные вихреразрешающего моделирования [19, 20, 22, 23] при предписанном ходе изменения поверхностного потока тепла показывают меньшие значения ${{\alpha }}$, от ${{\alpha }} = ~\,\,0.9$ до ${{\alpha }} = \,\,~1.2$. При наличии геострофического ветра и сдвиговой генерации турбулентности наблюдается замедление скорости затухания КЭТ [21, 22], до величины ${{\alpha }} \approx 0.7$. Полученные показатели ${{\alpha }}$ близки к приведенным ранее аналитическим оценкам для однородной турбулентности. Тем не менее вечерний переход в LES экспериментах характеризуется существенным влиянием сил плавучести на структуру течения, свойственной для всего периода анизотропией КЭТ, и разделяется на начальный период быстрого и последующего медленного затухания энергии [20, 29]. По этим причинам найденные значения ${{\alpha }}$ отражают в большей степени лишь эмпирическую оценку средней скорости затухания КЭТ для всего переходного периода. Наконец, отметим, что LES эксперименты в работе [30] с предписанным по данным измерений временным ходом температуры поверхности показывали ускорение затухания от ${{\alpha }} = \,\,~2$ до ${{\alpha }} = \,\,~6$ между начальной и поздней стадиями перехода, что согласуется с анализом натурных измерений [31].

Целью данного исследования является проверка возможности воспроизведения вечернего перехода в АПС с помощью RANS модели в сравнении с результатами LES экспериментов. Структура данной работы следующая: в разделе 2 описываются использующиеся в исследовании LES и RANS модели пограничного слоя, в разделе 3 приведена постановка численных экспериментов. В разделе 4 рассматриваются результаты вихреразрешающего моделирования вечернего перехода и обсуждается сравнение динамики затухающей турбулентности воспроизводимой LES и одномерными RANS моделями. В заключительном разделе представлено обобщение полученных результатов.

2. ЧИСЛЕННЫЕ МОДЕЛИ ПОГРАНИЧНОГО СЛОЯ

Для описания температурно-стратифицированного однородного по горизонтали пограничного слоя атмосферы будем рассматривать систему уравнений Навье–Стокса в приближении Буссинеска, включающую уравнения движения, неразрывности и переноса тепла.

В рамках LES подхода уравнения записываются относительно фильтрованных (по пространству) компонент вектора скорости $\bar {u}(x,t)$ = = $\left( {{{{\bar {u}}}_{1}},{{{\bar {u}}}_{2}},{{{\bar {u}}}_{3}}} \right) \equiv \left( {\bar {u},\bar {v},\bar {w}} \right)$, давления $\bar {p}\left( {x,t} \right)$ и потенциальной температуры ${{\bar {\Theta }}}\left( {x,t} \right)$ (см., например, [29, 32]):

(1)
$\begin{gathered} \frac{{\partial {{{\bar {u}}}_{i}}}}{{\partial t}} + \frac{{\partial {{{\bar {u}}}_{i}}{{{\bar {u}}}_{j}}}}{{\partial {{x}_{j}}}} = - \frac{{\partial {{{{\tau }}}_{{ij}}}}}{{\partial {{x}_{j}}}} - \frac{{\partial {{{\bar {p}}}_{*}}}}{{\partial {{x}_{i}}}} + {{\nu }}\frac{{{{\partial }^{2}}{{{\bar {u}}}_{i}}}}{{\partial {{x}_{j}}\partial {{x}_{j}}}} + \\ + \,\,{{{{\varepsilon }}}_{{ij3}}}f\left( {{{{\bar {u}}}_{j}} - {{G}_{j}}} \right) + {{{{\delta }}}_{{i3}}}{{\beta \bar {\Theta },}} \\ \end{gathered} $
(2)
$\frac{{\partial {{{\bar {u}}}_{i}}}}{{\partial {{x}_{i}}}} = 0,$
(3)
$\frac{{\partial {{\bar {\Theta }}}}}{{\partial t}} + \frac{{\partial {{{\bar {u}}}_{i}}{{\bar {\Theta }}}}}{{\partial {{x}_{i}}}} = - \frac{{\partial {{h}_{i}}}}{{\partial {{x}_{i}}}} + {{\chi }}\frac{{{{\partial }^{2}}{{\bar {\Theta }}}}}{{\partial {{x}_{j}}\partial {{x}_{j}}}},$
где $x = \left( {{{x}_{1}},{{x}_{2}},{{x}_{3}}} \right) \equiv \left( {x,y,z} \right)$, ${{\bar {p}}_{*}} = {{\bar {p}} \mathord{\left/ {\vphantom {{\bar {p}} {{\rho }}}} \right. \kern-0em} {{\rho }}}$, ${{\nu }}$ и ${{\chi }}$ – коэффициенты молекулярной кинематической вязкости и теплопроводности, ${{\rho }}$ – плотность воздуха, ${{\beta }}$ – коэффициент термического расширения, ${{G}_{j}}$ – компоненты вектора скорости геострофического ветра $\left( {{{U}_{g}},{{V}_{g}},0} \right)$, $t$ – время, ${{{{\delta }}}_{{ik}}}$ – символ Кронекера. Слагаемое ${{{{\varepsilon }}}_{{ij3}}}f\left( {{{{\bar {u}}}_{j}} - {{G}_{j}}} \right)$ соответствует действию силы Кориолиса, где ${{{{\varepsilon }}}_{{ijk}}}$ – тензор Леви-Чивиты, $f = 2{{\Omega }}\sin \phi $ – параметр Кориолиса для заданной широты $\phi $, ${{\Omega }}$ – угловая скорость вращения Земли.

Подсеточные/подфильтровые потоки импульса ${{{{\tau }}}_{{ij}}}$ и тепла ${{h}_{i}}$ заданы соотношениями:

(4)
${{{{\tau }}}_{{ij}}} = \overline {{{u}_{i}}{{u}_{j}}} - {{\bar {u}}_{i}}{{\bar {u}}_{j}},$
(5)
${{h}_{i}} = \overline {{{u}_{i}}{{\Theta }}} - {{\bar {u}}_{i}}{{\bar {\Theta },}}$

и содержат зависимость от не разрешаемых явно слагаемых $\overline {{{u}_{i}}{{u}_{j}}} $ и $\overline {{{u}_{i}}{{\Theta }}} $. Для замыкания системы уравнений (1)–(5) используется модель, основанная на определении эффективной турбулентной вязкости и диффузии, дополненная динамической процедурой.

При расчете подсеточного потока импульса анизотропная часть ${{\tau }}_{{ij}}^{a}$ тензора турбулентных напряжений ${{{{\tau }}}_{{ij}}}$ параметризуется в виде:

(6)
${{\tau }}_{{ij}}^{a} = {{{{\tau }}}_{{ij}}} - \frac{1}{3}{{{{\delta }}}_{{ij}}}{{{{\tau }}}_{{kk}}} = - 2{{K}_{{{{\Delta }},m}}}{{\bar {S}}_{{ij}}},$
где ${{\bar {S}}_{{ij}}} = \frac{1}{2}\left( {\frac{{\partial {{{\bar {u}}}_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{{\bar {u}}}_{j}}}}{{\partial {{x}_{i}}}}} \right)$ – тензор скоростей деформаций для фильтрованного поля скорости. Коэффициент турбулентной вязкости ${{K}_{{{{\Delta }},m}}}$ определяется согласно модели Смагоринского, предполагающей локальный баланс сдвиговой генерации подсеточной кинетической энергии турбулентных пульсаций и скорости ее диссипации:
(7)
${{K}_{{{{\Delta }},m}}} = {{\left( {{{C}_{s}}{{\bar {\Delta }}}} \right)}^{2}}\left| {\bar {S}} \right|,$
где ${{C}_{s}}$ – коэффициент Смагоринского, $\left| {\bar {S}} \right|$ = = $\sqrt {2{{S}_{{ij}}}{{S}_{{ij}}}} $ – норма тензора скоростей деформации, ${{\bar {\Delta }}}$ – ширина фильтра, в численной реализации равная шагу сетки. Схожим образом вклад подсеточного потока тепла выражается через коэффициент турбулентной диффузии ${{K}_{{{{\Delta }},h}}}$:
(8)
${{h}_{i}} = - {{K}_{{{{\Delta }},h}}}\frac{{\partial {{\bar {\Theta }}}}}{{\partial {{x}_{i}}}} = - {{K}_{{{{\Delta }},m}}}Pr_{{{\text{sgs}}}}^{{ - 1}}\frac{{\partial {{\bar {\Theta }}}}}{{\partial {{x}_{i}}}},$
где $P{{r}_{{{\text{sgs}}}}} = {{{{K}_{{{{\Delta }},m}}}} \mathord{\left/ {\vphantom {{{{K}_{{{{\Delta }},m}}}} {{{K}_{{{{\Delta }},h}}}}}} \right. \kern-0em} {{{K}_{{{{\Delta }},h}}}}}$ – подсеточное турбулентное число Прандтля.

Динамическая процедура [33, 34] используется для расчета коэффициента Смагоринского ${{C}_{s}} = {{C}_{s}}\left( {{\mathbf{x}},t} \right)$ и подсеточного числа Прандтля $P{{r}_{{{\text{sgs}}}}} = P{{r}_{{{\text{sgs}}}}}\left( {{\mathbf{x}},t} \right)$, что исключает необходимость привлечения эмпирических зависимостей для их задания в модели. Фильтрация исходной системы уравнений с помощью дополнительного “тестового” фильтра $\hat {a}\left( {{\mathbf{x}},t} \right) = {{F}_{{{{\hat {\Delta }}}}}}a\left( {{\mathbf{x}},t} \right)$ шириной ${{\hat {\Delta }}} = \eta {{\bar {\Delta }}}$, где $\eta > \,\,~1$, позволяет записать тождество Германо:

(9)
${{T}_{{ij}}} - \widehat {{{{{\tau }}}_{{ij}}}} = {{L}_{{ij}}} \equiv \widehat {{{{\bar {u}}}_{i}}{{{\bar {u}}}_{j}}} - \widehat {{{{\bar {u}}}_{i}}}\widehat {{{{\bar {u}}}_{j}}}.$

Здесь ${{T}_{{ij}}} = \widehat {\overline {{{u}_{i}}{{u}_{j}}} } - \widehat {{{{\bar {u}}}_{i}}}\widehat {{{{\bar {u}}}_{j}}}$ – тензор турбулентных напряжений, полученный при последовательном применении базового и тестового фильтров к уравнениям (1) и (2), а правая часть тождества (9) содержит зависимость только от фильтрованных компонент вектора скорости. Тогда, используя модель (6) для параметризации подсеточных напряжений ${{{{\tau }}}_{{ij}}}$ и ${{T}_{{ij}}}$, можно получить систему уравнений:

(10)
$C_{{{\Delta }}}^{2}{{M}_{{ij}}} = L_{{ij}}^{a} + {{e}_{{ij}}},$
где ${{C}_{{{\Delta }}}} = {{C}_{s}}{{\bar {\Delta }}}$, ${{M}_{{ij}}} = 2\left( {\widehat {\left| {\bar {S}} \right|{{{\bar {S}}}_{{ij}}}} - {{\eta }^{2}}\left| {\hat {\bar {S}}} \right|\widehat {{{{\bar {S}}}_{{ij}}}}} \right)$, $L_{{ij}}^{a}$ – девиатор тензора ${{L}_{{ij}}}$, ${{e}_{{ij}}}$ – невязка тождества Германо, связанная с неточностью описания подсеточной моделью истинного тензора турбулентных напряжений.

Для минимизации квадрата невязки системы (10) используется подход, предложенный в работах [35, 36] и основанный на осреднении вдоль лагранжевых траекторий, который при задании экспоненциально затухающих весовых функций сводится к решению нескольких эволюционных уравнений. Динамическая процедура с осреднением вдоль лагранжевых траекторий аналогично применяется и для расчета подсеточного потока тепла (5), что позволяет определить подсеточное число Прандтля $P{{r}_{{{\text{sgs}}}}}$ как функцию пространственных координат и времени.

В настоящей работе использовалась LES модель атмосферного пограничного слоя, разрабатываемая в НИВЦ МГУ и ИВМ РАН на основе единого гидродинамического кода, объединяющего как LES-, так и DNS- и RANS- подходы для расчета геофизических турбулентных течений при высоком пространственном и временном разрешении (см., например, [29, 37–40]). В численной модели используются консервативные конечно-разностные схемы [41] второго порядка точности для аппроксимации по пространству на прямоугольных сетках. Метод дробных шагов [42] применяется для интегрирования уравнений движения и неразрывности по времени при явной аппроксимации схемой Адамса-Башфорта третьего порядка операторов переноса импульса и тепла. Поправка к давлению, обеспечивающая выполнение уравнения неразрывности для поля скорости на каждом шаге по времени, находится из решения уравнения Пуассона с помощью итерационного метода бисопряженных градиентов с геометрическим многосеточным методом в качестве предобуславливателя. В динамической процедуре LES модели тестовый фильтр определяется согласно [32, 43], а отношение ширины базового и тестового фильтров $\eta $ вычисляется, следуя работе [44]. Программная реализация численной модели для параллельных вычислительных систем основана на гибридном MPI-OpenMP-CUDA подходе и позволяет проводить расчеты на суперкомпьютерах гетерогенной архитектуры.

Для горизонтально однородного стратифицированного турбулентного потока одномерные (по вертикали) уравнения RANS модели имеют вид:

(11)
$\frac{{\partial U}}{{\partial t}} + \frac{{\partial {{{{\tau }}}_{x}}}}{{\partial z}} = f\left( {V - {{V}_{g}}} \right),$
(12)
$\frac{{\partial V}}{{\partial t}} + \frac{{\partial {{{{\tau }}}_{y}}}}{{\partial z}} = - f\left( {U - {{U}_{g}}} \right),$
(13)
$\frac{{\partial {{\Theta }}}}{{\partial t}} + \frac{{\partial {{F}_{z}}}}{{\partial z}} = 0.$

Здесь $U$, $V$ и ${{\Theta }}$ – горизонтальные компоненты скорости ветра и потенциальная температура соответственно, осредненные по Рейнольдсу (ансамблю реализаций). Компоненты турбулентного потока импульса ${{{{\tau }}}_{x}},{{{{\tau }}}_{y}}$ и турбулентный кинематический поток тепла ${{F}_{z}}$ рассчитываются с помощью градиентного приближения:

(14)
${{{{\tau }}}_{x}} = - {{K}_{m}}\frac{{\partial U}}{{\partial z}},$
(15)
${{{{\tau }}}_{y}} = - {{K}_{m}}\frac{{\partial V}}{{\partial z}},$
(16)
${{F}_{z}} = - {{K}_{h}}\frac{{\partial {{\Theta }}}}{{\partial z}},$
где ${{K}_{m}}$ и ${{K}_{h}}$ есть коэффициенты турбулентной вязкости и теплопроводности, которые, в отличие от LES постановки, не зависят от масштабов длины, связанных с шириной фильтра или сеточным разрешением. Система уравнений (11)–(13) соответствует упрощенной модели пограничного слоя, используемой в крупномасштабных моделях атмосферы, и в случае верной параметризации турбулентных потоков должна быть согласована с результатами трехмерного вихреразрешающего моделирования.

Будем рассматривать двухпараметрическое замыкание, в котором коэффициенты ${{K}_{m}}$ и ${{K}_{h}}$ определяются из соотношений подобия:

(17)
${{K}_{m}} = {{S}_{m}}\frac{{E_{k}^{2}}}{{{\varepsilon }}},$
(18)
${{K}_{h}} = {{S}_{h}}\frac{{E_{k}^{2}}}{{{\varepsilon }}} \equiv {{{{K}_{m}}} \mathord{\left/ {\vphantom {{{{K}_{m}}} {P{{r}_{t}}}}} \right. \kern-0em} {P{{r}_{t}}}},$
где кинетическая энергия турбулентности ${{E}_{k}}$ и скорость ее диссипации ${{\varepsilon }}$ находятся из решения эволюционных уравнений:
(19)
$\frac{{\partial {{E}_{k}}}}{{\partial t}} - \frac{\partial }{{\partial z}}\frac{{{{K}_{m}}}}{{{{{{\sigma }}}_{k}}}}\frac{{\partial {{E}_{k}}}}{{\partial z}} = P + B - {{\varepsilon ,}}$
(20)
$\frac{{\partial {{\varepsilon }}}}{{\partial t}} - \frac{\partial }{{\partial z}}\frac{{{{K}_{m}}}}{{{{{{\sigma }}}_{{{\varepsilon }}}}}}\frac{{\partial {{\varepsilon }}}}{{\partial z}} = \frac{{{\varepsilon }}}{{{{E}_{k}}}}\left( {{{C}_{{1{{\varepsilon }}}}}P - {{C}_{{2{{\varepsilon }}}}}{{\varepsilon }} + {{C}_{{3{{\varepsilon }}}}}B} \right),$
здесь ${{S}_{m}}$ и ${{S}_{h}}$ – функции устойчивости, $P{{r}_{t}}$ – турбулентное число Прандтля, ${{{{\sigma }}}_{k}}$, ${{{{\sigma }}}_{{{\varepsilon }}}}$, ${{C}_{{1{{\varepsilon }}}}}$, ${{C}_{{2{{\varepsilon }}}}}$, ${{C}_{{3{{\varepsilon }}}}}$ – параметры замыкания, $P$ – сдвиговая генерация КЭТ, $B$ – генерация (или потребление) КЭТ силами плавучести:

(21)
$P = {{K}_{m}}\left[ {{{{\left( {\frac{{\partial U}}{{\partial z}}} \right)}}^{2}} + {{{\left( {\frac{{\partial V}}{{\partial z}}} \right)}}^{2}}} \right],$
(22)
$B = - \beta {{K}_{h}}\frac{{\partial \Theta }}{{\partial z}}.$

Значения параметров замыкания (17)–(20) были заданы в соответствии с работами [3, 11]: ${{\sigma }_{k}} = 1.0$, ${{\sigma }_{\varepsilon }} = 1.3$, ${{C}_{{1{{\varepsilon }}}}} = 1.44$, ${{C}_{{2{{\varepsilon }}}}} = 1.92$, ${{C}_{{3{{\varepsilon }}}}} = - 0.4$ при устойчивой стратификации, $B~\,\, < \,\,~0$, и C3ε = = –1.14 для конвективного случая, $B~\,\, > \,\,~0$. Безразмерные функции устойчивости для импульса и для тепла полагались постоянными ${{S}_{h}} = {{S}_{m}} \equiv 0.09$, подразумевая $P{{r}_{t}} = 1.0$. Несмотря на ряд упрощений, данный выбор позволяет, в частности, воспроизвести скорость затухания кинетической энергии пульсаций скорости для однородной турбулентности [11], вертикальное распределение скорости ветра, температуры, потоков импульса и тепла для квазистационарных устойчиво-стратифицированных пограничных слоев [3] и, как будет показано далее, согласуется с результатами вихреразрешающего моделирования для растущего конвективного пограничного слоя.

В двухпараметрической модели выражения для коэффициентов турбулентной вязкости (17) и теплопроводности (18), следуя работе [10], можно записать в виде ${{K}_{{m,h}}} \sim {{E}_{w}}{{t}_{T}}$, где ${{t}_{T}} = {{{{E}_{k}}} \mathord{\left/ {\vphantom {{{{E}_{k}}} {{\varepsilon }}}} \right. \kern-0em} {{\varepsilon }}}$ – турбулентный масштаб времени. Тогда использование постоянных функций устойчивости ${{S}_{{m,h}}}$ соответствует заданию фиксированной доли ${{{{E}_{w}}} \mathord{\left/ {\vphantom {{{{E}_{w}}} {{{E}_{k}}}}} \right. \kern-0em} {{{E}_{k}}}}$ вертикальной компоненты КЭТ. Замыкание также не учитывает и зависимость турбулентных потоков от характеристик устойчивой стратификации, например, в виде параметризации турбулентного числа Прандтля $P{{r}_{t}} = {{{{K}_{m}}} \mathord{\left/ {\vphantom {{{{K}_{m}}} {{{K}_{h}}}}} \right. \kern-0em} {{{K}_{h}}}}$. Подобные предположения могут нарушаться для вечернего перехода, в частности при воспроизведении интервала быстрого затухания КЭТ и последующего периода замедления затухания, где, как будет показано далее, анизотропия энергии и влияние сил плавучести при $B\,\,~ < \,\,~0$ существенны. Возможность использования известных функций устойчивости ${{S}_{{m,h}}}$ (см., например, [9, 10]), которые получены в предположении стационарности уравнений относительно вторых моментов, для описания вечернего перехода в АПС на наш взгляд не очевидна и требует детального изучения балансов одноточечных моментов в нестационарных режимах. Заметим также и то, что такие параметризации применимы лишь для горизонтально однородных течений и не используются, как правило, в трехмерных RANS моделях [16], где функции устойчивости полагаются постоянными.

3. ПОСТАНОВКА ЭКСПЕРИМЕНТОВ

В численных экспериментах рассматривался вечерний переход при мгновенной смене поверхностного потока тепла. В течение первого часа формировался конвективный ПС при постоянном кинематическом потоке тепла на поверхности ${{F}_{s}} = 0.35$ К м с–1, что соответствует потоку плавучести ${{B}_{s}} = \beta {{F}_{s}} \approx 0.0142$ м2 с–3, где $\beta = {g \mathord{\left/ {\vphantom {g {{{\Theta }_{0}}}}} \right. \kern-0em} {{{\Theta }_{0}}}}$, ${{\Theta }_{0}} = 241$ K, $g\,\,~ = \,\,~9.81$ м с–2 – ускорение свободного падения. Постановка данной части эксперимента согласуется с LES расчетами КПС в работе [45]. По истечении первого часа поток тепла мгновенно менялся на ${{F}_{s}} = 0$, после чего расчеты продолжались еще один час модельного времени.

Граничные условия для скорости на нижней границе задавались в виде потока импульса ${{\tau }_{{i3}}}\left( {x,y,t} \right)$, $i = 1,2$, рассчитанного в приближении логарифмического слоя:

(23)
${{\tau }_{{i3}}}\left( {x,y,t} \right) = - {{\left( {\frac{{\left| {{{{\bar {u}}}_{h}}} \right|\kappa }}{{\ln \left( {{{{{z}_{s}}} \mathord{\left/ {\vphantom {{{{z}_{s}}} {{{z}_{0}}}}} \right. \kern-0em} {{{z}_{0}}}}} \right)}}} \right)}^{2}}\frac{{{{{\bar {u}}}_{i}}}}{{\left| {{{{\bar {u}}}_{h}}} \right|}},$
где локальная мгновенная скорость ${{\bar {u}}_{i}} \equiv {{\bar {u}}_{i}}\left( {x,y,z,t} \right)$ и модуль горизонтальной скорости $\left| {{{{\bar {u}}}_{h}}} \right| \equiv \left| {{{{\bar {u}}}_{h}}} \right|(x,y,z,t)$ = = ${{\left( {{{{\bar {u}}}^{2}} + {{{\bar {v}}}^{2}}} \right)}^{{1/2}}}$ берутся на высоте ${{z}_{s}} = {{{{\Delta }_{z}}} \mathord{\left/ {\vphantom {{{{\Delta }_{z}}} 2}} \right. \kern-0em} 2}$, ${{{{\Delta }}}_{z}}$ – шаг расчетной ячейки по вертикали вблизи поверхности, $\kappa = \,\,~0.4$ – постоянная Кармана, ${{z}_{0}} = 0.1$ м – параметр динамической шероховатости. Граничное условие для вертикальной скорости соответствует непротеканию. На верхней границе потоки импульса и тепла полагались равными нулю.

Для моделирования свободной конвекции и конвекции со сдвигом задавались соответствующие значения геострофического ветра, ${{U}_{g}} = 0$ и ${{U}_{g}} = 7.5$ м с–1, при фиксированном параметре Кориолиса $f = 6.973 \times {{10}^{{ - 5}}}$ c–1. В начальный момент времени скорость потока полагалась постоянной $U = \left( {{{U}_{g}},0,0} \right)$, а вертикальное распределение температуры задавалось в виде перемешанного слоя $\Theta \left( {z < {{h}_{0}}} \right) = {{\Theta }_{0}}$ высотой ${{h}_{0}} = 250$ м и линейного градиента над ним $\Theta \left( {z > {{h}_{0}}} \right) = {{\Theta }_{0}} + \gamma \left( {z - {{h}_{0}}} \right)$, где $\gamma = 0.03$ К м–1 – градиент температуры в свободной атмосфере.

Для всех LES экспериментов размер вычислительной области составлял 2 км по всем координатам. По горизонтали использовались периодические граничные условия. В верхней части области к полям скорости и скаляров также применялось рэлеевское трение с целью дэмпфирования гравитационных волн, которые излучаются в слое вовлечения, и их дальнейшего переотражения обратно в расчетную область.

В работе [29] отмечается чувствительность интегральных характеристик вечернего перехода к выбору разрешения сетки и подсеточной LES модели. В настоящей работе вихреразрешающее моделирование проводилось на сетке из 5123 ячеек при пространственном разрешении около 4 метров, что на основе оценок [29] и с учетом использования динамического LES-замыкания представляется достаточным для воспроизведения динамики переходного периода.

Постановка RANS экспериментов повторяет LES расчеты. В численной реализации RANS модели (11)–(20) использовалась подробная сетка по вертикали и времени для исключения влияния погрешности дискретизации уравнений на результаты сравнений.

4. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ ЭКСПЕРИМЕНТОВ

Конвективный пограничный слой

На рис. 1 приведено вертикальное распределение температуры, скорости ветра, потоков импульса и тепла в конвективном пограничном слое в LES и RANS моделях до начала вечернего перехода. Мгновенные вертикальные распределения по данным вихреразрешающего моделирования получены с помощью горизонтального осреднения ${{\left\langle \phi \right\rangle }_{{x,y}}}$, где $\phi $ является, например, компонентой вектора скорости $\bar {u}\left( {x,t} \right)$ или потенциальной температурой $\bar {\Theta }\left( {x,t} \right)$. Тогда турбулентные потоки импульса и тепла определены как ${{\tau }_{x}} = {{\left\langle {u{\kern 1pt} 'w{\kern 1pt} '} \right\rangle }_{{x,y}}} + {{\left\langle {{{\tau }_{{13}}}} \right\rangle }_{{x,y}}}$ и ${{F}_{z}} = {{\left\langle {\Theta {\kern 1pt} 'w{\kern 1pt} '} \right\rangle }_{{x,y}}} + {{\left\langle {{{F}_{3}}} \right\rangle }_{{x,y}}}$, где ${{\tau }_{{13}}}$ и ${{F}_{3}}$ – подсеточный вклад в поток LES замыкания (4) и (5) соответственно, $\phi {\kern 1pt} ' = \bar {\phi } - {{\left\langle {\bar {\phi }} \right\rangle }_{{x,y}}}$ есть отклонение от средней величины. Результаты сравнения на рисунке 1 показаны для момента времени ${{t}_{n}} \approx 11.7$, где ${{t}_{n}} = {t \mathord{\left/ {\vphantom {t {{{t}_{*}}}}} \right. \kern-0em} {{{t}_{*}}}}$ – безразмерное время с начала эксперимента, ${{t}_{*}} = {{{{h}_{{CBL}}}} \mathord{\left/ {\vphantom {{{{h}_{{CBL}}}} {{{w}_{*}}}}} \right. \kern-0em} {{{w}_{*}}}}$ и ${{w}_{*}} = {{\left( {{{B}_{s}}{{h}_{{CBL}}}} \right)}^{{1/3}}}$ – конвективные масштабы времени и скорости [24], ${{h}_{{CBL}}}$ – высота пограничного слоя, которая, следуя работам [4, 11], рассчитывалась по высоте минимума потока тепла непосредственно до наступления вечернего перехода.

Рис. 1.

Распределение КЭТ по отдельным компонентам ${{E}_{u}}$ (штриховая линия), ${{E}_{v}}$ (штрихпунктирная линия) и ${{E}_{w}}$ (сплошная линия) во время вечернего перехода: (а), (б) средние по КПС значения ${{\left\langle {{{E}_{i}}} \right\rangle }_{z}}$ и (в), (г) анизотропия осредненных компонент; (д), (е) анизотропия энергии для высоты $z = 200$ м, $z \approx {{{{h}_{{CBL}}}} \mathord{\left/ {\vphantom {{{{h}_{{CBL}}}} 2}} \right. \kern-0em} 2}$. Левая колонка соответствует случаю свободной конвекции, правая – сдвигово-конвективному режиму.

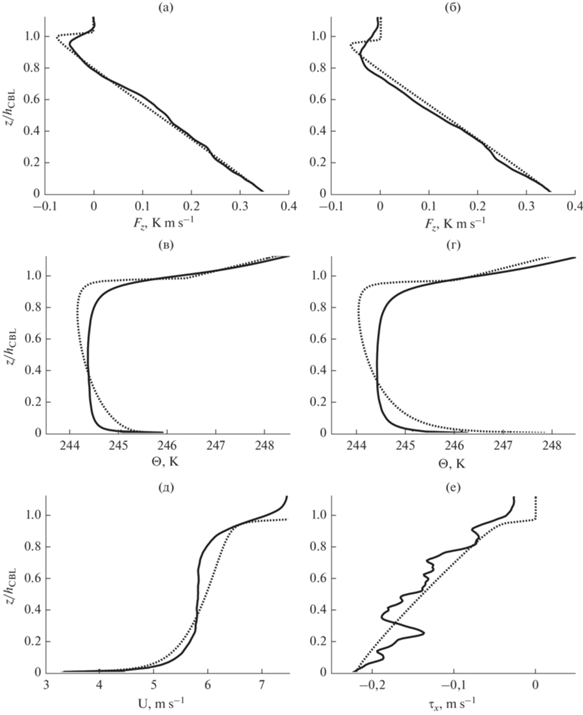
Одномерная RANS модель достаточно точно воспроизводит изменение высоты КПС со временем и толщину слоя вовлечения, а также значения потока тепла в нем (рис. 1a, б). До вечернего перехода в LES расчетах высота пограничного слоя составляла ${{h}_{{CBL}}} \approx 450$ м, а значения в RANS экспериментах отличалась на величины, сопоставимые с сеточным шагом. Однако использование градиентного приближения для параметризации турбулентного потока тепла (16) не позволяет воспроизвести перемешанный слой с почти постоянной по высоте температурой (рис. 1в, 1г), наблюдаемой в LES модели. Расхождения при схожем распределении потока импульса также наблюдаются в профиле скорости ветра (рис. 1д, 1е) в эксперименте при ${{U}_{g}} = 7.5$ м с–1, где RANS замыкание завышает градиент внутри КПС.

Затухание КЭТ в переходном периоде

Сравнение затухания КЭТ, осредненной по всей толщине пограничного слоя во время вечернего перехода для LES и RANS моделей, приведено на рис. 2, где ${{E}_{n}}\left( t \right) = w_{*}^{{ - 2}}{{\left\langle {{{E}_{k}}\left( {z,t} \right)} \right\rangle }_{z}} \equiv $ $ \equiv w_{*}^{{ - 2}}h_{{CBL}}^{{ - 1}}\int_0^{{{h}_{{CBL}}}} {{{E}_{k}}\left( {z,t} \right)dz} $. В вихреразрешающей модели на каждом шаге по времени рассчитывалась разрешаемая явно энергия турбулентных пульсаций поля скорости ${{E}_{k}}\left( {z,t} \right) = {{{{{\left\langle {u_{i}^{'}u_{i}^{'}} \right\rangle }}_{{x,y}}}} \mathord{\left/ {\vphantom {{{{{\left\langle {u_{i}^{'}u_{i}^{'}} \right\rangle }}_{{x,y}}}} 2}} \right. \kern-0em} 2}$. Подсеточная компонента кинетической энергии не учитывалась в связи с необходимостью привлечения дополнительных предположений в LES замыкании о спектральном распределении энергии для расчета следа тензора турбулентных напряжений. Оценки с помощью известных параметризаций (см., например, [46]) показывают, что доля осредненной по КПС подсеточной энергии составляет не более 5–10% от ${{E}_{n}}\left( t \right)$ во время вечернего перехода, а огрубление вычислительной сетки в два раза не приводит к значимым различиям в интегральных характеристиках затухания.

Рис. 2.

Затухание КЭТ в вечернем переходном периоде для LES (сплошная линия) и RANS (пунктирная линия) моделей в случае (а) свободной конвекции и (б) сдвигово-конвективного режима.

В LES экспериментах выделяются два интервала затухания КЭТ во время вечернего перехода. На рис. 2 отмечены показатели ${{\alpha }}$ для степенных зависимостей ${{E}_{n}}\left( t \right) \propto t_{n}^{{ - \alpha }}$ на временных интервалах с относительно постоянной скоростью затухания. Можно выделить начальный период быстрого затухания кинетической энергии продолжительности $ \sim {{t}_{*}}$, который сменяется периодом, где скорость затухания существенно замедляется. В двухпараметрическом замыкании в отсутствии геострофического ветра скорость затухания КЭТ близка к постоянной (рис. 2a), что приводит к завышению ${{E}_{n}}\left( t \right)$ в начале вечернего перехода, а на больших временах RANS модель, напротив, занижает величину осредненной по пограничному слою кинетической энергии турбулентности. Различия между величиной КЭТ в LES и RANS моделях при наличии геострофического ветра (рис. 2б) и, соответственно, источника сдвиговой генерации турбулентности уменьшаются при установлении стационарного состояния. Тем не менее по окончании переходного периода RANS замыкание завышает значение средней энергии. Наиболее значимые расхождения между моделями наблюдаются до ${{t}_{n}} \approx 20$, как в режиме свободной конвекции, так и для случая сдвигово-конвективного пограничного слоя.

Динамика анизотропии КЭТ

Рассмотрим основные различия в структуре течения в интервалах быстрого и медленного затухания КЭТ в LES экспериментах.

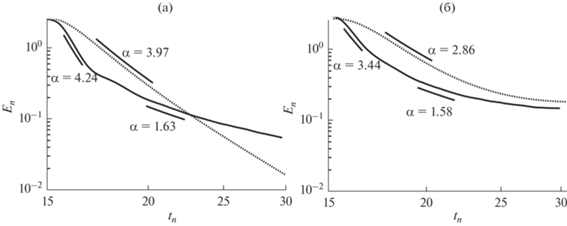
На рис. 3a и 3б приведено распределение разрешаемой явно кинетической энергии турбулентности между отдельными компонентами ${{E}_{u}} \equiv {{E}_{1}} = {{{{{\left\langle {{{{\left( {u{\kern 1pt} '} \right)}}^{2}}} \right\rangle }}_{{x,y}}}} \mathord{\left/ {\vphantom {{{{{\left\langle {{{{\left( {u{\kern 1pt} '} \right)}}^{2}}} \right\rangle }}_{{x,y}}}} 2}} \right. \kern-0em} 2}$, ${{E}_{v}} \equiv {{E}_{2}} = {{{{{\left\langle {{{{\left( {v{\kern 1pt} '} \right)}}^{2}}} \right\rangle }}_{{x,y}}}} \mathord{\left/ {\vphantom {{{{{\left\langle {{{{\left( {v{\kern 1pt} '} \right)}}^{2}}} \right\rangle }}_{{x,y}}}} 2}} \right. \kern-0em} 2}$ и Ew ≡ ${{E}_{3}} = {{{{{\left\langle {{{{\left( {w{\kern 1pt} '} \right)}}^{2}}} \right\rangle }}_{{x,y}}}} \mathord{\left/ {\vphantom {{{{{\left\langle {{{{\left( {w{\kern 1pt} '} \right)}}^{2}}} \right\rangle }}_{{x,y}}}} 2}} \right. \kern-0em} 2}$ во время вечернего перехода при осреднении по высоте КПС. Вертикальная составляющая затухает быстрее горизонтальных, что в особенности выражено в начале перехода. В случае отсутствия геострофического ветра (см. рис. 3в, 3д) доля ${{E}_{w}}$ как в среднем, так и локально в толще пограничного слоя последовательно уменьшается. Режим быстрого затухания КЭТ здесь сопровождается изотропизацией энергии, сменяющейся режимом медленного затухания, характеризующимся увеличением анизотропии и переходом к квазидвумерному течению, в котором энергия сосредоточена преимущественно в горизонтальных компонентах. При наличии геострофического ветра (см. рис. 3г, 3е) схожая динамика наблюдается в начале перехода, а затем анизотропия энергии за время около $5{{t}_{*}}$ приближается к значениям характерным для нейтрального и слабоустойчивого сдвигового ПС, где ${{{{E}_{w}}} \mathord{\left/ {\vphantom {{{{E}_{w}}} {{{E}_{k}}}}} \right. \kern-0em} {{{E}_{k}}}} \sim 0.2$, см., например, [10].

Рис. 3.

Распределение КЭТ по отдельным компонентам ${{E}_{u}}$ (штриховая линия), ${{E}_{v}}$ (штрихпунктирная линия) и ${{E}_{w}}$ (сплошная линия) во время вечернего перехода: (а), (б) средние по КПС значения ${{\left\langle {{{E}_{i}}} \right\rangle }_{z}}$ и (в), (г) анизотропия осредненных компонент; (д), (е) анизотропия энергии для высоты $z = 200$ м, $z \approx {{{{h}_{{CBL}}}} \mathord{\left/ {\vphantom {{{{h}_{{CBL}}}} 2}} \right. \kern-0em} 2}$. Левая колонка соответствует случаю свободной конвекции, правая – сдвигово-конвективному режиму.

На рис. 4 представлены гистограммы распределений для аномалий компонент скорости $\bar {u}$ и $\bar {w}$ в случае свободной конвекции и трех различных моментов времени, соответствующих конвективному режиму до начала вечернего перехода $t_{n}^{{\left( 1 \right)}} = 15$, окончанию интервала быстрого затухания КЭТ $t_{n}^{{\left( 2 \right)}} = 16.6$ и времени завершения эксперимента $t_{n}^{{\left( 3 \right)}} = 30$. В табл. 1 приведены оценки коэффициента асимметрии ${{{{\gamma }}}_{1}}$ и эксцесса ${{{{\gamma }}}_{2}}$ для этих моментов времени, здесь ${{\gamma }_{1}} = {{{{\mu }_{3}}} \mathord{\left/ {\vphantom {{{{\mu }_{3}}} {{{\sigma }^{3}}}}} \right. \kern-0em} {{{\sigma }^{3}}}}$ – коэффициент асимметрии, ${{{{\mu }}}_{3}}$ и ${{\sigma }}$ – третий центральный момент и среднеквадратичное отклонение случайной величины соответственно, ${{\gamma }_{2}} = {{{{\mu }_{4}}} \mathord{\left/ {\vphantom {{{{\mu }_{4}}} {{{\sigma }^{4}}}}} \right. \kern-0em} {{{\sigma }^{4}}}} - 3$ коэффициент эксцесса, ${{{{\mu }}}_{4}}$ – четвертый центральный момент случайной величины. В конвективном пограничном слое наблюдается характерная асимметрия в распределении вертикальной скорости, которая напрямую связана с крупномасштабными структурами в КПС, где положительные флуктуации скорости сконцентрированы в термиках – тонких и быстро всплывающих струях, а отрицательные в компенсирующем их медленном оседании в большей части конвективной ячейки.

Рис. 4.

Гистограммы распределения нормированных аномалий вертикальной $\bar {w}$ (а) и горизонтальной $\bar {u}$ (б) компонент скорости ветра внутри КПС для случая свободной конвекции.

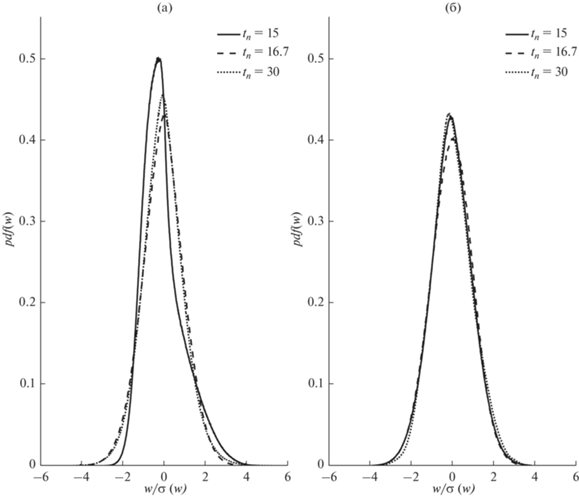
Таблица 1.  

Статистические характеристики компонент поля скорости

  $t_{n}^{{\left( 1 \right)}} = 15$ $t_{n}^{{\left( 2 \right)}} = 16.6$ $t_{n}^{{\left( 3 \right)}} = 30$
${{\left. {{{\gamma }_{1}}(\bar {w})} \right|}_{{{{t}_{n}}}}}$ 0.871 –0.027 0.167
${{\left. {{{\gamma }_{1}}(\bar {u})} \right|}_{{{{t}_{n}}}}}$ 0.019 –0.058 0.179
${{\left. {{{\gamma }_{2}}(\bar {w})} \right|}_{{{{t}_{n}}}}}$ 0.191 0.188 0.790
${{\left. {{{\gamma }_{2}}(\bar {u})} \right|}_{{{{t}_{n}}}}}$ 0.758 –0.004 0.105

В конце интервала быстрого затухания КЭТ распределение вертикальной скорости приближается к симметричной. Здесь оставшиеся термики в отсутствии источника плавучести по инерции всплывают и разрушаются в слое вовлечения. Поскольку конвергенция течения в струи у поверхности и расплывание термиков в слое вовлечения не зависят от горизонтального направления, асимметрия распределения компоненты $\bar {u}$ в КПС значительно ниже, по сравнению с оценкой для вертикальной скорости, и остается небольшой в конце периода изотропизации энергии. При замедлении скорости затухания КЭТ асимметрия как горизонтальной, так и вертикальной компонент скорости начинает расти.

Приведенная зависимость коэффициента ${{\gamma }_{1}}$ от времени для вечернего перехода согласуется с оценками в работе [21] по данным LES моделирования. Учитывая выраженную анизотропию КЭТ и преобладание энергии в горизонтальных компонентах в периоде медленного затухания, увеличение показателя асимметрии распределения может быть связано с менее эффективной передачей энергии по спектру из крупных масштабов в мелкие в формирующемся квазидвумерном течении, чем в изотропной турбулентности. На эту причину также указывает и изменение коэффициента эксцесса, который увеличивается как для горизонтальной, так и для вертикальной компонент скорости при переходе от быстрого интервала затухания к медленному. Рост ${{\gamma }_{2}}$ в интервале медленного затухания КЭТ соответствует уменьшению доли малых по амплитуде флуктуаций скорости, характерных для мелкомасштабной турбулентности.

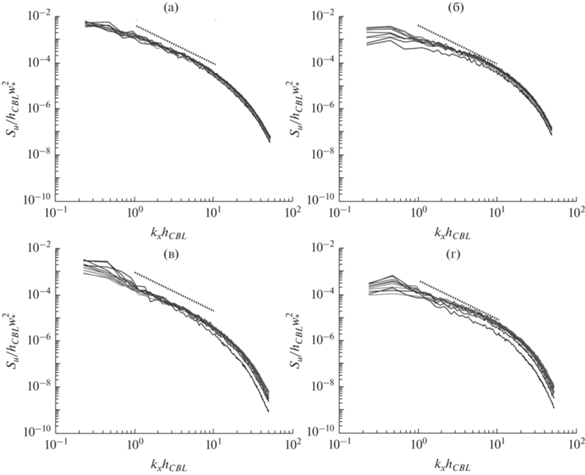
Различия в спектрах флуктуаций компонент $\bar {u}$ и $\bar {w}$ скорости во время вечернего перехода, приведенные на рис. 5, подтверждают формирование квазидвумерной турбулентности с преобладанием энергии в крупных горизонтальных масштабах в период медленного затухания КЭТ. Для горизонтальной компоненты $\bar {u}$ доля энергии, приходящейся на область малых волновых чисел ${{k}_{x}} \lesssim h_{{CBL}}^{{ - 1}}$, в конце интервала быстрого затухания КЭТ оказывается меньше, по сравнению с последующим периодом замедления скорости затухания (см. рис. 5a, 5в). Схожая зависимость наблюдается и для вертикальной компоненты скорости (см. рис. 5б, 5г), где к тому же энергия падает на порядок на всем спектре, что наблюдается и в затухании ${{E}_{w}}$ (рис. 3).

Рис. 5.

Нормированные одномерные (в продольном направлении $x$) спектры дисперсии горизонтальной (а), в) и вертикальной (б), (г) компонент скорости при ${{t}_{n}} \approx 16.7$ (а), (б) и ${{t}_{n}} \approx 21.6$ (в), (г) на высотах от 50 до 450 м внутри КПС для случая свободной конвекции. Пунктирная линия соответствует степенной зависимости ${{S}_{i}} \sim {{k}^{{ - 5/3}}}$ для инерционного интервала.

Баланс КЭТ в пограничном слое

Запишем уравнение баланса для энергии турбулентных пульсаций скорости ${{E}_{k}} = {{\left\langle {u_{i}^{'}u_{i}^{'}} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {u_{i}^{'}u_{i}^{'}} \right\rangle } 2}} \right. \kern-0em} 2}$ в LES модели:

(24)
$T~\,\, + \,\,~P\,\,~ + \,\,~B\,\,~ + \,\,~D\,\,~ - \,\,~\varepsilon = ~R,$
(25)
$T = - \frac{{\partial {{E}_{k}}}}{{\partial t}},$
(26)
$P = - \left( {\left\langle {u_{i}^{'}w{\kern 1pt} '\,} \right\rangle \, + \left\langle {{{{{\tau }}}_{{i3}}}} \right\rangle } \right)\frac{{\partial {{{\left\langle {\bar {u}} \right\rangle }}_{i}}}}{{\partial z}},$
(27)
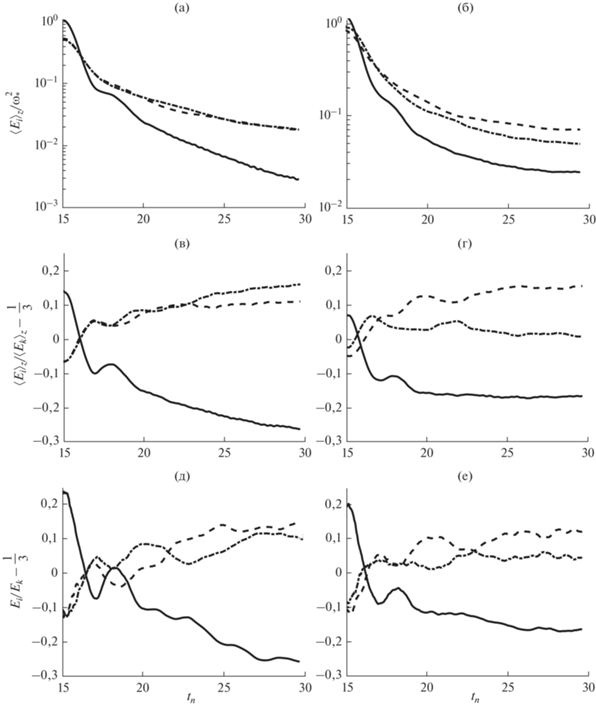
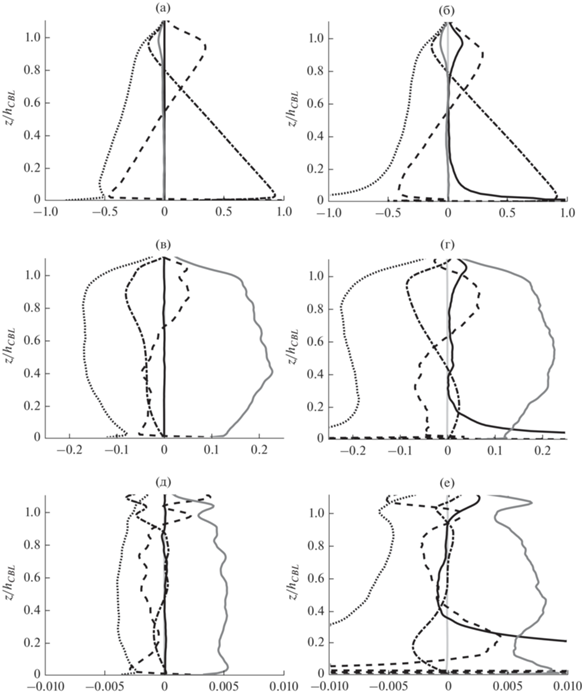
$B = \beta \left\langle {\Theta {\kern 1pt} 'w{\kern 1pt} '} \right\rangle ,$
(28)
$D = - \frac{1}{2}\frac{{\partial \left\langle {u_{i}^{'}u_{i}^{'}w{\kern 1pt} '} \right\rangle }}{{\partial z}} - \frac{{\partial \left\langle {p_{*}^{{\text{'}}}w{\kern 1pt} '} \right\rangle }}{{\partial z}} - \frac{{\partial \left\langle {{{{{\tau }}}_{{i3}}}u_{i}^{'}} \right\rangle }}{{\partial z}},$
(29)
$\varepsilon = \left\langle {{{K}_{{\Delta ,m}}}{{{\left| S \right|}}^{2}}} \right\rangle ,$
где $\left\langle \cdot \right\rangle $ есть осреднение по горизонтали и времени, $T$ – тенденция, $P$ – сдвиговая генерация кинетической энергии, $B$ – поток плавучести, $D$ – перенос турбулентных напряжений и пульсаций давления флуктуациями скорости, включающий и подсеточный диффузионный перенос, ${{\varepsilon }}$ – диссипативный член, описывающий передачу энергии в подсеточные масштабы, $R~\,\, \approx 0$ – невязка баланса, вследствие исключенных малых поправок на кинематическую вязкость воздуха и ошибок численной аппроксимации слагаемых. Далее будем считать, что уравнение (24) отражает изменение КЭТ, в частности ${{\varepsilon }}$ соответствует скорости диссипации за счет молекулярной вязкости. Тогда уравнение (19) относительно ${{E}_{k}}$ в RANS замыкании можно рассматривать как параметризацию баланса разрешаемой явно кинетической энергии пульсаций скорости в вихреразрешающей модели. Такое упрощение подтверждается оценками чувствительности к сеточному разрешению и к выбору подсеточного LES замыкания в работе [29].

На рис. 6 показано вертикальное распределение членов баланса кинетической энергии турбулентности (24) в конвективном ПС, при осреднении по времени на интервале $\delta {{t}_{n}} = \left[ {12.5,15.0} \right]$, и в вечернем переходе для периодов быстрого, ${{\delta }}{{t}_{n}} = \left[ {15.6,16.6} \right]$, и медленного затухания КЭТ, ${{\delta }}{{t}_{n}} = \left[ {19.2,23.2} \right]$. В начале вечернего перехода (см. рис. 6в, 6г) уменьшение КЭТ происходит за счет скорости диссипации и потока плавучести, который становится отрицательным. Здесь затухание КЭТ наиболее выражено в середине пограничного слоя. Действие механизмов переноса КЭТ (28) подобно конвективному режиму (см. рис. 6а, 6б) и приводит к перераспределению энергию в верхнюю часть пограничного слоя, где наблюдается минимум потока тепла. Сдвиговая генерация КЭТ при наличии геострофического ветра сосредоточена преимущественно вблизи поверхности (${z \mathord{\left/ {\vphantom {z {{{h}_{{CBL}}}}}} \right. \kern-0em} {{{h}_{{CBL}}}}} < 0.2$) и слабо влияет на затухание КЭТ со временем – накачка энергии средним течением локально компенсируется увеличением скорости диссипации. В периоде медленного затухания КЭТ (см. рис. 6д, 6е) влияние плавучести на изменение энергии становится малым. В отсутствии сдвига скорости энергия равномерно уменьшается по всей толщине ПС в основном за счет действия диссипации, а скорость затухания КЭТ для выбранного временного интервала ${{\delta }}{{t}_{n}}$ остается близкой к наблюдаемой в сдвигово-конвективном пограничном слое.

Рис. 6.

Вертикальное распределение нормированных на $w_{*}^{3}h_{{CBL}}^{{ - 1}}$ компонент баланса КЭТ (24) в КПС (а), (б); в периодах быстрого (в), (г) и медленного затухания кинетической энергии (д), (е): $P$ (сплошная черная линия), $D$ (штриховая линия), ${{\varepsilon }}$ (пунктирная линия), $B$ (штрихпунктирная линия), $T$ (сплошная тёмно-серая линия), $R$ (сплошная светло-серая линия). Левая колонка соответствует случаю свободной конвекции, правая – сдвигово-конвективному режиму.

На рис. 7 показаны нормальные компоненты тензора ${{R}_{{ij}}} = \left\langle {p{\kern 1pt} 'S_{{ij}}^{'}} \right\rangle $ корреляций “давление-скорости деформаций”, входящего в уравнения баланса для турбулентных напряжений (см., например, [11, 40]). След ${{R}_{{ij}}}$ в силу выполнения уравнения неразрывности (2) равен нулю и не влияет на изменение КЭТ, а его диагональные элементы описывают перераспределение энергии между отдельными ее компонентами. Профили ${{R}_{{ii}}}$ приведены для временных интервалов, рассмотренных ранее для оценки членов баланса КЭТ (см. рис. 6). В развивающемся КПС (рис. 7а, 7б) энергия, при наличии источника $B~\,\, > ~\,\,0$, передается из вертикальной компоненты ${{E}_{w}}$ в горизонтальные. В период быстрого затухания КЭТ (рис. 7в, 7г) подобный обмен продолжает происходить лишь внутри перемешанного слоя, тогда как у поверхности и в слое вовлечения наблюдается обратное перераспределение – из горизонтальных компонент энергии ${{E}_{u}}$ и Ev в вертикальную. Таким образом, наблюдаемая изотропизация энергии во время начала вечернего перехода (рис. 3) сильно неоднородна по высоте КПС.

Рис. 7.

Вертикальное распределение нормированных на $w_{*}^{3}h_{{CBL}}^{{ - 1}}$ диагональных компонент тензора ${{R}_{{ij}}}$ в КПС (а), (б); в периодах быстрого (в), (г) и медленного затухания кинетической энергии (д), (е): ${{R}_{{11}}}$ (штриховая линия), ${{R}_{{22}}}$ (штрихпунктирная линия) и ${{R}_{{33}}}$ (сплошная линия). Левая колонка соответствует случаю свободной конвекции, правая – сдвигово-конвективному режиму.

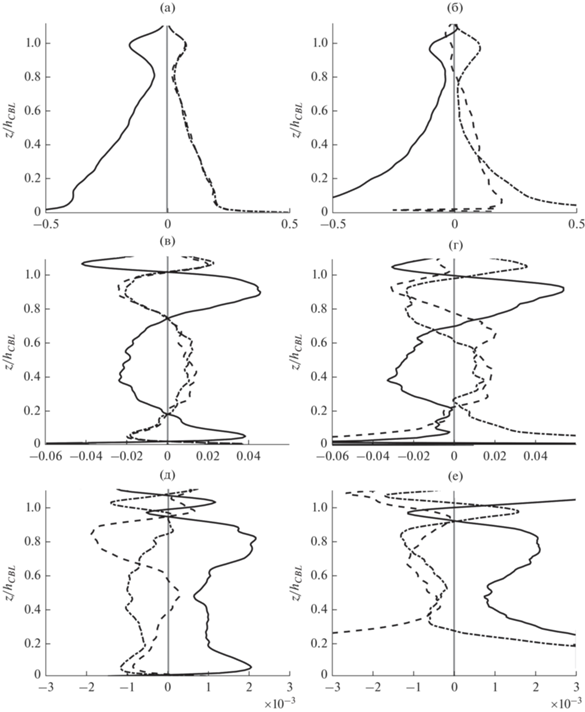
В период медленного затухания КЭТ и формирования квазидвумерного течения в режиме свободной конвекции (рис. 7д) изотропизация энергии за счет перераспределения в ${{E}_{w}}$ происходит по всей толще ПС, но не ограничивает рост анизотропии. При наличии геострофического ветра пограничный слой разделяется на две части (рис. 7е). В расположенном вблизи поверхности слое, который увеличивается со временем, наблюдается характерный для сдвигового ПС переход энергии из продольной компоненты ${{E}_{u}}$ в поперечную ${{E}_{v}}$ и вертикальную, а структура верхней части ПС остается схожей случаю свободной конвекции.

Двухпараметрические замыкания для переходного периода

Результаты LES экспериментов показывают, что динамика вечернего перехода состоит из интервала быстрого затухания КЭТ, в котором конвективный режим с преобладанием кинетической энергии в вертикальной компоненте ${{E}_{w}}$ сменяется изотропизацией за счет остаточного всплытия термиков. Данный процесс в последующем периоде медленного затухания КЭТ сопровождается формированием квазидвумерного течения, в котором энергия содержится преимущественно в крупных масштабах горизонтальных компонент. Здесь скорость диссипации КЭТ ниже, по сравнению с однородной изотропной турбулентностью. Двухпараметрическое RANS замыкание такую динамику воспроизводит неверно, что наблюдается в расхождениях скоростей затухания осредненной энергии пограничного слоя (рис. 2). Можно выделить несколько причин, способствующих этому.

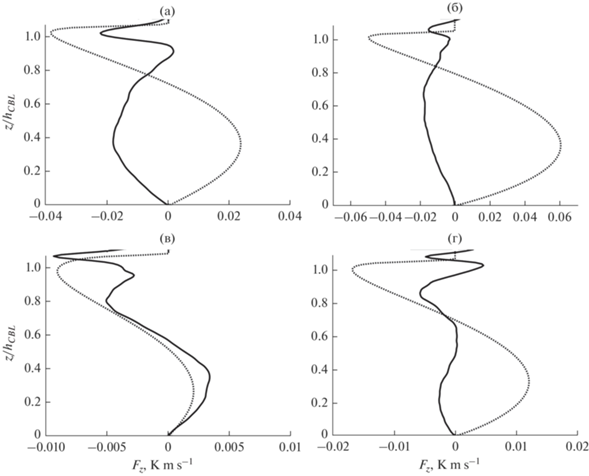
Одной из них является использование градиентного приближения для расчета кинематического потока тепла, что влияет не только на распределение температуры в КПС (рис. 1), но и на динамику вечернего перехода. На рис. 8 приведено мгновенное вертикальное распределение турбулентного потока тепла ${{F}_{z}}$ в интервалах быстрого и медленного затухания по данным LES и RANS моделей. Неверное описание с помощью двухпараметрического замыкания среднего профиля температуры, который остается неустойчивым в нижней части КПС во время затухания, приводит к сохранению положительного потока тепла в толще пограничного слоя во время вечернего перехода. Наличие такого источника генерации КЭТ в RANS модели не соответствует данным LES расчетов, где сток энергии за счет действия сил плавучести частично ускоряет изотропизацию энергии и затухание вертикальной компоненты КЭТ в интервале быстрого затухания. Отметим, что в RANS модели в верхней части КПС сохраняется остаточный слой вовлечения с отрицательными значениями потока тепла, а толщина такого слоя увеличивается со временем.

Рис. 8.

Вертикальное распределение кинематического потока тепла ${{F}_{z}}$ в LES (сплошная линия) и RANS (пунктирная линия) для быстрого периода затухания КЭТ, ${{t}_{n}} \approx 16.7$, (а, б) и при переходе к интервалу медленного затухания, ${{t}_{n}} \approx 18.3$ (в, г). На графиках приведены результаты экспериментов для случая (а, в) свободной конвекции и (б, г) сдвигово-конвективного режима.

Применение эмпирического уравнения (20) может приводить к неверной оценке скорости диссипации кинетической энергии турбулентности. Покажем это для режима вечернего перехода в отсутствие геострофического ветра. На рис. 9a пр-иведено затухание КЭТ в зависимости от выбора турбулентного числа Шмидта ${{{{\sigma }}}_{{{\varepsilon }}}}$ в уравнении для скорости диссипации. Наблюдаемая зависимость согласуется с результатами изучения чувствительности RANS модели к параметрам замыкания при воспроизведении вечернего перехода в работе [47] и показывает, что при значении ${{{{\sigma }}}_{{{\varepsilon }}}} = 1.3$ диффузия в уравнении (20) относительно слабо влияет на характеристики затухания КЭТ. Следовательно, пренебрегая оператором диффузии, уравнение для скорости диссипации можно приближенно записать в следующем виде:

(30)
$\frac{{\partial {{\varepsilon }}}}{{\partial t}} \approx - \frac{1}{{{{t}_{R}}}}\left( {{{\varepsilon }} - {{{{\varepsilon }}}_{0}}} \right).$
Рис. 9.

Затухание КЭТ в вечернем переходном периоде для случая свободной конвекции. (а) Влияние турбулентного числа Шмидта: ${{{{\sigma }}}_{{{\varepsilon }}}} = 1.3$ (пунктирная линия), ${{{{\sigma }}}_{{{\varepsilon }}}} = 0.3$ (штрихпунктирная линия) ${{{{\sigma }}}_{{{\varepsilon }}}} = 1000$ (штриховая линия). (б) Эксперимент с модифицированным уравнением для скорости диссипации КЭТ (сплошная серая линия). Сплошной черной линией отмечены результаты LES расчетов.

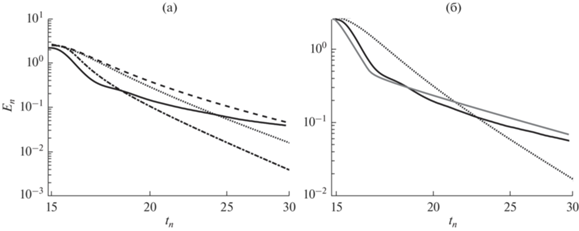
Уравнение (30) описывает приспособление скорости диссипации ${{\varepsilon }}$ к равновесному состоянию ${{\varepsilon }_{0}} = \left( {{{{{C}_{{3\varepsilon }}}} \mathord{\left/ {\vphantom {{{{C}_{{3\varepsilon }}}} {{{C}_{{2\varepsilon }}}}}} \right. \kern-0em} {{{C}_{{2\varepsilon }}}}}} \right)B$, где временной масштаб релаксации ${{t}_{R}} = {{C_{{2\varepsilon }}^{{ - 1}}{{E}_{k}}} \mathord{\left/ {\vphantom {{C_{{2\varepsilon }}^{{ - 1}}{{E}_{k}}} \varepsilon }} \right. \kern-0em} \varepsilon }$. В силу выбора значений параметров ${{C}_{{2{\kern 1pt} {{\varepsilon }}}}}$ и ${{C}_{{3{\kern 1pt} {{\varepsilon }}}}}$ в уравнении (20) равновесное решение всегда $0 \leqslant {{{{\varepsilon }}}_{0}} < \left| B \right|$, причем ${{ - {{{{\varepsilon }}}_{0}}} \mathord{\left/ {\vphantom {{ - {{{{\varepsilon }}}_{0}}} B}} \right. \kern-0em} B} \approx {1 \mathord{\left/ {\vphantom {1 5}} \right. \kern-0em} 5}$ при $B\,\,~ < \,\,~0$, а в случае неустойчивой стратификации ${{{{\varepsilon }_{0}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{0}}} B}} \right. \kern-0em} B} \approx {3 \mathord{\left/ {\vphantom {3 5}} \right. \kern-0em} 5}$. Таким образом, в случае малых ${{t}_{R}}$ или близости ${{\varepsilon }}$ к равновесному состоянию ${{{{\varepsilon }}}_{0}}$ (что и наблюдается в основной части растущего КПС) уравнение (30) может занижать скорость диссипации в начальной стадии затухания, по сравнению с данными вихреразрешающего моделирования, где ${\varepsilon \mathord{\left/ {\vphantom {\varepsilon {\left| B \right|}}} \right. \kern-0em} {\left| B \right|}} \approx 3$ (см. рис. 6). Для полной системы уравнений (11)–(20) результаты численных экспериментов показывают, что модуль потока плавучести и, соответственно, ${{{{\varepsilon }}}_{0}}$ уменьшаются быстрее скорости диссипации, однако соотношение ${{\varepsilon }} < \left| B \right|$ выполняется именно в начале вечернего перехода почти во всей толще ПС. Здесь основной сток кинетической энергии происходит в остаточном слое вовлечения, где $B~\,\, < \,\,~0$, а диффузия описывает перенос КЭТ из области, где поддерживается генерация плавучестью и $B~ - ~{{\varepsilon }} > ~\,\,0$, в верхнюю часть пограничного слоя. На больших временах, где поток плавучести мал и ${{{{\varepsilon }}}_{0}} \approx 0$, решения приближенно согласуются со скоростью затухания КЭТ в однородной турбулентности, которая в замыкании описывается степенной зависимостью от времени с показателем $\alpha = {1 \mathord{\left/ {\vphantom {1 {\left( {1 - {{C}_{{2{\kern 1pt} \varepsilon }}}} \right)}}} \right. \kern-0em} {\left( {1 - {{C}_{{2{\kern 1pt} \varepsilon }}}} \right)}}$, см. [28].

Согласно приведенным выше соображениям, можно изменить эмпирические параметры уравнения для скорости диссипации (20) так, чтобы воспроизвести затухание КЭТ в вечернем переходе, наблюдаемое в LES модели. На рис. 9б показан результат расчета с модифицированным замыканием, в котором равновесное состояние ${{{{\varepsilon }}}_{0}}$ определялось по оценкам, полученным в экспериментах с вихреразрешающей моделью, ${{\varepsilon }_{0}} \approx 3\left| B \right|$, а для описания перехода к интервалу медленного затухания КЭТ значение ${{C}_{{2{{\varepsilon }}}}}$ задавалось при ${{t}_{n}} > 16.7$ так, чтобы скорость затухания ${{\alpha }}$ уменьшалась и соответствовала данным LES моделирования. В данном случае двухпараметрическое замыкание позволяет верно воспроизвести изменение ${{E}_{n}}$ во время вечернего перехода, включая два интервала быстрой и медленной скорости затухания КЭТ. Приведенная модификация очевидно демонстрирует лишь особенности эмпирического уравнения для скорости диссипации и необходимость его обобщения для описания затухающей турбулентности при наличии плавучести и анизотропии КЭТ в пограничных слоях.

ЗАКЛЮЧЕНИЕ

В настоящей работе представлены результаты вихреразрешающего моделирования вечернего перехода в АПС. Численные эксперименты проводились для режима свободной конвекции и при наличии геострофического ветра. Динамика средней по пограничному слою кинетической энергии турбулентности и дисперсий компонент скорости, а также изменения в функциях распределения аномалий скорости и спектрах энергии, позволяют выделить два интервала вечернего перехода, характеризующихся в том числе различной скоростью затухания КЭТ.

В начале вечернего перехода наблюдается интервал быстрого затухания кинетической энергии флуктуаций скорости продолжительностью $ \sim {{t}_{*}}$. Конвективный режим, где анизотропия выражена и преобладает вертикальная компонента ${{E}_{w}}$, сменяется изотропизацией КЭТ, а распределения флуктуаций компонент скорости приближаются к нормальным. Поток плавучести становится отрицательным, что наряду с перераспределением энергии от ${{E}_{w}}$ в горизонтальные компоненты ${{E}_{u}}$ и ${{E}_{v}}$ ускоряет затухание вертикальной компоненты КЭТ.

Последующий второй интервал вечернего перехода для случая свободной конвекции сопровождается увеличением анизотропии КЭТ и формированием квазидвумерного течения, где энергия сосредоточена преимущественно в горизонтальных компонентах. Здесь затухание КЭТ продолжается с заметно меньшей скоростью. Увеличивается асимметрия распределений как вертикальной, так и горизонтальных компонент скорости ветра. В данном интервале затухание КЭТ преимущественно обусловлено диссипацией энергии, а вклад потока плавучести и консервативных членов, описывающих перенос вторых моментов, в баланс КЭТ уменьшается.

Наличие крупномасштабного градиента давления модифицирует как КПС, так и режим затухания в основном в областях с существенным сдвигом скорости, в начале перехода – у поверхности и в слое вовлечения. На временах, значительно превыщающих характерное время в КПС с начала вечернего перехода, толщина приповерхностного слоя, где сдвиговая генерация КЭТ значима, увеличивается, а структура турбулентного потока в нем становится характерной для нейтрального и слабо-устойчивого ПС.

Одномерная RANS модель пограничного слоя, в которой турбулентные потоки определяются двухпараметрическим замыканием, воспроизводит основные характеристики КПС, за исключением средних величин в перемешанном слое вследствие использования градиентного приближения. В то же время такая модель не позволяет верно описать динамику вечернего перехода, где отмечаются существенные различия с результатами LES экспериментов. В частности, отсутствует разделение на интервалы быстрого и медленного затухания энергии, а для случая свободной конвекции скорость затухания КЭТ близка к постоянной для всего переходного периода.

В начале вечернего перехода RANS модель поддерживает неустойчивый профиль потенциальной температуры и распределение потока тепла, которое характерно для КПС – положительный поток в перемешанном слое и отрицательный в слое вовлечения. Использование феноменологического уравнения для скорости диссипации (20) в данном случае приводит к тому, что сток кинетической энергии происходит преимущественно в верхней части ПС, где $B~\,\, < \,\,~0$, а в перемешанном слое генерация КЭТ за счет плавучести преобладает над диссипацией. Локальное затухание КЭТ в толще пограничного слоя происходит в таком случае за счет диффузионного переноса энергии в остаточный слой вовлечения.

Показана возможность изменения эмпирических параметров RANS замыкания, позволяющая воспроизвести динамику затухания КЭТ, подобную наблюдаемой в LES экспериментах. Приведенная модификация демонстрирует, что неточность описания вечернего перехода связана, в том числе, с неверной параметризацией стока кинетической энергии турбулентности в двухпараметрической модели во время интервала быстрого затухания энергии, а также завышенной оценкой скорости затухания КЭТ при формировании квазидвумерного течения в отсутствии геострофического ветра. Отметим, что с учетом неоднородности по времени затухания КЭТ калибровка замыканий по степенным зависимостям ${{E}_{n}}\left( {{{t}_{n}}} \right) \propto t_{n}^{{ - \alpha }}$, приближенно описывающих динамику всего переходного периода, по нашему мнению представляется недостаточно обоснованной.

Рассмотренная в работе идеализированная постановка свидетельствует о наличии значимых ошибок в воспроизведении вечернего перехода с помощью двухпараметрических замыканий, подходы к устранению которых требуют дальнейших исследований. В частности, для верного воспроизведения переходных режимов и суточного хода можно рассматривать замыкания более высокого порядка. Однако увеличение порядка модели, например, до второго, приведет к увеличению прогностических уравнений для моментов гидродинамических полей и также потребует привлечения дополнительных параметризаций для диссипативных членов системы. По этим причинам первоначальной задачей предполагается именно уточнение параметризации скорости диссипации кинетической энергии турбулентности. В общем случае неоднородность поверхности, обмен тепла и влажностью с почвой, радиационные процессы могут существенно влиять на структуру турбулентного пограничного слоя в переходном периоде. Например, в работе [21] отмечается, что для сдвигово-конвективного пограничного слоя в условиях городской застройки продолжительность вечернего перехода может увеличиваться за счет усиления сдвига скорости в слое вовлечения. Таким образом, исследование влияния подобных процессов также необходимо в дальнейшей работе по улучшению параметризаций АПС.

Работа выполнена при поддержке Российского фонда фундаментальных исследований, грант № ~20-05-00776, и гранта Президента РФ молодым ученым MK-1867.2020.5, а также при частичной поддержке научно-образовательной междисциплинарной школы Московского университета “Мозг, когнитивные системы, искусственный интеллект”. Работа выполнена с использованием оборудования Центра коллективного пользования сверхвысокопроизводительными вычислительными ресурсами МГУ имени М.В. Ломоносова.

Данные численных экспериментов доступны на ресурсе EUDAT инфраструктуры коллективного использования данных (EUDAT Collaborative Data Infrastructure (or EUDAT CDI)) [48].

Список литературы

  1. Stull R.B., Driedonks A.G.M. Applications of the transilient turbulence parameterization to atmospheric boundary-layer simulations // Bound.-Layer Meteorol. 1987. V. 40. № 3. P. 209–239.

  2. Debolskiy A., Mortikov E., Glazunov A., Lüpkes C. Evaluation of surface layer stability functions and their extension to first order turbulent closures for weakly and strongly stratified stable boundary layer // Bound.-Layer Meteorol. 2021. Under review.

  3. Мортиков Е.В., Глазунов А.В., Дебольский А.В., Лыкосов В.Н., Зилитинкевич С.С. О моделировании скорости диссипации кинетической энергии турбулентности // Доклады Академии Наук. 2019. Т. 489. № 4. С. 414–418.

  4. Svensson G., Holtslag A.A.M., Kumar, V., Mauritsen, T., Steeneveld G.J., Angevine W.M., Bazile E., Beljaars A., de Bruijn E.I.F., Cheng A., Conangla L., Cuxart J., Ek M., Falk M.J., Freedman F., Kitagawa H., Larson V.E., Lock A., Mailhot J., Masson V., Park S., Pleim J., Soderberg S., Weng W., Zampieri M. Evaluation of the diurnal cycle in the atmospheric boundary layer over land as represented by a variety of single-column models: The second GABLS experiment // Bound.-Layer Meteorol. 2011. V. 140. P. 177–206.

  5. Holtslag A.A.M., Svensson G., Baas P., Basu S., Beare B., Beljaars A.C.M., Bosveld F.C., Cuxart J., Lindvall J., Steeneveld G.J., Tjernstrom M., Van De Wiel B.J.H. Stable atmospheric boundary layers and diurnal cycles: Challenges for weather and climate models // Bull. Am. Meteorol. Soc. 2013. V. 94. № 11. P. 1691–1706.

  6. Angevine W.M., Edwards J.M., Lothon M., LeMone M.A., Osborne, S.R. Transition periods in the diurnally-varying atmospheric boundary layer over land // Bound.-Layer Meteorol. 2020. V. 177. P. 205–223.

  7. Taylor A.C., Beare R.J., Thomson D.J. Simulating dispersion in the evening-transition boundary layer // Bound.-Layer Meteorol. 2014. V. 153. P. 389–407.

  8. Copstein C.G. Simulating the Evening Transition in the PBL and Evaluating Its Contribution to the Next Day Prediction Ozone Peak Concentration // Doctoral dissertation. University of Houston. 2015. 125 p.

  9. Mellor G.L., Yamada T. Development of a turbulence closure model for geophysical fluid problems // Rev. Geophys. 1982. V. 20. № 4. P. 851–875.

  10. Zilitinkevich S.S., Elperin T., Kleeorin N., Rogachevskii I., Esau I. A hierarchy of energy- and flux-budget (EFB) turbulence closure models for stably-stratified geophysical flows // Bound.-Layer Meteorol. 2013. V. 146. P. 341–373.

  11. Burchard H. Applied turbulence modelling in marine waters // Berlin, Germany: Springer. 2002. 218 p.

  12. Detering H.W., Etling D. Application of the $E~ - ~\varepsilon $ turbulence model to the atmospheric boundary-layer // Bound.-Layer Meteorol. 1985. V. 33. P. 113–133.

  13. Sogachev A., Kelly M., Leclerc M.Y. Consistent two-equation closure modelling for atmospheric research: buoyancy and vegetation implementations // Bound.-Layer Meteorol. 2012. V. 145. P. 307–327.

  14. Zhang C., Wang Y., Xue M. Evaluation of an $E~ - ~\varepsilon $ and three other boundary layer parameterization schemes in the WRF model over the Southeast Pacific and the Southern Great Plains // Mon. Weather Rev. 2020. V. 148. № 3. P. 1121–1145.

  15. Langland E.H., Liou C.-S. Implementation of an $E~ - ~\varepsilon $ parameterization of vertical subgrid-scale mixing in a regional model // Mon. Weather Rev. May 1996. P. 905–918.

  16. Nuterman R., Mahura A., Baklanov A., Amstrup B., Zakey A. Downscaling system for modelling of atmospheric composition on regional, urban and street scales // Atmos. Chem. Phys. 2021. P. 1–16.

  17. Vu T.C., Asaeda T., Ashie Y. Development of a numerical model for the evaluation of the urban thermal environment // J. Wind Eng. Indust. Aero. 1999. V. 81. P. 181–196.

  18. Nakanishi M., Niino H. An improved Mellor-Yamada level-3 model with condensation physics: its design and verification // Bound.-Layer Meteorol. 2004. V. 112. P. 1–31.

  19. El Guernaoui O., Reuder J., Esau I., Wolf T., Maronga B. Scaling the decay of turbulence kinetic energy in the free-convective boundary layer // Bound.-Layer Meteorol. 2019. V. 173. № 1. P. 79–97.

  20. Nieuwstadt F.T.M., Brost R.A. The decay of convective turbulence // J. Atmos. Sci. 1986. V. 43. № 6. P. 532–546.

  21. Park S.-B., Baik J.-J., Han B.-S. Role of wind shear in the decay of convective boundary layers // Atmosphere. 2020. V. 11. № 6. P. 622.

  22. Pino D., Jonker H.J.J., de Arellano J.V.-G., Dosio A. Role of shear and the inversion strength during sunset turbulence over land: Characteristic length scales // Bound.-Layer Meteorol. 2006. V. 121. № 3. P. 537–556.

  23. Sorbjan Z. Decay of convective turbulence revisited // Bound.-Layer Meteorol. 1997. V. 82. № 3. P. 503–517.

  24. Deardorff J.W. Convective velocity and temperature scales for the unstable planetary boundary layer and for Rayleigh convection // J. Atmos. Sci. 1970. V. 27. № 8. P. 1211–1213.

  25. Колмогоров А.Н. К вырождению изотропной турбулентности в несжимаемой вязкой жидкости // Докл. Акад. Наук СССР. 1941. Т. 31. С. 538–540.

  26. Saffman P.G. The large-scale structure of homogeneous turbulence // J. Fluid Mech. 1967. V. 27. № 3. P. 581–593.

  27. Birkoff G. Fourier synthesis of homogeneous turbulence // Comm. Pure Appl. Math. 1954. V. 7. P. 19–44.

  28. Лыкосов В.Н. О проблеме замыкания моделей турбулентного пограничного слоя с помощью уравнений для кинетической энергии турбулентности и скорости ее диссипации // Изв. РАН. Физика атмосферы и океана. 1992. Т. 28. № 7. С. 696–704.

  29. Tkachenko E., Debolskiy A., Mortikov E. Intercomparison of subgrid scale models in large-eddy simulation of sunset atmospheric boundary layer turbulence: computational aspects // Lobachevskii Journal of Mathematics. 2021. V. 42. № 7. P. 1580–1595.

  30. Rizza U., Miglietta M.M., Degrazia G.A., Acevedo O.C., Marques Filho E.P. Sunset decay of the convective turbulence with large-eddy simulation under realistic conditions // Physica A. 2013. V. 392. P. 4481–4490.

  31. Nadeau D.F., Pardyjak E.R., Higgins C.W., Fernando H.J.S., Parlange M.B. A simple model for the afternoon and early evening decay of convective turbulence over different land surfaces // Bound.-Layer Meteorol. 2011. V. 141. № 2. P. 301–324.

  32. Glazunov A., Rannik U., Stepanenko V., Lykosov V., A-uvinen M., Vesala T., Mammarella I. Large-eddy simulation and stochastic modeling of Lagrangian particles for footprint determination in the stable boundary layer // Geosci. Model Dev. 2016. V. 9. P. 2925–2949.

  33. Germano M., Piomelli U., Moin P., Cabot W.H. A dynamic subgrid-scale eddy viscosity model // Phys. Fluids A. 1991. V. 3. № 7. P. 1760–1765.

  34. Lilly D.K. A proposed modification of the Germano subgrid-scale closure method // Phys. Fluids A. 1992. V. 4. № 3. P. 633–635.

  35. Bou-Zeid E., Meneveau C., Parlange M. A scale-dependent Lagrangian dynamic model for large eddy simulation of complex turbulent flows // Phys. Fluids. 2005. V. 17. № 2. P. 025105-1–025105-18.

  36. Meneveau C., Lund T.S., Cabot W.H. A Lagrangian dynamic subgrid-scale model of turbulence // J. Fluid Mech. 1996. V. 319. P. 353–385.

  37. Gladskikh D.S., Stepanenko V.M., Mortikov E.V. О влиянии горизонтальных размеров внутренних водоемов на толщину верхнего перемешанного слоя // Водные ресурсы. 2021. Т. 48. № 2. С. 155–163.

  38. Kadantsev E., Mortikov E., Zilitinkevich S. The resistance law for stably stratified atmospheric planetary boundary layers // Q.J.R. Meteorol. Soc. 2021. V. 147. № 737. P. 2233–2243.

  39. Mortikov E.V. Численное моделирование движения ледяного киля в стратифицированной жидкости // Изв. РАН. Физика атмосферы и океана. 2016. Т. 52. № 1. С. 120–128.

  40. Mortikov E.V., Glazunov A.V., Lykosov V.N. Numerical study of plane Couette flow: turbulence statistics and the structure of pressure-strain correlations // Russ. J. Numer. Analysis Math. Model. 2019. V. 34. № 2. P. 119–132.

  41. Morinishi Y., Lund T.S., Vasilyev O.V., Moin P. Fully conservative higher order finite difference schemes for incompressible flows // J. Comp. Phys. 1998. V. 143. P. 90–124.

  42. Brown D.L., Cortez R., Minion M.L. Accurate projection methods for the incompressible Navier-Stokes equations // J. Comp. Phys. 2001. V. 168. P. 464–499.

  43. Zang Y., Street R.L., Koseff J. A dynamic mixed subgrid-scale model and its application to turbulent recirculating flows // Phys. Fluids A. 1993. V. 5. № 12. P. 3186–3196.

  44. Lund T.S. On the use of discrete filters for large eddy simulation // Center for Turbulence Research, Annual Research Briefs. 1997. P. 83–95.

  45. Debolskiy A.V., Stepanenko V.M., Glazunov A.V., Zilitinkevich S.S. Интегральные модели проникающей конвекции со сдвигом скорости // Изв. РАН. Физика атмосферы и океана. 2019. Т. 55. № 2. С. 3–16.

  46. Wong V., Lilly D.K. A comparison of two subgrid closure methods for turbulent thermal convection // Phys. Fluids. 1994. V. 6. № 2. P. 1017–1023.

  47. Tkachenko E.V., Debolskiy A.V., Mortikov E.V. Analysis of turbulent kinetic energy decay power law in atmospheric boundary layer models // IOP Conference Series: Earth and Environmental Science. 2020. V. 611, N 1. P. 012-014.

  48. Tkachenko E., Debolskiy A., Mortikov E., Glazunov A. Large-eddy simulation and parameterization of decaying turbulence in the evening transition of atmospheric boundary layer // Supplementary dataset. 2021. Available at https://doi.org/10.23728/b2share.cb7f24996d234148a56b4444875226d0

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Физика атмосферы и океана

Архивы выпусков Информация о журнале Отправить рукопись в журнал