Известия РАН. Физика атмосферы и океана, 2022, T. 58, № 6, стр. 617-625

1. ВВЕДЕНИЕ

Описание волн, возбуждаемых движущимися источниками – одна из классических проблем гидродинамики. Начиная с работы Кельвина [1], основное внимание в литературе уделяется задаче о генерации поверхностных гравитационных волн стационарным движущимся источником. Описанию различных методов решения этой задачи посвящена обширная литература [2–9]. Следующий из решения задачи классический результат состоит в том, что движущийся источник индуцирует волновой след, расположенный строго позади источника. Примерами такого следа является знаменитый волновой клин Кельвина (картина корабельных волн) или волновой след в океане за движущимся интенсивным вихрем (ураганом) [10–12]. На примере акустических и поверхностных гравитационных волн в настоящей работе показано, что положение следа может принципиально измениться, если интенсивность движущегося источника осциллирует во времени. Движущийся осциллирующий источник может возбуждать волновые возмущения, расположенные как сзади, так и впереди источника. Возмущения впереди источника при этом можно рассматривать как волновые предвестники, сигнализирующие о приближении источника. Волновые предвестники от опасных метеорологических явлений экспериментально исследовались в работах [13–18], однако теоретические исследования вопроса о существовании предвестников крайне немногочисленны [19–28]. Внутренние гравитационные волны от движущихся осциллирующих источников теоретически исследовались в работах [22–28]. В настоящей работе рассмотрены возбуждаемые осциллирующим источником акустические и поверхностные гравитационные волны. Для описания структуры возникающего от источника волнового следа, использован развитый в работах [10–12] кинематический подход, основанный на лучевой теории волн. Для однородных сред (с постоянными значениями внешних параметров) этот подход позволяет получить явные параметрические уравнения для фазовых линий. В случае неоднородных сред, с параметрами, зависящими от времени и координат, формулируется система обыкновенных дифференциальных уравнений, определяющих положение следа.

2. ОБЩИЕ УРАВНЕНИЯ ДЛЯ ФАЗОВЫХ ВОЛНОВЫХ ПОВЕРХНОСТЕЙ (КРИВЫХ) ОТ ДВИЖУЩЕГОСЯ ОСЦИЛЛИРУЮЩЕГО ИСТОЧНИКА

Если в сплошной среде равномерно перемещается некоторый источник возмущений, то он создает вокруг себя волновую картину, основными особенностями которой являются поверхности (или линии – в двумерном случае) постоянной фазы. Структура этой картины на расстояниях много больших размеров источника, практически не зависит от его размеров и определяется в основном законом дисперсии и скоростью перемещения источника. Общие уравнения для фазовых поверхностей возбуждаемых волн можно получить из следующих соображений.

Будем рассматривать однородную сплошную среду, т.е. среду с постоянными значениями внутренних параметров. Предположение об однородности среды часто используется в современной теории волн. Будем считать, что в среде могут распространяться волны с заданным законом дисперсии$\omega = \Omega ({\mathbf{k}})$, где $\omega $ – циклическая частота, ${\mathbf{k}} = (k,l,m)$ волновой вектор. Внешний источник, осциллирующий с заданной частотой ${{\omega }_{0}}$ и движущийся с постоянной скоростью $U$, возбуждает в среде волны, с волновым вектором, удовлетворяющим соотношению

Данное соотношение представляет собой обычное дисперсионное соотношение для волн в движущейся с источником системе координат. При фиксированной частоте колебаний источника, соотношение (1) определяет некоторую поверхность (линию в двумерном случае) в пространстве волновых векторов. В случае ${{\omega }_{0}} = 0$ из (1) имеем соотношение ${\mathbf{kU}} = \Omega ({\mathbf{k}})$, определяющее волновую поверхность для стационарных источников.

Для получения общих уравнений для фазовых поверхностей возбуждаемых источником волн используем кинематический (вариационный) подход, предложенный в работе [12] для случая стационарных источников. Этот подход опирается на два условия а) фаза $S = {\mathbf{kr}}$ возбуждаемых волн постоянна на фазовых поверхностях (гребнях и впадинах волновой структуры), б) как функция волнового вектора ${\mathbf{k}}$ фаза $S$ стационарна при выполнении условия (1). Здесь ${\mathbf{r}} = (x,y,z)$ – радиус вектор точки с обычными декартовыми координатами.

В соответствии с условием б) фазовые поверхности находятся из решения задачи на условный экстремум для функционала

где $\lambda $ – лагранжев множитель. Условия экстремума $\partial L{\text{/}}\partial {\mathbf{k}} = 0$ дают где ${{{\mathbf{V}}}_{g}}({\mathbf{k}}) = \partial \Omega {\text{/}}\partial {\mathbf{k}}$ – групповая скорость волн. С учетом ${\mathbf{kr}} = S$, из соотношения (3) следует $\lambda ({\mathbf{k}}{{{\mathbf{V}}}_{g}} - {\mathbf{kU}}) = S$, откуда $\lambda = \frac{S}{{{\mathbf{k}}{{{\mathbf{V}}}_{g}} - {\mathbf{kU}}}}$. Подставляя данное $\lambda $ в (3) получим общие уравнения фазовых поверхностей (кривых) $S = {\text{const}}$

Поскольку, согласно (1), ${\mathbf{kU}} = \Omega ({\mathbf{k}}) - {{\omega }_{0}}$, уравнения (4) можно также представить в виде

Подчеркнем, что эти уравнения записаны в движущейся с источником системе координат и переменные $S,\,{{\omega }_{0}}$ играют роль внешних параметров, идентифицирующих каждую фазовую поверхность (кривую). При ${{\omega }_{0}} = 0$ из (5) следуют уравнения, сформулированные в [12] для случая стационарных источников. Подчеркнем, что в уравнениях (5) считается выполненным условие (1).

Приведем также более общий вывод уравнений (4), (5), использующий теорию уравнения Гамильтона-Якоби. В этом выводе рассматриваются волны в неоднородных средах с дисперсионным соотношением ${{\omega }_{0}} = \Omega ({\mathbf{k,r}})$, зависящим от координат. При наличии внешнего течения, удобно записать дисперсионное соотношение (1) в форме

Поскольку волновой вектор есть пространственный градиент фазы ${\mathbf{k}} = \nabla S$, дисперсионное соотношение (6) есть уравнение в частных производных (уравнение Гамильтона–Якоби) для нахождения фазы волн $S$. Согласно общей теории [2–4], решение уравнения сводится к интегрированию характеристической гамильтоновой системы уравнений, $d{\mathbf{r}}{\text{/}}dt = \partial {\rm H}{\text{/}}\partial {\mathbf{k}},\,\,\,d{\mathbf{k}}{\text{/}}dt = - \partial {\rm H}{\text{/}}\partial {\mathbf{r}}$, которую можно записать как

Здесь, как и ранее, ${{{\mathbf{V}}}_{g}} = \partial \Omega {\text{/}}\partial {\mathbf{k}}$ групповая скорость волн в неподвижной среде, $t$ – параметр на характеристиках, играющий роль времени. Изменение фазы вдоль характеристик находится из уравнения [2, 12]

В задаче о волнах от движущегося источника принципиальную роль играют неклассические “начальные” условия для характеристической системы (7). Соответствующие условия имеют вид

Первое условие требует, чтобы характеристики выходили из места положения источника ${\mathbf{r}} = {\mathbf{0}}$ (центрированная волна). Второе условие требует, чтобы при $t = 0$ волновой вектор ${\mathbf{k}} = {{{\mathbf{k}}}_{0}}$ удовлетворял условию (6). С геометрической точки зрения это условие (условие излучения) определяет некоторое двумерное многообразие (поверхность) в пространстве волновых векторов, которое можно задать в параметрическом виде ${{{\mathbf{k}}}_{0}} = {{{\mathbf{k}}}_{0}}(\alpha ,\beta )$ где – $\alpha ,\,\beta $ параметры. Для двумерных волн имеем одномерное многообразие (кривую).${{{\mathbf{k}}}_{0}} = {{{\mathbf{k}}}_{0}}(\alpha )$.

К условиям (4) присоединяется также естественное условие $t = 0:\,\,S = 0$. Для однородных сред (с постоянными параметрами) $\partial \Omega {\text{/}}\partial {\mathbf{r}} = 0$ и уравнения (7), (8) имеют простое аналитическое решение

Выразив $t$ через $S$ из третьего равенства, и подставив в первое, приходим к параметрическим уравнениям (4) для фазовых поверхностей

Эти уравнения были получены ранее из других соображений. Подчеркнем общий характер этих уравнений – они справедливы для волн с произвольным законом дисперсии. В случае стационарных источников, данные уравнения описывают знаменитый волновой клин Кельвина, образованный поверхностными гравитационными волнами (см. раздел 4). Определение фазовых линий для неоднородных сред сводится к интегрированию системы (7), (8). Пример такого интегрирования, иллюстрирующий влияние бета–эффекта на структуру внутренних волн, возбуждаемых движущимся стационарным источником (ураганом), представлен в работе [10]. В настоящей работе впервые рассмотрен случай нестационарных (пульсирующих) источников для модели однородной среды.

3. АКУСТИЧЕСКИЙ ВОЛНОВОЙ СЛЕД ОТ ДВИЖУЩЕГОСЯ ОСЦИЛЛИРУЮЩЕГО ИСТОЧНИКА

Используем уравнения (5) для описания фазовой структуры возбуждаемых движущимся осциллирующим источником акустических волн. Будем рассматривать двумерные волны с волновым вектором ${\mathbf{k}} = (k,l)$и частотой $\omega $. Удобно проводить рассмотрение в системе отсчета, связанной с источником, который считаем находящимся в начале координат. В неподвижной среде дисперсионное соотношение для акустических волн можно записать в виде [2–4]

где $c$ – скорость звука. Соответственно $\Omega ({\mathbf{k}}) = c\kappa $, где $\,\kappa = \left| {\mathbf{k}} \right| = \sqrt {{{k}^{2}} + {{l}^{2}}} $ – модуль волнового вектора. Для двумерных акустических волн групповая скорость

Следующее из (12) важное свойство акустических волн связано с отсутствием дисперсии, т.е. с выполнением соотношения ${\mathbf{k}}{{{\mathbf{V}}}_{g}} - \Omega ({\mathbf{k}}) = 0$. Уравнения (5) для фазовых кривых при этом сводятся к уравнениям

С учетом (12) и ${\mathbf{U}} = (U,0)$ векторный множитель в (13)

Преобразуем координаты (14) с использованием дисперсионного соотношения (1) (в движущейся с источником системе координат), которое запишем в виде $c\kappa = {{\omega }_{0}} + kU$. При этом

и в координатной форме уравнения (13) запишутся как

Дальнейшие преобразования используют квадрат дисперсионного соотношения (1) ${{(c\kappa )}^{2}} = {{({{\omega }_{0}} + kU)}^{2}}$, который, с учетом ${{\kappa }^{2}} = {{k}^{2}} + {{l}^{2}}$, запишем в форме уравнения

Левая часть уравнения есть квадратичная форма относительно координат волнового вектора $k,l$ и после выделения полных квадратов уравнение можно записать в виде

Используя (16) можно получить параметрические уравнения для фазовых линий (13). При этом нужно различать два случая. Первый случай отвечает ситуации, когда выполнено неравенство ${{U}^{2}} < {{c}^{2}}$, или, что эквивалентно, число Маха $M = U{\text{/}}c < 1$. В этом случае уравнение (16) удовлетворяется с использованием параметризации

где $\varphi $ – параметр. Отсюда найдем параметрическое представление для координат волнового вектора или

Подставим (17) в (15) с учетом соотношения ${{\omega }_{0}} + kU = \frac{{{{\omega }_{0}}c\left( {c + U{\kern 1pt} \cos {\kern 1pt} \varphi )} \right)}}{{{{c}^{2}} - {{U}^{2}}}} = \frac{{{{\omega }_{0}}(1 + M{\kern 1pt} \cos {\kern 1pt} \varphi )}}{{1 - {{M}^{2}}}}$. Вводя безразмерные координаты $\bar {x} = x{{\omega }_{0}}{\text{/}}c$, $\bar {y} = y{{\omega }_{0}}{\text{/}}c$, окончательно получим параметрические уравнения фазовых кривых (линий гребней и ложбин)

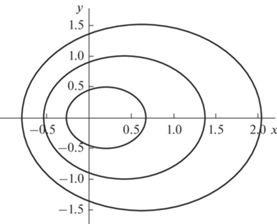
Представленная на рис. 1 картина фазовых кривых (18) образована системой деформированных окружностей, окружающих источник и вложенных друг в друга. Таким образом, осциллирующий источник, движущийся с дозвуковой скоростью, индуцирует волновые возмущения, расположенные как сзади, так и впереди источника (при $\bar {x} > 0$). Возмущения впереди источника и есть волновые предвестники, сигнализирующие о его приближении.

Совершенно другая волновая картина возникает в случае источников, движущихся со сверх звуковой скоростью, когда ${{U}^{2}} > {{c}^{2}}$ и число Маха $M = U{\text{/}}c > 1$. В этом случае дисперсионное соотношение (16) записывается в форме

и допускает параметризацию, использующую гиперболические функции

Выражая отсюда волновые числа $k,l$ через параметр $\varphi $ и подставляя в (15), после преобразований получим параметрические уравнения фазовых кривых

где, как и ранее, $\bar {x} = x{{\omega }_{0}}{\text{/}}c$ . $\bar {y} = y{{\omega }_{0}}{\text{/}}c$ . Картина фазовых кривых (19) принципиально отличается от рассмотренной ранее (рис. 2). Так, все фазовые кривые распложены строго позади источника, т.е. в области $\bar {x} < 0$. Из выражения $\bar {y}{\text{/}}\bar {x} = \operatorname{th} {\kern 1pt} \varphi {\text{/}}\sqrt {{{M}^{2}} - 1} $ следует, что все фазовые кривые заключены внутри волнового клина, ограниченного прямыми (наклонными асимптотами) $\bar {y}{\text{/}}\bar {x} = \pm 1{\text{/}}\sqrt {{{M}^{2}} - 1} $. Подчеркнем, что этот клин расположен позади источника.

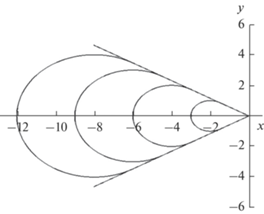
Таким образом, расположение области, охваченной волновыми возмущениями, принципиально зависит от скорости движения осциллирующего источника. Если эта скорость меньше скорости звука, волновые возмущения целиком охватывают круговую область и могут быть зарегистрированы средствами дистанционного зондирования атмосферы. При сверхзвуковой скорости движения источника область волновых возмущений расположена строго позади источника внутри волнового клина.

Представленный анализ позволяет получить простое описание эффекта Доплера, наблюдаемого при числах Маха $M = U{\text{/}}c < 1$. Действительно, дисперсионное соотношение (1) можно записать в виде ${{\omega }_{0}} = \omega - kU$или $\omega = {{\omega }_{0}} + kU$, где $\omega = \Omega ({\mathbf{k}})$ – частота волн в неподвижной системе координат, ${{\omega }_{0}}$ – частота колебаний источника. Преобразуем последнее выражения, используя выражение (17) для компоненты волнового вектора $k$. При этом

Таким образом, приходим к формуле

связывающей наблюдаемую в неподвижной системе координат частоту $\omega $ с частотой колебаний источника ${{\omega }_{0}}$. Из (20) следуют классические формулы теории эффекта Доплера [29]. Так, если $\varphi = 0$ (наблюдатель впереди источника), то

Регистрируемая частота больше частоты колебаний источника. Если $\varphi = \pi $ ( наблюдатель позади источника), то

т.е. позади источника наблюдаемая частота меньше частоты колебаний источника. Рассмотренный подход, таким образом, приводит к простому и наглядному описанию эффекта Доплера.

Отметим, что эффект Доплера фактически есть эффект волновых предвестников, однако этот факт специально не подчеркивается в литературе

4. ГРАВИТАЦИОННЫЕ ВОЛНЫ НА ГЛУБОКОЙ ВОДЕ

Рассмотрим теперь волновую картину, образованную поверхностными гравитационными волнами на глубокой воде с дисперсионным соотношением $\Omega = \sqrt {g\kappa } $, где $g$ – ускорение свободного падения. Вектор групповой скорости для этих волн ${{{\mathbf{V}}}_{g}} = \frac{1}{2}\sqrt {\frac{g}{{{{\kappa }^{3}}}}} {\mathbf{k}}$, соответственно модуль групповой скорости ${{V}_{g}} = 0.5\sqrt {g{\text{/}}\kappa } = 0.5\Omega {\text{/}}\kappa $. С учетом соотношений

уравнения (5) для фазовых кривых можно записать как Здесь, как и ранее, используется система координат с источником в центре.

С учетом приведенных соотношений дисперсионное соотношение (1) запишется в виде

Уравнения (21), (22) полностью определяют уравнения для фазовых кривых.

Рассмотрим вначале случай источника без осцилляций ${{\omega }_{0}} = 0$. В этом случае из (22) следует $\cos \varphi = \frac{{\sqrt {g\kappa } }}{{\kappa U}}$ или $\sqrt {g\kappa } = \frac{1}{{m{\kern 1pt} \cos {\kern 1pt} \varphi }}$, где $m = U{\text{/}}g$. Поскольку $\sqrt {g\kappa } > 0$ имеем ограничение $\cos {\kern 1pt} \varphi > 0$ , т.е. $ - \pi {\text{/}}2 < \varphi < \pi {\text{/}}2$. Подставляя выражение для $\sqrt {g\kappa } $ в (21) получим параметрические уравнения фазовых кривых

где $ - \pi {\text{/}}2 < \varphi < \pi {\text{/}}2$ . Графики кривых (23) для значений $S = - 1,\, - 2, - 3$. представлены на рис. 3. Значения координат нормированы на ${{U}^{2}}{\text{/}}g$. Эти кривые образуют знаменитый волновой клин Кельвины для волн от движущегося стационарного источника. Важно подчеркнуть, что в этом случае все волновые возмущении наблюдаются строго позади источника.

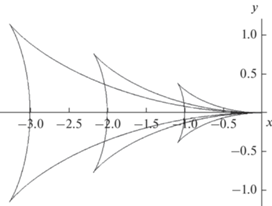
В связи с уравнениями (23) важно также отметить следующее обстоятельство. Выражение (10) для фазы $S$ в случае стационарных источников можно записать в виде $S = \left( {{\mathbf{k}}{{{\mathbf{V}}}_{g}} - \Omega ({\mathbf{k}})} \right)\,t$. Отсюда следует, что должно выполняться неравенство $t = S{\text{/}}\left( {{\mathbf{k}}{{{\mathbf{V}}}_{g}} - \Omega ({\mathbf{k}})} \right) > 0$. Поскольку для гравитационных волн ${\mathbf{k}}{{{\mathbf{V}}}_{g}} - \Omega ({\mathbf{k}}) = - (1{\text{/}}2)\sqrt {g\kappa } < 0$, допустимые значения фазы в уравнениях (23) должны быть отрицательны.

Рассмотрим теперь общий случай для движущегося осциллирующего источника. Обозначая $\sqrt {g\kappa } = a$ и $m = U{\text{/}}g$, дисперсионное соотношение (22) можно записать в форме квадратного уравнения

Отсюда получаем два корня

Нетрудно видеть, что при исчезающей частоте ${{\omega }_{0}} \to 0$ корень ${{a}_{1}}$ дает уравнение кривой (23), т.е определяет волновой клин Кельвина. При этом $ - \pi {\text{/}}2 < \varphi < \pi {\text{/}}2$. При исчезающей скорости $U \to 0$ ($m \to 0$) соотношение (26) сводится к соотношению $\sqrt {g\kappa } = {{\omega }_{0}}$, определяющие гравитационные волны на глубокой воде. При этом в (26) $0 < \varphi < 2\pi $, т.е. скорость движения источника не накладывает ограничений на угол $\varphi $. Движущийся осциллирующий источник, таким образом, возбуждает волны двух классов – волны Кельвина и обычные гравитационные волны.

Подставляя (25) в (21) получим уравнения для фазовых кривых, образованных волнами Кельвина от осциллирующего источника

$ - \pi {\text{/}}2 < \varphi < \pi {\text{/}}2$. Графики этих кривых для значений параметров $S = - 0.1,\,\, - 0.2,\, - 0,3.$ представлены на рис. 4. Подставляя (26) в (21) получим уравнения для фазовых кривых, образованных гравитационными волнами

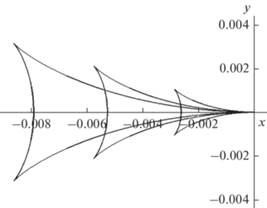
$0 < \varphi < 2\pi $. Графики этих кривых для значений параметров $S = - 0.1,\,\, - 0.2,\, - 0,3.$ представлены на рис. 5. Как видно, теперь фазовые кривые имеют форму деформированных окружностей, окружающих источник.

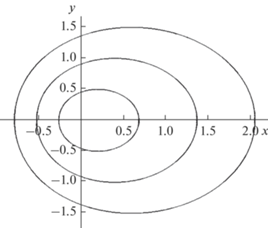
Таким образом, движущийся источник без осцилляций генерирует волновой клин Кельвина, расположенный строго позади источника. Движущийся осциллирующий источник наряду с волнами Кельвина, возбуждает гравитационные волны, фазовые линии которых имеют форму деформированных окружностей. Волновые возмущения при этом наблюдаются как сзади, так и впереди источника. Возмущения впереди источника есть волновые предвестники, свидетельствующие о приближении источника. Наличие предвестников может играть важную роль в задачах дистанционного зондирования атмосферы и океана.

В связи с волновыми предвестниками важно также отметить следующее обстоятельство. Их наличие будет иметь место для широкого класса диспергирующих волн при достаточно малых скоростях движения осциллирующего источника. Это прямо следует из дисперсионного соотношения (22). При условии ${{\omega }_{0}}{\text{/}}\kappa U \ll 1$ значения $\,\,\,\kappa $, удовлетворяющие (22), можно искать в форме разложения $\kappa = {{\kappa }_{0}} + {{\kappa }_{1}}$. При этом ${{\omega }_{0}} = \Omega ({{\kappa }_{0}})$, ${{\kappa }_{0}}\cos {\kern 1pt} \varphi U = \Omega {\kern 1pt} '({{\kappa }_{0}}){{\kappa }_{1}}$ или ${{\kappa }_{1}} = {{\kappa }_{0}}\cos {\kern 1pt} \varphi U{\text{/}}\Omega {\kern 1pt} '({{\kappa }_{0}})$. Подставляя $\kappa = {{\kappa }_{0}} + {{\kappa }_{1}}$ в соотношения (21) получим уравнения для фазовых кривых в форме деформированных окружностей, охватывающих область как впереди так и позади источника.

5. ЗАКЛЮЧЕНИЕ

С использованием лучевой теории исследована фазовая структура акустических и поверхностных гравитационных волн, возбуждаемых движущимся осциллирующим источником. Впервые получены явные уравнения для фазовых волновых линий возмущений от источника. Показано, что при достаточно малой скорости движения источника линии равной фазы имеют структуру колец, окружающих источник. При такой структуре всегда существуют волновые возмущения впереди источника, играющие роль волновых предвестников. На примере акустических волн показано, что если скорость движения источника больше скорости звука все фазовые кривые расположены в клиновидной области, находящейся строго позади источника. Полученные результаты могут играть важную роль в практических задачах дистанционного зондирования атмосферы и океана.

Автор благодарит М.В. Курганского и О.Г. Чхетиани за полезные обсуждения результатов. Работа выполнена при поддержке РНФ (номер проекта 22-27-00039).