Известия РАН. Физика атмосферы и океана, 2023, T. 59, № 2, стр. 173-191

Структурное описание геофизических случайных полей с негауссовой статистикой

И. Г. Якушкин^*, **

Институт физики атмосферы им. А.М. Обухова РАН
119017 Москва, Пыжевский пер., 3, Россия

^* E-mail: lgg@ifaran.ru
^** E-mail: iyakushkin@yandex.ru

Поступила в редакцию 30.08.2022
После доработки 14.11.2022
Принята к публикации 11.01.2023

EDN: HQDVLD
DOI: 10.31857/S0002351523020098

Аннотация

В статье рассмотрен подход к описанию случайных полей как совокупности интенсивных структур со случайными параметрами. Подобные структуры наблюдаются как в оптических полях, распространяющихся в неоднородных средах, так и в полях гидродинамического происхождения и образуются в результате фокусировок излучения или деформации течений. В статье рассмотрены способы фильтрации и эволюция подобных структур. Описаны различные режимы структур – режимы периодических и стохастических колебаний.

Ключевые слова: стохастические уравнения, хаос, структуры, вихри

1. ВВЕДЕНИЕ

Начиная, особенно с работ А.Н. Колмогорова и А.М. Обухова [Обухов, 1988], геофизические поля в атмосфере и океане стали рассматриваться как случайные, которые должны быть описаны на вероятностном языке. К числу таких полей относятся поля давления, температуры и плотности среды, а также векторное поле скорости ветра. Одновременно получали все большее значение и методы изучения природной среды с помощью акустических и радиоволн, а также вопросы точной передачи информации в условиях шумящей среды (атмосферы) [Рытов и др., 1978; Монин и др., 1965].

Все наблюдаемые во времени и пространстве геофизические, звуковые и электромагнитные поля имеют черты, как упорядоченности, так и случайности. Эти черты фиксируются и на малых и на больших масштабах наблюдения. На языке радиофизики, возникает различие между “сигналом”, который описывается уравнениями динамики, и “шумом”, который присутствует в этих уравнениях, но точно не определен. Ситуация требует решения двух задач – разработки модели “шума” и учета его влияния на несущий основную информацию “сигнал”. Согласно простейшей модели, шум приводит к некоторому изменению “среднего сигнала” и к его “флуктуациям”.

Среди специалистов по гидродинамике и геофизике особый интерес к этой проблематике возник в связи с изучением явления турбулентности на небольших масштабах. Разработке методов наблюдения, моделирования и описания, турбулентных полей наряду с основополагающими работами А.Н. Колмогорова и А.М. Обухова были посвящены многочисленные работы их сотрудников и учеников А.С. Монина, А.М. Яглома, Е.А. Новикова, В.И. Татарского, А.С. Гурвича, В.И. Кляцкина, В.В. Воробьева и других [Рытов и др., 1978; Татарский, 1967; Кляцкин, 2014]. Эта работа, происходила в сотрудничестве, как с математиками, так и с радиофизиками школы С.М. Рытова, и Нижегородской школы во главе с М.А. Миллером. Общей для геофизиков и радиофизиков оказалась задача о рассеянии волн различной природы в случайно – неоднородной (турбулентной) среде.

При изучении такого объекта, как случайное поле математической основой служит представление Фурье. Осредненные по протяженному участку реализации статистически – однородного случайного процесса или поля содержат компоненты Фурье, которые можно считать независимыми и распределенными по Гауссу. Это позволяет вычислять статистические средние, т.е. многоточечные моменты данного поля. Все высшие моменты выражаются через двухточечный момент, который носит название корреляционной функции и получается осреднением описывающей случайное поле квадратичной формы:

(1.1)

${{U}_{2}}\left( {\Delta r} \right) = \left\langle {{{U}_{2}}\left( {{\mathbf{r}},\Delta {\mathbf{r}}} \right)} \right\rangle = \left\langle {U\left( {{\mathbf{r}} + \Delta {\mathbf{r}}} \right)U\left( {{\mathbf{r}} - \Delta {\mathbf{r}}} \right)} \right\rangle $

которая определяет спектр случайного поля. Для векторного поля вводится соответствующий тензор. Если поля удовлетворяют линейным уравнениям, то их эволюция оставляет их гауссовыми. В случае же нелинейных уравнений или уравнений со случайными коэффициентами поле теряет гауссову структуру. Высшие моменты оказывают влияние на эволюцию второго момента, и отдельные спектральные компоненты оказываются статистически зависимыми. Задача вычисления моментов при этом требует некоторого замыкания, т.е. выражения высших моментов через низшие. Такое замыкание основано на предположении о слабой негауссовости поля и учете взаимодействия между его отдельными спектральными компонентами. На учете резонансных взаимодействий основана теория “слабой турбулентности”, характерной для сред с дисперсией, в том числе для “мелкой воды” [Заславский и др., 1988]. Теория мелкомасштабной турбулентности также основывается на представлении Фурье. Основной характеристикой турбулентного течения остается его пространственный спектр. Связь между спектральными компонентами описывается “каскадной” моделью, основанной на гипотезе Ричардсона о дроблении масштабов течения. Такое дробление происходит вплоть до малого масштаба, на котором имеет место диссипации энергии. Слабое взаимодействие спектральных компонент приводит к возникновению потока энергии по спектру. Характерной величиной является скорость диссипации энергии, которая в первоначальных работах Колмогорова и Обухова предполагалась постоянной. Впоследствии, по предложению Л.Д. Ландау, стали рассматриваться флуктуации этой величины. Различные эксперименты при этом показали, что эти флуктуации имеют негауссово, а скорее логнормальное распределение [Гледзер, 2005]. Наличие двух разных статистик, описывающих флуктуации поля на малых и более крупных масштабах, привело к понятию “перемежаемость турбулентности”. Установление вида спектра турбулентности в большом диапазоне масштабов позволило перейти к решению задачи о распространении волн в турбулентной атмосфере. Решение задачи было получено в работах В.И. Татарского и его коллег с использованием методов квазиоптики и выделения быстрых колебаний фазы поля. При этом подходе поле имело вид суммы не спектральных компонент, а вкладов от отдельных “лучей”.

Эксперименты А.С. Гурвича с сотрудниками показали, что картина флуктуаций интенсивности оптического поля представляет собой картину случайных фокусировок и указывает на негауссовость его статистики. Случайная фокусировка и дефокусировка когерентного излучения, приводит к образованию легко наблюдаемых глазом ярких структур. Аналитически этот эффект был описан как аномальный рост высших моментов интенсивности поля. При увеличении длины трассы поле переходит в стадию многолучевого распространения, где основную роль играет интерференция парциальных полей [Якушкин, 1985; Kravzov, 1992].

Из других работ следовало, что негауссовы случайные поля с интенсивными выбросами возникают и в акустике при формировании случайных ударных волн [Гурбатов, 1983], и при развитии неустойчивостей в различных средах. Во всех этих случаях имеет место статистическая зависимость между отдельными компонентами спектра поля.

На особенности негауссовых случайных полей, проявляющихся в различных физических ситуациях, было обращено внимание в статье Я.Б. Зельдовича с соавторами [Зельдович и др., 1987]. В этой статье указывалось на “перемежаемость” случайных процессов и полей. Так при астрофизических наблюдениях фиксируется резкое сгущение частиц или увеличение амплитуды случайных колебаний на отдельных интервалах времени или пространства. Касаясь явления турбулентности, авторы [Зельдович и др., 1987] указывали на различие двух свойств течений несжимаемой жидкости – завихренность и деформацию линий тока, которая приводит к созданию тонких вихревых нитей. Для авторов указанной статьи “перемежаемость” означала существование областей случайного поля, в которых его свойства заметно отличались от окружающего фона. Статистика таких полей имеет негауссовый характер и нуждается в отдельном описании.

В статье обращалось внимание на тот факт, что негауссовость возникающего в процессе эволюции распределения вероятности проявляется в аномальном росте моментов с ростом их номера. Это прослеживается, в частности, при исследовании быстрого “динамо” в проводящей жидкости, приводящего к концентрации магнитного поля. Важнейшую роль во всех этих ситуациях играет локальное нарушение статистической однородности поля, хотя в целом поле остается однородным.

На недостаточность описания случайных полей с помощью низших моментов указал также в своих работах В.И. Кляцкин [Кляцкин, 2014; Кляцкин, 2016]. Термин “перемежаемость” казался ему излишним. Общие (когерентные) свойства отдельной реализации можно описать с помощью модели статистически – однородного случайного поля. Основная информация о поле заключена не в его моментах, а в его одноточечной плотности вероятности:

(1.2)

$P\left( {U,{\mathbf{r}}} \right)\,\,{\text{или}}\,\,P\left( {\vec {U}\left( r \right),gradU,r} \right).$

Для векторного поля это плотности вероятности компонента вектора или каких-либо их комбинаций. Свойства отдельных реализаций поля проявляются при наблюдениях, охватывающих большие интервалы пространства. Для полей однородных во времени такой подход связывается с длительными наблюдениями в одной или нескольких соседних точках. На конечном участке времени или пространства отдельные реализации обладают частичной когерентностью.

Если брать гауссово поле за точку отсчета, то для негауссовых полей особое значение имеют “хвосты” плотности вероятности, т.е. ее поведение при больших значениях случайной величины. Закон спадания этих “хвостов” определяет и зависимость высших моментов от их номера. В качестве примера сильной негауссовости В.И. Кляцкин, как и авторы упомянутой выше статьи, указывал на логнормальные процессы и поля, для которых характерен факториальный рост моментов с номером. Подобные вероятностные распределения возникают и при решении уравнения первого порядка со случайным коэффициентом.

Для наглядного описания отдельной реализации случайного поля, а также и всего ансамбля реализаций В.И. Кляцкин предложил подход, названный им “статистической топографией” (термин употреблен ранее Займаном [Займан, 1982]). Этот подход обобщает теорию выбросов случайных процессов, в приложении к случайным полям. Первоначально подобный подход развивался Лонге–Хиггинсом [Longuet–Higgins, 1962]. Такое описание указывает на контраст между участками с разным рельефом. Эти участки могут занимать небольшую площадь, но сосредотачивать в себе большую часть “массы” поля. Такой подход возможен, хотя он менее нагляден, и при описании трехмерных и векторных полей.

Основу топографической картины составляет система линий уровня рельефа. Известная одноточечная плотность вероятности позволяет вычислить общую площадь областей ограниченных линиями данного уровня и полную длину ограничивающих контуров, а также их среднее число. Эти величины при большом интервале наблюдений оказываются детерминированными (когерентными) для любой реализации. Таким образом, координата точки наблюдения есть функция значения случайной величины. Представляя плотность вероятности в свою очередь как рельеф, мы можем наблюдать блуждания фиксированной точки по этому рельефу. Описание эволюции случайного рельефа следует из уравнения для плотности вероятности поля в точке. Уравнение получено и решено автором с помощью подхода, разработанного ранее для оптических полей. Результатом достаточно длительной эволюции является не зависящее от начальных условий состояние поля (его одноточечной плотности вероятности). Из полученных решений следует вывод о кластеризации поля плотности под воздействием случайного поля скорости течения в сжимаемой жидкости. Степень кластеризации зависит от дивергенции поля скорости. В несжимаемой жидкости происходит кластеризация пассивной примеси на поверхностях постоянной плотности, а также сжатие этих поверхностей. Возникающее вероятностное распределение сильно отличается от гауссова и ближе к логнормальному. Эти результаты говорят о некоторой структурности, присущей реализациям случайного поля. Вывод о структурности негауссовых полей столь же принципиален, как и вывод Э. Лоренца о хаотизации движения простейших динамических систем [Lorenz, 1963]. Cвязь между движениями разных масштабов ведет как к структурообразованию, так и к стохастизации поведения системы [Yakushkin et al., 1992; Якушкин, 1987].

Понятие структуры обсуждается в литературе применительно к различным физическим ситуациям, включая гидродинамику [Vallis, 2017; Blackwelder, 1987; Jimenez, 2018; Рабинович и др., 1998]. В целом, оно связано с понятием “формы” [Рабинович и др., 1998], которое предусматривает зависимость объекта от небольшого числа параметров. В данной работе, называя парциальные поля структурными, мы предполагаем, что они зависят от конечного набора принимающих случайные значения параметров, таких как точка расположения, амплитуда, ориентация и масштабы.

Для описания различных явлений в течениях жидкости, включая турбулентность, А.М. Обуховым и его коллегами [Гледзер и др., 1987; Должанский, 2011] было введено понятие системы гидродинамического типа, главной чертой которой является квадратичная нелинейность. Структуры, являющиеся следствием таких взаимодействий, имеют прообразы – вращающееся твердое тело или волновой триплет. На этой основе под руководством Ф. В. Должанского проводилось лабораторное изучение образования и эволюции вихревых структур в течениях с фиксированными границами. Для их интерпретации Ф.В. Должанским и его коллегами была развита аналогия вихревого течения в замкнутой области с вращающимся в поле силы тяжести твердым телом [Должанский и др., 1990].

Изучению волновых структур на границах области с заданными параметрами были посвящены труды Н.Н. Романовой [Romanova et al., 2001; Романова и др., 2005] и В.П. Гончарова [Гончаров и др., 2008] с соавторами, где был разработан подход к учету нелинейных взаимодействий на основе формализма Гамильтона. Большое внимание во всех перечисленных работах уделялось вопросам устойчивости структур. Как было показано [Должанский, 1990; Должанский и др., 2011; Romanova et al., 2005] неустойчивость развивается при взаимодействии простейших структур, а затем стабилизируется за счет взаимодействий со структурами посредниками. Возникающие режимы зависят от числа степеней свободы системы. Объединение структур сопровождается случайными изменениями границы и может описываться на вероятностном языке. Тем самым возникает необходимость движения исследователя по двум встречным путям: от сложного поля к простой структуре и от нее к ансамблю структур [Лоренц, 1970].

Рассматривая структурные объекты необходимо учитывать различие идеальных (гамильтоновых) и диссипативных систем. Сближение разных структур приводит к их соударениям, которые могут быть упругими и неупругими. В диссипативных структурах возникают многообразия типа странных аттракторов, тогда как гамильтоновы структуры сохраняют более регулярный характер. Поведение различных структур рассматривалось в работах Г.М. Заславского, М.И. Рабиновича и их соавторов [Заславский и др., 1991; Рабинович и др., 2000].

В настоящее время широко обсуждается вопрос о “солитонной турбулентности” [Pelinovsky et al., 2013], с которой связывают представление о “волнах – убийцах”. Это частный вид устойчивых волновых структур – солитонов, случайным образом расположенных в пространстве. Наблюдаемые природные объекты такого рода могут быть интерпретированы различным образом [Кляцкин, 2016].

Более точный учет вязкости заставляет обратиться к уравнениям высшего порядка. Отчасти сходные явления имеют место при переходе от геометрической оптики к волновой. Здесь учет высших производных поля позволяет описать интерференцию лучевых полей. Наложение полей в вязкой жидкости можно назвать их Конкуренцией [Кляцкин, 2016].

В настоящей статье обсуждаются структурные свойства случайных течений идеальной жидкости. Автор не ставил себе целью дать исчерпывающий обзор по данной теме, в основном учитывая работы коллег по Институту физики атмосферы. Эти исследования посвящались различным задачам, но фактически связаны между собой общим предметом исследования и математической основой процессов.

2. ОБЩИЕ СВОЙСТВА СЛУЧАЙНОГО ПОЛЯ

Задавая на случайном рельефе линии или поверхности уровня, мы выделяем интенсивные выбросы поля как ансамбль случайно расположенных и имеющих случайную форму “частиц”. Это могут быть или соприкасающиеся частицы сложной формы или изолированные частицы, выделенные из фона. Такому выделению соответствует разбиение полного вероятностного распределения на две части – малых и больших значений случайной величины.

Совокупность выделенных областей, представима как:

(2.1)

$U = \sum {{{U}_{i}}\left( {r - {{r}_{i}}} \right)} ,$

где ${{U}_{i}}$ – функция, соответствующая определенному уровню рельефа. Вектор ${{r}_{i}}$ указывает на расположение областей имеющих форму различных структур. Отдельные структуры принадлежат двум случайным ансамблям – локализованных образований и точек их расположения. На больших наблюдательных участках подобное поле остается статистически – однородным, но при уменьшении участка теряет это свойство. Используя преобразования (фильтрацию) поля, можно выделять такие структуры в преобразованном (фазовом) пространстве. Универсальным способом фильтрации является “оконное” преобразование Фурье, например, преобразование Габора [Баскаков, 1983]. Для одномерного поля оно имеет вид:

(2.2)

$F\left( {{{x}_{0}},k} \right) = \int {U\left( x \right)\exp \left\{ { - \frac{{{{{\left( {x - {{x}_{0}}} \right)}}^{2}}}}{{2{{a}^{2}}}} + ikx} \right\}dx} .$

Выражение (2.2) выделяет структуру данного размера, расположенную в точке фазового пространства. После обратного преобразования Фурье мы получаем структуры в комплексной форме с выделением амплитуды и фазы:

(2.3)

$U\left( x \right) = A\left( {x - {{x}_{0}}} \right)\exp \left[ {iS\left( {x - {{x}_{0}}} \right)} \right].$

К таким структурам относятся те, которые образуются на линиях уровня случайной величины и имеют вид волновых пакетов. Следует также учитывать, что простые “частицы” могут группироваться различным образом, что зависит от распределения их фазы. Группируясь между собой мелкие структуры, создают крупномасштабные кластеры. Для описания взаимного расположения структур следует использовать квадратичную форму:

${{U}_{2}}\left( {{\mathbf{r}},\Delta {\mathbf{r}}} \right) = U\left( {{\mathbf{r}} + \Delta {\mathbf{r}}} \right)U\left( {{\mathbf{r}} - \Delta {\mathbf{r}}} \right).$

Преобразование Фурье по разностной координате дает случайный спектр наблюдаемого поля, зависящий от точки наблюдения_, т.е. функцию Вигнера. Максимум информации о структурах можно получить, применяя преобразование Габора по двум переменным с разными масштабами:

(2.4)

$\begin{gathered} {{U}_{2}}\left( {{{x}_{0}},\Delta {{x}_{0}},K,\Delta K} \right)\, = \,\int {{{U}_{2}}\left( {x,\Delta {{x}_{0}}} \right)} \exp \left\{ { - {\kern 1pt} \frac{{{{{\left( {x\, - \,{{x}_{0}}} \right)}}^{2}}}}{{2{{a}^{2}}}}} \right. - \\ - \left. {\frac{{{{{\left( {\Delta x\, - \,\Delta {{x}_{0}}} \right)}}^{2}}}}{{2{{b}^{2}}}}\, - \,i\Delta Kx\, - \,iK\Delta x} \right\}dxd\Delta x. \\ \end{gathered} $

Изменяя размеры “окна”, мы выделяем структуры, связанные соотношением неопределенности, разных масштабов. Выделение наиболее ярких структур достигается за счет выбора масштабов фильтрации в соответствии с принципом максимального контраста, которому соответствует средний квадрат флуктуаций интенсивности. Примером такого подхода служит анализ изображений взволнованной поверхности фильтрация случайных полей акустических или внутренних гравитационных волн, регистрируемых в зависимости от времени в нескольких пространственных точках [Якушкин, 1990; Якушкин, 1998].

2.2 Локальные свойства случайных полей.

Прежде чем перейти к анализу эволюции ярких структур, наблюдаемых в случайных полях, необходимо расширить это понятие, включив в него свойства окрестности выбранной точки. Рассмотрим подробнее структуры, расположенные в физическом пространстве, лишь отчасти касаясь структур в пространстве фазовом.

Свойства окрестности скалярного поля $U\left( {\mathbf{r}} \right)$ содержатся в матрице вторых производных ${{U}_{{ij}}}$. При описании структур поля скорости или другого векторного поля ${\mathbf{V}}$ мы должны обратиться к анализу матрицы производных отдельных компонент поля ${{V}_{{ij}}}.$ Такие матрицы характеризуются набором инвариантов, к которым относятся определитель и след. Линии уровня этих величин могут быть нанесены на первоначальный статистический рельеф. Структуры спектрального типа, представленные через амплитуду и фазу $U = A\exp \left( {iS} \right)$ с наклонами фазового фронта ${\mathbf{K}} = {\text{grad}}S.$ В таком случае локальная структура определяется через связь волнового вектора с волновыми векторами других компонент поля. Одномерный рельеф $U\left( x \right)$ характеризуется величиной ${{U}_{{xx}}},$ знак которой указывает на тип деформации окрестности локального максимума или минимума поля. Скорость одномерного течения определяется как $V = {{dU} \mathord{\left/ {\vphantom {{dU} {dt}}} \right. \kern-0em} {dt}}.$ В таком поле возможно существование структур вида:

(2.5)

$V\left( x \right) = Ax - B{{x}^{2}}.$

Такая конструкция включает точки нулевой скорости и точку нулевой производной между ними. Все случайное поле разделяется при этом на части сгущения и растяжения. Другого типа структура связана с отдельной составляющей спектра Фурье и имеет вид волнового пакета:

$V\left( k \right) = V\left( {k - {{k}_{0}}} \right)\exp \left[ {ikx} \right].$

Наиболее наглядна топография двумерной поверхности $U\left( x \right) = U\left( {x,y} \right),$ которая в каждой точке характеризуется двумя инвариантами – средней и гауссовой кривизной, т.е. определителем и следом матрицы ${{U}_{{ij}}}$

(2.6)

${{K}_{m}} = {{U}_{{xx}}} + {{U}_{{yy}}},\,\,\,\,{{K}_{g}} = {{U}_{{xx}}}{{U}_{{yy}}} - {{U}_{{xy}}}{{U}_{{yx}}}.$

Второй момент ${{K}_{m}}$ и среднее значение ${{K}_{g}}$ выражаются через корреляционную функцию случайного поля. Вместе с тем линии уровня этих величин делят поверхность на зоны с различными свойствами. Точки нулевого градиента также делятся на точки экстремумов и перевальные в зависимости от знака ${{K}_{g}}.$

Двумерное поле скорости течения идеальной жидкости может быть выражено через две скалярных функции – потенциал и функцию тока:

(2.7)

${\mathbf{V}} = {\text{grad}}\varphi + {{{\mathbf{e}}}_{{\mathbf{z}}}} \times {\text{grad}}\left( {\psi + {{\psi }_{0}}} \right),\,\,\,\,\Delta {{\psi }_{0}} = 0.$

Наряду с вихревой и потенциальной, в полном поле скорости может быть выделена компонента с нулевой дивергенцией и завихренностью. Такое поле имеет инварианты: дивергенцию $D,$ завихренность $\Omega $ и функцию Окубо–Вайса $K$ [Okubo, 1970].

(2.8)

$\begin{gathered} D = \Delta \varphi = {{V}_{{xx}}} + {{V}_{{yy}}},\,\,\,\,\omega = \Delta \psi = {{V}_{{xy}}} - {{V}_{{yx}}}, \\ K = {{V}_{{xx}}}{{V}_{{yy}}} - {{V}_{{xy}}} = \frac{1}{4}{{\Omega }^{2}} - {{Q}^{2}}. \\ \end{gathered} $

Функция ${{Q}^{2}} = {{V}_{{xy}}}{{V}_{{yx}}} - \frac{1}{4}{{\left( {{{V}_{{xy}}} + {{V}_{{yx}}}} \right)}^{2}}$ представляет собой деформацию поля скорости. Линии $K = 0$ делят всю плоскость на части, в которых преобладают завихренность или деформация. Компонента ${{\psi }_{0}}$ создается сторонней завихренностью и вносит важный вклад в деформацию. Среднее значение $K$ характеризует степень квазиодномерности течения.

Простейшая структура течения несжимаемой жидкости предполагает, что около некоторой точки поля скорости задана постоянная завихренность, отделенная границей от остального течения. Если граница твердая, то нормальная скорость на ней равна нулю. Линии уровня имеют вид

(2.9)

$\Psi = a{{x}^{2}} + 2bxy + c{{y}^{2}} = C$

и в зависимости от знака $K$ описывают эллипсы или гиперболы. Или при учете линейного члена-параболу. Функция (2.9) может быть представлена как сумма вихревой и безвихревой части, которые описывают вращение и деформацию окрестности. В более общем случае линия уровня колеблется около среднего положения. Такая структура представляет собой квазиодномерное течение, сжимаемое в основном направлении.

Трехмерное поле в окрестности некоторой точки характеризуется кубической матрицей вторых производных. Матрица скалярного поля симметрична и поверхности уровня в окрестности экстремальной точки имеют вид эллипсоида или гиперболоида.

Трехмерное поле скорости течения представляется в виде суммы потенциальной и вихревой компонент. Разбиение кубической матрицы производных ${{V}_{{ij}}}$ на симметричную и антисимметричную части соответствует выделению разных компонент поля. Выделяя одно из пространственных направлений (в земных условиях вертикаль), это поле можно представить, как квазидвумерное, в виде

(2.10)

${\mathbf{V}} = {\text{grad}}\varphi + {{{\mathbf{e}}}_{{\mathbf{z}}}} \times {\text{grad}}\psi + w{{{\mathbf{e}}}_{{\mathbf{z}}}},$

где ${\text{grad}}$ вычисляется в плоскости $\left( {x,y} \right).$ Для несжимаемой жидкости имеем

(2.11)

$\varphi = \frac{{\partial {{\varphi }_{1}}}}{{\partial z}},\,\,\,\,w = {\text{div}}\,{\text{grad}}{{\varphi }_{1}}.$

Горизонтальное течение рассматривается как течение сжимаемой жидкости, а его дивергенция оказывается функцией вертикальной скорости. Представляют интерес и вертикальные “разрезы”, как их называют геоморфологи. В каждом сечении среда рассматривается как сжимаемая.

2.3. Случайные поля и эволюция структур

Процесс эволюции возмущений в идеальной жидкости представляет собой взаимодействие полей скорости и смещения точек среды. В полной системе уравнений идеальной жидкости поле скорости связано с полями давления $P,$ плотности $\rho ,$ температуры $T,$ которые определяются потенциальной энергией системы. Поле доступной потенциальной энергии подвергается деформации, т.е. растяжению и сжатию элементарного объема в различных направлениях. Пример эволюции вихревых структур, полученных в лабораторных условиях, показан на рисунке (1).

Рис. 1.

Фото вихревых структур на поверхности проводящей жидкости во вращающемся прямоугольном сосуде. Каждая строка соответствует своему периоду вращения $T = 22,10.1,6.2,2.8$ с. Каждому столбцу соответствует момент времени $t = 0,{T \mathord{\left/ {\vphantom {T 2}} \right. \kern-0em} 2},T.$ Градации цвета показывают скорость движения жидкости в ${{{\text{см}}} \mathord{\left/ {\vphantom {{{\text{см}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$. Графики взяты из [Kostrykin et al., 2014].

Локальная деформация выражается через тензора смещений ${{dR} \mathord{\left/ {\vphantom {{dR} {d{{R}_{0}}}}} \right. \kern-0em} {d{{R}_{0}}}}$ или ${{d{{R}_{0}}} \mathord{\left/ {\vphantom {{d{{R}_{0}}} {dR}}} \right. \kern-0em} {dR}},$ где ${{R}_{0}}$ – исходное положение точки. Детерминант этого тензора – плотность среды в точке. Для идеальной жидкости связь полей скорости и смещения точки выражается с помощью сохраняющегося гамильтониана (энергии) [Якушкин, 2005; Salmon, 1988], который имеет вид интеграла по одному из объемов:

(2.12)

$H = \int {{{H}_{1}}d} {{{\mathbf{R}}}_{0}} = \int {{{H}_{1}}\frac{{d{{{\mathbf{R}}}_{0}}}}{{dR}}d} {\mathbf{R}}.$

Точка зависимого объема выступает в роли канонической координаты в уравнениях Пуассона. Выбор представления определяет эйлерову или лагранжеву форму записи поля скорости. Возможен также выбор смешанного представления. Уравнения движения точки сплошной среды в форме Лагранжа, как и уравнения движения системы частиц имеют вид:

(2.13)

$\begin{gathered} \frac{{d{\mathbf{V}}}}{{dt}} = {\mathbf{F}}\left( {{\mathbf{R}},{{{\mathbf{R}}}_{0}}} \right),\,\,\,\,\frac{{d{\mathbf{R}}}}{{dt}} = {\mathbf{V}}\left( {{\mathbf{R}},t} \right), \\ {\mathbf{R}}\left( {t = 0} \right) = {{R}_{0}},\,\,\,\,{\mathbf{V}}\left( {t = 0} \right) = {{{\mathbf{V}}}_{0}}. \\ \end{gathered} $

Решая уравнения, мы следим за изменением формы ее окрестности, которая описывается тензором ${{d{\mathbf{R}}} \mathord{\left/ {\vphantom {{d{\mathbf{R}}} d}} \right. \kern-0em} d}{{{\mathbf{R}}}_{0}}.$

В эйлеровой форме уравнения имеют вид:

(2.14)

$\frac{{\partial {\mathbf{V}}}}{{\partial t}} + V\frac{{\partial {\mathbf{V}}}}{{\partial R}} = {\mathbf{F}}\left( {{\mathbf{R}},t} \right),\,\,\,\,\frac{{\partial {{{\mathbf{R}}}_{0}}}}{{\partial t}} + \left( {{\mathbf{V}}\frac{{\partial {{{\mathbf{R}}}_{0}}}}{{\partial {\mathbf{R}}}}} \right) = 0.$

Относительное движение траекторий определяется через ${{d{{{\mathbf{R}}}_{0}}} \mathord{\left/ {\vphantom {{d{{{\mathbf{R}}}_{0}}} {d{\mathbf{R}}}}} \right. \kern-0em} {d{\mathbf{R}}}}.$ В данном случае мы описываем траекторию ее начальными координатами. Это лагранжевы инварианты, сохраняющиеся вдоль траектории. Для каждого начального контура в случайном поле мы имеем три инварианта, задающие поверхность (семейство контуров), контур на поверхности и точку на контуре. Это система лагранжевых координат. В идеальной несжимаемой (изоэнтропической) жидкости особое значение имеют такие инварианты как плотность и потенциальная завихренность (скалярное произведение градиента плотности и завихренности). На топографической картине случайного поля два инварианта задают систему линий уровня каждой точке, которой соответствует свое значение третьего инварианта и своя траектория. Связывая поле скорости с системой лагранжевых инвариантов ${{H}_{i}}\left( R \right),$ получаем выражение для этого поля в форме Лина [Salmon, 1988]:

(2.15)

${\mathbf{V}} = \sum\limits_{i = 1}^3 {{{\lambda }_{i}}{\text{grad}}} {{H}_{i}}.$

Учитывая, что два инварианта определяют траекторию, а третий положение точки на ней форма записи поля скорости принимает вид:

(2.16)

${\mathbf{V}} = \sum\limits_{i = 1}^2 {{{\lambda }_{i}}{\text{grad}}} {{H}_{i}} + {\text{rad}}\varphi .$

Возмущения в равновесной системе лагранжевых инвариантов вызывают колебания линий уровня. При этом в различных ситуациях образуются когерентные (с фиксированной фазой) или частично-когерентные структуры. Они возникают в результате развития и стабилизации возмущений около точки нулевой частоты колебаний, играющей ту же роль что и точка фокусировка в оптике. На малых масштабах на структуры влияет диссипация энергии.

3. ЭВОЛЮЦИЯ СТРУКТУР В СРЕДЕ С ЗАДАННЫМИ СВОЙСТВАМИ

Эволюция течений жидкости описывается нелинейными уравнениями, и решение связанных с ней задач вызывает трудности. Возникают четыре возможные постановки задачи:

1. Кинематическое приближение. Поле скорости предполагается случайным или частично детерминированным векторным полем с заданной гауссовой статистикой: ${\mathbf{V}}\left( {{\mathbf{R}}{\text{,}}t} \right)$ или ${\mathbf{V}}\left( {{{{\mathbf{R}}}_{0}}{\text{,}}t} \right).$

2. Приближение сторонней силы. В этом приближении известными предполагаются свойства поля силы: ${\mathbf{F}}\left( {{\mathbf{R}}{\text{,}}t} \right)$ или ${\mathbf{F}}\left( {{{{\mathbf{R}}}_{0}}{\text{,}}t} \right).$

3. Система уравнений идеальной жидкости (уравнения Гамильтона). В этих уравнениях сила ${\mathbf{F}}$ зависит от точек $R$ и ${{R}_{0}},$ т.е. от начального и текущего состояния системы посредством полей давление $P,$ плотности $\rho $ и т.д. Случайными при такой постановке являются начальные условия.

4. Уравнения, учитывающие диссипацию. К такого рода описанию приводит и использование понятия турбулентной вязкости.

Два первых подхода позволяют, во-первых, выяснить общие закономерности взаимодействия полей скорости и смещения, во-вторых, служат для интерпретации эксперимента по наблюдению различных полей, например, поля пассивной примеси. При этом решение уравнений на их основе требует предположений о масштабах задаваемых полей.

Если средний квадрат скорости $V_{0}^{2},$ пространственный масштаб корреляции $\ell ,$ а временной масштаб ${{t}_{0}},$ то основное значение для динамики системы имеет сравнение масштабов ${{t}_{0}}$ и ${{T}_{0}} = {\ell \mathord{\left/ {\vphantom {\ell {{{V}_{0}}}}} \right. \kern-0em} {{{V}_{0}}}}.$ Если их отношение мало, то смещение точки на расстояние $\ell $ происходит в среднем за время $T = {{\left( {\frac{\ell }{V}{{t}_{0}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$ Если это отношение велико, то $T = {{T}_{0}}.$ По аналогии с оптической задачей время $T$ можно назвать временем фокусировки.

Важнейшим является предположение о дельта-корреляции полей ${\mathbf{V}}\left( {{\mathbf{R}},t} \right)$ или ${\mathbf{F}}\left( {{\mathbf{R}},t} \right)$ по времени. Это предположение широко использовалось в работах В.И. Татарского и других исследователей в задачах распространения волн в атмосфере [Рытов и др., 1978; Kravzov, 1992], а также в задаче о кластеризации примеси [Кляцкин, 2005; Данилов и др., 2000; Пономарев и др., 2009] и других.

3.1. Кинематическое приближение

Кинематическое приближение, сводится к решению уравнения для смещений при заданной скорости течения. При структурном подходе в окрестности точки нулевой скорости уравнения движения имеют вид:

(3.1)

$\frac{{d{{R}_{i}}}}{{dt}} = {{V}_{{ij}}}{{R}_{j}},\,\,\,\,\frac{{d{{R}_{{ik}}}}}{{dt}} = {{V}_{{ij}}}{{R}_{{jk}}},$

где ${{R}_{{ij}}} = {{d{{R}_{i}}} \mathord{\left/ {\vphantom {{d{{R}_{i}}} {{{R}_{{0j}}}}}} \right. \kern-0em} {{{R}_{{0j}}}}}$ – тензор относительных смещений. Тензор ${{V}_{{ij}}}$ содержит стационарную и зависящую от времени компоненты и характеризуется инвариантами симметричной и антисимметричной матриц. Стационарная компонента может быть результатом осреднения по времени. При постоянных или медленно меняющихся компонентах тензора ${{V}_{{ij}}}$ частное решение ищется в виде

(3.2)

${\mathbf{R}} = {{{\mathbf{R}}}_{0}}{{e}^{{is}}}.$

Величины $p = {{ds} \mathord{\left/ {\vphantom {{ds} {dt}}} \right. \kern-0em} {dt}}$ – корни кубического дисперсионного уравнения. Если мы имеем сумму матриц антисимметричной с элементами $a,b,c$ и диагональной с элементами ${{q}_{i}},$ то дисперсионное уравнение имеет вид

(3.3)

$\begin{gathered} {{p}^{3}} - \left( {{{q}_{1}} + {{q}_{2}} + {{q}_{3}}} \right){{p}^{2}} + \\ + \,\,\left( {{{a}^{2}} + {{b}^{2}} + {{c}^{2}} + {{q}_{1}}{{q}_{2}} + {{q}_{1}}{{q}_{3}} + {{q}_{2}}{{q}_{3}}} \right)p + \\ + \,\,{{q}_{1}}{{q}_{2}}{{q}_{3}} = 0. \\ \end{gathered} $

Решения уравнения описывают свойства поля, включающие вращение и деформацию структуры. Соотношение между корнями уравнения позволяет выделить различные режимы движения, которые в пространстве основных параметров (инвариантов матриц) разделяются сепаратрисами. Компоненты асимметричной матрицы $a,b,c$ указывают направление и частоту вращения. Деформация проявляется в сжатии и растяжении структуры в разных направлениях. Если след симметричной матрицы равен нулю, то не происходит изменение объема области жидкости, но меняется ее форма. Это соответствует изменению пространственного положения лагранжевых инвариантов.

Вращающаяся система может превращаться в тонкую трубку или диск. Если структура имеет форму гиперболоида, то эволюция приводит к кручению или сглаживанию ее фронтов. Это различные формы кластеризации, приводящие к возникновению больших градиентов. В двумерном течении вид траекторий и характер центральной точки определяются через след поля скорости и функцию Окубо–Вайса.

Зависимые от времени структурные коэффициенты меняют характер траекторий в точках поворота, где происходит слияние корней дисперсионного уравнения или один из корней обращается в ноль. Если время наблюдения не превышает времени фокусировки, то полное поле скорости представимо в виде суммы осредненного и случайного полей ${\mathbf{V}} = {{{\mathbf{V}}}_{0}} + {{{\mathbf{V}}}_{1}}.$ Равенство нулю величины $\int_0^\infty {{\mathbf{V}}\left( t \right)dt} $ требует дополнительного анализа [Кляцкин и др., 2000].

Другого типа модель поля скорости может быть задана в форме волнового пакета через его амплитуду и фазу. Решая уравнение Эйлера для смещения, мы получаем структуру имеющую вид триплета с волновыми числами, удовлетворяющими условию резонанса. Подобный триплет соответствует взаимодействию начального смещения траектории от положения равновесия и отклика на это возмущение.

Если поле скорости задается в виде ${\mathbf{V}}\left( {{{{\mathbf{R}}}_{0}}} \right),$ такая модель носит название приближения “фазового экрана”. Оно просто в использовании и дает глобальную картину эволюции течения на ограниченных интервалах времени. Оно используется для описания рассеянья волн на небольших по протяженности трассах.

3.2. Приближение сторонней силы

Это приближение предполагает, что сила задана своей корреляционной функцией и имеет много общего с кинематическим приближением. Характер траекторий все же меняется, т.к. становятся возможными колебательные режимы. Такое приближение широко используется в задаче о распространении оптического излучения в неоднородной случайной среде, а также и в теории турбулентности.

Задавая компоненты силы в виде ${{F}_{i}} = {{F}_{{ij}}}{{R}_{j}},$ получаем систему уравнений второго порядка

(3.4)

$\frac{{{{d}^{2}}{{R}_{i}}}}{{d{{t}^{2}}}} - {{F}_{{ij}}}{{R}_{j}} = 0.$

В трех измерениях дисперсионное уравнение имеет ту же структуру, как и уравнение (3.3), только относительно квадрата мгновенной частоты. Решение включает три ветви, отвечающие разному поведению траекторий, зависящие от соотношения элементов симметричной и антисимметричной матриц ${{F}_{{ij}}}.$ В двумерном случае дисперсионное уравнение имеет вид

(3.5)

${{p}^{4}} + {{p}^{2}}\left( {{{F}_{{xx}}} + {{F}_{{yy}}}} \right) + \left( {{{F}_{{xy}}}{{F}_{{yx}}} - {{F}_{{xx}}}{{F}_{{yy}}}} \right) = 0.$

Четыре решения этого уравнения дают картину траекторий, зависящую от инвариантов матрицы производных силы. Траектории соседних точек сближаются и расходятся, что может сопровождаться их колебаниями и взаимным пересечением. Если след матрицы равен нулю, движение происходит в режимах вращения, деформации или их сочетающих. При нестационарной силе переход между режимами происходит при слиянии корней дисперсионного уравнения и может рассматриваться как проявление неустойчивости течения. На большом масштабе движение описывается уравнением Эйлера для скорости:

(3.6)

$\frac{{\partial V}}{{\partial t}} + \left( {V\frac{\partial }{{\partial R}}} \right)V = F.$

Для малой по амплитуде и быстроменяющейся силе уравнение может быть проинтегрировано, что означает переход к кинематическому приближению. Для сравнительно медленных движений такой переход следует из условия:

$\left( {V\frac{\partial }{{\partial R}}} \right)V = - F.$

Это уравнение совместно с уравнением для смещения начальной точки описывает медленные движения около состояния частичного равновесия. По отношению к быстрым колебаниям медленные переменные представляют собой лагранжевы инварианты, сохраняющиеся вдоль траектории.

Если сила задается в виде волнового пакета, то эйлеровы уравнения описывают образование волновых триплетов. В комбинациях волновых чисел выделяются те, которые обеспечивают согласование фаз по текущей частоте (резонанс). Используя представление ${\mathbf{F}} = {\mathbf{F}}\left( {{{{\mathbf{R}}}_{0}},t} \right),$ мы получаем модель эквивалентную приближению фазового экрана.

3.3. Распространение излучения в случайной среде и фильтрация наблюдаемых полей

Образование структур в случайных полях легче проследить в задаче о распространении оптического излучения в случайно-неоднородной среде, которая соответствует задаче о потенциальном течении под действием сторонней силы [Рытов и др., 1978; Kravzov, 1992]. Постановка задачи связана с заданием модели среды распространения со случайными вариациями показателя преломления, на которых происходит рассеяние излучения. Так как масштаб неоднородностей много больше оптической длины волны, для описания процесса используется параболическое уравнение М.А. Леонтовича. Решение этого уравнения с граничным условием при $z = 0$ в плоскости наблюдения записывается как сумма полей, распространяющихся по отдельным лучам (траекториям):

(3.7)

$U = \sum\limits_i {{{U}_{i}}\left( r \right)} ,\,\,\,\,{{U}_{i}} = {{A}_{i}}\exp \left( {ik{{S}_{i}}} \right).$

Здесь $S$ – фаза отдельного лучевого поля, полученная методом геометрической оптики [Кравцов и др., 1980] для наклона фазового фронта ${\mathbf{p}} = {\text{grad}}\,S$ и координат точки в плоскости наблюдения ${\mathbf{R}}\left( {x,y} \right)$ в среде с показателем преломления $n\left( {{\mathbf{R}},z} \right).$ В задаче о течении потенциальной жидкости координата $Z$ играет роль времени, а угол наклона луча ${\mathbf{p}} = {\text{grad}}\,S$ эквивалентен скорости течения в заданной точке.

Интенсивность поля определяется шириной лучевой трубки:

(3.8)

$I = \left| {\frac{{d{{{\mathbf{R}}}_{0}}}}{{d{\mathbf{R}}}}} \right|.$

Если длина трассы распространения не превышает расстояния фокусировки, то мы имеем режим однолучевого распространения. В плоскости наблюдения распределение интенсивности представляет собой совокупность ярких полос и пятен, являющихся результатом случайных фокусировок. Вблизи точек, где лучевая амплитуда бесконечна, необходим учет дифракции. Описание случайных фокусировок излучения упрощается в приближении “фазового экрана” [Якушкин, 1974; Yakushkin, 1996], согласно которой скорость в точке наблюдения получается интегрированием показателя преломления по заданным линиям и ее распределение в плоскости $z = 0{\text{:}}$

(3.9)

$\begin{gathered} S\left( {x,y,z} \right) = S\left( {{{x}_{0}},{{y}_{0}}} \right), \\ x = {{x}_{0}} + z{{s}_{x}},\,\,\,\,y = {{y}_{0}} + z{{s}_{y}}, \\ {{s}_{x}} = {{s}_{{0x}}}\left( {{{x}_{0}},{{y}_{0}}} \right),\,\,\,\,{{s}_{y}} = {{s}_{{0y}}}\left( {{{x}_{0}},{{y}_{0}}} \right). \\ \end{gathered} $

Топография фазового фронта характеризуется его средней и гауссовой кривизной, которые меняются по длине трассы. Если в начальной точке

${{D}_{0}} = {{S}_{{0xx}}} + {{S}_{{0yy}}}\,\,{\text{и}}\,\,{{K}_{0}} = {{S}_{{xx}}}{{S}_{{yy}}} - S_{{xy}}^{2}$

то, обозначая ${{K}_{1}} = \frac{1}{{{{z}^{2}}}} + \frac{{{{D}_{0}}}}{z} + {{K}_{0}},$ получаем характеристики текущего фазового фронта:

(3.10)

$\begin{gathered} {{S}_{{xx}}} + {{S}_{{yy}}} = \frac{{\left[ {2{{K}_{1}}--{\text{ }}2{\text{ }} + {\text{ }}2D} \right]}}{{{{K}_{1}}}},\, \\ {{S}_{{xx}}}{{S}_{{yy}}} - S_{{yy}}^{2} = \frac{1}{{{{K}_{1}}}}. \\ \end{gathered} $

Амплитуда лучевого поля в плоскости наблюдения также определяются как функции характеристик волнового фронта в точке $\left( {{{x}_{0}},{{y}_{0}}} \right)$

(3.11)

$I = \left| {\frac{{d{{{\mathbf{R}}}_{0}}}}{{d{\mathbf{R}}}}} \right| = \frac{1}{{{{K}_{1}}{{z}^{2}}}} + \frac{{{{D}_{0}}}}{z} + {{K}_{0}}.$

На фазовом фронте фокусирующей являются область, где $D < 0.$ Параметры ярких структур связаны с масштабами рассеивающих центров в среде распространения. Измерения амплитуды и фазы в плоскости $Z$ позволяют восстановить свойства среды.

При увеличении длины трассы картина определяется интерференцией многих лучевых полей малой амплитуды. Однако число приходящих в точку лучей модулировано случайным образом, т.к. распределение фазы на экране представляет сумму структур больше и меньше масштаба фокусировки. Мелкие неоднородности размывают картину фокусировок. Проводя осреднение по этой компоненте, получаем частично когерентное описание наблюдаемого поля. Крупномасштабная компонента фазы приводит к слабым фокусировкам.

Для более точного описания картины фокусировок на трассах порядка фокусного расстояния можно прибегнуть к осреднению параметров среды по длине дистанции:

$F = {{F}_{1}} + {{F}_{2}},\,\,{\text{где}}\,\,{{F}_{1}} = \int\limits_0^z {F\left( {x,{{z}_{1}}} \right)} d{{z}_{1}}.$

При данном $z$ ${{F}_{1}}\left( {\mathbf{R}} \right)$ указывает ряд притягивающих в среднем точек, около которых группируются траектории. Между такими структурами происходят случайные блуждания отдельных траекторий.

Тот же подход целесообразен и для описания потенциальных течений (акустических волн) [Okubo, 1970]. В несжимаемой жидкости образование структур происходит сходным образом, хотя сами структуры имеют другой вид.

4. ГАМИЛЬТОНОВЫ СТРУКТУРЫ В ИДЕАЛЬНОЙ ЖИДКОСТИ

Более полное исследование образования и развития структур в течениях идеальной жидкости следует из уравнений Гамильтона. В этих уравнениях действующая сила выражается через поля давления $P$ и плотности $\rho $ и зависит от начального и текущего положения точек на траектории ${{F}_{1}}\left( {{\mathbf{R}},{{{\mathbf{R}}}_{0}}} \right).$ Структуры образуются вследствие отклонения начальной точки от равновесного состояния. Координаты начальной точки остаются постоянными, т.е. являются лагранжевыми инвариантами. Решение линейных уравнений описывает простые структуры, а более сложные возникают при развитии неустойчивости.

Потенциальное течение рассмотрим на примере распространения акустической волны большой амплитуды, которое сопровождаются образованием фронта ударных волн [Гурбатов и др., 1983], что описывается уравнением:

(4.1)

$\frac{{\partial V}}{{\partial t}} + V\frac{{\partial V}}{{\partial x}} = 0.$

Образование ударных фронтов происходит в точках, где производная скорости равна нулю. Определение ограничивающего ширину фронта масштаба следует из решения двух выходящих за пределы квадратичного приближения нелинейных уравнений. Другой путь – учет диссипации.

В несжимаемой жидкости динамика структур описывается уравнениями для завихренности и плотности. Поле скорости определяется полем завихренности и граничными условиями.

В баротропной жидкости все течение делится на области большой и малой завихренности. Область большой завихренности представляет собой вращающуюся структуру, форма которой изменяются под влиянием безвихревой скорости, возникающей или как следствие начального возмущения, или под воздействием других структур. Движение отдельной точки при этом носит двойственный характер – она движется по поверхности постоянного квадрата завихренности и смещается в пространстве вместе с этой поверхностью. Если в квазиодномерном струйном течении скорость в точке имеет компоненту ${{V}_{x}},$ то компоненты антисимметричной матрицы ${{V}_{{xz}}},$ ${{V}_{{xy}}}$ указывают на степень сжатия-растяжения трубки тока в направлении движения. Элементы ${{V}_{{yz}}}$ указывают на вращение трубки тока вокруг своей оси. Такие трубки разбиваются на отдельные участки с разной степенью сжатости, что может быть трактовано как турбулентная диффузия [Гурбатов и др., 1983; Jimenez, 2018]. Если зависящая от времени безвихревая компонента скорости задана как случайная, то траектории получают характер случайных блужданий. Все эти явления наблюдаются в лабораторных экспериментах по распространению пассивной примеси в вихревых течениях [Данилов и др., 2000; Пономарев и др., 2009].

В стратифицированной несжимаемой изоэнтропийной жидкости траектория определяется двумя лагранжевыми инвариантами: плотностью и потенциальной завихренностью ${\mathbf{\Omega }} \times {\text{grad}}\rho .$ Эти сохраняющиеся величины являются границами различных структур.

В линейной постановке система описывает колебания завихренности и плотности. Образующиеся благодаря квадратичной нелинейности структуры имеют характер триплета. В системе имеющей точку нулевой частоты развивается неустойчивость, которая соответствует кластеризации в акустике или фокусировкам в оптике. Свойства структур зависят от соотношения между геострофической и агеострофической компонентами движения. Геострофическое равновесие способствует образованию когерентных структур, тогда как агеострофическая вносит элемент случайности [Groesen, 1996]. Выражение для геострофического ветра

(4.2)

$ - {\text{rot}}\left[ {V \times \Omega } \right] = g \times {\text{grad}}\rho $

выделяет медленные колебания структуры. Определяемая таким образом завихренность имеет две компоненты: параллельную и ортогональную градиенту плотности. Первая присутствующая в трехмерных течениях, соответствует вращению системы, вторая связана с колебаниями поверхностей постоянной плотности.

При этом возникают две простейшие задачи – образование структур внутри областей с твердой границей и динамика границы при заданной завихренности и плотности внутри области. Ниже рассматриваются два примера структур, образующихся при развитии и стабилизации неустойчивости в областях с твердой и подвижной границей, которые позволяют проследить многие общие закономерности справедливые и для более сложных задач.

4.1. Волновые структуры

Обратимся к двумерной задаче о структурах на границе между течениями несжимаемой жидкости с разной плотностью [Romanova et al., 2005; Романова и др., 2016]. Завихренность в этом случае ортогональна плотности. На границах слоев с постоянной плотностью возбуждаются колебания, имеющие быструю и медленную ветви. Медленная ветвь представляет совместные колебания плотности (лагранжева инварианта) и завихренности, удовлетворяющие условию (4.2). Неустойчивость развивается при возмущениях течения вблизи точки нулевой частоты. Возмущение, взаимодействуя с откликом фонового течения, формирует структуру.

Такая задача была сформулирована в работах [Romanova et al., 2005; Романова и др., 2016], где был проведен анализ развития и стабилизации неустойчивости в трехслойном течении со сдвигом скорости. Взаимодействие границ в трехслойной системе ведет к развитию растущей “гибридной” моды. Завихренный слой растягивается в узкую полосу сходную с ударными фронтами. Неустойчивость стабилизируется или вследствие взаимодействия границ, выходящего за пределы квадратичного приближения [Guha et al., 2014] или путем образования резонансного триплета с двумя устойчивыми волнами [Loesch, 1974]. Этот триплет включает четыре волны на трех волновых числах:

(4.3)

${{A}_{i}} = {{b}_{i}}\exp \left[ {i{{k}_{i}}x - i\omega \left( {{{k}_{i}}} \right)t} \right]\,\,\,\,\left( {i = 1 - 4} \right).$

Волновые числа удовлетворяют условиям

(4.4)

$\begin{gathered} {{k}_{1}} - {{k}_{2}} - {{k}_{3}} = 0,\,\,\,\,\omega \left( {{{k}_{1}}} \right) - \omega \left( {{{k}_{2}}} \right) - \omega \left( {{{k}_{3}}} \right) = 0, \\ {{k}_{4}} = {{k}_{2}},\,\,\,\,\omega \left( {{{k}_{4}}} \right) = \omega \left( {{{k}_{2}}} \right). \\ \end{gathered} $

Компоненты ${{A}_{{2,4}}}$ представляют неустойчивые волны на двух границах слоя со сдвигом скорости, компоненты ${{A}_{{1,3}}}$ – устойчивые моды. Комплексные амплитуды ${{b}_{i}}$ удовлетворяют четырем уравнениям с тремя инвариантами

(4.5)

$\begin{gathered} {{I}_{1}} = {{b}_{1}}b_{1}^{ * } + {{b}_{3}}b_{3}^{ * },\,\,\,\,{{I}_{2}} = {{b}_{1}}b_{1}^{ * } + {{b}_{2}}b_{2}^{ * } + {{b}_{4}}b_{4}^{ * }, \\ {{I}_{3}} = \operatorname{Re} \left[ {{{b}_{2}}\left( {b_{1}^{ * }b_{3}^{ * } + b_{4}^{ * }} \right)} \right] \\ \end{gathered} $

${{I}_{3}}$ играет роль гамильтониана и определяет динамику системы. Если ${{I}_{3}} = 0,$ то система имеет дополнительные инварианты. Вводя обозначения ${{b}_{1}}{{b}_{3}} = \frac{1}{2}{{a}^{2}}sh\left( {2\mu {{e}^{{i{{\vartheta }_{{13}}}}}}} \right),$ ${{b}_{{2,4}}} = i{{R}_{{2,4}}}{{e}^{{i{{\vartheta }_{{2,4}}}}}}$ и переходя к переменным $x,y{\text{:}}$ ${\text{ch}}\left( {2\mu } \right) = {\text{ch}}x \times {\text{ch}}\left( {2\mu } \right),$ ${{y}^{2}} = R_{4}^{2} - y_{0}^{2}.$ Получаем

(4.6)

$\begin{gathered} {{I}_{3}} = {{R}_{2}}\left( {{{C}_{1}} + {{C}_{2}}} \right) = 0, \\ {{C}_{1}} = \frac{{{{a}^{2}}}}{2}{\text{sh}}\left( {2\mu } \right)\sin \left( {{{\vartheta }_{{13}}} - {{\vartheta }_{2}}} \right), \\ {{C}_{2}} = {{R}_{2}}\sin \left( {{{\vartheta }_{4}} - {{\vartheta }_{2}}} \right). \\ \end{gathered} $

При ${{I}_{3}} = 0$ имеем инвариантные величины ${{C}_{1}} = - {{C}_{2}}S = x - 2y$ и систему двух уравнений

(4.7)

$\frac{{dx}}{{dt}} = 2{{R}_{2}},\,\,\,\,\frac{{dy}}{{dt}} = - {{R}_{2}}.$

С инвариантом ${{I}_{2}}\, = \,R_{2}^{2} + \frac{{{{a}^{2}}}}{2}{\kern 1pt} {\text{ch}}\left( {2{{\mu }_{0}}} \right){\text{ch}}\left[ {S - 2y} \right] - $ $ - \,{{y}^{2}} - y_{0}^{2}.$ Такая система представляет собой нелинейный осциллятор, который совершает колебания между точками, где ${{R}_{2}} = 0$ с периодом $T.$ Инвариант ${{I}_{2}}$ определяет фазовые кривые на плоскости ${{R}_{2}},y.$ Система имеет две особенности. Во-первых, при $S \ne 0$ ее колебания несимметричны относительно средней точки, во-вторых, при некоторых значениях параметров она имеет в центре потенциальный барьер, разделяющий две области неустойчивости и стабилизации. Траектория на фазовой плоскости распадается на три интервала – центральную область развития, неустойчивости пограничные слои, где она стабилизируется. На плоскости параметров ${{\mu }_{0}}$ и $S,$ определяющих высоту и положение барьера множество траекторий разделяется на области ограниченные сепаратрисами.

В случае конечного значения третьего инварианта полная система уравнений описывает динамику структуры с тремя степенями свободы. Движение на фазовой плоскости ${{R}_{2}},y$ перестает быть периодическим, а переменные $S,\,\,{{\mu }_{0}}$ меняются от цикла к циклу. Это вызывает смещение траекторий относительно сепаратрис и блуждание системы по когерентным циклам. Быстрое изменение квазиинвариантов происходит вблизи границ цикла, где фазовые сдвиги меняют ход траекторий. Их смещение относительно сепаратрис приводит к хаотизации поведения системы. Фазовый портрет системы при разных значениях инварианта ${{I}_{3}}$ представлен на рис. 2.

Рис. 2.

Фазовый портрет системы на плоскости $R = {{r}_{2}},$ ${{\left( {{{y}^{2}} + y_{0}^{2}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = {{r}_{4}}$ разных значениях инварианта ${{I}_{3}} = 0,0.1,0.5$ (соответственно фигуры (а), (б), (в)). Графики взяты из [Романова Н.Н. и др., 2016].

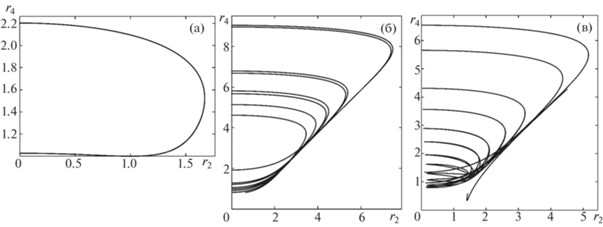
Ситуация напоминает маятник Капицы с колеблющейся точкой подвеса.

Рассмотрим движение системы между точками с одним значением ${{R}_{2}}$ как отображение Пуанкаре. Свойства отображения, показывающего смещение основных переменных за период, определяются матрицей Якоби [Лихтенберг и др., 1984; Заславский, 2004]. Отрицательные значения матрицы указывают на области, где возникает локальная неустойчивость по фазе. Эта неустойчивость зависит от величины основных инвариантов. При больших значениях первого инварианта третьего колебания системы имеют двоякопериодический характер. В противоположном случае система колеблется около сепаратрисы и поведение траекторий приобретает черты хаоса. При увеличении размаха колебаний хаос нарастает и движение системы переходит в “стохастическое море”. Наряду с этим растут амплитуды крупномасштабной и мелкомасштабной компонент движения. Вследствие этого возникают крутые фронты, сходные с фронтами ударных волн. Сценарий хаотизации в основном соответствует сценарию, описанному для простейших гамильтоновых систем в работах Г.М. Заславского и его соавторов [Заславский и др., 1991]. Вместе с тем фазовые кривые на плоскости $S,\,\,{{\mu }_{0}}$ показывают упорядоченное изменение компоненты, черпающей энергию от более быстрых колебаний.

Возмущение вида волнового пакета может быть представлено как сумма триплетов, зависящих от волнового числа. Описывая эволюцию каждого триплета, а затем, проводя суммирование триплетов, мы получаем представление меняющегося во времени полного поля. Поведение системы при этом осложняется колебаниями пространственной ширины пакета. Частота и амплитуда этих колебаний зависят от соотношения между шириной области неустойчивости и размерами области взаимодействия устойчивых волн, которое зависит от их групповых скоростей.

4.2. Вихревые структуры в идеальной жидкости (волчок Должанского)

Структуры, сходные с рассмотренными выше, возникают и при эволюции трехмерных вихревых образований. При структурном описании вихрей образующихся около некоторого центра, мы получаем систему уравнений относительно завихренности и градиента плотности

(4.8)

$\begin{gathered} \frac{{\partial {\mathbf{\Omega }}}}{{\partial t}} = \left( {{\mathbf{\Omega }}{\text{grad}}} \right)V - g \times {\text{grad}}\eta ,\, \\ \frac{{\partial \eta }}{{\partial t}} + {\text{grad}}\left( {V\eta } \right) = 0, \\ \end{gathered} $

где $\eta \left( t \right) = {\text{grad}}\rho .$ Поле скорости представляет сумму компонент, одна из которых определяет завихренность, а другая связана с условиями на границе. Граница области, представляет собой поверхность постоянной потенциальной завихренности может быть твердой или колеблющейся. Течения с твердой границей – это особый тип вихревых течений, реализуемый в лабораторных условиях.

К таким системам относится “волчок Должанского”, дающий описание колебаний жидкости в эллипсоиде, вращающемся в поле сил тяжести [Должанский и др., 2002]. В этой системе можно видеть “игрушечную” модель атмосферы [Должанский, 2011; Должанский, 2005]. Как показывают последние исследования, турбулентность также сохраняет подобные структурные особенности [Jimenez, 2018].

Система, следующая из (4.8) включает шесть уравнений и обладает тремя инвариантами: энергией, модулем градиента плотности и потенциальной завихренностью. Как и в рассмотренной выше задаче, система имеет три степени свободы [Должанский и др., 2002].

Линеаризуя систему при постоянных значениях вертикальных компонент завихренности и градиента плотности, получаем четыре уравнения для горизонтальных компонент этих векторов. Дисперсионное уравнение описывает две ветви – быстрых и медленных колебаний. Это соответствует разделению горизонтальной завихренности на две компоненты по отношению к поверхностям постоянной плотности.

Для разделения быстрых и медленных движений основное значение имеет условие квазигеострофического равновесия, которое принимает вид:

$\begin{gathered} {{\Omega }_{1}} = {{{{A}_{1}}{{\eta }_{1}}} \mathord{\left/ {\vphantom {{{{A}_{1}}{{\eta }_{1}}} {{{\Omega }_{3}}}}} \right. \kern-0em} {{{\Omega }_{3}}}},\,\,\,\,{{\Omega }_{2}} = {{{{A}_{2}}{{\eta }_{2}}} \mathord{\left/ {\vphantom {{{{A}_{2}}{{\eta }_{2}}} {{{\Omega }_{3}}}}} \right. \kern-0em} {{{\Omega }_{3}}}}, \\ {{A}_{1}} = {g \mathord{\left/ {\vphantom {g {\left( {{{I}_{3}} - {{I}_{1}}} \right)}}} \right. \kern-0em} {\left( {{{I}_{3}} - {{I}_{1}}} \right)}},\,\,\,\,{{A}_{2}} = - {g \mathord{\left/ {\vphantom {g {\left( {{{I}_{3}} - {{I}_{2}}} \right)}}} \right. \kern-0em} {\left( {{{I}_{3}} - {{I}_{2}}} \right)}}. \\ \end{gathered} $

Это условие уменьшает число переменных в системе:

(4.9)

$\begin{gathered} \frac{{d{{\eta }_{1}}}}{{dt}} = - {{\eta }_{2}}\left( { - {{\Omega }_{3}} + \frac{{{{A}_{1}}{{\eta }_{3}}}}{{{{\Omega }_{3}}}}} \right),\,\,\,\,\frac{{d{{\eta }_{2}}}}{{dt}} = {{\eta }_{1}}\left( {{{\Omega }_{3}} - \frac{{{{A}_{1}}{{\eta }_{3}}}}{{{{\Omega }_{3}}}}} \right), \\ \frac{{\partial {{\Omega }_{3}}}}{{\partial t}} = \left( {{{I}_{2}} - {{I}_{1}}} \right){{\eta }_{1}}{{\eta }_{1}}\frac{{{{A}_{1}}{{A}_{2}}}}{{\Omega _{3}^{2}}}. \\ \end{gathered} $

Коэффициенты ${{I}_{{1 - 3}}}$ обеспечивают равенство нулю нормальной компоненты скорости на границе эллипсоида. Линейная задача (4.9) указывает на область неустойчивости вблизи точки

$\left( {2{{I}_{3}} - {{I}_{2}} - {{I}_{1}}} \right)\Omega _{3}^{2} + 2g{{\eta }_{3}} = 0.$

Из уравнений (4.9) следует закон сохранения, используя который мы получаем описание стабилизирующего неустойчивость триплета: $X = \frac{{{{\eta }_{1}}}}{{{{\eta }_{{10}}}}},$ $Y = \frac{{{{\eta }_{2}}}}{{{{\eta }_{{20}}}}},$ $Z = {{Z}_{0}} + \frac{{{{\Omega }_{{33}}}}}{{{{\Omega }_{{30}}}}}$ [Должанский и др., 2002]. После соответствующей нормировки система приобретает вид

(4.10)

$\frac{{dX}}{{dt}} = - Y\left( {Z - {{Z}_{0}}} \right),\,\,\,\,\frac{{dY}}{{dt}} = XZ,\,\,\,\,\frac{{dZ}}{{dt}} = RXY.$

Нормировочные величины и параметры $R > 0,{{Z}_{0}}$ определяются коэффициентами исходной системы. Области соответствуют значения при $Z\left( {{{Z}_{0}} - Z} \right) < 0.$ Система обладает двумя инвариантами:

$R{{Y}^{2}} - {{Z}^{2}}{{C}_{1}}{{X}^{2}} + R{{\left( {Z - {{Z}_{0}}} \right)}^{2}} = {{C}_{2}}.$

И описывает нелинейный осциллятор, подобный рассмотренному в предшествующем разделе. В режиме периодических колебаний происходит вращение плоскости постоянной плотности с одновременным образованием фронтов с большими градиентами по горизонтали. Законы сохранения позволяют построить фазовый портрет системы. Фазовые траектории включают области развития и стабилизации неустойчивости. Периодичность нарушается при учете агеострофических колебаний, присутствующих в полной системе. Под их воздействием на границах основного периода возникают малые колебания инвариантов, вклады от которых приводят к смещению фазовых кривых основной системы и пересечению сепаратрисы, разделяющей разные режимы. Рост амплитуды колебаний делает поведение системы хаотическим. Степень хаотизации характеризуется значением матрицы Якоби, для отображения смещения переменных период $T.$ Результатом оказывается случайное блуждание фазовых траекторий сначала в сепаратрисном слое, а затем во всей области движения. Более сложная картина возникает при одновременных колебаниях границы.

Из разобранных примеров образования структур в идеальной жидкости следует сходство сценариев, по которым происходит эволюция поверхностей уровня лагранжевых инвариантов. В ее основе лежат колебания подобные колебаниям нелинейного осциллятора. Частота колебаний управляется дополнительными переменными, входящими в единый, синхронизированный по фазе триплет. Если эта синхронизация по фазе нарушается, то происходит частичная хаотизация движения. Общая картина возникновения крутых фронтов в несжимаемой жидкости подобна фокусировкам оптического излучения в неоднородной среде.

5. ДИССИПАТИВНЫ СТРУКТУРЫ

Диссипативные структуры, образуются в течениях жидкости с большими градиентами плотности и скорости [Рабинович и др., 1998; Рабинович и др., 2000]. Они ограничивают размеры кластеров, также как дифракция ограничивает размеры фокальных пятен. Они стабилизируют неустойчивость, выполняя ту же роль что и мелкомасштабные колебания в идеальной жидкости. Это соответствует соотношению упругих и неупругих соударений при столкновениях частиц. В сплошной среде это соотношение зависит от числа Рейнольдса. Совместное действие этих явлений ведет к возникновению турбулентности. Особенно важную роль играют структуры, образующиеся в пограничном слое около твердой стенки. Согласно современным воззрениям структуры среднего масштаба служат посредником между крупномасштабным течением и мелкомасштабной турбулентностью [Jimenez, 2018].

Простейшей моделью, учитывающей влияние диссипации на крупномасштабные течения, является модель линейного трения. Эта модель, восходящая к работе Чандрасекара, используется во многих работах посвященных интерпретации натурных и лабораторных экспериментов, включая работы Лоренца [Lorenz, 1963]. Важный вклад в апробацию этой модели внесли работы Ф.В. Должанского, непосредственно связанные с экспериментом [Должанский, 2011].

5.1. Линейное трение и система Лоренца

Рассмотрим влияние линейного трения на поведение игрушечной модели атмосферы, предложенной Ф.В. Должанским [Должанский, 2011]. Эта модель является развитием модели “волчка”, о которой говорилось выше. На основе квазигеострофического приближения с учетом сторонней температурной накачки и линейного трения уравнения имеют вид:

(5.1)

$\begin{gathered} \frac{{dX}}{{dt}} = - YZ - X + D, \\ \frac{{dY}}{{dt}} = XZ - Y,\,\,\,\,\frac{{dZ}}{{dt}} = XY - Z. \\ \end{gathered} $

Эти переменные указывают на колебания компонент вектора завихренности. В одном из горизонтальных направлений действует сторонняя сила $D.$ Как указано в [Должанский, 2011], система имеет два стационарных состояния – режимы Хедли и режим Россби

(5.2)

$X = D,\,\,\,\,Y = Z = 0\,\,\left( {{\text{Хедли}}} \right),$

(5.3)

$X = {{D}_{0}} = 1,\,\,\,\,YZ = \pm D_{0}^{{\frac{1}{2}}}{{\left[ {\left| D \right| - {{D}_{0}}} \right]}^{{\frac{1}{2}}}}\,\,\left( {{\text{Россби}}} \right).$

Система уравнений (5.1) также представляет собой триплет, который совершает периодические колебания с обменом энергией между компонентами. При этих колебаниях быстро достигается точка частичного равновесия: ${{Y}^{2}} = {{Z}^{2}}.$ Определяя $S$ как $X + 1 = {{dS} \mathord{\left/ {\vphantom {{dS} {dt}}} \right. \kern-0em} {dt}},$ имеем

(5.4)

$Y = {{Y}_{0}}\exp \left[ S \right].$

Для $S$ получаем уравнение осциллятора с трением и форсингом

(5.5)

$\frac{{{{d}^{2}}S}}{{d{{t}^{2}}}} + \frac{{dS}}{{dt}} - 1 + \left[ {Y_{0}^{2}\exp \left( {2S} \right) - D} \right] = 0.$

На фазовой плоскости $X,S$ при $D > 1$ возможны траектории различного типа. В окрестности режима Хедли в линеаризованной системе развивается неустойчивость. Это ведет к убыванию компоненты $X$ и переходу в окрестность одного из режимов Россби. Поведение траекторий в зависимости от амплитуды возмущения соответствует двум режимам. В одном случае возникает затухающее движение по отношению к точке равновесия режима Россби. В другом случае система колеблется между режимами Хедли и Россби. Такие колебания носят квазипериодический характер, включающий слабое блуждание точек поворота системы, не имеющей дополнительного интеграла. Такое блуждание в системе двух переменных является проявлением слабого хаоса.

Ситуация усложняется при учете $\beta $-эффекта, т.е. асимметрии системы относительно вертикального направления, что приводит уравнения к виду:

(5.6)

$\begin{gathered} \frac{{dX}}{{dt}} = - YZ - X - D, \\ \frac{{dY}}{{dt}} = XZ - Y,\,\,\,\,\frac{{dZ}}{{dt}} = RXY - \beta Y - Z. \\ \end{gathered} $

При $R = 0$ система эквивалентна известной системе Э. Лоренца [Lorenz, 1963].

Делая замену переменных аналогичную (5.4), получаем при отличном от нуля $\beta $ систему трех уравнений. Линеаризация уравнений для переменных $Y,Z$ при $X = {\text{Const}}$ показывает, что решение имеет растущую компоненту при $\beta X > 1.$ Уравнение для компоненты $X$ позволяет вычислить поправки к линейному решению, возникающие в пограничных слоях вблизи точек равновесия. При этом нарушается симметрия по переменной $Y.$ Эти поправки ведут к блужданиям системы по фазовым траекториям основного колебания. Блуждания усиливаются при переходе системы через сепаратрису, разделяющую разные типы ее поведения, смотри рис. 3. Система переходит в режим хаоса, как это было описано в предшествующих разделах. Однако хаотические колебания на фазовой плоскости происходят между точками равновесия Россби, так что в целом колебания амплитуды сохраняют периодический характер [Jimenez, 2018].

Рис. 3.

Фазовый портрет стохастического режима (а) и его спектральная диаграмма (б). Графики взяты из [Должанский, 2005].

5.2. Структуры в пограничных слоях

Приближение линейного трения понижает порядок системы уравнений, описывающих диссипацию. Однако, такой подход справедлив не всегда. Как уже указывалось, в нелинейной акустике вблизи фронта ударной волны образуется диссипативная структура. Дополняя уравнение (4.1) членом со второй производной, мы получаем уравнение Бюргерса, решение которого показывает структуру и масштабы ударного фронта [Гурбатов, 1983].

Особый интерес представляет формирование пограничных слоев вблизи твердого дна. При больших числах Рейнольдса условия на границе ведут к генерации вторичного течения во всей области, которое определяет влияние трения на основную компоненту скорости. Следующий отсюда коэффициент трения оказывается нелинейным [Должанский, 1999].

Другой пример дает модифицированная задача Кармана о течении вязкой жидкости над вращающимся диском под действием сторонней силы. Трехмерная задача в цилиндрических координатах без зависимости от угла и с линейной зависимостью от радиуса была рассмотрена [Кострыкин и др., 2011]. Задача формулируется для величины:

$K\left( z \right) = G + IF,$

где $G$ и $F$ вихревая и потенциальная компоненты течения в плоскости $z = {\text{Const}}{\text{.}}$ В стационарном режиме $K$ удовлетворяет уравнению:

(5.7)

$E\frac{{{{d}^{2}}K}}{{d{{z}^{2}}}} - H\frac{{dK}}{{dz}} + i\left( {{{K}^{2}} + P} \right) = - Q,$

где $E$ – коэффициент вязкости, $P$ – постоянное давление, $Q$ – сторонняя сила, $H$ – вертикальная скорость, удовлетворяющая условию ${{dH} \mathord{\left/ {\vphantom {{dH} {dz}}} \right. \kern-0em} {dz}} = - 2F.$ Граничные условия имеют вид:

(5.8)

$\begin{gathered} K = S,\,\,\,\,H = 0\left( {z = 0} \right), \\ \frac{{dK}}{{dz}} = 0,\,\,\,\,H = 0\left( {z = h} \right). \\ \end{gathered} $

Аналитическое решение задачи связано с введением линейного трения: $E{{{{d}^{2}}K} \mathord{\left/ {\vphantom {{{{d}^{2}}K} {d{{z}^{2}}}}} \right. \kern-0em} {d{{z}^{2}}}} = \gamma K.$ В простейшем случае это единое для всего слоя экмановское или стюартсоновское трение [Должанский, 1999]. Однако при больших числах Рейнольдса требуется более точное решение. Полагая $S = 1,$ $E \ll 1,$ будем искать решение в виде

(5.9)

$\begin{gathered} K = {{K}_{0}} + \left( {1 - {{K}_{0}}} \right)\exp \left( { - \gamma z} \right), \\ K_{0}^{2} = iQ - P,\,\,\,\,{{K}_{0}} = {{G}_{0}} + i{{F}_{0}}. \\ \end{gathered} $

Подставляя это выражение в уравнение, находим, что при $E \ll 1$

(5.10)

$\gamma = {{\left[ { - i\left( {1 + {{K}_{0}}} \right)} \right]}^{{\frac{1}{2}}}}.$

Вычисляя величину вертикальной скорости на верхней границе $H\left( 0 \right),$ получаем формулу для коэффициента нелинейного трения

(5.11)

${{F}_{0}} = - {{E}^{{\frac{1}{2}}}}\frac{{1 - {{G}_{0}}}}{{{{{\left( {1 + {{G}_{0}}} \right)}}^{{\frac{1}{2}}}}}}.$

Величина ${{G}_{0}}$ определяется условием ${{F}_{0}}{{G}_{0}} = Q.$ Это решение соответствует так называемому режиму Бэтчелора. Оно описывает стационарные структуры, образующиеся в пограничном слое около дна. Другой режим (Стюартсона), как показывает численное решение задачи [Якушкин, 1990] имеет место при $ - 1 < {{G}_{0}} < 0,$ когда основное течение и дно вращаются в разных направлениях. Анализ уравнения показывает существование между границами интенсивного вихря с горизонтальной осью. Основная структура течения определяется уравнением невязкой жидкости с учетом вертикальной скорости

(5.12)

$ - H\frac{{dK}}{{dz}} + i\left( {{{K}^{2}} + P} \right) = 0.$

Параметры этого спирального вихря определяются течением в пограничных слоях, где сторонняя сила уравновешивается диссипацией. Два типа стационарных структур до известной степени аналогичны структурам Хедли и Россби в системах с линейным трением. Совмещаясь в одном течении, такие структуры приводят к колебательным и хаотическим режимам. Нелинейное взаимодействие формирует трехмерные колебательные структуры [Jimenez, 2018]. В результате возникновения вторичного течения происходит деформация поля вертикальной завихренности и образование вертикальных пограничных слоев, как это было показано в линейной задаче для течения Колмогорова Ф.В. Должанским [Должанский, 1999].

6. ЗАКЛЮЧЕНИЕ

Рассматривая негауссовы случайные поля с точки зрения статистической топографии, мы видим, что их можно представить как совокупность интенсивных структур, выделяющихся на общем фоне. Таковы и волновые поля в неоднородной среде, и поля, описывающие гидродинамические течения, наблюдаемые в натурных или лабораторных условиях. Структурное описание является при этом альтернативным по отношению к описанию с помощью статистических моментов. Отдельные структуры с небольшим числом степеней свободы входят в единый ансамбль и описывают разнообразные явления. Расположение структур связано с экстремальными точками полей, фиксируемых в физическом и в фазовом пространстве. В оптических полях структуры являются результатом фокусировок излучения в неоднородной среде. В гидродинамике фокусировкам соответствуют явления кластеризации и деформации течений идеальной или вязкой жидкости. Такие явления связаны с развитием и стабилизацией неустойчивостей. И в том и в другом случае форма структур и ее эволюция содержат важную информацию о среде распространения или о свойствах течений жидкости.

Эволюция структур может быть описана в различных приближениях. При этом она определятся двумя процессами – собственной эволюцией и взаимодействием между структурами. Основные структуры среднего масштаба могут быть рассмотрены на основе квазигеострофического соотношения. Они образуются или около некоторых центров или на границах отдельных областей и представляют собой своего рода нелинейный осциллятор. Каждая структура характеризуется набором лагранжевых инвариантов, задающих ее пространственно – временные масштабы. Влияние колебаний на ограничение роста неустойчивости сходно с влиянием диссипации, что является следствием соударений между структурами, которые бывают упругими и не упругими.

Колебания такого осциллятора зависят от системы инвариантов, которые частично являются квазиинвариантами, так как подвергаются воздействию присутствующей в системе агеострофической компоненты. Другая система инвариантов испытывает внешнее воздействие со стороны соседних структур. Эти изменения приводят к тому, что колебания структуры становятся частично-когерентными и переходят в режим частичного хаоса. При взаимодействии структур разного масштаба мелкомасштабные структуры могут группироваться между собой, в результате чего возникают более сложные образования. Общее описание наблюдаемого поля должно быть основано на учете как детерминированного, так и случайного характера его эволюции на больших масштабах.

Автор выражает глубокую благодарность своим коллегам, с которыми обсуждал затронутые в статье проблемы и у которых постоянно учился. Особенную благодарность приношу А.А. Хапаеву за постоянное внимание и помощь.

Список литературы

Баскаков С.И. Радиотехнические цепи и сигналы. М.: Высшая школа, 1983. 544 с.
Гледзер Е.Б., Должанский Ф.В., Обухов А.М. Системы гидродинамического типа и их применение. М.: Наука, 1987. 366 с.
Гледзер Е.Б. Диссипация и перемежаемость турбулентности в рамках гидродинамических аппроксимаций // Изв. РАН Физика атмосферы и океана. 2005. Т. 41. № 6. С. 731–746.
Гончаров В.П., Павлов В.И. Гамильтоновая вихревая и волновая динамика. М.: ГЕОС, 2008. 432 с.
Гурбатов С.Н., Саичев А.И., Якушкин И.Г. Нелинейные волны и одномерная турбулентность в средах без дисперсии // УФН. 1983. Т. 141. № 2. С. 221–253.
Данилов С.Д., Довженко В.А., Якушкин И.Г. Перенос паcсивного скаляра и лагранжев хаос в гамильтоновой гидродинамической системе // ЖЭТФ. 2000. Т.118. Вып. 2. С. 483–494.
Должанский Ф.В., Крымов В.А., Манин Д.Ю. Устойчивость и вихревые структуры в квазидвумерных сдвиговых течениях // УФН. 1990. Т. 160. № 7. С. 1–45.
Должанский Ф.В. Поперечная структура квазидвумерных гидродинамических и магнитогидродинамических течений // Изв. РАН Физика атмосферы и океана. 1999. Т. 35. Вып. 2. С. 163–173.
Должанский Ф.В., Пономарев В.М. Простейшие медленные многообразия баротропных и бароклинных движений вращающейся жидкости // Изв. РАН. Физика атмосферы и океана. 2002. Т. 38. № 3. С. 316–330.
Должанский Ф.В. О механических прообразах фундаментальных гидродинамических инвариантов и медленных многообразий // УФН. 2005. Т.175. № 12. С. 1257–1288.
Должанский Ф.В. Основы геофизической гидродинамики. М.: Физматлит, 2011. 264 с.
Займан Д. Модели беспорядка. М.: Наука, 1982. 591 с.
Заславский Г.М., Сагдеев Р.З. Введение в нелинейную физику. М.: Наука, 1988. 368с.
Заславский Г.М., Сагдеев Р.З., Усиков Д.А., Черников А.А. Слабый хаос и квазирегулярные структуры. М.: Наука, 1991. 235 с.
Заславский Г.М. Физика хаоса в гамильтоновых системах. Москва–Ижевск: Ин-т компьютерных исследований, 2004. 288 с.
Зельдович Я.Б., Молчанов С.А., Рузмайкин А.А., Соколов Д.Д. Перемежаемость в случайной среде // УФН. 1987. Т. 152. № 1. С. 3–32.
Кляцкин В.И., Якушкин И.Г. Стохастический перенос в случайных волновых полях // ЖЭТФ. 2000. Т. 118. № 4. С. 849–862.
Кляцкин В.И. Статистический анализ когерентных явлений в стохастических динамических системах. М.: URSS, 2014. 768 с.
Кляцкин В.И. Стохастическое структурообразование в случайных средах // УФН. 2016. Т. 186. № 1. С. 76–105.
Кострыкин С.В., Хапаев А.А., Якушкин И.Г. Вихревые структуры в квазидвумерных течениях вязкой вращающейся жидкости // ЖЭТФ. 2011. Т. 139. № 2. С. 395–407.
Кравцов Ю.А., Орлов Ю.И. Геометрическая оптика неоднородных сред. М.: Наука, 1980. 306 с.
Лихтенберг А., Либерман М. Регулярная и стохастическая динамика. М.: Наука, 1984. 536 с.
Лоренц Э. Природа и теория общей циркуляции атмосферы // Л.: Гидрометеоиздат, 1970. 259 с.
Монин А.C., Яглом А.М. Статистическая гидродинамика. М.: Наука, 1965. Т. 1, 2. 639 с., 730 с.
Обухов А.М. Турбулентность и динамика атмосферы. Л.: Гидрометеоиздат, 1988. 412 с.
Пономарев В.А., Хапаев А.А., Якушкин И.Г. Влияние экмановского трения и асимметрия циклонических и антициклонических когерентных структур в гидродинамических течениях // ДАН сер Геофизика. 2009. Т. 425. № 6. С. 821–826.
Рабинович М.И., Езерский А.Б. Динамическая теория формообразования. М.: Янус-К, 1998. 191 с.
Рабинович М.И., Трубецков Д.И. Введение в теорию колебаний и волн. НИЦ: Регулярная и хаотическая динамика, 2000. 561 с.
Романова Н.Н., Якушкин И.Г. Гамильтоново описание движений в идеальной расслоенной жидкости // ДАН сер. Геофизика. 2001. Т. 380. № 5. С. 330–334.
Романова Н.Н., Чхетиани О.Г., Якушкин И.Г. Влияние нелинейных взаимодействий на развитие неустойчивости в волновых гидродинамических системах // ЖЭТФ. 2016. Т. 149. № 5. С.1043–1056.
Рытов С.М., Кравцов Ю.А, Татарский В.И. Введение в статистическую радиофизику. Часть 2. Случайные поля. М.: Наука, 1978. 464 с.
Татарский В.И. Распространение волн в турбулентной атмосфере. М.: Наука, 1967. 548 с.
Якушкин И.Г. Флуктуации интенсивности поля плоской волны за хаотическим фазовым экраном // Изв. Вузов. Радиофизика. 1974. Т. 13. № 9. С. 151–156.
Якушкин И.Г. Флуктуации интенсивности при малоугловом рассеянии волновых полей // Изв. Вузов. Радиофизика. 1985. Т.23. № 5. С. 535–566.
Якушкин И.Г. Многолучевое рассеяние волновых полей в неоднородных и нелинейных средах: Автореф. диссертации на соискание ученой степени докт. физ. мат. наук. М., 1987. 32 с.
Якушкин И.Г. О мерцаниях светового блика на морской поверхности // Изв. АН СССР Физика атмосферы и океана. 1990. Т. 26. № 10. С. 25–32.
Якушкин И.Г. Случайные внутренние гравитационные волны в атмосфере // Изв. РАН Физика атмосферы и океана. 1998. Т. 34. № 5. С. 651–657.
Якушкин И.Г. О лагранжевом и гамильтоновом описании моделей геофизических течений идеальной жидкости // Изв. РАН Физика атмосферы и океана. 2005. Т. 41. № 2. С. 156–166.
Blackwelder R.F.M. Coherent structures associated with turbulent transport // Proc. 2^nd Int. Sump. Tokyo. 1987. P. 1–20.
Groesen Van E. Deformation of coherent structures // UK Rep. Prog. Phys. 1996. V. 59. P. 511–600.
Guha A., Lawrence G.A. A wave interaction approach to studying non-modal homogeneous and stratified shear instabilities // J. Fluid Mech. 2014. V. 755. P. 336–364.
Jimenez J. Coherent structures in wall-bounded turbulence // J. Fluid Mech. 2018. V. 842. P. 1–100.
Kostrykin S.V., Khapaev A.A., Yakushkin I.G. The influence of nonlinear bottom friction on the properties of decaying cyclonic and anticyclonic vortex structures in a shallow rotated fluid // J. Fluid Mechanics. 2014. V. 753. P. 217–241.
Kravzov Y.A. Propagation of electromagnetic waves through turbulent atmosphere // Rep. Progr. Phys. 1992. P. 92–112.
Loesch A.Z. Resonant interactions between unstable and neutral baroclinic waves: Part I // J. Atmos. Sci. 1974. V. 31. P. 1177–1201.
Longuet–Higgins M.S. The statistical geometry of a random surface / In: Hydrodynamic Stability // Proc. 13-thSymp. Appl. Math. Am. Math. Soc. 1962. P. 105–142.
Lorenz E.N. Deterministic nonperiodic flow // J. Atmospheric Sciences. 1963. V. 20. № 3. P. 130–148.
Okubo A. Horizontal dispersion of floatable particles in the vicinity of velocity singularities such as convergences // Deep Sea Research. 1970. V. 17. P. 445–454.
Pelinovsky E.N., Shurgalina E.G., Sergeeva A.V., Talipova T.G., Grimshaw R.H.J. Two-Soliton Interaction as an Elementary Act of Soliton Turbulence in Integrable Systems // Physics Letters A. 2013. V. 377. P. 272–275.
Romanova N.N., Annenkov S.A. Three–wave resonant interactions in unstable media // J. Fluid Mech. 2005. V. 539. P. 57–91.
Salmon R. Hamiltonian fluid mechanics // Ann. Rev. Fluid Mech. 1988. V. 20. P. 225–256.
Vallis G.K. Atmospheric and Oceanic Fluid Dynamics: Fundamentals and Large-Scale Circulation // Cambridge University Press. 2017. 326 p.
Yakushkin I.G., Zavorotny V.U. Statistics evolution of Gaussian wave fields in random Media // Waves in Random media. 1992. V. 2 P.162–165.
Yakushkin I.G. Strong focusing of plane wave behind a power–law phase screen // Waves in Random Media. 1996. V. 6. P. 281–289.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Физика атмосферы и океана

Архивы выпусков Информация о журнале Отправить рукопись в журнал