Известия РАН. Физика атмосферы и океана, 2023, T. 59, № 3, стр. 352-372

ВВЕДЕНИЕ

Как показано в [Григорьев А.И. и др., 2003], капля, осциллирующая в материальной среде, будет излучать акустические волны, а если на капле имеется электрический заряд, то она одновременно будет излучать и электромагнитные волны [Калечиц В.И. и др., 1982], поскольку электрические заряды на ее поверхности при осцилляциях будут двигаться ускоренно. Акустическое и электромагнитное излучения неоднократно обсуждались в научной печати [Богатов Н.А., 2013; Григорьев А.И. и др., 2021; Григорьев А.И. и др., 2022], но, как правило, врозь, а не одновременно в одной публикации, в одной задаче математической физики, со сравнением интенсивностей и частот соответствующих излучений. Следует обратить внимание на то, что обсуждаемые волны различны по своей физической природе: акустические волны продольны, а электромагнитные поперечны. В данной статье мы попробуем исправить это упущение.

Прежде, чем исследовать и сравнивать по порядку величины интенсивности акустического и электромагнитного излучений, необходимо для начала обратиться к физическим понятиям электрического и акустического мультиполей. Общие положения и правила введения понятия акустических мультиполей подробно изложены в [Кошляков Н.С. и др., 1970], (глава 24). Кратко мультиполь (электрический, магнитный, акустический, гравитационный) можно определить как: физический объект, обладающий свойством создавать поля, подобные на бесконечной системе концентрических шаровых поверхностей произвольного радиуса. Под акустическим мультиполем следует понимать точечный источник, создающий в однородной среде акустическое поле со свойствами: а) удовлетворяет уравнению Гельмгольца, б) фаза колебаний поля зависит только от расстояния до источника (так что, в частности, в любой точке произвольной шаровой поверхности с центром в точке расположения источника фаза колебаний одинакова), в) акустические поля на всех шаровых поверхностях с центром в точке расположения источника поля подобны, г) удовлетворяется условие излучения Зоммерфельда [https:// www.ngpedia.ru/id166364p3.html].

Принято считать, что акустический мультиполь является точечным источником, создающим в материальной среде звуковое поле, обладающее в волновой зоне определенной направленностью излучения (см. [Кошляков Н.С. и др., 1970], стр. 430). При этом порядок акустических мультиполей связан с характеристикой направленности излучателя, которая описывается осесимметричным полиномом Лежандра соответствующего порядка (см. [Лепендин Л.Ф., 1978], стр. 216).

Как отмечается в [Лепендин Л.Ф., 1978], стр. 206, 209, монополь (излучатель нулевого порядка) создает во внешней среде сферические волны сжатия и разряжения и характеризуется ненаправленным излучением. Диполь (излучатель первого порядка) представляет собой совокупность двух противофазно пульсирующих близко расположенных монополей одинаковой производительности, вызывающих возмущения давлений внешней среды (разных по знаку). При этом диполь характеризуется направленным излучением и описывается поступательным движением точечного источника. Квадруполь (излучатель второго порядка) состоит из двух диполей, осциллирующих в противоположных фазах, и определяется направленным излучением.

Кроме того, в работах [Григорьев А.И. и др., 2003; Григорьев А.И. и др., 2022] было показано, что в асимптотических расчетах второго порядка малости по безразмерной амплитуде осцилляций $\varepsilon $ возбуждение центрально-симметричной (нулевой) моды капли, осциллирующей в материальной среде, приводит к появлению акустического излучения монопольного типа, а возбуждение трансляционной (первой) моды – к звуковому излучению дипольного типа.

В тоже время хорошо известно, что согласно существующим представлениям (см. [Ландау Л.Д. и др., 1973]) электрический мультиполь представляет собой систему зарядов, создающую на больших расстояниях $r$ в окружающем пространстве электрическое поле так, что потенциалы мультиполей различных порядков пропорциональны ${1 \mathord{\left/ {\vphantom {1 {{{r}^{{n + 1}}}}}} \right. \kern-0em} {{{r}^{{n + 1}}}}},$ где $n$ – целое число, равное порядку мультиполя.

В соответствии с общей теорией излучения электромагнитное излучение, создаваемое системой ускоренно движущихся зарядов, имеет мультипольное представление, основанное на изменении во времени мультипольных моментов излучателей. Разделение полного электромагнитного излучения на мультипольные компоненты (дипольную, квадрупольную и т.д.) проводится по малому параметру $\delta $ – квадрату отношения линейных размеров системы-излучателей к длине излучаемой электромагнитной волны [Савельев И.В., 1975]. Так, в задачах, приложенных к осциллирующей капле воды [Григорьев А.И. и др., 2021], дипольная составляющая излучения на 15 порядков величины интенсивнее квадрупольной.

Очевидный интерес представляет задача об одновременном исследовании акустического и электромагнитного излучений, генерируемых линейными осцилляциями заряженной капли, находящейся в материальной среде.

1. Физическая постановка задачи. Рассмотрим уединенную сферическую (для простоты) каплю радиуса $R$ идеальной несжимаемой идеально проводящей жидкости, имеющую массовую плотность ${{\rho }_{1}}$ и коэффициент поверхностного натяжения на границе со средой $\sigma .$ Пусть капля обладает зарядом $Q,$ находится в идеальной сжимаемой диэлектрической среде, характеризующейся массовой плотностью ${{\rho }_{2}},$ диэлектрической проницаемостью ${{\varepsilon }_{{{\text{ex}}}}}$ и скоростью распространения звука $\upsilon .$

Из-за теплового движения молекул жидкости в капле и в среде в обеих средах создается капиллярное волновое движение, приводящее к искажению границы раздела сред имеющего весьма малую амплитуду порядка $\left| \xi \right|\sim \sqrt {{{\kappa T} \mathord{\left/ {\vphantom {{\kappa T} \sigma }} \right. \kern-0em} \sigma }} ,$ где $\kappa $ – постоянная Больцмана, $T$ – абсолютная температура [Френкель Я.И., 1936]. Для большинства жидкостей амплитуда тепловых осцилляций $\left| \xi \right|$ не превосходит 1 × 10^–8 см.

Рассмотрение задачи естественно провести в сферической системе координат $\left( {r,\theta ,\varphi } \right),$ связанной с центром масс капли. Для упрощения дальнейших выкладок постановку задачи сведем к осесимметричному случаю, пренебрегая в функциях зависимостью от азимутальной координаты $\varphi .$

В случае идеально проводящей жидкости полный заряд $Q$ капли в любой момент времени равномерно распределен по ее возмущенной поверхности. При этом ускоренное движение собственного заряда $Q$ при осцилляциях капли приводит к генерации электромагнитных волн. Кроме того, волновое движение поверхности капли вызывает возмущение давления внешней среды, создающее продольную акустическую волну.

2. Математическая формулировка задачи. Уравнение возмущенной поверхности капли в произвольный момент времени $t$ зададим в виде:

где $\xi (\theta ,t)$ – деформация равновесной сферической формы, обусловленная капиллярным волновым движением: $\max \left| \xi \right| \ll R.$

Волновые движения внутренней и внешней сред капли будем полагать потенциальными, т.е. поле скоростей движения жидкостей внутри и вне капли выражаются через потенциалы скоростей [Ландау Л.Д. и др., 1986]:

Здесь величины, относящиеся к капле, отмечены нижним индексом 1, а к среде – нижним индексом 2. Заметим, что функции ${{\vec {V}}_{j}}(r,\theta ,t),$ ${{\psi }_{j}}(r,\theta ,t)$ имеют тот же порядок малости, что и возмущение $\xi (\theta ,t).$

В приближении идеально проводящей жидкости скорость перераспределения заряда по поверхности капли на много порядков больше гидродинамических скоростей. В виду этого электрическое поле, создаваемое зарядом $Q,$ будем принимать квазистационарным и характеризовать напряженностью поля $\vec {E}.$

Система уравнений электрогидродинамики, описывающая капиллярные осцилляции заряженной электропроводной капли и возникающих при этом акустическом и электромагнитном излучений, содержит уравнения Эйлера (уравнение движения внутренней и внешней сред капли):

уравнения непрерывности: волновое уравнение и уравнение непрерывности электрического поля: Равенство (4) после подстановки в него (2) при $j = 1$ сводится к уравнению Лапласа для потенциала поля скоростей течения жидкости в капле ${{\psi }_{1}}(r,\theta ,t){\text{:}}$

Используя (6), из уравнения (3) выпишем выражения для давлений внутри ${{P}_{1}}\left( {r,\theta ,t} \right)$ и вне капли ${{P}_{2}}\left( {r,\theta ,t} \right){\text{:}}$

В случае сжимаемой внешней среды из условий (4), (7) при $j = 2$ можно получить волновое уравнение для потенциала поля скоростей ${{\psi }_{2}}(r,\theta ,t){\text{:}}$

Потребуем, чтобы искомые величины удовлетворяли условиям ограниченности в центре масс капли и на бесконечности:

Потребуем, чтобы потенциал движения частиц внешней среды ${{\psi }_{2}}(r,\theta ,t)$ удовлетворял условию излучения Зоммерфельда [Лепендин Л.Ф., 1978] на бесконечном удалении от поверхности капли (расходящейся сферической волне, убывающей при $r \to \infty $):

Кроме того, на границе раздела сред r = R + $ + \,\,\xi \left( {\theta ,t} \right)$ потребуем выполнение граничных условий:кинематического:

динамического: а также условия эквипотенциальности:

Единичный вектор нормали $\vec {n}(r,\theta ,t)$ к свободной поверхности капли $F\left( {r,\theta ,t} \right) = r - R - \xi \left( {\theta ,t} \right) = 0$ вычисляется по общей формуле $\vec {n}\left( {r,\theta ,t} \right) = {{\nabla F} \mathord{\left/ {\vphantom {{\nabla F} {\left| {\nabla F} \right|}}} \right. \kern-0em} {\left| {\nabla F} \right|}},$ из которой несложно получить:

где ${{\vec {e}}_{r}},$ ${{\vec {e}}_{\theta }},$ ${{\vec {e}}_{\varphi }}$ – орты сферической системы координат.

Пользуясь (12), (15), приведем кинематическое граничное условие к виду:

В качестве дополнительных соотношений примем условия неизменности объема капли, неподвижности ее центра масс:

и постоянства полного заряда капли:

В (17) интегрирование производится по объему возмущенной капли $V = [0 \leqslant r \leqslant R + \xi (\theta ,t),$ $0 \leqslant \theta \leqslant \pi ,\,\,0 \leqslant \varphi \leqslant 2\pi ],$ а в (18) – по площади возмущенной поверхности $S = [r = R + \xi (\theta ,t),0 \leqslant $ $ \leqslant \theta \leqslant \pi ,\,\,0 \leqslant \varphi \leqslant 2\pi ].$ Заметим, что условия (17) позволяют определить ограничения снизу на спектр колебательных мод осциллирующей капли, участвующих в формировании искажения равновесной сферической формы.

В выписанных выражениях $\vec {\tau }$ – единичный вектор касательной к свободной поверхности, ${\text{O,}}$ $о$ – символы порядка малости [Найфе А.Х., 1976], $i$ – мнимая единица, ${{k}_{1}} = \frac{{\operatorname{Re} {{\omega }_{n}}}}{\upsilon }$ – волновое число, ${{\omega }_{n}}$ – комплексная частота, $n$ – номер моды, ${{P}_{{0j}}}$ – постоянные давления в капле ($j = 1$) и в среде ($j = 2$) в равновесном состоянии, ${{P}_{q}}\left( {r,\theta ,t} \right)$ – давление электрического поля собственного заряда на поверхность капли, ${{P}_{\sigma }}\left( {r,\theta ,t} \right)$ – давление сил поверхностного натяжения (лапласовское давление) под искаженной капиллярным волновым движением сферической поверхностью капли.

В итоге, система скалярных гидродинамических уравнений (6), (8) с граничными (9), (11) и дополнительными условиями (17), а также система векторных уравнений для электрического поля (5) с граничными (10), (14) и дополнительным (18) условиями описывает математическую модель решаемой задачи.

Дальнейшее решение задачи проведем в рамках теории возмущений [Найфе А.Х., 1976] в линейном приближении по малому параметру $\varepsilon ,$ равному отношению амплитуды капиллярных осцилляций капли к ее радиусу: $\varepsilon \equiv {{\left| \xi \right|} \mathord{\left/ {\vphantom {{\left| \xi \right|} R}} \right. \kern-0em} R} \ll 1.$ Искомые неизвестные функции $\xi (\theta ,t),$ ${{\psi }_{j}}(r,\theta ,t),$ $\vec {E}(r,\theta ,t)$ и давления ${{P}_{j}}\left( {r,\theta ,t} \right),$ ${{P}_{q}}\left( {r,\theta ,t} \right),$ ${{P}_{\sigma }}\left( {r,\theta ,t} \right),$ входящие в динамическое граничное условие (13), запишем в виде асимптотических разложений с точностью до членов первого порядка малости по $\varepsilon {\text{:}}$

В (19) верхним индексом “0” обозначены величины, относящиеся к равновесному состоянию системы (нулевого порядка по $\varepsilon $), а верхним индексом “1” отмечены величины, вызванные возмущением поверхности капли и имеющие первый порядок малости по $\varepsilon .$

Отметим, что в виду линейности векторных уравнений (5) им будет удовлетворять каждая из компонент напряженности электрического поля ${{\vec {E}}^{{\left( 0 \right)}}},$ ${{\vec {E}}^{{\left( 1 \right)}}}$ в разложении (19).

3. Решение задачи нулевого порядка малости по $\varepsilon .$ Подстановка разложений (19) в полную математическую формулировку задачи (5), (6), (8)–(11), (14), (17), (18) и выделение слагаемых $\sim {\kern 1pt} {{\varepsilon }^{0}}$ позволяет проанализировать равновесное состояние системы.

Выпишем краевую задачу для отыскания напряженности электростатического поля ${{\vec {E}}^{{\left( 0 \right)}}}$ в окрестности невозмущенной сферы:

где ${{\vec {n}}_{0}}$ – орт нормали к свободной поверхности сферы $F\left( r \right) = r - R = 0,$ определяемый в виде $\vec {n} = {{\vec {e}}_{r}}.$

Напряженность поля ${{\vec {E}}^{{\left( 0 \right)}}}$ будем искать через градиент электрического потенциала ${{\Phi }^{{\left( 0 \right)}}}$ в виде: ${{\vec {E}}^{{\left( 0 \right)}}} = - \nabla {{\Phi }^{{\left( 0 \right)}}}.$ Тогда выражение (20) обращается в тождество, а условие (21) преобразуется в уравнение Лапласа $\Delta {{\Phi }^{{\left( 0 \right)}}} = 0,$ решение которого в сферических координатах в случае осевой симметрии при удовлетворении условию ограниченности (22) имеет вид:

где ${{P}_{n}}\left( \mu \right)$ – нормированные полиномы Лежандра $n$ порядка [Абрамовиц М. и др., 1979], $n$ – целое неотрицательное число.

Неизвестную константу $С_{n}^{{\left( 0 \right)}}$ в (25) несложно определить из условия сохранения полного заряда капли (24):

В результате, подставляя (26) в (25), найдем напряженность электрического поля в отсутствие возмущения поверхности сферической капли:

Для невозмущенной сферы в силу ортогональности векторов $\vec {\tau },$ ${{\vec {e}}_{r}}$ условие эквипотенциальности (23) выполняется тождественно.

В нулевом приближении по $\varepsilon $ интегральные условия (17) удовлетворяются тождественно, а из баланса давлений

находится перепад постоянных давлений $\Delta P$ на границе раздела сред:

При этом равновесная форма капли совпадает с исходной сферической.

4. Решение задачи первого порядка малости по $\varepsilon .$ Подставляя асимптотические разложения (11) в систему (2)–(10) и группируя слагаемые $\sim {\kern 1pt} \varepsilon ,$ получим гидродинамическую задачу первого порядка по малому параметру $\varepsilon {\text{:}}$

где выражения для добавок к давлениям $P_{j}^{{\left( 1 \right)}},$ $P_{q}^{{\left( 1 \right)}},$ $P_{\sigma }^{{\left( 1 \right)}},$ вызванных волновым движением поверхности $\xi (\theta ,t),$ определятся соотношениями: $\hat {L}$ – угловая часть оператора Лапласа в сферических координатах.

В решаемой задаче об излучении электромагнитных и акустических волн зависимость от времени искомых величин положим экспоненциальной: $\xi (\theta ,t),$ ${{\psi }_{1}}(r,\theta ,t),$ ${{\psi }_{2}}(r,\theta ,t)$ $\sim \exp \left( {i{{\omega }_{n}}t} \right).$

Для функции $\xi (\theta ,t),$ описывающей искажение равновесной сферической поверхности, имеем:

где амплитуды ${{M}_{n}}$ записаны в первом порядке малости по $\varepsilon .$

В разложении (38) суммирование начинается с $n = 2,$ так как дополнительные интегральные условия (34) в первом порядке малости по $\varepsilon $ исключают радиальные пульсации капли, соответствующие нулевой моде ($n = 0$), и поступательное движение капли, связанное с возбуждением первой (трансляционной) моды ($n = 1$).

В силу граничного условия (30) решение уравнения Лапласа (28) будем искать в виде ряда по осесимметричным полиномам Лежандра:

где постоянные коэффициенты ${{A}_{n}}$ (имеющие первый порядок малости по $\varepsilon $) несложно определить, подставляя (38), (39) в кинематическое граничное условие (32) при $j = 1.$ В итоге, с учетом найденных коэффициентов ${{A}_{n}}$ выражение для гидродинамического потенциала ${{\psi }_{1}}(r,\theta ,t)$ примет вид:

Подставляя в (35) решение (40), получим окончательное выражение для линейной по $\varepsilon $ компоненты давления внутри капли:

Принимая во внимание периодическую зависимость от времени потенциала поля скоростей внешней среды ${{\psi }_{2}}(r,\theta ,t)\sim \exp \left( {i{{\omega }_{n}}t} \right),$ волновое уравнение (29) преобразуется в уравнение Гельмгольца:

решение которого при использовании условия излучения Зоммерфельда (31) выписывается в общем виде: где $h_{n}^{{\left( 2 \right)}}\left( {{{z}_{1}}} \right)$ – сферическая функция Бесселя третьего рода [Абрамовиц М. и др., 1979], константы ${{B}_{n}}$ являются малыми величинами первого порядка по $\varepsilon .$

Используя разложения (38), (42), легко найти связь неизвестных коэффициентов ${{B}_{n}}$ с амплитудами капиллярных осцилляций капли ${{M}_{n}}$ через кинематическое граничное условие (32) при $j = 2.$ Тогда для потенциала поля скоростей акустических волн ${{\psi }_{2}}(r,\theta ,t)$ сможем записать:

Применяя формулу (35), для поправки первого порядка малости к давлению внешней среды найдем:

Учитывая возмущение поверхности капли (38), линейную по $\varepsilon $ составляющую давления капиллярных сил (37) перепишем в виде:

Перейдем к вычислению входящего в граничное условие (14) орта касательной $\vec {\tau }$ к свободной поверхности капли. Отметим, что вектор $\vec {\tau }$ в плоскости, касательной к поверхности капли в данной точке, раскладывается на две составляющие: ${{\vec {\tau }}_{\varphi }}$ – орт касательной к параллелям и ${{\vec {\tau }}_{\theta }}$ – орт касательной к меридианам.

Для ортов ${{\vec {\tau }}_{\varphi }},$ ${{\vec {\tau }}_{\theta }}$ единичной длины запишем: ${{\vec {\tau }}_{\varphi }} = {{\vec {\tau }_{\varphi }^{*}} \mathord{\left/ {\vphantom {{\vec {\tau }_{\varphi }^{*}} {\left| {\vec {\tau }_{\varphi }^{*}} \right|}}} \right. \kern-0em} {\left| {\vec {\tau }_{\varphi }^{*}} \right|}},$ ${{\vec {\tau }}_{\theta }} = {{\vec {\tau }_{\theta }^{*}} \mathord{\left/ {\vphantom {{\vec {\tau }_{\theta }^{*}} {\left| {\vec {\tau }_{\theta }^{*}} \right|}}} \right. \kern-0em} {\left| {\vec {\tau }_{\theta }^{*}} \right|}}.$

Используя вектор касательной к параллелям $\vec {\tau }_{\varphi }^{*} = {{\vec {e}}_{z}} \times \vec {n}$ (в качестве произвольного постоянного вектора выбран орт оси симметрии ${{\vec {e}}_{z}}$), получим, что единичный вектор ${{\vec {\tau }}_{\varphi }}$ совпадает с азимутальным ортом ${{\vec {e}}_{\varphi }}$ сферической системы координат:

Учитывая, что касательная в меридиальном направлении $\vec {\tau }_{\theta }^{*}$ находится в соответствие с выражением $\vec {\tau }_{\theta }^{*} = \vec {\tau }_{\varphi }^{*} \times \vec {n},$ для орта ${{\vec {\tau }}_{\theta }}$ будет справедливо соотношение:

Чтобы рассчитать поправку к давлению электрического поля (28), необходимо определить в явном виде малую поправку к напряженности поля ${{\vec {E}}^{{\left( 1 \right)}}},$ возникающую из-за возмущения поверхности капли $\xi (\theta ,t).$ Для этого, подставляя орт нормали (15) в дополнительное условие (18), и орты касательных (46), (47) в граничное условие (14) и собирая слагаемые порядка $\varepsilon $ в первой степени в системе уравнений (5), (10), (14), (18), сформулируем краевую электрическую задачу:

где $E_{r}^{{\left( 1 \right)}},$ $E_{\theta }^{{\left( 1 \right)}},$ $E_{\varphi }^{{\left( 1 \right)}}$ – проекции вектора ${{\vec {E}}^{{\left( 1 \right)}}}$ на орты сферической системы координат.

Отыскивая решение вышеприведенной задачи (см. Приложение), найдем:

где ${{k}_{2}} = \frac{{\operatorname{Re} {{\omega }_{n}}}}{c}$ – волновое число, $c$ ‑ скорость света.

Вычислим добавку к давлению электрического поля на искаженную тепловым капиллярным движением сферическую поверхность, подставляя в (36) возмущение капли (38) и составляющие напряженности поля (27), (51):

Наконец, используя решения (41), (44), (45), (52), из баланса давлений (33) первого порядка малости по $\varepsilon $ с учетом ортогональности полиномов Лежандра [Абрамовиц М. и др., 1979], нетрудно выписать дисперсионное уравнение, связывающее комплексную частоту осцилляций ${{\omega }_{n}}$ с номером колебательной моды $n{\text{:}}$

Пользуясь соотношением для сферической функции Бесселя $h_{n}^{{\left( 2 \right)}}\left( z \right)$ [Абрамовиц М. и др., 1979; Градштейн И.С. и др., 1963]:

представим ${{H}_{0}}\left( {{{z}_{1}}} \right),$ ${{G}_{0}}\left( {{{z}_{2}}} \right),$ входящие в (53), в виде степенных рядов: При условии ${{z}_{1}} = {{z}_{{01}}} = {{k}_{1}}R \ll 1,$ ${{z}_{2}} = {{z}_{{02}}} = {{k}_{2}}R \ll 1$ функции (53), (54) примут асимптотический вид:

При записи уравнения (53) предполагается, что комплексная частота ${{\omega }_{n}}$ выражается соотношением: ${{\omega }_{n}} = \operatorname{Re} {{\omega }_{n}} + i\operatorname{Im} {{\omega }_{n}},$ в котором вещественная часть $\operatorname{Re} {{\omega }_{n}}$ дает собственную частоту осцилляций капли, а мнимая часть $\operatorname{Im} {{\omega }_{n}}$ в рамках модели идеальной жидкости характеризует декремент затухания, обусловленный потерей энергии капиллярных осцилляций капли на излучение звуковых и электромагнитных волн.

В случае $\operatorname{Im} {{\omega }_{n}} \ll \operatorname{Re} {{\omega }_{n}}$ правая часть дисперсионного уравнения (53) принимает вид: $\omega _{n}^{2} \approx {{\left( {\operatorname{Re} {{\omega }_{n}}} \right)}^{2}} + 2i\operatorname{Re} {{\omega }_{n}}\operatorname{Im} {{\omega }_{n}}.$ После подстановки в него асимптотических выражений (56) легко выпишем решение:

Здесь величина параметра Релея $W = \frac{{{{Q}^{2}}}}{{4\pi {{\varepsilon }_{{{\text{ex}}}}}\sigma {{R}^{3}}}}$ характеризует электрогидродинамическую устойчивость проводящей капли по отношению к собственному заряду. Критерий электростатической устойчивости n-ой моды осциллирующей капли выглядит как $W < \left( {n + 2} \right).$

Подставим (57) в (58) и с использованием ${{z}_{{01}}} = {{k}_{1}}R,$ ${{z}_{{02}}} = {{k}_{2}}R$ получим декремент затухания ${{\eta }_{1}},$ появляющийся вследствие излучения акустических волн:

и декремент затухания ${{\eta }_{2}},$ связанный с убыванием энергии капли за счет излучения электромагнитных волн:

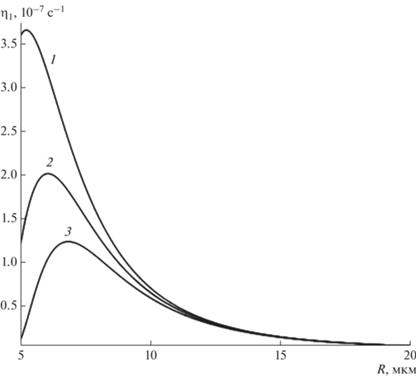
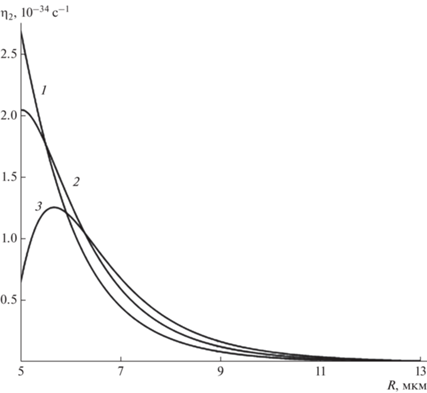
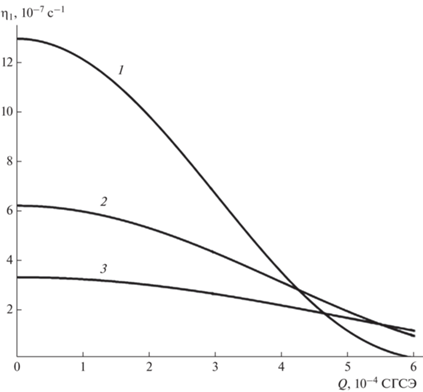
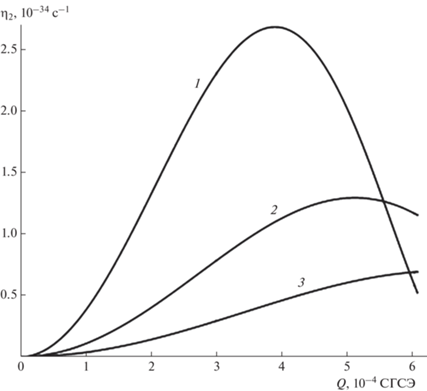
Для того, чтобы иметь возможность сравнить по порядку величины ${{\eta }_{1}},$ ${{\eta }_{2}},$ на рис. 1–4 для представлены рассчитанные по (59), (60) зависимости характеристик исследуемых излучений от размеров $R$ и зарядов $Q$ осциллирующих облачных капель при возбуждении второй (основной) колебательной моды $n = 2.$ Исходя из приведенных фигур, можно сделать вывод, что при прочих равных условиях, в частности, для одного значения частоты собственных осцилляций капли $\omega _{2}^{'},$ декремент затухания ${{\eta }_{1}}$ на 27–32 порядков величины (в зависимости от радиуса $R$) превышает ${{\eta }_{2}}$ в виду различий в физических механизмах генерации продольных звуковых и поперечных электромагнитных волн (их подробное толкование будет дано ниже).

Как видно графиков, изображенных на рис. 1, 2, при возрастании радиуса $R$ капли и величины ее собственного заряда $Q$ (не превышающего критического значения ${{Q}_{{{\text{кр}}}}}$) декременты затухания ${{\eta }_{1}},$ ${{\eta }_{2}},$ увеличиваясь до максимальных значений, начинают весьма быстро снижаться. Кроме того, на рис. 3, 4 видно различное поведение декрементов затухания ${{\eta }_{1}},$ ${{\eta }_{2}}$ при изменении величины собственного заряда $Q$ капли: ростом величины заряда $Q$ в случае убывания механической энергии капли на излучение акустических волн величина монотонно ${{\eta }_{1}}$ снижается, а в случае потерь на излучение электромагнитных волн ${{\eta }_{2}}$ возрастает и при достижении наибольшего значения быстро уменьшается.

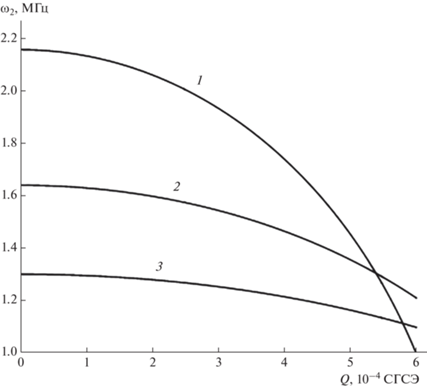
Из вида выражения (57) следует, что приближение заряда $Q$ к критическому значению ${{Q}_{{{\text{кр}}}}}$ для принятых размеров капли может приводить с снижению частоты излучения (осцилляций) в область звуковых длин волн, воспринимаемых человеческими органами слуха.

5. Акустическое излучение. Что касается мощности звукового излучения осциллирующей капли, удовлетворяющего условию ${{\lambda }_{1}} \gg R$ (${{\lambda }_{1}}$ – длина акустической волны), то ее можно рассчитать в соответствие с общей формулой [8, 10 ]:

В (61) интегрирование ведется по возмущенной поверхности капли S = [r = r(θ) + ξ(θ, t), $0 \leqslant \theta \leqslant \pi ,\,\,0 \leqslant \varphi \leqslant 2\pi ],$ а нормальная составляющая скорости движения частиц внешней среды в звуковой волне ${{\vec {V}}_{2}}(r,\theta ,t)$ имеет вид:

получающаяся отбрасыванием членов более высокого порядка, чем $1{\text{/}}r.$

Для нахождения потенциала скоростей ${{\psi }_{2}}(r,\theta ,t)$ вне капли в волновой зоне акустического поля на расстояниях $r \gg {{\lambda }_{1}},$ $R \ll r$ в исходном выражении (43) воспользуемся асимптотическим представлением сферической функции Бесселя $h_{n}^{{\left( 2 \right)}}\left( {{{z}_{1}}} \right)$ при больших значениях аргумента ${{z}_{1}} = {{k}_{1}}r \gg 1{\text{:}}$

и ее производной ${{\partial }_{{{{z}_{1}}}}}\left( {h_{n}^{{\left( 2 \right)}}\left( {{{z}_{1}}} \right)} \right)$ при малых z₁ = z₀₁ = $ = {{k}_{1}}R \ll 1{\text{:}}$

В итоге, потенциал ${{\psi }_{2}}(r,\theta ,t)$ преобразуется к виду:

а из (62) следует уравнение для скорости движения внешней среды ${{\vec {V}}_{2}}(r,\theta ,t){\text{:}}$

Заметим, что (63) описывает суперпозицию расходящихся сферических волн.

Входящее в (61) среднее значение квадрата поля скоростей $\overline {V_{2}^{2}} $ нетрудно найти по формуле $\overline {{{{\left| {{{V}_{2}}} \right|}}^{2}}} = {{{{{\left| {{{V}_{2}}} \right|}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left| {{{V}_{2}}} \right|}}^{2}}} 2}} \right. \kern-0em} 2},$ скалярно умножая соотношение (64) на комплексно ему сопряженное. В результате имеем:

Производя интегрирование (61) при использовании ортогональности полиномов Лежандра [Абрамовиц М. и др., 1979] и выражая волновое число ${{k}_{1}} = \frac{{\omega _{n}^{'}}}{\upsilon },$ определим интенсивность звукового излучения единичной заряженной капли, осциллирующей во внешней сжимаемой среде:

Учитывая явный вид частоты $\omega _{n}^{'},$ (65) перепишем в виде:

Представляет интерес провести численные оценки интенсивности (66) генерируемого на частотах (57) акустического излучения от различных жидкокапельных объектов искусственного и естественного происхождения.

Возможным источником акустического излучения являются мелкие осциллирующие капли, составляющие конвективные облака в период их образования. Согласно справочным данным [Мазин И.П. и др., 1989] характерные размеры таких капель колеблются от 3 до 30 мкм со средней концентрацией в облаке, равной 10³ см^–3. При этом наибольшая концентрация приходится на капли радиусом 3–7 мкм. На стадии развития кучево-дождевых облаков внутриоблачные водяные капли в результате их коагуляции укрупняются в дождевые капли, радиус которых колеблется в диапазоне от 0.025 до 0.35 см. Однако более мелкие дождевые капли при $R$ от 0.01 до 0.025 см относятся к мороси, а наиболее крупные падающие капли осадков радиусом более 0.35 см разрушаются из-за сопротивления воздушных потоков [Тверской П.Н., 1962].

Как показывают данные натурных исследований [Стерлядкин В.В., 1988], наличие внешних силовых воздействий (аэродинамическое сопротивление, коагуляция и столкновение капель разных размеров, гидродинамическое и электрическое взаимодействие с соседними частицами) вызывают осцилляции капель достаточно большой амплитуды (могут достигать порядка радиусов $\sim {\kern 1pt} R$).

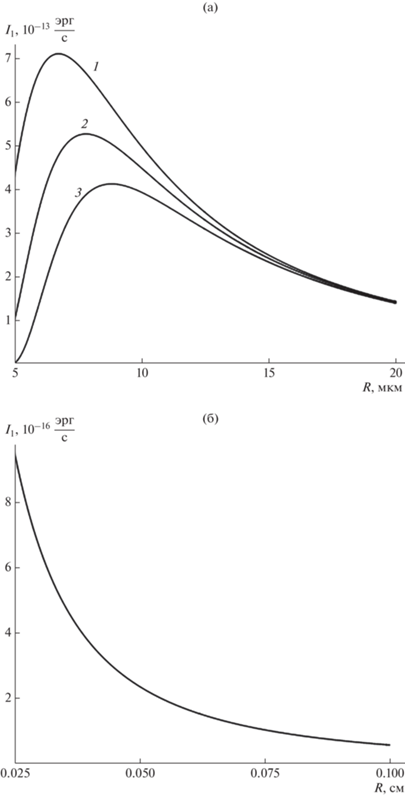
Для нижеследующих оценок положим величину безразмерной амплитуды осцилляций $\varepsilon = 0.1.$ Примем, что рассматриваемые капли совершают осцилляции с амплитудами ${{M}_{n}} = 0.1R$ за счет возбуждения основной (второй) колебательной моды $n = 2.$ Воспользуемся средними характеристиками внутриоблачных капель: $\sigma = 73$ дин/см, ${{\rho }_{1}} = 1$ г/м³, $Q = 2 \times {{10}^{{ - 5}}}$ СГСЭ ($\sim {\kern 1pt} 0.06{{Q}_{{{\text{кр}}}}}$ при R = = 3 мкм и $\sim {\kern 1pt} 0.002{{Q}_{{{\text{кр}}}}}$ при $R = 30$ мкм), где ${{Q}_{{{\text{кр}}}}}$ – критическое значение заряда. Кроме того, примем: ${{\varepsilon }_{{{\text{ex}}}}} = 1,$ ${{\rho }_{2}} = 1.3 \times {{10}^{{ - 3}}}$ г/м³, $\upsilon = 3.3 \times {{10}^{4}}$ см/с. В итоге, при $R = 3$ мкм получена оценка интенсивности акустического излучения ${{I}_{1}}\sim 7 \times {{10}^{{ - 12}}}$ эрг/с на частоте ${{\omega }_{2}} \approx 4.6$ МГц. Для радиуса $R = 8$ мкм оценка излучения составила ${{I}_{1}}\sim 9 \times {{10}^{{ - 13}}}$ эрг/с на частоте ${{\omega }_{2}} \approx 1$ МГц. При $R = 30$ мкм найдена мощность излучения ${{I}_{1}}\sim 7 \times {{10}^{{ - 14}}}$ эрг/с с частотой ${{\omega }_{2}} \approx 147$ кГц.

Моделируя грозовое облако диаметром 10 км ансамблем мелких водяных капель одинакового размера $R = 30$ мкм и учитывая, что на 1 см³ внутриоблачного пространства приходится ~10³ капель [Мазин И.П. и др., 1983], из (66) несложно найти: ${{I}_{{1{\text{in}}}}}\sim 3 \times {{10}^{7}}$ эрг/с на ультразвуковой частоте $147$ кГц.

Принимая средний заряд дождевой капли $Q = 7 \times {{10}^{{ - 4}}}$ СГСЭ ($\sim {\kern 1pt} 3 \times {{10}^{{ - 3}}}{{Q}_{{{\text{кр}}}}}$ при $R = 0.025$ см и $\sim {\kern 1pt} 6 \times {{10}^{{ - 5}}}{{Q}_{{{\text{кр}}}}}$ при $R = 0.35$ см), оценка звукового излучения наименьшей дождевой капли $R = 0.025$ см дает ${{I}_{1}}\sim 1 \times {{10}^{{ - 15}}}$ эрг/с на частоте ${{\omega }_{2}} \approx 6$ кГц. Для $R = 0.25$ см мощность излучения равна I₁ ~ 1 × $ \times \,{{10}^{{ - 17}}}$ эрг/с при частоте ${{\omega }_{2}} \approx 0.2\,\,{\text{кГц}}{\text{.}}$ Для наиболее крупной капли $R = 0.35$ см получим I₁ ~ $\sim 5 \times {{10}^{{ - 18}}}$ эрг/с при частоте ${{\omega }_{2}} \approx 0.1\,\,{\text{кГц}}{\text{.}}$

Для оценки интегрального акустического излучения ливневого дождя из пространства объемом 1 км³ из [Мазин И.П. и др., 1989] возьмем концентрацию капель, равную 0.3 см^–3, для $R = 0.025$ см. Тогда по формуле (66) получим ${{I}_{{1{\text{in}}}}}\sim 0.3$ эрг/с, соответствующее частоте $ \approx {\kern 1pt} 6$ кГц.

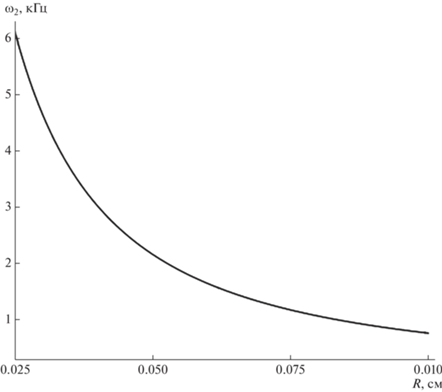
Для иллюстрации на рис. 5 приведены зависимости частоты ${{\omega }_{2}}$ акустического излучения единичной дождевой капли от величин $R,$ рассчитанные по (57). Как видно, увеличение радиуса $R$ капли приводит к быстрому снижению частоты ${{\omega }_{2}}$ звукового излучения. Зависимость ${{\omega }_{2}}$ от заряда капли крайне слаба, в рассматриваемом диапазоне зарядов частота изменяется лишь в шестом знаке после запятой.

Из приведенных оценок и рис. 5 видно, что внутриоблачные капли излучают в ультразвуковом диапазоне акустических волн, а дождевые капли (большего размера) излучают звуковые волны в слышимом диапазоне с меньшей (на три-пять порядков величины) мощностью акустического излучения.

Проведенные расчеты справедливы и для туманов с характерными размерами капель $R = 2 - 10$ мкм [Грин Х. и др., 1969]. Согласно (66) капли тумана обладают достаточно большой интенсивностью излучения, соответствующей ультразвуковым частотам.

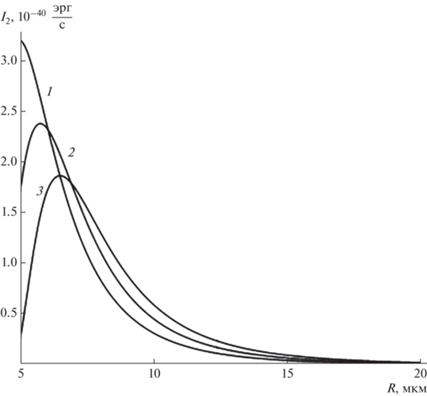
На рис. 6, 7 представлены зависимости интенсивности от размеров ${{I}_{1}}\left( R \right)$ и зарядов ${{I}_{1}}\left( Q \right)$ одиночных капель. Приведенные графики качественно схожи с графиками для декремента затухания ${{\eta }_{1}}\left( R \right),$ ${{\eta }_{1}}\left( Q \right)$ (рис. 1, 3). Зависимость интенсивности излучения от заряда капли кране слаба, в рассматриваемом диапазоне зарядов частота изменяется лишь в четвертом знаке после запятой.

Используя полученные оценки, а также рис. 6, 7, следует сделать заключение о том, что мощности акустического излучения осциллирующих заряженной капли и незаряженной капли, находящейся во внешнем электрическом поле [Григорьев А.И. и др., 2022], совпадают по порядку величины. Это обстоятельство объясняется тем, что величины собственного и индуцированнных электрическим полем зарядов оказывают слабое влияние на величину интенсивности излучения.

Кроме того, следует уделить внимание физическому механизму звукового излучения. Исходя из общефизических соображений, отметим, при передаче механической энергии тепловых осцилляций капли в окружающую материальную среду приводятся в движение частицы этой среды. При этом уменьшение скорости движения молекул жидкости в приповерхностном слое осциллирующей капли влечет снижение ее температуры. Очевидно, что в состоянии теплового равновесия первоначально запасенная механическая энергия в капле, расходуемая на излучение продольных акустических волн, компенсируется поступающей тепловой энергией из внешней среды.

В силу закона Фурье [Кикоин А.К. и др., 1976, стр. 25], описывающего количество теплоты $dQ,$ поступающее на элемент поверхности $dS$ за промежуток времени $dt{\text{:}}$

рассчитаем полное количество теплоты, передаваемое от внешней среды сферической капле в единицу времени: где $\alpha $ – коэффициент теплопроводности среды. Заметим, что в виду малости амплитуды осцилляций (${{\left| \xi \right|} \mathord{\left/ {\vphantom {{\left| \xi \right|} R}} \right. \kern-0em} R} \ll 1$) форма капли принимается невозмущенной сферической: $r = R.$

Исходя из того, что в стационарных условиях интенсивность переносимого тепла $Q$ из внешней среды равна интенсивности ${{I}_{1}}$ расходования энергии на звуковое излучение: $Q = {{I}_{1}},$ и пологая ${{dT} \mathord{\left/ {\vphantom {{dT} {dn}}} \right. \kern-0em} {dn}} \approx {{\Delta T} \mathord{\left/ {\vphantom {{\Delta T} {\Delta n}}} \right. \kern-0em} {\Delta n}},$ из (67) выпишем соотношение для разности температур капли и среды $\Delta T$ в виде:

где в качестве расстояния по нормали $\Delta n$ принимается длина свободного пробега молекулы воздуха.

Уравнение (68) показывает, что величина $\Delta T$ обеспечивает поступающий на каплю поток тепловой энергии, необходимый для поддержания непрерывного акустического излучения.

Если принять параметры внешней среды (воздуха) $\Delta n = 6 \times {{10}^{{ - 6}}}$ см, $\alpha = 2 \times {{10}^{3}}$ эрг/с см град, то из (68) для одиночной внутриоблачной капли размером $R = 30$ мкм получим $\Delta T \approx 2 \times {{10}^{{ - 18}}}$ град. Перепад температур между воздушной средой и уединенной дождевой каплей $R = 0.025$ см составит $\Delta T \approx 4 \times {{10}^{{ - 22}}}$ град.

6. Электромагнитное излучение. Следуя закону сохранения энергии, излучение электромагнитных волн осциллирующей каплей при наличии заряда вызывается уменьшением запасенной в ней энергии. В связи со сказанным с учетом малости величины ${{{{\eta }_{2}}} \mathord{\left/ {\vphantom {{{{\eta }_{2}}} {\omega _{n}^{'}}}} \right. \kern-0em} {\omega _{n}^{'}}} \ll 1$ мощность электромагнитного излучения равна скорости убывания энергии поверхностных затухающих колебаний $n$-ой моды ${{\vartheta }_{n}}$ [Калечиц В.И. и др., 1982]:

Согласно теореме вириала ${{\vartheta }_{n}}$ определяется удвоенной средней за период кинетической энергией движения молекул жидкости в капле:

Подставляя в (69) поле скоростей движения внутренней среды ${{\vec {V}}_{1}}(r,\theta ,t)$ в виде:

и вычисляя интеграл по объему равновесной сферы $V = [0 \leqslant r \leqslant R,\,\,0 \leqslant \theta \leqslant \pi ,\,\,0 \leqslant \varphi \leqslant 2\pi ],$ получим:

Таким образом, учитывая (60), (70), перейдем к окончательному выражению для мощности излучения электромагнитных волн, связанного с $n$-ой колебательной модой:

Заметить, что (71) согласуется с интенсивностью электромагнитного излучения, возникающего при осцилляциях заряженной капли, находящейся в идеальной несжимаемой диэлектрической среде. Отметим тот факт, что характеристики электромагнитного излучения при наличии внешней несжимаемой среды остаются справедливыми и для капли, осциллирующей в несжимаемой среде.

В анализируемом случае генерируемое линейными осцилляциями заряженной капли электромагнитное излучение, найденное в соответствие с общей теорией излучения, относится к квадрупольному типу, обнаруживаемому на основе общей теории излучения в расчетах второго порядка по малому параметру $\delta \equiv {{\left( {{R \mathord{\left/ {\vphantom {R {{{\lambda }_{2}}}}} \right. \kern-0em} {{{\lambda }_{2}}}}} \right)}^{2}}\sim {{10}^{{ - 15}}}$ (${{\lambda }_{2}}$ – длина электромагнитной волны) [Григорьев А.И. и др., 2021]. Отметим, что в линейном приближении по $\varepsilon $ и $\delta $ дипольная составляющая полного излучения отсутствует, так как в первом порядке малости по $\varepsilon $ смещение положения центра заряда и, следовательно, дипольный момент равны нулю (трансляционная мода не возбуждается в силу неподвижности центра масс) равны нулю ${{\vec {R}}_{Q}} = 0,$ $\vec {d} = Q{{\vec {R}}_{Q}} = 0.$ Более интенсивное чем квадрупольное (на 15 порядков величины) дипольное излучение заряженной капли, осциллирующей в отсутствии внешнего электростатического поля, находится в электрогидродинамических расчетах второго порядка по $\varepsilon $ [Григорьев А.И. и др., 2021].

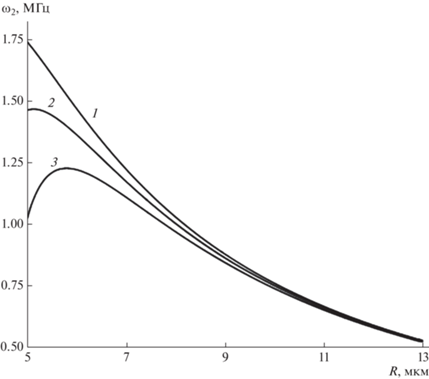
Для оценки по порядку величины воспользуемся вышеприведенными значениями физических величин для внутриоблачных капель. Тогда из (71) следует, что при минимальном радиусе $R = 3$ мкм интенсивность излучения составляет ${{I}_{2}}\sim 4 \times {{10}^{{ - 41}}}$ эрг/с на частоте ${{\omega }_{2}} \approx 4.6$ МГц. Если размер капли принять $R = 8$ мкм, то интенсивность излучения равна ${{I}_{2}}\sim 3 \times {{10}^{{ - 43}}}$ эрг/с при ${{\omega }_{2}} \approx 1$ МГц. Для капли радиусом $R = 30$ будет ${{I}_{2}}\sim 4 \times {{10}^{{ - 46}}}$ эрг/с при ${{\omega }_{2}} \approx 147$ кГц.

В модельном рассмотрении мощность электромагнитного излучения грозового облака протяженностью 10 км будет уже в $5 \times {{10}^{{20}}}$ раз выше по сравнению с единичной каплей, если принять, что все капли радиуса $R = 30$ мкм осциллируют синфазно.

Из рис. 8, 9, где представлены зависимости частот электромагнитного излучения от параметров капли $R,$ $Q,$ нетрудно видеть, что приближение величины собственного заряда $Q$ внутриоблачной капли к критическому значению ${{Q}_{{{\text{кр}}}}}$ при фиксированном радиусе $R$ приводит к заметному снижению частоты ${{\omega }_{2}}$ излучения. Из рис. 8, 9 следует, что облачные капли излучают электромагнитные волны на частотах от десятых долей до единиц мегагерц, что соответствует низким, средним и высоким радиочастотам.

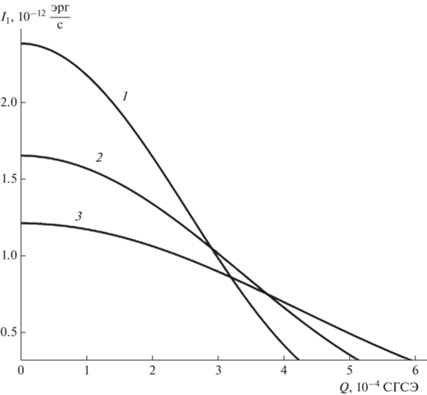
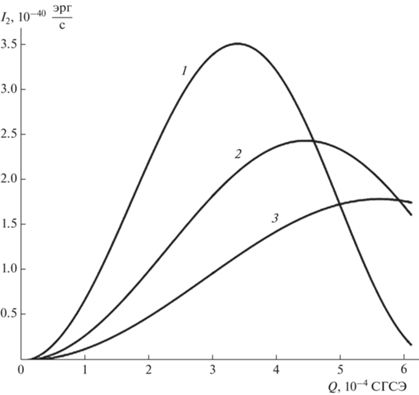
На рис. 10, 11 изображены зависимости интенсивности ${{I}_{2}}$ от величин $R,$ $Q,$ аналогичные показанным на рис. 6, 7. Из сравнения приведенных графиков можно видеть, в случае электромагнитного излучения (в отличие от акустического излучения) прослеживается более выраженная зависимость мощности ${{I}_{2}}$ от величины общего заряда $Q,$ так как в генерировании электромагнитных волн участвует именно заряд $Q.$ Нетрудно заметить, что поведение зависимостей ${{I}_{2}}\left( R \right),$ ${{I}_{2}}\left( Q \right)$ (рис. 10, 11) качественно аналогично поведению зависимостей декремента затухания ${{\eta }_{2}}\left( R \right),$ ${{\eta }_{2}}\left( Q \right)$ (рис. 2, 4).

Анализируя численные оценки и рис. 6, 7, 10, 11 получим, что при тех же значениях физических величин мощность акустического излучения единичной облачной капли, осциллирующей в материальной среде, на 27–32 порядков величины (в зависимости от принятых радиусов капель) превышает мощность ее электромагнитного излучения.

Интересно отметить сильную зависимость интенсивности ${{I}_{2}}$ от номера колебательной моды $n.$ Так, при возрастании номера моды $n$ на единицу излучаемая мощность электромагнитных волн уменьшается на 15 порядков величины, тогда как интенсивность акустического излучения ${{I}_{1}}$ снижается всего лишь на два порядка величины.

Говоря о физическом механизме электромагнитного излучения, отметим, что согласно общефизическим представлениям расходование энергии осциллирующей заряженной капли на излучение электромагнитных волн сопровождаются замедлением ускоренно движущихся поверхностных зарядов и молекул проводящей жидкости, что приводит к уменьшению температуры капли. В условиях теплового равновесия разность температур капли и окружающей среды найдем по аналогии с (68):

при которой поступающая из внешней среды тепловая энергия восполняет потери исходной механической энергии капли и обеспечивает непрерывное электромагнитное излучение.

Используя выше принятые характеристики отдельной облачной капли $R = 30$ мкм, осциллирующей в материальной среде, оценим разницу температур $\Delta T \approx 1 \times {{10}^{{ - 50}}}$ град, что на 32 порядка величины меньше по сравнению с величиной $\Delta T$ в случае акустического излучения.

7. В заключение отойдем от принятой при расчетах модели идеальной жидкости и зададимся вопросом: как может повлиять на капиллярные осцилляции и интенсивность излучения вязкость жидкости? Здесь следует отметить, что вязкость по-разному сказывается на осцилляциях мелких и крупных капель [Григорьев А.И., 2001]. Чтобы выяснить роль вязкости в осцилляциях капель следует перейти к безразмерным переменным, например, таких $\rho = \sigma = R = 1,$ тогда можно сравнивать между собой капли разных размеров и плотностей с различными коэффициентами поверхностного натяжения. В указанных безразмерных переменных безразмерная вязкость определяется параметром $\mu \equiv \nu \sqrt {{\rho \mathord{\left/ {\vphantom {\rho {\sigma R}}} \right. \kern-0em} {\sigma R}}} ,$ здесь $\nu $ – коэффициент кинематической вязкости. Когда вязкость мала $\mu \ll 1,$ капля осциллирует и излучает электромагнитные и акустические волны. При $\mu \sim 1$ осцилляции подавляются вязкостью [Григорьев А.И., 2001] и капля не излучает. Несложно видеть, что параметр $\mu $ кроме собственно коэффициента кинематической вязкости зависит от радиуса капли $R,$ коэффициента поверхностного натяжения $\sigma $ и массовой плотности $\rho .$ Для воды осцилляции капель прекращаются для капель с $R \leqslant 1\,\,\mu {\text{m}}.$ Более крупные капли осциллируют и излучают частотой, определяющейся $\nu $ – коэффициентом кинематической вязкости, радиусом $R,$ коэффициентом поверхностного натяжения $\sigma $ и массовой плотностью $\rho .$

ЗАКЛЮЧЕНИЕ

В аналитических асимптотических расчетах первого порядка малости по $\varepsilon $ – отношению амплитуды капиллярных осцилляций к радиусу сферической заряженной капли, находящейся во внешней материальной среде, показано, что акустическое излучение оказывается более интенсивным (на 27–32 порядков величины в зависимости от радиуса внутриоблачной капли), чем электромагнитное излучение. Полученный результат объясняется разными физическими механизмами генерации продольных акустических волн, приходящихся на диапазоны звуковых (для дождевых капель) и ультразвуковых частот (для облачных капель), и поперечных электромагнитных волн радиочастотного диапазона от десятых долей до единиц мегагерц (соответствующих низким, средним и высоким радиочастотам) при излучении облачных капель.

Показано, что в линейном по $\varepsilon $ приближении аналитическая оценка мощности электромагнитного излучения, рассчитанного в соответствие с законом сохранения энергии, по порядку величины совпадает с мощностью квадрупольной компоненты излучения [Григорьев А.И., 2021], найденного на основе общей теории излучения во втором порядке по малому параметру $\delta $ – квадрату отношения радиуса капли к длине излучаемой электромагнитной волны. Однако более интенсивная (на 15 порядков величины) дипольная компонента полного электромагнитного излучения, обнаруживаемая в линейном приближении по $\delta ,$ отсутствует, так как в расчетах первого порядка малости по $\varepsilon $ возбуждение трансляционной (первой) моды невозможно из-за выполнения условия неподвижности центра масс капли [Григорьев А.И., 2021; Ландау Л.Д. и др.,1986].

Акустическое излучение, генерируемое линейными осцилляциями при возбуждении второй (основной) моды $n = 2,$ оказалось слабее монопольной компоненты излучения, связанного с наличием в спектре капиллярных осцилляций второго порядка по $\varepsilon $ амплитуды нулевой моды ($n = 0$), и дипольной составляющей излучения, характеризуемого появлением во втором порядке малости по $\varepsilon $ амплитуды первой моды ($n = 1$), соответствующей поступательному движению капли [Григорьев А.И., 2022].

ПРИЛОЖЕНИЕ

ВЫЧИСЛЕНИЕ ДОБАВКИ К НАПРЯЖЕННОСТИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ ${{\vec {E}}^{{\left( 1 \right)}}},$ ВЫЗВАННОЙ ВОЗМУЩЕНИЕМ ПОВЕРХНОСТИ КАПЛИ $\xi (\theta ,t).$

Для отыскания поправки первого порядка малости к напряженности электрического поля ${{\vec {E}}^{{\left( 1 \right)}}}$ исходную векторную систему уравнений (48) будем решать методом скаляризации, подробно описанным в [Лазарянц А.Э., 2020]. Для этого искомый вектор ${{\vec {E}}^{{\left( 1 \right)}}}$ запишем в виде суперпозиции трех более простых векторов:

получающихся действием ортогональных векторных дифференциальных операторов ${{\vec {N}}_{j}}$ на произвольные скалярные функции ${{{\text{Ф}}}_{j}}.$

В сферической системе координат векторные операторы ${{\vec {N}}_{j}}$ представляются в виде:

а эрмитово сопряженные к ним операторы имеют вид: удовлетворяющие условиям ортогональности: и условиям коммутативности с оператором Лапласа ($\Delta $):

В этих выражениях $\vec {r}$ – радиус-вектор, знак “+” означает эрмитовое сопряжение.

Подставка разложения (1П) в уравнение непрерывности электрического поля (48) при использовании свойства ортогональности (3П) позволяет получить уравнение Лапласа для скалярной функции ${{{\text{Ф}}}_{1}}{\text{:}}$

Подставим (1П) в волновое уравнение (48) и с учетом свойства коммутативности (4П) получим систему трех скалярных уравнений для функций ${{{\text{Ф}}}_{j}}{\text{:}}$

Будем исходить из того, что функции ${{{\text{Ф}}}_{j}}$ изменяются во времени гармонически: ${{{\text{Ф}}}_{j}}\sim \exp \left( {i{{\omega }_{n}}t} \right).$ Тогда умножая (6П) слева скалярно на векторные операторы $\vec {N}_{j}^{ + }$ и вновь используя свойство ортогональности (3П), перейдем к уравнениям Гельмгольца:

Из системы уравнений (5П), (7П) для скалярной функции ${{{\text{Ф}}}_{1}}$ легко получить решение: ${{{\text{Ф}}}_{1}} = 0,$ при использовании которого уравнение (1П) перепишем в виде суперпозиции вихревых (полоидальной и тороидальной) составляющих электрического поля:

Используя представление дифференциальных операторов ${{\vec {N}}_{2}},$ ${{\vec {N}}_{3}}$ в общем виде (2П), выпишем компоненты вектора (7П) в сферических координатах $\left( {r,\;\theta ,\;\varphi } \right)$ для осесимметричного случая:

Далее решение сформулированной электрической задачи (46) сводится к отысканию в явном виде скалярных функций ${{{\text{Ф}}}_{2}},$ ${{{\text{Ф}}}_{3}}.$

Решений уравнений Гельмгольца при $j = 2,3$ с учетом условия ограниченности на бесконечности (49) будем искать в виде разложений:

где $h_{n}^{{\left( 2 \right)}}\left( {{{z}_{2}}} \right)$ – сферическая функция Бесселя третьего рода, $D_{n}^{{\left( j \right)}}$ – неизвестные коэффициенты первого порядка малости по $\varepsilon ,$ определяемые из граничных условий (50).

Подставляя разложения (9П), (10П) в (50), найдем, что для полоидальной компоненты электрического поля интегральное условие постоянства полного заряда капли выполняется тождественно, а условие эквипотенциальности приводится к виду: $\frac{{\partial {{{\text{Ф}}}_{2}}}}{{\partial \theta }} = 0,$ из которого с учетом (11П) определим, что все константы $D_{n}^{{\left( 2 \right)}}$ в решении для функции ${{{\text{Ф}}}_{2}}$ обращаются в ноль.

Учитывая данный результат, получим, что ${{\vec {E}}^{{\left( 1 \right)}}}$ содержит лишь тороидальную компоненту: ${{\vec {E}}^{{\left( 1 \right)}}} = {{\vec {N}}_{3}}{{{\text{Ф}}}_{3}},$ а с использованием разложений (10П), (11П) при $j = 3$ напряженность поля ${{\vec {E}}^{{\left( 1 \right)}}}$ представим в виде:

Исходя из найденных соотношений ${{\vec {E}}^{{\left( 1 \right)}}}$ и $\xi \left( {\theta ,t} \right),$ из граничных условий (50) для тороидальной составляющей электрического поля несложно получить постоянные коэффициенты $D_{n}^{{\left( 3 \right)}}$ в виде:

В итоге, решение для линейной по малому параметру $\varepsilon $ поправки к напряженности электрического поля запишем в виде:

Работа выполнена при финансовой поддержке Российского научного фонда (проект 19-19-00598 “Гидродинамика и энергетика капли и капельных струй: формирование, движение, распад, взаимодействие с контактной поверхностью”, https://rscf. ru/project/19-19-00598/).