1. На главную
  2. Электронные версии
  3. Журнал физической химии
  4. T. 96, № 3, 2022

Журнал физической химии, 2022, T. 96, № 3, стр. 442-447

Поверхностное натяжение и состав поверхностного слоя бинарных металлических систем

Х. С. Умархаджиев a, Р. Х. Дадашев b, С. М. Умархаджиев a, b, Д. З. Элимханов b, *

a Комплексный научно-исследовательский институт им. Х.И. Ибрагимова РАН
Грозный, Россия

b Академия наук Чеченской Республики
Грозный, Россия

* E-mail: edzhabrail@mail.ru

Поступила в редакцию 20.09.2021
После доработки 05.10.2021
Принята к публикации 08.10.2021

Полный текст (PDF)

Аннотация

Аналитическими методами установлена функциональная связь между содержанием компонента в поверхностном слое и объемной фазе, в которой учтена зависимость коэффициента пропорциональности от состава раствора. С использованием этого соотношения из адсорбционного уравнения Гиббса получены более точные выражения для изотерм поверхностного натяжения и состава поверхностного слоя раствора. По полученным уравнениям проведены расчеты поверхностного натяжения и состава поверхностного слоя расплавов олово–таллий, индий–таллий, галлий–висмут, золото–серебро, натрий–цезий, натрий–калий. Показано, что для этих систем теоретические изотермы в пределах погрешности эксперимента совпадают с экспериментальными.

Ключевые слова: усредненный состав поверхностного слоя, поверхностное натяжение, химический потенциал, изотерма поверхностного натяжения, идеальный раствор

Физико-химические свойства поверхностного слоя могут существенно отличаться от их значений в сосуществующих объемных фазах. Этим частично обусловлены уникальные свойства наноматериалов, отличительная особенность которых – наличие огромной площади поверхности. Значения большинства объемных свойств с достаточной точностью можно определить экспериментально. При этом экспериментальное измерение многих практически важных свойств поверхностного слоя сопряжено с огромными, а порой и принципиально непреодолимыми трудностями. Поэтому разработка теоретических методов определения свойств поверхностного слоя, а также установление функциональной связи физико-химических свойств поверхностного слоя и объемной фазы [1–3] имеет научное и практическое значение.

Следует отметить, что, если для твердых тел имеются надежные методы определения состава поверхности [4], то для жидкостей наиболее точно измеряемое свойство поверхностности – поверхностное натяжение [5]. К настоящему времени достигнуты определенные успехи в установлении связи параметров поверхностного слоя с экспериментально определимыми свойствами объемных фаз [1, 5, 6]. Однако, несмотря на достигнутые успехи, до сих пор нерешенными остаются многие практически важные проблемы, к числу которых относится и задача получения строгих термодинамических выражений, устанавливающих связь поверхностного натяжения и усредненного состава поверхностного слоя с содержанием компонента в растворе.

В связи с этим в работе для двухкомпонентного раствора получены уравнения, которые устанавливают зависимость содержания компонентов в поверхностном слое и поверхностного натяжения от состава объемной фазы.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Если известна концентрационная и температурная зависимости поверхностного натяжения растворов, то по имеющимся фундаментальным уравнениям поверхностного слоя можно определить важные свойства поверхности. Поэтому неудивительно, что разработке уравнений изотерм поверхностного натяжения растворов уделяется большое внимание [1, 2]. Одно из основных направлений решения этой проблемы – попытки получения выражения для изотермы поверхностного натяжения интегрированием адсорбционного уравнения Гиббса. В методе слоя конечной толщины для этих целей используют выражения для мольных долей компонента в поверхностном слое [7]. Однако для интегрирования указанных уравнений необходимы теоретические или полуэмпирические выражения зависимости адсорбции или состава поверхностного слоя от состава раствора. Строгие теоретические выражения этой зависимости даже для бинарных растворов к настоящему времени отсутствуют. Поэтому при решении различных задач исследователи вынуждены прибегать к различным приближенным соотношениям.

Приближенные выражения, устанавливающие связь между содержанием компонента в поверхностном слое и в объемной фазе были получены А.А. Жуховицким [2], а затем А.И. Русановым [1, 5]. Выражение А.А. Жуховицкого для этой зависимости имеет вид [2]:

(1)
$\frac{{1 - x_{{}}^{\omega }}}{{{{{(x_{{}}^{\omega })}}^{\beta }}}} = \frac{{1 - x}}{x}\exp \left( {\frac{{{{\sigma }_{2}} - {{\sigma }_{1}}}}{{RT}}{{\omega }_{1}}} \right),\quad \beta = \frac{{{{V}_{1}}}}{{{{V}_{2}}}}.$
Позднее А.И. Русанов предложил для этой зависимости более простое выражение [1]:
(2)
$\frac{{1 - x_{{}}^{\omega }}}{{x_{{}}^{\omega }}} = m\frac{{1 - x}}{x}.$
В выражениях (1) и (2) $x_{{}}^{\omega }$ и х – мольные доли компонента в поверхностном слое и в объемной фазе соответственно, ${{\sigma }_{1}}$ и ${{\sigma }_{2}}$ – поверхностные натяжения компонентов 1 и 2, ${{\omega }_{1}}$ – молярная площадь первого компонента, V1 и V2 – мольные объемы компонентов, m – некоторая постоянная, не зависящая от состава раствора.

В полученных выражениях коэффициенты пропорциональности m или $\exp \left( {\frac{{{{\sigma }_{2}} - {{\sigma }_{1}}}}{{RT}}{{\omega }_{1}}} \right)$ считаются не зависящими от состава расплава. Это допущение, как показывают результаты вычисления состава поверхностного слоя большого количества расплавов двойных систем [5], существенно сужает область применения полученных уравнений. Об этом свидетельствует также и то, что уравнения изотерм поверхностного натяжения, полученные с использованием этих выражений [7, 8] дают результаты, заметно отличающиеся от экспериментальных данных.

В связи с этим цель данной работы – установить аналитическую связь между составами поверхностного слоя и объемной фазы и на этой основе получить более строгое уравнение изотерм поверхностного натяжения двойных систем. При выводе этого уравнения учтена функциональная зависимость коэффициента пропорциональности от состава раствора. На основе полученных выражений нами разработан метод вычисления состава поверхностного слоя и поверхностного натяжения бинарного раствора.

Рассмотрим двухфазную двухкомпонентную систему с поверхностью разрыва между сосуществующими фазами. Для зависимости химических потенциалов от усредненного состава этой системы в работе [1] получены следующие выражения:

(3)
$\mu _{1}^{\omega } = \mu _{{01}}^{\omega } - (\sigma (x_{{}}^{\omega }) - {{\sigma }_{1}}){{\omega }_{1}} + RT\ln x_{{}}^{\omega },$
(4)
$\mu _{2}^{\omega } = \mu _{{02}}^{\omega } - (\sigma (x_{{}}^{\omega }) - {{\sigma }_{2}}){{\omega }_{2}} + RT\ln (1 - x_{{}}^{\omega }),$
где $x_{{}}^{\omega }$ – средняя мольная доля компонента в рассматриваемой двухфазной системе, $\mu _{i}^{\omega }$ – усредненные химические потенциалы компонентов в двухфазной системе, $T$ – температура и $R$ – газовая постоянная, $\sigma $ – поверхностное натяжение, ${{\omega }_{i}}$ – парциально-молярная поверхность $i$-го компонента.

Как подчеркнуто в работе [1], выражения (3) и (4) “применимы не только к самому поверхностному слою, но и к двухфазной системе в целом” [1, с. 56]. Поэтому мы вправе записать их в такой форме и для поверхностного слоя, который включает в себя небольшие прослойки однородных фаз. В пределе, при приближении толщины двухфазной системы к эффективной толщине поверхностного слоя, мы получим усредненные значения мольных долей и химических потенциалов компонентов в поверхностном слое.

Следует отметить также, что выражения (3) и (4) получены для модели жесткого поверхностного слоя, в которой парциально-молярные поверхности не зависят от поверхностного натяжения, а, следовательно, парциально-молярная поверхность i-го компонента равна молярной поверхности этого компонента (т.е. поверхности, деленной на общее число молей $i$-го компонента в рассматриваемой двухфазной системе).

Запишем выражения для химических потенциалов компонентов в идеальном растворе, т.е. допустим, что коэффициенты активности компонентов $f = 1$

(5)
$\mu _{1}^{{}} = \mu _{{01}}^{{}} + RT\ln x,$
(6)
$\mu _{2}^{{}} = \mu _{{02}}^{{}} + RT\ln (1 - x).$
Отметим, что нами рассматривается двухфазная система, в которой объемная фаза и поверхностный слой считаются идеальными растворами. Кроме того, поверхностный слой считается и абсолютно жестким. Следует подчеркнуть, что эта модель двухфазной системы служит неплохим приближением при рассмотрении поверхностного слоя конденсированных фаз вдали от критического состояния. При этом, как подчеркивал А.А. Жуховицкий [2], предположение об идеальности поверхностного слоя является более строгим приближением, чем модель идеального раствора. Обусловлено это, по мнению А.А. Жуховицкого [2], тем, что на свободной поверхности раствора частицы (атомы и молекулы) обладают дополнительными степенями свободы, и вероятность образования идеального поверхностного слоя на границе жидкость–пар должна быть выше, чем вероятность образования идеального раствора.

В случае равновесия рассматриваемой термодинамической системы, следуя условиям равновесия фаз Гиббса, мы вправе приравнять значения химических потенциалов компонентов в поверхностном слое и в прослойках объемных фаз. Следовательно, приравнивая выражения химических потенциалов в поверхностном слое $\mu _{i}^{\omega }$ (3), (4) и в растворе $\mu _{i}^{{}}$ (5), (6) имеем:

(7)
$\begin{gathered} (\sigma (x_{{}}^{\omega }) - {{\sigma }_{1}}){{\omega }_{1}} = RT\ln \frac{{x_{{}}^{\omega }}}{x}, \\ (\sigma (x_{{}}^{\omega }) - {{\sigma }_{2}}){{\omega }_{2}} = RT\ln \frac{{1 - x_{{}}^{\omega }}}{{1 - x}}. \\ \end{gathered} $

Из выражений (7) после несложных преобразований можно получить формулы, выражающие связь состава поверхностного слоя и объемной фазы:

$\begin{gathered} \frac{{1 - x_{{}}^{\omega }}}{{1 - x}} = \exp \left( {\frac{{(\sigma (x_{{}}^{\omega }) - {{\sigma }_{1}}){{\omega }_{1}}}}{{RT}}} \right) \times \\ \times \;\exp \left( {\frac{{(\sigma (x_{{}}^{\omega }) - {{\sigma }_{2}}){{\omega }_{2}}}}{{RT}} - \frac{{(\sigma (x_{{}}^{\omega }) - {{\sigma }_{1}}){{\omega }_{1}}}}{{RT}}} \right) = \\ = \;\frac{{x_{{}}^{\omega }}}{x}\exp \left( {\frac{{\sigma (x_{{}}^{\omega })({{\omega }_{2}} - {{\omega }_{1}}) + {{\sigma }_{1}}{{\omega }_{1}} - {{\sigma }_{2}}{{\omega }_{2}}}}{{RT}}} \right) \\ \end{gathered} $
или
(8)
$\begin{gathered} \frac{{1 - x_{{}}^{\omega }}}{{x_{{}}^{\omega }}} = \frac{{1 - x}}{x} \times \\ \times \;\exp \left( {\frac{{\sigma (x_{{}}^{\omega })({{\omega }_{2}} - {{\omega }_{1}}) + {{\sigma }_{1}}{{\omega }_{1}} - {{\sigma }_{2}}{{\omega }_{2}}}}{{RT}}} \right). \\ \end{gathered} $
Полученное выражение (8) устанавливает функциональную связь между мольными долями компонентов в поверхностном слое ($x_{{}}^{\omega }$) и объеме раствора ($x$). Однако, выразить из этого равенства $x_{{}}^{\omega }$ через $x$ не представляется возможным, поскольку аргумент экспоненты в правой части содержит неизвестную функцию $\sigma (x_{{}}^{\omega })$, которая устанавливает зависимость поверхностного натяжения от состава поверхностного слоя. Однако, из этого выражения без особых трудностей можно выразить мольные доли компонента в объемной фазе через мольные доли этого компонента в поверхностном слое. Действительно, из этого выражения после несложных преобразований имеем:
(9)
$\begin{gathered} x = \\ = \frac{{x_{{}}^{\omega }}}{{x_{{}}^{\omega } + (1 - x_{{}}^{\omega })\exp \left( { - \frac{{\sigma (x_{{}}^{\omega })({{\omega }_{2}} - {{\omega }_{1}}) + {{\sigma }_{1}}{{\omega }_{1}} - {{\sigma }_{2}}{{\omega }_{2}}}}{{RT}}} \right)}}. \\ \end{gathered} $
Выражение (9) устанавливает в явном виде связь между мольными долями компонентов в поверхностном слое и в объемной фазе. Однако это выражение содержит неизвестную функцию $\sigma (x_{{}}^{\omega })$. Поэтому для проведения расчетов по уравнению (9) необходимо найти выражение для зависимости поверхностного натяжения от мольных долей компонентов в поверхностном слое.

Для определения этой зависимости воспользуемся дифференциальным уравнением, которое устанавливает связь поверхностного натяжения раствора с усредненными мольными долями компонента в поверхностном слое и в объемной фазе [9]:

(10)
$d\sigma (x_{{}}^{\omega }) = \frac{{RT}}{\omega }\frac{{x - x_{{}}^{\omega }}}{{x(1 - x)}}dx.$
Если дополнить это уравнение начальным условием $\sigma (0) = {{\sigma }_{2}}$, то, с математической точки зрения, получим задачу Коши для нахождения функции $\sigma (x_{{}}^{\omega })$. Однако, при решении уравнения (10) возникают трудности, обусловленные тем, что оно содержит еще одну неизвестную функцию, которая дает зависимость молярной поверхности от содержания компонентов в поверхностном слое или в объемной фазе.

Существуют различные подходы к определению этой зависимости, подробный анализ которых дан в работе [5]. Рассмотрим те варианты, которые могут быть использованы на практике.

1) Иногда при решении теоретических задач делается предположение о том, что молярная площадь не зависит от состава раствора $\omega (x) = {\text{const}}$ [8]. Однако это предположение для большинства бинарных систем не выполняется.

2) Молярную площадь можно представить и в виде линейной функции состава раствора, т.е. молярная поверхность представляется в виде аддитивной функции состава раствора $\omega = {{\omega }_{1}}{{x}_{1}} + {{\omega }_{2}}{{x}_{2}}$. Однако и это предположение, хотя и более строгое, для большинства систем не выполняется. Обусловлено это тем, что молярная площадь является термодинамическим параметром не объемной фазы, а поверхностного слоя.

3) Исходя из изложенного выше, логичнее предположить, что молярная площадь аддитивна относительно мольных долей компонентов в поверхностном слое:

(11)
$\omega = {{\omega }_{1}}x_{{}}^{\omega } + {{\omega }_{2}}(1 - x_{{}}^{\omega }),$
где ${{x}^{\omega }}$ – мольная доля компонента в поверхностном слое, ${{\omega }_{i}}$ – молярная поверхность i-го компонента.

Результаты вычислений термодинамических параметров поверхностного слоя большого количества двойных и тройных систем, проведенные автором [5], показали, что зависимость молярной площади от состава поверхностного слоя значительно ближе к аддитивной прямой, чем ее зависимость от состава расплава. Поэтому дальнейшие рассуждения и выкладки проведены нами по формуле (11), которая получена в предположении о том, что молярная площадь $\omega $ является линейной функцией состава поверхностного слоя.

Заменив в выражении (10) переменную $x$ согласно (9), получим обыкновенное дифференциальное уравнение:

(12)
$d\sigma = \frac{{RT\left( {1 - \exp \left( { - \frac{{({{\omega }_{2}} - {{\omega }_{1}})\sigma + {{\omega }_{1}}{{\sigma }_{1}} - {{\omega }_{2}}{{\sigma }_{2}}}}{{RT}}} \right)} \right)}}{{{{\omega }_{2}}(1 - {{x}^{\omega }})\exp \left( { - \frac{{({{\omega }_{2}} - {{\omega }_{1}})\sigma + {{\omega }_{1}}{{\sigma }_{1}} - {{\omega }_{2}}{{\sigma }_{2}}}}{{RT}}} \right) + {{\omega }_{1}}{{x}^{\omega }}}}d{{x}^{\omega }}.$
Рассматривая полученное равенство как уравнение относительно функции ${{x}^{\omega }}(\sigma )$, получим линейное уравнение:
$\frac{{d{{x}^{\omega }}}}{{d\sigma }} = \frac{{{{\omega }_{2}}(1 - {{x}^{\omega }})\exp \left( { - \frac{{({{\omega }_{2}} - {{\omega }_{1}})\sigma + {{\omega }_{1}}{{\sigma }_{1}} - {{\omega }_{2}}{{\sigma }_{2}}}}{{RT}}} \right) + {{\omega }_{1}}{{x}^{\omega }}}}{{RT\left( {1 - \exp \left( { - \frac{{({{\omega }_{2}} - {{\omega }_{1}})\sigma + {{\omega }_{1}}{{\sigma }_{1}} - {{\omega }_{2}}{{\sigma }_{2}}}}{{RT}}} \right)} \right)}}$
с краевым условием ${{x}^{\omega }}({{\sigma }_{2}}) = 0$. Решение этого уравнения относительно ${{x}^{\omega }}(\sigma )$ имеет вид:
(13)
$\begin{gathered} {{x}^{\omega }}(\sigma ) = \frac{{\exp \left( {\frac{{{{\omega }_{1}}(\sigma - {{\sigma }_{1}})}}{{RT}}} \right) - \exp \left( { - \frac{{({{\omega }_{2}} - {{\omega }_{1}})\sigma + {{\omega }_{1}}{{\sigma }_{1}} - {{\omega }_{2}}{{\sigma }_{2}}}}{{RT}}} \right)}}{{1 - \exp \left( { - \frac{{({{\omega }_{2}} - {{\omega }_{1}})\sigma + {{\omega }_{1}}{{\sigma }_{1}} - {{\omega }_{2}}{{\sigma }_{2}}}}{{RT}}} \right)}}, \\ {{\sigma }_{1}} \leqslant \sigma \leqslant {{\sigma }_{2}}. \\ \end{gathered} $
Подставив выражение (13) в формулу (9), получим:
(14)
$\begin{gathered} x(\sigma ) = \frac{{1 - \exp \left( { - \frac{{{{\omega }_{2}}(\sigma - {{\sigma }_{2}})}}{{RT}}} \right)}}{{1 - \exp \left( { - \frac{{({{\omega }_{2}} - {{\omega }_{1}})\sigma + {{\omega }_{1}}{{\sigma }_{1}} - {{\omega }_{2}}{{\sigma }_{2}}}}{{RT}}} \right)}}, \\ {{\sigma }_{1}} \leqslant \sigma \leqslant {{\sigma }_{2}}. \\ \end{gathered} $
Полученные формулы (13) и (14) дают зависимость состава поверхностного слоя от состава объемной фазы в параметрическом виде с параметром $\sigma $:
(15)
$\left\{ \begin{gathered} x = \frac{{1 - \exp \left( { - \frac{{(\sigma - {{\sigma }_{2}}){{\omega }_{2}}}}{{RT}}} \right)}}{{1 - \exp \left( { - \frac{{({{\omega }_{2}} - {{\omega }_{1}})\sigma + {{\omega }_{1}}{{\sigma }_{1}} - {{\omega }_{2}}{{\sigma }_{2}}}}{{RT}}} \right)}}, \hfill \\ {{x}^{\omega }} = \frac{{\exp \left( {\frac{{(\sigma - {{\sigma }_{1}}){{\omega }_{1}}}}{{RT}}} \right) - \exp \left( { - \frac{{({{\omega }_{2}} - {{\omega }_{1}})\sigma + {{\omega }_{1}}{{\sigma }_{1}} - {{\omega }_{2}}{{\sigma }_{2}}}}{{RT}}} \right)}}{{1 - \exp \left( { - \frac{{({{\omega }_{2}} - {{\omega }_{1}})\sigma + {{\omega }_{1}}{{\sigma }_{1}} - {{\omega }_{2}}{{\sigma }_{2}}}}{{RT}}} \right)}}, \hfill \\ \end{gathered} \right.\quad {{\sigma }_{1}} \leqslant \sigma \leqslant {{\sigma }_{2}}.$
При этом в качестве параметра $\sigma $ выступает поверхностное натяжение раствора. Кроме этого, выражение (14) позволяет выразить зависимость поверхностного натяжения от состава объемной фазы $\sigma (x)$ в параметрическом виде:

(16)
$\begin{gathered} \left\{ \begin{gathered} x = \frac{{1 - \exp \left( { - \frac{{(t - {{\sigma }_{2}}){{\omega }_{2}}}}{{RT}}} \right)}}{{1 - \exp \left( { - \frac{{({{\omega }_{2}} - {{\omega }_{1}})t + {{\omega }_{1}}{{\sigma }_{1}} - {{\omega }_{2}}{{\sigma }_{2}}}}{{RT}}} \right)}} \hfill \\ \sigma = t, \hfill \\ \end{gathered} \right., \\ {{\sigma }_{1}} \leqslant t \leqslant {{\sigma }_{2}}. \\ \end{gathered} $

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

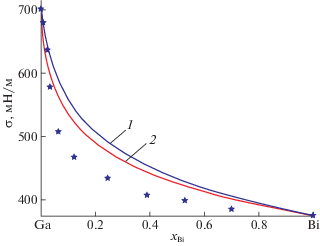
В качестве апробации полученных формул нами проведены расчеты изотерм состава поверхностного слоя и поверхностного натяжения двойных систем индий–таллий [5], олово–таллий [5], галлий–висмут [5], золото–серебро [10], натрий–цезий [11], натрий–калий, по поверхностным свойствам которых в литературе имеются надежные экспериментальные данные. Сопоставление теоретических изотерм с экспериментальными показывает, что для всех исследованных нами систем полученное уравнение качественно, а для большинства из них и количественно описывает концентрационную зависимость поверхностного натяжения. Поэтому на рис. 1, 2 представлены результаты по поверхностным свойствам бинарных расплавов галлий–висмут (система, в которой получены максимальные отклонения теоретических значений от экспериментальных данных) и натрий–цезий (система, в которой теоретические значения совпадают с экспериментальными в пределах ошибки эксперимента). Причин расхождений вычисленных значений от экспериментальных, по-видимому, несколько. К ним можно отнести и те факторы, которые обусловлены тем, что в работе рассмотрена идеальная модель двухфазной системы, в которой и конденсированная фаза, и поверхностный слой считаются идеальными растворами.

Рис. 1.

Изотермы поверхностного натяжения расплавов галлий–висмут, при Т = 573 K; (1 – результаты расчетов по уравнению Жуховицкого [2]; 2 – результаты теоретических расчетов (15); точки – экспериментальные данные [5]).

Рис. 2.

Изотермы поверхностного натяжения расплавов натрий–цезий, при Т = 373 K; 1 – результаты расчетов по уравнению Жуховицкого [2]; 2 – результаты теоретических расчетов (15); точки – экспериментальные данные [11].

Как видно из рис. 2, вычисленные изотермы поверхностного натяжения в пределах погрешности эксперимента совпадают с экспериментальными. Изотермы мольных долей цезия имеют небольшие количественные отличия, которые незначительно превышают ошибку вычислений. Обусловлено это, на наш взгляд, тем, что состав поверхностного слоя в методе слоя конечной толщины [1] определяется через производную поверхностного натяжения по мольным долям компонента в растворе, что сопряжено с относительно большими ошибками (10–15%).

Таким образом, получены выражения, устанавливающие зависимость мольных долей компонентов в поверхностном слое и поверхностного натяжения от состава объемной фазы. Проведены расчеты мольных долей компонентов в поверхностном слое и поверхностного натяжения расплавов индий–таллий, галлий–висмут [5] золото–серебро [10], натрий–цезий, натрий–калий [11]. На основе сопоставления результатов проведенных расчетов с экспериментальными данными показано, что теоретические изотермы поверхностного натяжения в изученных системах (рис. 3, 4) ближе к экспериментальным кривым, чем изотермы поверхностного натяжения, полученные по уравнению А.А. Жуховицкого.

Рис. 3.

Изотермы мольных долей висмута в поверхностном слое (хω) расплавов галлий–висмут Т = = 773 K (х – мольные доли висмута в объеме); 1 – результаты теоретических расчетов (15), 2 – кривые, полученные по экспериментальным изотермам поверхностного натяжения [5].

Рис. 4.

Изотермы мольных долей серебра в поверхностном слое (хω) расплавов золото–серебро при Т = = 1273 K (х – мольные доли серебра в объеме); 1 – результаты теоретических расчетов, 2 – кривые, полученные по экспериментальным изотермам поверхностного натяжения [10].

Теоретические изотермы мольных долей компонентов в поверхностном слое качественно передают зависимость состава поверхностного слоя от состава раствора. Имеющиеся количественные расхождения теоретических значений от экспериментальных данных не выходят за пределы погрешности расчетов мольных долей компонентов в поверхностном слое.

Список литературы

  1. Rusanov A.I. Phasengleichgewichte und Oberflachener-scheinungen. Berlin, Academie-Verlag, 1978. 678 p.

  2. Жуховицкий А.А. // Журн. физ. химии. 1944. T. I8. Вып. 5–6. С. 214.

  3. Пригожин И., Дефей Р. Химическая термодинамика. Новосибирск: Наука, 1966. 510 с.

  4. Ашхотов О.Г., Шебзухов А.А., Хоконов Х.Б. // Докл. АН СССР. 1984. Т. 274. № 6. С. 1349.

  5. Дадашев Р.Х. Термодинамика поверхностных явлений. М.: Физматлит, 2008. 287 с.

  6. Гиббс Дж.В. Термодинамика. Статистическая механика. М.: Наука, 1982. 582 с.

  7. Dadashev R.Kh., Elimkhanov Dj.Z., Bichueva Z.I., Khokonov Kh.B. // Bulletin of the Russian Academy of Sciences: Physics. 2007. V. 71. № 2. P. 257.

  8. Мехдиев. И.Г. // Журн. физ. химии. 2001. 75. № 4. С. 749.

  9. Русанов А.И., Левичев С.А. // Поверхностные явления в расплавах. Киев: Наукова думка, 1968. С. 63–68.

  10. Dogan A., Arslan H. // Philosophical Magazine. 2017. P. 1–17. https://doi.org/10.1080/14786435.2017.1356483

  11. Алчагиров Б.Б. Поверхностное натяжение, плотность и работа выхода электрона некоторых бинарных металлических расплавов: Автореф. дис…. канд. физ.-мат. наук. Кабард.-Балкар. гос. ун-т, Нальчик, 1974. 23 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал физической химии

Архивы выпусков Информация о журнале Отправить рукопись в журнал