Физика металлов и металловедение, 2019, T. 120, № 10, стр. 1011-1015

1. Повышенный интерес в последнее время к магнитнокалорическим эффектам (МКЭ) связан с поиском ферро- и ферримагнитных соединений, дающих максимальный эффект в области комнатных температур и поэтому потенциально пригодных для разработки охлаждающих устройств в этой температурной области [1–6]. Однако в целом это направление исследований МКЭ пока еще находится на стадии поисков перспективных материалов, тогда как на практике уже давно существует другое, хорошо развитое направление применения МКЭ, которое связано с использованием МКЭ в парамагнетиках для получения сверхнизких температур и сжижения газов [7].

При этом следует иметь в виду, что обычно для этих целей используют МКЭ в таких парамагнетиках, в которых ближайшее кристаллическое окружение парамагнитного иона обладает кубической симметрией (например, квасцы [7, 8]) и эффекты кристалличесикх полей относительно слабы, так что в первом приближении МКЭ в таких соединениях можно рассматривать как изотропный. В то же время существуют парамагнетики, в которых симметрия кристаллического окружения магнитных ионов носит одноосный характер (например, гексагональные редкоземельные этилсульфаты [9] или двойные нитраты с тригональной симметрией [10]). В этих парамагнитных соединениях магнитная анизотропия достаточна сильна, а ее влияние на МКЭ еще слабо изучено.

Недавно было показано [11], что в одноосных парамагнетиках с некрамерсовыми ионами (с целочисленными спинами $S = 1,2,...$) в случае одноионной анизотропии типа легкая плоскость намагничивание в трудном направлении приводит к появлению аномального обратного МКЭ в области низких температур и слабых полей, и что эта аномалия возникает из-за эффекта пересечения энергетических уровней иона в магнитном поле. Так как эффекты пересечения энергетических уровней парамагнитного иона в магнитном поле при наличии одноионной анизотропии типа легкая плоскость могут существовать и для крамерсовых ионов с полуцелочисленными спинами $S = {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2},{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2},...,$ то интересно понять, каковы будут особенности низкотемпературных МКЭ в одноосных парамагнетиках с крамерсовыми ионами. Мы в основном ограничимся модельными расчетами изменения магнитной энтропии при изотермическом намагничивании и случаем крамерсова иона со спином $S = {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2},$ но для полноты картины исследуем намагничивание как в легком, так и в трудном направлениях.

2. Гамильтониан крамерсова парамагнитного иона со спинами $S = {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}$ и одноионной анизотропией второго порядка типа легкая плоскость (параметр анизотропии $D > 0$) в магнитном поле имеет вид:

где первое выражение берется в случае магнитного поля $H{\text{||}}OZ,$ параллельного трудному направлению $OZ,$ и второе – при намагничивании в легкой плоскости вдоль легкого направления с $H{\text{||}}OX.$ Обозначение ${{\mu }_{Z}} \equiv {{\mu }_{{\text{B}}}}{{g}_{Z}}$ или ${{\mu }_{X}} \equiv {{\mu }_{{\text{B}}}}{{g}_{X}}$ (здесь ${{\mu }_{{\text{B}}}}$ – магнетон Бора) учитывает возможную анизотропию фактора спектроскопического расщепления $g$ (фактор Ланде) в парамагнитном кристалле [8].

В случае намагничивания в трудном направлении $H{\text{||}}OZ$ гамильтониан ${{H}_{{{\text{hd}}}}}$ (1) имеет собственные значения

причем каждому собственному значению энергии соответствует собственное значение $Z$-проекции спина ${{S}_{Z}}.$ Тогда намагниченность $m_{Z}^{{{\text{hd}}}}(T,H)$ в трудном направлении (на один ион) равна

Для нахождения изменения магнитной энтропии $\Delta {{S}_{M}}$ при изотермическом намагничивании от начального магнитного поля ${{H}_{i}}$ до конечного поля ${{H}_{f}}$ необходимо знать температурную производную намагниченности ${{\partial m_{Z}^{{{\text{hd}}}}(T,H)} \mathord{\left/ {\vphantom {{\partial m_{Z}^{{{\text{hd}}}}(T,H)} {\partial T}}} \right. \kern-0em} {\partial T}}{\text{:}}$

причем знак $\Delta {{S}_{{\text{M}}}}$ (при $\Delta {{S}_{{\text{M}}}} < 0$ – прямой эффект и при $\Delta {{S}_{{\text{M}}}} > 0$ – обратный эффект) определяется знаком температурной производной намагниченности $\partial m_{Z}^{{{\text{hd}}}}(T,H)$ на интервале интегрирования по полю $\Delta H = {{H}_{f}} - {{H}_{i}}.$

При намагничивании в трудном направлении температурная производная намагниченности равна

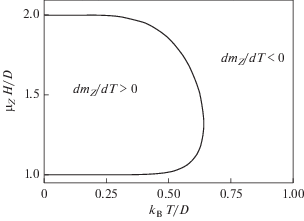
Если выражение (5) преобразовать к безразмерным переменным – полю ${{{{\mu }_{Z}}H} \mathord{\left/ {\vphantom {{{{\mu }_{Z}}H} D}} \right. \kern-0em} D}$ и температуре ${{{{k}_{{\text{B}}}}T} \mathord{\left/ {\vphantom {{{{k}_{{\text{B}}}}T} D}} \right. \kern-0em} D},$ то можно убедиться, что на плоскости переменных $({{{{k}_{{\text{B}}}}T} \mathord{\left/ {\vphantom {{{{k}_{{\text{B}}}}T} D}} \right. \kern-0em} D})$ – $({{{{\mu }_{Z}}H} \mathord{\left/ {\vphantom {{{{\mu }_{Z}}H} D}} \right. \kern-0em} D})$ температурная производная $\partial \left( {{{m_{Z}^{{{\text{hd}}}}(T,H)} \mathord{\left/ {\vphantom {{m_{Z}^{{{\text{hd}}}}(T,H)} {{{\mu }_{Z}}{{k}_{{\text{B}}}}}}} \right. \kern-0em} {{{\mu }_{Z}}{{k}_{{\text{B}}}}}}} \right)\partial ({T \mathord{\left/ {\vphantom {T D}} \right. \kern-0em} D})$ ~ ${{\partial m_{Z}^{{{\text{hd}}}}} \mathord{\left/ {\vphantom {{\partial m_{Z}^{{{\text{hd}}}}} {\partial T}}} \right. \kern-0em} {\partial T}}$ может быть как положительной, так и отрицательной. На рис. 1 представлены результаты расчета границы между областями нормального $\left( {{{\partial m_{Z}^{{{\text{hd}}}}} \mathord{\left/ {\vphantom {{\partial m_{Z}^{{{\text{hd}}}}} {\partial T}}} \right. \kern-0em} {\partial T}} < 0} \right)$ и аномального $\left( {{{\partial m_{Z}^{{{\text{hd}}}}} \mathord{\left/ {\vphantom {{\partial m_{Z}^{{{\text{hd}}}}} {\partial T > 0}}} \right. \kern-0em} {\partial T > 0}}} \right)$ температурного поведения намагниченности $m_{Z}^{{{\text{hd}}}}$ на плоскость безразмерных температур $\left( {{{{{k}_{{\text{B}}}}T} \mathord{\left/ {\vphantom {{{{k}_{{\text{B}}}}T} D}} \right. \kern-0em} D}} \right)$ и полей $\left( {{{{{\mu }_{Z}}H} \mathord{\left/ {\vphantom {{{{\mu }_{Z}}H} D}} \right. \kern-0em} D}} \right).$ Очевидно, что, если намагничивание в интервале полей $\Delta H$ = ${{H}_{f}} - {{H}_{i}}$ будет захватывать области положительных значений температурной производной намагниченности ${{\partial m_{Z}^{{{\text{hd}}}}} \mathord{\left/ {\vphantom {{\partial m_{Z}^{{{\text{hd}}}}} {\partial T}}} \right. \kern-0em} {\partial T}} > 0,$ то в случае преобладания вкладов от этих областей полевая зависимость $\Delta S_{{\text{M}}}^{{{\text{hd}}}}(T,\Delta H)$ будет иметь аномальный положительный знак $\Delta {{S}_{{\text{M}}}}(T,\Delta H) > 0.$

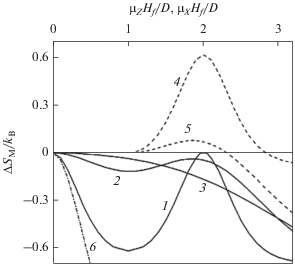
На рис. 2 представлены результаты расчета изменения магнитной энтропии $\Delta S_{{\text{M}}}^{{{\text{hd}}}}$ как функции безразмерного конечного магнитного поля ${{{{\mu }_{Z}}{{H}_{f}}} \mathord{\left/ {\vphantom {{{{\mu }_{Z}}{{H}_{f}}} D}} \right. \kern-0em} D}$ при двух вариантах выбора начального поля намагничивания: ${{{{\mu }_{Z}}{{H}_{i}}} \mathord{\left/ {\vphantom {{{{\mu }_{Z}}{{H}_{i}}} D}} \right. \kern-0em} D} = 0$ и ${{{{\mu }_{Z}}{{H}_{i}}} \mathord{\left/ {\vphantom {{{{\mu }_{Z}}{{H}_{i}}} D}} \right. \kern-0em} D} = 1.$ Кривые 1 и 2 отражают немонотонное поведение $\Delta S_{{\text{M}}}^{{{\text{hd}}}}$ для температур ${{{{k}_{{\text{B}}}}T} \mathord{\left/ {\vphantom {{{{k}_{{\text{B}}}}T} D}} \right. \kern-0em} D} = 0.2$ и ${{{{k}_{{\text{B}}}}T} \mathord{\left/ {\vphantom {{{{k}_{{\text{B}}}}T} D}} \right. \kern-0em} D} = 0.5$ при нулевом начальном поле ${{{{\mu }_{Z}}{{H}_{i}}} \mathord{\left/ {\vphantom {{{{\mu }_{Z}}{{H}_{i}}} D}} \right. \kern-0em} D} = 0,$ кривые 4 и 5 – для температур ${{{{k}_{{\text{B}}}}T} \mathord{\left/ {\vphantom {{{{k}_{{\text{B}}}}T} D}} \right. \kern-0em} D} = 0.2$ и ${{{{k}_{{\text{B}}}}T} \mathord{\left/ {\vphantom {{{{k}_{{\text{B}}}}T} D}} \right. \kern-0em} D} = 0.5$ при начальном поле ${{{{\mu }_{Z}}{{H}_{i}}} \mathord{\left/ {\vphantom {{{{\mu }_{Z}}{{H}_{i}}} D}} \right. \kern-0em} D} = 1.$ Кривая 3 показывает монотонную зависимость $\Delta S_{{\text{M}}}^{{{\text{hd}}}}$ от ${{{{\mu }_{Z}}{{H}_{f}}} \mathord{\left/ {\vphantom {{{{\mu }_{Z}}{{H}_{f}}} D}} \right. \kern-0em} D}$ при ${{{{k}_{{\text{B}}}}T} \mathord{\left/ {\vphantom {{{{k}_{{\text{B}}}}T} D}} \right. \kern-0em} D} = 1$ и начальном поле ${{{{\mu }_{Z}}{{H}_{i}}} \mathord{\left/ {\vphantom {{{{\mu }_{Z}}{{H}_{i}}} D}} \right. \kern-0em} D} = 0.$ Немонотонность кривых 1, 2 и 4, 5 для $\Delta S_{{\text{M}}}^{{{\text{hd}}}}$ связана с тем, что при изменении конечного поля ${{{{\mu }_{Z}}{{H}_{f}}} \mathord{\left/ {\vphantom {{{{\mu }_{Z}}{{H}_{f}}} D}} \right. \kern-0em} D}$ и выборе температур ${{{{k}_{{\text{B}}}}T} \mathord{\left/ {\vphantom {{{{k}_{{\text{B}}}}T} D}} \right. \kern-0em} D} = 0.2$ и $0.5$ изотермическое намагничивание захватывает область аномального температурного поведения намагниченности ${{\partial m_{Z}^{{{\text{hd}}}}} \mathord{\left/ {\vphantom {{\partial m_{Z}^{{{\text{hd}}}}} {\partial T}}} \right. \kern-0em} {\partial T}} > 0$ (см. рис. 1), тогда как при ${{{{k}_{{\text{B}}}}T} \mathord{\left/ {\vphantom {{{{k}_{{\text{B}}}}T} D}} \right. \kern-0em} D} = 1$ изменение $\Delta S_{{\text{M}}}^{{{\text{hd}}}} < 0$ (сплошная кривая 3) связано с намагничиванием только в областях нормального поведения намагниченности ${{\partial m_{Z}^{{{\text{hd}}}}} \mathord{\left/ {\vphantom {{\partial m_{Z}^{{{\text{hd}}}}} {\partial T}}} \right. \kern-0em} {\partial T}} < 0.$

Из рис. 2, во-первых, видно, что на кривых $\Delta S_{{\text{M}}}^{{{\text{hd}}}}$ с немонотонным поведением (кривые 1, 2, 4, 5) существуют участки парадоксальной зависимости от конечного поля намагничивания ${{H}_{f}},$ когда при увеличении ${{H}_{f}}$ абсолютная величина эффекта $\left| {\Delta S_{{\text{M}}}^{{{\text{hd}}}}} \right|$ начинает уменьшаться. Во-вторых, видно, что в рассмотренной ситуации знак величины изменения магнитной энтропии $\Delta S_{{\text{M}}}^{{{\text{hd}}}}$ перестает быть однозначной характеристикой магнитного состояния вещества, так как теперь этот знак существенно зависит от выбора границ интервала намагничивания. Например, если сравнить величину $\Delta S_{{\text{M}}}^{{{\text{hd}}}}$ при одинаковом конечном поле ${{{{\mu }_{Z}}{{H}_{f}}} \mathord{\left/ {\vphantom {{{{\mu }_{Z}}{{H}_{f}}} D}} \right. \kern-0em} D}$ = 1.5 и одинаковой температуре ${{{{k}_{{\text{B}}}}T} \mathord{\left/ {\vphantom {{{{k}_{{\text{B}}}}T} D}} \right. \kern-0em} D}$ на кривых 1 и 4, (но при разных начальных полях намагничивания: ${{{{\mu }_{Z}}{{H}_{i}}} \mathord{\left/ {\vphantom {{{{\mu }_{Z}}{{H}_{i}}} D}} \right. \kern-0em} D}$ = 0 и ${{{{\mu }_{Z}}{{H}_{i}}} \mathord{\left/ {\vphantom {{{{\mu }_{Z}}{{H}_{i}}} D}} \right. \kern-0em} D}$ = 1), то на кривой 1 будет $\Delta S_{{\text{M}}}^{{{\text{hd}}}} < 0,$ а на кривой 4 будет $\Delta S_{{\text{M}}}^{{{\text{hd}}}} > 0.$ Очевидно, что это можно рассматривать и как прямой МКЭ уменьшения магнитной энтропии $\Delta S_{{\text{M}}}^{{{\text{hd}}}} < 0$ (по отношению к ее значению при ${{H}_{i}} = 0$), и как обратный МКЭ увеличения магнитной энтропии $\Delta S_{{\text{M}}}^{{{\text{hd}}}} > 0$ (но по отношению к ее значению при $\mu {{_{Z}{{H}_{i}}} \mathord{\left/ {\vphantom {{_{Z}{{H}_{i}}} D}} \right. \kern-0em} D}$ = 1).

Таким образом, без точной конкретизации границ намагничивания разговор о прямом и обратном характере МКЭ утрачивает смысл.

Добавим, что, как видно из рис. 2, все аномалии на кривых зависимости $\Delta {{S}_{{\text{M}}}}$ от ${{H}_{f}},$ соответствующие увеличению магнитной энтропии при увеличении магнитного поля, возникают при конечных полях намагничивания, попадающих в интервал значений $D \leqslant {{\mu }_{Z}}{{H}_{f}} \leqslant 2D.$ Легко убедиться, что этот интервал полей является следствием пересечения энергетических уровней иона (2) в магнитном поле. В слабых магнитных полях ${{\mu }_{Z}}{{H}_{f}} \leqslant D$ энергетические уровни (2) выстраиваются по возрастанию энергии в следующей последовательности:

где уровень ${{E}_{1}}$ и значение $Z$-проекции спина ${{S}_{Z}} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$ отвечают основному состоянию. Однако в интервале полей $D \leqslant {{\mu }_{Z}}{{H}_{f}} \leqslant 2D$ эта последовательность сменяется на

когда ближайшим возбужденным уровнем над основным состоянием вместо уровня ${{E}_{2}}({{S}_{Z}} = {{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2})$ с Z-проекцией спина ${{S}_{Z}} = {{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}$ становится уровень ${{E}_{3}}({{S}_{Z}} = {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2})$ с ${{S}_{Z}} = {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}.$ Тогда при низких температурах тепловое возбуждение в первую очередь подмешивает к основному состоянию с ${{S}_{Z}} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$ возбужденное состояние с ${{S}_{Z}} = {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2},$ а не с ${{S}_{Z}} = {{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2},$ что приводит к аномальному температурному росту среднего значения $Z$-проекции спина $\left\langle {{{S}_{Z}}(T,H)} \right\rangle $ и, соответственно, намагниченности $m_{Z}^{{{\text{hd}}}}(T,H)$ = ${{\mu }_{Z}}\left\langle {{{S}_{Z}}(T,H)} \right\rangle .$ Дальнейшее увеличение поля ${{\mu }_{Z}}{{H}_{f}} \geqslant 2D$ приводит к смене местами уровней основного и ближайшего возбужденного состояния на ${{E}_{3}}({{S}_{Z}} = {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2})$ < ${{E}_{1}}({{S}_{Z}} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}),$ что восстанавливает нормальное температурное поведение намагниченности ${{\partial m_{Z}^{{{\text{hd}}}}} \mathord{\left/ {\vphantom {{\partial m_{Z}^{{{\text{hd}}}}} {\partial T}}} \right. \kern-0em} {\partial T}} < 0.$

Наконец укажем, что, если рассматривать случай анизотропии легкая плоскость с намагничиванием вдоль трудного направления и последующими значениями крамерсовых спинов $S = {5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2},{7 \mathord{\left/ {\vphantom {7 2}} \right. \kern-0em} 2},...,$ то эффект пересечения энергетических уровней в магнитном поле приведет к появлению дополнительных областей аномального температурного поведения намагниченности и аномалий в МКЭ по сравнению со случаем с $S = {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}.$ Так, например, для $S = {5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}$ в интервале более высоких магнитных полей $3D \leqslant {{\mu }_{Z}}{{H}_{f}} \leqslant 4D$ дополнительно возникает область температурной аномалии намагниченности, когда ближайшим возбужденным уровнем к уровню основного состояния ${{E}_{3}}({{S}_{Z}} = {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2})$ с ${{S}_{Z}} = {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}$ станет уровень ${{E}_{5}}({{S}_{Z}} = {5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2})$ с более высоким значением $Z$-проекции спина ${{S}_{Z}} = {5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}.$

3. В случае намагничивания легкоплоскостного парамагнетика в легком направлении вдоль оси OX собственные значения гамильтониана ${{H}_{{{\text{ed}}}}}(1)$ равны

Тогда намагниченность ${{m}_{X}}(T,H)$ в легком направлении (на один ион) становится равной

где

и температурная производная намагниченности равна

Анализ знаков производных ${{\partial m_{X}^{{{\text{ed}}}}(T,H)} \mathord{\left/ {\vphantom {{\partial m_{X}^{{{\text{ed}}}}(T,H)} {\partial T}}} \right. \kern-0em} {\partial T}}$ на плоскости безразмерных переменных $({{{{k}_{{\text{B}}}}T} \mathord{\left/ {\vphantom {{{{k}_{{\text{B}}}}T} D}} \right. \kern-0em} D})$ – $({{{{\mu }_{X}}H} \mathord{\left/ {\vphantom {{{{\mu }_{X}}H} D}} \right. \kern-0em} D})$ показывает, что эта производная всегда отрицательна, и поэтому изменение магнитной энтропии $\Delta S_{{\text{M}}}^{{{\text{ed}}}}(T,\Delta H = {{H}_{f}} - {{H}_{i}})$ при изотермическом намагничивании в легком направлении будет всегда отрицательным (прямой МКЭ).

Для примера на рис. 2 приведен результат расчета $\Delta S_{{\text{M}}}^{{{\text{ed}}}}(T,\Delta H = {{H}_{f}} - {{H}_{i}})$ как функция безразмерного конечного поля намагничивания ${{{{\mu }_{X}}{{H}_{f}}} \mathord{\left/ {\vphantom {{{{\mu }_{X}}{{H}_{f}}} D}} \right. \kern-0em} D}$ при выборе нулевого начального поля ${{{{\mu }_{X}}{{H}_{i}}} \mathord{\left/ {\vphantom {{{{\mu }_{X}}{{H}_{i}}} D}} \right. \kern-0em} D}$ = 0 и безразмерной температуры ${{{{k}_{{\text{B}}}}T} \mathord{\left/ {\vphantom {{{{k}_{{\text{B}}}}T} D}} \right. \kern-0em} D}$ = 0.5 (кривая 6). Положим для простоты ${{\mu }_{Z}} = {{\mu }_{X}},$ т.е. пренебрежем анизотропией факторов Ланде ${{\mu }_{{\text{B}}}}{{g}_{Z}} = {{\mu }_{{\text{B}}}}{{g}_{X}}$ и тем самым выберем одинаковую шкалу безразмерных полей намагничивания в обоих направлениях ${{{{\mu }_{Z}}H} \mathord{\left/ {\vphantom {{{{\mu }_{Z}}H} D}} \right. \kern-0em} D}$ = ${{{{\mu }_{X}}H} \mathord{\left/ {\vphantom {{{{\mu }_{X}}H} D}} \right. \kern-0em} D}.$ Тогда сравнение кривой 6 $\Delta S_{{\text{M}}}^{{{\text{ed}}}}(T,\Delta H = {{H}_{f}})$ и кривой 2 $\Delta S_{{\text{M}}}^{{{\text{hd}}}}(T,\Delta H = {{H}_{f}})$ показывает, что в области низких температур МКЭ в анизотропном одноосном парамагнетике при намагничивании в легком направлении намного больше, чем при намагничивании в трудном направлении.

4. Рассмотрение изменения магнитной энтропии $\Delta {{S}_{{\text{M}}}}$ в одноосном парамагнетике с крамерсовыми ионами (спин $S = {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}$) и одноионной анизотропией типа легкая плоскость показывает, что изотермическое намагничивание в легкой плоскости намного сильнее уменьшает магнитную энтропию, чем намагничивание при той же температуре, но в трудном направлении, поперек легкой плоскости. Вообще говоря, аналогичное явление, расчеты которого мы не приводим в настоящей статье, существует и в парамагнетике с одноионной анизотропией типа легкая ось, где изменение энтропии $\Delta {{S}_{{\text{M}}}}$ при намагничивании вдоль легкой оси оказывается на порядки сильнее, чем намагничивание поперек легкой оси.

Кроме того, обнаружено, что при достаточно низких температурах намагничивание легкоплоскостного парамагнетика в трудном направлении для определенных интервалов полей может приводить к обратному МКЭ – при увеличении поля магнитная энтропия начинает возрастать, а не падать. Подобное аномальное явление наблюдается и при поперечном намагничивании легкоплоскостного парамагнетика с некрамерсовыми спинами [11], и разница между этими случаями состоит в том, что для некрамерсовых спинов ($S = 1,2,..$) нижняя граница такого полевого интервала аномального поведения начинается с нулевого магнитного поля, а для крамерсовых спинов $\left( {S = {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2},{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2},...} \right)$ – с конечного поля. Например, если взять два легкоплоскостных парамагнетика с одинаковым параметром анизотропии второго порядка $D > 0,$ то в случае некрамерсовых спинов наинизший интервал таких магнитных полей равен $0 < H < {D \mathord{\left/ {\vphantom {D {{{\mu }_{Z}}}}} \right. \kern-0em} {{{\mu }_{Z}}}},$ а в случае крамерсовых ионов границы такого интервала будут ${D \mathord{\left/ {\vphantom {D {{{\mu }_{Z}}}}} \right. \kern-0em} {{{\mu }_{Z}}}} < H < {{2D} \mathord{\left/ {\vphantom {{2D} {{{\mu }_{Z}}}}} \right. \kern-0em} {{{\mu }_{Z}}}}.$ Разумеется, при низких температурах в этих же интервалах полей с аномальным изотермическим ростом магнитной энтропии поперечное адиабатическое намагничивание легкоплоскостных парамагнетиков будет приведено к аномальному уменьшению температуры парамагнетика.

Работа выполнена при частичной поддержке Проекта УрО РАН № 18-2-2-1 и гранта РФФИ № 18-02-00281.