Физика металлов и металловедение, 2019, T. 120, № 3, стр. 251-256

I

Магнитокалорические эффекты (МКЭ) в парамагнетиках ланжевеновского типа максимальны вблизи температуры абсолютного нуля, что дало возможность эффективно использовать эти соединения в процессах получения сверхнизких температур [1–4]. С физической точки зрения это связано с тем, что магнитная восприимчивость ${{\chi }^{L}}$ ланжевеновского парамагнетика расходится как ${1 \mathord{\left/ {\vphantom {1 T}} \right. \kern-0em} T} \to \infty $ при температуре $T \to 0,$ стремящийся к нулю. Соответственно этому МКЭ, связанный с изменением магнитной энтропии при изотермическом намагничивании и пропорциональный температурной производной ${{d{{\chi }^{L}}} \mathord{\left/ {\vphantom {{d{{\chi }^{L}}} {dT}}} \right. \kern-0em} {dT}},$ будет вести себя как ${1 \mathord{\left/ {\vphantom {1 {{{T}^{2}} \to - \infty }}} \right. \kern-0em} {{{T}^{2}} \to - \infty }}$ при $T \to 0.$

Интересно сравнить низкотемпературное поведение МКЭ ланжевеновского парамагнетика с МКЭ поляризационного ван-флековского парамагнетика, у которых температурная зависимость магнитной восприимчивости ${{\chi }^{{VV}}}$ очень слаба, поскольку основное состояние магнитных ионов ван-флековского парамагнетика является синглетным [5]. В работе [6] исследован МКЭ в модели одноосного ван-флековского парамагнетика для некрамеровских ионов с целочисленными спинами S = 1,2, …, находящимися в кристаллическом поле типа легкая плоскость, причем был обнаружен обратный МКЭ в низкотемпературной области при намагничивании в трудном направлении. Однако рассмотрнная в [6] модель ван-флековского парамагнетика применима только для гидратированных парамагнитных солей, где магнитные моменты d- или f-ионов разделены молекулами кристаллизационной воды и поэтому не связаны между собой обменным взаимодействием. В более общем случае между магнитными ионами существует обменная связь, однако основное синглетное состояние ван-флековского парамагнетика будет сохраняться до тех пор, пока отношение параметров обмена и одноионной анизотропии типа легкая плоскость не превысит порогового значения. Поэтому цель настоящей работы состоит в том, чтобы понять, как наличие обменного взаимодействия повлияет на МКЭ ван-флековского парамагнетика.

II

Рассмотрим сначала случай, когда внешнее магнитное поле H приложено в плоскости легкого намагничивания (H||OX) одноосного ван-флековского парамагнетика. Исходный гамильтониан имеет вид:

где $D > 0$ – параметр одноионной анизотропии типа легкая плоскость, ${{\mu }_{0}} = g{{\mu }_{{\text{B}}}}$ (${{\mu }_{{\text{B}}}}$ – магнетон Бора, $g$ – фактор Ланде) и обменное взаимодействие учтено в приближении ближайших соседей ($J > 0$ – ферромагнитный параметр обмена, $z$ – число ближайших магнитных соседей). Считаем, что $S = 1$ – целочисленный некрамерсов спин, так что в отсутствие обмена ($J = 0$) и внешнего поля ($H = 0$) каждый ион находится в синглетном основном состоянии.

В приближении молекулярного поля гамильтониан ${{H}_{{||}}}$ (1) преобразуется к сумме одноузельных спин-гамильтонианов:

где введены обозначения:

С помощью ${{H}_{{||}}}{{(n)}^{{MFA}}}$ (2) легко получить самосогласованное уравнение для термодинамического среднего значения X-проекции спина ${{\sigma }_{X}}$ (при $S = 1$):

Это уравнение позволяет найти соотношение параметров анизотропии $D$ и обмена $Jz,$ определяющее область существования синглетного состояния исследуемого магнетика при $T = 0.$

Для этого предположим, что в отсутствие внешнего поля H = 0 в магнетике существует спонтанный ферромагнетизм вдоль оси OX в плоскости легкого намагничивания с параметром порядка ${{\sigma }_{X}}(H = 0,T) \equiv {{\sigma }_{{{{X}_{0}}}}}(T).$ Тогда в пределе $T \to 0$ из уравнения (4) найдем

С другой стороны, линеаризуя правую часть (4) в пределе бесконечно малого параметра ${{\sigma }_{X}}(T) \to 0,$ можно получить линейное уравнение для определения температуры Кюри ${{T}_{{{{{\text{C}}}_{X}}}}},$ при которой возникает спонтанный ферромагнетизм вдоль оси OX. Эта температура Кюри ${{T}_{{{{{\text{C}}}_{X}}}}}$ равна

Тогда из (5) и (6) можно получить известный результат (см., например, [7]), что и ${{\sigma }_{{{{X}_{0}}}}}(T = 0)$ (5), и точка Кюри ${{T}_{{{{{\text{C}}}_{X}}}}}$ (6) одновременно исчезают, когда параметр обмена $J$ уменьшается до критического значения

Таким образом, при $T = 0$ спонтанный ферромагнетизм существует только при условии $2Jz > D,$ а при $2Jz < D$ возникает область ван-флековского парамагнетизма с синглетным основным состоянием магнитных ионов. Поэтому дальше будем исследовать изотермическое намагничивание ван-флековского парамагнетика с ограничением $2Jz < D$ на энергетические параметры взаимодействий.

Если к одноосному ван-флековскому парамагнетику приложить магнитное поле $H||OX$ в плоскости легкого намагничивания, то на каждом узле магнитной решетки индуцируется намагниченность ${{m}_{X}} = {{\mu }_{0}}{{\sigma }_{X}}.$ Для невысоких полей, в линейном приближении по полю H, можно выразить поляризационную намагниченность из формулы (4) через линейную магнитную восприимчивость $\chi _{X}^{{VV}}{\text{:}}$

Для низких температур ($D \gg {{k}_{{\text{B}}}}T$) из (8) следует, что низкотемпературная восприимчивость $\chi _{X}^{{VV}}$ фактически не зависит от температуры T, так как температурные поправки к значению восприимчивости $\chi _{X}^{{VV}}(T = 0)$ при нулевой температуре

будут экспоненциально малы

Однако важно отметить, что абсолютная величина $\chi _{X}^{{VV}}(T = 0)$ существенно зависит от величины разности $D - 2Jz$, отражающей степень близости ван-флековского парамагнитного состояния к границе перехода в феромагнитное состояние и что на границе перехода (по соотношению параметров взаимодействия) восприимчивость ${\chi }_{X}^{{VV}}(T = 0)$ расходится

Для области высоких температур ($D \ll {{k}_{{\text{B}}}}T$) восприимчивость ван-флековского парамагнетика носит кюри-вейссовский характер:

причем положительная парамагнитная точка Кюри ${{\theta }_{{pX}}}$ включает вклады как от ферромагнитного обмена, так и от кристаллического поля.

Выражение ${{m}_{X}}$ (8) позволяет найти температурную производную ${{\partial {{m}_{X}}(T,H)} \mathord{\left/ {\vphantom {{\partial {{m}_{X}}(T,H)} {\partial T}}} \right. \kern-0em} {\partial T}}$ и с ее помощью найти МКЭ, описывающий изменение магнитной энтропии ван-флековского парамагнетика $\Delta S_{M}^{{VV}}(T,H||OX)$ (на один магнитный атом) при изотермическом намагничивании от нулевого начального поля ${{H}_{i}} = 0$ до конечного поля ${{H}_{f}}$ [1–3]

Для низких температурD ⪢ k_BT выражение (13) преобразуется к виду

а при высоких температурах D ⪡ k_BT приближенно равно

Таким образом, в противоположность ланжевеновскому парамагнетику, в котором $\Delta S_{M}^{L}(T,{{H}_{f}})$ расходится при $T \to 0,$ в ван-флековском парамагнетике изменение энтропии $\Delta S_{M}^{{VV}}(T,\left. {{{H}_{f}}} \right\|OX)$ стремится к нулю при $T \to 0.$ Поэтому заметной величины изменения энтропии $\Delta S_{M}^{{VV}}(T,\left. {{{H}_{f}}} \right\|OX)$ в низкотемпературной области можно ожидать лишь в ван-флековских парамагнетиках, близких к границе перехода в спонтанное ферромагнитное состояние при $D \to 2Jz + {{0}^{ + }}.$

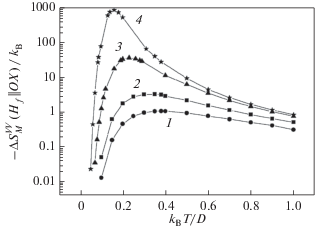
На рис. 1 представлено поведение изменения энтропии $\Delta S_{M}^{{VV}}(T,\left. {{{H}_{f}}} \right\|OX)$ (13) как функции безразмерной температуры ${{{{k}_{{\text{B}}}}T} \mathord{\left/ {\vphantom {{{{k}_{{\text{B}}}}T} D}} \right. \kern-0em} D}$ при изотермическом намагничивании от начального нулевого поля до конечного H_f, безразмерная величина которого задана условием ${{{{\mu }_{0}}{{H}_{f}}} \mathord{\left/ {\vphantom {{{{\mu }_{0}}{{H}_{f}}} D}} \right. \kern-0em} D} = 1.$ При этом исследовано 4 варианта отношений параметров обмена $Jz$ и анизотропии $D$, а именно: 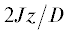= 0; 0.5; 0.9 и 0.99. Видно, что величина $\Delta S_{M}^{{VV}}(T,\left. {{{H}_{f}}} \right\|OX) < 0$ – отрицательна (нормальный МКЭ) и что максимальная абсолютная величина эффекта резко возрастает при уменьшении разности $D - 2Jz$, сдвигаясь в сторону более низких температур. Этот результат согласуется с расходимостью изменения энтропии $\Delta S_{M}^{{VV}}(T,\left. {{{H}_{f}}} \right\|OX) \to - \infty $ при $D \to 2Jz,$ т.е. с приближением состояния ван-флековского парамагнетика к границе перехода в ферромагнитное состояние по мере изменения энергетических параметров системы.

III

Теперь исследуем изменение магнитной энтропии ван-флековского парамагнетика $\Delta S_{M}^{{VV}}$ $(T,\left. {{{H}_{f}}} \right\|OZ)$ в случае изотермического намагничивания в трудном направлении вдоль оси OZ, перпендикулярной плоскости легкого намагничивания OXY. Учитывая наличие ферромагнитного обмена $J > 0$ и появление в магнитном поле $\left. H \right\|OZ$ индуцируемых магнитных моментов на узлах ${{m}_{Z}}(n),$ в приближении молекулярного поля эту ситуацию можно описать одноузельным гамильтонианом $H_{ \bot }^{{MFA}}(n){\text{:}}$

где обозначено

Для спина $S = 1$ термодинамическое среднее значение $Z$-проекции спина ${{\sigma }_{Z}} \equiv \left\langle {{{S}_{Z}}(n)} \right\rangle $ определяется уравнением

Тогда в линейном приближении по магнитному полю $H$ намагниченность узла ${{m}_{Z}}(n)$ выражается из (18) через восприимчивость $\chi _{Z}^{{VV}}(T)$ [7] как

Теперь, в отличие от случая намагничивания в легком направлении с $\chi _{X}^{{VV}}$ (9) и (10), низкотемпературная магнитная восприимчивость ($D \gg {{k}_{{\text{B}}}}T$) стремится к нулю:

Высокотемпературная магнитная восприимчивость ($D \ll {{k}_{{\text{B}}}}T$) ван-флековского парамагнетика вдоль трудного направления намагничивания, как и в случае намагничивания в легком направлении, имеет кюри-вейссовский вид. Однако парамагнитная точка Кюри ${{\Theta }_{{pZ}}}$ теперь будет отрицательна:

Используя (19), находим, что температурная производная ${{\partial {{m}_{Z}}} \mathord{\left/ {\vphantom {{\partial {{m}_{Z}}} {\partial T}}} \right. \kern-0em} {\partial T}}$ равна

Тогда изменение магнитной энтропии при намагничивании в трудном направлении ($H||OZ$) от ${{H}_{i}} = 0$ до ${{H}_{f}}$ имеет вид

В области низких температур ($D \gg {{k}_{{\text{B}}}}T$) это изменение положительно

а при высоких температурах ($D \ll {{k}_{{\text{B}}}}T$) будет отрицательным

Из (23) следует, что смена знака изменения магнитной энтропии определяется условием

Тогда из (26) получаем, что при температурах ${{{{k}_{{\text{B}}}}T} \mathord{\left/ {\vphantom {{{{k}_{{\text{B}}}}T} {D < 0.683}}} \right. \kern-0em} {D < 0.683}}$ будет наблюдаться аномальный (обратный) МКЭ – рост магнитной энтропии при изотермическом намагничивании $\Delta S_{M}^{{VV}}$ $(T,\left. {{{H}_{f}}} \right\|OZ),$ а при ${{{{k}_{{\text{B}}}}T} \mathord{\left/ {\vphantom {{{{k}_{{\text{B}}}}T} {D > 0.683}}} \right. \kern-0em} {D > 0.683}}$ будет реализовываться нормальный (прямой) МКЭ с $\Delta S_{M}^{{VV}}(T,\left. {{{H}_{f}}} \right\|OZ) < 0.$

На рис. 2 приведены расчеты температурной зависимости величины изменения энтропии $\Delta S_{M}^{{VV}}(T,\left. {{{H}_{f}}} \right\|OZ)$ при изотермическом намагничивании в трудном направлении от нулевого начального поля ${{H}_{i}} = 0$ до конечного поля ${{H}_{f}}.$ Величина конечного поля ${{H}_{f}}$ в безразмерных единицах, как и в случае намагничивания в легком направлении, выбрана как ${{{{\mu }_{0}}{{H}_{f}}} \mathord{\left/ {\vphantom {{{{\mu }_{0}}{{H}_{f}}} D}} \right. \kern-0em} D} = 1.$ Результаты расчетов представлены для двух крайних вариантов отношения параметров обмена и анизотропии: для ${{2Jz} \mathord{\left/ {\vphantom {{2Jz} D}} \right. \kern-0em} D} = 0$ (кривая 1) – случая отсутствия ферромагнитного обмена и для ${{2Jz} \mathord{\left/ {\vphantom {{2Jz} D}} \right. \kern-0em} D} = 0.99$ (кривая 2) – случая близости отношения параметров к критическому значению, отвечающему границе перехода в ферромагитное состояние.

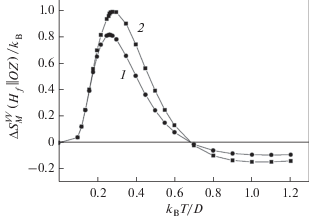
Видно, что различие в величине $\Delta S_{M}^{{VV}}$ $(T,\left. {{{H}_{f}}} \right\|OZ)$ между этими крайними вариантами отношения ${{2Jz} \mathord{\left/ {\vphantom {{2Jz} D}} \right. \kern-0em} D}$ незначительно. Аналогичные кривые для $\Delta S_{M}^{{VV}}(T,\left. {{{H}_{f}}} \right\|OZ)$ при выборе каких-либо промежуточных отношений параметров ${{2Jz} \mathord{\left/ {\vphantom {{2Jz} D}} \right. \kern-0em} D}$ из интервала ${{0 < 2Jz} \mathord{\left/ {\vphantom {{0 < 2Jz} {D < 1}}} \right. \kern-0em} {D < 1}}$ лежат между этими двумя кривыми, и поэтому они не приведены на рисунке. Кроме того, видно, что в низкотемпературной области при ${{{{k}_{{\text{B}}}}T} \mathord{\left/ {\vphantom {{{{k}_{{\text{B}}}}T} {D < 0.683}}} \right. \kern-0em} {D < 0.683}}$ наблюдается аномальный МКЭ – намагничивание увеличивает энтропию $\left( {\Delta S_{M}^{{VV}}(T,\left. {{{H}_{f}}} \right\|OZ) > 0} \right),$ тогда как при ${{{{k}_{{\text{B}}}}T} \mathord{\left/ {\vphantom {{{{k}_{{\text{B}}}}T} {D > 0.683}}} \right. \kern-0em} {D > 0.683}}$ при намагничивании энтропия уменьшается.

Наконец, если сравнить теперь абсолютные значения величин $\left| {\Delta S_{M}^{{VV}}(T)} \right|$ в точках экстремумов на кривых температурных зависимостей для намагничивания в легком (рис. 1) и трудном (рис. 2) направлениях, то можно заметить, что абсолютные величины эффектов в максимумах для этих двух вариантов намагничивания сопоставимы только при очень слабом обмене ${{2Jz} \mathord{\left/ {\vphantom {{2Jz} {D \ll 1}}} \right. \kern-0em} {D \ll 1}}.$ Однако в случае близости ван-флековского парамагнитного состояния к границе перехода в ферромагнитное состояние (т.е. при ${{2Jz} \mathord{\left/ {\vphantom {{2Jz} {D \cong 1}}} \right. \kern-0em} {D \cong 1}}$) абсолютная величина нормального МКЭ при намагничивании в легкой плоскости будет на 2–3 порядка больше, чем абсолютная величина аномального МКЭ при изотермическом намагничивании в трудном направлении.

IV

Мы показали, что в одноосном ван-флековском парамагнетике с некрамерсовыми спинами $S = 1$ и одноионной анизотропией типа легкая плоскость МКЭ (изменение магнитной энтропии при изотермическом намагничивании $\Delta S_{M}^{{VV}}(T,H)$) наиболее интересен в низкотемпературной области ${{k}_{{\text{B}}}}T < D,$ в которой характер и величина эффекта радикально отличаются при намагничивании в легком и трудном направлениях. При намагничивании в легком направлении (в легкой плоскости вдоль оси OX) МКЭ имеет нормальный характер, так как $\Delta S_{M}^{{VV}}(T,\left. {{{H}_{f}}} \right\|OX) < 0$ и магнитная энтропия уменьшается при намагничивании. При этом абсолютная величина эффекта $\left| {\Delta S_{M}^{{VV}}(T)} \right|$ при заданной температуре $T$ сильно зависит от соотношения между энергетическими параметрами анизотропии $D$ и ферромагнитного обмена $Jz$, достигая аномально больших величин при увеличении $Jz$ до пороговых значений ${{(Jz)}_{{{\text{crit}}}}} = D,$ отвечающих границе перехода в ферромагнитное состояние.

При намагничивании в трудном направлении, перпендикулярно плоскости легкого намагничивания ($\left. H \right\|OZ$), МКЭ в низкотемпературной области ${{k}_{{\text{B}}}}T < 0.683D$ носит аномальный характер, так как $\Delta S_{M}^{{VV}}(T,\left. {{{H}_{f}}} \right\|OZ) > 0$ и магнитная энтропия растет при намагничивании. Однако при этом изменение соотношения между параметрами $Jz$ и $D$ мало влияет на величину эффектов $\Delta S_{M}^{{VV}}(T,\left. {{{H}_{f}}} \right\|OZ),$ температурное поведение которых практически зависит только от отношения ${{{{k}_{{\text{B}}}}T} \mathord{\left/ {\vphantom {{{{k}_{{\text{B}}}}T} D}} \right. \kern-0em} D}.$

Наконец, в области температур ${{k}_{{\text{B}}}}T > D$ намагничивание и в легком, и в трудном направлениях дают нормальные МКЭ, хотя даже в пределе очень высоких температур ${{k}_{{\text{B}}}}T \gg D$ намагничивание в легком направлении дает несколько большие значения эффекта $\left| {\Delta S_{M}^{{VV}}(T,\left. {{{H}_{f}}} \right\|OX)} \right|$ > > $\left| {\Delta S_{M}^{{VV}}(T,\left. {{{H}_{f}}} \right\|OZ)} \right|.$

Работа выполнена в рамках темы государственного задания № 0389-2015-0024 и частично поддержана Комплексной программой фундаментальных научных исследований УрО РАН на 2018-2020г.г. (проект № 18-2-2-1).