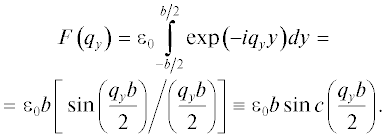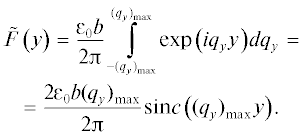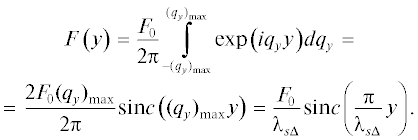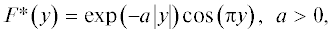Физика металлов и металловедение, 2019, T. 120, № 5, стр. 457-463

ВВЕДЕНИЕ

Двойники превращения возникают непосредственно в ходе роста мартенситных кристаллов, составляя их тонкую структуру в виде чередующихся пластинчатых компонент. Они наблюдаются достаточно часто при мартенситных превращениях (МП), как в случае ярко выраженных признаков фазовых переходов I рода (например, в сплавах железа [1]), так и при МП, близких к фазовым переходам II рода (например, в ряде сплавов цветных металлов [2]) Типичное различие компонент двойниковой структуры (ДС) заключается в различии ориентаций главных осей деформации, как правило, ортогональных друг другу в исходной фазе. Установление физических механизмов формирования вариантов двойников превращения при мартенситных реакциях представляет одно из интереснейших направлений исследования в теории МП. Напомним, что при формальном кристаллогеометрическом подходе [3], использующем постулат о габитусной плоскости как макроскопически инвариантом объекте, двойникование в качестве неоднородного сдвига способствует выполнению постулата. При этом конкретной ориентации габитуса сопоставляются вполне определенные доли двойниковой δ и основной (1–δ) составляющих ДС. Однако данные [4] показали изменение величины δ в пределах одного и того же тонкопластинчатого мартенситного кристалла с габитусами типа {3 10 15}, а в [5] для некоторых кристаллов с аналогичными габитусами двойники превращения не фиксировались.

При сравнительно невысоких (дозвуковых) скоростях роста мартенситных кристаллов в качестве механизма роста допустимо использование дислокационных представлений при трактовках ДС (см., например, [6]). При высоких же скоростях роста кристаллов, обладающих ДС, естественно опираться на динамические (волновые) трактовки, использующие концепцию управляющего волнового процесса (УВП). В предыдущих работах было показано, что концепция УВП позволяет описать не только идеальную (строго регулярную) ДС [7, 8], но и, базируясь на модели формирования регулярной ДС, ставить и решать задачу интерпретации реальных неоднородных вариантов ДС, учитывая действие детерминированных и стохастических факторов, обеспечивающих отклонения наблюдаемых ДС от регулярных [9–13]. Одним из принципиальных итогов такого анализа является вывод о фрагментации ДС, причем каждый фрагмент порождается единственной спонтанно возникшей возбужденной ячейкой.

Цель данной работы – обсудить на примере образования ДС важную роль таких факторов, как дифракционная расходимость волновых пучков, входящих в состав УВП, и конфигурация начального возбужденного состояния.

ОСНОВНЫЕ ПРЕДСТАВЛЕНИЯ О ВОЗНИКНОВЕНИИ УВП

Напомним, что в динамической модели роста мартенситных кристаллов за описание габитусных плоскостей отвечают пары относительно длинноволновых квазипродольных смещений в составе УВП ($\ell $-волны), тогда как ориентации плоскостей {110} контакта двойников превращения задают пары относительно коротковолновых продольных смещений (s-волны), распространяющихся вдоль ортогональных осей 〈100〉 и 〈010〉 исходной фазы (направления ∆ в первой зоне Бриллюэна) со скоростями ${{v}_{{s\Delta }}}$.

При простейшей идеализации двухволнового управления ростом мартенситного кристалла рассматривается модель двух плоских продольных волн, распространяющихся в ортогональных направлениях (обозначим их х и у), инициирующих в области наложения пороговую деформацию сжатия-растяжения [14]. При этом размеры фронтов неограниченны, а поперечные размеры b_y, b_x области наложения, которая имеет форму вытянутого прямоугольного параллелепипеда, и внутри которой предполагается потеря устойчивости исходной фазы (аустенита), удовлетворяют неравенствам

Ясно, что при однородной деформации на фронтах каждой из плоских волн имеется бесконечное число аналогичных параллелепипедов, и выбор какого-либо из них должен быть связан с нарушением подобной однородности. Например, такие нарушения могут иметь вид “всплесков” амплитуды на фронтах волн с центральными максимумами и чередующимися убывающими, по мере удаления от центрального максимума, побочными экстремумами минимумов и максимумов деформаций. В качестве предельного варианта “всплеска” выступает одиночный локализованный в пространстве импульс, задающий ширину фронта волнового пучка ~λ/2.

Очевидно, что в отсутствие внешних источников плоских волн в состав УВП могут входить только волновые пучки.

Само формирование УВП является следствием возникновения начального “всплеска” – начального возбужденного (колебательного) состояния (НВС). Причем пары $\ell $-волн в форме плоских волновых пучков имеют волновые векторы k_𝓵1 и k_𝓵2 c направлениями, близкими к ориентациям собственных векторов ξ₁ и ξ₂ тензора деформации упругого поля дислокационного центра зарождения (ДЦЗ), соответствующих главным значениям растяжения ε₁ и сжатия ε₂ (деформация ε₃ вдоль третьего вектора ξ₃ равна нулю, либо мала по сравнению с |ε_{1, 2}|). Конфигурация НВС близка к форме прямоугольного вытянутого параллелепипеда, построенного на векторах ξ_i, поскольку считается, что переохлажденный ниже точки равновесия фаз аустенит теряет устойчивость в области НВС, и при этом выделяется энергия (в основном в виде колебаний), достаточная для преодоления межфазного барьера при распространении волн, инициированных колебательным процессом в НВС. Если возникновение НВС, инициирующего 𝓵-волны (НВС_𝓵), сопровождается более или менее синхронизованным возникновением области локализации внутри НВС_𝓵 и возбужденной области НВС_s в форме тонкого колеблющегося параллелепипеда, инициирующего возбуждение пар s-волн, то результирующий УВП способен корректно описать формирование тонкоплстинчатых двойникованных кристаллов (или двойникованных мидрибов линзовидных кристаллов). Причем основная компонента ДС физически выделена, так как именно эта компонента инициируется, главным образом, действием s-волн, тогда как двойниковая возникает в качестве прослойки между ближайшими основными компонентами (в силу когерентной связи контактирующих областей решетки), т.е. процесс ее формирования имеет подчиненный характер.

Наиболее интересным в описанной картине является процесс индуцированного воспроизводства возбужденной s-ячейки (возникшей первоначально спонтанно) в ходе распространения УВП. Возможность такого воспроизводства предполагает, что ближайшая к исходной s-ячейка возникает после прохождения за одно и тоже время двух катетов треугольника в направлениях [1$\bar {1}$0] и [110] суперпозицией s-волн, а гипотенузы треугольника со скоростью, равной $v_{{{\text{2}}\ell }}^{'}$ – проекции на плоскость (001) скорости 𝓵-волны v_2𝓵, несущей деформацию сжатия (рис. 1).

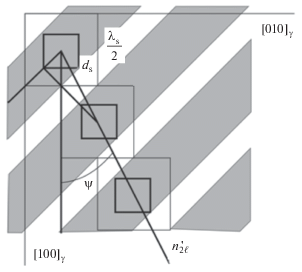
В предположении, что оба катета проходятся со скоростью $\sqrt 2 {{v}_{{s\Delta }}}$, получаем условие

где ψ – острый угол между $v_{{{\text{2}}\ell }}^{'}$ и ${{v}_{{s{\Delta }}}}$||〈001〉_γ.

СПЕКТР ПРОСТРАНСТВЕННЫХ ГАРМОНИК, СОПОСТАВЛЯЕМЫХ ПЛОСКОМУ ВОЛНОВОМУ ПУЧКУ

Необходимость учета уширения волновых пучков была отмечена в [13] в связи с обсуждением сценария изменения длин волн λ_s коротковолновых смещений в составе УВП. Рассмотрим вначале простейший двумерный вариант.

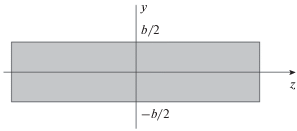
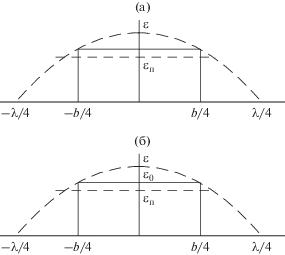
Пусть волновой пучок, описывающий поле продольных деформаций ε (и смещений), распространяется вдоль направления x, имеет в начальный момент времени плоский однородный фронт (во всех точках деформация ε₀ = const) с шириной b (от –b/2 до +b/2) в направлении y, а в направлении z гораздо больший размер, как показано на рис. 2.

Такое упрощенное описание фронта пучка можно ввести, полагая, что величина ε₀ соответствует деформации, превышающей некоторое пороговое значение ε_п (0 < ε_п < ε₀), и заменяя неоднородную деформацию на фронте вида $\varepsilon = {{\varepsilon }_{{\max }}}\cos \left( {\frac{{\pi y}}{{2b}}} \right)$ на однородную, т.е. заменяя часть косинусоидального импульса на прямоугольный. На рис. 3 такая замена иллюстрируется для полуволнового импульса.

Фурье-образ F(q_y) функции

дается выражением:

Уместно подчеркнуть, что величины ${{q}_{y}}$ являются проекциями на ось y волновых векторов q, имеющих и проекции на направление х распространения плоского пучка. Действительно, для точек фронта волны, несущей возмущения среды колебательного типа, характерна синфазность возмущений в произвольный момент времени. Это соответствует условию изочастотности спектра пространственных гармоник с векторами q, что возможно лишь для волновых векторов, не принадлежащих поверхности фронта.

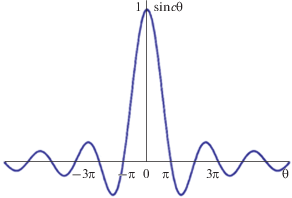
График функции $\sin c{\theta }$ приведен на рис. 4.

Обычно за полуширину $\Delta {{q}_{y}}$ спектра гармоник принимают величину$\quad{{q}_{y}},$ при которой впервые обращается в нуль функция $\sin c\left( {{{{{q}_{y}}b} \mathord{\left/ {\vphantom {{{{q}_{y}}b} 2}} \right. \kern-0em} 2}} \right),$ тогда

Симметричный дополнительный вклад в спектр задается равенством ${{{{q}_{y}}b} \mathord{\left/ {\vphantom {{{{q}_{y}}b} 2}} \right. \kern-0em} 2} = - {\pi }{\text{.}}$

В простейшем варианте рост кристалла мартенсита управляется парой налагающихся волновых пучков с близкими значениями ширин фронтов и длин волн, но распространяющихся в ортогональных направлениях (на рис. 1 для s-пучков имеет место точное равенство). Причем, ограничения ширин фронтов неравенствами (1) диктуются фазировкой деформационных процессов, так что ширина фронта каждого из пучков задается пучком-партнером по паре.

Тогда из (1) и (5) следует

Качественно, по порядку величины, расходимости узких волновых пучков в ближней волновой зоне можно задать отношениями

При близких значениях длин волн ${{{{{\lambda }}_{x}}} \mathord{\left/ {\vphantom {{{{{\lambda }}_{x}}} {{{{\lambda }}_{y}}\sim 1}}} \right. \kern-0em} {{{{\lambda }}_{y}}\sim 1}},$ tg φ_x ≈ tgφ_y ≥ 2, и, следовательно, ${{{\varphi }}_{{x\quad}}} \approx {{{\varphi }}_{{y\quad}}} \geqslant 63.4^\circ .$ Заметим, что полному уширению пучка соответствует удвоение угла ${\varphi }{\text{.}}$

Существенная расходимость (дифракционного типа) характерна лишь для узких волновых пучков и приводит к быстрому уширению и цилиндрическому искривлению уединенных фронтов. Однако из физической постановки задачи об управлении ростом кристалла мартенсита следует, что уединенные пучки без энергетической поддержки (за счет выделения энергии в области наложения пучков) будут быстро затухать. Следовательно, имеет смысл рассматривать только области непрерывного наложения пучков в ближней волновой зоне, где обеспечивается энергетическая поддержка процесса. Вполне достаточным является учет в спектре (3) фурье-компонент до ${{{\varphi }}_{{x\quad}}} \approx {{{\varphi }}_{{y\quad}}} \approx 45^\circ .$ Действительно, при формировании ДС основную роль играют пары гармоник с квазиимпульсами вдоль ортогональных осей симметрии 4-го порядка (направления 〈100〉). Отклонения q_x и q_y от этих осей в плоскостях симметрии {001} означают переход к гармоникам, распространяющимся с бóльшими скоростями (при факторе упругой анизотропии А > 1). Причем максимальных значений скорость достигает вдоль 〈110〉 направлений (Σ – направления в первой зоне Бриллюэна, составляющие углы $ \pm 45^\circ $ с ближайшими направлениями $\Delta $). Ясно, что распространение потоков упругой энергии преимущественно вдоль осей Σ способствовало бы образованию основных компонент ДС, так как эти компоненты растут в тех же направлениях со скоростями $\sqrt {2\quad} $${{v}_{{s{\Delta }}}}$. Данному варианту на рис. 5 приближенно соответствует сечение изочастотной поверхности обратных скоростей (поверхность медленностей или рефракции) близкое по форме к квадратному (отличие в области вершин “квадрата”, где прямоугольные сочленения сторон заменяют овалы).

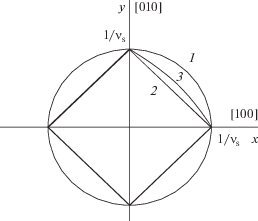
Направления групповых скоростей упругих волн, как известно [15, 16], ортогональны поверхности рефракции, поэтому при указанной форме поверхности рефракции отклонения волновых нормалей от направлений [100] и [010] сопровождаются переходом к групповым скоростям, коллинеарным направлениям [110], либо [1$\bar {1}$0]. Такое “каналирование” упругой энергии является оптимальным с позиций волнового механизма инициации роста основной компоненты ДС. Уместно напомнить, что подобное “каналирование”, обусловленное особенностями анизотропии упругой среды, отражают и термином “фононная фокусировка” [16].

Ограничение фурье-компонентами, ассоциированными с угловым интервалом $0 \leqslant {{{\varphi }}_{\quad}} \leqslant 45^\circ ,$ соответствует учету больших значений $F\left( {{{q}_{y}}} \right).$ Ограничиваясь оптимальным вариантом, в области волновых векторов, где еще можно пренебречь дисперсией, и учитывая изочастотность гармоник, имеем

Тогда максимальное отклонение ${{q}_{y}}$ – компоненты в совокупности векторов q

Заметим, что использовать ${{({{q}_{y}})}_{{{\text{max}}}}}$ как эквивалент $\Delta {{q}_{y}}$ в формулах (7) для оценки расходимости не следует, так как оценка (7) неявно предполагает равенство проекций волновых векторов всех гармоник на направление $\Delta ,$ что для рассматриваемого спектра векторов q изочастотных гармоник заведомо не выполнимо.

Таким образом, при ${{({{q}_{y}})}_{{{\text{max}}}}} = {{\pi } \mathord{\left/ {\vphantom {{\pi } {{{{\lambda }}_{{s\Delta }}}}}} \right. \kern-0em} {{{{\lambda }}_{{s\Delta }}}}},$ $b = {{{{{\lambda }}_{{s\Delta }}}} \mathord{\left/ {\vphantom {{{{{\lambda }}_{{s\Delta }}}} 4}} \right. \kern-0em} 4}$ значение $\quad{\theta } = {{{{q}_{y}}b} \mathord{\left/ {\vphantom {{{{q}_{y}}b} 2}} \right. \kern-0em} 2} = {{\pi } \mathord{\left/ {\vphantom {{\pi } 8}} \right. \kern-0em} 8},$ sincθ ≈ 0.9745 и $F\left( {{{q}_{y}}} \right)$ принадлежит интервалу

вблизи центрального максимума ${{{\varepsilon }}_{0}}b$ функции ${{{\varepsilon }}_{0}}b{\;}\sin c\left( {{{{{q}_{y}}b} \mathord{\left/ {\vphantom {{{{q}_{y}}b} 2}} \right. \kern-0em} 2}} \right).$

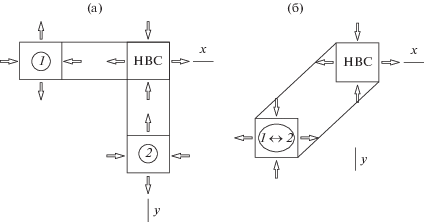
Если полагать [14], что волновые пучки имеют не только узкие фронты (один из поперечных размеров фронта порядка половины длины волны), но и существуют в виде узких “полуволновых” импульсов с размерами вдоль направления движения $ \leqslant {{\lambda } \mathord{\left/ {\vphantom {{\lambda } 2}} \right. \kern-0em} 2},$ то, в отсутствие поперечного дифракционного уширения, пучки, возбуждаемые НВС, не могли бы налагаться. Схематично это показано на рис. 6а, где бегущие в ортогональных направлениях отдельные пучки 1 и 2, не налагаясь, будут быстро затухать, поскольку в отдельном пучке не будет сохраняться (как по амплитудам, так и по фазам) пороговая деформация типа “растяжение–сжатие”, которая должна наследоваться от состояния НВС, и, значит, не будет выделяться энергия для поддержки УВП. В частности, фазировка смещений может быть противоположной фазировке в области НВС, как для контраста показано на рис. 6а. Напротив, при существенном дифракционном уширении пучки образуют область наложения с сохранением типа пороговой деформации, наследуемой УВП от состояния НВС. Рис. 6б иллюстрирует вариант ${{{\varphi }}_{x}} = {{{\varphi }}_{y}} = 45^\circ $ для плоских фронтов уширяющихся пучков. Области наложения пучков соответствует сечение пластинчатой области между двумя параллельными линиями (изображение относится к тому же квадранту, что и на рис. 1.)

ОБРАТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ С УЧЕТОМ АКТУАЛЬНОГО ИНТЕРВАЛА ВОЛНОВЫХ ВЕКТОРОВ ПРОСТРАНСТВЕННЫХ ГАРМОНИК

Близость амплитуд актуальных компонент волновых векторов ${{q}_{y}}$ (10) позволяет ставить задачу определения вклада$\quad\tilde {F}\left( у \right)$ актуальных гармоник в функцию 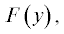задавая амплитудный спектр гармоник в виде прямоугольного импульса:

Тогда находим

В частности, из (12) при $b = {{{{{\lambda }}_{{s\Delta }}}} \mathord{\left/ {\vphantom {{{{{\lambda }}_{{s\Delta }}}} 4}} \right. \kern-0em} 4},$ (q_y)_max = = π/λ_sΔ следует, что максимальное значение функции $\tilde {F}\left( y \right)$ в 4 раза меньше значения исходного прямоугольного импульса ${{{\varepsilon }}_{{0\quad}}}$ в (3) (при этом полуширина y = ${{{\lambda }}_{{s\Delta }}}$ (из условия ${{\pi y} \mathord{\left/ {\vphantom {{\pi y} {{{{\lambda }}_{{s\Delta }}}}}} \right. \kern-0em} {{{{\lambda }}_{{s\Delta }}}}} = \pi $) в 4 раза больше исходного значения $b = {{{{{\lambda }}_{{s\Delta }}}} \mathord{\left/ {\vphantom {{{{{\lambda }}_{{s\Delta }}}} 4}} \right. \kern-0em} 4}$).

Таким образом, проведенная оценка показывает, что представления о локализации НВС в координатном пространстве и необходимости поддержания некоторого надпорогового уровня деформаций ${{{\varepsilon }}_{{0\quad}}}$ на стадии роста за счет вклада актуальных гармоник в области наложения дифрагирующих пучков требуют не менее четырехкратного усиления амплитуд гармоник.

Выявление спектра актуальных гармоник позволяет поставить задачу о форме начального “всплеска” в решетке (ассоциированного с понятием НВС), как функции формы локализованного распределения амплитуд только актуальных гармоник в пространстве волновых векторов.

Для прямоугольного импульса $F\left( {{{q}_{y}}} \right),$ согласно (11), (12), находим

Если сопоставить максимальному значению “всплеска” при у = 0 значение ${{{\varepsilon }}_{{{\text{max}}}}},$ то амплитуды гармоник ${{F}_{0}} = {{{\varepsilon }}_{{{\text{max}}}}}{{{\lambda }}_{{s{\Delta }}}}.$

Поскольку актуальные гармоники являются естественным базисом реального физического носителя пороговой деформации в волновом режиме, именно распределение $F\left( {{{q}_{y}}} \right)$ уместно брать за основу. Представляют интерес варианты отклонения $F\left( {{{q}_{y}}} \right)$ от ${\text{rect}}\left( {\quad{{q}_{y}}} \right).$ Два простых примера такого отклонения приведены на рис. 7.

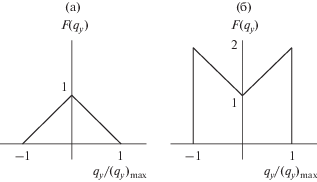
Нетрудно убедиться, что треугольной функции (случай рис. 7а)

соответствует

Поскольку М-образная фунция F_M (q_y) (случай рис. 7б) дается выражением

ее координатное представление

Очевидно, что варианту эффективного перекрытия волновых пучков для реализации пороговой деформации соответствует вариант на рис. 7б.

Прежде всего, подчеркнем, что установление актуального спектра гармоник – реального физического спектра пороговой деформации, позволяет отдать предпочтение локализации фурье-образа начального “всплеска” в пространстве волновых чисел по сравнению с другим предельным случаем – жесткой пространственной локализации “всплеска”. “Паритет” между пространственной и импульсной формами “всплеска” достигается при гауссовских формах распределения амплитуд гармоник и пространственного “всплеска”.

Отдельно отметим, что физически приемлемой является форма “всплеска” в виде затухающей в пространстве косинусоиды

где y = 0 cоответствует центральной точке “всплеска”. Характерно, что форме (19) соответствует фурье-образ, центральная область которого ассоциируется с актуальным спектром гармоник и имеет сходство с М-образной кривой [17].

Уместно напомнить, что обсуждавшийся в [13] сценарий изменения длины волны λ_s без учета дифракционного уширения пучков приводил к быстрому снижению толщин основных и дополнительных компонент ДС и, как следствие, к малым размерам фрагментов ДС. Учет же дифракционного уширения $b \to \tilde {b}$ позволяет замедлить сокращение фрагментов ДС и даже, в принципе, допускает их стабилизацию.

Старт МП с предельно узкого пространственного всплеска шириной b < λ/2, в принципе, допустим, но при инициировании роста кристалла мартенсита с участием актуального спектра гармоник требует существенного усиления волн, что вполне возможно в неравновесных условиях. Данный вывод в равной мере касается как s-, так и $\ell $-волн. По-видимому, более оптимальным является старт с менее локализованных в пространстве НВС. Отметим, наконец, что, при известных пространственной форме НВС и фононных дисперсионных кривых, дифракционное уширение может быть рассчитано, и, следовательно, относится к детерминированным факторам, однако форма НВС при спонтанном формировании мартенсита является стохастическим факторам.

ЗАКЛЮЧЕНИЕ

Учет дифракционного уширения узких волновых пучков играет важную роль как при создании пространственных областей, где выполняются условия инициации МП, так и в качестве фактора, противостоящего процессам сокращения размеров фрагментов ДС.

Проведенный анализ позволяет продвинуться в понимании еще одного стохастического фактора, которым является начальная форма “всплеска”, обеспечивающего эффективное перекрытие волновых пучков, необходимое для начала роста мартенситного кристалла. Очевидно, что каждый фрагмент ДС может иметь отличающуюся, хотя и качественно подобную, структуру “всплеска”.