1. На главную
  2. Электронные версии
  3. Физика металлов и металловедение
  4. T. 120, № 6, 2019

Физика металлов и металловедение, 2019, T. 120, № 6, стр. 637-646

Изучение распределения зерен по размерам в аустенитной нержавеющей стали AISI 316L на стадии предварительного нагрева до горячей деформации

Дж. Расти *

Машиностроительный факультет, Кумский технологический университет (QUT)
Кум, Иран

* E-mail: rasti@qut.ac.ir

Поступила в редакцию 22.06.2018
После доработки 22.10.2018
Принята к публикации 27.12.2018

Полный текст (PDF)

Аннотация

Размер зерна и распределение зерен по размерам – важнейшие микроструктурные характеристики аустенитных нержавеющих сталей. Они оказывают значительное влияние на механические свойства материала. Характер распределения зерен по размерам на стадии предварительного нагрева материала до горячей деформации, главным образом сказывается на равномерности распределения деформации внутри зерен и, следовательно, на однородности развития таких процессов в материале, как статическая, динамическая и метадинамическая рекристаллизация. Распределение зерен по размерам может быть выражено с использованием точечного метода Йенсена–Гундерсена наряду с привлечением таких часто используемых функций распределения (ФР), как логнормальная, гамма – функция, уравнения Вейбулла, Луата или Хилерта. В данном исследовании, для прогнозирования кинетики роста зерен и их распределения по размерам в процессе отжига и для установления, какая из перечисленных ФР реализуется, был использован 3D-метод Монте-Карло Поттса. Для подтверждения результатов компьютерного моделирования нами было проведено изучение эволюции зеренной структуры на поперечных сечениях цилиндрических образцов стали AISI 316L, отожженной при 1200°C в течение 5, 10 и 15 минут. Результаты моделирования показали, что вид распределения зерен по размерам зависит от исходного числа зерен, а именно, при их относительно небольшом количестве реализуется логнормальное распределение, а при большем количестве зерен распределение описывается гамма-функцией. Более того, на базе логнормального распределения предложен новый метод расчета параметра стандартного отклонения размера зерна.

Ключевые слова: размер зерна, метод Монте-Карло, гамма-функция, логнормальное распределение, распределение Вейбулла

ВВЕДЕНИЕ

Размер зерен и их распределение по размерам – одни из наиболее важных характеристик микроструктуры аустенитных нержавеющих сталей, поскольку эти сплавы обычно являются однофазными и не испытывают каких-либо фазовых превращений в процессе традиционной термической обработки [1]. Горячее деформирование этих сплавов предусматривает стадию предварительного нагрева и выдержки при температурах 1100−1250°C, на которой происходит рост зерен, и их размер и соответствующее распределение изменяются. Это сказывается на равномерности распределения деформации внутри зерен, что влечет за собой однородность развития в материале таких процессов, как статическая, динамическая и метадинамическая рекристаллизация [2–5]. Внимание данной статьи сосредоточено на явлениях роста зерен на стадии предварительного нагрева материала, и цель ее состоит в отыскании формулы, подходящей для описания кинетики, и функции распределения, способной адекватно описать распределение зерен по размерам (РЗР).

Предложенный Джеффрисом планиметрический метод, а также метод секущих, сориентированы на установление среднего (по ASTM E112-82) размера зерна и основаны на подсчете числа зерен в “поле зрения” и длин отрезков, отсекаемых границами зерен на каждой из выбранных в планарных сечениях прямых линий, соответственно [6]. Однако зерна в кристаллах являются трехмерными объектами, с их особой, присущей 3-м измерениям, формой, и в реальных кристаллических материалах объемы этих зерен отличны друг от друга и показывают определенную особенность распределения.

Для установления экспериментальным путем распределения зерен по размерам имеется несколько методов, таких как, например, методы серийных послойных срезов и разделения зерен [7–9], или предложенный в [10] “диссекторный” подход. Авторы работ [10, 11] отмечали, что анализ послойных срезов материала – наиболее информативный метод для установления всего объема параметров зеренной структуры. С другой стороны, применение метода “диссектор” отнимает много сил и времени и требует пристального внимания при отборе и подсчете “объектов” анализа [10].

Пространственное (3D) распределение зерен по размерам можно описать двумя способами: (i) распределение, основанное на учете числовых долей зерен каждого размерного класса, т.е. такое РЗР (${{f}_{N}}(v)$), когда его характер определяется в первую очередь, количеством зерен в каждом классе размеров R, и (ii) РЗР, которое определяется суммарным объемом зерен в каждом размерном классе, такое распределение (${{f}_{N}}(v)$) указывает произведение числа зерен и среднего объема зерна в каждом размерном классе [11, 12]. Помимо этих функций распределения, мы вводим в рассмотрение и такие параметры, как ${{\bar {V}}_{N}}$ – средневзвешенный объем зерна, как объем частицы среднего размера $\bar {R},$ $C{{V}_{N}}$ – коэффициент вариации количественно-взвешенного распределения зерен ${{f}_{N}}(v),$ ${{\bar {V}}_{v}}$ – средний объем зерна как среднее по всем объемам зерен, $C{{V}_{v}}$ – коэффициент вариации объемно-взвешенного распределения зерен ${{f}_{v}}(v).$ Эти параметры могут быть представлены в следующем виде [8]:

(1)
$\begin{gathered} {{{\bar {V}}}_{x}} = \left\langle {{{V}_{x}}} \right\rangle = \sum {{{{{{({{V}_{x}})}}_{i}}} \mathord{\left/ {\vphantom {{{{{({{V}_{x}})}}_{i}}} N}} \right. \kern-0em} N}} ; \\ {{\sigma }_{x}} = {{\left( {\frac{{\sum {{{{\left( {{{{({{V}_{x}})}}_{i}} - {{{\bar {V}}}_{x}}} \right)}}^{2}}} }}{N}} \right)}^{{0.5}}} = \sqrt {\left\langle {V_{x}^{2}} \right\rangle - {{{\left\langle {{{V}_{x}}} \right\rangle }}^{2}}} ; \\ C{{V}_{x}} = {{{{\sigma }_{x}}} \mathord{\left/ {\vphantom {{{{\sigma }_{x}}} {{{{\bar {V}}}_{x}}}}} \right. \kern-0em} {{{{\bar {V}}}_{x}}}} \\ \end{gathered} $
где индекс x принимает значения N или $v,$ а индекс i соответствует i-ому размерному классу R. Используются также еще две статистические характеристики РЗР, а именно, коэффициент асимметрии ФР (СSx) и коэффициент эксцесса распределения (СEx), определяемые как:

(2)
$\begin{gathered} C{{S}_{x}} = \frac{{\sum {{{{\left( {{{{({{V}_{x}})}}_{i}} - {{{\bar {V}}}_{x}}} \right)}}^{3}}} }}{{N\sigma _{x}^{3}}}; \\ C{{E}_{x}} = \frac{{\sum {{{{\left( {{{{({{V}_{x}})}}_{i}} - {{{\bar {V}}}_{x}}} \right)}}^{4}}} }}{{N\sigma _{x}^{4}}} - 3. \\ \end{gathered} $

Величина параметра ${{\bar {V}}_{v}}$ может быть достаточно легко определена с помощью процедуры, предложенной Йенсеном и Гундерсеном [13]. Эта процедура предполагает случайную выборку зерен на поперечном сечении образца и последующие измерения длин li отрезков, проходящих через точки Pi, спроецированные на изображение исследуемой зеренной структуры. На основе таких измерений средний объем зерна ${{\bar {V}}_{v}}$ может быть оценен по формуле

(3)
$\left\langle {{{V}_{v}}} \right\rangle = \frac{\pi }{3}\left\langle {{{l}^{3}}} \right\rangle .$

Коэффициент вариации $C{{V}_{v}}$ (распределения ${{f}_{v}}(v)$), с другой стороны, может быть вычислен по формуле

(4)
$C{{V}_{v}} = {{\left[ {\frac{{36k\left\langle {{{a}^{3}}} \right\rangle }}{{\pi {{{\left\langle {{{l}^{3}}} \right\rangle }}^{2}}}} - 1} \right]}^{{0.5}}},$
где a – площадь зерна, границе которого принадлежит точка Pi, а k –константа со значением в интервале от 0.071 до 0.083. (Величина k зависит от формы зерен и предполагается постоянной для большой группы поликристаллических материалов. Ее значение может быть определено либо экспериментальным путем, либо посредством подходящего моделирования).

Вышеупомянутый метод можно использовать для установления значений параметров ${{\bar {V}}_{v}}$ и $C{{V}_{v}}$ в их привязке к конкретному изучаемому сечению. А посредством использования подходящей ФР могут быть получены и соответствующие количественно-взвешенные параметры ${{\bar {V}}_{N}}$ и $C{{V}_{N}},$ характеризующие те РЗР, поведение которых определяется числом зерен в каждом размерном классе.

Информацию о виде квазистационарных ФР можно почерпнуть из литературных обзоров [11–17]. Среди этих ФР мы найдем логнормальное распределение (L), ФР на основе гамма-функции (G), распределения Вейбулла (W), Луата, Рэлея, Хилерта. Перечисленные функции распределения сведены в табл. 1.

Таблица 1.  

Примеры различных функций распределения зерен по размерам в их ${{f}_{N}}(v)$ представлении

Уравнение Параметры
Логнормальное распределение [11, 12]: ${{f}_{N}}(v) = \frac{1}{{Av\sqrt {2\pi } }}\exp \left[ { - \frac{1}{2}{{{\left( {\frac{{\ln (v) - B}}{A}} \right)}}^{2}}} \right]$ A – стандартное отклонение (СО) и B – средне арифметическое от логарифма объема зерна ($\ln (v)$), соответственно
Распределение Вейбулла [14, 16]:
${{f}_{N}}(v) = \frac{\beta }{{{{\alpha }^{\beta }}}}{{v}^{{\beta - 1}}}\exp \left[ { - {{{\left( {\frac{v}{\alpha }} \right)}}^{\beta }}} \right]$		 Где β > 0 – параметр формы, а величина $\alpha = {1 \mathord{\left/ {\vphantom {1 \Gamma }} \right. \kern-0em} \Gamma }(1 + {1 \mathord{\left/ {\vphantom {1 \beta }} \right. \kern-0em} \beta })$ – подгоночный параметр распределения (Γ – гамма функция)
гамма-функция [11]: ${{f}_{N}}(v) = \frac{{{{v}^{{a - 1}}}}}{{{{b}^{a}}\Gamma (a)}}\exp \left( { - \frac{v}{a}} \right)$ Величина ab2 – дисперсия распределения, а ab – среднее по распределению
Хилерт [17]: ${{f}_{N}}(r) = {{(2e)}^{2}}\frac{{2r}}{{{{{(2 - r)}}^{4}}}}\exp \left( { - \frac{4}{{2 - r}}} \right)$ r – приведенный размер зерна
Louat [25]: ${{f}_{N}}(v) = 2kv\exp ( - k{{v}^{2}})$ k – подгоночный параметр
Рэлей [15]: ${{f}_{N}}(v) = \frac{{{8 \mathord{\left/ {\vphantom {8 3}} \right. \kern-0em} 3}}}{{\sqrt \pi }}{{k}^{{\frac{5}{2}}}}v\exp ( - k{{v}^{2}})$ То же, что для ФР Вейбулла с β = 2, т.е., k = ${{\left\{ {\Gamma (1 + {1 \mathord{\left/ {\vphantom {1 {\beta )}}} \right. \kern-0em} {\beta )}}} \right\}}^{2}}$

Теория Хилерта своими корнями уходит в классическую теорию коалесценции частиц. Само распределение Хилерта до сих пор редко наблюдалось в эксперименте [18]. Браун подверг детальному анализу классические результаты теории ЛСВ (Лифшица и Слёзова [19] и Вагнера [20]) в контексте укрупнения частиц и пришел к выводу, что имеется бесконечное число квазистационарных распределений, из которых ЛСВ распределения являются лишь частным случаем [21].

Согласно результатам работ [22] и [23], а также благодаря усилиям команды авторов статьи [24], можно считать доказанным, что более или менее удачное совпадение квазистационарного распределения зерен по размерам с логнормальной функцией или одной из функций: Вейбулла, Рэлея и Хилерта, может быть получено с помощью придания одному единственному подгоночному параметру в каждой из формул табл. 1 того или иного численного значения.

В табл. 2 показано соотношение между объемно-взвешенными и количественно-взвешенными параметрами ФР с использованием наиболее часто упоминаемых функций, таких как логнормальное, гамма-распределение или распределение Вейбулла.

Таблица 2.  

Корреляция между объемно-взвешенными и количественно-взвешенными параметрами функций распределения

Логнормальное распределение [11] Гамма функция [11] Распределение Вейбулла*
$\left\langle {{{V}_{N}}} \right\rangle = \frac{{{{{\left\langle {{{V}_{v}}} \right\rangle }}^{3}}}}{{\left\langle {V_{v}^{2}} \right\rangle }}$ $\left\langle {{{V}_{N}}} \right\rangle = 2\left\langle {{{V}_{v}}} \right\rangle - \frac{{\left\langle {V_{v}^{2}} \right\rangle }}{{\left\langle {{{V}_{v}}} \right\rangle }}$ $\left\langle {{{V}_{v}}} \right\rangle = 2a\frac{{\Gamma ({2 \mathord{\left/ {\vphantom {2 \beta }} \right. \kern-0em} \beta })}}{{\Gamma ({1 \mathord{\left/ {\vphantom {1 \beta }} \right. \kern-0em} \beta })}}$
$C{{V}_{N}} = C{{V}_{v}}$ $C{{V}_{N}} = \frac{{C{{V}_{v}}}}{{\sqrt {1 - CV_{v}^{2}} }}$ $C{{V}_{v}} = \sqrt {\frac{{3\Gamma ({1 \mathord{\left/ {\vphantom {1 \beta }} \right. \kern-0em} \beta })\Gamma \left( {{3 \mathord{\left/ {\vphantom {3 \beta }} \right. \kern-0em} \beta }} \right)}}{{4{{\Gamma }^{2}}\left( {{2 \mathord{\left/ {\vphantom {2 \beta }} \right. \kern-0em} \beta }} \right)}}} $
$A = \sqrt {\ln (1 + CN_{N}^{2})} $ $a = \frac{1}{{CV_{N}^{2}}}$ $\left\langle {{{V}_{N}}} \right\rangle = \frac{\alpha }{\beta }\Gamma ({1 \mathord{\left/ {\vphantom {1 \beta }} \right. \kern-0em} \beta })$
$B = \ln \left\langle {{{V}_{N}}} \right\rangle - 0.5{{A}^{2}}$ $b = \frac{{\left\langle {{{V}_{N}}} \right\rangle }}{a}$ $C{{V}_{N}} = \sqrt {2\beta \frac{{\Gamma ({2 \mathord{\left/ {\vphantom {2 {\beta )}}} \right. \kern-0em} {\beta )}}}}{{{{\Gamma }^{2}}({1 \mathord{\left/ {\vphantom {1 {\beta )}}} \right. \kern-0em} {\beta )}}}}} $

* Соотношения для ФР Вейбулла выведены в данной работе.

Как только значения параметров ${{\bar {V}}_{v}}$ и $C{{V}_{v}}$ получены из обработки планарного сечения методом поточечной выборки, так сразу с помощью соотношений, приведенных в табл. 2, можно получить соответствующие параметры ${{\bar {V}}_{N}}$ и $C{{V}_{N}}.$ После этого, через эти параметры может быть записана выбираемая функция распределения.

Представленные функции распределения оказываются совершенно разными по своей форме. Здесь возникает вопрос: которая из этих ФР могла бы описывать квазистационарное распределение зерен по размерам наилучшим образом? В поисках ответа на этот вопрос и заключалась данная работа. При этом было использовано два подхода: анализ серийных послойных срезов и метод Монте-Карло.

Использование модели Поттса является наиболее многообещающим подходом при изучении процесса роста зерен методами Монте-Карло и получении детальной информации об эволюции микроструктуры.

В нашем моделировании методом Монте-Карло [14, 16], на кубическую решетку с полным набором периодических граничных условий отображалась непрерывная микроструктура. Каждому узлу решетки было приписано положительное целое число Si (от 1 до N), отвечавшее ориентации зерна, отображенного на эту кубическую решетку. Каждое зерно было представлено набором узлов решетки, каждый из которых был снабжен индивидуальным, неповторяющимся номером, отвечавшим ориентации зерна, которому они принадлежали. Каждый зернограничный сегмент задавался как лежащий между узлами, принадлежавшими зернам несовпадающих ориентаций. Величина зернограничной энергии задавалась в терминах энергии узлов решетки следующим образом:

(5)
${{E}_{i}} = J\sum\limits_{j = 1}^{{{N}_{n}}} {\left( {{{\delta }_{{{{S}_{i}}{{S}_{j}}}}} - 1} \right)} ,\,\,\,\,{{\delta }_{{{{S}_{i}}{{S}_{j}}}}} = \left\{ {\begin{array}{*{20}{c}} {1,}&{{{S}_{i}} = {{S}_{j}}} \\ {0,}&{{{S}_{i}} \ne {{S}_{j}}} \end{array}} \right.,$
где J – положительная константа размерности энергии, определяющая ее зернограничное значение; Nn – общее число ближайших соседей j для i-го узла (здесь принятое равным 26 для первой координационной сферы); и, наконец, ${{\delta }_{{{{S}_{i}}{{S}_{j}}}}}$ – символ Кронекера. Каждый зернограничный сегмент имел положительную энергию, тогда как каждому узлу внутри объема зерна была приписана нулевая энергия.

Моделирование роста зерен предусматривало случайную выборку узла с ориентацией Si и его попытку к переориентации. Осуществление этой переориентации было ограничено выбором произвольного узла j, прилегающего к выбранному узлу. Таким образом, итоговое изменение энергии, связанное с попыткой к переориентации, может быть представлено как

(6)
$\Delta E = {{E}_{{i2}}} - {{E}_{{i1}}},$
где Ei2 и Ei1 – значения зернограничной энергии i‑го узла до и после попытки изменить ориентировку. Вероятность осуществление такой переориентации равна:
(7)
$w = \left\{ \begin{gathered} 1, \hfill \\ \exp \left( { - \frac{{\Delta E}}{{kT}}} \right), \hfill \\ \end{gathered} \right.\,\,\,\,\begin{array}{*{20}{c}} {\Delta E \leqslant 0} \\ {\Delta E > 0} \end{array},$
где k – постоянная Больцмана, а T – абсолютная температура; в действительности, оба этих параметра – тепловые константы. N попыток переориентации являются своего рода мерилом единицы времени, именуемой далее MCS (один шаг процедуры Монте-Карло), причем N есть ни что иное, как полное число узлов решетки. Наша система состояла из N (200 × 200 × 200) узлов в исходном очень мелкозернистом состоянии, т.е. положительное целое число от 1 до Q было присвоено каждому узлу решетки, где Q представляло различные кристаллографические направления для зерен. Показано, что для Q > 30 итоговые результаты совершенно не зависят от Q [26], а здесь величина Q представляла 4000 ориентаций.

При моделировании роста зерна, из-за огромного числа очень мелких зерен в микроструктуре (как рассредоточенных точек), при статистическом расчете размера зерна, в качестве веса зерен каждого размерного класса была выбрана величина V2 (квадрат их объема), с тем, чтобы ограничить вклад этих мелких зерен в итоговый результат. Отсюда значения среднего объема зерен и коэффициента вариации были определены из следующих выражений:

(8)
$\left\langle {{{V}_{{N,MC}}}} \right\rangle = \frac{{\left\langle {V_{N}^{3}} \right\rangle }}{{\left\langle {V_{N}^{2}} \right\rangle }};$
(9)
$C{{V}_{{N,MC}}} = \frac{{\sqrt {\frac{{(V_{N}^{4})}}{{(V_{N}^{2})}} - {{{\left\langle {{{V}_{N}}} \right\rangle }}^{2}}} }}{{\left\langle {{{V}_{N}}} \right\rangle }}.$

1. МЕТОДИКА ЭКСПЕРИМЕНТА

В данной работе использовалась аустенитная нержавеющая сталь AISI 316L, химический состав которой приведен в табл. 3. Образцы цилиндрической формы диаметром 10 мм прошли отжиг при 1200°C в течение 5, 10 и 15 мин, с последующей быстрой закалкой в стоячей воде. Эти образцы затем были порезаны, отшлифованы, отполированы и протравлены в реактиве ниталь (2%-ный раствор) для выявления микроструктуры. Оценку распределения зерен по размерам осуществляли методом последовательных послойных “срезов” (ППС). В этом ППС-методе, вплоть до глубины, равной двум диаметрам наибольшего зерна, образцы последовательно подвергались шлифовке со снятием слоя материала толщиной в 1% от размера наибольшего зерна, и, после стандартного приготовления металлографических шлифов, производили их съемку. По результатам обработки этих последовательных изображений, строили затем 3D распределение зерен по размерам. При этом, был использован пакет компьютерных программ для анализа изображений микроструктуры, CLEMEX.

Таблица 3.  

Химический состав аустенитной нержавеющей стали AISI 316L, использованной в данной работе (вес. %)

C Cr Ni Mo Si Mn Ti P S Fe
0.026 17.6 10.6 1.88 0.36 1.94 0.08 0.045 <0.02 Ост.

На рис. 1 представлены два последовательных снимка, полученных с образца, отожженного в течение 15 мин при 1200°C. На снимках одни и те же цифры обозначают одни и те же зерна. Толщина слоя материала, удаленного в результате повторной шлифовки, полировки и травления образца, т.е. расстояние между поверхностями, с которых были получены изображения, составляла примерно 0.02 мм. Произведение средней площади каждого из пронумерованных зерен на обоих снимках и толщины слоя материала, их разделявшего (т.е. 0.02 мм), рассматривалось равным малой части объема каждого из одинаково пронумерованных зерен. Многократное повторение процедуры указанного перемножения после каждого механического удаления материала (с последующим фиксированием зеренной структуры очередного “среза”) дало объем примерно 80–150 зерен, что позволило получить экспериментальное 3D распределение зерен по размерам.

Рис. 1.

Иллюстрация метода [7] последовательных послойных “срезов”: Два последовательных изображения поверхностей “среза”, сделанных с образца, прошедшего отжиг при 1200°C в течение 15 минут. На этих “снимках” одни и те же цифры обозначают одни и те же зерна.

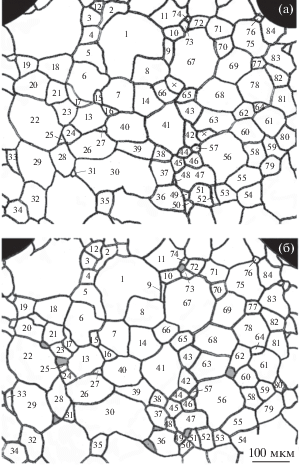
В образце были просверлены два отверстия, на поверхностях последовательных “срезов” их след выступал в качестве реперных точек, чтобы быть уверенными в принадлежности набора карт зеренной структуры одной и той же области образца.

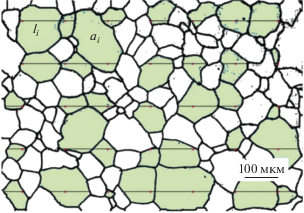
На рис. 2 проиллюстрирована процедура метода Йенсена–Гундерсена. На изображении представлена микроструктура образца после отжига в течение 10 мин при температуре 1200°C. Показан пример случайной точечной выборки зерен на поперечном сечении и последующего измерения длин li отрезков, проходящих через точки ${{P}_{i}},$ которые спроецированы на изображение исследуемой зеренной структуры. Символом ai отмечена площадь тех зерен, через которые целиком проходит отрезок. Т.о., все готово для определения величин среднего объема ${{\bar {V}}_{v}}$ и коэффициента вариации $C{{V}_{v}}$ зерен с помощью формул (3) и (4), соответственно. Окончательно, используя соотношения табл. 2, можно рассчитать параметры $\left\langle {{{V}_{N}}} \right\rangle $ и $C{{V}_{N}}$ – константы ФР.

Рис. 2.

Микроструктура образца, отожженного в течение 10 минут при 1200°C. К иллюстрации метода случайной выборки зерен Йенсена–Гундерсена [13].

2. РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

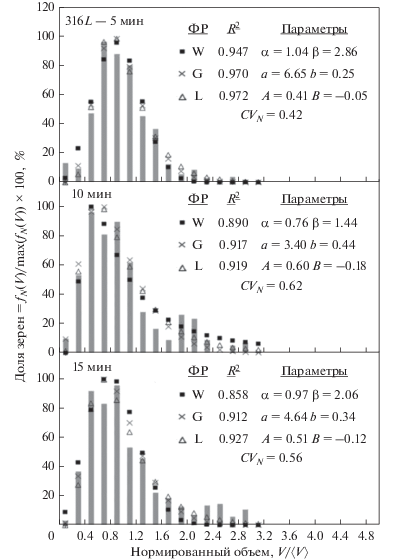
На рис. 3 представлена микроструктура аустенитной нержавеющей стали AISI 316L в исходном состоянии и после отжига при 1200°C в течение 5, 10 и 15 мин. Для определения величины параметров ${{\bar {V}}_{v}}$ и $C{{V}_{v}},$ нами был использован метод случайной выборки зерен (СВЗ), предложенный Йенсеном и Гундерсеном [13]. Имея в виду различные ФР и соотношения их параметров, сведенные в табл. 2, мы смогли рассчитать значения подгоночных параметров, а также ${{\bar {V}}_{N}}$ и $C{{V}_{N}},$ и построить графически 3D распределение зерен по размерам. Пример такого построения приведен на рис. 4 для образца, отожженного в течение 5 мин при 1200°C. Средний диаметр зерен и эквивалентный ему диаметр, полученный методом секущих, могут быть рассчитаны по формулам ${{D}_{v}} = {{\left( {{{6\left\langle {{{V}_{v}}} \right\rangle } \mathord{\left/ {\vphantom {{6\left\langle {{{V}_{v}}} \right\rangle } \pi }} \right. \kern-0em} \pi }} \right)}^{{\frac{1}{3}}}}$ и ${{D}_{{\operatorname{int} }}} = \frac{{{{D}_{v}}}}{{1.68}}$ соответственно [6].

Рис. 3.

Микроструктура стали в исходном состоянии и после отжига, с указанием среднего диаметра, полученного разными методами, и соответствующего коэффициента вариации.

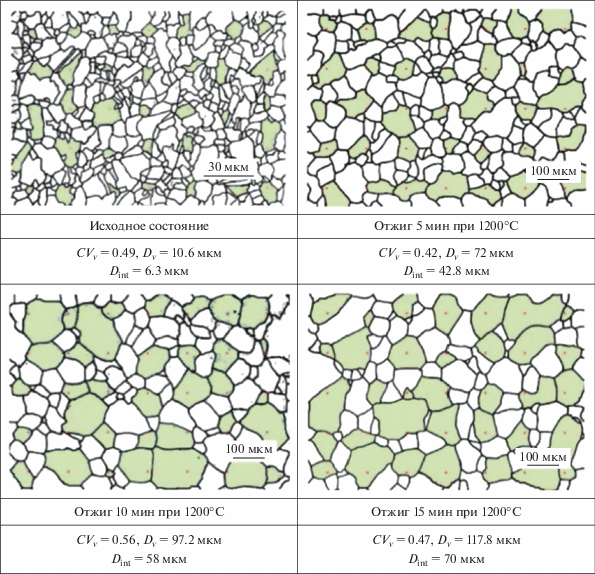
Рис. 4.

Функции распределения зерен по размерам для образца стали AISI 316L после отжига при 1200°C в течение 5 мин.

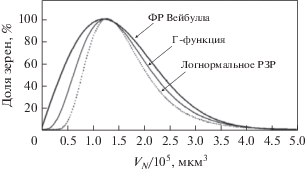
Как можно видеть на рис. 4, представленные функции распределения оказываются совершенно различными по форме. Проблема остается: какая из приведенных ФР наилучшим образом описывает наше экспериментальное 3D распределение. На рис. 5 представлены полученные методом ППС гистограммы РЗР, соответствующие показанным на рис. 3 микроструктурам. Тут же на рис. 5 точками показаны различные ФР, построенные по данным, полученным методом СВЗ Йенсена–Гундерсена.

Рис. 5.

Гистограммы РЗР, основанные на данных метода ППС, и результаты подгонки различных ФР, полученные в рамках метода СВЗ Йенсена–Гундерсена с учетом соотношений из табл. 2 для определения подгоночных параметров функций распределения из табл. 1.

По рис. 5 можно утверждать, что экспериментальное РЗР почти во всех точках соответствует логнормальному распределению, со средними параметрами ${{A}_{{{\text{ave}}}}} = 0.5,$ ${{B}_{{{\text{ave}}}}} = - 0.125,$ или гамма-функции, со средними параметрами ${{a}_{{{\text{ave}}}}} = 4.1$ и ${{b}_{{{\text{ave}}}}} = 0.26.$ Как можно видеть, логнормальная ФР лучше всего отвечает экспериментальным данным. Поэтому характерное 3D распределение зерен по размерам может быть получено из двумерных сечений, если использовать СВЗ-метод накопления данных о зеренной структуре и принять логнормальную ФР.

С другой стороны, функции гамма и логнормального распределения очень похожи, и одних только экспериментальных данных недостаточно для выбора одной из них в силу ограниченности числа зерен, формирующих статистику. Компьютерное моделирование показало, что распределение зерен ближе к гамма функции [27]. Чтобы убедиться в этом было проведено 3D моделирование методом Монте-Карло (МК).

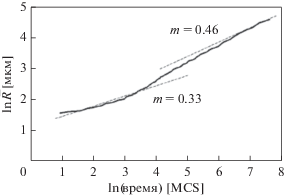
Для проверки соответствия действительности результатов моделирования методом МК, обычной практикой является рассмотрение степенного показателя m в кинетическом уравнении $\bar {R} = k{{t}^{m}},$ предложенном в работе [28]. При этом, само уравнение было получено в рамках МК-метода как результат зависимости величины среднего размера зерен от числа шагов МК-процедуры (MCS). Так что указанный критерий может быть сформулирован так: чем ближе m к 0.5, тем выше качество подхода к описанию кинетики.

В рамках МК-метода, средний радиус зерен можно рассчитать по формуле

$\bar {R} = \sqrt[3]{{\frac{{3\left\langle {{{V}_{{v,{\text{MC}}}}}} \right\rangle }}{{4\pi }}}},$
где ${{V}_{{v,{\text{MC}}}}}$ – средний объем зерен. На рис. 6 показано изменение среднего радиуса $\bar {R}$ с продолжительностью (здесь, единицей времени является MCS) отжига в логарифмическом масштабе. Величина степенного показателя m, на ранних стадиях отжига материала, в значительной степени отклоняется от своего теоретического значения 0.5. При этом, однако, m увеличивается со временем и при t > 800 MCS приближается к 0.46. На рис. 7 показана 3D микроструктура, полученная в результате МК моделирования при времени отжига 800 MCS. Здесь средний радиус зерен $\bar {R}$ равен ~ 40 мкм.

Рис. 6.

Предсказание МК моделирования по изменению среднего радиуса $\bar {R}$ со временем (MCS) отжига.

Рис. 7.

3D микроструктура при времени отжига 800 MCS как результат МК-моделирования.

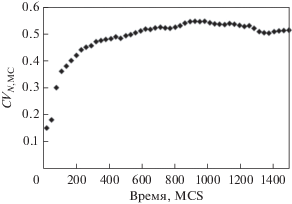
Рассмотрение значений коэффициента вариации, $C{{V}_{{N,{\text{MC}}}}},$ при различной длительности отжига показывает, что при MCS > 600, его величина достигает почти стабильного значения 0.52, что соответствует диапазону значений, получаемых в эксперименте, а именно, 0.4−0.8 (рис. 8).

Рис. 8.

Коэффициент вариации $C{{V}_{{N,{\text{MC}}}}}$ в зависимости от продолжительности отжига, при МК моделировании.

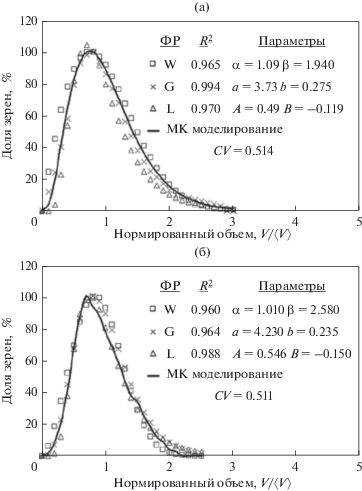
По результатам МК-моделирования может быть рассчитана функция распределения зерен по размерам в количественно-взвешенном (${{f}_{N}}(v)$) представлении. На рис. 9 эти РЗР приведены в моменты времени 800 и 1400 MCS. Как можно видеть, число зерен в ансамбле влияет на вид ФР: на ранних стадиях отжига (800 MCS) при относительно большом числе зерен (4200) формирующееся распределение хорошо согласуется с гамма-функцией (рис. 9a), тогда как при относительно больших временах отжига (1400 MCS) для меньших зеренных ансамблей (из 1100 зерен) наилучшее соответствие получено для логнормального распределения (рис. 9б). Отметим, что подгонка РЗР исторически включала этапы использования логнормального распределения, зависящего от одного, двух и трех параметров [29].

Рис. 9.

3-D распределение зерен по объемам в ${{f}_{v}}(v)$ представлении, полученное по результатам МК моделирования, в сравнении с известными ФР на момент времени отжига (a) 800 MCS, и (б) 1400 MCS.

В данной статье был предложен новый метод для представления стандартного отклонения размера зерна, основанный на использовании логнормальной ФР. Этот метод предполагает использование коэффициента вариации объема.

Полагая, что распределение зерен по размерам носит логнормальный характер, стандартное отклонение (для объема зерна) определяется формулой

(10)
${{\sigma }_{{\ln (v)}}} = A = \sqrt {\ln (1 + CV_{v}^{2})} .$

Если распределение объемов зерен является логнормальным, тогда распределение зерен по “эквивалентным” диаметрам также будет логнормальным при известных допущениях относительно формы зерна, но стандартное отклонение для “эквивалентных” диаметров будет равным $\frac{1}{3}{{\sigma }_{{\ln (v)}}} = \frac{A}{3}$ [24]. Тем самым, логарифм “эквивалентного” диаметра зерна с одним стандартным отклонением в качестве допуска, может быть представлен в следующем виде:

(11)
$\begin{gathered} \ln ({{{\bar {D}}}_{{\operatorname{int} }}}) \pm {A \mathord{\left/ {\vphantom {A 3}} \right. \kern-0em} 3} = \\ = \ln ({{{\bar {D}}}_{{\operatorname{int} }}}\exp ( \pm {A \mathord{\left/ {\vphantom {A 3}} \right. \kern-0em} 3})) \cong \ln ({{{\bar {D}}}_{{\operatorname{int} }}}(1 \pm {A \mathord{\left/ {\vphantom {A 3}} \right. \kern-0em} 3})). \\ \end{gathered} $

Это соотношение (11) означает, что ${A \mathord{\left/ {\vphantom {A 3}} \right. \kern-0em} 3}$ может рассматриваться в нем как член, соответствующий допустимому отклонению “эквивалентного” диаметра зерен, так что средний размер зерна может быть представлен как

(12)
${{\bar {D}}_{{\operatorname{int} }}} \pm \sqrt {\ln (1 + {{CV_{v}^{2})} \mathord{\left/ {\vphantom {{CV_{v}^{2})} 3}} \right. \kern-0em} 3}} ,$
где $C{{V}_{v}}$ – коэффициент вариации, который можно вычислить просто, используя метод случайной выборки зерен, предложенный Йенсеном и Гундерсеном.

ВЫВОДЫ

Получены следующие результаты:

1. 3D распределение зерен по размерам может быть получено в результате (i) обработки двумерных сечений по методу случайной выборки зерен, предложенному Йенсеном и Гундерсеном, и (ii) выбора подходящей функции распределения.

2. 3D распределение зерен по размерам, построенное с привлечением метода последовательных послойных “срезов”, лучше всего согласуется с логнормальной функцией распределения.

3. Результаты 3D моделирования по методу Монте-Карло показали, что распределение зерен по объемам находится в хорошем согласии с гамма или логнормальным распределением в случае относительно большого или малого числа зерен, соответственно.

4. На основе рассмотрения логнормального распределения предложен новый подход к определению параметра стандартного отклонения размера зерна.

Данное исследование было спонсировано из Фонда вице-президента по учебно-образователь-ной и научно-исследовательской работе Кумского технологического университета (QUT).

Список литературы

  1. Kuck D., Niewielski G., Cwajna J. Influence of deformation parameters and initial grain size on the microstructure of austenitic steels after hot-working processes // Mat. Characterization. 2006. V. 56. P. 318–324.

  2. Esedoglu S. Grain size distribution under simultaneous grain boundary migration and grain rotation in two dimensions // Computational Mater. Sci. 2016. V. 121. C. 209–216.

  3. Uhlirov T., Pabst W., Gregorov E., Hostasa J. Stereology of dense polycrystalline materials-from interface density and mean curvature integral density to Rayleigh distributions of grain sizes // J. European Ceramic Society. 2016. V. 36. P. 2319–2328.

  4. Wahabi M.EI., Gavard L., Montheillet F., Cabrera J.M., Prado J.M. Effect of initial grain size on dynamic recrystallization in high purity austenitic stainless steels // Acta Materialia. 2005. V. 53. P. 4605–4612.

  5. Maki T. Stainless steel: progress in thermomechanical treatment/ in Metals and Alloys. McGraw Hill, 2001. P. 290–295.

  6. Thorvaldsen A. The intercept method-1. Evaluation of grain shape// Acta Mater. 1997. V. 45. № 2. P. 587–594.

  7. Rhines F.N., Craig K.R., Rousse D.A. Measurement of average grain volume and certain topological parameters by serial section analysis // Metall. Trans. A 1976. V. 7. P. 1729–1734.

  8. Liu G., Yu H. On the sampling of serial sectioning technique for three dimensional space-filling grain structures// Image Anal. Stereol. 2000. V. 19. P. 81–84.

  9. Matsuura K., Itoh Y., Kudoh M., Ohmi T., Ishii K. Three-dimensional grain size distribution in SUS304 stainless steel // ISIJ Int. 1994. V. 34. № 2. P. 186–190.

  10. Liu G., Yu H., Li W. Efficient and unbiased evaluation of size and topology of space filling grains// Acta Stereol. 1994. V. 13. P. 281–286.

  11. Yu H., Liu G., Song X. On the relation between the number-weighted and volume-weighted grain volume distribution parameters// Metall. Mater. Trans. A. 1998. V. 29. P. 3081–3086.

  12. Yin F., Sakurai A., Song X. Determination of spatial grain size with the area-weighted grain area distribution of the planar sections in polycrystalline materials // Metall. Mater. Trans. A 2006. V. 37. P. 3707–3714.

  13. Kurzydtowski K.J., Bucki J.J. A method for grain size and grain size uniformity estimation- application to polycrystalline // Scripta Metall. 1992. V. 27. P. 117–120.

  14. Sun Y., Liu G., Wang C. On the Grain Size Distributions Obtained from Different Grain Growth Simulation Techniques // J. Mat. Sci. 2004. V. 39. P. 2553–2556.

  15. Gusak A.M., Tu K.N. Theory of normal grain growth in normalized size space// Acta Materialia. 2003. V. 51. P. 3895–3904.

  16. Wang C., Liu G. Grain size distribution obtained from Monte-Carlo simulation and the analytical mean field model // ISIJ Int. 2003. V. 43. P. 774–776.

  17. Hillert M. On the theory of normal and abnormal grain growth // Acta Metall. 1965. V. 13. № 3. P. 227–238.

  18. Atkinson H.V. Overview no. 65: Theories of normal grain growth in pure single phase systems // Acta Metall. 1998. V. 36. № 3. P. 469–491.

  19. Lifshitz I.M., Slyosov V.V. The kinetics of precipitation from supersaturated solid solutions // J. Phys. Chem. Solids. 1961. V. 19. P. 35–50.

  20. Wagner C. Theorie der Alterung von Niederschlagen durch Umlosen (Ostwald-Reifung) // Z. Elektrochem 1961. V. 65. P. 581–591.

  21. Brown L.C. A new examination of classical coarsening theory // Acta Metall. 1989. V. 37. № 1. P. 71–77.

  22. Yu H., PhD dissertation, University of Science and Technology, Beijing, Beijin, 1997. 5 p.

  23. Rios P.R. Comparison between a computer simulated and an analytical grain size distribution // Scripta Mater. 1999. V. 40. № 6. P. 665–668.

  24. Coughlan S.D., Fortes M.A. Self similar size distributions in particle coarsening // Scripta. Metall. Mater. 1993. V. 28. P. 1471–1476.

  25. Louat N.P., Duesbery M.S., Sadananda K. On the role of random walk in normal grain growth // Mater. Sci. Forum. 1992. V. 94–96. P. 67–76.

  26. Anderson M.P., Srolovitz D.J., Grest G.S., Sahni P.S. Computer simulation of grain growth – I. Kinetics // Acta Metall. 1984. V. 32. P. 783–792.

  27. Nunez C., Domingo S. Grain shape and its influence on the experimental measurement of grain size // Metall. Trans. A. 1988. V. 19A. P. 933–940.

  28. Burke J.E. Some factors affecting the rate of grain growth in metals // Trans. Am. Inst. Min. Eng. 1949. V. 180. P. 73–91.

  29. Murray D., Fredlund D., Fredlund G., Wilson G.W. An equation to represent grain-size distribution // Can. Geotech. 2000. V. J 37. P. 817–827.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика металлов и металловедение

Архивы выпусков Информация о журнале Отправить рукопись в журнал