Физика металлов и металловедение, 2019, T. 120, № 7, стр. 771-777

ВВЕДЕНИЕ

Известно, что пластические свойства материалов существенно зависят от условий деформирования. Так, при фиксированной температуре пластичность металлов значительно повышается при увеличении величины внешнего давления [1]. Этот эффект во многом определяет возможности получения наноструктурированных металлических систем в процессах пластического деформирования [2].

Пластичность металлов определяется коллективным поведением основных носителей пластической деформации: точечных, линейных и планарных дефектов кристаллической решетки. Основные механизмы разрушения кристаллов, свойства пор и микротрещин также тесно связаны со свойствами решеточных дефектов [1, 3]. Следовательно, давление, повышая пластичность металлов, должно оказывать определенное влияние на поведение дефектов кристаллической решетки.

С другой стороны, в термодинамике давление рассматривается как обобщенная термодинамическая сила, сопряженная объему. Поэтому влияние давления на поведение дефектов должно означать, что они могут давать определенный вклад в величину объема материала. Однако современная теория дефектов обычно не рассматривает такую возможность. К примеру, в общепринятой линейной теории деформаций вклад дислокаций в полное изменение объема материала равен нулю [3].

Существуют два основных подхода к решению этой проблемы. Первый связан с формальным применением методов нелинейной теории упругости к анализу дислокационных полей дисторсии (см., например, в [4]). Однако его следует признать неполным, поскольку дислокации вносят в материал не только обратимые, но и необратимые, т.е. неупругие деформации.

Второй подход основан на прямых вычислениях объемов для ограниченных конфигураций одиночных дислокаций (например, дислокационных диполей) с использованием модельных представлений о потенциалах межатомных взаимодействий или первопринципных расчетов [5, 6]. Однако эти подходы сталкиваются со значительными трудностями при описании деформационных полей от скоплений дислокаций одного знака.

Цель работы состоит в исследовании объемно-зависимых свойств дислокаций и их скоплений в рамках нелинейной теории необратимых деформаций, основанной на континуальной модели Дебая и приближении Грюнайзена [7].

ТЕОРЕТИЧЕСКИЕ МОДЕЛИ

Избыточный объем и свойства потенциалов межатомных взаимодействий

Рассмотрим структурные особенности прямолинейной краевой дислокации в простой кубической (ПК) решетке. В объеме ПК-решетки выберем произвольную плоскость из семейства {100}, делящую кристалл на две части. Зафиксируем форму каждой из частей и внедрим между ними лишнюю атомную полуплоскость, предварительно отключив все типы атомных взаимодействий. В результате получим новую кристаллическую решетку, структура которой представлена на рис. 1a (ось z ортогональна плоскости рисунка).

Рис. 1.

Структура ПК решетки вокруг прямолинейной краевой дислокации; при отключении межатомных взаимодействий (a), при включенном межатомном взаимодействии (б). Пояснения в тексте.

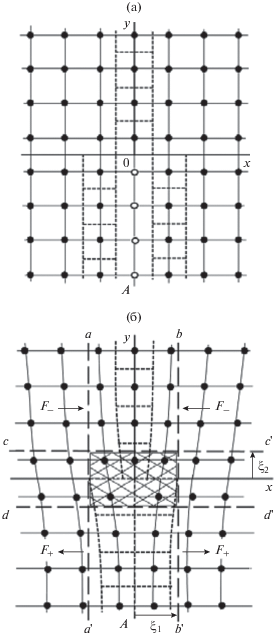
Новая структура отличается от начальной тем, что между смещенными со своих мест недеформированными частями кристалла, вдоль плоскости y0z (ее проекция на плоскость рисунка совпадает с линией y0A) образовалась зона необратимых изменений (деформаций) распределения атомов по узлам решетки.

Заштрихованные символы на рис. 1а обозначают положения атомов, незаштрихованные – положения вакансий в узлах вновь образованной кристаллической решетки. Тонкие сплошные линии соответствуют атомным плоскостям, пунктирными линиями обозначены границы недеформированных элементарных ячеек.

Если в этой структуре включить межатомные взаимодействия, решетка испытает деформацию так, как это условно показано на рис. 1б. При этом размеры зоны необратимых деформаций решетки могут измениться. В рамках континуального приближения эта зона ограничена плоскостями $aa{\text{'}}$ и $bb{\text{'}}.$ В области материала, заключенной между ними: $\left| x \right| \leqslant {{\xi }_{1}},$ решетка подвержена полным необратимым деформациям, величина которых определяется суммой начальных и релаксационных изменений атомной структуры. Эту область относят к структуре ядра краевой дислокации. Величину ${{\xi }_{1}}$ принято называть полушириной ядра дислокации. В остальной части решетки $\left| x \right| \geqslant {{\xi }_{1}}$ предполагается, что деформирование происходит в упругой области. Здесь описание деформационных полей дислокации обычно проводят в рамках линейной теории упругости [1–3].

Механизм возникновения избыточного объема у дислокации тесно связан с различиями в поведении потенциалов межатомных взаимодействий $U(r)$ (r – расстояние между атомами) при растяжении и сжатии решетки.

В области ядра атомные смещения антисимметричны относительно плоскости скольжения. Это согласуется с расчетами полей напряжений в упругой области $\left| x \right| \geqslant {{\xi }_{1}}.$ Прямолинейная дислокация Вольтерра создает распределение давления [3]

(1)

$p(x,y) \approx - {{K}_{0}}{{\varepsilon }_{W}}(x,y),$

где

(2)

${{\varepsilon }_{W}}(x,y) = \frac{{{{\mu }_{0}}b(1 + \nu )}}{{3\pi {{K}_{0}}(1 - \nu )}}\frac{y}{{{{x}^{2}} + {{y}^{2}}}}$

– поле дилатации. Предполагается, что линия дислокации не ограничена в пространстве и в системе координат (x, y, z) параллельна оси z; μ₀ и ${{K}_{0}}$ – модуль сдвига и модуль изотермического сжатия недеформированного материала соответственно, b – вектор Бюргерса дислокации, параллельный оси 0x, $\nu $ – коэффициент Пуассона.

Нормальная компонента силы, действующей на единицу площади в плоскости $aa{\text{'}}$ (или $bb{\text{'}}$) со стороны упругой области, равна

(3)

${\mathbf{F}}( \pm {{\xi }_{1}},y) \approx - {\text{sign}}(x){{{\mathbf{e}}}_{x}}p( \pm {{\xi }_{1}},y).$

Здесь ${{{\mathbf{e}}}_{x}}$ – единичный вектор в направлении оси 0x. На рис. 1б x-компоненты этих сил обозначены символами ${{{\mathbf{F}}}_{ - }}$ в области сжатия и ${{{\mathbf{F}}}_{ + }}$ в области расширения решетки. Из соотношений (1)–(3) следует, что вдоль границ $aa{\text{'}}$ и $bb{\text{'}}$ выполняются условия

(4)

${{{\mathbf{F}}}_{ - }}( \pm {{\xi }_{1}},y) = - {{{\mathbf{F}}}_{ + }}( \pm {{\xi }_{1}}, - y).$

Источником поля сил, определенных выражением (3), являются межатомные взаимодействия в области ядра дислокации. В связи с этим рассмотрим условия равновесия атомов в зоне необратимых деформаций.

Одним из таких условий является равенство химических потенциалов отдельных атомов или групп сильно связанных атомов. При абсолютной температуре $T = 0$ оно сводится к равенству потенциальных энергий $U$ этих групп в решетке. В частности, в антисимметричных точках зоны $\left| x \right| \leqslant {{\xi }_{1}}$ должно выполняться соотношение

(5)

$U\{ u(y)\} = U\{ u( - y)\} .$

Здесь $u(y)$ – функция, характеризующая среднее изменение расстояний между атомами в группах ближайшего окружения. Координата $y$ указывает на положение центра группы или атома в ее центре. При сжатии материала $u(y) < 0,$ при растяжении $u(y) > 0.$

Если функция $U(u)$ симметрична относительно значения $u = 0{\text{:}}$

$U(u) = U( - u),$

то для выполнения условия (5) необходимо чтобы $u(y) = - u( - y).$ Тогда сжатие решетки, в области $y > 0$ полностью компенсируется ее растяжением в области $y < 0,$ и избыточный объем дислокации становится равным нулю. Если же потенциал $U(u)$ несимметричен: $U(u) \ne U( - u),$ такой компенсации не происходит, поскольку для выполнения условия (5) теперь нужно чтобы $u(y) \ne - u( - y).$ В этом случае дислокация может иметь избыточный объем.

При $T \ne 0$ условие равновесия зоны $\left| x \right| \leqslant {{\xi }_{1}}$ требует учета изменений энтропии системы. Однако в теории деформационных полей дефектов кристаллической решетки этими поправками обычно пренебрегают [1–6].

Асимметрия поведения материалов по отношению к сжатию и растяжению проявляется и в нелинейной зависимости давления p от необратимой дилатации $\varepsilon ,$ полученной в рамках континуального приближения (см. Приложение):

(7)

$p(\varepsilon ) = \frac{{{{K}_{0}}}}{{2\gamma + 1}}\left\{ {{{{(1 - \varepsilon )}}^{{2{\gamma } + 1}}} - 1} \right\}.$

Здесь $\gamma $ – постоянная Грюнайзена. Из формулы (7) следует, что условие антисимметрии по давлению в зоне необратимых деформаций p(y) = = –p(–y) не выполняется при нулевом избыточном объеме, который соответствует равенству $\varepsilon (y) = - \varepsilon ( - y).$

Выражения (1)–(4) дают условие механического равновесия сил на границе зоны необратимых деформаций на плоскостях $aa{\text{'}}$ и $bb{\text{'}}.$ Для неограниченной среды его можно записать в виде соотношения

(8)

$\int\limits_{ - \infty }^\infty {p( \pm {{\xi }_{1}},y)dy = 0} ,$

которое означает равенство нулю полной силы, действующей на каждую из плоскостей $aa{\text{'}}$ и $bb{\text{'}}$ со стороны упругой области $\left| x \right| \geqslant {{\xi }_{1}}.$

МЕТОД ЭКСПЕРИМЕНТАЛЬНОГО ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ МОДЕЛИ

Континуальная теория дает лишь одно уравнение для двух неизвестных величин ${{\xi }_{D}}$ и ${{\text{v}}_{0}}.$ Второе уравнение для этих параметров можно получить либо при более детальном рассмотрении атомной структуры в плоскости скольжения дислокации, либо из анализа экспериментальных данных.

В частности, известно, что зависимость коэффициентов самодиффузии в объеме материала от абсолютной температуры T определяется соотношением [8, 9]

Здесь W – энергия активации самодиффузии, k_B – постоянная Больцмана.

Величина W зависит от давления p: $W(p)$ = = ${{W}_{{V,0}}} + p{{V}_{a}}(p),$ ${{V}_{a}}(p)$ = ${{{{V}_{{a,0}}}} \mathord{\left/ {\vphantom {{{{V}_{{a,0}}}} {(1 - \varepsilon (p))}}} \right. \kern-0em} {(1 - \varepsilon (p))}}$ – активационный объем, ${{W}_{{V,0}}}$ и ${{V}_{{a,0}}}$ – энергия активации объемной диффузии и активационный объем среды при нормальных условиях соответственно, $\varepsilon (p)$ – поле дилатации.

Отсюда следует, что процесс самодиффузии вдоль дислокационной линии можно интерпретировать как процесс объемной диффузии с учетом давления p, создаваемого дислокацией вдоль своего ядра. В этом случае величина $W(p)$ равна энергии активации диффузии ${{W}_{D}}$ по ядру дислокации.

В реальности, процесс самодиффузии протекает не только по ядру дислокации, но и по его ближайшей окрестности. Это означает, что общепринятый коэффициент диффузии по ядру носит эффективный характер, суммируя все объемные эффекты, вызванные дислокацией в материале. При расчетах это можно учесть, равномерно распределив весь избыточный объем ${{v}_{0}}$ по дислокационной трубке радиуса ${{\xi }_{D}}.$

Необходимо также учесть, что диффузионные процессы протекают не по всему ядру дислокации, а лишь по его части, подвергнутой суммарному растяжению за счет упругой и неупругой дилатации.

Оценим параметры процессов самодиффузии вдоль дислокационных линий в Ag. Для этого рассмотрим основную систему дислокаций ГЦК решетки с вектором Бюргерса $b = {{\left\langle {110} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {110} \right\rangle } 2}} \right. \kern-0em} 2}$ в плоскостях $\{ 111\} .$

Для этой системы график изменения давления в растянутой части ядра $ - p(\xi )$ приведен на рис. 2. Штриховыми линиями на нем отмечены граничные значения $ - p({{\xi }_{0}})$ и $ - p({{\xi }_{{PN}}}).$ ${{\xi }_{{PN}}}$ – полуширина дислокации в модели Пайерлса–Набарро.

Рис. 2.

Зависимость давления в растянутой части ядра краевой дислокации в Ag от полуширины дислокации.

Зависимость давления от суммарной дилатации ${{\varepsilon }_{C}},$ равномерно распределенной по растянутой части ядра дислокации, рассчитывали по формуле (30). При проведении расчетов для Ag параметры в формулах (1), (2), (8), (11)–(19) выбирали в следующем виде: ${{\mu }_{0}} = 29.4$ ГПа, ${{K}_{0}}$ = = ${{{2 \mathord{\left/ {\vphantom {2 {3{{\mu }_{0}}(1 + v)}}} \right. \kern-0em} {3{{\mu }_{0}}(1 + v)}}} \mathord{\left/ {\vphantom {{{2 \mathord{\left/ {\vphantom {2 {3{{\mu }_{0}}(1 + v)}}} \right. \kern-0em} {3{{\mu }_{0}}(1 + v)}}} {(1 - 2v)}}} \right. \kern-0em} {(1 - 2v)}},$ $\gamma = 2.4,$ $v = 0.37,$ $d = {a \mathord{\left/ {\vphantom {a {\sqrt 3 }}} \right. \kern-0em} {\sqrt 3 }},$ $b = {a \mathord{\left/ {\vphantom {a {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}.$ Здесь a – параметр ГЦК-решетки: ${{a}^{3}} = 4\Omega ,$ $\Omega $ – атомный объем $\Omega = 1.71 \times {{10}^{{ - 30}}}$ м³ [8].

Для определения значения параметра ${{\xi }_{D}}$ использовали экспериментальные данные по энергиям активации самодиффузии в Ag из работы [9]. При температуре T ≈ 600 К имеем: ${{W}_{V}} \approx 169$ кДж моль^–1, ${{W}_{D}} \approx 82.5$ кДж моль^–1, ${{V}_{{a,0}}} \approx \Omega .$ Подставив эти величины в формулу (30), получим среднее значение давления в ядре дислокации: $p({{\xi }_{D}}) \approx - 7.7$ ГПа. На рис. 2 оно отмечено сплошной горизонтальной линией. По точке пересечения этой линии с графиком можно определить эффективный радиус дислокационной трубки в Ag: ${{\xi }_{D}} \approx 0.6{{\xi }_{{PN}}} \approx 0.3a.$ Значение полной дилатации в растянутой части ядра ${{\varepsilon }_{C}}({{\xi }_{D}}) \approx 0.092,$ а необратимой объемной деформации ${{\varepsilon }_{0}}({{\xi }_{D}}) \approx 0.063.$ Учитывая экспоненциальный характер зависимости (19) от давления, можно показать, что учет деформации ${{\varepsilon }_{0}}({{\xi }_{D}})$ повышает коэффициент самодиффузии вдоль дислокационных линий на несколько порядков.

ДИСЛОКАЦИОННЫЕ СКОПЛЕНИЯ

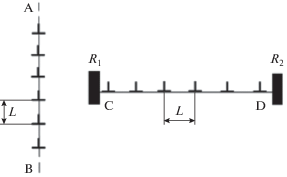
Рассмотрим задачу об определении избыточного объема, приходящегося на единицу длины краевой дислокации, входящей в состав плоского вертикального (AB) и горизонтального скопления (CD), схематично показанных на рис. 3. Такие скопления используются для исследования свойств межкристаллитных и межфазных границ раздела в материалах [3].

Рис. 3.

Плоские дислокационные скопления. Пояснения в тексте.

При проведении вычислений величины ${{\text{v}}_{0}}$ скопление AB удобно считать неограниченным по вертикали. Для расчетов следует использовать формулы (17), (18), в которые вместо распределения упругой дилатации от одиночной дислокации ${{\varepsilon }_{V}}({{\xi }_{1}},y)$ нужно подставить распределение упругой дилатации от всего скопления в виде суперпозиции отдельных вкладов:

Скопление CD представляет собой супердислокацию с векторов Бюргерса $B = Nb$ (N – число дислокаций в скоплении), ядро которой равномерно распределено по всей длине скопления. Следовательно, для получения конечных результатов число N должно быть ограничено. На практике длина скоплений типа CD всегда ограничена некоторыми препятствиями R₁ и R₂.

Основная особенность поля упругой дилатации любых дислокаций, и супердислокации, в частности, состоит в том, что оно всегда принимает экстремальные значения в центре ядра. Это означает, что величина ${{v}_{0}}$ у каждой дислокации из скопления будет зависеть от ее положения в ядре супердислокации. Поэтому величину ${{v}_{0}}$ для дислокаций скопления CD следует отмечать дополнительным индексом k = {1, 2, 3,…, N}, нумерующим дислокации: ${{v}_{{0,k}}}.$ В этом случае уравнение (18) для избыточного объема k-той дислокации на плоскости (z0x) принимает вид:

Здесь ${{x}_{k}}$ – координата центра ядра k-той дислокации.

Результаты расчетов суммарной необратимой дилатации ${{\varepsilon }_{0}}$ в ядрах отдельных дислокаций для различных скоплений в Ag приведены на рис. 4. При расчетах параметр ${{\xi }_{1}}$ был фиксирован для всех дислокаций обоих скоплений. В этом случае условие (8) исключает влияние избыточного объема дислокаций на деформационные поля в объеме материала.

Рис. 4.

Зависимость дилатации, вносимой отдельными дислокациями в скоплениях AB и CD, от расстояния L между ними. Пояснения в тексте.

Кривая 1 относится к скоплению типа AB. Избыточный объем дислокации ${{v}_{0}} = {{\varepsilon }_{0}}S,$ где $S \approx 4\xi _{D}^{2}$ – площадь поперечного сечения ядра дислокации. Из графика 1 видно, что величина избыточного объема каждой из дислокаций уменьшается при увеличении их линейной плотности в стенке. Это происходит за счет частичной компенсации упругих полей соседних дислокаций. Кривые 2, 3, 4, и 5 описывают зависимость дилатации у крайних дислокаций скопления CD от расстояния L для значений $N$ = 2, 5, 10 и 20 соответственно. Они показывают, что с увеличением мощности супердислокации избыточный объем крайних дислокаций увеличивается. Этот вывод относится ко всем дислокациям скопления CD.

Полученные результаты были использованы при исследовании процессов структурно-фазовых превращений и разрушения, протекающих при интенсивном пластическом деформировании металлов и сплавов под давлением [10]. Они также могут оказаться полезными при изучении механизмов влияния давления на процессы диффузионного массопереноса в деформируемых наноматериалах.

ВЫВОДЫ

1. Основной причиной возникновения избыточного объема у дислокаций является асимметрия поведения потенциалов межатомных взаимодействий при растяжении и сжатии кристаллической решетки материалов.

2. Избыточный объем отдельных дислокаций в скоплениях может изменяться в широких пределах в зависимости от структуры и размера скопления.

Работа выполнена по НИР рег. № АААА-А17-117022250038-7.