Физика металлов и металловедение, 2020, T. 121, № 10, стр. 1019-1025

ВВЕДЕНИЕ

Известно, что взаимодействие дислокаций с границами зерен играет важную роль в процессах пластической деформации и разрушения поликристаллов. В частности, на границах зерен и их морфологических особенностях (фасетках, уступах и изломах) и в стыках зерен при неоднородном пластическом течении формируются специфические мезодефекты – линейные ротационные мезодефекты в виде дисклинаций, расположенных в стыках зерен или в вершинах фасеток, и планарные мезодефекты, представляющие собой распределенные вдоль границ зерен и фасеток системы виртуальных скользящих дислокаций [1]. Упругие поля напряжений от этих мезодефектов, в зависимости от их типа, мощности и других факторов, могут релаксировать либо путем аккомодационного скольжения дислокаций в приграничных областях зерен с образованием оборванных дислокационных границ [2, 3], полос скольжения [4, 5] полос переориентации [6], либо, при отсутствии этой возможности, путем зарождения микротрещин [7–9].

В свою очередь, перечисленные морфологические особенности границ могут иметь ростовое происхождение, появляться в процессе предшествующей термической обработки материала, или иметь деформационное происхождение. В последнем случае их формирование естественно связать с процессами прохождения пластических сдвигов через границы зерен. При этом, в зависимости от вида и степени локализации пластической деформации (осуществляющейся путем распространения полос скольжения, полос сдвига, полос переориентации, плоских скоплений решеточных дислокаций), величины прошедшего через границу сдвига и ориентации относительно нее плоскостей скольжения дислокаций, на границе могут возникать уступы, изломы и фасетки различных размеров и ориентаций [4, 6, 10–12], характеризующиеся различной дефектной структурой. Как показывают экспериментальные данные, склонность материала к деформационному фасетированию границ зерен зависит от размера зерна, спектра разориентировок границ, температуры и других факторов [13]. Для понимания этих закономерностей, а также описания развивающихся в окрестности фасеток процессов структурообразования и разрушения материала, необходимо разработать адекватные модели формирования фасеток деформационного происхождения, позволяющие рассчитать их кристалло-геометрические характеристики (ориентацию и длину фасеток) и характеристики их дефектной структуры, реализующиеся при различных схемах взаимодействия решеточных дислокаций с границами зерен.

Различные аспекты этого взаимодействия рассматривались в работах [4, 7, 14–19]. При этом теоретический анализ прохождения решеточных дислокаций через границы ограничивался рассмотрением прохождения одиночных дислокаций через специальные границы зерен c появлением на границе ступенек атомного размера [17]. Но как показывают экспериментальные данные в процессе пластической деформации на границах зерен могут создаваться достаточно протяженные фасетки субмикронного и микронного размера [6, 11, 12], требующие для своего появления прохождения через границу большого числа дислокаций. Как показывают экспериментальные исследования [15], для прохождения сдвига через границу наиболее благоприятные условия реализуются в случае минимального рассогласования линий пересечения плоскостей скольжения дислокаций с плоскостью границы. Фактически это означает, что прохождение дислокаций через границу, имеющую даже небольшую компоненту кручения, существенно затруднено. Наиболее благоприятный случай для прохождения сдвига реализуется для границы наклона, когда эти линии соосны.

В настоящей работе проведен анализ условий формирования и рассчитаны характеристики фасеток, возникающих при взаимодействии плоского скопления дислокаций с большеугловой границей наклона.

ОПИСАНИЕ МОДЕЛИ

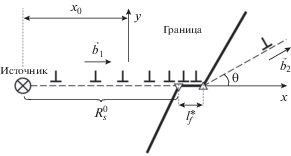
Рассмотрим расположенное в плоскости скольжения, действующей в первом зерне, скопление, состоящее из дислокаций с вектором Бюргерса ${{\vec {b}}_{1}},$ поджатое внешним напряжением $\hat {\sigma }$ к большеугловой границе наклона с разориентировкой $\theta .$ Для прохождения дислокации через границу необходимо переориентировать вектор Бюргерса дислокации первого зерна ${{\vec {b}}_{1}}$ в вектор Бюргерса дислокации ${{\vec {b}}_{2}}$ второго зерна. Другими словами, необходимо осуществить реакцию диссоциации ${{\vec {b}}_{1}} = {{\vec {b}}_{2}} + \Delta \vec {b}$ дислокации первого зерна на дислокацию второго зерна ${{\vec {b}}_{2}}$ ($\left| {{{{\vec {b}}}_{1}}} \right| = \left| {{{{\vec {b}}}_{2}}} \right| = b$) и дислокацию ориентационного несоответствия с разностным вектором Бюргерса $\Delta \vec {b}.$ В результате такой реакции и выхода дислокации ${{\vec {b}}_{2}}$ во второе зерно на границе создается ступенька, ориентированная вдоль исходной плоскости скольжения дислокаций в первом зерне. Ее длина $\Delta l$ определяется проекцией вектора Бюргерса дислокации ${{\vec {b}}_{2}}$ на плоскость ступеньки: $\Delta l = b\cos \theta .$ Кроме того, на этой ступеньке остается дислокация ориентационного несоответствия. В дальнейшем будем считать, что температура деформации такова, что диффузионными процессами переползания дислокаций вдоль границы и проскальзывания по границам можно пренебречь. По мере ухода дислокации ${{\vec {b}}_{2}}$ во второе зерно, дислокационное скопление поджимается внешним напряжением к границе и при выполнении определенных условий (рассмотренных ниже) происходит прохождение через границу следующей дислокации. Последовательное повторение этого процесса приводит к образованию на границе фасетки длиной ${{l}_{f}} = n\Delta l,$ где $n$ – число ушедших во второе зерно дислокаций. Раскладывая вектор Бюргерса дислокаций ориентационного несоответствия на нормальную и тангенциальную к плоскости фасетки компоненты, ее дефектное содержание можно описать как суперпозицию двух планарных распределений виртуальных дислокаций. Первое из них можно представить в виде дислокационной стенки наклона, сформированной сидячими дислокациями, порождающими на фасетированном участке границы зерна дополнительную разориентировку $\Delta \theta = {{\Delta {{b}_{n}}} \mathord{\left/ {\vphantom {{\Delta {{b}_{n}}} {{{l}_{f}}}}} \right. \kern-0em} {{{l}_{f}}}}$. Далее будем ее рассматривать как двухосный диполь клиновых дисклинаций длины ${{l}_{f}}$ и мощности ${{w}_{d}} = \Delta \theta .$ Второе из них можно представить в виде распределенных в плоскости фасетки виртуальных скользящих дислокаций. В отличие от стенки сидячих дислокаций, скользящие компоненты дислокаций распределены вдоль фасетки в поле внешних и внутренних напряжений неравномерно. Их суммарный вектор Бюргерса зависит как от числа прошедших через границу дислокаций, так и от числа находящихся на фасетке дислокаций первого зерна. В дальнейшем, для упрощения расчетов, при анализе условий, необходимых для прохождения пластического сдвига через границу, скопление дислокаций в первом зерне и его головную часть, расположенную на фасетке, будем рассматривать в виде единого скопления континуально распределенных скользящих дислокаций.

Проанализируем условия прохождения пластического сдвига через границу наклона и параметры формирующейся при этом фасетки. Рассмотрим случай, когда по мере ухода дислокаций во второе зерно, заторможенное границей зерна скопление дислокаций пополняется за счет срабатывания дислокационного источника в первом зерне. Схематическое представление процесса формирования фасетки для случая, когда угол между плоскостями скольжения решеточных дислокаций 1-го и 2-го зерна совпадает с углом разориентировки, показано на рис. 1. При этом будем считать заданными расстояние от источника до границы зерна $R_{s}^{0},$ критическое напряжение срабатывания источника ${{\sigma }_{s}},$ внешнее напряжение $\hat {\sigma }$ и разориентировку границы $\theta .$ При дальнейших расчетах удобно также задать параметры, характеризующие систему на каждом этапе формирования фасетки, а именно, текущий суммарный вектор Бюргерса дислокаций скопления $\vec {B} = (\begin{array}{*{20}{c}} B&0 \end{array})$ и текущую длину фасетки ${{l}_{f}}.$ Выберем систему координат, связанную с фасеткой зерна так, как показано на рис. 1 с началом координат помещенным в центр дислокационного скопления. Поскольку диполь дисклинаций расположен в плоскости фасетки ориентированной вдоль плоскости скольжения дислокации первого зерна и, следовательно, не взаимодействует с дислокациями скопления, то длина скопления $L$ и распределение модуля плотности вектора Бюргерса $\rho (x)$ определяются известными выражениями [20]:

где ${{\sigma }_{1}}$ – сдвиговое напряжение в плоскости скольжения дислокации ${{\vec {b}}_{1}},$ $G$ и $\nu $ – модуль сдвига и коэффициент Пуассона материала соответственно.

В рамках рассматриваемой модели процесс прохождения пластического сдвига через границу зерна возможен при одновременном выполнении двух условий:

1) энергетические затраты, необходимые для создания новых участков границы (по мере увеличения длины фасетки) и формирования скользящей решеточной дислокации в плоскости скольжения во втором зерне (будем считать, что по завершению процесса отщепления дислокации она расположена на расстоянии от границы равном удвоенному радиусу ядра дислокации ${{r}_{c}}$), должны компенсироваться работой внешних напряжений (критерий № 1);

2) при выполнении критерия № 1 должны обеспечиваться условия ухода дислокации во второе зерно. Это возможно в том случае, когда суммарная сила отталкивания, действующая на эту дислокацию со стороны скопления дислокаций и внешнего сдвигового напряжения в плоскости скольжения во втором зерне, превышает силу притяжения между уходящей дислокацией и расположенным на фасетке диполем дисклинаций (критерий № 2).

Первый критерий запишем в виде

где

– упругая энергия скопления до ($i = 1$) и после ($i = 2$) осуществления процесса отщепления дислокации во второе зерно,

В выражении (5) учтено то обстоятельство, что после отщепления дислокации во второе зерно в области фасетки $\left( {{{x}_{b}},{L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}} \right)$ остается дислокация ориентационного несоответствия с модулем плотности вектора Бюргерса $2\rho (x)\sin \left( {{\theta \mathord{\left/ {\vphantom {\theta 2}} \right. \kern-0em} 2}} \right).$ Величина ${{x}_{b}}$ определяется из выражения

В выражении (3) ${{W}_{{{\alpha ,\beta }}}}$ – функция погонной энергии взаимодействия двух единичных дислокаций с координатами $({{x}_{{\alpha }}},{{y}_{{\alpha }}})$ и $({{x}_{{\beta }}},{{y}_{{\beta }}}){\text{:}}$

где $D = \frac{G}{{2\pi (1 - {v})}},$ $\vec {R} = \left( {{{x}_{{\alpha }}} - {{x}_{{\beta }}}\,\,{{y}_{{\alpha }}} - {{y}_{{\beta }}}} \right),$ $\vec {e}_{{\alpha }}^{{(i)}}$ и $\vec {e}_{{\beta }}^{{(i)}}$ – единичные вектора направленные вдоль векторов Бюргерса, взаимодействующих дислокаций. $E_{{\gamma }}^{{(1)}},$ $E_{{\gamma }}^{{(2)}}$ – поверхностная энергия фасетки до и после осуществления процесса отщепления дислокации во второе зерно: где $\gamma $ – удельная поверхностная энергия. ${{E}_{{{{b}_{2}}}}}$ – упругая энергия дислокации ${{\vec {b}}_{2}}$ с радиусом ядра ${{r}_{c}}{\text{:}}$

${{E}_{{p,{{b}_{2}}}}}$ – энергия упругого взаимодействия скопления и отщепившейся во второе зерно дислокации. При численных расчетах эта дислокация рассматривается как равномерно распределенное скопление континуальных дислокаций с плотностью вектора Бюргерса ${{\rho }_{{{{b}_{2}}}}}({{x}_{{{{b}_{2}}}}}) = {b \mathord{\left/ {\vphantom {b {2{{r}_{c}}}}} \right. \kern-0em} {2{{r}_{c}}}}{\text{:}}$

${{E}_{{d,{{b}_{2}}}}}$ – энергия взаимодействия диполя дисклинаций и дислокации ${{\vec {b}}_{2}}{\text{:}}$

E_{d, Δb} – энергия упругого взаимодействия диполя дисклинаций с дислокацией ориентационного несоответствия $\Delta \vec {b}{\text{:}}$

${{A}_{{pl}}}$ – работа пластической деформации, осуществляемая при смещении дислокаций скопления на расстояние $\Delta l = b\cos \theta $ и перемещении дислокации ${{\vec {b}}_{2}}$ на расстояние $2{{r}_{c}}$ вдоль плоскости скольжения во втором зерне:

где ${{\sigma }_{2}}$ – сдвиговое напряжение в плоскости скольжения дислокации ${{\vec {b}}_{2}}.$

Критерий ухода дислокации во второе зерно (критерий № 2) запишем в виде:

где ${{\sigma }_{{th}}}$ – напряжение Пайерлса, ${{\sigma }_{p}}(x,y)$ – сдвиговое напряжение от скопления в плоскости скольжения дислокации второго зерна, где $\vec {n}$ – единичный вектор нормали к плоскости скольжения дислокации ${{\vec {b}}_{2}},$ ${{\vec {e}}_{{{{b}_{2}}}}}$ – единичный вектор направленный вдоль вектора Бюргерса ${{\vec {b}}_{2}},$ $G(x - x{\kern 1pt} ',y)$ – функция напряжений от расположенной в точке $(x{\kern 1pt} ',0)$ дислокации скопления с единичным вектором Бюргерса, направленным вдоль оси $Ox$ [20]. ${{\sigma }_{d}}(x,y) = \vec {n} \cdot {{\hat {\sigma }}_{d}}(x,y) \cdot {{\vec {e}}_{{{{b}_{2}}}}}$ – сдвиговое напряжение от диполя дисклинаций в плоскости скольжения во втором зерне, где ${{\hat {\sigma }}_{d}}$ – функция тензора напряжений от диполя дисклинаций [21 ] .

РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ И ОБСУЖДЕНИЕ

Численные расчеты проводились для случая простой кубической решетки. Рассматривалась граница наклона с осью разориентировки $\left[ {001} \right]$, направленной вдоль оси Oz. Отметим, что дислокации могут уходить во второе зерно как по плоскости скольжения, показанной на рис. 1, так и по плоскости скольжения, повернутой на угол (90° – θ). Из этих двух вариантов прохождения дислокаций через границу наиболее энергетически выгоден тот, при котором вектор Бюргерса дислокации ориентационного несоответствия, возникающей в границе при отщеплении дислокации во второе зерно, имеет минимальное значение [15]. Нетрудно видеть, что, исходя из этого критерия, первый из рассмотренных вариантов прохождения реализуется при углах разориентировки границы θ < 45°. В противном случае реализуется второй вариант прохождения. Результаты расчетов характеристик фасетки, проведенных для второго варианта прохождения, в силу симметрии полей внутренних напряжений от скопления дислокаций и дислокационного диполя относительно плоскости скольжения в первом зерне, несущественно отличаются от приведенных ниже результатов расчетов, выполненных для первого варианта прохождения.

При расчете длины фасетки считалось, что процесс ее формирования (при последовательном прохождении дислокаций скопления через границу) прекращался, как только переставали действовать рассмотренные выше критерии. Численный анализ критериев прохождения дислокационного скопления через границу зерна и расчеты длины фасетки были проведены для следующих значений параметров и варьируемых величин: $b = 2.7 \times {{10}^{{ - 4}}}\,\,{\text{мкм}},$ ${{r}_{c}} = b,$ ${v} = 0.3,$ ${{\sigma }_{s}} = 3.8 \times {{10}^{{ - 3}}}G,$ ${{\sigma }_{{{\text{th}}}}} = 0.6 \times {{10}^{{ - 4}}}G,$ $\theta = 10^\circ {\text{--}}45^\circ ,$ $\gamma = {{Gb} \mathord{\left/ {\vphantom {{Gb} {24}}} \right. \kern-0em} {24}},$ ${{\sigma }_{1}} = \left( {5 \times {{{10}}^{{ - 3}}} - 8 \times {{{10}}^{{ - 3}}}} \right)G$ (в расчетах использовалось значение $G = 45\,\,{\text{ГПа}}$ для меди), $R_{s}^{0} = 0.5{\text{--}}10\,\,{\text{мкм}},$ $B = \left( {2{\text{--}}200} \right)b.$

Результаты расчетов зависимости длины фасетки $l_{f}^{*}$ от количества дислокаций в скоплении ${B \mathord{\left/ {\vphantom {B b}} \right. \kern-0em} b}$ при различных значениях угла разориентировки границы $\theta $ и внешнего напряжения $\hat {\sigma }$ представлены на рис. 2.

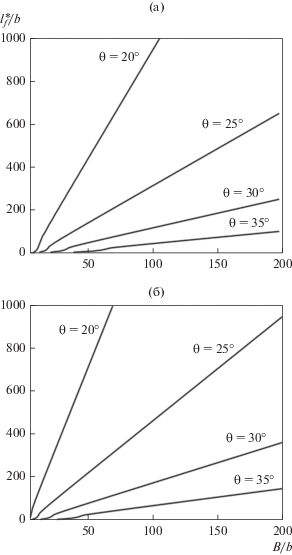
Как показывают результаты расчета, появление фасетки на границе зерна при взаимодействии границы с плоским скоплением дислокаций возможно только при превышении суммарного вектора Бюргерса скопления некоторого критического значения, величина которого зависит от внешнего напряжения и разориентировки границы. В исследуемом диапазоне значений параметров критическое число дислокаций в скоплении относительно невелико (10–15 штук). При увеличении числа дислокаций в скоплении увеличивается и длина фасетки.

Очевидно, что максимальное значение $B$ и, соответственно, максимальная длина фасетки $l_{f}^{*}$ связаны с расстоянием от дислокационного источника до границы зерна $R_{s}^{0}$ и пороговым напряжением срабатывания источника ${{\sigma }_{s}}.$

Связь этих величин можно определить из следующих соображений. Суммарный вектор Бюргерса $B$ скопления связан с длиной скопления $L$ соотношением (1), а суммарное сдвиговое напряжение ${{\sigma }^{\Sigma }},$ действующее в точке расположения дислокационного источника, связано с длиной скопления и координатой источника ${{x}_{0}}$ выражением [20]:

Выражая отсюда ${{x}_{0}},$ и принимая во внимание, что $R_{s}^{*} = \left| {{{x}_{0}}} \right| + \frac{L}{2}$ получим

где $R_{s}^{*}$ – расстояние от границы до источника после того, как процесс прохождения дислокаций через границу завершился. Найденная величина $R_{s}^{*}$ связана с исходным расстоянием от источника до границы $R_{s}^{0}$ выражением:

Для того чтобы получить зависимость длины фасетки $l_{f}^{*}$ от $R_{s}^{0}$ при заданных $\sigma $ и $\theta ,$ необходимо выразить $L$ через $l_{f}^{*}.$ Это можно сделать, используя выражение (1) и зависимости $l_{f}^{*}(B),$ полученные при моделировании. При достаточно большом количестве дислокаций в скоплении $l_{f}^{*}(B)$ можно аппроксимировать линейной функцией:

где коэффициенты $\alpha (\sigma ,\theta )$ и $\beta (\sigma ,\theta )$ находятся с помощью метода регрессии. Тогда:

Подставляя данное выражение в (17) получим:

где $\chi = \frac{{\alpha (\sigma ,\theta )\left( {{{\sigma }^{2}} - \sigma _{s}^{2}} \right)}}{{2D\sigma }}.$

Результаты расчета зависимости длины фасетки $l_{f}^{*}$ от исходного расстояния между источником и границей $R_{s}^{0}$ при различных значениях $\theta $ и $\hat {\sigma }$ приведены на рис. 3.

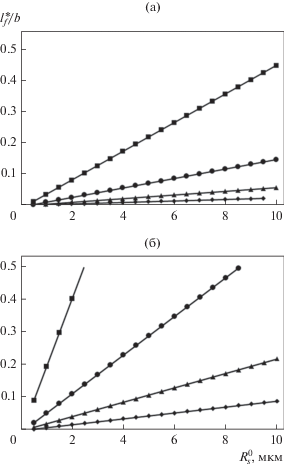
В интервале использованных в расчетах значений $\sigma $ и $\theta $ размер фасеток составляет десятые доли $R_{s}^{0}$ (рис. 3). Поскольку величина $R_{s}^{0}$ не может превышать размер зерна поликристалла, то отсюда следует важный вывод о том, что при измельчении зеренной структуры материала склонность границ зерен к деформационному фасетированию должна уменьшаться.

Зависимость длины фасетки $l_{f}^{*}$ от разориентировки границы $\theta $ при разной величине внешнего напряжения и фиксированном суммарном векторе Бюргерса скопления $B$ показаны на рис. 4.

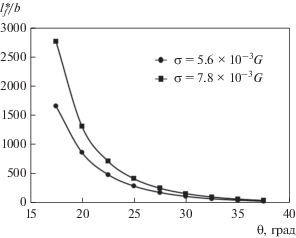
Как видно из этого рисунка, длина фасетки уменьшается при увеличении разориентировки границы. Таким образом, наибольшую склонность к фасетированию должны проявлять мало- и среднеугловые границы зерен.

Отметим, что при деформационном измельчении зерен поликристалла при больших пластических деформациях происходит не только уменьшение среднего размера зерна, но и смещение спектра разориентировок границ зерен поликристалла в область больших углов разориентировки [2]. Оба эти фактора работают на подавление фасетирования границ на поздних стадиях фрагментации поликристаллов.

Еще одним очевидным следствием рассмотренной модели деформационного фасетирования границ является образование во втором зерне полосы сдвига. Это следует из того, что при уходе дислокации во второе зерно и увеличении длины фасетки плоскость скольжения каждой следующей испущенной дислокации во втором зерне смещается относительно плоскости скольжения предыдущей на одно межплоскостное расстояние. Ширина такой полосы $h$ связана с длиной фасетки соотношением: $h = l_{f}^{*}\sin \theta .$

В заключение отметим, что формирование фасетки может сопровождаться аккомодационными процессами пластической деформации. Рассмотрение этих процессов будет проведено в последующих публикациях.

ЗАКЛЮЧЕНИЕ

Рассмотренная для случая взаимодействия плоского скопления решеточных дислокаций с границей наклона модель формирования деформационной фасетки хорошо согласуется с наблюдаемыми на эксперименте основными закономерностями фасетирования границ при пластическом деформировании поликристаллов. Из нее следует, что при измельчении зеренной структуры материала и смещении спектра разориентировок границ в область больших углов разориентировки склонность границ зерен к деформационному фасетированию уменьшается.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 20-08-00867.