Физика металлов и металловедение, 2020, T. 121, № 3, стр. 257-269

ВВЕДЕНИЕ

Известные гальваномагнитные явления в металлах и полупроводниках – магниторезистивный эффект и эффект Холла – обусловлены влиянием магнитного поля B на движение электронов проводимости, вызываемое электрическим полем E [1]. Влияние магнитного поля на переносимый электронами электрический ток плотности j обусловлено силой Лоренца eE + $\frac{e}{c}[v \times B],$ которая действует на движущийся со скоростью v электрон, несущий на себе электрический заряд e. Исторически первая работа по наблюдению влияния магнитного поля на электрический ток была опубликована Эдвином Холлом еще в 1879 г. [2]. Эффект Холла проявляется как появление в образце электрического поля, перпендикулярного направлению пропускаемого через образец тока, при помещении образца в поперечное магнитное поле. Для реального образца конечных размеров эффект Холла приводит к появлению вблизи граней образца областей накопления электрического заряда, которые и являются источником поперечного электрического поля.

Помимо электрического заряда, электроны несут на себе собственный механический момент, спин и соответствующий ему магнитный момент. Спин-орбитальное взаимодействие электронов с кристаллической решеткой и ее дефектами ведет к тому, что электроны с разным значением проекции спина, участвующие в создании электрического тока, будут отклоняться в разные стороны перпендикулярно направлению плотности тока j. Это явление, получившее название спинового эффекта Холла, было теоретически предсказано Дьяконовым и Перелем в 1971 г. [3, 4]. В отличие от классического эффекта Холла [2], спиновый эффект Холла [3, 4] возникает при протекании тока в отсутствие какого-либо внешнего магнитного поля и проявляется в появлении вблизи граней образца областей аккумуляции неравновесной спиновой плотности. Наличие у электронов проводимости спина ведет естественным образом и к спиновой зависимости классического эффекта Холла. В работе [5] описан спин-зависящий классический эффект Холла без учета спин-орбитального взаимодействия – возбуждение электрическим током перпендикулярного ему спинового потока в геометрии классического эффекта Холла, когда поперечным к току магнитным полем создана спиновая поляризация Паули.

Спин-орбитальное взаимодействие в условиях протекания электрического тока в поперечном магнитном поле приводит к появлению спиновой аккумуляции вблизи граней образца, зависящей от величины магнитного поля. Как было показано в работе [6], приложенное магнитное поле уменьшает величину спиновой поляризации в области поверхностной аккумуляции, что в результате приводит к эффекту положительного магнитосопротивления. Этот эффект дает возможность изучать явление спиновой аккумуляции с помощью гальваномагнитных измерений.

Во всех вышеупомянутых гальваномагнитных эффектах магнитное поле B по умолчанию предполагается однородным. Между тем неоднородность магнитного поля может играть в спин-транспортных явлениях существенную роль. Отвлечемся (в дидактических целях) от квантовой природы спина и представим электрон как классическую частицу, обладающую магнитным моментом μ. Тогда при рассмотрении движения электрона в неоднородном магнитном поле мы должны принять во внимание действующую на него силу $\nabla (\mu \cdot B),$ равную с обратным знаком пространственному градиенту от энергии взаимодействия магнитного момента μ с полем B.

Здесь уместно будет упомянуть работу Штерна и Герлаха [7], в которой именно особенности движения частиц – носителей спина в неоднородном магнитном поле были использованы для доказательства квантовой природы спина.

В выполненных к настоящему времени работах по спин-зависящим гальваномагнитным явлениям вопросы учета неоднородностей магнитного поля рассматривали лишь фрагментарно. Поэтому сегодня актуальной задачей является построение квантовой теории спин-транспортных явлений, пригодной для описания спиновых токов и гальваномагнитных явлений в металлах и полупроводниках в неоднородных внешних полях с учетом спин-орбитальных взаимодействий.

Вопросы описания спиновых транспортных явлений в проводящих твердых телах составляют предмет многочисленных исследований в области спинтроники. Исследование эффектов, для которых понятие “спиновый ток” является ключевым, является одним из “горячих” направлений современной физики конденсированного состояния вещества. Здесь уместно будет сослаться на монографию [8], 25 глав которой дают полное представление о прогрессе в изучении эффектов, связанных со спиновыми токами, а также на коллективную монографию [9], в которой описан широкий круг спин-зависимых оптических, электрических и магнитных свойств полупроводников.

Главная задача настоящей работы – сформулировать основные уравнения для описания электрических и спиновых токов, протекающих в системе, помещенной в неоднородное магнитное поле. В случае, когда речь идет об электронах проводимости парамагнитных металлов и полупроводников, действующие на электрон силы могут создаваться неоднородным внешним магнитным полем. Если же нас интересует электронный спиновый транспорт в магнитоупорядоченных проводниках, в которых реализуется неоднородное магнитное состояние, то под неоднородным магнитным полем, действующем на спин электрона, можно понимать эффективное обменное поле, усредненное по элементарному объему магнетика и пропорциональное неоднородной спонтанной намагниченности вещества. Задача последнего раздела – дать описание спинового и электрического транспорта в киральных гелимагнетиках, где эффекты неоднородного магнитного состояния могут наблюдаться экспериментально.

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ. СПИНОВЫЙ ТОК

Последовательное описание транспорта заряда и спина в электронной системе в металлах и полупроводниках может быть реализовано с помощью аппарата квантового кинетического уравнения для квантовой функции распределения $\hat {f}(r,p,t),$ зависящей от координаты r, электронного квазиимпульса p и времени t, но являющейся оператором в спиновом пространстве. Будучи квантовым обобщением хорошо известного и повсеместно применяемого уравнения Больцмана на случай наличия у носителей заряда спинового момента, квантовое кинетическое уравнение для $\hat {f}(r,p,t)$ является, возможно, наиболее простым и эффективным теоретическим инструментом для изучения транспорта заряда и спина в условиях, когда орбитальное движение электронов может быть рассмотрено на языке классической механики.

Итак, наша задача – описание кинетических явлений в системе электронов проводимости твердого тела, которые являются носителями электрического заряда e, а также спинового и связанного с ним магнитного момента μ. Величина магнитного момента μ определяется значением g-фактора электрона соотношением μ = gμ_B/2, где μ_B – магнетон Бора. Результатом решения поставленной задачи должны стать материальные уравнения – соотношения, связывающие потоки электрического заряда и спинового (магнитного) момента электронов с индуцирующими их внешними электрическим и магнитным полями.

Пусть ${{\varepsilon }_{p}}$ – энергетический спектр электронов проводимости кристалла. Закон зависимости энергии ${{\varepsilon }_{p}}$ от квазиимпульса $p$ определяет скорость электрона $v = ({\partial \mathord{\left/ {\vphantom {\partial {\partial p}}} \right. \kern-0em} {\partial p}}){{\varepsilon }_{p}}.$ Пусть $\hat {\mu }~$ – оператор магнитного момента электрона. Ниже мы будем использовать известное представление оператора $\hat {\mu }~$ через спиновые матрицы Паули $\hat {\sigma }{\text{:}}$

Поскольку квантовая функция распределения $\hat {f}~\left( {r,p,t} \right)$ представляет собой оператор в спиновом пространстве, который может быть представлен как матрица по спиновым переменным, без каких-либо ограничений общности можно представить $\hat {f}$ в виде

Вновь введенные функции $n\left( {r,p,t} \right)$ и $s\left( {r,p,t} \right)~$ определяются следующими соотношениями:

Здесь и ниже ${\text{Tr}}\hat {M}$ – операция взятия следа (шпура) матрицы $\hat {M}.$

Функция $n\left( {r,p,t} \right)$ имеет смысл функции распределения электронной плотности в импульсном пространстве. Суммируя $n\left( {r,p,t} \right)$ по всем возможным $p{\text{,}}$ получаем величину $N\left( {r,t} \right)~$ – плотность числа электронов в данной точке пространства в заданный момент времени:

Просуммировав по всем $p~$ произведение $v~n\left( {r,p,t} \right),$ получаем величину $I\left( {r,t} \right)~$ – плотность потока электронов в точке пространства $r$ в момент времени $t{\text{:}}$

Произведение $eN\left( {r,t} \right)$ дает нам плотность электрического заряда, тогда как $eI\left( {r,t} \right)$ суть плотность электрического тока $j\left( {r,t} \right).$

Введенная определением (4) функция $s\left( {r,p,t} \right)$ по аналогии с $n\left( {r,p,t} \right)$ может быть названа функцией распределения спиновой плотности. Суммируя $s\left( {r,p,t} \right)$ по всем возможным $p{\text{,}}$ получаем величину $S\left( {r,t} \right),$ которую ниже будем называть спиновой плотностью:

Просуммировав по $p~$ тензорное произведение векторов $v \otimes s\left( {r,p,t} \right),$ получаем величину $J\left( {r,t} \right),$ которую мы будем называть плотностью спинового тока:

Здесь необходимо сделать одно важное замечание. При записи определения спинового тока (8) мы использования знак $ \otimes ~$ для обозначения математической операции тензорного произведения векторов. В результате выполнения операции тензорного произведения векторов v и s получается тензор – диада $v \otimes s{\text{,}}$ который в матричном представлении имеет компоненты ${{(v{\text{\;}} \otimes s)}_{{ij}}} = {{v}_{i}}{{s}_{j}}.$ Для обозначения тензоров мы будем использовать “наклонный жирный” шрифт, тогда как векторы будут обозначаться “прямым жирным” шрифтом. Таким образом, введенная нами величина $J\left( {r,t} \right)$ – тензор плотности спинового тока. Произведение $\frac{\hbar }{2}S\left( {r,t} \right)$ дает нам вектор плотности спинового момента электронов, тогда как $\frac{\hbar }{2}J\left( {r,t} \right)~$ суть тензор плотности потока спинового момента электронов. Заметим здесь также, что введенная нами величина спиновой плотности $S\left( {r,t} \right)$ имеет ту же самую размерность, что и электронная плотность $N\left( {r,t} \right).$ Аналогично, одинаковую размерность имеют плотность потока электронов $I\left( {r,t} \right)$ и плотность спинового тока $J\left( {r,t} \right).$

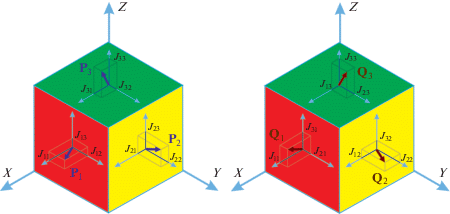
Тензор спинового тока в конкретном базисе ортогональных единичных векторов $\left\{ {{{e}_{i}}} \right\},$ может быть представлен как $J = {{J}_{{ij}}}{{e}_{i}} \otimes {{e}_{j}},$ где ${{J}_{{ij}}}~$ – координаты тензора спинового тока. Иногда вместо тензора $J~$ удобно использовать его проекции на орты $\left\{ {{{e}_{i}}} \right\}.$ Этими проекциями могут быть либо три вектора ${{P}_{i}}$ = ${{e}_{i}} \cdot J,$ либо тройка векторов ${{Q}_{i}}$ = = $J \cdot {{e}_{i}}.$ В матричном представлении ${{P}_{i}} = {{J}_{{ij}}}{{e}_{j}}$ и ${{Q}_{j}} = {{J}_{{ij}}}{{e}_{i}}.$ Последние равенства показывают, что векторы ${{P}_{i}}$ – это вектор-строки, а векторы ${{Q}_{j}}$ – это вектор-столбцы матрицы ${{J}_{{ij}}},$ представляющей тензор $J.$ Вектор ${{P}_{i}}$ по способу определения может быть назван поляризацией спинового тока, текущего в направлении i. Вектор ${{Q}_{i}}$ характеризует направление, в котором течет компонента спиновой плотности ${{S}_{i}}$, и может быть назван потоком i-той компоненты спиновой плотности. Таким образом, получаем два альтернативных представления тензора спинового тока:

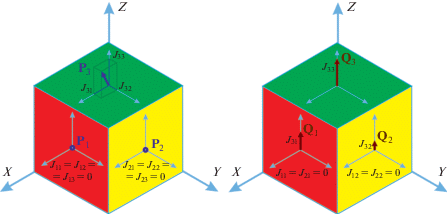
Иллюстрация представления произвольного тензора спинового тока $J$ на языке векторов ${{P}_{i}}~$ и ${{Q}_{i}}~$ дана на рис. 1. На рис. 2 приведены $P$- и $Q$-представления тензора спинового тока $J$ для случая, когда отличны от нуля только три компоненты одной z-строки матрицы ${{J}_{{ij}}}.$ В этом случае среди всех векторов ${{P}_{i}}$ отличен от нуля только один вектор поляризации тока ${{P}_{3}},$ который может иметь произвольное направление, а все три вектора ${{Q}_{i}}~$ направлены вдоль одной оси z.

КВАНТОВОЕ КИНЕТИЧЕСКОЕ УРАВНЕНИЕ

Квантовое кинетическое уравнение для $\hat {f}~\left( {r,p,t} \right)$ может быть получено последовательным образом из уравнения для одночастичного статистического оператора $\hat {\rho },$ удовлетворяющего уравнению фон Неймана

в котором ${{\hat {H}}_{0}}$ – оператор кинетической и потенциальной энергии электрона в поле идеальной кристаллической решетки, ${{\hat {H}}_{E}} = - e~E \cdot r$ и ${{\hat {H}}_{B}} = \mu ~B \cdot \hat {\sigma }$ – операторы взаимодействия с электрическим полем напряженности $E\left( {r,t} \right)$ и магнитным полем индукции $B\left( {r,t} \right)$ соответственно. Оператор $\hat {V} = U - \frac{\hbar }{{4{{m}^{2}}{{c}^{2}}}}\hat {\sigma }$ ⋅ $\left[ {p \times \frac{\partial }{{\partial r}}U} \right]$ описывает спин-орбитальное взаимодействие электрона с рассеивателями – всевозможными дефектами кристаллической решетки, создающими потенциал $U.$ Собственные значения гамильтониана ${{\hat {H}}_{0}}$ – суть энергетический спектр электрона ${{\varepsilon }_{p}}.$

Квантовое кинетическое уравнение для $\hat {f}~\left( {r,p,t} \right)$ может быть получено из (9) путем записи уравнения для оператора $\left\langle {\hat {\rho }} \right\rangle ,$ где скобки 〈…〉 означают операцию усреднения по всем возможным конфигурациям рассеивающего потенциала $\hat {V}.$ Последующий переход к квазиклассическому пределу в уравнении для $\left\langle {\hat {\rho }} \right\rangle $ при описании только орбитального движения электронов и дает интересующее нас квантовое кинетическое уравнение для $\hat {f}~\left( {r,p,t} \right).$ Не имея возможности описать в данном сообщении детали этой довольно громоздкой процедуры, мы приведем здесь только конечное уравнение:

В уравнении (10) сумма второго и третьего члена – это квазиклассический предел квантовой скобки Пуассона $\frac{i}{\hbar }\left[ {{{{\hat {H}}}_{0}} + {{{\hat {H}}}_{E}},\left\langle {\hat {\rho }} \right\rangle } \right],$ тогда как сумма четвертого и пятого членов – это квазиклассический предел от $\frac{i}{\hbar }\left[ {{{{\hat {H}}}_{B}},\left\langle {\hat {\rho }} \right\rangle } \right].$ Последний член $\hat {R}$ – это квазиклассический предел усредненной по конфигурациям рассеивающего потенциала квантовой скобки Пуассона $\left\langle {\frac{i}{\hbar }\left[ {\hat {V},\hat {\rho }} \right]} \right\rangle .$ Этот член описывает релаксацию квантовой функции распределения $\hat {f}~$ к своему локально-равновесному значению ${{\hat {f}}_{{\text{L}}}}$ и выражается через отклонение $\delta \hat {f} = \hat {f} - {{\hat {f}}_{{\text{L}}}}.$

Заметим, что сумма четвертого и пятого членов в уравнении (10) может быть записана как скалярное произведение векторного оператора $\hat {F} = eE + \frac{e}{c}\left[ {v \times B} \right]$ – $\mu \frac{\partial }{{\partial r}}\left( {\hat {\sigma } \cdot B} \right)$ и производной $\frac{{\partial{ \hat {f}}}}{{\partial p}}.$ Последнее слагаемое в выражении для оператора $\hat {F}$ можно трактовать как квантовую добавку к классической силе Лоренца $eE + \frac{e}{c}\left[ {v \times B} \right],$ действующей на электрон в неоднородном поле в силу наличия у него спина.

Уравнение (10) для $\hat {f}$ с точностью до использованных обозначений совпадает с уравнением, приведенным в работах [10, 11], в которых интеграл столкновений $\hat {R}$ был записан феноменологически в приближении времени релаксации. В отличие от этих работ, мы в следующем разделе приведем строгий результат квантовомеханического рассмотрения интеграла столкновений, справедливый для любого рассеивающего потенциала $\hat {V}.$ Отметим, что продуктивность идеи использования аппарата квантового кинетического уравнения для построения теории спин-транспортных явлений была продемонстрирована в работах [12, 13] по выводу граничных условий для функций распределения, описывающих спиновые процессы рассеяния электронов на дефектах поверхности металла.

Возьмем след от уравнения (10) и выполним ту же операцию после умножения уравнения (10) на $\hat {\sigma }{\text{,}}$ в результате получим систему связанных кинетических уравнений для функций распределения электронной плотности и спиновой плотности электронов:

где введены обозначения $R = {\text{Tr}}\hat {R},$ $R = {\text{Tr}}\hat {\sigma }\hat {R}.$

Кинетические уравнения (11), (12) необходимо использовать при описании транспортных свойств систем, в которых длина свободного пробега электронов проводимости сравнима или превышает характерный масштаб изменения полей B и E, а также характерные линейные размеры образца. В этом случае из уравнений (11), (12) после их решения будет получена существенно нелокальная связь потоков и полей. В обратном предельном случае, когда длина свободного пробега электронов является наименьшим параметром размерности длины, можно существенно упростить решение задачи, если перейти от описания системы на языке функций распределения к описанию на языке плотностей и потоков. Пренебрегая в этом случае пространственной дисперсией, исходя из уравнений (11), (12) для функций распределения, ниже мы получим замкнутую систему уравнений для плотностей $N\left( {r,t} \right),$ $S\left( {r,t} \right)$ и потоков $I\left( {r,t} \right),$ $J\left( {r,t} \right).$

ПЕРЕХОД К “СОКРАЩЕННОМУ” ОПИСАНИЮ СПИНОВОЙ КИНЕТИКИ

В отсутствие внешних полей система находится в состоянии полного термодинамического равновесия и описывается статистическим оператором ${{\hat {f}}_{0}} = F\left( {{{\varepsilon }_{p}} - {{\zeta }_{0}}} \right),$ где $F\left( \varepsilon \right)$ = ${1 \mathord{\left/ {\vphantom {1 {({\text{exp}}\left( {{\varepsilon \mathord{\left/ {\vphantom {\varepsilon {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}}) + 1} \right)}}} \right. \kern-0em} {({\text{exp}}\left( {{\varepsilon \mathord{\left/ {\vphantom {\varepsilon {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}}) + 1} \right)}}$ – функция Ферми, ${{\zeta }_{0}}$ – химический потенциал, определяемый из условия $\sum\nolimits_p {2F\left( {{{\varepsilon }_{p}} - {{\zeta }_{0}}} \right)} $ = ${{N}_{0}},$ где ${{N}_{0}}$ – равновесная плотность электронов.

Определим мгновенное локально-равновесное значение квантовой функции распределения системы, помещенной в магнитное поле $B\left( {r,t} \right),$ как оператор ${{\hat {f}}_{{\text{L}}}} = F\left( {{{\varepsilon }_{p}} + \mu ~B \cdot \hat {\sigma } - {{\zeta }_{{\text{L}}}}} \right).$ Здесь ${{\zeta }_{{\text{L}}}}$ – локальный химический потенциал, определяемый из условия $\sum\nolimits_p {{\text{Tr}}F\left( {{{\varepsilon }_{p}} + \mu ~B \cdot \hat {\sigma } - {{\zeta }_{{\text{L}}}}} \right)~} = N.$ Считая энергию спинового расщепления $\mu B$ и изменения химпотенциала ${{\zeta }_{{\text{L}}}} - {{\zeta }_{0}}$ малыми по сравнению с энергией Ферми, запишем ${{\hat {f}}_{{\text{L}}}}$ в линейном по внешним полям приближении как

где $F{\kern 1pt} '\left( \varepsilon \right)$ – производная функции $F\left( \varepsilon \right).$ Соответствующая этому состоянию спиновая функция распределения ${{s}_{{\text{L}}}}\left( {r,p,t} \right)$ = $2F{\kern 1pt} '\left( {{{\varepsilon }_{p}} - {{\zeta }_{0}}} \right)~\mu B{\text{,}}$ тогда как спиновая плотность ${{S}_{{\text{L}}}}\left( {r,t} \right)$ = $2\sum\nolimits_p {F{\kern 1pt} '\left( {{{\varepsilon }_{p}} - {{\zeta }_{0}}} \right)~\mu B} {\text{.}}$ Локально равновесная спиновая функция распределения ${{s}_{{\text{L}}}}\left( {r,p,t} \right)$ может быть выражена через спиновую плотность ${{S}_{{\text{L}}}}$ соотношением

Локальное изменение химпотенциала ${{\zeta }_{{\text{L}}}} - {{\zeta }_{0}}$ определяет отклонение локально-равновесной функции распределения числа частиц ${{n}_{{\text{L}}}}\left( {r,p,t} \right)$ от равновесного значения ${{n}_{0}} = 2F\left( {{{\varepsilon }_{p}} - {{\zeta }_{0}}} \right)$ как ${{n}_{{\text{L}}}} - {{n}_{0}}$ = $ - 2F{\kern 1pt} '\left( {{{\varepsilon }_{p}} - {{\zeta }_{0}}} \right)~\left( {{{\zeta }_{{\text{L}}}} - {{\zeta }_{0}}} \right).$ Это отклонение выражается через отклонение локальной плотности электронов N от ${{N}_{0}}$ соотношением

Переход от описания системы на языке функций распределения к “сокращенному” описанию на языке плотностей и потоков подразумевает возможность непосредственного выражения функций распределения через плотности и потоки.

“Сокращенное” представление ${{\hat {f}}_{{\text{R}}}}$ оператора $\hat {f}~$ мы определим формальным операторным уравнением ${{\hat {f}}_{{\text{R}}}} = F\left( {{{\varepsilon }_{{p - \hat {\pi }}}} + \mu ~B \cdot \hat {\sigma } - \hat {\zeta }} \right),$ в котором $\hat {\zeta }$ описывает локальные изменения энергии электронов из-за изменения плотностей $N\left( {r,t} \right),$ $S\left( {r,t} \right),$ а вектор $\hat {\pi }$ определяет локальный сдвиг распределения квантовой функции распределения в импульсном пространстве, обусловленный потоками заряда и спина $I\left( {r,t} \right),$ $J\left( {r,t} \right).$ В линейном по внешним полям приближении для ${{\hat {f}}_{{\text{R}}}}$ получаем уравнение

Химпотенциал $\zeta $ и векторный оператор $\hat {\pi }$ определяются из уравнений

После нахождения из уравнений (16), (17) операторов $\hat {\zeta }$ и $\hat {\pi }$ получаем выражение для ${{\hat {f}}_{{\text{R}}}}{\text{:}}$

где $\overline {v_{E}^{2}} = \sum\nolimits_p {v_{E}^{2}F{\kern 1pt} '} {{\left[ {\sum\nolimits_p {F{\kern 1pt} '} } \right]}^{{ - 1}}},$ ${{v}_{E}}$ – проекция скорости электрона на направление электрического поля. При получении соотношений (19), (20) для простоты мы считали спектр ${{\varepsilon }_{p}}$ электронов изотропным. Далее мы будем считать спектр ${{\varepsilon }_{p}}$ изотропным и квадратичным, введя в рассмотрение эффективную массу электронов m.

Перейдем теперь непосредственно к получению уравнений для плотностей и токов из уравнений (11), (12) для функций распределения. Просуммируем по $p$ уравнения (11) и (12), а затем просуммируем эти же уравнения после умножения их на скорость $v{\text{,}}$ в результате получим систему уравнений вида

где введены обозначения ${{\Omega }_{{\text{L}}}} = \frac{{2\mu }}{\hbar }B$ и ${{\Omega }_{{\text{C}}}} = \frac{{\left| e \right|}}{{mc}}B{\text{.}}$ Величина ${{\Omega }_{{\text{L}}}}$ – это Ларморовская частота, характеризующая прецессионное движение спина электронов, тогда как ${{\Omega }_{{\text{C}}}}$ – циклотронная частота, отвечающая движению электрона по циклотронным орбитам вследствие действия на заряд электрона силы Лоренца.

Система уравнений (21)–(24) не является замкнутой, поскольку вторые слагаемые в левых частях уравнений (23) и (24) выражаются через свертку функций распределения с квадратичными комбинациями вектора скорости электрона. Чтобы замкнуть систему уравнений, мы при вычислении вышеуказанных слагаемых пренебрежем отличием функций распределения $n$ и $s$ от функций ${{n}_{{\text{R}}}}$ и ${{s}_{{\text{R}}}},$ определенных уравнениями (19) и (20) соответственно. В результате получаем

Аналогично мы поступим и при вычислении сумм по квазиимпульсам от интегралов столкновений R и $R{\text{.}}$

ИНТЕГРАЛ СТОЛКНОВЕНИЙ

Дальнейшее рассмотрение требует конкретизации вида интегралов столкновений R и $R{\text{.}}$ Можно показать, что описывающий релаксацию интеграл столкновений $\hat {R}$ может быть записан в следующем виде:

где $~\delta {{\hat {f}}_{p}} \equiv \delta \hat {f}~\left( {r,p,t} \right),$ $\hat {T}_{{pp{\kern 1pt} '}}^{ \pm }\left( E \right)$ – матричные элементы оператора амплитуды рассеяния, который определяется рассеивающим потенциалом $\hat {V}$ и находится как решение уравнения Липпмана–Швингера

Первое слагаемое в (27), выражающееся через $\delta {{\hat {f}}_{p}},$ – это так называемый “уходный” член интеграла стокновений, описывающий уход электронов из состояния p во все возможные состояния при рассеянии на потенциале $\hat {V}.$ Второе слагаемое в (27), выражающееся через сумму по p' от слагаемых, содержащих $\delta {{\hat {f}}_{{p{\kern 1pt} '}}}$ – это так называемый “приходный” член интеграла столкновений, описывающий приход электронов в состояние p из всех других состояний p'.

Мы ограничимся здесь рассмотрением случая, когда рассеиватели электронов, формирующие потенциал $\hat {V}$ и определяющие вид оператора амплитуды рассеяния $\hat {T},$ не обладают собственным спином. Некоторые важные данные о структуре оператора $\hat {T}$ можно получить путем анализа свойств симметрии взаимодействия $\hat {V},$ поскольку амплитуду рассеяния можно представить в виде матричного элемента оператора рассеяния, а свойства симметрии оператора $\hat {T}$ совпадают со свойствами симметрии гамильтониана системы. Гамильтониан рассматриваемой системы предполагаем инвариантым относительно произвольных поворотов и пространственной инверсии. Следовательно, и оператор амплитуды рассеяния должен быть инвариантен относительно этих преобразований. Опираясь на эти фундаментальные свойства оператора $\hat {T},$ найдем его общий вид. Поскольку $\hat {T}$ является оператором в пространстве спиновых функций, его всегда можно представить в виде линейной комбинации матриц Паули $\hat {\sigma }$ и единичного оператора:

В разложении (29) величины $A~$ и $C~$ являются комплексно-значными функциями квазиимпульсов p и p'. Оператор амплитуды рассеяния $\hat {T}$ будет инвариантом произвольного поворота и инверсии только в том случае, если $A$ будет скаляром, а величина C − некоторым псевдовектором.

Введем в рассмотрение три единичных вектора:

Векторы c, c₊, c_– попарно ортогональны, а поэтому могут быть взяты в качестве базиса трехмерного пространства. Тогда вектор C можно представить в виде разложения $C = Cc$ + ${{C}_{ + }}{{c}_{ + }} + {{C}_{ - }}{{c}_{{ - ~,}}}$ где C, C₊, C_– − некоторые скалярные или псевдоскалярные функции p и p'. При инверсии векторы p и p' изменяют знак, а поэтому изменяют знак также векторы c₊ и c_–. Поэтому из инвариантности оператора $\hat {T}$ относительно пространственной инверсии следует, что ${{C}_{ + }} = 0,~~{{C}_{ - }} = 0$, а зависящие от p и p' величины $A$ и $C$ − скаляры. Эти функции зависят от p и p' только через скалярные комбинации p ⋅ p, p' ⋅ p' и p · p', т.е. являются функциями энергии и угла рассеяния – угла между p и p'. Таким образом, оператор амплитуды рассеяния имеет следующий общий вид:

где c − единичный вектор нормали к плоскости рассеяния, определяемый первым из выражений (30).

Можно показать, что определяющие оператор $\hat {T}~$ величины $A$ и $C$ связаны следующим соотношением, которое известно как “оптическая теорема”:

С использованием определения (27) для оператора интеграла столкновений $\hat {R},$ уравнений (31) и (32), интегралы столкновений $R = {\text{Tr}}\hat {R}$ и $R = {\text{Tr}}\hat {\sigma }\hat {R}~$ можно представить в виде:

При записи интегралов столкновений (33), (34) мы для краткости использовали обозначения $\delta {{n}_{p}}~$ и $\delta {{s}_{p}}$ для функций $\delta n\left( {r,p,t} \right)$ и $\delta s\left( {r,p,t} \right)$ соответственно, а также ввели следующие величины:

Величина $W_{{pp{\kern 1pt} '}}^{{\left( {{\text{nsf}}} \right)}}$ имеет смысл дифференциальной вероятности рассеяния электрона без изменения спинового состояния (non spin-flip) из состояния с квазиимпульсом $p{\kern 1pt} '$ в состояние с квазиимпульсом p за единицу времени, тогда как $W_{{pp{\kern 1pt} '}}^{{\left( {{\text{sf}}} \right)}}$ – это дифференциальная вероятность рассеяния с переворотом спина (spin-flip) за единицу времени. Величина $W_{{pp{\kern 1pt} '}}^{{\left( {{\text{as}}} \right)}}$ характеризует асимметричное, так называемое “косое” (askew) спиновое рассеяние, является комплексно-значной функцией квазиимпульсов электрона до и после рассеяния и поэтому не имеет простого смысла вероятности какого-либо процесса. Суммируя дифференциальную вероятность $W_{{pp{\kern 1pt} '}}^{{\left( {{\text{sf}}} \right)}}$ рассеяния электрона из состояния с квазиимпульсом p' в состояние с квазиимпульсом p за единицу времени с переворотом спина по всем возможным состояниям электрона p после рассеяния, получаем интегральную вероятность рассеяния из состояния с квазиимпульсом p' за единицу времени с переворотом спина

Интегральную вероятность изменения орбитального состояния электрона с квазиимпульсом p', от величины которой будут зависеть транспортные характеристики электронной системы, определим как

Интегральная вероятность процессов “косого” спинового рассеяния из состояния p' характеризуется величиной

БАЗОВЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ДЛЯ ПЛОТНОСТЕЙ И ПОТОКОВ

Подставим (33), (34) в уравнения (21)–(24), с использованием соотношений (25), (26) и определений (35)–(40), после выполнения всех суммирований получим искомую систему уравнений для плотностей и потоков:

Здесь введены следующие величины, характеризующие скорость различных процессов релаксации:

– скорость релаксации спина ${1 \mathord{\left/ {\vphantom {1 {{{\tau }_{{\text{S}}}}}}} \right. \kern-0em} {{{\tau }_{{\text{S}}}}}}$ (как характеристика процессов рассеяния с переворотом спина)

– скорость релаксации импульса ${1 \mathord{\left/ {\vphantom {1 {{{\tau }_{{\text{O}}}}}}} \right. \kern-0em} {{{\tau }_{{\text{O}}}}}}$ (как характеристика влияния рассеяния на изменение орбитального движения электронов, определяющее их транспортные свойства):

– скорость релаксации, обусловленной “косым” рассеянием электронов ${1 \mathord{\left/ {\vphantom {1 {{{\tau }_{{{\text{SO}}}}}}}} \right. \kern-0em} {{{\tau }_{{{\text{SO}}}}}}}$ (как характеристика интенсивности асимметричного спин-орбитального рассеяния)

В определениях (45)–(47) чертой над функцией обозначена операция ее усреднения по p с весом F': $\overline {\left( \ldots \right)} = {{\sum\nolimits_p {\left( \ldots \right)F{\kern 1pt} '} } \mathord{\left/ {\vphantom {{\sum\nolimits_p {\left( \ldots \right)F{\kern 1pt} '} } {\sum\nolimits_p {F{\kern 1pt} '} }}} \right. \kern-0em} {\sum\nolimits_p {F{\kern 1pt} '} }},$ а величина e в уравнениях (43), (44) есть абсолютно антисимметричный единичный тензор 3-го ранга.

Легко видеть, что уравнение (41) не что иное, как уравнение непрерывности для потока электронов. Наличие в левой части этого уравнения двух членов отражает выполнение закона сохранения числа частиц: скорость изменения плотности частиц в данной точке равна с обратным знаком дивергенции вектора плотности потока частиц в этой точке.

Уравнение (42) – известное уравнение движения для спиновой плотности, которое также можно рассматривать как уравнение непрерывности для спинового тока, однако в этом уравнении заложена возможность диссипации спина, которая описывается последним членом в левой части уравнения. Скорость спиновой релаксации электронов проводимости ${1 \mathord{\left/ {\vphantom {1 {{{\tau }_{{\text{S}}}}}}} \right. \kern-0em} {{{\tau }_{{\text{S}}}}}}$ и, соответственно, время спиновой релаксации ${{\tau }_{{\text{S}}}}$ определяются, как можно видеть из уравнений (45) и (36), процессами рассеяния с переворотом спина. Третий член в левой части (42) описывает прецессионное движение электронов с частотой ${{\Omega }_{{\text{L}}}}.$ Второй член отвечает за локальное изменение спиновой плотности, обусловленное переносом спина, который имеет место при протекании спинового тока $J$ из одной области пространства с фиксированной спиновой плотностью в другую область, имеющую иную по величине или направлению спиновую плотность. В силу малости времени релаксации квазиимпульса ${{\tau }_{{\text{O}}}}$ по сравнению с временем спиновой релаксации ${{\tau }_{{\text{S}}}},$ описанное выше движение спина электрона можно описывать как диффузионный процесс. При этом коэффициент спиновой диффузии определяется как $D = \overline {{v}_{E}^{2}} {{\tau }_{{\text{O}}}}.$

Уравнение (43) – уравнение для нахождения вектора плотности потока электронов или связанного с ним вектора плотности электрического тока $j = eI\left( {r,t} \right)$ при заданных полях E и B. Второй член в левой части описывает диффузионную компоненту потока частиц, величина которой определяется коэффициентом диффузии $D = \overline {{v}_{E}^{2}} {{\tau }_{{\text{O}}}}.$ Третий член описывает ток проводимости, индуцируемый полем $E$, величина которого определяется удельной электропроводностью металла $\sigma = {{N{{e}^{2}}{{\tau }_{{\text{O}}}}} \mathord{\left/ {\vphantom {{N{{e}^{2}}{{\tau }_{{\text{O}}}}} m}} \right. \kern-0em} m}.$ Четвертый описывает изменение плотности электрического тока из-за действия силы Лоренца, заставляющей электроны двигаться по циклотронным орбитам с частотой ${{\Omega }_{{\text{C}}}}$ и приводящей к появлению эффекта Холла. Пятое слагаемое учитывает изменение проводимости металла из-за зависимости действующего в металле магнитного поля от координат. Именно этот вклад определяет новые эффекты в проводимости неоднородно-намагниченных проводников. Шестое слагаемое описывает скорость изменения орбитального состояния электронов, определяемую транспортным временем релаксации импульса ${{\tau }_{{\text{O}}}}$. Наконец, последнее слагаемое в левой части уравнения (43) отвечает за учет асимметричного спинового рассеяния электронов, интенсивность которого задается временем релаксации ${{\tau }_{{{\text{SO}}}}}.$ Это слагаемое, как и последний член в левой части уравнения (44), описывает специфические особенности физического явления, получившего название “спиновый эффект Холла”.

Уравнение (44) – уравнение для нахождения тензора спинового тока J. Второй член в левой части (44) описывает диффузионную компоненту потока спина, величина которой определяется коэффициентом диффузии спина $D = \overline {{v}_{E}^{2}} {{\tau }_{{\text{O}}}}.$ Третий член описывает эффекты дрейфа спиновой плотности под действием электрического поля. Четвертое слагаемое, векторное произведение вектора ${{\Omega }_{{\text{C}}}}$ и тензора спинового тока J, описывает влияние силы Лоренца, аналогично четвертому члену уравнения (43). Пятый член, векторное произведение тензора спинового тока J и вектора ${{\Omega }_{{\text{L}}}},$ описывает спиновую прецессию движущихся электронов. Шестое слагаемое описывает влияние неоднородностей магнитного поля на спиновый транспорт, а седьмое учитывает затухание спинового тока со скоростью релаксации импульса ${1 \mathord{\left/ {\vphantom {1 {{{\tau }_{{\text{O}}}}}}} \right. \kern-0em} {{{\tau }_{{\text{O}}}}}}.$ Последний член в левой части (44), как уже отмечалось, отражает существование спинового эффекта Холла.

СПИНОВЫЙ ТРАНСПОРТ В КИРАЛЬНЫХ ГЕЛИМАГНЕТИКАХ

Для иллюстрации влияния неоднородного магнитного поля на спиновый транспорт применим полученные уравнения для описания транспортных свойств киральных гелимагнетиков. Интерес к спиновому транспорту в киральных гелимагнетиках обусловлен возможностью использования их уникальных свойств при создании магнитокиральных наноструктур для применений в спинтронике [14–16].

Пусть ось простой магнитной спирали гелимагнетика и электрическое поле E направлены вдоль оси OZ: E = E_ze_z. Помимо внешнего магнитного поля на электронные спины действует эффективное магнитное поле обменного происхождения H^(ex). Для геликоидального магнетика со спиновым упорядочением типа “простая спираль” поле H^(ex) может быть представлено в виде ${{H}^{{\left( {{\text{ex}}} \right)}}}\left( z \right) = {{H}^{{\left( {{\text{ex}}} \right)}}}h\left( z \right),$ где ${{H}^{{\left( {{\text{ex}}} \right)}}}$ – величина обменного поля, $h\left( z \right)$ – единичный вектор, характеризующий направление H^(ex)(z) в плоскости xy в точке z. Введем в рассмотрение вектор производной вектора H^(ex)(z) по координате z, ${{H}^{{\left( {{\text{ex}}} \right){\kern 1pt} '}}}\left( z \right)$ ≡ $({d \mathord{\left/ {\vphantom {d {dz}}} \right. \kern-0em} {dz}}){{H}^{{\left( {{\text{ex}}} \right)}}}\left( z \right),$ и единичный вектор $h{\kern 1pt} '\left( z \right) = {{{{H}^{{\left( {{\text{ex}}} \right){\kern 1pt} '}}}\left( z \right)} \mathord{\left/ {\vphantom {{{{H}^{{\left( {{\text{ex}}} \right){\kern 1pt} '}}}\left( z \right)} {\left| {{{H}^{{\left( {{\text{ex}}} \right){\kern 1pt} '}}}\left( z \right)} \right|}}} \right. \kern-0em} {\left| {{{H}^{{\left( {{\text{ex}}} \right){\kern 1pt} '}}}\left( z \right)} \right|}},$ задающий направление вектора ${{H}^{{\left( {{\text{ex}}} \right){\kern 1pt} '}}}\left( z \right).$ Полагая, что компоненты вектора $h\left( z \right)$ изменяются по гармоническому закону, ${{h}_{x}}\left( z \right)\sim \cos qz,$ ${{h}_{у}}\left( z \right)\sim \sin qz,$ где q – волновой вектор магнитной спирали, получаем, что единичные вектора $h\left( z \right)$ и $h{\kern 1pt} '\left( z \right)$ взаимно ортогональны в каждой точке z. Направление “закручивания” спирали однозначно определяется вектором $k = \left[ {h \times h{\kern 1pt} '} \right],$ который мы будем называть вектором киральности магнитной спирали.

Для наглядности изложения при записи системы уравнений (41)–(44) применительно к гелимагнетикам мы будем полагать, что внешнее магнитное поле отсутствует, полагая ${{\Omega }_{{\text{C}}}} = 0,$ и будем рассматривать стационарный перенос заряда и спина в условиях электрической нейтральности системы, полагая $\delta N = 0.$ Кроме того, пренебрежем эффектами “косого” спин-орбитального рассеяния, опуская все члены, содержащие ${1 \mathord{\left/ {\vphantom {1 {{{\tau }_{{{\text{SO}}}}}}}} \right. \kern-0em} {{{\tau }_{{{\text{SO}}}}}}}.$

Решение уравнения (43) для потока I в этом случае можно записать в явном виде

Из выражения (48) следует, что неоднородное магнитное поле изменяет поток электронов, причем изменение определяется скалярным произведением вектора $\frac{\partial }{{\partial z}}{{H}^{{\left( {{\text{ex}}} \right)}}}$ и вектора неравновесной спиновой плотности $\delta S{\text{.}}$ Представим $\delta S$ в виде суммы продольной $\delta {{S}_{{\text{l}}}}$ и поперечной $\delta {{S}_{{\text{t}}}}$ (по отношению к оси спирали) компонент: $\delta S = \delta {{S}_{{\text{l}}}} + \delta {{S}_{{\text{t}}}}.$ С учетом того, что вектор $\frac{\partial }{{\partial z}}{{H}^{{\left( {{\text{ex}}} \right)}}}$ перпендикулярен вектору оси e_z, получаем, что изменение потока электронов в (48) определяется только поперечной компонентой неравновесной спиновой плотности $\delta {{S}_{{\text{t}}}}.$

Из уравнений (42)–(44) получаем следующую связь продольной $\delta {{S}_{{\text{l}}}}$ и поперечной $\delta {{S}_{{\text{t}}}}$ компонент:

Среди введенных ранее векторов поляризации спинового тока ${{P}_{i}}$ в рассматриваемом случае оказывается отличным от нуля только вектор ${{P}_{z}},$ удовлетворяющий уравнению

В линейном по электрическому полю приближении в формуле (50) можно пренебречь отличием спиновой плотности $S$ от ее локально-равновесного значения ${{S}_{{\text{L}}}}.$ Тогда получаем, что ${{P}_{z}} \bot {{e}_{z}},$ $\left. {{{P}_{z}}} \right\|{{\Omega }_{{\text{L}}}}.$ Учет нелинейных членов в (50) приводит к появлению у вектора поляризации ${{P}_{z}}$ компоненты, направленной вдоль оси геликоиды.

С использованием соотношений (49), (50), из уравнения (42) получаем следующее уравнение для поперечной компоненты спиновой плотности:

Уравнение движения (51) для геликоиды, характеризуемой волновым вектором q, с учетом того обстоятельства, что вектора $\delta {{S}_{{\text{t}}}}~$и ${{\Omega }_{{\text{L}}}}$ взаимно перпендикулярны, может быть записано в виде

где введено эффективное время спиновой релаксации в гелимагнетике ${{\tau }_{{\text{G}}}},$ определяемое соотношением

Эффективная скорость спиновой релаксации в гелимагнетике $\tau _{{\text{G}}}^{{ - 1}}$ есть сумма трех составляющих: $\tau _{{\text{S}}}^{{ - 1}},$ $\tau _{{\text{L}}}^{{ - 1}}$ и $\tau _{{\text{D}}}^{{ - 1}}.$

Вклад $\tau _{{\text{S}}}^{{ - 1}}$ – это скорость спин-решеточной релаксации, обусловленной диссипацией неравновесного спина электронов проводимости на дефектах решетки, которая может быть рассчитана по формуле (45).

Составляющая эффективной скорости релаксации $\tau _{{\text{L}}}^{{ - 1}}$ определяется как

Физической причиной появления такого вклада является ларморовская прецессия спина электрона в условиях, когда ось прецессионного движения меняет свое направление при движении электрона по орбите вдоль оси геликоиды. Этот механизм спиновой релаксации электронов проводимости в гелимагнетиках естественно называть прецессионным.

Вклад $\tau _{{\text{D}}}^{{ - 1}},$ определяемый как

описывает скорость изменения спиновой плотности в данной точке пространства из-за диффузионного “ухода” спинов электронов из данной точки в процессе протекания спинового тока. Следует заметить, что спиновая диффузия в проводящем гелимагнетике – это не процесс “перетекания” спина из области пространства, где концентрация электронов с заданной проекцией спина велика, в область, где таких электронов меньше. В гелимагнетике значения вектора неравновесной спиновой плотности в соседних точках оси геликоиды отличаются только по направлению и поэтому диффузия в данном случае обеспечивает релаксацию спина электронов исключительно “по направлению”. С учетом того, что коэффициент диффузии прямо пропорционален времени релаксации импульса ${{\tau }_{{\text{O}}}},$ $D = \overline {{v}_{E}^{2}} {{\tau }_{{\text{O}}}},$ частота “диффузионной” составляющей скорости спиновой релаксации также пропорциональна ${{\tau }_{{\text{O}}}}{\text{:}}$ $\tau _{{\text{D}}}^{{ - 1}} = ~\Omega _{q}^{2}{{\tau }_{{\text{O}}}},$ где $\Omega _{q}^{2} = {{q}^{2}}~\overline {{v}_{E}^{2}} .$ Представление диффузионного вклада в эффективную частоту спиновой релаксации в виде соотношения $\tau _{{\text{D}}}^{{ - 1}} = ~\Omega _{{\text{D}}}^{2}{{\tau }_{{\text{O}}}}$ по форме зависимости от времени релаксации импульса ${{\tau }_{{\text{O}}}}$ совпадает с известным выражением для скорости спиновой релаксации электронов в полупроводниках, предложенным Дьяконовым и Перелем.

Соотношение между величинами $\tau _{{\text{D}}}^{{ - 1}}$ и $\tau _{{\text{S}}}^{{ - 1}}$ определяется отношением характерного линейного размера неоднородности поля ${{q}^{{ - 1}}}$ и спин-диффузионной длины ${{L}_{{\text{S}}}} = \sqrt {D{{\tau }_{{\text{S}}}}} .$ Для длиннопериодных неоднородностей $q{{L}_{{\text{S}}}} \ll 1$ и диффузионным механизмом спиновой релаксации можно пренебречь. Для короткопериодных неоднородностей $q{{L}_{{\text{S}}}} \gg 1$ и скорость релаксации спиновой плотности определяется в основном диффузионным механизмом.

Легко видеть, что приведенные выше рассуждения о дополнительных механизмах спиновой релаксации – “прецессионном” и “диффузионном” – применимы не только к периодическим магнитно-неоднородным системам типа геликоидальных магнетиков. Для непериодических магнитоупорядоченных систем частота ${{\Omega }_{{\text{L}}}}$ будет определяться среднеквадратичной величиной флуктуаций обменного поля в магнетике, а волновое число $q~$ будет иметь смысл характерного обратного линейного размера этих флуктуаций.

Решение уравнения (51) с учетом определения (53) дает результат:

где $\chi $ – восприимчивость Паули электронного газа.

Из выражений (56), (57) немедленно следует, что отношение абсолютных значений $\delta {{S}_{{\text{l}}}}$ и $\delta {{S}_{{\text{t}}}}$ зависит только от значения параметра ${{\Omega }_{{\text{L}}}}{{\tau }_{{\text{S}}}}{\text{:}}$

Если обменное поле ${{H}^{{\left( {{\text{ex}}} \right)}}}$ невелико и ${{\Omega }_{{\text{L}}}}{{\tau }_{{\text{S}}}} \ll 1~,$ то параллельная оси геликоиды неравновесная компонента спиновой плотности мала. В противном случае сильных обменных полей, когда ${{\Omega }_{{\text{L}}}}{{\tau }_{{\text{S}}}} \gg 1,$ неравновесная спиновая плотность практически параллельна оси геликоиды.

Отдельного обсуждения заслуживает вопрос о направлении вектора продольной поляризации $\delta {{S}_{{\text{l}}}}$. Из выражения (57) следует, что вектор $\delta {{S}_{{\text{l}}}}$ коллинеарен вектору киральности k. Записывая вектор киральности в виде $k = K{{e}_{z}},$ получаем, что для правозакрученной магнитной спирали с киральностью $K = 1$ коллинеарные векторы спиновой плотности $\delta {{S}_{{\text{l}}}}$ и плотности потока электронов I являются сонаправленными, $\delta {{S}_{{\text{l}}}} \uparrow \uparrow I.$ Этот вывод справедлив и для пары векторов неравновесной плотности намагниченности электронов $\delta {{m}_{{\text{l}}}}$ и плотности электрического тока j. Соответственно, для левозакрученной магнитной спирали с киральностью $K = - 1$ коллинеарные векторы спиновой плотности $\delta {{S}_{{\text{l}}}}$ и плотности потока электронов I являются противоположно направленными, $\delta {{S}_{{\text{l}}}} \uparrow \downarrow I,$ как и векторы $\delta {{m}_{{\text{l}}}}$ и j.

Из уравнения (48) следует, что плотность электрического тока $j = eI,$ индуцируемого в гелимагнетике вдоль его оси электрическим полем E, записывается как

где ${{\sigma }_{0}} = {{{{N}_{0}}{{e}^{2}}{{\tau }_{{\text{O}}}}} \mathord{\left/ {\vphantom {{{{N}_{0}}{{e}^{2}}{{\tau }_{{\text{O}}}}} m}} \right. \kern-0em} m}$ – проводимость Друде электронного газа, а добавка $\left( { - \delta \sigma } \right)$ к проводимости, обусловленная спиральной структурой обменных полей в гелимагнетике, определяется выражением

Таким образом, согласно (60), величина эффектов неоднородности магнитного состояния гелимагнетиков определяется двумя факторами. Во-первых, это величина отношения обменной энергии $\mu {{H}^{{\left( {{\text{ex}}} \right)}}}$ к энергии Ферми ${{\varepsilon }_{{\text{F}}}}.$ Именно этот фактор, зависящий только от электронной и магнитной структуры гелимагнетика, ограничивает относительную величину изменения электропроводности сверху. Во-вторых, на величину изменения электропроводности будут влиять транспортные свойства материала. Этот фактор в формуле (60) записан как отношение ${{{{\tau }_{{\text{G}}}}} \mathord{\left/ {\vphantom {{{{\tau }_{{\text{G}}}}} {{{\tau }_{{\text{D}}}}}}} \right. \kern-0em} {{{\tau }_{{\text{D}}}}}}.$ Это отношение при любом соотношении вкладов различных механизмов спиновой релаксации всегда меньше единицы и достигает максимального единичного значения в условиях, когда диффузионный механизм релаксации является определяющим. Оставаясь в пределах применимости базовых уравнений (41)–(44), мы должны считать параметр ${{\mu {{H}^{{\left( {{\text{ex}}} \right)}}}} \mathord{\left/ {\vphantom {{\mu {{H}^{{\left( {{\text{ex}}} \right)}}}} {{{\varepsilon }_{{\text{F}}}}}}} \right. \kern-0em} {{{\varepsilon }_{{\text{F}}}}}}$ малым по сравнению с единицей и, следовательно, численное значение величины ${{\delta \sigma } \mathord{\left/ {\vphantom {{\delta \sigma } {{{\sigma }_{0}}}}} \right. \kern-0em} {{{\sigma }_{0}}}},$ определяемой формулой (60), может быть оценено сверху именно значением этого малого параметра. В случае сильных обменных полей, когда ${{\mu {{H}^{{\left( {{\text{ex}}} \right)}}}} \mathord{\left/ {\vphantom {{\mu {{H}^{{\left( {{\text{ex}}} \right)}}}} {{{\varepsilon }_{{\text{F}}}}}}} \right. \kern-0em} {{{\varepsilon }_{{\text{F}}}}}} \leqslant 1,$ формула (60) может дать оценку лишь по порядку величины.

ЗАКЛЮЧЕНИЕ

Полученная система уравнений (41)–(44) описывает весь круг гальваномагнитных явлений в металлах и полупроводниках, обусловленных наличием электрического заряда и спинового момента у электронов проводимости, включая как известные эффекты – магнитосопротивление, эффект Холла и спиновый эффект Холла, так и не описанные ранее эффекты, обусловленные неоднородностями внешнего магнитного поля и внутренних полей обменного происхождения. Неоднородности действующего на электрон в металле эффективного магнитного поля приводят как к изменению величины электрического тока, индуцированного электрическим полем, так и к существенному изменению картины протекания спиновых токов в рассматриваемой геометрии эксперимента.

Полученные уравнения движения применены для описания электронного спинового транспорта в киральных гелимагнетиках. Показано, что направление индуцируемой электрическим полем неравновесной спиновой плотности определяется киральностью гелимагнетика. Предсказано существование в киральных магнетиках двух дополнительных механизмов спиновой релаксации: диффузионного и прецессионного. Рассчитано уменьшение электропроводности гелимагнетика, обусловленное действием геликоидальных обменных полей.

Работа выполнена в рамках государственного задания по теме “Спин” AAAA-A18-118020290104-2, проект № 32-1.1.3.5, при поддержке РФФИ, проект № 19-02-00057.