1. На главную
  2. Электронные версии
  3. Физика металлов и металловедение
  4. T. 121, № 4, 2020

Физика металлов и металловедение, 2020, T. 121, № 4, стр. 352-358

Спин-переориентационные переходы в мультиферроиках с циклоидальным спиновым упорядочением

З. В. Гареева a, *, Л. А. Калякин b, И. Р. Каюмов c, А. К. Звездин c, d, **

a Институт физики молекул и кристаллов УФИЦ РАН
450075 Уфа, пр. Октября, 151, Россия

b Институт математики с вычислительным центром УФИЦ РАН,
450008 Уфа, ул. Чернышевского, 112, Россия

c Институт общей физики им. Прохорова РАН
119991 Москва, ул. Вавилова, 38, Россия

d Национальный исследовательский университет “Высшая школа экономики” Факультет физики
101000 Москва, ул. Мясницкая, 20, Россия

* E-mail: gzv@anrb.ru
** E-mail: zvezdin@gmail.com

Поступила в редакцию 16.09.2019
После доработки 24.10.2019
Принята к публикации 19.11.2019

Полный текст (PDF)

Аннотация

Исследованы фазовые переходы в мультиферроиках, основным состоянием которых являются пространственно-модулированные структуры. Обсуждаются основные физические механизмы, необходимые для реализации модулированных состояний различного вида (циклоидальных и геликоидальных магнитных фаз), а также условия фазовых переходов внутри модулированных состояний. Для монокристаллов и пленок феррита висмута определена область физических параметров, при которых основное состояние спиновой циклоиды теряет свою устойчивость. Показано, что области существования и устойчивости спиновых циклоид различны, получены аналитические оценки их границ. Исследовано поведение спиновой системы в магнитном поле в (110) пленке BiFeO3, построены диаграммы основных магнитных состояний.

Ключевые слова: мультиферроики, пространственно-модулированные структуры, фазовые переходы

ВВЕДЕНИЕ

В настоящее время активные исследования проводятся в области физики мультиферроиков, магнитоэлектричества, спиновой киральности, которые затрагивают приоритетные направления современного магнетизма. Широкий спектр перспективных приложений этих явлений в спинтронике, информационных и энергосберегающих технологиях, возможность обнаружения фундаментальных физических эффектов представляют большой исследовательский интерес.

Магнитоэлектичество и киральный магнетизм относятся к классу взаимно пересекающихся явлений. С точки зрения симметрийного подхода для реализации мультиферроидных свойств кристаллов и стабилизации киральных магнитных структур необходимым условием является отсутствие операции пространственной инверсии в группе симметрии магнитных кристаллов.

Прогресс в создании мультиферроиков идет по двум основным направлениям: 1) дизайн и инженерия стрейтронных магнитоэлектрических гетероструктур; 2) синтез однофазных мультиферроиков, в которых за счет легирования, процессов роста, замещения магнитных катионов удается реализовывать новые магнитные, сегнетоэлектрические структуры, в том числе геометрически управляемые, а также существенно повысить магнитоэлектрический отклик системы.

Пространственно-модулированные структуры (ПМС) реализуются в широком классе антиферромагнитных кристаллов, обладающих мультиферроидными свойствами – манганитах, ортоферритах, борацитах: наличие нескольких магнитных подрешеток в слабых ферромагнетиках благоприятствует спиновой модуляции [1–6]. При наличии существенного спин-орбитального взаимодействия, взаимодействия Дзялошинского–Мория (DMI), ПМС возникают в тонких пленках мультиферроиков и гетероструктурах, величину DMI можно регулировать за счет подбора ориентирующих подложек (с включением Pt, Au, Ag) гетероструктур [7], варьирования стехиометрического состава и модификации кристаллической структуры однофазных мультиферроиков [3–6].

Одним из материалов, в котором наиболее ярко прослеживается взаимосвязь магнитоэлектрических эффектов с ПМС, является высокотемпературный мультиферроик феррит висмута, ПМС могут реализовываться в кристаллах и пленках BiFeO3 [2, 4–26]. С наличием ПМС в BiFeO3 связана сложная спин-волновая динамика, возможность электроиндуцированного управления процессами спиновой переориентации, а также увеличение величины магнитоэлектрического эффекта [2]. Несмотря на обширный экспериментальный и теоретический материал [3–27], многие вопросы, связанные с ПМС, требуют дополнительного исследования.

В данной работе мы рассмотрим свойства циклоидных магнитных фаз, акцентируя внимание на вопросах, которые являются отправными точками при исследовании процессов спиновой переориентации и спиновой динамики – устойчивости циклоид, их внутренней структуре, условиях перехода в новое магнитное состояние, управляющих параметрах перехода и особенностях фазовых диаграмм мультиферроиков, симметрия которых разрешает существование ПМС циклоидного типа.

2. КРИСТАЛЛИЧЕСКАЯ И МАГНИТНАЯ СТРУКТУРА BiFeO3, ГАМИЛЬТОНИАН СИСТЕМЫ

Феррит висмута BiFeO3 – сегнетоэлектрик, относящийся к классу слабых антиферромагнетиков с ромбоэдрической структурой. Кристаллическая структура BiFeO3 представляет собой искаженную структуру ABO3 перовскитов, в результате структурных дисторсий (искажений), элементарная кубическая ячейка перовскита удваивается и вытягивается в направлении главной оси кристалла 〈111〉. Незначительные искажения кристаллической структуры приводят к существенному изменению физических свойств материала: в результате смещения катионов Bi3+и Fe3+ друг относительно друга возникает электрическая поляризация; смещение ионов Fe3+ из симметричных B-позиций перовскита и разворот кислородных октаэдров (11°–14°) приводит к появлению двух эффектов: слабому ферромагнетизму на фоне антиферромагнитного упорядочения G-типа и спиновой модуляции – возникновению длиннопериодической модулированной структуры с периодом ~62 нм [8].

С кристаллическими искажениями связано понижение симметрии, в случае монокристаллов BiFeO3 она понижается до ромбоэдрической, C3 || 〈111〉 является главной осью симметрии, плоскостями симметрии – плоскости $(1\bar {1}0),$ $(110),$ $(101),$ $(\bar {1}01),$ $(01\bar {1}),$ $(011).$ Вектор электрической поляризации направлен вдоль главной оси; в монокристаллах в модулированной фазе вектор модуляции лежит в плоскостях симметрии: в них возможна реализация шести энергетически эквивалентных циклоидных фаз, расположенных по звезде волнового вектора k || 〈110〉. Пространственная группа симметрии BiFeO3 – R3c, отсутствие операции пространственной инверсии делает возможным с симметрийных позиций существование магнитоэлектрического эффекта и спин-модулированных фаз.

Гамильтониан рассматриваемой системы имеет вид

(1)
$\begin{gathered} H = - \sum\limits_{i < j} {{{J}_{{ij}}}\left( {{{s}_{i}} \cdot {{s}_{j}}} \right)} + \sum\limits_{i < j} {{{D}_{{ij}}}\left[ {{{s}_{i}} \times {{s}_{j}}} \right]} + \\ + \,\,{{K}_{1}}{{\sum\limits_i {\left( {{{s}_{i}} \cdot {{n}_{u}}} \right)} }^{2}} + {{K}_{2}}{{\sum\limits_i {\left( {{{s}_{i}} \cdot {{n}_{z}}} \right)} }^{2}}, \\ \end{gathered} $
где ${{J}_{{ij}}} = J$ – обменный интеграл, ${{D}_{{ij}}} = V\left[ {{{r}_{i}} \times {{r}_{j}}} \right]$ – вектор Дзялошинского, V – константа взаимодействия Дзялошинского–Мория (${{V}_{{{\text{BiFe}}{{{\text{O}}}_{{\text{3}}}}}}}$ ~ 1.1 мэВ/A2), ri, rj – радиус-векторы, соединяющие немагнитный ион O2– с ближайшими ионами Fe3+, K1, K2 – константы магнитной анизотропии, nu, nz – единичные векторы, направленные по нормали и в плоскости пленки.

Плотность свободной энергии, полученной на основе гамильтониана (1) при условии малого изменения вектора антиферромагнетизма на межатомных расстояниях, имеет вид

(2)
$\begin{gathered} E = \frac{1}{{2{{\chi }_{ \bot }}}}M_{0}^{2}{{m}^{2}} - \left( {m \cdot \left[ {D \times l} \right]} \right) + A{{(\nabla l)}^{2}} + \\ + \,\,\gamma {{e}_{p}}\left( {\left( {l \cdot \nabla } \right) \cdot l - l \cdot \left( {\nabla \cdot l} \right)} \right) + \\ + \,\,{{K}_{1}}{{\left( {{{{\mathbf{n}}}_{u}}l} \right)}^{2}} + {{K}_{2}}{{\left( {{{{\mathbf{n}}}_{z}}l} \right)}^{2}}, \\ \end{gathered} $
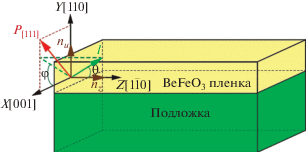
где ${{\chi }_{ \bot }}$ – поперечная магнитная восприимчивость (для BiFeO3 ${{\chi }_{ \bot }}$ ~ 5 × 10–5), $m = \frac{{{{M}_{1}} + {{M}_{2}}}}{{2{{M}_{0}}}},$ $l = \frac{{{{M}_{1}} - {{M}_{2}}}}{{2{{M}_{0}}}}$ – вектора ферро- и антиферромагнетизма, А – константа неоднородного обменного взаимодействия, γ – константа неоднородного магнитоэлектрического взаимодействия, ${{e}_{p}} = P{\text{/}}P$ – единичный вектор электрической поляризации, считаем P || [111]. Минимизация (2) по параметру m при условиях ${{m}^{2}} + {{l}^{2}} = 1,$ $\left( {m \cdot l} \right) = 0$ приводит к выражению
(3)
$\begin{gathered} E = - \frac{{{{\chi }_{ \bot }}}}{2}\left( {H_{{{\text{eff}}}}^{2} - {{{\left( {{{H}_{{{\text{eff}}}}}{\mathbf{l}}} \right)}}^{2}}} \right) + A{{(\nabla {\mathbf{l}})}^{2}} + \\ + \,\,\gamma {{e}_{p}}\left( {\left( {{\text{grad }}{\mathbf{l}}} \right) \cdot {\mathbf{l}} - {\mathbf{l}} \cdot \left( {{\text{div }}{\mathbf{l}}} \right)} \right) + {{K}_{1}}{{\left( {{{n}_{u}}{\mathbf{l}}} \right)}^{2}} + {{K}_{2}}{{\left( {{{{\mathbf{n}}}_{z}}{\mathbf{l}}} \right)}^{2}}, \\ \end{gathered} $
${{H}_{{{\text{eff}}}}} = H + {{H}_{{\text{D}}}}\left[ {{\mathbf{l}} \times {{{\mathbf{e}}}_{{p[111]}}}} \right],$
${{H}_{{\text{D}}}} = \frac{D}{{{{M}_{0}}}}$ – поле Дзялошинского–Мория (для BiFeO3${{H}_{{\text{D}}}} = 1.4 \times {{10}^{5}}\,\,{\text{Э}}$ [26].

Мы исследуем особенности ПМС на примере (110) пленок BiFeO3, геометрия задачи показана на рис. 1.

Рис. 1.

Геометрия задачи.

В кристаллографическом базисе ${{{\mathbf{e}}}_{x}}\,\,{\text{||}}\,\,\left[ {001} \right],$ ${{{\mathbf{e}}}_{y}}\,\,{\text{||}}\,\,\left[ {110} \right],$ ${{{\mathbf{e}}}_{z}}\,\,{\text{||}}\,\,\left[ {1\bar {1}0} \right],$ где единичный вектор нормали к поверхности ${{{\mathbf{n}}}_{u}} = \left( {1,1,0} \right),$ единичный вектор, ориентированный по направлению электрической поляризации ${{{\mathbf{e}}}_{p}} = \left( {\frac{1}{{\sqrt 3 }},\sqrt {\frac{2}{3}} ,0} \right),$ свободная энергия (3) примет вид:

(4)
$\begin{gathered} E = \frac{1}{2}\left[ {{{{\left( {\frac{{\partial {{l}_{x}}}}{{\partial x}}} \right)}}^{2}} + {{{\left( {\frac{{\partial {{l}_{y}}}}{{\partial x}}} \right)}}^{2}} + {{{\left( {\frac{{\partial {{l}_{z}}}}{{\partial x}}} \right)}}^{2}} + {{{\left( {\frac{{\partial {{l}_{x}}}}{{\partial z}}} \right)}}^{2}} + } \right. \\ \left. { + \,\,{{{\left( {\frac{{\partial {{l}_{y}}}}{{\partial z}}} \right)}}^{2}} + {{{\left( {\frac{{\partial {{l}_{z}}}}{{\partial z}}} \right)}}^{2}}} \right] + \left( {\sqrt {\frac{2}{3}} \left( {{{l}_{x}}\frac{{\partial {{l}_{y}}}}{{\partial x}} - {{l}_{y}}\frac{{\partial {{l}_{x}}}}{{\partial x}}} \right) + } \right. \\ \left. { + \,\,\sqrt {\frac{2}{3}} \left( {{{l}_{z}}\frac{{\partial {{l}_{y}}}}{{\partial z}} - {{l}_{y}}\frac{{\partial {{l}_{z}}}}{{\partial z}}} \right) + \frac{1}{{\sqrt 3 }}\left( {{{l}_{z}}\frac{{\partial {{l}_{x}}}}{{\partial z}} - {{l}_{x}}\frac{{\partial {{l}_{z}}}}{{\partial z}}} \right)} \right) + {{E}_{{{\text{an}}}}}, \\ \end{gathered} $
(5)
$\begin{gathered} {{E}_{{{\text{an}}}}} = \frac{1}{2}{{\kappa }_{1}}l_{y}^{2} + \frac{1}{2}{{\kappa }_{m}}{{(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {h} ,\vec {l})}^{2}} - \sqrt {{{\kappa }_{d}}{{\kappa }_{m}}} \left( { - \sqrt {\frac{2}{3}} {{l}_{z}}{{h}_{x}} + } \right. \\ \left. { + \,\,\frac{1}{{\sqrt 3 }}{{l}_{z}}{{h}_{y}} - \frac{1}{{\sqrt 3 }}({{l}_{y}} - \sqrt 2 {{l}_{x}}){{h}_{z}}} \right) - \frac{{{{\kappa }_{d}}}}{2}\left( {l_{z}^{2} + \frac{1}{3}{{{({{l}_{y}} - \sqrt 2 {{l}_{x}})}}^{2}}} \right), \\ \end{gathered} $
где ${{\kappa }_{1}} = - \frac{{4{{K}_{1}}A}}{{{{\beta }^{2}}}},$ ${{\kappa }_{m}} = \frac{{2A}}{{{{\beta }^{2}}{{P}^{2}}}}M_{0}^{2},$ ${{\kappa }_{d}} = {{\kappa }_{m}}{{\left( {\frac{{{{\chi }_{ \bot }}{{H}_{D}}}}{{{{M}_{0}}}}} \right)}^{2}},$ ${{h}_{{[110]}}} = \frac{{4{{M}_{s}}HA}}{{{{\gamma }^{2}}}},$ $x = \frac{\beta }{{2A}}X,$ $y = \frac{\beta }{{2A}}Y,$ $z = \frac{\beta }{{2A}}Z$ – нормированные переменные: A = (2–4) × 10−7 эрг/см, 104 эрг/см3< K1< 106 эрг/см3, M0 = 640 G, γ = 0.6, D = 1.2 × 105 Э, χ⊥ = 4 × 10−5.

3. ПМС В ФЕРРИТЕ ВИСМУТА. ОСНОВНЫЕ УРАВНЕНИЯ ДЛЯ РАСЧЕТА ЦИКЛОИД В ПЛЕНКАХ

ПМС являются основным магнитным состоянием BiFeO3, об экспериментальном обнаружении ПМС в монокристаллах BiFeO3 на основе нейтронографических исследований впервые сообщили в 1982 г. [8, 9]. Теоретическое обоснование существования циклоидного упорядочения было представлено в 1995 г. [10] на основе учета инварианта Лифшица, связанного с DMI в разложении свободной энергии BiFeO3. Наличие спиновой циклоиды приводит к дополнительному вкладу в поляризацию BiFeO3 за счет неоднородного магнитоэлектрического взаимодействия (инварианта Лифшица) [11]. Спиновое упорядочение в ПМС зависит от ряда факторов. В работах [12] на основе измерения спектров ЯМР было впервые показано, что изменение температуры приводит к ангармоническому распределению спинов в циклоиде. Циклоидное упорядочение может быть разрушено за счет внешних воздействий. Эксперименты [13, 14] продемонстрировали, что сильные магнитные поля индуцируют магнитный фазовый переход и резкое увеличение электрической поляризации; замещения катионов Bi редкоземельными ионами в монокристаллах [15], изменение температуры [16]; структурные деформации, обусловленные процессами роста мультиферроидных пленок на основе BiFeO3 также приводят к росту поляризации и разрушению циклоидного порядка [17–25].

В случае монокристаллических пленок BiFeO3 ростовые напряжения индуцируют наведенную магнитную анизотропию, которая оказывает существенное влияние на формирование и свойства ПМС. Особую актуальность исследование свойств ПМС в пленках приобретает в связи с развитием новых технологий доменной инженерии и стрейнтроники. Последние экспериментальные и теоретические работы, посвященные ПМС в пленках BiFeO3 представлены в [19–26].

Воздействие магнитной анизотропии на циклоиды может проявляться в двух аспектах: 1) снимается вырождение направления спиновой модуляции [23–25]; 2) наблюдается трансформация спиновых циклоид. Проблеме спиновой модуляции (выделению направления распространения циклоид в (110) пленках BiFeO3) посвящены работы [24, 25].

В данном исследовании мы остановимся на вопросах, связанных с устойчивостью спиновой циклоиды и возможностью реализации фазовых переходов разного рода внутри циклоидной фазы. А именно, рассмотрим 1) переход в однородное магнитное состояние, который, в случае ПМС, как известно [27], является непрерывным фазовым переходом второго рода и осуществляется через образование промежуточной доменной структуры, 2) переход из циклоиды в ПМС конусного типа, характер которого (скачкообразный переход первого рода или переход второго рода, сопровождающийся плавным изменением распределения спиновой плотности) до сих пор полностью не определен.

Фазовые переходы в монокристаллах, а также в (111) и (001)-ориентированных пленках BiFeO3 исследованы в [19–23]. Как было показано в [24], в (110) пленках возможна реализация циклоид, распространяющихся в направлениях $[1\bar {1}0]$, [001], также в [24] определены условия, необходимые для выделения определенного направления модуляции ПМС.

В данной работе мы исследуем циклоиды, модулированные в направлении [001] в (110)-пленках BiFeO3 в геометрии H || [110]. В этом случае $\partial \theta {\text{/}}\partial z = 0,$ $\partial \varphi {\text{/}}\partial z = 0,$ плотность энергии системы (4), (5) запишется в виде

(6)
$\begin{gathered} E = \frac{1}{2}\left[ {{{{\left( {\frac{{\partial {{l}_{x}}}}{{\partial x}}} \right)}}^{2}} + {{{\left( {\frac{{\partial {{l}_{y}}}}{{\partial x}}} \right)}}^{2}} + {{{\left( {\frac{{\partial {{l}_{z}}}}{{\partial x}}} \right)}}^{2}}} \right] + \\ + \,\,\sqrt {\frac{2}{3}} \left( {{{l}_{x}}\frac{{\partial {{l}_{y}}}}{{\partial x}} - {{l}_{y}}\frac{{\partial {{l}_{x}}}}{{\partial x}}} \right) + \frac{1}{2}{{\kappa }_{1}}l_{y}^{2} + \frac{1}{2}{{\kappa }_{m}}h_{{[110]}}^{2}l_{y}^{2} - \\ - \,\,\sqrt {{{\kappa }_{d}}{{\kappa }_{m}}} \frac{1}{{\sqrt 3 }}{{l}_{z}}{{h}_{{[110]}}} - \frac{{{{\kappa }_{d}}}}{2}\left( {l_{z}^{2} + \frac{1}{3}{{{({{l}_{y}} - \sqrt 2 {{l}_{x}})}}^{2}}} \right). \\ \end{gathered} $

В угловых переменных энергия (6) приводится к виду

(7)
$\begin{gathered} E = \frac{1}{2}{{\left( {\frac{{d\theta }}{{dx}}} \right)}^{2}} + {{E}_{{\varphi }}}{{\sin }^{2}}\theta - \frac{k}{2}{{\cos }^{2}}\theta + h\cos \theta , \\ {{E}_{{\varphi }}} = \frac{1}{2}{{\left( {\frac{{d\tilde {\varphi }}}{{dx}}} \right)}^{2}} + \sqrt {\frac{2}{3}} \frac{{d\tilde {\varphi }}}{{dx}} + \frac{b}{2}{{\sin }^{2}}\varphi , \\ \end{gathered} $
(8)
${\text{где}}\,\,\tilde {\varphi } = \varphi + \alpha ,$

$\alpha = \frac{1}{2}{\text{arctg}}\frac{{2\sqrt 2 {{\kappa }_{d}}}}{{3{{\kappa }_{1}} + {{\kappa }_{d}}}}.$

Коэффициенты, связанные с исходными физическими параметрами соотношениями

$\begin{gathered} h = {{h}_{{[110]}}}\sqrt {\frac{{{{\kappa }_{d}}{{\kappa }_{m}}}}{3}} ,\,\,\,\,k = \frac{{{{\kappa }_{1}} + {{\kappa }_{m}}h_{{[110]}}^{2} + {{\kappa }_{d}} - b}}{2}, \\ b = \pm \sqrt {{{{\left( {{{\kappa }_{1}} + {{\kappa }_{m}}h_{y}^{2} + {{{{\kappa }_{d}}} \mathord{\left/ {\vphantom {{{{\kappa }_{d}}} 3}} \right. \kern-0em} 3}} \right)}}^{2}} + {{8\kappa _{d}^{2}} \mathord{\left/ {\vphantom {{8\kappa _{d}^{2}} 9}} \right. \kern-0em} 9}} \\ \end{gathered} $
являются независимыми (несвязанными между собой) параметрами задачи. Выбор знака у коэффициента b зависит от исходных параметров
${\text{sign}}b = {\text{sign}}\left( {{{\kappa }_{1}} + {{\kappa }_{m}}h_{{[110]}}^{2} + 3{{\kappa }_{d}}} \right)$
среди которых имеется знакопеременный κ1.

В дальнейшем мы будем считать, что новый знакопеременный параметр b выступает в качестве управляющего параметра фазового перехода.

Уравнения Эйлера–Лагранжа дают систему уравнений:

(9)
$\begin{gathered} \frac{{{{d}^{2}}\theta }}{{d{{x}^{2}}}} - \left[ {2{{E}_{{\varphi }}} + k} \right]\sin \theta \cos \theta + h\sin \theta = 0; \\ \frac{d}{{dx}}\left( {{{{\sin }}^{2}}\theta \frac{{d\varphi }}{{dx}}} \right) + 2\sqrt {\frac{2}{3}} \sin \theta \cos \theta \frac{{d\theta }}{{dx}} - \\ - \,\,b{{\sin }^{2}}\theta \sin \varphi \cos \varphi = 0, \\ \end{gathered} $
для которой первый интеграл определяется соотношением

(10)
$\begin{gathered} H = \frac{1}{2}\left[ {{{{\left( {\frac{{d\theta }}{{dx}}} \right)}}^{2}} + {{{\sin }}^{2}}\theta {{{\left( {\frac{{d\varphi }}{{dx}}} \right)}}^{2}}} \right] - \frac{b}{2}{{\sin }^{2}}\theta {{\sin }^{2}}\varphi + \\ + \,\,\frac{k}{2}{{\cos }^{2}}\theta - h\cos \theta . \\ \end{gathered} $

Рассмотрим два случая:

1) ${{h}_{{[110]}}} = 0;$ 2) ${{h}_{{[110]}}} \ne 0.$

При ${{h}_{{[110]}}} = 0,$ θ → π/2, система уравнений (9) редуцируется к уравнению

(11)
$\frac{{{{d}^{2}}\tilde {\varphi }}}{{d{{s}^{2}}}} \mp \sin \tilde {\varphi }\cos \tilde {\varphi } = 0,\,\,\,\,s = x\sqrt {\left| b \right|} .$

Периодические решения уравнения (11), ZX‑решения, определяются функциями вида

(12)
$\cos \tilde {\varphi } = {\text{sn}}\left( {\frac{{\sqrt b x}}{m},m} \right),$
которые описывают плоскую спиновую циклоиду с плоскостью разворота спинов (ZX) и периодом

$T\left( {{{H}_{ \pm }}} \right) = \int\limits_0^{\pi } {\frac{1}{{\sqrt {2{{H}_{ \pm }} \pm {{{\sin }}^{2}}\varphi } }}d\varphi } .$

Значение первого интеграла, на котором реализуется минимальное решение, находится из условия

(13)
$\int\limits_0^{\pi } {\sqrt {2{{H}_{ \pm }} \pm {{{\sin }}^{2}}\varphi } } d\varphi = \frac{\pi }{{\sqrt {{{3\left| b \right|} \mathord{\left/ {\vphantom {{3\left| b \right|} 2}} \right. \kern-0em} 2}} }}.$

Область существования ZX-решений с минимальной энергией ограничивается значением параметра

(14)
$\left| b \right| < {{\pi }^{2}}/6.$

При включении магнитного поля ${{h}_{{[110]}}} \ne 0,$ как следует из уравнений (8), решение вида плоской циклоиды (12) не реализуется, магнитное поле создает ПМС с более сложной структурой.

4. АНАЛИЗ УСТОЙЧИВОСТИ СПИНОВЫХ ЦИКЛОИД. ПМС НОВОГО ТИПА

Исследуем устойчивость решений (12) по отношению к малому возмущению ε:

$\begin{gathered} \theta = \pi {\text{/}}2 + \varepsilon \vartheta (s) + O({{\varepsilon }^{2}}), \\ \varphi = \phi (s) + O(\varepsilon ),\,\,\,\,\varepsilon \to 0. \\ \end{gathered} $

В этом случае первое уравнение системы (8) примет вид уравнения Хилла

(15)
$\begin{gathered} \frac{{{{d}^{2}}\vartheta }}{{d{{s}^{2}}}} + p(s,k,b)\vartheta + h{\text{/}}\varepsilon = 0; \\ p(s,k,b) = k + 2{{E}_{m}}(s,b); \\ k = \frac{1}{2}\left( {\frac{{{{\kappa }_{1}} + {{\kappa }_{m}}{{h}^{2}} + {{\kappa }_{d}}}}{{\left| b \right|}} - \frac{b}{{\left| b \right|}}} \right); \\ {{E}_{m}}(s,b) = E_{{\varphi }}^{ \pm }(s,{{H}_{m}}(b),\left| b \right|). \\ \end{gathered} $

Слагаемое h/ε делает уравнение Хилла неоднородным. Учитывать или не учитывать это слагаемое зависит от амплитуды ε рассматриваемого возмущения. Влияние h существенно на решениях с малой амплитудой ε ≈ h. Для решений со сравнительно большим возмущением h $ \ll $ ε $ \ll $1 этим слагаемым можно пренебречь. Отметим, что здесь не обсуждается задача о минимизации энергии с учетом первой поправки ε. В такой задаче следует учитывать первую поправку порядка O(ε) в ZX-решении, что выходит за рамки данной работы. Конечно, при таком упрощении надо контролировать устойчивость выявляемых свойств относительно возмущения коэффициента p.

На устойчивость в уравнении Хилла сильно влияет среднее значение коэффициента $p(s,k,b)$ = $ = k - 2{{H}_{m}}(b).$

Здесь ${{H}_{m}}(b)$ – первый интеграл, соответствующий минимуму энергии ${{E}_{m}}(s,b).$

Известные на этот счет результаты в основном опираются на условие положительности среднего [28]. Проведенный анализ показывает, что в области параметров системы ${{\kappa }_{1}} + {{\kappa }_{m}}{{h}^{2}} > 0,$ $\left| b \right| < {{{{\pi }^{2}}} \mathord{\left/ {\vphantom {{{{\pi }^{2}}} 6}} \right. \kern-0em} 6},$ существует подобласть, определяемая соотношениями

(16)
$0 < k - 2{{H}_{m}}(b) < \frac{1}{2}\left( {\sqrt {\frac{3}{2}} - 1} \right),$
в которой среднее значение коэффициента Хилла положительно, причем граница области положительности p (s, k, b) определяется условиями

(17)
$\begin{gathered} \int\limits_0^{\pi } {\sqrt {\tilde {k} + {{{\sin }}^{2}}\phi } } d\phi = \frac{\pi }{{\sqrt {{{3\left| b \right|} \mathord{\left/ {\vphantom {{3\left| b \right|} 2}} \right. \kern-0em} 2}} }},\,\,\,\,b > 0; \\ \tilde {k} = \frac{1}{2}\left( {\frac{{{{\kappa }_{1}} + {{\kappa }_{m}}{{h}^{2}} + {{\kappa }_{d}}}}{{\left| b \right|}} - 1} \right). \\ \end{gathered} $

Соотношения (16), (17) определяют границы области существования устойчивых решений уравнения Хилла. В этой области возможна реализация ПМС. Отметим тот факт, что условия (16), (17) не совпадают с условием (14), которое определяет границу области существования сепаратрисных решений (11). Это дает основание полагать, что в промежуточной области, регулируемой значением магнитной анизотропии ${{\kappa }_{1}},$ также в отсутствие внешних магнитных полей, возможна реализация модулированных магнитных состояний, со структурой, отличной от циклоиды. Соотношения (17) показывают, что в пленках BiFeO3 новые ПМС могут быть реализованы при (b > 0), что физически соответствует деформациям растяжения пленки.

При учете магнитного поля система уравнений (9) не может быть редуцирована к уравнению (11), описывающему плоскую циклоиду. Таким образом, в магнитном поле спины в ПМС выходят из плоскости разворота (110), и модулированная фаза имеет другую (конусную) структуру.

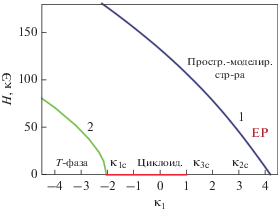
На рис. 2 показана диаграмма магнитных состояний, реализуемых в (110) пленке BiFeO3 в магнитном поле, приложенном вдоль нормали к поверхности пленки. Линии потери устойчивости однородных магнитных состояний (угловой T-фазы и фазы “легкая плоскость” EP) определены на основе анализа потери устойчивости однородных состояний. Линия на отрезке $\left[ {{{\kappa }_{{1с}}}{{\kappa }_{{3с}}}} \right]$ на оси абсцисс отмечает область существования циклоидной ПМС при отсутствии магнитного поля, ${{\kappa }_{{1с}}},$ ${{\kappa }_{{2с}}},$ ${{\kappa }_{{3с}}}$ – критические точки потери устойчивости легкоплоскостной, угловой однородных магнитных фаз и спиновой циклоиды.

Рис. 2.

Фазовая диаграмма (110) пленки BiFeO3 в магнитном поле H || [110].

ЗАКЛЮЧЕНИЕ

В работе исследованы проблемы существования, трансформации и устойчивости ПМС в мультиферроиках. В качестве модельного объекта исследования выбраны (110) пленки BiFeO3, однако предложенный подход является общим, он применим к описанию ПМС мультиферроиков с разрешенным симметрией взаимодействием Дзялошинского–Мория (DMI).

Взаимодействие Дзялошинского–Мория, которое представлено инвариантом Лифшица в разложении свободной энергии магнетика, с одной стороны, приводит к возникновению ПМС, с другой стороны, способствует их неустойчивости.

Изучение областей существования и устойчивости ПМС, а также структуры модулированных фаз требует проведения дополнительных исследований, которые могут быть реализованы в рамках различных подходов.

В данной работе на основе анализа уравнений Хилла определены области существования периодических решений, эквивалентных ПМС, реализующихся в пленках мультиферроика BiFeO3. Показано, что область устойчивости и область существования спиновых циклоид различны. Получены аналитические оценки границы существования и устойчивости циклоидных фаз. В общем случае значения материальных параметров, определяющих области реализации периодических решений не совпадают с параметрами, определяющими переход в однородное состояние намагниченности (сепаратрисные фазовые траектории), что говорит о возможности реализации ПМС со структурой, отличной от циклоидной.

Отметим, что переходы между модулированными состояниями (возможность образования нескольких видов ПМС – спиновых циклоид и конусных фаз) является отличительной особенностью магнетиков, симметрия которых разрешает формирование спиновых циклоид. В магнетиках с геликоидальными спиновыми структурами фазовые переходы внутри ПМС не реализуются.

Работа поддержана грантами РФФИ офи-м № 16‑29-14037, № 19-52-80024.

Список литературы

  1. Tokura Y. Multiferroics as quantum electromagnets // Science. 2006. V. 312. P. 1481–1482.

  2. Звездин А.К., Пятаков А.П. Фазовые переходы и гигантский магнитоэлектрический эффект в мультиферроиках // УФН. 2004. Т. 174. С. 465–470.

  3. Mochizuki M., Furukawa N. Microscopic model and phase diagrams of the multiferroic perovskite manganites // Phys. Rev. B. 2009. V. 80. P. 134 416(22).

  4. Park J.G, Le M.D., Jeong J., Lee S. Structure and spin dynamics of multiferroic BiFeO3 // J. Phys. Cond. Matter. 2014. V. 26. P. 433 202.

  5. Shi X.X., Liu X.Q., Chen X.M. Readdressing of Magnetoelectric Effect in Bulk BiFeO3 // Adv. Funct. Mater. 2017. V. 27. P. 1604037.

  6. Lebeugle D., Colson D., Forget A., Vire, M., Bataille A.M., Gukasov A. Electric – field – induced spin flop in BiFeO3 single crystals at room temperature // Phys. Rev. Lett. 2008. V. 100. P. 227602.

  7. Siemens A., Zhang Y., Hagemeister J., Vedmedenko E.Y., Wiesendanger R. Minimal radius of magnetic skyrmions: statics and dynamics // New J. Phys. 2016. V. 18. P. 045 021.

  8. Sosnowska I., Neumaier T., Steichele E. Spiral magnetic ordering in bismuth ferrite. // J. Phys. C. Solid State Phys. 1982. V. 15. P. 4835.

  9. Sosnovska I.M. Spatially modulated spin structure (SMSS) in BiFeO3 – 30 years later // J. Phys. Cond. Matter. 2016. V. 28. P. 421 002.

  10. Sosnowska I., Zvezdin A. Origin of the Long Period Magnetic Ordering in BiFeO3 J. Magn. Magn. Mater. 1995. V. 140. P. 167.

  11. Sparavigna A., Strigazzi A., Zvezdin A.K. Electric-field effects on the spin-density wave in magnetic ferroelectrics // Phys. Rev. B. 1994. V. 50. P. 2953.

  12. Zalessky A.V.; Frolov A.A.; Khimich T.A.; Bush A.A.; Pokatilov V.S.; Zvezdin A.K. 57Fe NMR Study of Spin-Modulated Magnetic Structure in BiFeO3 // EPL 2000. V. 50(4). P. 547

  13. Popov Y.F., Zvezdin A.K., Vorob’ev G.P., Kadomtseva A.M., Murashev V.A., Rakov D.N. Linear magnetoelectric effect and phase transitions in bismuth ferrite, BiFeO3 // JETP Lett. 1993 V. 57. P. 69–73.

  14. Tokunaga Y., Iguchi S., Arima T., Tokura Y. Magnetic-Field-Induced Ferroelectric State in DyFeO3 // Phys. Rev. Lett. 2008. V. 101. P. 097205.

  15. Gabbasova Z., Kuz’min M., Zvezdin A., Dubenko I., Murashov V., Rakov D., Krynetsky I. Bi1 –xRxFeO3 (R = rare earth): a family of novel magnetoelectrics // Phys. Lett. A. 1991. V. 158. P. 491.

  16. Przeniosło R., Palewicz A., Regulski M., Sosnowska I., Ibberson R.M., and Knight K.S. Does the modulated magnetic structure of BiFeO3 change at low temperatures? // J. Phys. Condens. Matter. 2006. V. 18. P. 2069.

  17. Bai F., Wang J., Wuttig M., Li J., Wang N., Pyatakov A.P., Viehland D. Destruction of Spin Cycloid in (111)c-Oriented BiFeO3 Thin Films by Epitiaxial Constraint: Enhanced Polarization and Release of Latent Magnetization // Appl. Phys. Lett. 2005. V. 86(3). P. 032 511.

  18. Fishman R.S. Sin wave spectra and spatially modulated structures in BiFeO3 // Phys. Rev. B. 2013. V. 87. P. 224 419.

  19. Sando D., Agbelele A., Rahmedov D., Liu J., Rovillain P., Toulouse C., Infante I.C., Pyatakov A.P., Fusil S., Jacque E., Carretero C., Deranlot C., Lisenkov S., Wang D., Le Breton J.-M., Cazayous M., Sacuto A., Juraszek J., Zvezdin A.K., Bellaiche L., Dkhil B., Barthelemy A., Bibes M. Crafting the Magnonic and Spintronic Response of BiFeO3 Films by Epitaxial Strain // Nature Mater. 2013. V. 12. P. 641.

  20. Agbelele A., Sando D., Toulouse C.,Paillard C., Johnson R.D., Ruffer R., Popkov A.F., Carretero C., Rovillain P., Breton J.-M., Dkhil B., Gallais Y., Neasson M.-A., Sacuto A., Manuel P., Zvezdin A.K., Barthelemy A., Juraszek J., Bebes M. Strain and Magnetic Field Induced Spin-Structure Transitions in Multiferroic BiFeO3 // Adv. Mater. 2017. V. 29. Iss. 9. P. 1 602 327.

  21. Кулагин Н.Е., Попков А.Ф., Звездин А.К. Пространственно-модулированные антиферромагнитные структуры в легкоплоскостном мультиферроике // ФТТ 2011. Т. 53 № 5. С. 912–918.

  22. Gareeva Z.V., Popkov A.F., Soloviov S.V., Zvezdin A.K. Field-induced phase transitions and phase diagrams in BiFeO3-like multiferroics // Phys. Rev. B. 2013. V. 87. P. 214 413–214 425.

  23. Кулагин Н.Е., Попков А.Ф., Соловьёв С.В., Звездин А.К. Индуцированные магнитным полем спин-модуляционные переходы в эпитаксиальных плeнках BiFeO3 с ориентацией (001) // ФТТ. 2019. Т. 61 № 2. С. 248–256.

  24. Gareeva Z.V., Zvezdin K.A., Pyatakov A.P., Zvezdin A.K. Novel type of spin cycloid in epitaxial bismuth ferrite films // J. Magn. Magn. Mater. 2019. V. 469. P. 593–597.

  25. Burns S., Sando D., Xu B., Dupe B., Russell L., Den G., Seidel J., Bellaiche L., Valanoor N., Ulrich C. Expansion of the spin cycloid in multiferroic BiFeO3 thin films // Quantum Mater. 2019. V. 4. № 18. P. 1–7.

  26. Tokunaga M., Azuma M., Shimakawa Y. High- field study of strong magnetoelectric coupling in single-domain crystals of BiFeO3 // J. Phys. Soc. Jpn. 2010. V. 79. P. 064 713.

  27. Изюмов Ю.А., Сыромятников В.Н. Фазовые переходы и симметрия кристаллов. М.: Наука, 1984, 245 с.

  28. Якубович В.А., Старжинский В.М. Линейные дифференциальные уравнения с периодическими коэффициентами и их применение. М.: Наука. 1972. 720 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика металлов и металловедение

Архивы выпусков Информация о журнале Отправить рукопись в журнал