Физика металлов и металловедение, 2020, T. 121, № 8, стр. 781-788
Аналитическое представление вихревой структуры доменной границы Блоха
В. С. Семенов *
Институт проблем управления им. В.А. Трапезникова РАН
117997 Москва, ул. Профсоюзная, 65, Россия
* E-mail: vsemsem@mail.ru
Поступила в редакцию 14.11.2019
После доработки 16.03.2020
Принята к публикации 06.04.2020
Аннотация
Предложен аналитический метод определения вихревого асимметричного распределения намагниченности в двумерной доменной границе (ДГ) Блоха. Для получения асимметричного двумерного распределения намагниченности в ДГ использованы простые аналитические зависимости, содержащие минимальное число переменных параметров. Исследована структура и энергия ДГ Блоха в магнитных пленках типа пермаллоя для широкого диапазона значений толщины пленки. Проведено сравнение полученных результатов расчета с результатами расчета других авторов.
ВВЕДЕНИЕ
Существование вихревой асимметричной структуры $180^\circ $ доменной границы (ДГ) Блоха в тонких магнитных пленках типа пермаллоя в области толщин пленки (50–200 нм) впервые было показано в работах [1, 2]. В [1] двумерное распределение намагниченности получено численным методом, а в [2] двумерное распределение получено c использованием аналитических потенциальных функций. Распределения намагниченности в обоих случаях практически совпадают.
Экспериментальные исследования [3–5] подтвердили, что $180^\circ $ ДГ Блоха имеют, по крайней мере, двумерное распределение намагниченности.
С момента появления этих работ и по настоящее время происходит интенсивное исследование статической и динамической структуры доменных границ на основе численного моделирования [6–11].
В работах [12–18] рассмотрены аналитические модели, в которых для описания распределения намагниченности в ДГ используются очень сложные функции с большим числом переменных параметров, и при этом значения полной энергии ДГ намного превышают значения энергии, полученные в работах [1, 2]. Использование аппроксимирующих функций для описания структуры двумерной ДГ Блоха в этих работах основано на интуиции автора. Наличие же метода для выбора таких функций позволило бы использовать простые аналитические функции.
В данной работе предлагается метод, который позволяет для представления распределения намагниченности в двумерной ДГ Блоха использовать простые аналитические функции с минимально необходимым числом переменных параметров.
АНАЛИТИЧЕСКАЯ МОДЕЛЬ ДВУМЕРНОЙ ДГ БЛОХА
Рассмотрим пленку толщиной $2{\kern 1pt} D$ с осью легкого намагничивания, параллельной оси $z.$ $180^\circ $ ДГ разделяет два домена, намагниченных вдоль оси $ \pm z.$ Распределение намагниченности в ДГ определяется изменением вектора намагниченности $\vec {M} = {{M}_{{\text{S}}}}\vec {m}$ = ${{M}_{{\text{S}}}}({{m}_{x}}\vec {i} + {{m}_{y}}\vec {j} + {{m}_{z}}\vec {k})$ ($\left| {\vec {M}} \right|$ = ${{M}_{{\text{S}}}}$ – намагниченность насыщения пленки).
Рассматриваются двумерные модели, в которых направляющие косинусы ${{m}_{x}}(x,y),$ ${{m}_{y}}(x,y)$ и ${{m}_{z}}(x,y)$ совпадают с осями $x,$ $y$ и $z$ прямоугольной системы координат.
Для определения направляющих косинусов используется потенциальная функция
Зависимость $p(t)$ задает изменение намагниченности по ширине ДГ, а зависимость $\,g(s)$ – по толщине пленки, где $t = {x \mathord{\left/ {\vphantom {x D}} \right. \kern-0em} D}$ и $s = {y \mathord{\left/ {\vphantom {y D}} \right. \kern-0em} D}$ – относительные переменные.
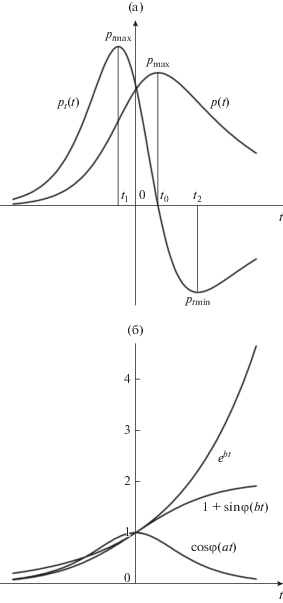
В работе [19] при описании двумерной структуры ДГ Блоха изменение $p(t)$ происходит монотонным образом от максимального значения ${{p}_{{\max }}}$ при $t = {{t}_{0}}$ (рис. 1а), а изменение производной ${{p}_{t}}(t)$ происходит от ${{p}_{t}}(t = {{t}_{0}}) = 0$ до максимального значения ${{p}_{t}}(t = {{t}_{1}}) = {{p}_{{t\max }}}$ (рис. 1а). Для создания асимметрии в двумерной ДГ Блоха в смежной области ${{t}_{0}} \leqslant t \leqslant {{t}_{2}}$ используется зависимость ${{p}_{b}}(t),$ изменение которой происходит от максимального значения ${{p}_{{\max }}}$ при $t = {{t}_{0}},$ а изменение производной ${{d{{b}_{b}}(t)} \mathord{\left/ {\vphantom {{d{{b}_{b}}(t)} {dt}}} \right. \kern-0em} {dt}}$ = ${{p}_{{bt}}}(t)$ происходит от значения ${{p}_{{bt}}}(t = {{t}_{0}}) = 0$ до минимального значения ${{p}_{{bt}}}(t = {{t}_{2}})$ = ${{p}_{{t\min }}}.$ В качестве переменных параметров в этой модели используются величины: ${{p}_{{\max }}},$ ${{p}_{{t\max }}}$ и ${{p}_{{t\min }}}.$ Проведенный расчет полной энергии ДГ для толщины пленки $2{\kern 1pt} {\kern 1pt} D = 100$ нм показал значение практически равное значению полной энергии, полученному в работе [1].
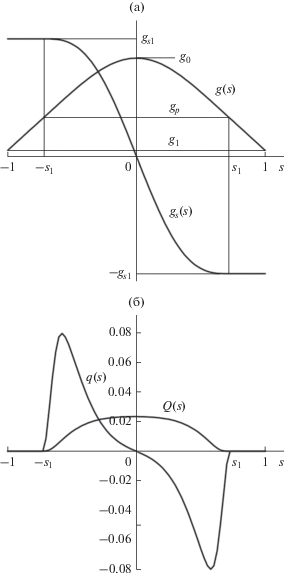
Рис. 1.
а – Зависимости $p(t)$ и${{p}_{t}}(t)$ (пояснения в тексте); б – четная зависимость $\cos {\kern 1pt} \varphi (a{\kern 1pt} t)$ и монотонно возрастающие зависимости ${{p}_{0}}(t) = 1 + \sin \varphi (bt)$ и ${{p}_{0}}(t) = {{e}^{{bt}}}.$
Представим зависимость $p(t)$ в (1) в виде произведения двух функций:
где четная функция ${\kern 1pt} \cos {\kern 1pt} \varphi (a{\kern 1pt} t)$ соответствует изменению намагниченности в одномерной ДГ Блоха для массивных материалов [20]:Направляющие косинусы с использованием потенциальной функции (1) согласно [2] определяются следующим образом:
где ${{p}_{t}}(t) = {{dp(t)} \mathord{\left/ {\vphantom {{dp(t)} {dt}}} \right. \kern-0em} {dt}},$ ${{g}_{s}}(s) = {{dg(s)} \mathord{\left/ {\vphantom {{dg(s)} {ds}}} \right. \kern-0em} {ds}},$ ${{x}_{0}}(s)$ – линия перехода, вдоль которой по толщине пленки происходит изменение намагниченности с одного направления на противоположное.
Для получения модели двумерной ДГ Блоха с асимметричным распределением намагниченности четную функцию $\cos {\kern 1pt} \varphi (a{\kern 1pt} t)$ в (2) необходимо умножить на монотонную функцию ${{p}_{0}}(t),$ имеющую один знак (положительный или отрицательный) для всей области $t < \left| \infty \right|.$
На рис. 1б показана четная функция ${\kern 1pt} \cos {\kern 1pt} \varphi (a{\kern 1pt} t)$ и две монотонно возрастающие зависимости: 1) ${{p}_{0}}(t)$ = $1 + \sin \varphi (bt)$ и 2) ${{p}_{0}}(t) = {{e}^{{bt}}}.$ На рис. 1а показаны зависимости $p(t)$ и ее производной ${{p}_{t}}(t).$
Зависимость $p(t)$ характеризуется максимальным значением ${{p}_{{\max }}}$ при ${{t}_{0}}{\text{:}}$ $p(t = {{t}_{0}}) = {{p}_{{\max }}},$ а зависимость ${{p}_{t}}(t)$ характеризуется двумя экстремальными значениями: ${{p}_{t}}(t = {{t}_{1}}) = {{p}_{{t\max }}}$ и ${{p}_{t}}(t = {{t}_{2}}) = {{p}_{{t\min }}}$ и при этом значение ${{p}_{{t\max }}} > \left| {{{p}_{{t\min }}}} \right|.$
Линия перехода находится из совместного решения следующих уравнений:
(4б)
$\begin{gathered} {{m}_{x}}({{x}_{0}}(s),s)\frac{{d{{m}_{x}}(t,s)}}{{\partial t}}\left| {{{x}_{0}}(s),s + } \right. \\ \left. { + \,\,{{m}_{y}}({{x}_{0}}(s),s)\frac{{d{{m}_{y}}(t,s)}}{{\partial t}}} \right|{{x}_{0}}(s),s = 0. \\ \end{gathered} $Для определения неизвестной функции $g(s)$ и ее производной ${{g}_{s}}(s)$ найдем опорные значения этих функций из уравнений для линии перехода (4).
Для середины пленки $s = 0$ изменение намагниченности в двумерной ДГ Блоха происходит как в одномерной ДГ Блоха, т.е. ${{m}_{x}}(t,s = 0) = 0,$ и согласно (3a) значение производной ${{g}_{s}}(s = 0) = 0.$ Для координаты линии перехода ($t = {{t}_{1}},$ $s = 0$) из (4a) получаем $m_{y}^{2}(t = {{t}_{1}},\,\,s = 0)$ = $p_{t}^{2}(t = {{t}_{1}}){{g}^{2}}(s = 0)$ = = $p_{{t\max }}^{2}g_{0}^{2} = 1.$ Из этого равенства находим максимальное значение функции ${{g}_{0}} = g(s = 0),$ которое определяется максимальным значением функции ${{p}_{t}}(t = {{t}_{1}}){\kern 1pt} = {{p}_{{t\max }}}{\kern 1pt} $ (рис. 1а), т.е.
(5)
${{g}_{0}} = g(s = 0) = {1 \mathord{\left/ {\vphantom {1 {{{p}_{t}}(t = {{t}_{1}})}}} \right. \kern-0em} {{{p}_{t}}(t = {{t}_{1}})}} = {1 \mathord{\left/ {\vphantom {1 {{{p}_{{t\max }}}}}} \right. \kern-0em} {{{p}_{{t\max }}}}}.$При изменении координаты $t$ в пределах ${{t}_{1}} \leqslant t \leqslant {{t}_{0}}$ линия перехода изменяется от x0(t = t1, s = 0 до ${{x}_{0}}(t = {{t}_{0}},\,\,\,\,s = \pm {{s}_{1}}).$ Для координаты $t = {{t}_{0}}$ ${{m}_{y}}({{t}_{0}},s) = 0,$ т. к. ${{p}_{t}}(t = {{t}_{0}}) = 0$ (рис. 1а), и из (4a) получаем: ${{p}^{2}}(t = {{t}_{0}})g_{s}^{2}(s) = 1.$ Выполнение этого равенства означает, что для приповерхностных областей (${{s}_{1}} \leqslant \left| s \right| \leqslant 1$) производная ${{g}_{s}}(s)$ имеет постоянное значение
(6)
$\begin{gathered} {{g}_{{s1}}} = {{g}_{s}}({{s}_{1}} \leqslant \left| s \right| \leqslant 1) = \\ = - {\text{sign}}(s)\frac{1}{{p(t = {{t}_{0}})}} = - {\text{sign}}(s)\frac{1}{{{{p}_{{\max }}}}}. \\ \end{gathered} $Для нахождения зависимости $g(s)$ и ее производных в области $ - {{s}_{1}} \leqslant s \leqslant {{s}_{1}}$ в качестве исходной функции используем нечетную функцию для третьей производной в следующем виде: ${{g}_{{sss}}}(s) = {{a}_{1}}\sin ({{\pi s} \mathord{\left/ {\vphantom {{\pi s} {{{s}_{1}}}}} \right. \kern-0em} {{{s}_{1}}}}),$ которая при $s = \pm {{s}_{1}}$ принимает значения ${{g}_{{sss}}}(s = \pm {{s}_{1}}) = 0.$ С учетом опорных значений, что
получаем выражения для функции $g(s)$ и ее производных:
(7)
$\begin{gathered} g(s) = {{g}_{0}} - \frac{{{{g}_{{s1}}}{{s}_{1}}}}{{{{\pi }^{2}}}}\left( {1 - \cos ({{\pi s} \mathord{\left/ {\vphantom {{\pi s} {{{s}_{1}}}}} \right. \kern-0em} {{{s}_{1}}}})} \right) - \frac{{{{g}_{{s1}}}}}{{2{{s}_{1}}}}{{s}^{2}}, \\ {{g}_{s}}(s) = - \frac{{{{g}_{{s1}}}}}{\pi }\sin ({{\pi s} \mathord{\left/ {\vphantom {{\pi s} {{{s}_{1}}}}} \right. \kern-0em} {{{s}_{1}}}}) - \frac{{{{g}_{{s1}}}}}{{{{s}_{1}}}}s, \\ {{g}_{{ss}}}(s) = - \frac{{{{g}_{{s1}}}}}{{{{s}_{1}}}}\cos ({{\pi s} \mathord{\left/ {\vphantom {{\pi s} {{{s}_{1}}}}} \right. \kern-0em} {{{s}_{1}}}}) - \frac{{{{g}_{{s1}}}}}{{{{s}_{1}}}}, \\ {{g}_{{sss}}}(s) = \frac{{\pi {{g}_{{s1}}}}}{{s_{1}^{2}}}\sin ({{\pi s} \mathord{\left/ {\vphantom {{\pi s} {{{s}_{1}}}}} \right. \kern-0em} {{{s}_{1}}}}). \\ \end{gathered} $Зависимость $g(s)$ изменяется от максимального значения $g(s = 0) = {{g}_{0}}$ до значения $g(s = \pm {{s}_{1}}) = {{g}_{p}}{\text{:}}$
(8)
${{g}_{p}} = {{g}_{0}} - \frac{{2{{g}_{{s1}}}{{s}_{1}}}}{{{{\pi }^{2}}}} - \frac{{{{g}_{{s1}}}{{s}_{1}}}}{2}.$Для приповерхностных областях ${{s}_{1}} \leqslant \left| s \right| \leqslant 1$ изменение функции $g(s)$ вследствие постоянного значения ее производной (6) происходит по линейной зависимости:
(9)
$\begin{gathered} \tilde {g}(s) = {{g}_{p}} - {{g}_{{s1}}}({\text{sign}}(s)s - {{s}_{1}}), \\ {{{\tilde {g}}}_{s}}(s) = - {\text{sign}}(s){{g}_{{s1}}},\,\,\,\,{{{\tilde {g}}}_{{ss}}}(s) = 0,\,\,\,\,{{g}_{{sss}}}(s) = 0. \\ \end{gathered} $Зависимость $\tilde {g}(s)$ изменяется от значения $\tilde {g}$(s = = ±s1) = $g(s = \pm {{s}_{1}}) = {{g}_{p}}$ до значения $\tilde {g}(s = \pm 1) = {{g}_{1}}.$ Значение ${{g}_{1}}$ характеризует выход намагниченности на поверхностях пленки: ${{g}_{1}} = {{g}_{p}}$ – ${{g}_{{s1}}}(1 - {{s}_{1}}).$ Это выражение запишем в следующем виде:
Из равенства выражений (8) и (10) находим значение
(11)
${{s}_{1}} = {{(1 - {{g}_{{01}}})} \mathord{\left/ {\vphantom {{(1 - {{g}_{{01}}})} {({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2} - {2 \mathord{\left/ {\vphantom {2 {{{\pi }^{2}}}}} \right. \kern-0em} {{{\pi }^{2}}}})}}} \right. \kern-0em} {({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2} - {2 \mathord{\left/ {\vphantom {2 {{{\pi }^{2}}}}} \right. \kern-0em} {{{\pi }^{2}}}})}},$Уравнения (4) для линии перехода справедливы для середины пленки c координатой x0(t = = t1, s = 0) и для приповерхностных областей ${{x}_{0}}(t = {{t}_{0}},\,\,\,\,{{s}_{1}} \leqslant \left| s \right| \leqslant 1),$ в которых зависимость $\tilde {g}(s)$ и ее производные определяются выражениями (9) и направляющие косинусы – выражениями (3).
Для области $ - {{s}_{1}} \leqslant s \leqslant {{s}_{1}}$ зависимость $g(s)$ определяется выражением (7), и уравнения (4) для линии перехода не имеют совместного решения, так как значение функции (4a) меньше единицы.
Для определения направляющих косинусов в этой области используется потенциальная функция [2]
с новой переменной
Если ввести обозначение $q(s) = {{dQ(s)} \mathord{\left/ {\vphantom {{dQ(s)} {ds}}} \right. \kern-0em} {ds}},$ то направляющие косинусы определяются следующими выражениями:
(14)
$\begin{gathered} {{m}_{x}}(\xi ,s) = - \frac{{\partial A(\xi ,s)}}{{\partial s}} = \\ = - (p(\xi ){{g}_{s}}(s) + q(s){{p}_{t}}(\xi )g(s)), \\ {{m}_{y}}(\xi ,s) = - \frac{{\partial A(\xi ,s)}}{{\partial t}} = {{p}_{t}}(\xi )g(s), \\ {{m}_{z}}(\xi ,s) = {\text{sign}}(\xi - {{x}_{0}}(s)) \times \\ \times \,\,\sqrt {1 - m_{x}^{2}(\xi ,s) - m_{y}^{2}(\xi ,s)} . \\ \end{gathered} $Для области $ - {{s}_{1}} \leqslant s \leqslant {{s}_{1}}$ из решения системы уравнений (15) методом Ньютона находим зависимости для линии перехода ${{x}_{0}}(s)$ и $q(s),$ где в качестве начальных значений берутся значения для $s = 0$(${{x}_{0}}(s = 0) = {{t}_{1}},$ $q(s = 0) = 0$): $m_{x}^{2}({{x}_{0}}(s),s)$ + + $m_{y}^{2}({{x}_{0}}(s),s) = 1,$
(15)
$\begin{gathered} {{m}_{x}}({{x}_{0}}(s),s)\frac{{d{{m}_{x}}(\xi ,s)}}{{\partial t}}\left| {{{x}_{0}}(s),s + } \right. \\ \left. { + \,\,{{m}_{y}}({{x}_{0}}(s),s)\frac{{d{{m}_{y}}(\xi ,s)}}{{\partial t}}} \right|{{x}_{0}}(s),s = 0. \\ \end{gathered} $На рис. 2б показаны зависимости $q(s)$ и $Q(s)$ по толщине пленки. Зависимость $Q(s) = \int_{ - 1}^s {q(s)ds} .$ В дополнительных областях ${{s}_{1}} \leqslant \left| s \right| \leqslant 1$ линия перехода совпадает с координатой ${{x}_{0}}(s = 0) = {{t}_{0}}$ и для этих областей $q(s) = 0.$
Перечислим основные пункты создания двумерных моделей ДГ Блоха:
1. Согласно (2) выбираем монотонно возрастающую (убывающую) функцию ${{p}_{0}}(t)$ одного знака;
2. Определяем максимальные значения p(t = t0) = = pmax и ${{p}_{t}}(t = {{t}_{1}}) = {{p}_{{t\max }}};$
3. Согласно (5) и (6) находим значения ${{g}_{0}}$ и ${{g}_{{s1}}};$
4. Определяем зависимости $g(s)$ (7) и $\tilde {g}(s)$ (9);
5. Находим значение ${{s}_{1}}$ (11);
6. Из решения системы уравнений (15) находим зависимости для линии перехода ${{x}_{0}}(s)$ и $q(s)$ для $ - {{s}_{1}} \leqslant s \leqslant {{s}_{1}}$ и ${{x}_{0}}(s) = {{t}_{0}},$ $q(s) = 0$ для ${{s}_{1}} \leqslant \left| s \right| \leqslant 1;$
7. Определяем направляющие косинусы (15): ${{m}_{x}}(\xi ,s),$ ${{m}_{y}}(\xi ,s)$ и ${{m}_{z}}(\xi ,s).$
ЭНЕРГИЯ ДОМЕННОЙ ГРАНИЦЫ
Равновесное состояние ДГ определяется минимумом полной энергии
где ${{E}_{A}}$ – обменная энергия, ${{E}_{K}}$ – энергия анизотропии и ${{E}_{S}}$ – магнитостатическая энергия.Обменная энергия на единицу длины
(16)
${{E}_{A}} = A\int\limits_{ - \infty }^\infty {dx} \int\limits_{ - D}^D {\left[ {{{{(\nabla {{m}_{x}})}}^{2}} + {{{(\nabla {{m}_{x}})}}^{2}} + {{{(\nabla {{m}_{x}})}}^{2}}} \right]} dy,$Энергия анизотропии на единицу длины
(17)
${{E}_{K}} = K\int\limits_{ - \infty }^\infty {dx} \int\limits_{ - D}^D {\left( {m_{x}^{2} + m_{y}^{2}} \right)dy} ,$Магнитостатическая энергия на единицу длины при отсутствии объемных зарядов определяется поверхностными магнитными зарядами на верхней $y = D$ и нижней $y = - D$ поверхностях пленки: ${{\sigma }_{m}}(x,y = D)$ = ${{M}_{{\text{S}}}}{{m}_{y}}(x,y = D),$ ${{\sigma }_{m}}(x,y = - D)$ = = $ - {{M}_{{\text{S}}}}{{m}_{y}}(x,y = - D)$
и
(18)
$\begin{gathered} {{E}_{S}} = M_{{\text{S}}}^{2}\int\limits_{ - \infty }^\infty {{{m}_{y}}(x,y = D)} \int\limits_{ - \infty }^\infty {{{m}_{y}}(x{\kern 1pt} ',y{\kern 1pt} ' = - D)} \times \\ \times \,\,\ln \left[ {1 + \frac{{{{{(2D)}}^{2}}}}{{{{{(x - x{\kern 1pt} ')}}^{2}}}}} \right]dxdx{\kern 1pt} '. \\ \end{gathered} $Для сравнения с результатами, полученными другими авторами, используются относительные значения полной энергии $\omega = {E \mathord{\left/ {\vphantom {E A}} \right. \kern-0em} A}$ и ее составляющие (${{\omega }_{A}} = {{{{E}_{A}}} \mathord{\left/ {\vphantom {{{{E}_{A}}} A}} \right. \kern-0em} A},$ ${{\omega }_{K}} = {{{{E}_{K}}} \mathord{\left/ {\vphantom {{{{E}_{K}}} A}} \right. \kern-0em} A},$ ${{\omega }_{S}} = {{{{E}_{S}}} \mathord{\left/ {\vphantom {{{{E}_{S}}} A}} \right. \kern-0em} A}$).
РАСЧЕТ И РЕЗУЛЬТАТЫ РАСЧЕТА
Вычисления были выполнены для тонкой магнитной пленки типа пермаллоя со значениями обменной константы $A = {{10}^{{ - 6}}}$ эрг/см, константы анизотропии $K = {{10}^{3}}$ эрг/см$^{3}$ и намагниченности насыщения ${{M}_{{\text{S}}}} = 800$ Гс. Для численного вычисления полной энергии и ее составляющих толщина пленки делится на ${{N}_{y}}$-слоев, параллельных поверхности пленки.
Толщина слоя $\Delta $ = 1.25 нм, и число слоев определяется толщиной пленки: ${{N}_{y}} = {{2D} \mathord{\left/ {\vphantom {{2D} \Delta }} \right. \kern-0em} \Delta }.$
Область изменения направляющих косинусов по ширине ДГ определяется бесконечными значениями: $ - \infty < t < \infty ,$ поэтому для проведения численных расчетов по ширине ДГ ограничимся областью$p(t) > {{10}^{{ - 3}}}.$
Расчет проведем на примере трех моделей, которые отличаются друг от друга зависимостью ${{p}_{0}}(t)$ в $p(t)$ (2): 1) ${{p}_{0}}(t) = 1;$ 2) ${{p}_{0}}(t)$ = $1 + \sin \varphi (bt)$ и 3) ${{p}_{0}}(t) = {{e}^{{bt}}}.$
1-ая модель: ${{p}_{0}}(t) = 1$
Вычисления для данной модели были выполнены для толщины пленки $2{\kern 1pt} D$ = 100 нм. Распределение намагниченности для этой модели получается симметричным относительно координаты ${{t}_{0}} = 0$ с двумя линиями, удовлетворяющим уравнениям линии перехода (рис. 3а).
Рис. 3.
Распределение намагниченности в симметричной ДГ Блоха, где одна сплошных линий соответствует линии перехода (а) и зависимости $p(t)$ и ${{p}_{t}}(t)$ по ширине границы (б).
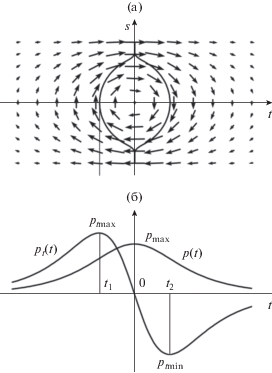
На рис. 3б показаны зависимости $p(t)$ и ${{p}_{t}}(t).$ Максимальное значение $p(t = {{t}_{0}} = 0)$ = pmax = 1.0, экстремальные значения ${{p}_{t}}(t = {{t}_{1}}) = {{p}_{{t\max }}}$ = –pt(t = = t2) = –pt min = 1.26 симметрично расположены относительно центра ДГ ($t = {{t}_{0}} = 0,$ $s = 0$): ${{t}_{2}} = - {{t}_{1}}$ = = 0.35. Значение ${{s}_{1}}$ = 0.81. Равновесное значение полной энергии соответствует двум переменным параметрам: $a$ = 2.52 и ${{g}_{1}}$ = 0.033. Значения полной энергии $\omega $ = 28.76 и ее составляющих ${{\omega }_{A}}$ = = 28.62, ${{\omega }_{K}}$ = 0.052, ${{\omega }_{S}}$ = 0.087.
2-ая модель: ${{p}_{0}}(t) = 1 + \sin \varphi (b{\kern 1pt} t)$
Для этой модели вычисления были выполнены для четырех значений толщины пленки: $2{\kern 1pt} D$ = 50, 100, 150 и 200 нм. Зависимость $p(t)$(2) в этой модели подобна зависимости, используемой в [21]. Распределение намагниченности имеет асимметричный характер ${{p}_{{t\max }}} > - {{p}_{{t\min }}}$ с одной линией перехода (сплошная линия на рис. 4а).
Рис. 4.
Распределение намагниченности в асимметричной ДГ Блоха, где сплошная линия соответствует линии перехода (а) и зависимости $p(t)$ и ${{p}_{t}}(t)$ по ширине границы (б).
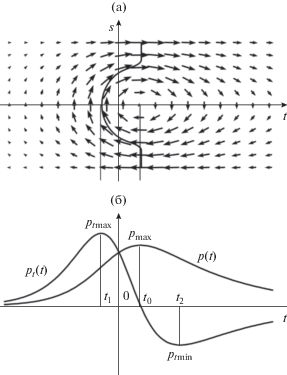
Зависимости $p(t)$ и ${{p}_{t}}(t)$ по ширине границы показаны на рис. 4б, а основные характеристики этой модели (${{p}_{{\max }}},$ ${{p}_{{t\max }}},$ ${{p}_{{t\min }}},$ ${{s}_{1}},$ ${{t}_{1}},$ ${{t}_{0}},$ ${{t}_{2}}$) представлены в табл. 1. Равновесное значение полной энергии достигается при изменении трех переменных параметров: $a,$ $b$и ${{g}_{1}}.$ В табл. 2 представлены значения переменных параметров, полной энергии ДГ и ее составляющих. Асимметричное распределение значительно понижает обменную энергию, и полная энергия значительно ниже по сравнению с симметричным распределением.
Таблица 1.
Результаты расчета основных характеристик двумерной ДГ Блоха (2-я модель)
| $2D,$ нм | ${{p}_{{\max }}}$ | ${{p}_{{t\max }}}$ | ${{p}_{{t\min }}}$ | ${{s}_{1}}$ | ${{t}_{1}}$ | ${{t}_{0}}$ | ${{t}_{2}}$ |
|---|---|---|---|---|---|---|---|
| 50 | 1.43 | 1.65 | –0.89 | 0.76 | –0.10 | 0.50 | 1.10 |
| 100 | 1.35 | 1.62 | –0.96 | 0.68 | –0.13 | 0.43 | 0.98 |
| 150 | 1.32 | 1.60 | –0.98 | 0.67 | –0.13 | 0.39 | 0.91 |
| 1000 | 1.34 | 1.63 | –0.98 | 0.64 | –0.13 | 0.41 | 0.94 |
Таблица 2.
Результаты расчета переменных параметров, полной энергии и ее составляющих для двумерной ДГ Блоха (2-я модель)
| $2D,$ нм | $a$ | $b$ | ${{g}_{1}}$ | ${{\omega }_{A}}$ | ${{\omega }_{K}}$ | ${{\omega }_{S}}$ | $\omega $ |
|---|---|---|---|---|---|---|---|
| 50 | 1.12 | 1.60 | 0.064 | 20.83 | 0.017 | 0.143 | 20.99 |
| 100 | 1.32 | 1.52 | 0.027 | 21.63 | 0.063 | 0.098 | 21.79 |
| 150 | 1.40 | 1.48 | 0.016 | 21.95 | 0.138 | 0.076 | 22.15 |
| 1000 | 1.36 | 1.52 | 0.010 | 22.15 | 0.248 | 0.055 | 22.46 |
Функция${{p}_{0}}(t)$ во 2-ой модели упрощена по сравнению с данной функцией, используемой в [20]:
В качестве функции, определяющей изменение намагниченности по толщине пленки, в [21] использовалась зависимость следующего вида:
Данная зависимость включает пять дополнительных переменных параметров и полностью исключает выход намагниченности на поверхность пленки и, таким образом, в данной модели полностью отсутствует магнитостатическая энергия.
3-ая модель: ${{p}_{0}}(t) = {{e}^{{bt}}}$
Вычисления были выполнены для следующих значений толщины пленки: $2{\kern 1pt} D$ = 50, 100, 150, 200, 300, 500 и 1000 нм. Распределение намагниченности аналогично распределению по 2-ой модели и носит также асимметричный характер с одной линией перехода (сплошная линия на рис. 4а). Основные характеристики этой модели представлены в табл. 3. Полная энергия ДГ Блоха для данной модели ниже по сравнению с полной энергией, полученной по второй модели. С ростом толщины пленки магнитостатическая энергия уменьшается и полностью отсутствует для толщины пленки $2{\kern 1pt} D$ = 1 мкм. В табл. 4 представлены значения переменных параметров, полной энергии ДГ и ее составляющих.
Таблица 3.
Результаты расчета основных характеристик двумерной ДГ Блоха (3-я модель)
| $2D,$ нм | ${{p}_{{\max }}}$ | ${{p}_{{t\max }}}$ | ${{p}_{{t\min }}}$ | ${{s}_{1}}$ | ${{t}_{1}}$ | ${{t}_{0}}$ | ${{t}_{2}}$ |
|---|---|---|---|---|---|---|---|
| 50 | 1.13 | 1.30 | –0.72 | 0.81 | –0.23 | 0.27 | 0.77 |
| 100 | 1.15 | 1.37 | –0.74 | 0.72 | –0.21 | 0.28 | 0.76 |
| 150 | 1.14 | 1.39 | –0.76 | 0.69 | –0.21 | 0.26 | 0.74 |
| 200 | 1.15 | 1.41 | –0.75 | 0.67 | –0.20 | 0.28 | 0.76 |
| 300 | 1.14 | 1.39 | –0.76 | 0.64 | –0.21 | 0.26 | 0.74 |
| 500 | 1.10 | 1.37 | –0.82 | 0.64 | –0.23 | 0.22 | 0.67 |
| 1000 | 1.10 | 1.37 | –0.82 | 0.63 | –0.23 | 0.22 | 0.67 |
Таблица 4.
Результаты расчета переменных параметров, полной энергии и ее составляющих для двумерной ДГ Блоха (3-я модель).
| $2D,$ нм | $a$ | $b$ | ${{g}_{1}}$ | ${{\omega }_{A}}$ | ${{\omega }_{K}}$ | ${{\omega }_{S}}$ | $\omega $ |
|---|---|---|---|---|---|---|---|
| 50 | 1.96 | 0.96 | 0.099 | 20.37 | 0.016 | 0.202 | 20.52 |
| 100 | 2.04 | 1.04 | 0.043 | 21.18 | 0.063 | 0.168 | 21.41 |
| 150 | 2.08 | 1.04 | 0.024 | 21.53 | 0.137 | 0.120 | 21.78 |
| 200 | 2.08 | 1.08 | 0.017 | 21.69 | 0.247 | 0.111 | 22.05 |
| 300 | 2.08 | 1.04 | 0.011 | 21.86 | 0.55 | 0.104 | 22.52 |
| 500 | 2.12 | 0.92 | 0.003 | 22.09 | 1.47 | 0.020 | 23.58 |
| 1000 | 2.12 | 0.92 | 0.0 | 22.24 | 5.91 | 0.0 | 28.15 |
В табл. 5 для толщины пленки $2{\kern 1pt} D$ = 100 нм приведено сравнение полной энергии и ее составляющих для различных аналитических моделей. В 1 и 2 строках таблицы представлены значения полной энергии ДГ Блоха и ее составляющих для 2 и 3 аналитических моделей, и полная энергия для этих моделей имеет самое низкое значение по сравнению с полной энергией для аналитических моделей, полученных в работах [21] (строка 3), [14] (строка 4) и [18] (строка 5).
Таблица 5.
Сравнение результатов расчета полной энергии и ее составляющих для двумерной ДГ Блоха, полученных в данной работе (строки 1 и 2) и в цитируемых работах (строки 3–6)
Однако полная энергия для рассмотренных моделей ДГ Блоха выше полной энергии ДГ (строка 6), представленной в работе [1], распределение намагниченности в которой получено численным методом. Это отличие, видимо, объясняется тем, что в рассмотренных аналитических моделях не учитывается магнитостатическая энергия от объемных зарядов. Значение магнитостатической энергии, полученное численным методом, включает, видимо, магнитостатическую энергию как от поверхностных магнитных зарядов, так и от объемных магнитных зарядов, что уменьшает обменную энергию и приводит к меньшему значению полной энергии ДГ.
ЗАКЛЮЧЕНИЕ
В работе предложен аналитический метод определения вихревого асимметричного распределения намагниченности в двумерной ДГ Блоха. Этот метод основан на использовании потенциальной функции, которая определяется как произведение двух функций, одна из которых задает изменение намагниченности по ширине ДГ, а другая задает изменение намагниченности по толщине пленки. Асимметричное распределение намагниченности в ДГ задается изменением потенциальной функции по ширине ДГ, которая определяется как произведение четной функции на монотонно возрастающую (или убывающую) функцию. Данная функция и ее производная характеризуются максимальными значениями, которые из решения системы уравнений линии перехода определяют опорные (максимальные) значения функции, которая задает изменение намагниченности по толщине пленки. Таким образом, изменение намагниченности по ширине границы взаимосвязано с изменением намагниченности по толщине пленки.
Для получения асимметричного двумерного распределения в данной работе использованы простые аналитические зависимости, содержащие минимальное число переменных параметров, и при этом были получены более низкие значения полной энергии по сравнению со значениями полной энергии в цитируемых работах.
Список литературы
La Bonte A.E. Two-dimensional Bloch-type domain walls in ferromagnetic films // J. Appl. Phys. 1969. V. 40. № 6. P. 2450–2458.
Hubert A. Stray-field-free magnetization configurations // Phys. Stat. Sol. 1969. V. 32. P. 519–534.
Suzuki T., Hubert A. Determination of ferromagnetic domain wall widths by high voltage Lorentz microscopy // Phys. Stat. Sol. 1970. V. 38. P. K5–K8.
Suzuki T. Investigations of ferromagnetic domain walls by Lorentz microscopy // Zeitschrift angew. Phys. 1971. V. 32. № 2. P. 75–80.
Hothersall D.C. Electron images of two-dimensional domain walls // 'Phys. Stat. Sol. (b). 1972. V. 51. P. 529–536.
Филиппов Б.Н. Статические свойства и нелинейная динамика доменных границ с вихреподобной внутренней структурой в магнитных пленках // ФНТ. 2002. Т. 28. № 10. С. 991–1032.
Корзунин Л.Г., Филиппов Б.Н., Кассан-Оглы Ф.А. О вихревом характере распределения намагниченности в магнитных пленках // ФММ. 2009. Т. 108. № 6. С. 572–576.
Дубовик М.Н., Зверев В.В., Филиппов Б.Н. Двумерное микромагнитное моделирование доменных структур в пленках с комбинированной анизотропией // ФТТ. 2013. Т. 55. № 10. С. 1942–1949.
Зверев В.В., Филиппов Б.Н. Переходные микромагнитные структуры в асимметричных вихреподобных доменных стенках (статические решения и динамические перестройки) // ЖЕТФ. 2013. Т. 144. Вып. 1(7). С. 126–140.
Дубовик М.Н., Зверев В.В., Филиппов Б.Н. Нелинейная перестройка структуры доменных границ в тонкой пленке с одноосной плоскостной анизотропией // ФММ. 2014. Т. 115. № 11. С. 1226–1244.
Корзунин Л.Г., Филиппов Б.Н., Кассан-Оглы Ф.А., Чайковский И.А. Статические свойства асимметричных вихреподобных доменных стенок в магнитно-одноосных пленках больших толщин // ФТТ. 2006. Т. 48. Вып. 9. С. 1636–1640.
Aharoni A. Two-dimensional approximation to of Bloch walls in magnetic films // Phil. Mag. 1971. V. 25. № 4. P. 993–999.
Aharoni A. Ritz model for asymmetric domain walls // Phil. Mag. 1972. V. 26. № 6. P. 1473–1479.
Aharoni A. Asymetry in domain walls // Phys. Stat. Sol.(a) 1973. V. 18. P. 661–667.
Aharoni A. Two-dimensional walls in ferromagnetic films. I. General theory // J. Appl. Phys. 1975. V. 46. № 2. P. 908–913.
Aharoni A. Two-dimensional walls in ferromagnetic films. II. Cubic anisotropy // J. Appl. Phys. 1975. V. 46. № 2. P. 914–916.
Aharoni A. Two-dimensional walls in ferromagnetic films. III. Uniaxial anisotropy // J. Appl. Phys. 1975. V. 46. № 4 P. 1783–1783.
Jakubovics J.P. Analytic representation of Bloch walls in thin ferromagnetic films // Phil. Mag. 1974. V. 30. № 5. P. 983–993.
Семенов В.С. Аналитический метод определения вихревой структуры доменной границы Блоха // Изв. РАН. Сер. Физическая. 2019. Т. 83. № 7. С. 900–903.
Landau D., Lifshits E. On the theory of the dispersion of magnetic permeability in ferromagnetic bodies // Phys. Zeitsch. Sow. 1935. V. 8. P. 153–169.
Hubert A. Stray-field-free and related domain wall configurations in thin magnetic films (II) // Phys. Stat. Sol. 1970. V. 38. P. 699–713.
Дополнительные материалы отсутствуют.
Инструменты
Физика металлов и металловедение