Физика плазмы, 2019, T. 45, № 1, стр. 37-50
Математические модели плазмы в проектах МорозоваК. В. Брушлинский
К. В. Брушлинский *
Институт прикладной математики им. М.В. Келдыша РАН
Москва, Россия
* E-mail: brush@keldysh.ru
Поступила в редакцию 29.05.2018
После доработки 05.07.2018
Принята к публикации 02.08.2018
Аннотация
Представлен обзор математических моделей и расчетов плазменных процессов в научно-технических проектах, предложенных и в значительной степени реализованных А.И. Морозовым. Плазмодинамические модели основаны на уравнениях магнитной газодинамики и ее обобщениях и посвящены исследованиям течений плазмы в каналах-соплах плазменных ускорителей. Результаты расчетов внесли заметный вклад в теорию МГД-аналога сопла Лаваля и содействовали успешной разработке и созданию квазистационарного сильноточного плазменного ускорителя большой мощности. Плазмостатические модели в терминах краевых задач с уравнением Грэда–Шафранова реализованы в расчетах равновесных магнитоплазменных конфигураций в ловушках с погруженными в плазму токонесущими проводниками. А.И. Морозов назвал такие ловушки галатеями. Результаты расчетов относятся к геометрии, количественным характеристикам рассмотренных конфигураций и ряду закономерностей в вопросах удержания плазмы магнитным полем. Обсуждаются также общие вопросы, касающиеся математических моделей взаимодействия процессов реакции и диффузии. Проведены расчеты геометрии магнитного поля в вакууме, образующего магнитные поверхности, предназначенные для удержания плазмы в ловушках.
1. ВВЕДЕНИЕ
Алексей Иванович Морозов (1928–2009) – один из выдающихся советских физиков первого послевоенного поколения выпускников Московского государственного университета им. М.В. Ломоносова. Он внес существенный вклад в возникшую в 1940–1950-е годы новую область науки – физику плазмы, интерес к которой был вызван надеждами получить дешевый источник энергии управляемого термоядерного синтеза (УТС), широкими возможностями плазменной техники, увлекательными проблемами астрофизики. Им предложены и по его инициативе разработаны и внедрены в практику несколько поколений плазменных ускорителей с широкой перспективой применения. В исследованиях термоядерной проблемы значительное место занимают ловушки для удержания плазмы магнитным полем – единственно возможным “материалом”, способным контактировать со сжатой плазмой, нагретой до температур, исчисляемых десятками миллионов градусов. Здесь А.И. Морозов уделил серьезное внимание ловушкам сложной геометрии с расположенными внутри плазмы токонесущими проводниками и инициировал целое направление разработки и исследований специального класса этих ловушек, названных им галатеями.
Физика за все время своего существования – с античных времен до наших дней традиционно имеет дело с двумя основными группами методов исследований – теоретическими и экспериментальными. И те и другие используют язык математики – уравнения, формулы, обработку результатов наблюдений. Однако в середине XX в. сложность теории, громоздкость и дороговизна экспериментов, а иногда и принципиальная невозможность их осуществления потребовали более широкого и глубокого применения математики в виде приближенного решения больших задач в немыслимых ранее объемах. Это стало возможным благодаря созданию в тех же целях новой вычислительной техники: электронно-вычислительные машины (ЭВМ) и составленные из них высокопроизводительные комплексы повысили скорость расчетов на много порядков по сравнению с ручными или электромеханическими средствами. Постановка задач, численные методы их решения, программирование и расчеты на ЭВМ, анализ результатов составили новую – третью, наряду с теорией и экспериментом, группу методов исследований, получившую название математическое (или численное) моделирование исследуемых процессов. Подготовлено большое число успешно работающих здесь специалистов. Однако для эффективного исследования какого-либо явления в целом естественно взаимодействие всех трех групп методов, и для этого необходимо, чтобы его возглавил специалист, хорошо ориентирующийся во всех методах, знающий и понимающий возможности каждого из них. Примером успешного применения больших объемов расчетов наряду с традиционными подходами являются решение атомной проблемы в СССР под руководством И.В. Курчатова, Ю.Б. Харитона, Я.Б. Зельдовича, И.Е. Тамма и работы на ту же тему в США.
В физике плазмы одной из первых работ с применением расчетов на ЭВМ была математическая модель динамики Z-пинча опубликованная С.И. Брагинским, И.М. Гельфандом и Р.П. Федоренко в 1958 г. [1]. Систематическому внедрению прикладной математики в эту область способствовал А.И. Морозов. Физик-теоретик по образованию, он хорошо владел логикой экспериментов и не только раньше многих оценил необходимость численного решения задач физики плазмы, но и сумел организовать взаимодействие всех трех групп методов в реализации предложенных им научно-технических проектов.
В 1960 году он инициировал в Отделении прикладной математики МИАН СССР (ныне ИПМ – Институт прикладной математики им. М.В. Келдыша РАН) работы по расчетам магнитных поверхностей и их устойчивости в вакууме, которым предназначалась роль магнитного каркаса в тороидальных ловушках для удержания плазмы. Эти работы возглавил и принял в них личное участие И.М. Гельфанд. Полученные нетривиальные и представляющие интерес за пределами упомянутого приложения результаты опубликованы в серии журнальных статей 1961–63 годов [2–5] и составили содержание обзора [6]. Они же послужили основой для большой серии исследований плазменных конфигураций в магнитных ловушках, проведенных впоследствии Л.С. Соловьевым, Н.М. Зуевой и др. (см. [7]).
Постоянной темой работ ИПМ являются численные исследования ускорения плазмы, инициированные А.И. Морозовым в связи с разработками предложенных им мощных установок, в которых плазма – проводник с током – ускоряется в магнитном поле осесимметричного канала, образованного двумя коаксиальными электродами. Идея такой установки возникла у А.И. Морозова во время его педагогической работы в техникуме г. Людиново [8]. После его перехода на работу в Институт атомной энергии (ныне РНЦ “Курчатовский институт”) она была опубликована [9] и поддержана Л.А. Арцимовичем, под руководством которого в том же году проведены первые эксперименты по ускорению плазмы [10].
Расчеты динамики плазмы в каналах велись параллельно с разработкой ускорителей начиная с 1961 года. Математические модели основаны на численном решении начально-краевых задач с уравнениями магнитной газодинамики с последующим ее расширением за счет конечной электропроводности, эффекта Холла, моделей процесса ионизации. Цикл работ на эту тему облегчил и ускорил разработку плазменных ускорителей, составил существенную главу вычислительной плазмодинамики, способствовал созданию теории магнитного аналога сопла Лаваля. Итогом разработки коаксиальных ускорителей стало создание к началу 1990-х годов квазистационарного сильноточного плазменного ускорителя (КСПУ) кооперацией ряда институтов Москвы, Ленинграда, Троицка, Харькова и Минска, организованной А.И. Морозовым и поддержанной А.П. Александровым, который в 1980-е годы руководил одновременно Академией Наук СССР и ИАЭ им. И.В. Курчатова. КСПУ продемонстрировал рекордные параметры скорости и энергии выходящего из него потока (сила тока 1 МА, напряжение 20 кV, скорость 500 км/с [11]) и рассчитан на многоцелевое применение. В частности, он может быть мощным маршевым электрореактивным двигателем, если удастся создать адекватный его возможностям компактный источник электроэнергии и разместить его на спутнике. Основными публикациями по тематике коаксиальных ускорителей являются обзор [11] и книги [12, 13] А.И. Морозова, теоретический обзор [14], серия статей в журнале “Физика плазмы” вып. 2 1990 года. Работы по численному моделированию обобщены в обзоре [15] и монографии [16].
Тематика плазменных ускорителей представляет интерес и в настоящее время. Уделяется внимание течениям в каналах в присутствии продольного магнитного поля, которое дополнительно создается с помощью, например, соленоида, окружающего установку. На эту тему известны экспериментальные результаты В.Б. Тихонова и Г.А. Дьяконова [17], а математические модели представлены серией работ, выполненных К.В. Брушлинским с учениками в последние годы и цитированных в [18]. Развитию численных моделей и расчетов течения ионизующегося газа в канале посвящены работы А.Н. Козлова (см. [19, 20] и библиографию в них).
На противоположном КСПУ конце диапазона мощностей находятся компактные стационарные плазменные ускорители (СПД) малой тяги, но с длительным ресурсом работы. С 1971 года они постоянно используются в качестве двигателей для корректировки орбит спутников Земли [21]. За изобретение СПД А.И. Морозов награжден памятными медалями международного Сообщества, занятого электроракетными двигателями, и Французской национальной академии атмосферы и космоса. Принципы работы СПД сложнее, и теория физических процессов в них менее разработана. Цикл работ, посвященных началам теории и численным моделям выполнен А.И. Морозовым и В.В. Савельевым (см. обзоры [22, 23]).
Численные модели магнитных ловушек связаны с исследованием геометрии и расчетами параметров конфигураций плазмы, удерживаемых в равновесии магнитным полем. Здесь широко распространены плазмостатические МГД-модели строго равновесных конфигураций. Если конфигурации допускают симметрию (плоскую, осевую, винтовую), математический аппарат моделей сводится к двумерным краевым задачам с одним скалярным уравнением типа Грэда–Шафранова [24, 25] для функции магнитного потока. Эти задачи приближенно описывают квазиравновесие, поскольку они не учитывают конечную проводимость плазмы, которая способствует разрушению строгого равновесия в процессе медленной диффузии магнитного поля. Они также не дают ответа на вопрос о том, каким образом может сформироваться та или иная конфигурация. Более полное исследование требует плазмодинамических моделей, в которых нестационарные МГД задачи с учетом конечной, хотя и высокой, проводимости решаются численно. Они позволяют исследовать условия, при которых формируются конфигурации нужного типа, существующие в квазиравновесном режиме.
В серии работ подробно исследованы конфигурации в нескольких тороидальных ловушках-галатеях и их распрямленных в цилиндр аналогах. На перспективность галатей А.И. Морозов обратил внимание в статье [26]. Результаты первых расчетов равновесных конфигураций в “стелларатор-галатее” (СГ) опубликованы в [27]. Обзор теоретических, численных и экспериментальных работ 1990-х годов содержится в [28]. Из работ последнего времени по численным исследованиям равновесия в галатеях укажем на статью [29] с необходимой библиографией. Вопросы, связанные с задачами о равновесии и примеры плазмодинамических моделей формирования магнитоплазменных конфигураций рассмотрены в [30, 31].
2. МОРФОЛОГИЯ МАГНИТНОГО ПОЛЯ
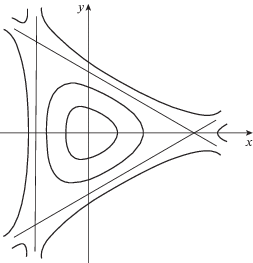
Ранние работы по численному моделированию магнитных ловушек связаны с исследованиями конструкционного материала для “сосудов”, удерживающих плазму, т.е. поверхностей, образованных силовыми линиями магнитного поля. Структуру этих поверхностей естественно рассмотреть сначала в вакууме до наполнения их плазмой. Объектом исследования являются форма поверхностей и ее изменение при возмущении поля. Рассмотрим их на одном из простейших примеров безвихревого трехзаходного магнитного поля H в прямом цилиндре, описываемое скалярным потенциалом
(1)
$\begin{gathered} {\mathbf{H}} = \nabla \Phi ; \\ \Phi = z + 3{{I}_{3}}(3r)\sin {\kern 1pt} 3({\varphi } - z) + {{h}_{0}}{{I}_{0}}(3r)\sin {\kern 1pt} 3z \\ \end{gathered} $3. ПЛАЗМОДИНАМИЧЕСКИЕ МОДЕЛИ УСКОРЕНИЯ ПЛАЗМЫ В ПОПЕРЕЧНОМ МАГНИТНОМ ПОЛЕ
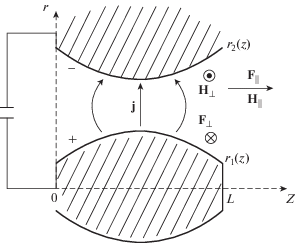
Значительную часть обсуждаемых работ по численному моделированию плазмы составили расчеты МГД-течений в коаксиальных каналах плазменных ускорителей. Схема основного процесса ускорения представлена на рис. 3. Канал образован двумя коаксиальными электродами, включенными в сеть с источником питания. Плазма подается в него слева, электрический ток радиального направления в ней взаимодействует с азимутальным магнитным полем, созданным продольным током в центральном электроде, и ускоряет плазму в осевом направлении. Канал имеет форму сопла, что обеспечивает ускорение с переходом через скорость быстрого магнитного звука. В результате скорость и энергия плазменного потока на выходе могут существенно превосходить их значения в жидкостных и газовых реактивных двигателях, поскольку в кинетическую энергию здесь переходит не только тепловая, но и магнитная энергия системы. Диапазон характерных параметров плазмы в рассматриваемых ускорителях позволяет толковать ее как сплошную среду, поэтому в основе математического аппарата моделей исследуемых явлений лежат уравнения магнитной газодинамики
(2)
$\begin{gathered} \frac{{\partial {\rho }}}{{\partial t}} + \nabla \cdot ({\rho }{\mathbf{v}}) = 0 \\ {\rho }\frac{{d{\mathbf{v}}}}{{dt}} + \nabla p = {\mathbf{j}} \times {\mathbf{H}} \\ {\rho }\frac{{d{\varepsilon }}}{{dt}} + p\nabla \cdot {\mathbf{v}} = {\nu }{{j}^{2}} \\ \frac{{\partial {\mathbf{H}}}}{{\partial t}} = \nabla \times ({\mathbf{v}} \times {\mathbf{H}}) - \nabla \times \left( {{\nu }{\mathbf{j}}} \right), \\ \end{gathered} $Уравнения приведены в безразмерной форме: единицы измерения всех величин, а также безразмерные параметры β и ν составлены из характерных размерных величин, участвующих в постановке задач [15, 16]. Из диссипативных процессов уравнения учитывают “магнитную вязкость” ν, обратно пропорциональную проводимости σ, поскольку в некоторых вопросах она принципиально необходима, а гидродинамическая вязкость и теплопроводность в рассматриваемых задачах несущественны.
Течения плазмы в канале ускорителя (рис. 3) допускают осевую симметрию, поэтому рассматриваемые задачи двумерны: $\partial {\text{/}}\partial {\varphi } \equiv 0$ в цилиндрических координатах $\left( {z,r,{\varphi }} \right)$. Время разряда имеющихся источников питания на порядки превосходит пролетное время установки, поэтому основной интерес представляет стационарный режим течения, который устанавливается в процессе решения нестационарных задач.
Основной объем расчетов относится к исследованиям течений плазмы в собственном поперечном по отношению к направлению потока магнитном поле. В этом случае
где $H = {{H}_{{\varphi }}}$, $u = {{v}_{z}}$, $v = {{v}_{r}}$. Смешанная краевая задача с уравнениями (2) ставится для $t > 0$ в области переменных $\left( {z,r} \right)$ на рис. 3. Граничными условиями на входе являются где ${{r}_{0}}$ характерное значение радиуса во входном сечении. Кроме того, задано направление $v{\text{/}}u$ предполагаемых траекторий. На выходе из канала $\left( {z = Z} \right)$ в предположении установления трансзвукового течения гидродинамические граничные условия не нужны, а четвертое уравнение системы (2), параболическое при ${\nu } > 0$, требует задать какую-либо связь магнитного поля H с током ${{j}_{r}} = - \partial H{\text{/}}\partial z$. Боковые стенки канала предполагаются сплошными и эквипотенциальными, откуда следуют граничные условияНачальными условиями в задачах об установлении стационарного течения могут быть любые значения искомых функций при t = 0, которые обеспечивают разгон плазмы в направлении оси z, например, монотонно убывающие значения давлений – газового p и магнитного H2, согласованные с граничными условиями.
Для численного решения задач уравнения (2) используются в консервативной форме. Чтобы избавиться от криволинейных границ ${{r}_{1}}\left( z \right)$ и ${{r}_{2}}\left( z \right)$ вводятся координаты $\left( {z,y} \right)$:
которые превращают расчетную область в прямоугольник $0 < z < Z$, $0 < y < 1$. Численное решение проведено в разное время несколькими разностными методами, в частности, при ${\nu } \equiv 0$ удалось реализовать известный в газодинамике метод Годунова в решении двумерных МГД-задач с поперечным магнитным полем при двух значениях показателя адиабаты ${\gamma } = 5{\text{/}}3$ и ${\gamma } = 2$ [33]. В последнее время в основном используется метод коррекции потоков в вариантах Бориса–Бука и Залесака [34].Результаты численного решения поставленной задачи и ее модификаций можно систематизировать следующим образом.
1. Большая часть расчетов выполнена первоначально в предположении бесконечно проводящей плазмы $({\sigma } = \infty ,\;{\nu } = 0)$, исходя из того, что оценки электропроводности плазмы в ускорителе типа КСПУ ${\nu } = 1{\text{/}}{{\operatorname{Re} }_{m}} \lesssim {{10}^{{ - 3}}}$ позволяют считать ее влияние несущественным. Результаты относятся к основным простейшим свойствам течений.
– Стационарные течения получены в процессе установления за время порядка пролетного $t \sim Z{\text{/}}u$, где Z – длина канала, u – характерное значение установившейся продольной скорости. Это говорит об устойчивости течения относительно возмущений той же размерности, т.е. двумерных, которые могут оказаться наиболее опасными. Некоторые результаты о затухании трехмерных возмущений в линейном приближении представлены в работе [35].
– Исследован разброс скорости u(Z, r) по радиусу на выходе из канала, который характеризует свойства ускорителя. В слабом магнитном поле (большие значения параметра β) этот разброс незначителен, при возрастании поля он увеличивается, но при этом всегда остается слабее, чем разброс на входе напряженности поля $H\left( {0,r} \right)\sim 1{\text{/}}r$.
– В каналах с сильно профилированными электродами плотность плазмы может оказаться немонотонно убывающей вдоль траекторий течения, а распределение электрического тока может содержать вихри, т.е. участки с обратным направлением тока, препятствующим ускорению. Эти результаты нашли теоретическое объяснение в работах А.И. Морозова и Л.С. Соловьева [14]. В последнее время упомянутые явления подробно исследованы в каналах с сильно профилированными электродами [18, 36].
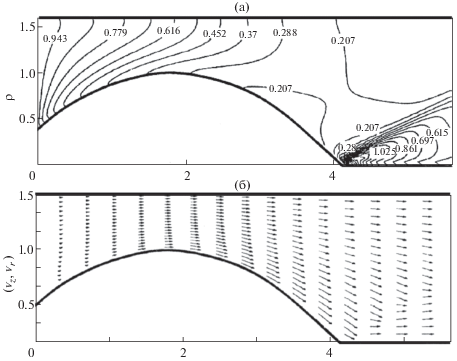
– В каналах с укороченным центральным электродом плазма выходит на ось системы, где образуется зона компрессии – область с высокими значениями плотности и температуры, которые возрастают скачком на конической ударной волне. Распределение плотности и поля скоростей в канале, представленные на рис. 4, получены в расчетах методами Годунова [33] и коррекции потоков [37].
Рис. 4.
Стационарное МГД-течение и зона компрессии на оси канала: линии уровня плотности (а), поле скоростей (б).
2. При повышении мощности ускорителя для адекватного описания течений плазмы в каналах изложенной МГД-модели оказалось недостаточно. Ожидаемые ускорительные свойства течения по-прежнему воспроизводятся в расчетах, однако они не совпадают с экспериментальными данными. Эксперименты показали, что процессы в прилегающих к электродам слоях, во-первых, зависят от полярности электродов, которую не учитывает МГД-модель, и во-вторых, препятствуют ускорению: здесь электрический ток отклоняется от радиального направления и скользит вдоль поверхности электрода, где образуются скачки потенциала. Исследовать эти процессы удалось в терминах модифицированной МГД-модели, включающей эффект Холла. Она допускает конечное различие скоростей ионов и электронов
и связанное с ним взаимодействие тока с магнитным полем в законе Ома [13–16]. В модифицированной системе уравнений (2) два последних уравнения имеют вид(5)
$\begin{gathered} {\rho }\frac{{d{\varepsilon }}}{{dt}} + p\nabla \cdot {\mathbf{v}} = {\nu }{{j}^{2}} + \frac{\xi }{2}{\varepsilon }{\mathbf{j}} \cdot \nabla s \\ \frac{{\partial {\mathbf{H}}}}{{\partial t}} = \nabla \times \left( {{\mathbf{v}} \times {\mathbf{H}}} \right) - \nabla \times \left( {{\nu }{\mathbf{j}}} \right) - \\ - \;\xi \nabla \times \frac{{{\mathbf{j}} \times {\mathbf{H}} - \nabla p{\text{/}}2}}{{\rho }}, \\ \end{gathered} $В расчетах течений плазмы в изложенной МГД-модели с учетом эффекта Холла стационарный режим устанавливается только при ограничении на параметр обмена
Результаты расчетов отражают упомянутое выше отклонение тока от радиального направления, сильно выраженное вблизи электродов. Если неравенство (6) нарушено, течение носит взрывной характер в первую очередь у анода (“анодные взрывы”). При ${\nu } \equiv 0$ течение оказалось неустойчивым, и при его анализе обнаружена возможная некорректность задачи Коши с модифицированными МГД-уравнениями [15]. Строгий анализ задачи, критерий ее корректности и примеры расчетов устойчивых и неустойчивых течений изложены в [16, 38, 39].
3. Другой пример выхода за пределы классической МГД связан с моделированием процесса ионизации газа в каналах. В экспериментальных исследованиях течений ионизующегося газа, например, в каналах ускорителей первой ступени КСПУ, наблюдаются как квазистационарные с ярко выраженным фронтом, так и нестационарные пульсирующие режимы с сильными колебаниями температуры. Последние имеют, по-видимому, общую природу с явлениями при расширении плазменного цилиндра и ускорения плазмы в установках рельсотронного типа: периодически возникающие высокотемпературные слои обнаружены в численных экспериментах группой авторов под руководством А.Н. Тихонова и А.А. Самарского и составили предмет открытия, названного Т-слоем [40]. Анализу указанных явлений в коаксиальных каналах посвящены работы по их численному моделированию, в которых существенную роль играет нелинейная зависимость проводимости плазмы от температуры. Рассмотрено несколько постепенно усложняющихся математических моделей, которые предполагают втекающий в канал газ слегка ионизованным. Простейшая из них использует скачкообразную зависимость проводимости среды от температуры
(7)
${\sigma }\left( T \right) = \left\{ \begin{gathered} {{{\sigma }}_{1}} \ll 1,\quad T < {{T}^{*}} \hfill \\ {{{\sigma }}_{2}} \gg {{{\sigma }}_{1}},\quad T > {{T}^{*}}, \hfill \\ \end{gathered} \right.$Последующие модели имеют дело с трехкомпонентной сплошной средой, состоящей из электронов, ионов и нейтральных атомов. Отношение концентраций этих компонент, т.е. степень ионизации подчиняется законам локально-термодинамического равновесия (ЛТР) и описывается формулой Саха.
В расчетах здесь также устанавливаются либо стационарные либо пульсирующие режимы течения, которые отличаются друг от друга отношением ${{J}^{2}}{\text{/}}\dot {M}$ квадрата разрядного тока к потоку массы в канале, выраженному в токовых единицах: в стационарных режимах этот параметр выше, чем в пульсирующих [19, 41]. Это значит, что поддержание стационарного процесса ионизации в потоке заданной величины требует достаточно сильного электрического тока.
В упомянутых моделях фронт ионизации размыт по сравнению с имеющимися экспериментальными наблюдениями. Относительно узкий фронт, более соответствующий экспериментам, удалось получить в моделях, учитывающих кинетику ионизации и рекомбинации с отклонениями от термодинамического равновесия [42].
В работах последних лет обращено внимание на сильные колебания температуры в пульсирующих режимах, в связи с чем в математическую модель включены процессы теплопроводности и излучения [19, 43]. Основной результат расчетов состоит в том, что излучение не оказывает принципиального влияния на процесс ионизации, но излучение определенного диапазона может глубоко проникать в объем поступающего в канал газа и способствовать его предварительной ионизации [20].
4. ТЕЧЕНИЯ ПЛАЗМЫ В КАНАЛАХ В ПРИСУТСТВИИ ПРОДОЛЬНОГО МАГНИТНОГО ПОЛЯ
Теоретические и численные исследования течений плазмы в каналах-соплах направлены также на выяснение влияния продольного магнитного поля на природу стационарных течений. Продольное поле может быть создано дополнительно, например, с помощью внешних проводников с током или соленоида, окружающих установку (рис. 3). Очевидно, что поле осевого направления, взаимодействуя с радиальным током, вращает плазму вокруг оси симметрии. Общая картина течения и количественные характеристики его особенностей составляют объект исследований, проведенных в МГД-модели невязкой нетеплопроводной бесконечно проводящей плазмы. Некоторые результаты о стационарных течениях в узких трубках течения упомянуты в обзоре А.И. Морозова и Л.С. Соловьева [14], где приведены первые интегралы МГД-уравнений в квазиодномерном приближении и обращено внимание на существенное различие между сверхальфвеновскими и доальфвеновскими (“до- и закритическими” [14]) течениями.
Подробное исследование квазиодномерных стационарных течений в канале с постоянным средним радиусом $R\left( z \right) = {\text{const}}$ и переменной площадью сечения $S\left( z \right)$ выполнено в терминах обыкновенных дифференциальных уравнений (безразмерных):
(8)
$\begin{gathered} \frac{{d{\rho }}}{{dz}} = - \frac{{\left( {{{u}^{2}} - C_{A}^{2}} \right)}}{{\left( {{{u}^{2}} - C_{s}^{2}} \right)\left( {{{u}^{2}} - C_{f}^{2}} \right)}}\frac{{{\rho }{{u}^{2}}}}{S}\frac{{dS}}{{dz}} \\ \frac{{du}}{{dz}} = \frac{{{\gamma }p\left( {{{u}^{2}} - C_{A}^{2}} \right) + {{u}^{2}}H_{{\varphi }}^{2}}}{{\left( {{{u}^{2}} - C_{s}^{2}} \right)\left( {{{u}^{2}} - C_{f}^{2}} \right)}}\frac{u}{{{\rho }S}}\frac{{dS}}{{dz}} \\ \frac{{d{{H}_{{\varphi }}}}}{{dz}} = - \frac{{{{H}_{{\varphi }}}{{u}^{4}}}}{{\left( {{{u}^{2}} - C_{s}^{2}} \right)\left( {{{u}^{2}} - C_{f}^{2}} \right)}}\frac{{dS}}{{Sdz}} \\ \frac{{dw}}{{dz}} = \frac{{{{H}_{z}}}}{{{\rho }u}}\frac{{d{{H}_{{\varphi }}}}}{{dz}};\quad \frac{d}{{dz}}\left( {\frac{p}{{{{{\rho }}^{{\gamma }}}}}} \right) = 0;\quad \frac{{d{{H}_{z}}S}}{{dz}} = 0, \\ \end{gathered} $Рис. 5.
Классификация стационарных течений плазмы в каналах-соплах в присутствии продольного магнитного поля: графики скорости течений различных типов (сплошные линии) и скоростей магнитного звука (штриховые линии).
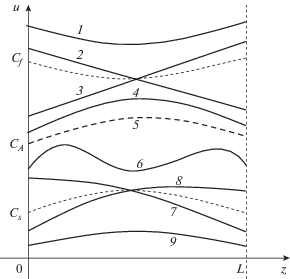
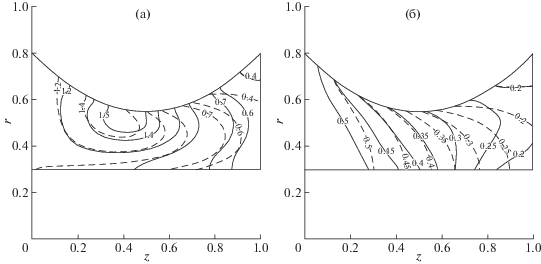
Более полное исследование МГД-течений в каналах проведено в терминах численного решения двумерных нестационарных задач [18, 37, 47]. В качестве результатов получены примеры установившихся течений сверх- и доальфвеновских типов, а также комбинированных, т.е. разных типов в разных частях канала. Специальное внимание уделено трансзвуковым сверхальфвеновским течениям в каналах с заметно выраженной кривизной электродов. На рис. 6–7 представлено распределение плотности плазмы и электрического тока (линии уровня ${{H}_{{\varphi }}}r = {\text{const}}$) в каналах с выпуклыми внутрь отдельно центральным и внешним электродами в присутствии продольного поля и без него. Здесь видно, что процесс ускорения выглядит более равномерным и эффективным в первом варианте геометрии, который реализован в КСПУ. Второй вариант характеризуется немонотонным распределением плотности вдоль внешнего электрода, что дополнительно усиливается продольным полем. В обоих вариантах геометрии присутствие продольного поля отклоняет электрический ток от радиального направления, что может оказаться полезным для нейтрализации отклонения тока в противоположную сторону, обязанного упомянутому выше эффекту Холла.
Рис. 6.
Распределение плотности (а) и электрического тока (б) в канале с профилированным центральным электродом в присутствии продольного магнитного поля (сплошные линии) и без него (штриховые линии).
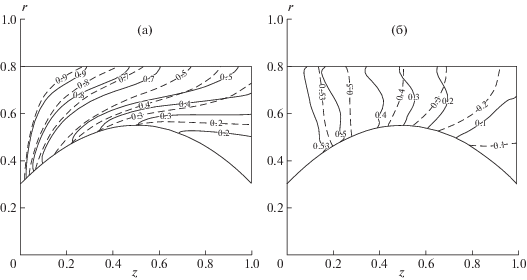
Рис. 7.
Распределение плотности (a) и электрического тока (б) в каналах с профилированным внешним электродом в присутствии продольного магнитного поля (сплошные линии) и без него (штриховые линии).
Некоторые результаты расчетов течений плазмы в каналах с продольным полем в модифицированных моделях с учетом эффекта Холла и конечной проводимости изложены в [48].
5. ПЛАЗМОСТАТИЧЕСКИЕ МОДЕЛИ РАВНОВЕСИЯ В МАГНИТНЫХ ЛОВУШКАХ ДЛЯ УДЕРЖАНИЯ ПЛАЗМЫ
Численные исследования равновесия плазмы в магнитном поле ловушек используют математический аппарат плазмостатики. Возможные конфигурации плазмы, поля и электрического тока полностью характеризуются распределением в пространстве трех функций: давления p, напряженности поля H и плотности электрического тока j. Они удовлетворяют уравнению МГД-равновесия и двум уравнениям Максвелла
(9)
$\nabla p = {\mathbf{j}} \times {\mathbf{H}},\quad {\mathbf{j}} = \nabla \times \,{\mathbf{H}},\quad \nabla \cdot {\mathbf{H}} = 0,$(10)
$r\frac{\partial }{{\partial r}}\left( {\frac{1}{r}\frac{{\partial \psi }}{{\partial r}}} \right) + \frac{{{{\partial }^{2}}\psi }}{{\partial {{z}^{2}}}} + {{r}^{2}}\frac{{dp}}{{d\psi }} + I\frac{{dI}}{{d\psi }} = 0,$Его разновидности имеют вид: в случае плоской симметрии
(11)
$\frac{{{{\partial }^{2}}\psi }}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}\psi }}{{\partial {{y}^{2}}}} + \frac{{dp}}{{d\psi }} + I\frac{{dI}}{{d\psi }} = 0,$(12)
$\frac{1}{r}\frac{\partial }{{\partial r}}\left( {\frac{r}{{\eta }}\frac{{\partial \psi }}{{\partial r}}} \right) + \frac{1}{{{{r}^{2}}}}\frac{{{{\partial }^{2}}\psi }}{{\partial {{{\theta }}^{2}}}} + \frac{{dp}}{{d\psi }} - \frac{{2{\alpha }I}}{{{{{\eta }}^{2}}}} + \frac{I}{{\eta }}\frac{{dI}}{{d\psi }} = 0,$Каждая из разновидностей уравнения содержит две произвольные функции $p(\psi )$ и $I(\psi )$ искомой величины ψ, которые должны быть заданы с помощью дополнительных требований к решению конкретной задачи или информации о нем. В этом проявляется некоторая недоопределенность краевых задач плазмостатики. Ее причина заключается в том, что при выводе уравнений (10)–(12) из (8) не использовано МГД-уравнение индукции магнитного поля (2), которое в равновесии означало бы $\nabla \times ({\nu }{\mathbf{j}}) = 0$, т.е. не учтена проводимость плазмы, а также какие-либо дополнительные обстоятельства или источники, которые могли быть отражены в уравнениях МГД. Поэтому они в лучшем случае описывают строгое равновесие бесконечно проводящей плазмы. Равновесных решений существует бесконечно много, т.к. они зависят от выбора функций $p(\psi )$ и $I(\psi )$. Поскольку проводимость плазмы реально конечна, полученные любым способом идеальные равновесия фактически оказываются квазиравновесными и медленно разрушаются вследствие слабой диффузии магнитного поля [30, 31]. Применимость уравнения Грэда–Шафранова к описанию равновесия реальной плазмы в сильном магнитном поле подробно обсуждена в статье Л.Е. Захарова и В.Д. Шафранова [51].
А.И. Морозовым инициирован цикл работ по расчетам плазмостатических моделей конфигураций в ловушках-галатеях с погруженными в плазму проводниками с током. Чтобы не выделять из расчетной области островки с сечениями проводников, краевые задачи ставятся и решаются в односвязной области, охватывающей ловушку в целом, а ток в проводнике задается с помощью дополнительного слагаемого типа.
(13)
${{j}^{{ex}}}\left( {x,y} \right) = \sum\limits_k {{{j}_{0}}} {\text{exp}}\left( { - \frac{{{{{\left( {x - {{x}_{k}}} \right)}}^{2}} + {{{\left( {y - {{y}_{k}}} \right)}}^{2}}}}{{r_{c}^{2}}}} \right)$Первые работы упомянутого цикла посвящены расчетам цилиндрического плазменного шнура с тремя винтовыми проводниками в нем – “стелларатор-галатеи” (СГ). Идея ловушки предложена в [52]. Винтовые проводники образуют сложную систему магнитных поверхностей, сечение которых плоскостью $z = {\text{const}}$ представлено на рис. 8. Дополнительно предполагается винтовая симметрия всей задачи с заданным шагом винта проводников. Функция $p\left( {\psi } \right)$ соответствует требованиям сосредоточить плазму в нужном месте и избежать ее соприкосновения с проводниками и внешней границей. Им удовлетворяет, например,
(14)
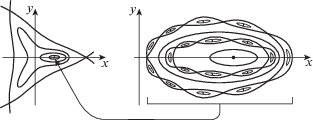
$p\left( \psi \right) = {{p}_{0}}\exp \left( { - {{{\left( {\frac{{\psi - {{\psi }_{0}}}}{q}} \right)}}^{2}}} \right)$Рис. 8.
Сечение магнитных поверхностей плоскостью $z = {\text{const}}$ в цилиндрической стелларатор-галатее.
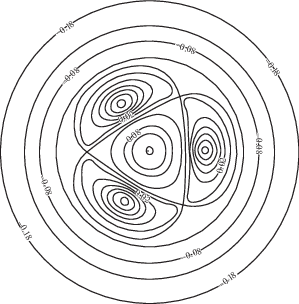
Параметр ${{\psi }_{0}}$ равен значению ψ на магнитной поверхности, в окрестности которой предполагается расположить плазму. Рассмотрено две возможности выбора ${{\psi }_{0}}$. Во-первых, ${{\psi }_{0}} = \psi \left( {0,0} \right)$ в центре области. При этом проводники фактически расположены вне плазменного шнура, и эта конфигурация аналогична традиционным стеллараторам. Во-вторых, ${{\psi }_{0}} = {{\psi }_{{sep}}}$ – значение ψ на сепаратрисе магнитного поля, которая охватывает все три проводника, не касаясь их, т.е. плазменная конфигурация относится к классу галатей. Функция $I\left( \psi \right) = {\alpha /}2{\pi }$ соответствует постоянному значению винтовой компоненты напряженности магнитного поля. Краевая задача с уравнением (12), дополненным слагаемым типа (13), ставится в круге с условием $\psi = {\text{const}}$ на его непрозрачной для магнитного поля границе. Ее разностный аналог решается численно итерационным методом установления. Результатом расчетов являются геометрия и количественные характеристики равновесных магнитоплазменных конфигураций и их зависимость от параметров задачи – максимального давления ${{p}_{0}}$, отнесенного к магнитной единице, и шага винта проводников. Из них можно сделать два основных вывода.
Во-первых, единственная при заданных условиях равновесная конфигурация устанавливается в итерационном процессе численного решения задач лишь при ограниченных сверху значениях давления
Физический смысл его в том, что ловушка с заданными геометрией и величиной тока в проводниках способна удержать плазму лишь ограниченного давления. Подобного рода ограничения возникают в широком классе задач о моделях взаимодействия физических процессов реакции и диффузии, например, в теории горения [16, 45, 53]. Они имеют общую математическую природу. Решение краевых задач с уравнениями типа
c коэффициентами, не зависящими от времени t, и граничным условием ${\psi } = {{{\psi }}_{{\text{Г }}}}$ стремится к равновесному решению, если решение линейной задачи о погрешности итераций(17)
$\frac{{\partial u}}{{\partial t}} = \Delta u + \frac{{\partial g}}{{\partial \psi }}u;\quad {{\left. u \right|}_{\Gamma }} = 0$Второй вывод относится к конкретной ловушке СГ. Из двух рассмотренных вариантов расположения плазмы предпочтительнее с точки зрения удержания оказался тот, в котором максимальное давление сосредоточено вдоль сепаратрисы: значения $р _{0}^{{cr}}$ здесь оказалось втрое выше, чем в конфигурациях, сосредоточенных в центре. Таким образом, расчеты подтвердили преимущества и перспективность концепции ловушек-галатей по сравнению с традиционными стеллараторами [55]. Расчеты конфигураций в СГ, связанные с ними соображения и соответствующая библиография изложены в [16, 27, 56–58].
Следующие работы “галатейного” цикла посвящены моделям и расчетам конфигураций в тороидальной ловушке “Галатея-Пояс” с двумя кольцевыми проводниками внутри плазменного объема. Ловушка предложена А.И. Морозовым и А.Г. Франк [59] в связи с предполагаемым сходством с конфигурациями типа токового слоя, который является постоянной темой экспериментальных исследований в ИОФАН в развитие идей С.И. Сыроватского о природе солнечных вспышек [60]. Подробно исследован распрямленный в цилиндр квадратного сечения аналог “Пояса” с двумя проводниками, параллельными оси. Плазму предполагается сосредоточить вне проводников вдоль проходящей через центр магнитной сепаратрисы. В результате расчетов получено распределение поля и плазмы (рис. 9а). Плазменная конфигурация расположена в центре области и имеет форму криволинейного четырехугольника с выпуклыми внутрь границами, к которому примыкает тонкая периферия, окружающая проводники вдоль сепаратрисы. Электрический ток в плазме $j = - dp{\text{/}}d{\psi }$, отрицательный внутри сепаратрисы и положительный вне ее, взаимодействует с магнитным полем, ориентированным против часовой стрелки, и создает амперову силу ${\mathbf{j}} \times {\mathbf{H}}$, направленную в сторону сепаратрисы, которая не позволяет плазме контактировать с проводниками [61, 62]. Распределение плазменного тока в “Поясе” в отличие от токовых слоев имеет характер “бислоя”: ток равен нулю там, где давление плазмы максимально, а его величина разных знаков на внутренней и внешней границах конфигурации максимальна у этих границ. Сравнительный анализ плазмостатических моделей конфигураций в галатее и токовом слое, а также плазмодинамических моделей их формирования представлен в [63].
Рис. 9.
Распределение магнитного поля и давления плазмы в цилиндрическом (а) и тороидальном (б) вариантах галатеи-пояса.
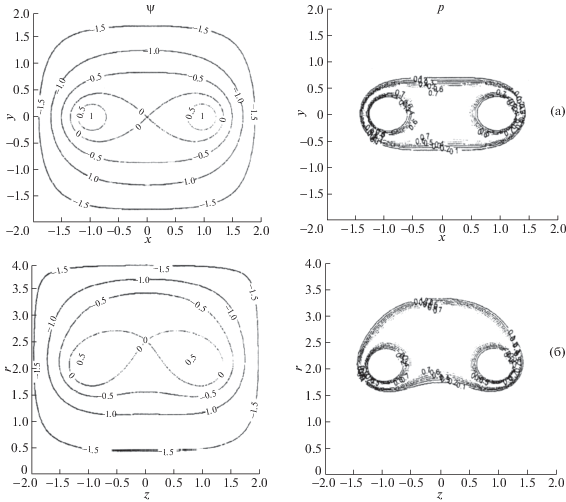
Изложенные результаты для цилиндрического аналога “Пояса” характеризуют качественную природу и основные закономерности рассмотренных ловушек. Чтобы установить количественные характеристики тороидальной ловушки и их отличия от цилиндрической, проведены расчеты тех же конфигураций в торах квадратного сечения с разными значениями их большого радиуса и сопоставлены с аналогичными результатами в цилиндре. Квадратная форма области выбрана для простоты расчетов в торе, что практически не влияет на результаты, т.к. плазменная конфигурация сосредоточена влали от границы, совпадающей с магнитной поверхностью. Конфигурации в торе деформированы по сравнению с цилиндрическими и смещены в направлении большого радиуса, что иллюстрирует теоретические положения статьи [51]. Они также отличаются от последних уменьшением полоидального магнитного потока и критического значения $p_{0}^{{cr}}$. На рис. 9б приведено распределение магнитного поля и давления плазмы в торе для сравнения с аналогичной равновесной конфигурацией в цилиндре на рис. 9а. Подробная количественная информация о различии конфигураций в обоих вариантах геометрии представлена в [29, 64–66].
Список литературы
Брагинский С.И., Гельфанд И.М., Федоренко Р.П. // Физика плазмы и проблема управляемых термоядерных реакций / Ред. М.А. Леонтович. Изд. АН СССР, 1958. Т. 4. С. 201.
Гельфанд И.М., Граев М.И., Зуева Н.М., Морозов А.И., Соловьев Л.С. // ЖТФ. 1961. Т. 31. № 10. С. 1164.
Гельфанд И.М., Граев М.И., Зуева Н.М., Михайло-ва М.С., Морозов А.И. // ДАН СССР. 1962. Т. 143. № 1. С. 81.
Гельфанд И.М., Граев М.И., Зуева Н.М., Михайло-ва М.С., Морозов А.И., // ДАН СССР. 1963. Т. 148. № 6. С. 1286.
Зуева Н.М., Михайлова М.С., Морозов А.И. // ДАН СССР. 1963. Т. 153. № 4. С. 801.
Морозов А.И., Соловьев Л.С. // Вопросы теории плазмы / Ред. М.А. Леонтович. М.: Госатомиздат, 1963. Вып. 2. С. 3.
Зуева Н.М., Соловьев Л.С. // Матем. моделирование. 1998. Т. 10. № 10. С. 88.
Морозов А.И. // Межд. cеминар “Межд. сотрудничество в будущих космических полетах, использующих электродвигатели” Светлогорск, Россия, 15–16 сент. 2005.
Морозов А.И. // ЖЭТФ. 1957. Т. 32. Вып. 2. С. 305.
Арцимович Л.А., Лукьянов С.Ю., Подгорный И.М., Чуватин С.А. // ЖЭТФ. 1957. Т. 33. Вып. 1. С. 3.
Морозов А.И. // Энциклопедия низкотемпературной плазмы / Ред. В.Е. Фортов. М.: Наука, 2000. Вводный том III. Раздел IX. С. 393.
Морозов А.И. Физические основы космических электрореактивных двигателей. М.: Атомиздат, 1978.
Морозов А.И. Введение в плазмодинамику. 2-е изд. М.: ФИЗМАТЛИТ, 2008.
Морозов А.И., Соловьев Л.С. // Вопросы теории плазмы / Ред. М.А. Леонтович. М.: Атомиздат, 1974. Вып. 8. С. 3.
Брушлинский К.В., Морозов А.И. // Вопросы теории плазмы / Ред. М.А. Леонтович. М.: Атомиздат, 1974. Вып. 8. С. 88.
Брушлинский К.В. Математические и вычислительные задачи магнитной газодинамики М.: БИНОМ. Лаборатория знаний. 2009.
Дьяконов Г.А., Тихонов В.Б. // Физика плазмы. 1994. Т. 20. № 6. С. 533.
Брушлинский К.В., Жданова Н.С., Стёпин Е.В. // ЖВМ и МФ. 2018. Т. 58. № 4. С. 607.
Брушлинский К.В., Козлов А.Н., Коновалов В.С. // ЖВМ и МФ. 2015. Т. 55. № 8. С. 1405.
Kozlov A.N., Konovalov V.S. // Communications in Nonlinear Science and Numerical Simulation (CNSNS). 2017. V. 51. P. 169.
Архипов А.С., Ким В.П., Сидоренко Е.К. Стационарные плазменные двигатели Морозова. М.: МАИ, 2012.
Morozov A.I., Savelyev V.V. // Reviews of Plasma Physics / Ed. B.B. Kadomtsev and V.D. Shafranov. Consultant Bureau. NY, Boston, Dordrecht, London, Moscow. 2000. V. 21. P. 203.
Морозов А.И. // Физика плазмы. 2003. Т. 29. № 3. С. 261.
Шафранов В.Д. // ЖЭТФ. 1957. Т. 33. Вып. 3(9). С. 710.
Grad H., Rubin H. // Proc. 2-nd United Nations Int. Conf. Peaceful Uses Atomic Energy. Geneva. 1958. V. 31. NY: Columbia Univ. Press. 1959. P. 190.
Морозов А.И. // Физика плазмы. 1992. Т. 18. Вып. 3. С. 305.
Брушлинский К.В., Зуева Н.М., Михайлова М.С., Морозов А.И., Пустовитов В.Д., Тузова Н.Б. // Физика плазмы. 1994. Т. 20. № 3. С. 284.
Морозов А.И., Савельев В.В. // УФН. 1998. Т. 168. № 11. С. 1153.
Брушлинский К.В., Кондратьев И.А. // Матем. моделирование. 2018. Т. 30. № 6. С. 76.
Брушлинский К.В., Чмыхова Н.А. // Матем. моделирование. 2010. Т. 22. № 6. С. 3.
Брушлинский К.В., Чмыхова Н.А. // Вестн. НИЯУ МИФИ. 2014. Т. 3. № 1. С. 40.
Арнольд В.И. // УМН. 1963. Т. 18. Вып. 6 (144). С. 91.
Ратникова Т.А. // Матем. моделирование. 1997. Т. 9. № 8. С. 3.
Oran E., Boris J.P. Numerical simulation of reactive flow. Elsevier. NY, Amsterdam, London. 1987 (перевод: Оран Э., Борис Дж. Численное моделирование реагирующих потоков. М.: Мир. 1990).
Белова И.В., Брушлинский К.В., Морозов А.И. // Матем. моделирование. 1992. Т. 4. № 10. С. 3.
Brushlinskii K.V., Styopin E.V. // J. Phys: Conf. Ser. 2017. V. 788. 012009.
Брушлинский К.В., Жданова Н.С. // Физика плазмы. 2008. Т. 34. № 12. С. 1120.
Брушлинский К.В., Ратникова Т.А. // Матем. моделирование. 1996. Т. 8. № 2. С. 75.
Брушлинский К.В., Ратникова Т.А. // Физика плазмы. 1995. Т. 21. № 9. С. 784.
Тихонов А.Н., Самарский А.А., Заклязьминский Л.А., Волосевич П.П., Дегтярев Л.М., Курдюмов С.П., Попов Ю.П., Соколов В.С., Фаворский А.П. // ДАН СССР. 1967. Т. 173. № 4. С. 808.
Брушлинский К.В. // Энциклопедия низкотемпературной плазмы / Ред. В.Е. Фортов. 2008. Сер. Б. Т. VII-1, Часть 2. С. 84.
Козлов А.Н. // Изв. АН. Механика жидкости и газа. 2000. № 5. С. 181.
Kozlov A.N. // Plasma Phys. Control. Fusion. 2017. V. 59. № 11. 115004.
Брушлинский К.В., Жданова Н.С. // Изв. РАН. МЖГ. 2004. № 3. Р. 135.
Брушлинский К.В. Математические основы механики жидкости, газа и плазмы. Долгопрудный: Изд. Дом “Интеллект”, 2017.
Стёпин Е.В. // Вестник НИЯУ МИФИ. 2014. Т. 3. № 5. С. 517.
Brushlinskii K.V., Styopin E.V. // J. Phys: Conf. Ser. 2017. V. 937. 012007.
Козлов А.Н. // Физика плазмы. 2012. Т. 38. № 1. С. 15.
Johnson J.L., Oberman C.R., Kulsrud R.M., Frieman E.A. // Phys. Fluids. 1958. V. 1. № 4. P. 281.
Пустовитов В.Д., Шафранов В.Д. // Вопросы теории плазмы / Ред. Б.Б. Кадомцев. М.: Энергоиздат. 1987. Вып. 15. С. 146.
Захаров Л.Е., Шафранов В.Д. // Вопросы теории плазмы / Ред. М.А. Леонтович и Б.Б. Кадомцев. М.: Энергоиздат, 1982. Вып. 11. С. 118.
Морозов А.И., Пустовитов В.Д. // Физика плазмы. 1991. Т. 17. Вып. 10. С. 1276.
Ильгисонис В.И., Поздняков Ю.И. // Физика плазмы. 2004. Т. 30. № 12. С. 1064.
Арсенин В.Я. Методы математической физики и специальные функции. М.: Наука. Гл. ред. физ.-мат. лит-ры, 1974.
Брушлинский К.В., Морозов А.И., Петровская Н.Б. // Матем. моделирование. 1998. Т. 10. № 11. С. 29.
Брушлинский К.В., Зуева Н.М., Михайлова М.С., Петровская Н.Б. // Матем. моделирование. 1995. Т. 7. № 4. С. 73.
Брушлинский К.В., Савельев В.В. // Матем. моделирование. 1999. Т. 11. № 5. С. 3.
Brushlinskii K.V. // Comp. Phys. Comm. 2000. V. 26. P. 37.
Морозов А.И., Франк А.Г. // Физика плазмы. 1994. Т. 20. № 11. С. 982.
Франк А.Г. // УФН. 2010. Т. 180. № 9. С. 982.
Брушлинскимй К.В., Игнатов П.А. // ЖВМиМФ. 2010. Т. 50. № 12. С. 2184.
Брушлинский К.В., Гольдич А.С., Десятова А.С. // Матем. моделирование. 2012. Т. 24. № 8. С. 81.
Брушлинский К.В., Гольдич А.С., Давыдова Н.А. // Матем. моделирование. 2016. Т. 28. № 7. С. 107.
Брушлинский К.В., Гольдич А.С. // Дифф. уравнения. 2016. Т. 52. № 7. С. 887.
Brushlinskii K.V., Goldich A.S. // J. Phys.: Conf. Ser. 2017. V. 788. 012008
Brushlinskii K.V., Kondratyev I.A. // J. Phys.: Conf. Ser. 2017. V. 937. 012006.
Дополнительные материалы отсутствуют.