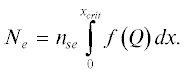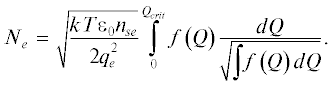Физика плазмы, 2019, T. 45, № 1, стр. 76-96
Анализ длительности перехода между режимом дебаевского слоя с виртуальным катодом и обратным режимомГ. Р. Джонсон, М. Д. Кампанелл
Г. Р. Джонсон a, *, М. Д. Кампанелл a
a Ливерморская национальная лаборатория имени Эрнеста Лоуренса
94551 Калифорния, Ливермор, США
* E-mail: GrantRandolphJohnson@gmail.com
Поступила в редакцию 05.06.2018
После доработки 12.07.2018
Принята к публикации 02.08.2018
Аннотация
Накопление холодных ионов, захваченных внутри дебаевского слоя с виртуальным катодом, приводит к разрушению слоя, вызывая переход в обратный режим. Главным процессом, приводящим к появлению захваченных ионов, является перезарядка, происходящая при столкновениях быстрых ионов с холодными нейтралами. Из-за сложности процессов, происходящих в постоянно меняющемся слое пространственного заряда, предсказать продолжительность перехода непросто. В зависимости от характеристик плазмы, а также эмитированных электронов и нейтралов, продолжительность перехода может составить от миллисекунд до часов. При проведении экспериментов важно понимать, произойдет ли переход дебаевского слоя с виртуальным катодом в обратный режим за время, выделенное для наблюдений. В данной статье изложена теория, позволяющая определить длительность перехода слоя при известных параметрах плазмы. Расчеты включают приближенные аналитические оценки длины виртуального катода, количества заряженных частиц в каждом зарядовом слое дебаевского слоя с виртуальным катодом и времени, необходимого для его перехода в обратный дебаевский слой. Результаты, полученные в рамках теоретической модели, сравниваются с результатами одномерного кинетического моделирования дебаевского слоя с виртуальным катодом с учетом процессов перезарядки. Результаты используются для оценки масштаба длительности перехода в лабораторных плазменных экспериментах, в фотоэлектронной оболочке Луны и в экспериментах на токамаках.
1. ВВЕДЕНИЕ
Исследования слоев пространственного заряда критически важны для понимания взаимодействия плазмы с поверхностью. Основополагающей работой, посвященной взаимодействию плазмы со стенкой, является работа Тонкса и Ленгмюра [1], в которой дано количественное описание пристеночного слоя пространственного заряда в зависимости от параметров плазмы в случае, когда поверхностью, взаимодействующей с плазмой, является катод с электрическим смещением. В случаях, когда протекающий через поверхность ток равен нулю, поверхность принято называть плавающей. В этом случае стенка приобретает потенциал, который способствует поддержанию равных результирующих потоков электронов и ионов.
Нормальный режим, при котором потенциал монотонно спадает по направлению к плавающей поверхности, называют классическим режимом. Классический режим нарушается, когда коэффициент эмиссии электронов со стенки (количество эмитированных электронов на каждый электрон, упавший на стенку и поглощенный ею) превышает некое критическое значение (0.81 для водородной плазмы [2]). Для более высоких коэффициентов эмиссии было предсказано, что система переходит в дебаевский слой с виртуальным катодом (ДСВК). Режим ДСВК впервые был рассмотрен в [2]. Решение, соответствующее ДСВК, было подробно исследовано в [3–7], однако, результаты нуждаются в проверке. Прямые экспериментальные измерения слоев пространственного заряда затруднены. В то же время, при компьютерном моделировании зачастую не учитываются важные процессы, происходящие в плазме, поскольку их учет требует весьма мелкого разбиения моделируемой области и, соответственно, существенно больших компьютерных ресурсов даже в случае 1D-моделирования (это будет продемонстрировано в разд. 3). Таким образом, до сих пор не ясно, является ли модель ДСВК вполне адекватной.
В литературе можно найти и другие модели слоев пространственного заряда, альтернативные модели ДСВК. Морозов и Соловьев предложили модель слоя, названную “антидебаевским слоем” [8] или же “обратным дебаевским слоем” [9], в котором потенциал увеличивается в направлении от границы слоя к стенке. В этой модели предполагается, что скорость потока ионов, проникающих в слой, велика, и, они достигают стенки. Предполагается также, что ионы ускоряются вне дебаевского слоя плазмы за счет наличия большой разности потенциала в предслое. В [10] был рассмотрен другой тип “обратного режима”, при котором вблизи стенки формируется обратный дебаевский слой, но, в отличие от модели Морозова, ионы плазмы удерживаются в дебаевском слое в отсутствие предслоя, ускоряющего ионы. Обратный режим значительно отличается от всех остальных режимов. В отсутствие разности потенциалов в предслое, ускоряющей ионы, баланс сил в плазме значительно меняется, и поток ионов на стенку становится минимальным [10].
В [10] было показано, что удержание ионов в обратном режиме является наиболее стабильным состоянием, возникающим при взаимодействии плазмы с поверхностью при наличии сильной эмиссии. Моделирование показало, что когда эмиссия электронов с поверхности сильно возрастает, то дебаевский слой сначала превращается в ДСВК, но процессы перезарядки при столкновениях в слое постепенно приводят к захвату все большего числа ионов в потенциальной яме, провоцируя переход слоя в обратный режим. В большинстве фундаментальных теоретических и расчетных работ, рассматривающих эмиссию электронов в слоях пространственного заряда, влияние столкновений не учитывается, однако, для получения адекватных физических результатов, такой учет необходимо сделать.
Интерес представляет определение продолжительности перехода между режимом ДСВК и обратным режимом. Продолжительность времени перехода может существенно меняться в зависимости от параметров плазмы. В случае низкой скорости процессов перезарядки при столкновениях длительность перехода может превышать продолжительность эксперимента, что означает, что ДСВК режим сохраняется в течение эксперимента. При промежуточных значениях длительности перехода, в течение стационарного эксперимента можно наблюдать медленную эволюцию дебаевского слоя из режима ДСВК в обратный режим.
В настоящей работе предлагается теоретическая модель вычисления продолжительности перехода между режимом ДСВК и обратным режимом. Для проверки достоверности модели приведены результаты одномерного моделирования взаимодействия поверхности с плазмой с учетом электронной эмиссии. Затем рассмотрены примеры применения модели для нескольких практически важных случаев. Первый пример касается исследований взаимодействия низкотемпературной лабораторной плазмы с поверхностями, с которых происходит эмиссия электронов. Во втором примере рассмотрены слои пространственного заряда вблизи лунной поверхности, эмиссия электронов с которой вызвана фотоэмиссионными процессами. И, наконец, рассмотрен случай сильной вторичной или термоэлектронной эмиссии с диверторных пластин токамака, расположенных в тени лимитера (scrape-of-layer (SOL)).
2. ТЕОРИЯ
2.1. Переход дебаевского слоя из ДСВК режима в обратный
Интересующие нас распределения потенциалов в дебаевских слоях для различных режимов представлены на рис. 1a. Общепринятая теория предсказывает, что вблизи обращенной к плазме поверхности, которая эмитирует электроны с коэффициентом γ большим, чем некоторое критическое значение, которое составляет примерно один эмитируемый электрон на один электрон, падающий на поверхность, образуется ДСВК [2]. Слой, существующий на пороге перехода между классическим и ДСВК режимами, принято называть пограничным ДСВК слоем. Он был подробно исследован в [2], и также представляет интерес с точки зрения эксперимента [11]. Тем не менее, захват ионов слоем вследствие процессов перезарядки при столкновениях нейтрализует ДСВК слой, и в случае, если у холодных ионов нет возможности его покинуть, образуется обратный слой [10]. Для обратного слоя должен сформироваться соответствующий обратный предслой. Благодаря относительно небольшому падению напряжения между средней плоскостью слоя и его краем, обратный предслой значительно отличается от предслоев, которые формируются в ДСВК и классическом режимах.
Рис. 1.
а) – Качественные распределения потенциала в классическом, ДСВК и обратном режимах. Чтобы подчеркнуть различия между решениями для пограничного ДСВК и ДСВК режимов, также показано распределение потенциала в пограничном ДСВК режиме, описанном в [2]; б) – образование двойного зарядового слоя в пограничном ДСВК. Распределения плотностей электронов и ионов демонстрируют фундаментальные структуры слоя, полученные при моделировании и подробно обсуждаемые в разд. 3.
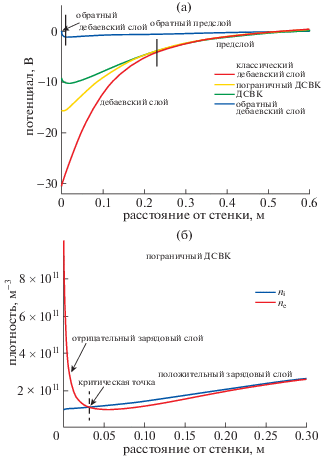
Для понимания временной динамики перехода слоя в обратное состояние сначала необходимо объяснить разницу между решениями, соответствующими стационарным состояниям дебаевского слоя в ДСВК и обратном режимах. Из общих соображений, чтобы экранировать плазму, заряд стенки должен быть равен по величине и противоположен по знаку общему заряду дебаевского слоя. В классическом режиме стенка заряжена отрицательно, а дебаевский слой всюду заряжен положительно. Для случая пограничного ДСВК, распределение плотности электронов показано на рис. 1б. Вблизи границы слоя ионная плотность превышает электронную, что следует из критерия Бома, который имеет тот же вид, что и в случае классического дебаевского слоя. Отрицательно заряженный слой вблизи стенки возникает благодаря тому, что здесь плотность эмитированных электронов является высокой. Общий заряд в случае пограничного ДСВК приблизительно равен нулю, заряд стенки также равен нулю и, соответственно, электрическое поле на стенке также равно нулю (нет потенциальной ямы), что видно на рис. 1а. В ДСВК и обратном режимах, заряд стенки положителен.
В ДСВК формируется “виртуальный катод”, в котором потенциал имеет минимум (см. рис. 2). Слева от минимума существует слой с большим отрицательным зарядом, который компенсируется положительно заряженной стенкой, что приводит к формированию виртуального катода (см. рис. 2). Структура ДСВК в области, расположенной дальше от стенки, чем минимум потенциала, та же, что и у пограничного ДСВК. Отрицательно заряженный слой в основном состоит из электронов, эмитированных со стенки (плотность электронов плазмы в этой области ниже). На расстоянии от поверхности, большем, чем некоторая критическая точка в слое, в которой плотность ионов ni равна плотности электронов ne, плотность эмитированных электронов становится низкой, и ионы плазмы становятся основными носителями заряда. Потенциальная яма вблизи стенки притягивает некоторые из эмитированных электронов обратно на стенку. Она также может служить ловушкой для пришедших извне ионов, которые были ускорены разностью потенциалов предслоя, а затем произошла их перезарядка при столкновении с холодными нейтралами в области потенциальной ямы.
Рис. 2.
а) – Структура дебаевского слоя с виртуальным катодом; б) – распределение электростатического потенциала, соответствующее зарядовым слоям, показанным на рис. 2а.
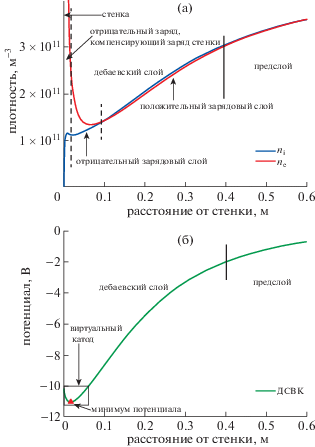
Ключевая идея состоит в следующем: чтобы поверхность с сильной эмиссией поддерживалась в плавающем состоянии, необходим потенциальный барьер с амплитудой $\sim {\kern 1pt} {{T}_{{emit}}}\ln (\gamma )$. Тогда накопление ионов не будет нарушать структуру потенциала слева стороны от минимума потенциала. Вместо этого, захваченные ионы будут нейтрализовывать отрицательный заряд, имеющийся справа от минимума потенциала. Поскольку общий заряд слоя с правой стороны от минимума потенциала должен быть приблизительно равен нулю, положительный заряд слоя будет также уменьшаться. В итоге, падение напряжения в области слоя, где существует пограничный ДСВК режим, уменьшится до нуля, формируя эмиссионный барьер (то есть, обратный слой). Корректность такого описания процессов, происходящих в дебаевском слое, подтверждается результатами моделирования. Типичные для обратного слоя распределения плотности частиц и потенциала представлены на рис. 3, на котором видно, что слой представляет собой одиночный слой отрицательного заряда. На рис. 3а электронная плотность вблизи стенки обрезана по вертикальной оси, потому что ее максимальная величина примерно на порядок больше, чем ионная плотность.
Рис. 3.
а) – Распределения плотностей электронов и ионов вблизи стенки в обратном дебаевском слое и предслое, построенные по данным моделирования, представленным в разд. 3. Отметим, что вблизи стенки существует только один зарядовый слой, который уравновешивает заряд стенки. Этот слой нескомпенсированного заряда вблизи стенки включает в себя весь обратный дебаевский слой, ширина которого меньше, чем ширина ДСВК; б) – распределение электростатического потенциала, соответствующее этому зарядовому слою.
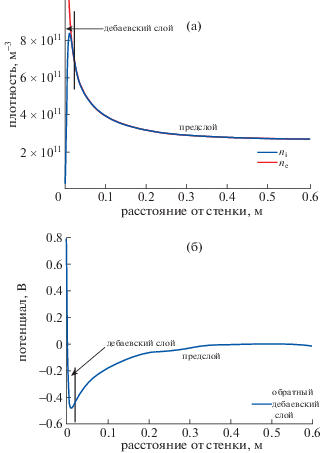
На рис. 3б видно, что в обратном режиме потенциал стенки выше, чем в остальной части плазмы. Падение напряжения между средней плоскостью и границей слоя мало, хотя и не равно нулю (см. рис. 3б). Сравнивая рис. 1а и 3б, можно видеть, что падение напряжения в предслое в обратном режиме гораздо меньше, чем в случае формирования Бомовского предслоя, в котором происходит ускорение ионов в классическом и ДСВК режимах. В обратном режиме большинство ионов удерживаются в слое, но небольшой “хвост” высокоэнергетичных ионов может убегать на стенку. Другая уникальная особенность обратного режима состоит в том, что плотность плазмы нарастает в направлении от средней плоскости к краю слоя. Трансформация ДСВК в обратный дебаевский слой сопровождается формированием соответствующего предслоя.
Поскольку переход ДСВК в обратный дебаевский слой приводит к столь сильным изменениям в слое пространственного заряда и плазме, то весьма важно количественно определить временной масштаб длительности этого процесса по сравнению с продолжительностью интересующего нас эксперимента. Длительности перехода могут отличаться на несколько порядков по величине, в зависимости от свойств системы. Мы построим модель, которая позволит приближенно выразить продолжительность перехода через известные параметры системы. Начнем с определения количества ионов, необходимого для того, чтобы нейтрализовать зарядовые слои в ДСВК (разд. 2.2 и 2.3).
2.2. Распределение заряда в пограничном ДСВК режиме
В качестве исходного условия, предположим, что количество захваченных ионов, необходимых для разрушения ДСВК, примерно равно начальному отрицательному заряду слоя, который ионам предстоит нейтрализовать. Это эквивалентно вычислению отрицательного заряда в отрицательно заряженном слое пограничного ДСВК (см. рис. 1б). Начнем с уравнения Пуассона, в котором плотность заряда можно выразить через плотности трех сортов заряженных частиц, присутствующих в слое: ионов ${{n}_{i}}$, электронов плазмы ${{n}_{{pe}}}$, и эмитированных электронов ${{n}_{{ee}}}$,
(1)
$\frac{{{{d}^{2}}\varphi }}{{d{{x}^{2}}}} = - \frac{{{{q}_{e}}}}{{{{\varepsilon }_{0}}}}\left( {{{n}_{i}} - {{n}_{{pe}}} - {{n}_{{ee}}}} \right).\quad$В работе [2] аналитически описаны все разновидности заряженных частиц присутствующих в дебаевском слое. Уравнение Пуассона, записанное для случая пограничного ДСВК с учетом свойств плазмы, имеет вид
(2)
$\begin{gathered} \frac{{{{d}^{2}}\varphi }}{{d{{x}^{2}}}} = \frac{{{{q}_{e}}{{n}_{{se}}}}}{{{{\varepsilon }_{0}}}}\left( { - \sqrt {\frac{E}{{E - {{q}_{e}}\varphi }}} \mathop + \limits_{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}^{^{{^{{^{{^{{^{{^{{}}}}}}}}}}}}} } \right. \\ + \;\exp \left( {\frac{{{{q}_{e}}\varphi }}{{kT}}} \right)\left( {\frac{{\gamma \sqrt { - \frac{{E{{m}_{e}}}}{{{{m}_{i}}{{q}_{e}}{{\varphi }_{{wall}}}}}\quad} }}{{\gamma - 1}} + 1} \right) + \\ \left. { + \;\frac{{\gamma \left( {\sqrt {\frac{{E{{m}_{e}}}}{{{{m}_{i}}{{q}_{e}}\left( {\varphi - {{\varphi }_{{wall}}}} \right)}}} } \right)}}{{1 - \gamma }}} \right). \\ \end{gathered} $Уравнение (2) представляет собой уравнение Пуассона (1) для плазмы, находящейся вблизи поверхности, эмитирующей электроны. Здесь, qe – заряд электрона, nse – плотность плазмы на границе дебаевского слоя, E – тепловая энергия электронов, φ – электростатический потенциал, T – температура электронов плазмы (в Кельвинах), k – постоянная Больцмана, γ – коэффициент эмиссии (количество электронов, эмитированных поверхностью на каждый падающий электрон), me – масса электрона, mi – масса иона, φwall – потенциал стенки по отношению к потенциалу на границе слоя, который принят равным нулю, ε0 – диэлектрическая проницаемость вакуума.
Для случая пограничного ДСВК, уравнение (2) приводится к более простому виду за счет подстановок $\gamma = 1 - 8.3\sqrt {{{{{m}_{e}}} \mathord{\left/ {\vphantom {{{{m}_{e}}} {{{m}_{i}}}}} \right. \kern-0em} {{{m}_{i}}}}} $, $E = 0.58kT$ и ${{\varphi }_{{wall}}} = $ $ = - 1.02kT{\text{/}}{{q}_{e}}$ [2]. Предположение, что масса иона много больше массы электрона (${{m}_{e}} \gg {{m}_{i}}$) позволяет еще больше упростить результат. Группируя оставшиеся члены, получаем уравнение
(3)
$\begin{gathered} \frac{{{{d}^{2}}\varphi }}{{d{{x}^{2}}}} = \frac{{{{q}_{e}}{{n}_{{se}}}}}{{{{\varepsilon }_{0}}}}\left( { - \sqrt { - \frac{{29}}{{50\frac{{{{q}_{e}}\varphi }}{{kT}} - 29}}} \mathop + \limits_{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}}}}}^{^{{^{{^{{^{{^{{^{{^{{^{{^{{}}}}}}}}}}}}}}}}}}} } \right. \\ \left. { + \;\quad0.9091\exp \left( {\frac{{{{q}_{e}}\varphi }}{{kT}}} \right) + \frac{{\sqrt {\frac{{29}}{{50\frac{{{{q}_{e}}\varphi }}{{kT}} + 51}}} }}{{8.3}}} \right). \\ \end{gathered} $Уравнение (3) может быть решено численно для конкретных распределений потенциала и заряда вдоль оси x (расстояние от стенки) в пограничном ДСВК.
2.3. Численный расчет профиля потенциала
Подставив в уравнение (3) выражения для потенциала и его второй производной в виде $\varphi = QkT{\text{/}}{{q}_{e}}$ и $\varphi '' = Q''kT{\text{/}}{{q}_{e}}$, получим уравнение
(4)
$\begin{gathered} \frac{{{{d}^{2}}Q}}{{d{{x}^{2}}}} = \frac{{q_{e}^{2}{{n}_{{se}}}}}{{kT{{\varepsilon }_{0}}}}\left( { - \sqrt { - \frac{{29}}{{50Q - 29}}} \mathop + \limits_{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}^{^{{^{{^{{^{{^{{^{{}}}}}}}}}}}}} } \right.\quad \\ \left. { + \;0.9091\exp \left( Q \right) + \frac{{\sqrt {\frac{{29}}{{50Q + 51}}} }}{{8.3}}} \right) = \frac{{q_{e}^{2}{{n}_{{se}}}}}{{kT{{\varepsilon }_{0}}}}f\left( Q \right). \\ \end{gathered} $Преимуществом такой подстановки является то, что все зависимости от параметров плазмы теперь описываются функцией f(Q). Функция f(Q) в правой части уравнения (4) представляет собой зависимость плотности заряда от безразмерной переменной Q.
Подставляя $\varphi '' = Q''kT{\text{/}}{{q}_{e}}$ в уравнение Пуассона (1) и решая его относительно заряда, получаем уравнение
(5)
$\left( {{{n}_{{pe}}} + {{n}_{{ee}}} - {{n}_{i}}} \right) = \frac{{kT{{\varepsilon }_{0}}}}{{q_{e}^{2}}}\frac{{{{d}^{2}}Q}}{{d{{x}^{2}}}}.$Подставляя уравнение (4) в уравнение (5) и интегрируя по x обе части уравнения в пределах границ одиночного заряженного слоя, получаем плотность на границе слоя, помноженную на некоторую константу с размерностью длины. Введем переменную Ne для описания общего заряда слоя внутри дебаевского слоя. Поскольку оба слоя являются практически одинаковыми, мы будем искать решение для положительно заряженного слоя, поскольку в этом случае уравнение легче решается, чем для случая отрицательно заряженного слоя, когда на стенке оно расходится до бесконечности,
Функция в правой части уравнения (6) не является функций переменной x. Чтобы провести интегрирование, мы должны найти соответствие между dx и dQ, чтобы затем найти решение для заряженного слоя. Оно может быть легко получено из уравнения (5) с помощью подстановки u = dQ/dx в уравнение (5), однократного интегрирования, обратной подстановки в u, и переписывания выражения для dx. Вычисление неопределенного интеграла добавляет константу C, которая обращается в ноль при задании граничных условий u = 0 и Q = 0 (граничные условия на стенке в случае пограничного ДСВК, где потенциал равен нулю и электрическое поле равно нулю). Подставляя выражение для dx в уравнение (6), получаем
Для обеспечения необходимой точности интеграл в выражении (7) вычислялся с использованием трапециедального суммирования по десяти миллионам точек. Пределы интегрирования по Q были найдены путем построения графика функции и определения точки, где она обращается в ноль, которая и является критической точкой Qcrit = 0.986, отмеченной на рис. 1б. Такое интегрирование дает значение интеграла, равное 0.509. Подставив это значение в формулу (7), получим выражение для полного заряда одиночного слоя на единицу площади поверхности (в м2),
Заметим, что выражение (8) может быть переписано в терминах дебаевской длины путем умножения числителя и знаменателя на $\sqrt {{{n}_{{se}}}} $, что дает Ne = 0.360nseλD.
2.4. Ширина виртуального катода в ДСВК
Поскольку ионы, которые участвуют в процессах перезарядки при столкновениях в области виртуального катода, оказываются захваченными, то, естественно, скорость захвата ионов зависит от пространственного размера виртуального катода. Чтобы рассчитать общую ширину виртуального катода, мы сперва рассчитаем расстояние от стенки до минимума потенциала (см. рис. 2б), решив уравнение Пуассона для этой области. Поскольку плотность частиц в этой области определяется эмитированными электронами, мы пренебрежем плотностями электронов и ионов плазмы. При описании эмитированных электронов необходимо учитывать, что их поток со стенки Γee, равен произведению коэффициента эмиссии γ на поток электронов, падающих на стенку Γe: Γee = γΓe. Эти потоки могут быть выражены через соответствующие плотности электронов. Потоки эмитированных электронов и электронов плазмы можно записать, соответственно, в виде уравнений [10, 12]
(9)
$\begin{gathered} {{{\Gamma }}_{{ee}}} = {{n}_{{ee}}}\sqrt {\frac{{2k{{T}_{{emit}}}}}{{\pi {{m}_{e}}}}} \quad,\quad \\ {{{\Gamma }}_{e}} = {{n}_{{se}}}\sqrt {\frac{{kT}}{{2\pi {{m}_{e}}}}} \exp \left( {\frac{{{{q}_{e}}{{\varphi }_{{wall}}}}}{{kT}}} \right), \\ \end{gathered} $(10)
${{n}_{{ee}}} = \frac{{\gamma {{n}_{{se}}}}}{2}\sqrt {\frac{T}{{{{T}_{{emit}}}}}} \exp \left( {\frac{{{{q}_{e}}{{\varphi }_{{wall}}}}}{{kT}}} \right).$В [2] было показано, что падение потенциала на участке от границы слоя до минимума потенциала равно ${{\varphi }_{{wall}}} = - 1.02kT{\text{/}}{{q}_{e}}$. Подставляя это значение в формулу (10), получаем выражение для плотности электронов вблизи стенки. Для данной величины φwall, значение экспоненты равно ~0.360. Далее представим зависимость плотности заряда от расстояния до стенки как зависимость ее от электростатического потенциала. Используя приближение Больцмана, получим выражение
(11)
${{n}_{{ee}}} = 0.180\gamma {{n}_{{se}}}\sqrt {\frac{T}{{{{T}_{{emit}}}}}} \exp \left( {\frac{{{{q}_{e}}\varphi }}{{k{{T}_{{emit}}}}}} \right).$В условиях сильной эмиссии влияние ионного потока на потенциал “плавающей” поверхности значительно меньше, чем влияние, связанное с нарушением баланса электронов плазмы и эмитированных электронов. Так что в случае ДСВК величина потенциала в минимуме сопоставима с соответствующей величиной в случае обратного слоя [14], которая описывается выражением (см. [10])
Подстановка выражения (11) в уравнение (1) дает уравнение Пуассона, в котором правая часть является функцией потенциала,
(13)
$\frac{{{{d}^{2}}\varphi }}{{d{{x}^{2}}}} = 0.180\gamma {{n}_{{se}}}\frac{{{{q}_{e}}}}{{{{\varepsilon }_{0}}}}\sqrt {\frac{T}{{{{T}_{{emit}}}}}} \exp \left( {\frac{{{{q}_{e}}\varphi }}{{k{{T}_{{emit}}}}}} \right).$Здесь сделана та же самая подстановка, что и в разд. 2.3, с той лишь разницей, что здесь входящая в уравнение температура является температурой эмитированных электронов, а не электронов плазмы. Подстановки $\varphi = QkT{\text{/}}{{q}_{e}}$ и $\varphi '' = Q''kT{\text{/}}{{q}_{e}}$ приводят к исчезновению всех констант в экспоненциальном члене в уравнении (13),
(14)
$\frac{{{{d}^{2}}Q}}{{d{{x}^{2}}}} = \frac{{0.180\gamma q_{e}^{2}{{n}_{{se}}}}}{{k{{T}_{{emit}}}{{\varepsilon }_{0}}}}\sqrt {\frac{T}{{{{T}_{{emit}}}}}} \exp \left( Q \right).$Уравнение (14) сводится к виду $y'' = Cf\left( y \right)$ и является особым дифференциальным уравнением, которое называется автономным дифференциальным уравнением второго порядка. Такие уравнения могут быть напрямую решены относительно переменной x [15]. Для начала, упростим правую часть уравнения (14), приведя ее к виду Cf(y),
Это автономное дифференциальное уравнение второго порядка с разделяющимися переменными. После подстановки u = dQ/dx, уравнение (15) может быть сведено к дифференциальному уравнению первого порядка. Заметим, что если мы выразим dx через u в использованном для подстановки выражении, то получим dx = dQ/u. Перенося dQ в правую часть уравнения и, проинтегрировав обе его части, получим уравнение
Константу C1 в уравнении (16) можно найти, используя граничные условия в минимуме потенциала: u = 0 и Q = 0. Отсюда получаем ${{C}_{1}} = - {{\gamma }^{{ - 1}}}$. Следовательно, величина u, которая является градиентом Q, также равна нулю. В точке, где u = 0 (в минимуме потенциала), Q представляет собой разность потенциалов между стенкой и точкой минимума, что, в соответствии с уравнением (12), дает значение Q равное $ - \ln \gamma $.
Решая уравнение (16) относительно u и затем, подставляя u = dQ/dx обратно в уравнение, получаем другое дифференциальное уравнение первого порядка, которое можно проинтегрировать, чтобы найти длину x. Пределы интегрирования по Q определяются пределами изменения потенциала, который меняется от φwall = 0 до $\varphi = - {{T}_{{emit}}}\ln (\gamma )k{\text{/}}{{q}_{e}}$,
(17)
$ \pm \mathop \smallint \nolimits^ dx = \mathop \smallint \limits_0^{ - \ln \left( \gamma \right)} \frac{{dQ}}{{\sqrt {2C\left( {\exp \left( Q \right) - {{\gamma }^{{ - 1}}}} \right)} }}.$Подставляя C обратно в уравнение (17) и вычисляя интеграл, получаем
(18)
$\begin{gathered} {{x}_{{wall - dip}}} = \sqrt {\frac{{k{{T}_{{emit}}}{{\varepsilon }_{0}}}}{{0.180\gamma q_{e}^{2}{{n}_{{se}}}}}} {{\left( {\frac{{{{T}_{{emit}}}}}{T}} \right)}^{{1/4}}} \times \\ \times \;2\sqrt \gamma \left( {\arctan \left( {\sqrt {\gamma - 1} } \right)} \right). \\ \end{gathered} $Упрощение уравнения (18) приводит к выражению для расстояния между минимумом потенциала и стенкой, выраженной через параметры плазмы,
(19)
$\begin{gathered} {{x}_{{wall - dip}}} = 4.71\left( {\sqrt {\frac{{{{\varepsilon }_{o}}k{{T}_{{emit}}}}}{{q_{e}^{2}{{n}_{{se}}}}}} } \right){{\left( {\frac{{{{T}_{{emit}}}}}{T}} \right)}^{{1/4}}} \times \\ \times \;\left( {\arctan \left( {\sqrt {\gamma - 1} } \right)} \right). \\ \end{gathered} $Выражение (19) позволяет рассчитать расстояние от стенки до минимума потенциала (виртуального катода). Заметим, что дебаевская длина зависит от некоторых параметров плазмы, таких как плотность плазмы и температура эмитированных электронов. Отметим, что поскольку максимальное значение арктангенса равно π/2, то значение xwall-dip является конечным даже в пределе γ, стремящегося к бесконечности. Из выражения (19) следует, что расстояние от стенки до минимума потенциала также возрастает с ростом температуры эмитированных электронов, что можно легко объяснить. Температура электронов плазмы T обусловлена потоком эмитированных электронов, который пропорционален потоку электронов плазмы на стенку (по определению коэффициента вторичной эмиссии γ). При термоэлектронной эмиссии и фотоэлектронной эмиссии, когда испускаемый поток Γee практически не связан с T, расстояние между минимумом потенциала и стенкой может быть аналогичным образом выражено через поток Γee.
Расчет длины остальной части виртуального катода (т. е. расстояния от минимума потенциала до правой границы потенциальной ямы) является более сложным, чем расчет xwall-dip. Плотность эмитированных электронов быстро уменьшается вследствие их ускорения, поэтому электроны и ионы плазмы также начинают влиять на распределение потенциала. Не существует простой аналитической оценки длины этой области, да она и не нужна, поскольку при разрушении дебаевского слоя структура этой области сильно меняется. Поэтому, в качестве грубого приближения, мы предположим, что виртуальный катод является практически симметричным, что означает, что lVC ≈ 2xwall-dip. Это приводит к выражению
2.5. Зависимость длительности перехода от величины ионного потока
Теперь, когда у нас есть оценка длины виртуального катода (выражение (20)), нам нужно определить входящий в интересующую нас область поток частиц, который затем захватывается в этой области. Поток частиц, который испытывает столкновения, сопровождающиеся перезарядкой, во время прохождения области виртуального катода, может быть рассчитан по формуле
(21)
${{\Gamma }_{{cx}}} = {{\Gamma }_{{se}}}\left( {1 - \exp \left( { - \frac{{{{l}_{{{\text{VC}}}}}}}{{{{i}_{{mfp}}}}}} \right)} \right).$Однако, поскольку ширина виртуального катода во многих случаях много меньше длины свободного пробега, то для описания процессов достаточно использовать первый порядок разложения экспоненты,
(22)
${{\Gamma }_{{cx}}} = \left( {\frac{{{{l}_{{{\text{VC}}}}}}}{{{{i}_{{mfp}}}}}} \right){{\Gamma }_{{se}}}.$Поток ионов из области квазинейтральной плазмы определяется структурой предслоя. В режиме ДСВК предслой практически идентичен предслою в классическом режиме. Пристеночный слой является единственной областью, структура которой меняется при переходе из классического режима в режим ДСВК, а классический предслой остается неизменным для поддержания Бомовского потока ионов на стенку. В [2] для потока ускоренных ионов, поступающих из области вблизи средней плоскости плазмы к краю пристеночного слоя, было получено выражение Γse = = nsecs, где cs – ионно-звуковая скорость в плазме. Когда температура ионов много меньше температуры электронов, ионно-звуковая скорость дается выражением ${{c}_{s}} \approx \sqrt {{{kT} \mathord{\left/ {\vphantom {{kT} {{{m}_{i}}}}} \right. \kern-0em} {{{m}_{i}}}}} $ (см. [13], стр. 15), поэтому поток ионов, поступающих в слой, на границе слоя может быть записан в виде ${{\Gamma }_{{se}}} = $ $ = {{n}_{{se}}}\sqrt {{{kT} \mathord{\left/ {\vphantom {{kT} {{{m}_{i}}}}} \right. \kern-0em} {{{m}_{i}}}}} $.
Если средняя длина свободного пробега ионов для столкновений, сопровождающихся перезарядкой, неизвестна, то она может быть найдена исходя из плотности нейтралов и сечения процесса перезарядки, imfp = (σcxnn)–1. Переписав выражение (22) для потока ионов, поступающих в область виртуального катода, с использованием выражений для средней длины свободного пробега ионов, ионного потока и длины виртуального катода lVC, получим следующее выражение для потока ионов, входящих в область виртуального катода, в которое входят параметры плазмы:
(23)
$\begin{gathered} {{\Gamma }_{{cx}}} = {{\sigma }_{{cx}}}{{n}_{n}}9.42\left( {\sqrt {\frac{{{{\varepsilon }_{0}}k{{T}_{{emit}}}}}{{q_{e}^{2}{{n}_{{se}}}}}} } \right){{\left( {\frac{{{{T}_{{emit}}}}}{T}} \right)}^{{1/4}}} \times \\ \times \;\left( {\arctan \left( {\sqrt {\gamma - 1} } \right)} \right)\left( {\sqrt {\frac{{kT}}{{{{m}_{i}}}}} } \right){{n}_{{se}}}. \\ \end{gathered} $Поскольку из наших предыдущих вычислений нам известна величина отрицательного заряда Ne, который необходимо нейтрализовать, то мы можем оценить время, которое потребуется для накопления соответствующего количества захваченных ионов,
(24)
${{t}_{{accum}}} = \frac{{{{N}_{e}}{{i}_{{mfp}}}}}{{{{l}_{{{\text{VC}}}}}{{{\Gamma }}_{{se}}}}}\quad,{\text{ и л и }}\quad{{t}_{{accum}}} = \frac{{{{N}_{e}}}}{{{{\Gamma }_{{{\text{cx}}}}}}}.$Подставляя выражения (8) и (23) в выражение (24), получим
(25)
${{t}_{{accum}}} = 0.0382\frac{{{{i}_{{mfp}}}\sqrt {{{m}_{i}}} }}{{\sqrt {kT} \arctan \left( {\sqrt {\gamma - 1} } \right)}}{{\left( {\frac{T}{{{{T}_{{emit}}}}}} \right)}^{{3/4}}}.$Выражение (25) может служить грубой оценкой времени перехода между ДСВК и обратным режимами дебаевского слоя. Не стоит ожидать высокой точности оценки, поскольку при ее выводе был использован целый ряд приближений. Например, заряд Ne одного из слоев в ДСВК-режиме был рассчитан с использованием модели Хоббса–Вессона, где ионы не участвуют в столкновениях. Те же столкновения, которые приводят к захвату ионов в области виртуального катода, приведут и к изменению распределения плотности в остальной части слоя пространственного заряда, если только длина свободного пробега достаточно велика. Кроме того, наше предположение о том, что захваченные ионы должны компенсировать заряд Ne в исходном слое, является всего лишь эвристическим предсказанием, которое не учитывает сложную динамику разрушающегося слоя. При разрушении дебаевского слоя потенциальная яма расширяется, увеличивая ширину виртуального катода lVC и ускоряя захват ионов. В общем случае, длительность перехода, вычисленная в соответствии с выражением (25), изменяется, как и ожидалось, в зависимости от значений параметров системы. Например, переход происходит быстрее при более высоких значениях γ или Temit из-за того, что ширина виртуального катода становится больше.
В случае, когда ширина виртуального катода не является малой по сравнению с длиной свободного пробега ионов, можно по аналогии получить следующее выражение для длительности перехода:
(26)
${{t}_{{accum}}} = \frac{{{{N}_{e}}}}{{{{\Gamma }_{{se}}}\left( {1 - \exp \left( { - \frac{{{{l}_{{{\text{VC}}}}}}}{{{{i}_{{mfp}}}}}} \right)} \right)}}.$Заметим, что выражения (25) и (26) дают оценку длительности перехода дебаевского слоя из ДСВК режима в обратный, но эта оценка не является оценкой времени, которое требуется для установления стационарного распределения потенциала в остальной плазме вдали от дебаевского слоя. Для формирования соответствующего обратного предслоя требуется больше времени, и оно происходит под действием различных физических процессов.
3. СРАВНЕНИЕ РЕЗУЛЬТАТОВ ТЕОРИИ И МОДЕЛИРОВАНИЯ
3.1. Численный код
Численный код, использованный для проверки нашей теоретической модели, был подробно описан в [10]. Здесь будет дано лишь краткое описание. С помощью кода проводится моделирование незамагниченной плазмы с 1D-1V функциями распределения скоростей электронов и ионов, которые в начальный момент времени являются максвелловскими по скоростям и однородными во всех точках x-пространства. Вид начальных распределений электронов и ионов дается выражением
(27)
${{f}_{s}}\left( {x,v} \right) = {{n}_{s}}\left( {\sqrt {\frac{{{{m}_{s}}}}{{2\pi k{{T}_{s}}}}} } \right)\exp \left( { - \frac{{{{m}_{s}}{{v}_{s}}^{2}}}{{2k{{T}_{s}}}}} \right).$Динамика частиц в фазовом пространстве рассчитывается с использованием уравнения Власова
(28)
$\frac{{\partial {{f}_{s}}}}{{\partial t}} = - {{v}_{s}}\frac{{\partial {{f}_{s}}}}{{\partial x}} \pm \frac{{{{q}_{s}}}}{{{{m}_{s}}}}\frac{{\partial \varphi }}{{\partial x}}\frac{{\partial {{f}_{s}}}}{{\partial {{v}_{s}}}} + {{S}_{{ch\left( s \right)}}} + {{S}_{{coll\left( s \right)}}}$Использование сетки из 801 точки по оси x и 300 точек по оси v фазового пространства позволило обеспечить достаточно мелкое разбиение области моделирования. Если не указано иное, то на рисунках приведены результаты, полученные при следующих параметрах: плотность плазмы 3 × 1011 м–3, электронная температура плазмы 8 эВ, длина плазмы 1 м, коэффициент электронной эмиссии 10, температура испускаемых электронов 0.3 эВ, длина свободного пробега электронов и ионов 0.2 м. Для наглядности, в рассматриваемых здесь случаях слой пространственного заряда не является идеализированным тонким слоем, а занимает значительную часть плазменного промежутка.
3.2. Формирование виртуального катода в ДСВК
Поскольку ищется решение уравнения Власова (28), зависящее от времени, то учитывается взаимодействие плазмы со стенкой. Вначале предполагается, что дебаевский слой приходит в равновесие по классическому сценарию. При этом, когда начинается электронная эмиссия со стенки, считается, что ускоряющий ионы предслой уже сформировался. Начиная со значения, соответствующего классическому равновесию, коэффициент эмиссии стенки постепенно увеличивается до тех пор, пока не образуется сначала пограничный ДСВК, а затем и сам ДСВК. На рис. 4 можно проследить изменение таких параметров дебаевского слоя, как потенциал и зарядовые слои.
Рис. 4.
(а)–(д) Временная эволюция профилей плотности электронов и ионов; (е) – профили потенциала, соответствующие профилям плотности на рис. 4а–4д. Когда плотность электронов достигает величины 4 × 1011 м–3, электронный слой отрывается от стенки. Затем плотность увеличивается на порядок по сравнению с плотностью нейтральной плазмы, составляющей 3 × 1011 м–3.
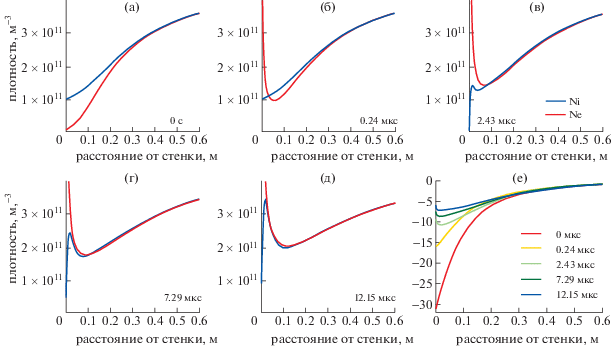
На рис. 4а–д показаны пять последовательно рассчитанных распределений ионной и электронной плотности для различных моментов времени, начиная с 4а и кончая 4д. Графики позволяют проследить, как эти распределения изменяются во времени. На рис. 4а показаны распределения, соответствующие начальному классическому дебаевскому слою, который представляет собой один положительно заряженный слой, нейтрализующий отрицательно заряженную стенку. На рис. 4б видно, что, после начала электронной эмиссии, вблизи стенки популяция электронов становится доминирующей, в то время как профиль ионной плотности остается практически неизменным. Рисунки 4в–4д дают возможность проследить за ростом ионной плотности во времени, который происходит из-за захвата ионов. При сопоставлении этих распределений с рис. 4е, становится очевидным, что накопление ионов вызывает разрушение исходных зарядовых слоев в ДСВК, и, соответственно, разрушение распределения потенциала в слое. Необходимо отметить, что на протяжении всего процесса разрушения дебаевского слоя положение потенциального барьера между минимумом потенциала и стенкой всегда остается неизменным, так же как и положение отрицательно заряженного слоя. Эта область не может быть нейтрализована захваченными ионами, поскольку барьер для эмитированных электронов необходим для поддержания плавающего состояния поверхности в условиях сильной эмиссии электронов. Этим барьером и станет обратный дебаевский слой после того, как произойдет переход.
Чтобы можно было сравнить результаты расчетов в рамках нашей теоретической модели с результатами моделирования, были разработаны различные диагностические инструменты для всестороннего анализа плазмы. Ионы, захваченные в виртуальном катоде, можно изобразить в фазовом пространстве, сосчитав все ионы в каждой точке сетки по x и $v$, которые не обладают достаточной энергией, чтобы выйти из электростатической потенциальной ямы (см. рис. 5).
Рис. 5.
(а) – Распределение потенциала вблизи стенки относительно потенциала средней плоскости слоя в один из моментов времени во время перехода (см. рис. 4); (б) – область фазового пространства ионов. Отрицательное значение скорости означает, что частицы перемещаются влево (по направлению к стенке). Черными отрезками показаны погрешности в определении положения ионов, захваченных в виртуальном катоде ДСВК, в фазовом пространстве, где вертикальный отрезок соответствует диапазону скоростей, при которых ионы удерживаются электростатическими силами в потенциальной яме. Вычисления были проведены для длины свободного пробега ионов 0.5 м.
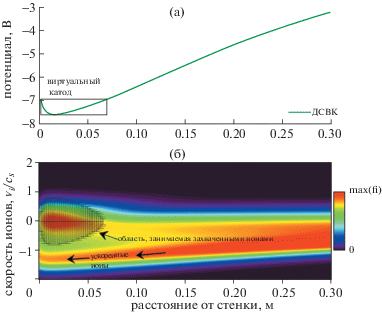
На рис. 5а показано распределение потенциала в ДСВК, в котором имеется минимум вблизи стенки. Заметим, что виртуальный катод образуется вблизи стенки, вдаваясь вглубь плазмы на длину 0.0676 м. Эта ширина хорошо согласуется с теоретической оценкой 0.0574 м длины виртуального катода при заданных начальных условиях, которая может быть получена с помощью выражения (20).
На рис. 5б показана область фазового пространства, занимаемая захваченными ионами, которая присутствует в виртуальном катоде ДСВК и которая содержит ионы, энергия которых недостаточна для того, чтобы покинуть область виртуального катода. Частицы в этой области осциллируют между областями виртуального катода, одна из которых ограничена стенкой, а другая обращена к плазме. В нашей теоретической модели предполагалось, что размеры правой (справа от минимума потенциала) и левой половин виртуального катода равны. На рис. 5а соотношение размеров правой и левой частей виртуального катода в несколько раз больше, однако, это не приводит к большой ошибке при вычислении скорости захвата ионов. Обратим внимание, что в пространстве скоростей ниже области захваченных ионов можно видеть пучок быстрых ионов, ускорившихся при прохождении предслоя и ДСВК.
3.3. Моделирование обратных слоя и предслоя
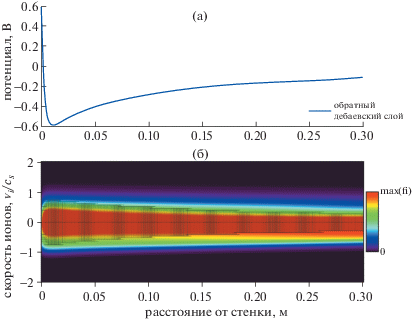
Продолжим анализ динамики дебаевского слоя, начиная с состояния, показанного на рис. 4. Накопление ионов в ДСВК в итоге приводит к переходу в обратный режим. По мере того, как предслой в режиме ДСВК, разрушаясь, переходит в обратный предслой, пучок ускоренных ионов, бомбардирующих стеку, прекращается. Из рис. 6 видно, что почти все ионы удерживаются в плазме. Поток ионов, достигающих стенки, не нулевой, но он очень мал по сравнению с потоком в режиме ДСВК.
Рис. 6.
Область, занимаемая захваченными ионами, после формирования обратного дебаевского слоя и предслоя. Моделирование показывает, что в этот момент произошло уширение области, занимаемой захваченными ионами, поскольку холодные ионы из предслоя больше не могут преодолеть потенциальный барьер вблизи стенки.
3.4. Сравнение моделирования и теории
Чтобы сравнить результаты теории и моделирования, мы взяли тестовый пример с достаточно мелкой численной сеткой, состоящей из 801 точки в x-пространстве и 300 точек в пространстве скоростей, и теми же параметрами, которые были определены в начале разд. 3.1. Аналогично случаю классических дебаевского слоя и предслоя, коэффициент электронной эмиссии γ постепенно повышался до 10, что является достижимым значением в экспериментах по термоэлектронной эмиссии в низкотемпературной плазме.
При сравнении результатов теории и моделирования важно использовать при моделировании источник объемного заряда. Ионы, попавшие на стенку, повторно вводятся в плазму в виде ион-электронных пар, распространяющихся по всему вычислительному домену, включая слой пространственного заряда. В пределе бесконечно протяженной плазмы и бесконечно тонкого слоя, при описании слоя член, описывающий источник, становится пренебрежимо малым. Однако, при моделировании, член, описывающий источник, приводит к появлению ненулевого количества ионов, захваченных в ДСВК, дополнительно к ионам, захваченным вследствие столкновений, сопровождающихся перезарядкой. Формула для длительности перехода в пределе ${{l}_{{{\text{VC}}}}}{\text{/}}{{i}_{{mfp}}} \ll 1$ может быть переписана в виде
(29)
${{t}_{{accum}}} = \frac{{{{N}_{e}}}}{{\left( {\frac{{{{l}_{{VC}}}}}{{{{i}_{{mfp}}}}}} \right){{\Gamma }_{{se}}} + \left( {\frac{{{{l}_{{{\text{VC}}}}}}}{{{{l}_{{plasma}}}}}} \right){{\Gamma }_{{se}}}}}.$Аналогом выражения (26) для произвольного значения lVC/imfp является выражение
(30)
${{t}_{{accum}}} = \frac{{{{N}_{e}}}}{{\left( {\left( {1 - \exp \left( { - \frac{{{{l}_{{{\text{VC}}}}}}}{{{{i}_{{mfp}}}}}} \right)} \right) + \left( {\frac{{{{l}_{{{\text{VC}}}}}}}{{{{l}_{{plasma}}}}}} \right)} \right){{\Gamma }_{{se}}}}}.$Причиной для того, чтобы не исключать из рассмотрения член, описывающий источник внутри дебаевского слоя, является то, что он создает искусственное нарушение непрерывности в точке осечки [10]. Если не указано иное, в выражении (30), использовавшемся для расчета всех величин в разд. 3 и 4, считалось, что длина плазмы составляет один метр.
Переход из режима ДСВК, показанный на рис. 4, продолжается до тех пор, пока не устанавливается стационарное состояние, а именно, обратный режим. Распределения потенциала и ионной плотности в этом режиме показаны на рис. 6а и б соответственно. Данные о распределении потенциала, накоплении заряда и длительности перехода собраны в табл. 1, где сравниваются результаты теоретических расчетов и моделирования.
Таблица 1.
Количественное сравнение теоретических расчетов и результатов моделирования при значениях параметров, описанных в последнем параграфе разд. 3.1
| Пограничный ДСВК, число частиц/м2 | Расстояние от стенки до минимума потенциала, м | Ширина виртуального катода, м | Время нейтрализации заряда, с | |
|---|---|---|---|---|
| Моделирование | 2.30 × 109 | 1.92 × 10–2 | 5.84 × 10–2 | 3.50 × 10–6 |
| Теория | 2.78 × 109 | 2.87 × 10–2 | 5.74 × 10–2 | 2.44 × 10–6 |
В табл. 1 результаты моделирования приведены в сравнении с результатами теоретических расчетов, выполненных по формулам (8), (19), (20), (30). Из результатов моделирования видно, что формирование минимума потенциала внутри дебаевского слоя указывает на начало формирования положительно заряженной поверхности, а также пограничного ДСВК. Именно в этот момент и рассчитывался заряд положительного слоя внутри ДСВК. При моделировании был получен положительный заряженный слой вместо отрицательного, поскольку он не граничил со стенкой и был примерно равен по величине и противоположен по знаку отрицательному заряду слоя.
Расстояние от минимума потенциала до стенки и ширина виртуального катода при моделировании определяли путем усреднения их по всем моментам времени, начиная от времен образования пограничного ДСВК вплоть до времен окончания перехода между режимами. Эта усредненная величина является более информативной, поскольку в начале трансформации дебаевского слоя в ДСВК виртуальный катод имеет очень маленькую ширину, но, по мере роста эмиссии до ее окончательного значения, ширина виртуального катода также достигает своего стационарного значения. В итоге, время, необходимое для разрушения двух слоев, и является суммарным временем, прошедшим от момента образования виртуального катода до момента, когда накопленные в потенциальной яме заряженные ионы нарушают равенство зарядов положительного и отрицательного слоев.
Чтобы получить данные, которые можно было бы сравнить с теорией, обрабатывались зависимости, рассчитанные при достаточно мелком разбиении области моделирования и полученные при различных значениях параметров плазмы и, соответственно, при различных временах перехода (см. рис. 7).
Рис. 7.
Зависимости длительности перехода от некоторых параметров, влияющих на накопление ионов в слое. Зеленым и синим цветом показаны, соответственно, результаты моделирования и теоретических расчетов.
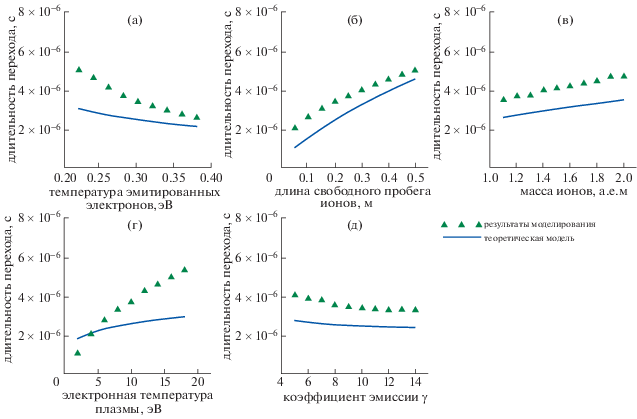
Из рис. 7 видно, что теоретические расчеты, учитывающие скорость захвата ионов, удовлетворительно (с точностью до двойки) совпадают с результатами моделирования. Однако, существуют численные ограничения при моделировании и проведении теоретических расчетов, которые следует обсудить. По мере уменьшения температуры эмитированных электронов, ширина виртуального катода уменьшается вплоть до значений, при которых она становится плохо разрешимой, и ионы физически уже не могут захватываться. Именно поэтому данные на рис. 7а приведены, начиная со значения 0.22 эВ, а не от нуля.
На рис. 7б показана длительность перехода в зависимости от длины свободного пробега ионов. Из рисунка видно, что с ростом длины свободного пробега ионов длительность перехода стремится к некоторому постоянному значению. Это объясняется тем, что объемный источник заряда в дебаевском слое начинает играть заметную роль. Качественная оценка, полученная из данных моделирования, показывает, что для длины свободного пробега ионов 0.2 м, объемный источник заряда создает 15% ионов, захваченных в дебаевском слое. При длине свободного пробега ионов 0.5 м доля объемного источника в числе захваченных ионов составляет уже 33%.
Данные, приведенные на рис. 7в, на котором показана зависимость длительности перехода от массы ионов, подтверждают, что, как и ожидалось, для более тяжелых ионов длительность перехода оказывается большей, поскольку они движутся медленнее. Массы ионов были взяты в несколько раз меньшими, чем атомная единица массы, для сокращения времени вычислений.
Электронная температура плазмы, зависимость от которой показана на рис. 7г, оказывает влияние на все характеристики слоя, делая затруднительным построение обобщенной зависимости на основе одного уравнения. По мере увеличения температуры плазмы, слои заряда внутри ДСВК растут, требуя все большего количества захваченных ионов для совершения перехода. Это компенсируется увеличением потока ионов, который пропорционален квадратному корню из электронной температуры плазмы. Рисунок 7д был получен для постоянных значений коэффициента эмиссии стенки, превышающих единицу, поскольку при стремлении коэффициента эмиссии к единице ширина виртуального катода становится слишком малой и не разрешается при выбранной сетке.
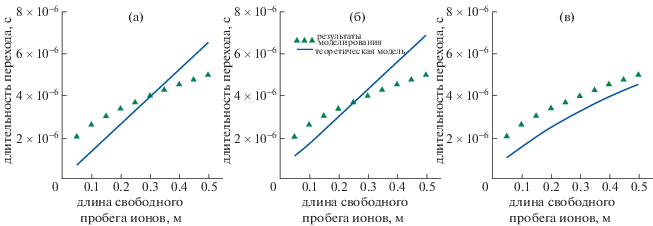
Если при моделировании вклад объемного источника мал, то время накопления ионов будет линейно зависеть от длины их свободного пробега, описываемой выражением (25). Если ширина виртуального катода близка к длине свободного пробега ионов, то для получения точных результатов необходимо использовать выражение (26). В итоге, если объемный источник не является пренебрежимо малым, а именно так обстоит дело при обсуждаемом моделировании, то выражение (30) будет более точно описывать время накопления ионов. Рисунок 8, на котором результаты расчета в рамках трех моделей сравниваются с результатами моделирования, подтверждает это.
Рис. 8.
Сравнение результатов расчетов длительности перехода при использовании различных теоретических моделей: (а) линейная аппроксимация, (б) экспоненциальное решение, (в) экспоненциальное решение с учетом поправки на источник объемного заряда.
Как определить, когда переход дебаевского слоя из одного режима в другой завершен? Хотя и нельзя указать точный момент времени, но переход дебаевского слоя в другой режим может быть установлен несколькими способами. Один из них – проследить процесс преобразования зарядовых слоев, показанный на рис. 4. Другим способом является наблюдение за потенциалом на краю слоя по отношению к потенциалу стенки. В данной работе, мы определяли эту разность потенциалов в режиме пограничного ДСВК и временем окончания перехода считали время, когда эта разность потенциалов уменьшится на 80%. На рис. 9 сравниваются результаты, полученные с помощью этих двух методов. Находится отношение времени накопления заряда, необходимого для разрушения двойных зарядовых слоев, ко времени, когда разность потенциалов между границей слоя и стенкой уменьшается на 80%.
Рис. 9.
Длительность перехода дебаевского слоя, нормированная на время, за которое потенциал на краю слоя уменьшается на 80%, оцененная по результатам теоретических расчетов и моделирования. Показаны зависимости от тех же параметров, что и на рис. 7.
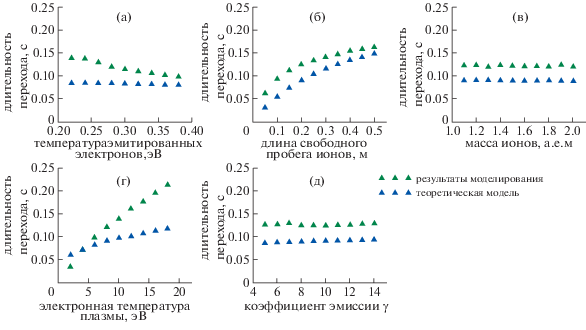
Синие треугольники на всех панелях рис. 9 соответствуют теоретическому времени накопления заряда в виртуальном катоде, деленному на время, когда разность потенциалов между границей слоя и стенкой при моделировании уменьшается на 80%. Зелеными треугольниками на рис. 9 показано отношение времени, полученного при моделировании, при котором виртуальный катод накопил соответствующее количество заряда в одном зарядовом слое пограничного ДСВК, ко времени, при котором разность потенциалов между границей слоя и стенкой уменьшается на 80%.
Одним из полученных результатов является то, что время, необходимое для накопления ионов для нейтрализации исходного отрицательного слоя заряда, хорошо согласуется с предсказаниями теории (в результате чего синие и зеленые треугольники расположены близко). Однако, это время не является точной оценкой времени, необходимого для 80% уменьшения разности потенциалов между границей слоя и стенкой. Треугольники на рис. 9а, в и д группируются вокруг значений 0.1–0.15, что означает, что уменьшение потенциала на 80% требует примерно в 8–10 раз большего времени. На рис. 9б расхождение возрастает при уменьшении длины свободного пробега ионов. Вероятно, это связано с тем, что теоретические расчеты зарядового слоя базируются на бесстолкновительной теории дебаевского слоя Хоббса–Вессона. Теория Хоббса–Вессона также неприменима, когда температура плазмы приближается к температуре эмитированных электронов, что, возможно, объясняет зависимости, представленные на рис. 9г.
3.5. Ограничения при моделировании и чувствительность к низкому разрешению
Важно отметить, что моделирование дебаевского слоя на основе уравнения Власова может дать неточные результаты, если разбиение области моделирования (разрешение) недостаточно мелкое для определения положения виртуального катода. Поэтому важно обеспечить хорошее разрешение. При тех же значениях параметров плазмы, что и в разд. 3.1, было проведено моделирование при различных разрешениях численной сетки. При непротиворечивых значениях параметров в пределе высокого разрешения в решении не наблюдается никаких изменений. При компьютерном моделировании разрешение (число узлов сетки) в x-пространстве последовательно изменялось на 100, а разрешение в v-пространстве поддерживалось на уровне 3/8 от разрешения в x-пространстве. На рис. 10 показано время перехода в зависимости от разрешения в x-пространстве.
Рис. 10.
Длительность перехода в зависимости от разрешения по пространственной координате х при одинаковых начальных значениях параметров плазмы. Показано влияние недостаточного пространственного разрешения.
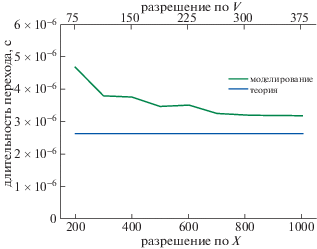
Из рис. 10 видно, что значительные проблемы возникают при низком разрешении. Время перехода увеличивается, поскольку захваченные ионы, которые должны удерживаться в потенциальной яме в соответствии с законом сохранения энергии, имеют возможность покинуть яму вследствие численных ошибок, возникающих в том случае, когда разрешение недостаточно для четкого определения положения виртуального катода в x-пространстве. Аномальное убегание ионов усиливается, когда захваченные ионы с низкой энергией также имеют плохое разрешение и в пространстве скоростей, поскольку это увеличивает ошибки, связанные с нарушением сохранения энергии при перемещении. Это является причиной возникновения расхождений на графиках, построенных в условиях низкой температуры эмитированных электронов, высокой электронной температуры плазмы и низких значениях коэффициента эмиссии. При более высоком разрешении длительность перехода стремится к пределу, показанному на рис. 10. Основываясь на рис. 10, при вычислениях мы использовали сетку не хуже, чем 801 точку в x-пространстве и 300 точек в пространстве скоростей, чтобы обеспечить получение результатов с необходимым разрешением.
3.6. Качественные оценки перехода и более строгие модели
Переход ДСВК в другой режим происходит быстрее по времени, чем переход предслоя. Обратный дебаевский слой должен сформироваться до того, как начнется формирование обратного предслоя и будет достигнуто его стационарное состояние. Формирование предслоя зависит от скорости перемещения захваченных ионов по области, размеры которой велики по сравнению с размерами самого предслоя. В нашей теоретической модели считается, что на протяжении перехода поток входящих ионов является постоянным. Это приближение является допустимым, поскольку за время перехода значительных изменений предслоя еще не произошло, и он продолжает ускорять ионы. Однако, как только предслой начинает подстраиваться к сформировавшемуся обратному дебаевскому слою, поток ионов начинает меняться. Изменение ионного потока в совокупности с изменениями распределений плотности и потенциала значительно затрудняют оцифровывание данных в процессе перехода предслоя в другой режим, поэтому, основываясь на данных моделирования в условиях, определенных в разд. 3.1, мы можем представить здесь лишь беглый качественный обзор.
Свойства дебаевского слоя и предслоя при переходе из ДСВК режима в обратный делают аналитическую модель непригодной для описания процессов, происходящих после разрушения ДСВК. В начале процесса разрушения ДСВК потенциал на границе слоя меняется линейно (см. рис. 11), и теоретическая модель в рамках сделанных нами предположений хорошо описывает этот процесс до тех пор, пока ДСВК не оказывается разрушенным примерно на 30% от своего начального размера. В процессе перехода предслой трансформируется так, чтобы соответствовать обратному дебаевскому слою, а пучок ускоренных ионов разрушается. После уменьшения потенциала на границе слоя по отношению к стенке на 80% по сравнению с его величиной в пограничном ДСВК, потенциал продолжает постепенно падать до тех пор, пока он, в конечном итоге, не становится ниже потенциала стенки. Обратный дебаевский слой приходит в стационарное состояние, когда общий поток ионов становится равен общему потоку электронов, покидающих систему.
Рис. 11.
Уменьшение потенциала средней плоскости слоя при переходе дебаевского слоя из режима ДСВК в обратный. По горизонтальной оси отложено время в течение перехода, а на вертикальной оси показано уменьшение падения потенциала (в процентах) между краем слоя и средней плоскостью по сравнению с его начальным значением в ДСВК.
В дальнейшем, более строгие модели могут быть разработаны на основе модели, представленной в этой статье. Для корректного решения уравнения для плотности заряда необходимо пересмотреть предположение о том, что масса ионов пренебрежимо мала. При расчете плотностей частиц необходимо использовать функцию ошибок, учитывающую число эмитированных электронов, которые не возвращаются обратно, а теряются в плазме. Повышению точности также способствовал бы учет того, что в области между стенкой и минимумом потенциала присутствуют электроны и ионы плазмы. В итоге, вторая половина виртуального катода должна быть исследована при наличии всех трех групп заряженных частиц.
4. ПРИЛОЖЕНИЯ
4.1. Холодная лабораторная плазма
Наиболее доступными экспериментами, в которых можно наблюдать и исследовать переход между ДСВК и обратным режимами дебаевского слоя, являются эксперименты с разрядами в низкотемпературной лабораторной плазме. Здесь мы приведем пример теоретического предсказания, которое может быть проверено в лабораторных условиях. Типичная плотность лабораторной плазмы была взята из работ [17, 18], где исследовалась плазма в условиях эмиссии стенок в диоде, в котором поддерживался режим, аналогичный рассмотренному выше, а именно, режим анодного свечения [19]. Заметим, что мы применяли наши теоретические модели только к плавающим поверхностям. Однако, поверхности со смещением потенциала подобны им во многих отношениях. В частности, недавно было показано, что в режиме анодного свечения вблизи горячего катода формируется обратный дебаевский слой [19]. В условиях, представленных в табл. 2, мы можем теоретически вычислить свойства формирующегося обратного дебаевского слоя (см. табл. 3).
Таблица 2.
Значения параметров, использованные в [15, таблица II ] при моделировании режима анодного свечения между катодом и анодом. Заметим, что условия формирования плавающего потенциала поверхности в этом случае были другими, в расчетах использовалась масса ионов аргона, и для коэффициента эмиссии использовалось значение, характерное для термоэлектронного разряда, которое хорошо воспроизводилось экспериментально
| Плотность плазмы n, м–3 | Температура эмитированных электронов Temit, эВ | Коэффициент эмиссии γ | Масса иона mi, кг | Длина свободного пробега иона imfp, м | Электронная температура плазмы T, эВ |
|---|---|---|---|---|---|
| 5 × 1012 | 0.0757 | 10.0 | 6.68 × 10–26 | 0.0422 | 8.0 |
Таблица 3.
Результаты расчетов в рамках теоретической модели, разработанной в данной статье, при параметрах плазмы, приведенных в табл. 1
| Расстояние от стенки до минимума потенциала xwall–dip, м | Ширина виртуального катода lVC, м | Плотность электронов в зарядовом слое Ne, м–2 | Дебаевская длина λD, м | Длительность перехода taccum, с | |
|---|---|---|---|---|---|
| Теория | 2.50 × 10–3 | 5.01 × 10–3 | 1.14 × 1010 | 9.41 × 10–3 | 9.72 × 10–6 |
В этом случае ожидается, что длительность перехода слоя составит несколько микросекунд, а сам переход произойдет очень близко к стенке. Низкая температура эмитированных электронов является причиной малой ширины виртуального катода. Для формирования более протяженного виртуального катода нужны более высокие температуры электронов, при которых будет увеличиваться расстояние от стенки до точки с минимальным потенциалом. Однако, в данном случае температура эмитированных электронов поддерживается на минимальном уровне, поскольку при использовании таких диагностических методов, как лазерная флуоресценция, при просвечивании плазмы выгодно уменьшить паразитную засветку, источником которой являются пластина и горячие эмитированные электроны [20]. В экспериментах, в которых коэффициент эмиссии приближается к единице, виртуальный катод является очень узким, если он вообще может образоваться, и переход в обратный режим вообще может не произойти за время эксперимента, поэтому зарегистрировать его довольно трудно.
4.2. Слой пространственного заряда вблизи поверхности Луны
Освещенная Солнцем сторона Луны – это большая взаимодействующая с плазмой поверхность, на которой идут процессы фотоэмиссии. Из-за солнечного ветра общая плотность заряженных частиц плазмы в отдельных местах составляет порядка 109 м–3 [21]. Фотоэмиссия, вызванная излучением Солнца, характеризуется коэффициентом эмиссии ~4 [22], что является вполне достаточным, чтобы вызвать переход дебаевского слоя из классического в ДСВК режим. Тем не менее, остаются вопросы, возможен ли вообще такой переход, и если возможен, то сколько времени потребуется, чтобы слой пространственного заряда вблизи поверхности Луны превратился в обратный дебаевский слой за счет захвата холодных ионов в виртуальном катоде.
Средняя плотность нейтральных атомов на освещенной Солнцем поверхности Луны в лунный полдень представлена в табл. 4 [23–25], в которой приведены только данные для частиц, являющихся преобладающими в атмосфере Луны. Теоретические модели предсказывают содержание молекулярного водорода на уровне 6 × 109 м–3, что было подтверждено данными орбитальной спектроскопии атмосферы Луны [25, 26].
Максимальную длительность перехода можно найти, рассматривая захват любого из присутствующих видов ионов в результате перезарядки при столкновениях. Чтобы получить более точную длительность перехода дебаевского слоя вблизи поверхности Луны, необходимо учесть фотоэмиссию нейтралов атмосферы, зарядку пылевых частиц и наличие в атмосфере аргона, неона и гелия. Столь подробный анализ выходит за рамки данной статьи, но учет этих эффектов мог бы только способствовать ускорению перехода из ДСВК режима дебаевского слоя в обратный. Основная реакция перезарядки, происходящая в лунной атмосфере, на которой мы сфокусируем наше внимание в данной работе, происходит при столкновении протонов, приносимых солнечным ветром, с атомами водорода, находящимися на поверхности Луны,
где p – протон, H – атом водорода и H2 – молекула водорода. Эта реакция является доминирующей при столкновениях частиц в дебаевском слое вблизи лунной поверхности и сопровождается перезарядкой. В потоке частиц, приносимых солнечным ветром, средняя плотность ионизованных атомов водорода составляет 6 × 109 м–3 [27]. Другие частицы также приносятся солнечным ветром, но они составляют в среднем около 4% от общего числа частиц в плазме [27], и, для простоты, мы не будем их учитывать. Площадь поперечного сечения нейтральной молекулы H2 составляет приблизительно 7.3 × 10–20 м2 [28], а примерное значение коэффициента электронной эмиссии на освещенной стороне Луны равно γ = 4. [22] Температура электронов плазмы, приносимой солнечным ветром, на расстоянии в 1 а.е. в среднем составляет 140000 К (или ~12 эВ) [29]. Последней величиной, которую нам необходимо задать, чтобы можно было использовать нашу модель, является температура эмитированных электронов. При фотоэлектронной эмиссии электроны вылетают с поверхности Луны с температурой 2.2 эВ [22]. (Корректно было бы рассчитывать ширину реального распределения электронов как полуширину распределения Ферми–Дирака [30], однако, это не повлияет на вид нашего решения.) При этих значениях параметров можно вычислить максимальное теоретическое значение длительности перехода. Используя выражение (25) для расчета времени, необходимого для накопления ионов для нейтрализации заряда двойного слоя, для длительности перехода получим 1.24 × × 104 c ≈ 3.5 часа. Поскольку в расчетах были использованы некоторые приближения и неопределенности, эта оценка является лишь оценкой по порядку величины. По крайней мере, эти расчеты дают мотивацию к дальнейшим исследованиям и предлагают интересную идею, состоящую в том, что, благодаря накоплению холодных ионов, дебаевский слой вблизи поверхности Луны может постепенно эволюционировать в течение каждого лунного дня.
Возникает вопрос, а могут ли захваченные ионы покинуть потенциальную яму вследствие термализации при столкновениях? Воспользуемся выражением (12) для амплитуды потенциала в минимуме для ДСВК и обратного режимов дебаевского слоя. Оно дает значение потенциала в минимуме –2.72 В. Ионы, захваченные в потенциальной яме, должны иметь температуру ~31500 К, чтобы иметь возможность покинуть эту область, что маловероятно, так как температура нейтралов в атмосфере Луны составляет ~400 К в течение лунного дня [26]. Другие факторы, такие как зарядка пылевых частиц, могут приводить к увеличению заряда, захваченного в виртуальном катоде. Кроме того, изменение скорости фотоионизации в данном случае на порядок величины не будет заметно влиять на захват ионов [26].
В целом, холодный молекулярный водород, который ионизуется в области виртуального катода, электростатически связан и не может покидать дебаевский слой по нормали к лунной поверхности. Переход дебаевского слоя от классического режима через ДСВК к обратному режиму может происходить каждым лунным утром, когда Солнце восходит над поверхностью Луны. Когда Солнце начинает садиться, иначе говоря, угол между солнечными лучами и освещенной поверхностью начинает увеличиваться и коэффициент эмиссии падает до значений меньших γ = 0.81–1, обратный режим дебаевского слоя начинает преобразовываться в классический режим, и все удерживаемые ионы покидают слой и попадают на поверхность.
4.3. Замагниченная плазма, в которой может сохраняться обратный режим дебаевского слоя
В термоядерных установках с магнитным удержанием электронная плотность в области SOL составляет порядка 1019–1020 м–3 [13, 31–33]. Высокая плотность плазмы приводит к интенсивному рециклингу нейтралов вблизи поверхности лимитеров и диверторых пластин. На токамаке DIII-D, с использованием диагностики быстрых ионов по излучению Dα, на последней замкнутой магнитной поверхности регистрировались плотности нейтралов до 8.1 × 1015 м–3 [33]. Как показали измерения по излучению быстрых ионов на токамаке NSTX-U [32], плотность нейтралов в этой области экспоненциально возрастает до значения 1.1 × 1017 м–3 на стенке [33].
Наихудший сценарий для длительности перехода в токамаке может быть оценен с помощью теоретической модели, представленной в данной статье. Предположив, что коэффициент электронной эмиссии равен 1.5, что может быть обеспечено за счет термоэлектронной эмиссии [34], вторичной эмиссии [35] или же комбинации обоих видов эмиссии, можно получить теоретическую оценку длительности перехода. Предполагается, что температура эмитированных электронов Temit при термоэлектронном разряде в дейтерии равна 0.1 эВ [30, 36], и наличием других видов частиц в плазме можно пренебречь. Длина свободного пробега определяется сечением столкновений ионов дейтерия с энергией порядка 10 эВ с нейтралами [13], для которых сечение столкновений, сопровождающихся перезарядкой, составляет примерно 3.2 × 10–19 м–2 [37]. Столкновения с нейтралами происходят в области SOL, значения параметров для которого приведены в табл. 5, а соответствующие теоретические оценки даны в табл. 6.
Таблица 5.
Значения параметров в экспериментах на токамаке DIII-D. Плотность нейтралов вблизи стенки получена с помощью диагностики пучком быстрых ионов. Значение коэффициента электронной эмиссии приведено для низкотемпературной термоэлектронной эмиссии с поверхности
| Плотность нейтралов nn, м–3 | Температура эмитированных электронов Temit, эВ | Коэффициент эмиссии γ | Масса иона mi, кг | Длина свободного пробега ионов imfp, м | Электронная температура T, эВ |
|---|---|---|---|---|---|
| 1.10 × 1017 | 0.10 | 1.50 | 3.40 × 10–27 | 20.1 | 25.0 |
Таблица 6.
Результаты расчетов с использованием модели, разработанной в данной статье, выполненных при значениях параметров, указанных в табл. 5, которые являются типичными для установок с магнитным удержанием плазмы
| Расстояние от стенки до минимума потенциала xwall–dip, м | Ширина виртуального катода lVC, м | Плотность электронов в заряженном слое Ne, м–2 | Дебаевская длина λD, м | Длительность перехода t, с | |
|---|---|---|---|---|---|
| Теория | 1.56 × 10–5 | 3.13 × 10–5 | 2.98 × 1012 | 1.12 × 10–4 | 1.13 × 10–3 |
Для наихудшего сценария эмитирующей стенки, при котором температура эмитированных электронов низкая, длина свободного пробега большая, а коэффициент эмиссии низкий, длительность перехода составляет порядка нескольких миллисекунд. При более высоких значениях плотности нейтралов в плазме, коэффициента эмиссии, температуры эмитированных электронов, и при меньшей длине свободного пробега ионов, испытывающих столкновения, сопровождающиеся перезарядкой, длительность перехода будет меньше.
4.4. Другие приложения
Холловские двигатели [3, 5], пылевые частицы [10], горячие катоды [17–19, 38], эмиссионные зонды, и освещенные солнцем оболочки космических кораблей [39] также являются эмитирующими поверхностями, находящимися в контакте с плазмой, и вокруг них также могут образовываться обратные дебаевские слои, если эмиссия достаточно сильная. Эти случаи не исследованы в рамках данной статьи, но следует отметить, что формирование обратного дебаевского слоя возможно в любом из этих случаев. Все сильно эмитирующие поверхности, находящиеся в контакте с плазмой, потенциально могут сформировать обратный дебаевский слой. В каждом из этих случаев с помощью аналитической модели, представленной в настоящей статье, можно получить приблизительную оценку времени, которое потребуется для формирования обратного дебаевского слоя после того, как эмиссия поверхности станет достаточно сильной.
5. ВЫВОДЫ
5.1. Краткий обзор результатов
Рассчитаны ширина виртуального катода, заряд одиночного слоя пограничного ДСВК и скорость захвата ионов, испытавших столкновения, сопровождающиеся перезарядкой, и приблизительно оценена длительность перехода дебаевского слоя из ДСВК режима в обратный. Пригодность модели была проверена с помощью одномерного моделирования, и результаты расчета длительности перехода, выполненные этими двумя способами, совпали с удовлетворительной точностью. Уменьшение потенциала на границе слоя сложнее описать количественно, но оно занимает примерно в 8–10 раз больше времени, чем нейтрализация исходного зарядового слоя.
Было также показано, что при очень низкой плотности нейтралов, что, например, имеет место около поверхности Луны, где длины свободного пробега ионов очень велики, длительность перехода может составлять несколько часов. Поэтому необходимы дальнейшие исследования влияния захвата ионов на эволюцию дебаевского слоя вблизи поверхности Луны. Однако, для поверхностей с сильной эмиссией, контактирующих с лабораторной плазмой с короткой длиной свободного пробега ионов, включая газоразрядную плазму и плазму токамаков, длительность перехода дебаевского слоя в обратный режим составляет несколько миллисекунд. Это означает, что слой гарантированно превратится в обратный дебаевский слой в течение эксперимента, продолжающегося секунды.
5.2. Будущие эксперименты и рекомендации в отношении дальнейших исследований
В будущих экспериментах по изучению переходов между различными режимами дебаевского слоя можно использовать лазерную флуоресценцию для измерения ионных потоков в плазме без возмущения самого плазменного слоя. В [20] было показано, как можно использовать лазерную флуоресценцию для измерения потоков ионов аргона и ксенона, и приведена схема экспериментальной установки. Предложения по исследованию режима с отталкиванием ионов (обратный дебаевский слой) и выявлению его отличий от режима с притяжением ионов (ДСВК или классический дебаевский слой) обсуждались ранее в [10].
Прямое наблюдение обратного дебаевского слоя может оказаться весьма непростой задачей, поскольку ширина его примерно на порядок меньше, чем ширина классического дебаевского слоя или ДСВК. Поэтому легче было бы измерить параметры соответствующего предслоя, которые, в свою очередь, позволят судить о структуре самого обратного слоя. Если поток ионов, направленный на эмитирующую стенку, находящуюся подплавающим потенциалом, отсутствует, тогда дебаевский слой должен быть обратным.
Дополнительные исследования, направленные на более глубокое понимание процесса захвата ионов в многомерных потенциальных ямах, могут дать ценную информацию о геометрических конфигурациях, в которых может иметь место обратный режим дебаевского слоя. В [40] было теоретически показано, что убегание ионов из ловушки в направлении, параллельном поверхности, может препятствовать полному переходу дебаевского слоя из ДСВК режима в обратный. Скорость поперечного убегания ионов зависит от структуры электрического поля в этом направлении, которая еще не изучена. В настоящей работе, предполагалось, что захваченные в виртуальном катоде ионы остаются в ловушке до тех пор, пока дебаевский слой не перейдет в обратный режим, что верно в случае одномерного анализа, или же когда существует магнитное поле, препятствующее движению ионов параллельно поверхности. Дальнейший анализ механизмов захвата и потерь ионов в ловушке позволит более подробно исследовать процессы, происходящие при переходе дебаевского слоя из ДСВК режима в обратный.
Работа выполнена в Ливерморской национальной лаборатории имени Эрнеста Лоуренса при поддержке Министерства энергетики США (контракт № DE-AC52-07NA27344).
Список литературы
L. Tonks and I. Langmuir, Phys. Rev. 34, 876 (1929).
G. D. Hobbs and J. A. Wesson, Plasma Phys. 9, 85 (1967).
F. Taccogna, Europhys. J. 68, 7, (2014).
R. T. Farouki, S. Hamaguchi, and M. Dalvie, Phys Rev. A. 44, 2664 (1991).
J. P. Sheehan, Ph.D. Dissertation (University of Wisconsin, Madison, 2012).
J. P. Sheehan, N. Hershkowitz, I. D. Kaganovich, H. Wang, Y. Raitses, E. V. Barnat, B. R. Weatherford, and D. Sydorenko, Phys. Rev. Lett. 111, 075002, (2013).
D. Sydorenko, I. Kaganovich, Y. Raitses, and A. Smolyakov, Phys. Rev. 103, 145004, (2009).
A. I. Morozov and V. V. Savel’ev, Plasma Phys. Rep. 30, 299 (2004).
A. I. Morozov and V. V. Savel’ev, Plasma Phys. Rep. 33, 20 (2007).
M. D. Campanell and M. V. Umansky, Phys. Plasmas 24, 057101 (2017).
X.Wang, J. Pilewskie, H.-W. Hsu, and M. Horányi,Geophys. Res. Lett.43, 525 (2016).
M. D. Campanell, Phys. Rev. E 97, 043207 (2018).
P. C. Stangeby, The Plasma Boundary of Magnetic Fusion Devices (IOP, Bristol, 2000).
M. D. Campanell, Phys. Rev. E 88, 033103 (2013).
A. D. Polyanin and V. F. Zaitsev, Handbook of Exact Solutions for Ordinary Differential Equations (CRC Press, Boca Raton, FL, 2003).
P. L. Bhatnagar, E. P. Gross, and M. Krook, Phys. Rev. 94, 511 (1954).
F. Greiner, T. Klinger, and A. Piel, Phys. Plasmas 2, 1810 (1995).
T. Klinger, F. Greiner, A. Rohde, and A. Piel, Phys. Plasmas 2, 1822 (1995).
M. D. Campanell and M. V. Umansky, Plasma Sources Sci. Technol. 26, 124002 (2017).
C. Yip, N. Hershkowitz, G. Severn, and S. D. Baalrud, Phys. Plasmas 23, 050703 (2016).
A. J. Dessler, Rev. Geophys. 5(1), 1(1967).
W. M. Farrell, A. R. Poppe, M. I. Zimmerman, J. S. Ha-lekas, G. T. Delory, and R. M. Killen, J. Geophys. Res. 118, 1114 (2013).
J. H. Hoffman, Report NASA-CR-150946 (Texas Univ. at Dallas, Richardson, TX, 1975).
M. Benna, P. R. Mahaffy, J. S. Halekas, R. C. Elphic, and G. T. Delory, Geophys. Res. Lett. 42, 3723 (2015).
R. R. Hodges, Jr., J. Geophys. Res. 78, 8055 (1973).
S. A. Stern, Rev. Geophys. 37, 453 (1999).
R. Schwenn, Encyclopedia of Astronomy and Astrophysics (IOP, Bristol, 2000).
W. L. Fite, R. T. Brackmann, and W. R. Snow, Phys. Rev. 112, 1161 (1958).
J. A. Newbury, Eos77, 471 (1996).
M. S. Sodha and S. K. Mishra, Phys. Plasmas 21, 093704 (2014).
J. A. Wesson, The Science of JET (JET Joint Undertaking, Abingdon, 1999), p. 56.
G. Z. Hao, W. W. Heidbrink, D. Liu, M. Podesta, L. Stagner, R. E. Bell, A. Bortolon, and F Scotti, Plasma Phys. Controlled Fusion 60, 025026 (2018).
N. G. Bolte, W. W. Heidbrink, D. Pace, M. V. Zeeland, and X. Che,Nucl. Fusion 56, 112023 (2016).
W. W. Dolan and W. P. Dyke, Phys. Rev. 95, 327 (1954).
M. E. Woods, B. J. Hopkins, G. F. Matthews, G. M. McCracken, P. M. Sewell, and H. Fahrang, J. Phys. D 20, 1136 (1987).
W. B. Nottingham, Phys. Rev. 49, 78 (1936).
E. W. Thomas and W. M. Stacey, Phys. Plasmas 4, 678 (1997).
O. Biblarz, R. C. Dolson, and A. M. Shorb, J. Appl. Phys. 46, 3342 (1975).
H. B. Garrett, Rev. Geophys. 19, 577 (1981).
B. F. Kraus and Y. Raitses, Phys. Plasmas 25, 030701 (2018).
Дополнительные материалы отсутствуют.
Инструменты
Физика плазмы