Физика плазмы, 2019, T. 45, № 1, стр. 70-75
Опыт применения уравнений Морозова–Соловьева для тороидальной магнитной ловушкиВ. В. Савельев
a Институт прикладной математики им. М.В. Келдыша РАН
Москва, Россия
b Национальный исследовательский ядерный университет МИФИ
Москва, Россия
* E-mail: ssvvvv@rambler.ru
Поступила в редакцию 09.06.2018
После доработки 16.07.2018
Принята к публикации 02.08.2018
Аннотация
В статье А.И. Морозова и Л.С. Соловьева в сборнике “Вопросы теории плазмы”, вып. 8 (1974 г.) была выписана общая система уравнений гидродинамики двухкомпонентной идеальной плазмы для стационарного случая. Эта система чрезвычайно сложная и громоздкая. Для случая аксиальной симметрии авторам удалось записать ее в более обозримой форме, введя три функции потока (магнитного поля, электронов и ионов). Ситуация напоминает получение уравнения Грэда–Шафранова, когда задача о статическом равновесии плазмы свелась одному уравнению второго порядка для функции потока магнитного поля. При этом, чтобы замкнуть задачу, требовалось задать две произвольные функции-параметры. Когда рассматриваются течения, а не статическое равновесие, количество функций-параметров увеличивается. В настоящей работе уравнения Морозова–Соловьева используются для описания стационарных конфигураций плазмы в тороидальных магнитных ловушках.
1. ВВЕДЕНИЕ. УРАВНЕНИЯ МОРОЗОВА–СОЛОВЬЕВА
Полный набор соотношений, составляющих уравнения Морозова–Соловьева (МС) приведен в [1, 2]. Фактически авторы исходят из полной системы двухжидкостной гидродинамики электрон-ионной плазмы [3], добавляя к ним уравнения Максвелла. Далее происходит редукция этой очень сложной системы к более простой. В частности, к двухжидкостной гидродинамике квазинейтральной плазмы. Это и соответствует физической ситуации (характерным значениям плотности плазмы в интересных для авторов приложениях), и значительно упрощает задачу. Вводя функции потоков, как часто делается в гидродинамике, для стационарных течений получают так называемые “трехпотоковые” уравнения двухжидкостной плазмы. Эти уравнения используются в [1, 2] для получения, прежде всего, качественных выводов о свойствах течений.
Мы также будем предполагать в дальнейшем выполненным условие квазинейтральности (ni = = ne = n).
Условие покоя двухкомпонентной плазмы часто трактуют как равенство нулю среднемассовой скорости плазмы. Но это условие с точностью до величины порядка отношения масс электрона и иона совпадает с условием неподвижности ионов. Тем самым мы приходим к “двухпотоковому” варианту уравнений МС. Поэтому, далее будем называть конфигурацию плазмы стационарной (равновесной), если ионная компонента неподвижна в действующих самосогласованных электрическом и магнитном полях. Далее приводится краткий вывод уравнений МС для этого случая.
Введем стандартные определения функции магнитного потока $\Psi (r,z)$ и функции полного тока $J(r,z)$ в цилиндрических координатах r, z (z – ось симметрии задачи)
(1)
$\begin{gathered} {{B}_{r}} = - \frac{1}{{2\pi r}}\frac{{\partial \Psi }}{{\partial z}},\quad {{B}_{z}} = \frac{1}{{2\pi r}}\frac{{\partial \Psi }}{{\partial r}},\quad {{B}_{\varphi }} = \frac{{2J}}{{cr}}, \\ {{j}_{r}} = - \frac{1}{{2\pi r}}\frac{{\partial J}}{{\partial z}},\quad {{j}_{z}} = \frac{1}{{2\pi r}}\frac{{\partial J}}{{\partial r}}, \\ {{j}_{\varphi }} = - \frac{c}{{8{{\pi }^{2}}r}}{{\Delta }^{*}}\Psi ,\quad {{\Delta }^{*}}\Psi = \frac{{{{\partial }^{2}}\Psi }}{{\partial {{r}^{2}}}} - \frac{1}{r}\frac{{\partial \Psi }}{{\partial r}} + \frac{{{{\partial }^{2}}\Psi }}{{\partial {{z}^{2}}}}. \\ \end{gathered} $В терминах этих двух функций уравнения МС при сделанных предположениях имеют вид
(2)
$\begin{gathered} {{\Delta }^{*}}\Psi - \frac{{8{{\pi }^{2}}e}}{{c{{m}_{e}}}}n\left[ {\frac{1}{{2\pi }}\frac{e}{c}(\Psi + \pi {{r}^{2}}{{H}_{z}}) + K(J)} \right] = 0, \\ \frac{{{{m}_{e}}}}{{4{{\pi }^{2}}{{e}^{2}}}}\left[ {\frac{\partial }{{\partial z}}\left( {\frac{1}{{rn}}\frac{{\partial J}}{{\partial z}}} \right) + \frac{\partial }{{\partial r}}\left( {\frac{1}{{rn}}\frac{{\partial J}}{{\partial r}}} \right)} \right] - \\ - \;rn\left( {\frac{{dF}}{{dJ}} - {{m}_{e}}{{T}_{e}}\frac{{d{{s}_{e}}}}{{dJ}}} \right) - \frac{{{{j}_{\varphi }}}}{e}\frac{{dK}}{{dJ}} - \frac{1}{{\pi {{c}^{2}}}}\frac{J}{r} = 0. \\ \end{gathered} $Здесь $K(J)$ – интеграл углового момента электронов (имеется аксиальная симметрия)
(3)
$\frac{{{{m}_{e}}}}{{en}}r{{j}_{\varphi }} + \frac{e}{{2\pi c}}(\Psi + \;\pi {{r}^{2}}{{H}_{z}}) = - K(J),$(4)
$\frac{{{{m}_{e}}}}{{2{{e}^{2}}}}\frac{{{{{\mathbf{j}}}^{2}}}}{{{{n}^{2}}}} + {{m}_{i}}{{W}_{i}}(n) + {{m}_{e}}{{W}_{e}} = F(J),$Для случая идеального политропного электронного газа имеем
Считая ${{P}_{i}}(n) = {{G}_{i}}{{n}^{\gamma }}\;({{G}_{i}} = \operatorname{const} )$, получим ${{W}_{i}}(n) = $ $ = \frac{\gamma }{{(\gamma - 1){{m}_{i}}}}{{G}_{i}}{{n}^{{\gamma - 1}}}$. Тогда уравнение для J и закон Бернулли конкретизируются
(6)
$\begin{gathered} \frac{{{{m}_{e}}}}{{4{{\pi }^{2}}{{e}^{2}}}}\left[ {\frac{\partial }{{\partial z}}\left( {\frac{1}{{rn}}\frac{{\partial J}}{{\partial z}}} \right) + \frac{\partial }{{\partial r}}\left( {\frac{1}{{rn}}\frac{{\partial J}}{{\partial r}}} \right)} \right] - \\ - \;rn\left( {\frac{{dF}}{{dJ}} - \frac{{{{n}^{{\gamma - 1}}}}}{{\gamma - 1}}\frac{{d{{G}_{e}}}}{{dJ}}} \right) - \frac{{{{j}_{\varphi }}}}{e}\frac{{dK}}{{dJ}} - \frac{1}{{\pi {{c}^{2}}}}\frac{J}{r} = 0, \\ \frac{\gamma }{{(\gamma - 1)}}({{G}_{i}} + {{G}_{e}}(J)){{n}^{{\gamma - 1}}} + \frac{{{{m}_{e}}}}{{2{{e}^{2}}}}\frac{{{{{\mathbf{j}}}^{2}}}}{{{{n}^{2}}}} = F(J). \\ \end{gathered} $Закон Бернулли (6) дает алгебраическое уравнение для нахождения n. Если $\gamma = 3$ (ниже ограничимся этим случаем), это уравнение становится биквадратным, и получаем явное выражение для концентрации частиц n (заметим, что решение уравнения Грэда–Шафранова (ГШ) позволяет определить только распределение давления плазмы с точностью до аддитивной константы)
(7)
$\begin{gathered} {{n}^{2}} = \frac{{Q \pm \sqrt {{{Q}^{2}} - \frac{{3{{m}_{e}}}}{{4{{\pi }^{2}}{{e}^{2}}{{r}^{2}}}}({{G}_{i}} + {{G}_{e}}(J)){{{(\nabla J)}}^{2}}} }}{{3({{G}_{i}} + {{G}_{e}}(J))}}, \\ Q = F(J) - \frac{1}{{2{{m}_{e}}{{r}^{2}}}}{{\left( {\frac{1}{{2\pi }}\frac{e}{c}\Psi + K + \frac{{{{r}^{2}}}}{2}\frac{e}{c}{{H}_{z}}} \right)}^{2}}. \\ \end{gathered} $Формула (7) дает два выражения для n. Оказывается [4], что в области параметров отвечающих знаку “+” (“плотная” плазма), система (2) эллиптическая, а для знака “–” (“разреженная” плазма) – гиперболическая. Мы будем рассматривать только эллиптический случай – знак “+” в формуле (7).
2. КРАЕВАЯ ЗАДАЧА ДЛЯ ТОРОИДАЛЬНОЙ ЛОВУШКИ
Рассматриваем осесимметричную тороидальную камеру с классическим круговым поперечным сечением, удерживающую плазму в “равновесии” (рис. 1). На границе круга ставятся условия
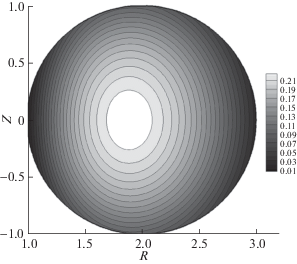
где ${{J}_{0}},\;{{\Psi }_{0}}$ – константы. Линии $J = \operatorname{const} $ – линии тока электронов в плоскости r, z, величина ${{J}_{0}}$ равна току во внешней тороидальной обмотке. Линии $\Psi = \operatorname{const} $ – линии магнитного поля в плоскости r, z, величина ${{\Psi }_{0}}$ равна потоку магнитного поля через центральное отверстие тора.Рис. 1.
Распределение по сечению камеры функции полного тока $J(r,z)$ (линии уровня этой функции – линии тока электронов) при значениях параметров ${{\xi }^{2}} = 0.6$, $\beta = 50$, $\alpha = 4$, $\delta = 0.05$, $\eta = 0.001$, ${{h}_{z}} = 2.5$.
Для удобства численного решения будем использовать новые единицы измерения, обращаясь к характерным физическим параметрам, входящим в постановку задачи. Единицей длины возьмем расстояние ${{L}_{0}}$ между осью z и камерой. Магнитное поле будем измерять в единицах ${{B}_{0}} = 2{{J}_{0}}{\text{/}}c{{L}_{0}}$. Единицы плотности и температуры образуем из известных характерных значений функций $F(J) = {{F}_{0}}f(J{\text{/}}{{J}_{0}})$, ${{G}_{e}}(J) = {{G}_{{e0}}}g(J{\text{/}}{{J}_{0}})$, $K(J) = {{K}_{0}}k(J{\text{/}}{{J}_{0}})$, а именно,
В новых единицах условия (8) примут вид
(9)
$J = 1,\quad \Psi = \frac{{{{B}_{{p0}}}}}{{{{B}_{0}}}} = \delta ,\quad {{B}_{{p0}}} = \frac{{{{\Psi }_{0}}}}{{2\pi L_{0}^{2}}},$(10)
${{\xi }^{2}}\frac{{r{{j}_{\varphi }}}}{n} + \Psi + \alpha k(J) + \frac{{{{r}^{2}}}}{2}{{h}_{z}} = 0,$(11)
$\frac{{{{\xi }^{2}}}}{\beta }\frac{{{{{\mathbf{j}}}^{2}}}}{{{{n}^{2}}}} + \frac{3}{2}(\eta + g(J)){{n}^{2}} = f(J),$(12)
$\begin{gathered} {{\xi }^{2}}\left( {\frac{{{{\partial }^{2}}A}}{{\partial {{z}^{2}}}} + \frac{\partial }{{\partial r}}\left( {\frac{1}{r}\frac{{\partial rA}}{{\partial r}}} \right)} \right) - \frac{n}{r}\left( {rA + \alpha k(J) + \frac{{{{r}^{2}}}}{2}{{h}_{z}}} \right) = 0, \\ {{\xi }^{2}}\left[ {\frac{\partial }{{\partial z}}\left( {\frac{1}{{rn}}\frac{{\partial J}}{{\partial z}}} \right) + \frac{\partial }{{\partial r}}\left( {\frac{1}{{rn}}\frac{{\partial J}}{{\partial r}}} \right)} \right] - \\ - \;\frac{\beta }{2}rn\left( {\frac{{df}}{{dJ}} - \frac{1}{2}{{n}^{2}}\frac{{dg(J)}}{{dJ}}} \right) - \alpha {{j}_{\varphi }}\frac{{dk}}{{dJ}} - \frac{J}{r} = 0. \\ \end{gathered} $Формула для вычисления плотности n
(13)
$\begin{gathered} {{n}^{2}} = \frac{{q + \sqrt {{{q}^{2}} - 6\frac{{{{\xi }^{2}}}}{{\beta {{r}^{2}}}}(\eta + g(J)){{{(\nabla J)}}^{2}}} }}{{3(\eta + g(J))}}, \\ q = f(J) - \frac{1}{{{{\xi }^{2}}\beta {{r}^{2}}}}{{\left( {\Psi + \alpha k(J) + \frac{{{{r}^{2}}}}{2}{{h}_{z}}} \right)}^{2}}. \\ \end{gathered} $В задаче появляются безразмерные параметры
(14)
$\begin{gathered} {{\xi }^{2}} = \frac{{{{c}^{2}}{{m}_{e}}}}{{4\pi {{e}^{2}}L_{0}^{2}{{n}_{0}}}},\quad \beta = \frac{{8\pi {{k}_{B}}{{n}_{0}}{{T}_{{e0}}}}}{{B_{0}^{2}}},\quad \eta = \frac{{{{T}_{{i0}}}}}{{{{T}_{{e0}}}}}, \\ \alpha = \frac{{{{c}^{2}}{{K}_{0}}}}{{2e{{L}_{0}}{{J}_{0}}}} = \frac{c}{e}\frac{{{{K}_{0}}}}{{{{B}_{0}}L_{0}^{2}}},\quad \delta = \frac{{{{B}_{{p0}}}}}{{{{B}_{0}}}},\quad {{h}_{z}} = \frac{{{{H}_{z}}}}{{{{B}_{0}}}} \\ \end{gathered} $Уравнение Грэда–Шафранова [5] получаются из уравнений (12) в пределе ${{\xi }^{2}} \ll 1$ [4]. Поскольку параметр ${{\xi }^{2}}$ входит в систему (12) сингулярно – стоит при старших производных, то уравнение ГШ – не только предельный, но и вырожденный случай уравнений МС. Заметим еще, что малый параметр $\mu = {{m}_{e}}{\text{/}}{{m}_{i}}$ вообще не входит в задачу. Если характерный размер неоднородности в решении ~ 1 см, то при плотности n ~ 1012 см–3 значение ${{\xi }^{2}}$ будет ~0.3. При n ~ 1011 см–3 получим ${{\xi }^{2}}$ ~ 3. Роль малого параметра может быть очень существенной при наличии областей с резким изменением решения.
Требование положительности плотности в (13) позволяет легко получить необходимое условие существования решения краевой задачи для уравнений (12). Из положительности величины q (13) следует такое ограничение на параметры:
(15)
${{\xi }^{2}}\beta > \max \left\{ {\frac{{{{{\left( {\alpha + \delta + \frac{{r_{{\min }}^{2}}}{2}{{h}_{z}}} \right)}}^{2}}}}{{r_{{\min }}^{2}}},\frac{{{{{\left( {\alpha + \delta + \frac{{r_{{\max }}^{2}}}{2}{{h}_{z}}} \right)}}^{2}}}}{{r_{{\max }}^{2}}}} \right\}.$При ${{h}_{z}} = 0$ должно быть $\;{{\xi }^{2}}\beta > {{(\alpha + \delta )}^{2}}$.
3. РЕЗУЛЬТАТЫ РАСЧЕТОВ
В настоящее время существует много действующих тороидальных магнитных ловушек, в том числе токамаков, и огромная литература по эксперименту и теории (что касается токамаков, см., например, [6, 7]). Их параметры: геометрические размеры, величины полей и токов, – могут различаться весьма значительно. Целью первых расчетов стационарных конфигураций в рамках уравнений МС было, прежде всего, желание убедиться, что уравнения (12) имеют разумные решения, в которых есть удержание плазмы. Под удержанием плазмы здесь понимаем такие решения, в которых давление плазмы максимально где-то в центральной области камеры и имеет меньшие значения вблизи ее границы. Какой-либо точной привязки к конкретной установке и соответствующим параметрам не проводилось. По этой причине в расчетах использовались простейшие зависимости для функций-параметров f, g, k, а именно, $f(J) \equiv 1$, $g(J) \equiv 1$, $k(J) \equiv 1$. Уравнения (12) при таком выборе этих функций несколько упрощаются. Для реальных систем эти функции могут быть значительно сложнее.
На рис. 1–5 даны распределения по сечению ловушки основных величин определяющих характер решения при следующих значениях параметров ${{\xi }^{2}} = 0.6$, $\beta = 50$, $\alpha = 4$, $\delta = 0.05$, $\eta = 0.001$, ${{h}_{z}} = 2.5$. Представлены линии уровня пяти функций $J(r,z)$, $\Psi (r,z)$, ${{P}_{e}}(r,z)$, ${{B}_{\varphi }}(r,z)$, ${{j}_{\varphi }}(r,z)$. Это один из ряда вариантов расчетов, при которых наблюдается удержание плазмы. Хорошо видно, что в двухжидкостной модели МС линии уровня трех из этих функций ($J,\;\Psi ,\;{{P}_{e}}$), вообще говоря, не совпадают, как для уравнения ГШ, где давление и функция полного тока являются функциями Ψ.
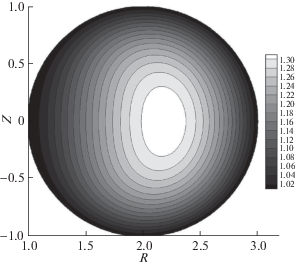
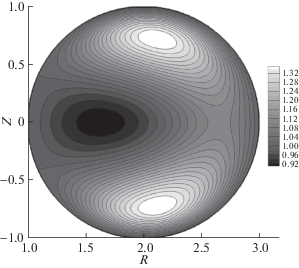
Рис. 2.
Распределение по сечению камеры функции полного тока $J(r,z)$ (линии уровня этой функции – линии тока электронов) при тех же значениях параметров, что на рис. 1.
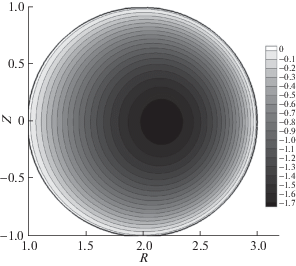
Рис. 4.
Распределение по сечению камеры азимутальной компоненты магнитного поля при тех же параметрах, что на рис. 1.
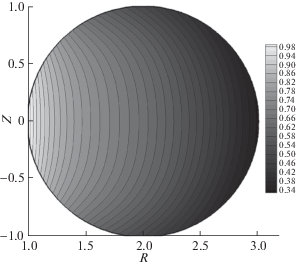
Рис. 5.
Распределение по сечению камеры азимутальной компоненты плотности электрического тока при тех же параметрах, что на рис. 1.
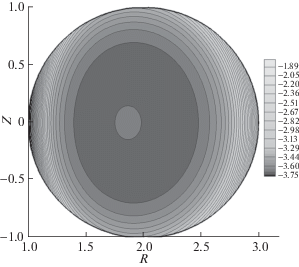
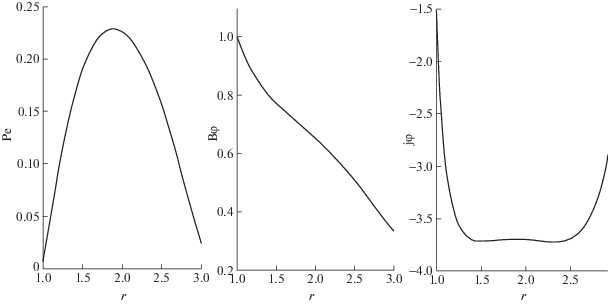
Давление (рис. 3) меняется в пределах камеры примерно в 20 раз, достигая максимума в ее центральной части. На наружной стенке давление несколько больше, чем на внутренней стенке. Изменение параметра ${{h}_{z}}$ позволяет управлять положением максимума давления, сдвигая его “влево” или “вправо”. Азимутальная компонента магнитного поля (рис. 4) меняется в этом варианте расчета довольно плавно, убывая примерно пропорционально расстоянию от оси, т.е. в этом варианте расчетов плазма не влияет заметно на тороидальное магнитное поле. Это объясняется малой величиной характерного полоидального поля по сравнению с тороидальным ($\delta = 0.05$). Тороидальная плотность тока ${{j}_{\varphi }}$ (рис. 5) везде отрицательна и достигает минимума в центральной части камеры, быстро увеличиваясь при подходе к стенкам. В дополнение к двумерным картинкам, на рис. 6 даны (при тех же параметрах) одномерные профили давления ${{P}_{e}}$, тороидальной компоненты магнитного поля ${{B}_{\varphi }}$ и тороидальной компоненты плотности тока ${{j}_{\varphi }}$ как функции радиуса r в сечении $z = 0$.
Рис. 6.
Распределения по радиусу при z = 0: а) – давления; б) – азимутальной компоненты магнитного поля; в) – азимутальной компоненты электрического тока. Параметры те же, что на рис. 1.
Приведенные первые и во многом поисковые результаты показывают, что уравнения МС могут давать решения, по крайней мере, качественно близкие (по распределению давления) к решениям, полученным на основе уравнения ГШ. Но, разумеется, есть и другие решения. В качестве примера приведем только один вариант расчетов с параметрами ${{\xi }^{2}} = 0.1$, $\beta = 300$, $\alpha = 3$, $\delta = 1.0$, $\eta = 1$, ${{h}_{z}} = 2.5$. На рис. 7 представлена картина линий тока (линии уровня $J(r,z)$) для этого варианта. В нем, в частности, значительно больше величина полоидального поля ($\delta = 1$). В плоскости r, z появились вихри. И этот результат вполне естественен, если иметь в виду следующее соображение. Как известно, решения уравнения ГШ имеют гидродинамическую аналогию: при соответствующей замене переменных [5] получаются уравнения, описывающие стационарное течение несжимаемой жидкости и, таким образом, каждое решение уравнения ГШ имеет аналог в виде некоторого стационарного течения. В случае с уравнениями МС ситуация несколько сложнее. Как показано в [4], здесь имеется такого же смысла аналогия, но теперь с вихревым течением сжимаемого газа. Появление же вихрей при течении сжимаемого газа в тороидальной области с условием непротекания на стенке вполне ожидаемо.
Рис. 7.
Распределение по сечению камеры функции полного тока $J(r,z)$ (линии уровня этой функции – линии тока электронов) при значениях параметров ${{\xi }^{2}} = 0.1$, $\beta = 300$, $\alpha = 3$, $\delta = 1.0$, $\eta = 1$, ${{h}_{z}} = 2.5$.
Численное решение задачи проводилось методом конечных элементов второго порядка на треугольной сетке.
4. ОБСУЖДЕНИЕ
Целью этой работы было привлечь внимание к полученным А.И. Морозовым и Л.С. Соловьевым еще в 1974 г. уравнениям, описывающим стационарные двумерные течения двухжидкостной плазмы. Насколько известно автору, до сих пор эти уравнения не нашли сколько-нибудь широкого применения в теории плазмы. Представляется, что их можно использовать для получения новых результатов как в теории ускорения плазмы, так и для исследования стационарных конфигураций в различных плазменных ловушках. Физический смысл их вполне ясен и фундаментален.
В представленных вариантах расчетов (их всего два) значения параметров ${{\xi }^{2}}$, β и т.д. (14) могут показаться не вполне естественными, они не близки к значениям для реальных ловушек. Вопрос с параметрами не очевидный. Как, например, определить параметр β? В работе он формируется из параметров заданных на границе функций $f(J)$, $s(J)$ с нормировкой $f(1) = s(1) = 1$. Кроме того, имеется еще одно ограничение, следующее исключительно из математической природы уравнений, – $\;{{\xi }^{2}}\beta > {{(\alpha + \delta )}^{2}}$ (это простейший случай). Таким образом, параметры ξ2, β, α, δ связаны неким условием. Это точное необходимое условие существования решения рассматриваемой краевой задачи для уравнений МС. Проводить расчеты при параметрах, не удовлетворяющих этому условию, бессмысленно. Имеются ли решения с малым β? Ответа общего и однозначного здесь нет. При каких-то геометриях, при каких-то значениях других параметров, не исключено, есть и положительный ответ.
Параметр ${{\xi }^{2}}$ – чрезвычайно важный параметр задачи. Вопрос о его влиянии очень непростой и пока ясен только с формально математической стороны дела. В работе [4] строго показано, что уравнение ГШ является предельным и вырожденным случаем уравнений МС при ${{\xi }^{2}} \to 0$. Чтобы решить это уравнение, нужно задать две функции ${{P}_{0}}(\Psi )$ и ${{J}_{0}}(\Psi )$ (функции давления и полного тока). При предельном переходе ${{\xi }^{2}} \to 0$ они появятся просто как члены нулевого порядка, удовлетворяющие уравнению ГШ. Ясно, что просто положить ${{\xi }^{2}} = 0$ нельзя. Конечно, можно проводить вычисления, взяв ${{\xi }^{2}}$ достаточно малой величиной. Но выяснить, к какому конкретно решению уравнения ГШ происходит стремление, очень затруднительно. Очевидно только, что будут увеличиваться градиенты решения, прежде всего на границе.
Автор благодарен М.Б. Гаврикову за полезные обсуждения.
Работа выполнена при поддержке Российского научного фонда (грант № 16-11-10278).
Список литературы
Морозов А.И., Соловьев Л.С. Вопросы теории плазмы. Вып. 8 / Под ред. М.А. Леонтовича. М.: Атомиздат, 1974. С. 3.
Морозов А.И. Введение в плазмодинамику. М.: Физматлит, 2006.
Брагинский С.И. Вопросы теории плазмы. Вып. 1 / Под ред. М.А. Леонтовича. М.: Госатомиздат, 1963. С.183.
Gavrikov M.B., Savelyev V.V. //J. Mathematical Sciences. 2009. V. 168. № 1. P. 1.
Шафранов В.Д. Вопросы теории плазмы/ Вып. 2 / Под ред. М.А. Леонтовича. М.: Госатомиздат, 1963. С. 92.
Кадомцев Б.Б. Итоги науки и техники. Сер. Физика плазмы. Т. 10. Ч. 1. М.: ВИНИТИ, 1990. С. 1.
Wesson J. Tokamaks. Oxford University Press, 2004.
Дополнительные материалы отсутствуют.