Физика плазмы, 2019, T. 45, № 12, стр. 1088-1102
Расширение теории равновесия шафранова на описание срывов тока при учете диссипации в резистивной стенке в токамаках
a Национальный исследовательский центр “Курчатовский институт”
Москва, Россия
b Национальный исследовательский ядерный университет МИФИ
Москва, Россия
* E-mail: Pustovitov_VD@nrcki.ru
Поступила в редакцию 25.03.2019
После доработки 20.05.2019
Принята к публикации 25.06.2019
Аннотация
Уравнение для положения плазменного шнура в токамаке получено с учетом реакции резистивной стенки на изменения параметров плазмы. Подобную задачу рассматривал В.Д. Шафранов [Атомная энергия 13, 521 (1962)], но при фиксированном токе плазмы. Здесь этот ток рассматривается как функция времени, что позволяет покрыть срывы тока (current quenches) и расширить исследование на анализ срывов. Показано, что полный тороидальный ток, наводимый в стенке во время срыва тока (не учтенный в упомянутой и связанных существующих аналитических моделях), может значительно повлиять на равновесие плазмы. Представлен общий алгоритм, применимый к произвольным токамакам. Для “круглого” токамака с большим аспектным отношением выполнен полный цикл пошаговой редукции задачи, вплоть до уравнения для эволюции смещения плазмы. Метод и результаты готовы к использованию в сочетании со стандартными кодами и моделями равновесия.
1. ВВЕДЕНИЕ
На развитие концепции токамака существенно повлияли теоретические результаты по равновесию тороидальной плазмы с магнитным удержанием, полученные В.Д. Шафрановым. Один из них – хорошо известная формула [1, 2]
(1)
$B_{ \bot }^{{eq}} \equiv - {{B}_{J}}\frac{b}{{2{{R}_{{pl}}}}}\left( {\ln \frac{{8{{R}_{{pl}}}}}{b} + \Lambda - \frac{1}{2}} \right)$– полоидальное поле ${{B}_{\theta }}$ на границе плазмы,
(3)
$J \equiv \int\limits_{pl} {{\mathbf{j}} \cdot d{{{\mathbf{S}}}_{{pl}}}} = \frac{1}{{2\pi }}\int\limits_{pl} {{\mathbf{j}} \cdot \nabla \zeta d\tau } $– полный ток в плазме, b – ее малый радиус, ${{R}_{{pl}}}$ – большой,
– “полоидальная бэта”, p – давление плазмы, черта сверху обозначает среднее по поперечному сечению плазмы,
– внутренняя индуктивность на единицу длины плазменного шнура, а ${{\mu }_{0}} = 4\pi \times {{10}^{{ - 7}}}$ Г/м – магнитная проницаемость вакуума (атрибут используемой здесь системы СИ). В (3) первый интеграл берется по поперечному сечению, а второй – по полному объему плазмы, ζ – тороидальный угол.
Анализ, приведший к появлению (1), был стимулирован экспериментами с плазмой в тороидальной камере с толстой проводящей стенкой без ныне неотъемлемой системы управления равновесием. В таком раннем предшественнике токамаков никогда не достигалось стационарное состояние, а разряд был очень коротким: плазма смещалась к стенке, касалась ее и быстро исчезала [3]. Уравнение (1) было ответом на возникшие тогда вопросы. Был сделан вывод, что для предотвращения такого катастрофического сценария необходима специальная система, создающая поперечное поле $ = {\kern 1pt} \;B_{ \bot }^{{eq}}$.
На пути к (1) В.Д. Шафранов попутно рассмотрел возможность поддержания равновесия плазмы по большому радиусу за счет одних только токов, возбуждаемых в стенке камеры при смещении плазмы. Эти токи должны создавать магнитное поле $B_{ \bot }^{w} = B_{ \bot }^{{eq}}$, но их затухание из-за резистивности стенки приводит к уменьшению $\left| {B_{ \bot }^{w}} \right|$. Как следствие, смещение плазменного шнура наружу по большому радиусу нарастает.
Результат в конечном итоге представлялся формулой (66) в [1] (здесь мы приводим ее в компактной форме)
(7)
$\frac{d}{{dt}}\left( {J\frac{{{{\Delta }_{b}} - {{\Delta }_{{iw}}}}}{{{{b}_{w}}}}} \right) = \frac{J}{{{{t}_{{con}}}}}$(8)
${{t}_{{con}}} = {{\tau }_{w}}\frac{{{{R}_{{pl}}}}}{b}{{\left( {\ln \frac{{8{{R}_{{pl}}}}}{b} + \Lambda - \frac{1}{2}} \right)}^{{ - 1}}},$В [5] ограничение $dJ{\text{/}}dt = 0$ было косвенно, но ясно оговорено указанием, что ток в стенке возбуждается только за счет расширения шнура. Никаких комментариев по поводу $dJ{\text{/}}dt$ в [1] и [4] не приводилось, а присутствие J в (7) вызывает естественный вопрос о применимости (7) к случаям с изменяющимся J.
Ответ должен быть отрицательным по причинам, объясненным ниже. Чтобы выявить их, нужно погрузиться в математические операции в [1, 4, 5]. Здесь наша цель состоит в том, чтобы найти замену (7), которая покрыла бы события с $dJ{\text{/}}dt \ne 0$. Такое расширение необходимо для лучшего моделирования переходных процессов, включая срывы со срывом тока – current quench (CQ).
Уравнение (7) было получено для радиального движения плазмы, при котором толщина скин-слоя ${{d}_{{sk}}}$ в стенке существенно превышает ее толщину ${{d}_{w}}$. Возникший в задаче временной масштаб ${{t}_{{{\text{cont}}}}}$ оказывается порядка ${{\tau }_{w}}$, что согласуется с этим ограничением.
Срывы тока, которые естественно происходят в токамаках [6], также попадают в диапазон ${{d}_{{sk}}} > {{d}_{w}}$, потому что их длительность ${{\tau }_{{cq}}}$ всегда сопоставима или даже слегка превышает “резистивные времена стенки” ${{\tau }_{w}}$, см. рис. 3 в [6] для ${{\tau }_{{cq}}}$ и табл. 1 в [7] для величины ${{\tau }_{w}}$, введенной уравнением (9), которая часто используется в теории устойчивости как характерный масштаб для винтовых мод, частично стабилизируемых резистивной стенкой (Resistive Wall Modes, RWMs) [7, 8].
Отметим, что, для токамака с ${{R}_{{pl}}}{\text{/}}b = 3$, ${{\beta }_{J}} = 1$ и ${{\ell }_{i}} = 0.8$ мы получим в точности ${{t}_{{con}}} = {{\tau }_{w}}$ из (8). Однако в [2] то же самое время ${{t}_{{con}}}$ дано формулой (6.18), которая отличается от (8) отсутствием степени −1 и поэтому предсказывает ${{t}_{{con}}} = 9{{\tau }_{w}}$ при упомянутых параметрах. Позже [5] утверждалось (рядом с уравнением (4.72) в [5]), что движение шнура по большому радиусу характеризуется постоянной времени ${{\tau }_{w}}{{R}_{{pl}}}{\text{/}}b$, что сводится к $3{{\tau }_{w}}$. В приложениях к задачам срывов эта неопределенность с разбросом от ${{\tau }_{w}}$ до $9{{\tau }_{w}}$ уже за пределами допустимого. Это еще одна причина, по которой необходим пересмотр подхода, ведущего к (7) или к его более поздним замещающим аналогам.
Теория равновесия плазмы с магнитным удержанием создавалась для описания статических конфигураций, но она применима, как и в случаях, рассмотренных в [1, 2, 4, 5], даже при очень больших $\partial {\mathbf{B}}{\text{/}}\partial t \ne 0$, если сила инерции в уравнении силового баланса для плазмы
мала. Здесь ρ – массовая плотность плазмы, v – скорость ее движения, p – ее давление, t – время, B – магнитное поле, ${\mathbf{j}} = \nabla \times {\mathbf{B}}{\text{/}}{{\mu }_{0}}$ – плотность тока.Использование уравнения
и стандартных методов теории равновесия является общепринятым даже для описания срывов в токамаках, когда управление разрядом потеряно, см. [9–16]. Это оправдано тем, что быстрому глобальному движению плазмы препятствуют индукционные токи в стенке, существенно ограничивая ее направленную скорость, как, в частности, демонстрирует (7). Кроме того, массовая плотность плазмы в термоядерных системах ничтожно мала. Как следствие электромагнитные нагрузки на стенку камеры токамака при срыве могут в 106–108 раз превзойти силу инерции, см. оценки в [11–13]. Естественно поэтому привлечь для анализа подобных событий аналитическую теорию равновесия плазмы.Это делалось в работах [12, 17, 18] для быстрых процессов, какими обычно бывают тепловые срывы в токамаках [19–21]. При этом приближение идеальной стенки с $\delta ({{\Delta }_{b}} - {{\Delta }_{{iw}}}) = 0$, что было явно использовано в [18], вполне пригодно. Теперь мы усложняем задачу, включая в рассмотрение резистивное затухание токов в стенке. Интерес представляет также и описание сопутствующего движения плазменного шнура. Уравнение (7) дает нам решение лишь для частного переходного процесса. Здесь мы установим область применимости (7) и получим обобщение этого уравнения, покрывающее более широкий круг явлений, вплоть до срывов.
2. МОДЕЛЬ И ПОСТАНОВКА ЗАДАЧИ
Стандартная аналитическая теория [1, 2, 4, 5], которая вошла в учебники [22–26], была развита для плазмы и стенки с круглыми сечениями, как показано на рисунках 1 и 2. Эта модель используется ниже на заключительной стадии выкладок. Основным неизвестным в задаче будет ${{\Delta }_{b}} = {{R}_{{pl}}} - {{R}_{w}}$, смещение центра границы плазмы относительно центра почти коаксиальной стенки.
Рис. 1.
Схематический вид токамака и цилиндрических координат $(r,\zeta ,z)$, связанных с его главной осью. ζ – тороидальный угол, b – малый радиус плазмы. Рисунок сделан Д.В. Мироновым.
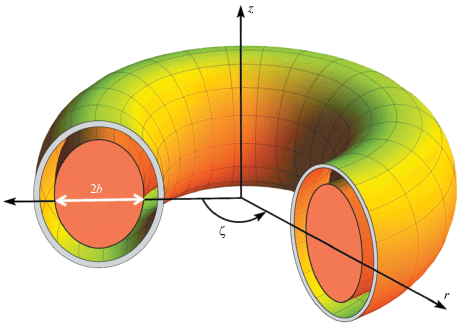
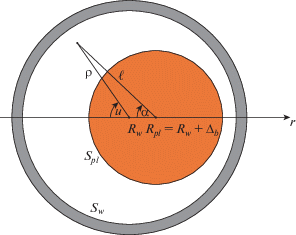
Рис. 2.
Схематический вид системы в поперечном сечении $\zeta = \operatorname{const} $. Здесь плазма и стенка круглые. $(\rho ,u)$ и $(\ell ,\alpha )$ – полярные координаты, связанные с геометрическими центрами внутренней стороны стенки ${{\Gamma }_{w}}$ и границы плазмы ${{\Gamma }_{{pl}}}$, соответственно. ${{\Delta }_{b}} \equiv {{R}_{{pl}}} - {{R}_{w}}$ – смещение плазменного шнура относительно стенки. Рисунок сделан Д.И. Кирамовым.
Мы движемся к уравнению для ${{\Delta }_{b}}$ через несколько уровней редукции. Сначала система считается аксиально симметричной, что означает независимость всех физических величин от тороидального угла ζ в цилиндрических координатах $(r,\zeta ,z)$, связанных с главной осью тора, как на рис. 1. Начинаем только с этого предположения и оперируем с уравнениями, которые могут быть применимы к любой токамако-подобной конфигурации. Позже мы вводим приближение большого аспектного отношения и выполняем разложение по $\ell {\text{/}}{{R}_{{pl}}}$ и $\rho {\text{/}}{{R}_{w}}$. Окончательно рассматривается геометрия, показанная на рис. 2.
В задаче фигурируют три области: плазма, стенка и вакуумный промежуток между ними, см. рис. 1 и 2. Плазма действует как толстый подвижный и деформируемый проводник с током, который всегда должен подчиняться условию (11). Последнее требует ${\mathbf{B}} \cdot \nabla p = 0$ и приносит ограничение
на границе плазмы ${{S}_{{pl}}}$, форма которой и положение являются главными неизвестными, влияющими на поле B снаружи (${{{\mathbf{n}}}_{{pl}}}$ – единичный вектор нормали к ${{S}_{{pl}}}$). Связь внутренних и внешних решений через (12) на адаптируемой тороидальной поверхности ${{S}_{{pl}}}$ является главной трудностью в стандартной (в других отношениях) электромагнитной задаче вычисления ${\mathbf{B}}({\mathbf{r}},t)$.Поведение тока в плазме и стенке определяется полным магнитным полем
где pl, e и w обозначают, соответственно, вклады от тороидальной плазмы, внешних катушек и стенки вакуумной камеры. При стандартной работе токамака поле ${{{\mathbf{B}}}^{w}}$ и токи в стенке малы, но могут стать очень большими при переходных процессах с генерацией электрического поля E вне плазмы. Индуцированное поле ${{{\mathbf{B}}}^{w}}$, которое должно быть найдено как функция изменяющихся параметров плазмы, подчиняется закону Ампера в сочетании с законом Ома для плотности тока в стенке и законом ФарадеяВ дальнейшем проводимость стенки $\sigma $ будет считаться постоянной.
В осесимметричных системах магнитное поле B, удовлетворяющее уравнению $\nabla \cdot {\mathbf{B}} = 0$, может быть представлено в виде
где(18)
$\psi (r,z;t) \equiv \int\limits_0^r {\int\limits_0^{2\pi } {{\mathbf{B}} \cdot {{{\mathbf{e}}}_{z}}rdrd\zeta } } = 2\pi r{{A}_{\zeta }},$– полоидальный поток и ток, соответственно, через мембрану, ограниченную окружностью на плоскости $z = {\text{const}}$, ${{{\mathbf{e}}}_{z}} \equiv \nabla z$, ${{A}_{\zeta }}$ – тороидальная компонента векторного потенциала A, так что
а(21)
${\mathbf{j}} = \nabla \times {\mathbf{B}}{\text{/}}{{\mu }_{0}} = {{{\mathbf{j}}}^{{pl}}} + {{{\mathbf{j}}}^{e}} + {{{\mathbf{j}}}^{w}}$– плотность тока с тремя составляющими, возникающими из (13).
При аксиальной симметрии электромагнитные уравнения для $({{{\mathbf{j}}}_{p}},{{B}_{\zeta }},{{{\mathbf{E}}}_{p}})$ и $({{j}_{\zeta }},{{{\mathbf{B}}}_{p}},{{E}_{\zeta }})$, где нижний индекс p означает полоидальную компоненту (перпендикулярную к $\nabla \zeta $), становятся расцепленными. Описание ${\mathbf{j}}_{p}^{w}$ и полного полоидального тока ${{I}_{w}}$, возбуждаемого в стенке, может быть найдено в [9] и [27]. Здесь нам нужна величина $j_{\zeta }^{w}$, что требует рассмотрения реакции стенки на изменения ${{{\mathbf{B}}}_{p}}$. Соответствующий анализ подразумевает операции с $({{j}_{\zeta }},{{{\mathbf{B}}}_{p}},{{E}_{\zeta }})$, включая основное уравнение для стенки
(22)
$j_{\zeta }^{w} = \sigma {{E}_{\zeta }} = - \sigma {{\left. {\frac{{\dot {\psi }}}{{2\pi r}}} \right|}_{{wall}}} = - \sigma {{\left. {{{{\dot {A}}}_{\zeta }}} \right|}_{{wall}}},$Правая часть содержит вклад ${{\psi }^{w}}$ (или $A_{\zeta }^{w}$), создаваемый $j_{\zeta }^{w}$ и поэтому зависящий от него. В целом связи токов с потоками подчиняются уравнению
(23)
${{{\mathbf{A}}}^{v}}({\mathbf{x}}) = \frac{{{{\mu }_{0}}}}{{4\pi }}\int\limits_v {\frac{{{\mathbf{j}}({\mathbf{x}}{\kern 1pt} ')}}{{\left| {{\mathbf{x}} - {\mathbf{x}}{\kern 1pt} '} \right|}}d{\mathbf{x}}{\kern 1pt} '} ,$(24)
$rA_{\zeta }^{v} \equiv \frac{{{{\psi }^{v}}}}{{2\pi }} = {{\mu }_{0}}\int\limits_v {G(r,z;r{\kern 1pt} ',z{\kern 1pt} '){{j}_{\zeta }}(r{\kern 1pt} ',z{\kern 1pt} ')dr{\kern 1pt} 'dz{\kern 1pt} ',} $(25)
$G \equiv \frac{{\sqrt {rr{\kern 1pt} '} }}{{\pi k}}\left[ {\left( {1 - \frac{{{{k}^{2}}}}{2}} \right)K(k) - E(k)} \right],$(26)
${{k}^{2}} \equiv \frac{{4rr{\kern 1pt} '}}{{{{{(r + r')}}^{2}} + {{{(z - z{\kern 1pt} ')}}^{2}}}}.$Прямой вывод (24) из (23) основан на формулах
(27)
${{{\mathbf{e}}}_{\zeta }} = - {{{\mathbf{e}}}_{x}}\sin \zeta + {{{\mathbf{e}}}_{y}}\cos \zeta ,$(28)
${{{\mathbf{e}}}_{\zeta }} \cdot {\mathbf{e}}_{\zeta }^{'} = \cos (\zeta - \zeta {\kern 1pt} ')$(29)
$\begin{gathered} \frac{1}{{\left| {{\mathbf{x}} - {\mathbf{x}}{\kern 1pt} '} \right|}} = \\ \, = \frac{1}{{\pi \sqrt {rr{\kern 1pt} '} }}\left[ {{{Q}_{{ - 1/2}}}(\chi ) + 2\sum\limits_{n = 1}^\infty {{{Q}_{{n - 1/2}}}(\chi )\cos n(\zeta - \zeta {\kern 1pt} ')} } \right], \\ \end{gathered} $Здесь мы намеренно отделяем электромагнитную часть задачи и, чтобы сделать выкладки прямыми и прозрачными, начинаем с общеизвестного равенства (23) и его точных следствий. Эта часть связана с плазмой только граничным условием (12). До момента применения его к операциям с (21)–(24) мы остаемся в области чистой и хорошо развитой математики. Этот подход позволяет отложить введение малых параметров, типичных для аналитической теории равновесия плазмы [1, 2, 4, 5]. Обычно разложение в приближении большого аспектного отношения (допустимое при $b{\text{/}}{{R}_{{pl}}} \ll 1$) вводится с самого начала вычислений, а плазма считается круглой. Тем самым точность и применимость всех последующих результатов ограничены, как в [1, 2, 4, 5]. В противоположность этому, здесь и в следующих двух разделах соотношения свободны от данных ограничений и справедливы для произвольной конфигурации токамака.
Стратегия здесь состоит в том, чтобы соединить (22), (24) и
с (12). Это покроет все интересующие нас случаи. Затем на пути к замене (7) уравнением, позволяющим анализ CQ, мы выполним редукцию к геометрии, показанной на рис. 2.3. ИНТЕГРАЛЬНЫЕ ФОРМУЛИРОВКИ ВНЕШНЕЙ ЗАДАЧИ С ПРИВЯЗКОЙ К ПЛАЗМЕ
Трудности нахождения распределения тока ${{j}_{\zeta }}$ в плазме токамака известны [33–47]. С далеко не полной экспериментальной информацией о ${{j}_{\zeta }}({\mathbf{r}})$ связанная неточность в вычислении ${{\psi }^{{pl}}}$ становится намного меньшей после преобразования (24) к поверхностному интегралу по ${{S}_{{pl}}}$ как функции B на ${{S}_{{pl}}}$, потому что такое B может быть вполне надежно оценено из магнитных измерений [4, 5, 48]. Это известное преобразование, основанное только на уравнениях Максвелла, может быть сделано для произвольной системы токов [33, 49], не обязательно удовлетворяющей (12). Для полноты и связности, несколько ключевых уравнений приведены ниже.
Из (29), (30), равенств
(32)
${{\nabla }^{2}}\frac{1}{{\left| {{\mathbf{x}} - {\mathbf{x}}{\kern 1pt} '} \right|}} = - 4\pi \delta ({\mathbf{x}} - {\mathbf{x}}{\kern 1pt} ')$(33)
$\oint {\delta ({\mathbf{x}} - {\mathbf{x}}{\kern 1pt} ')\cos n(\zeta - \zeta {\kern 1pt} ')d\zeta {\kern 1pt} '} = \frac{{\delta (r - r{\kern 1pt} ')\delta (z - z{\kern 1pt} ')}}{r},$(34)
${\text{div}}\frac{{\nabla G}}{{{{r}^{2}}}} = - \frac{{\delta (r - r{\kern 1pt} ')\delta (z - z{\kern 1pt} ')}}{r}.$С этим соотношением и следствием (17) и (21)
(35)
${\text{div}}\frac{{\nabla \psi }}{{{{r}^{2}}}} = - \frac{{2\pi {{\mu }_{0}}}}{r}{{j}_{\zeta }},$(36)
${{\psi }^{{pl}}} - {{\eta }_{{pl}}}\psi = \frac{1}{{2\pi }}\oint\limits_{pl} {\left( {\psi \frac{{\nabla G}}{{{{r}^{2}}}} - G\frac{{\nabla \psi }}{{{{r}^{2}}}}} \right) \cdot d{{{\mathbf{S}}}_{{pl}}}} ,$(37)
${{\eta }_{{pl}}}({\mathbf{x}}) \equiv - \frac{1}{{2\pi }}\int\limits_{pl} {{\text{div}}\frac{{\nabla G}}{{{{r}^{2}}}}} d{\mathbf{x}} = \left\{ {\begin{array}{*{20}{l}} {1\quad {\text{внутри}}\;{{S}_{{pl}}}} \\ {0.5\quad {\text{на}}\;{{S}_{{pl}}}} \\ {0\quad {\text{вне}}\;{{S}_{{pl}}}} \end{array}} \right.,$Общее электромагнитное равенство (36) справедливо для любого аксиально-симметричного распределения тока в тороидальной трубке ${{S}_{{pl}}}$. Для удерживаемой магнитным полем изотропной плазмы, подчиняющейся уравнению (11), есть сильное ограничение (12), которое в сочетании с симметрией и (17) требует
где ${{{\mathbf{n}}}_{{pl}}}$ и– нормальный и тангенциальный к ${{S}_{{pl}}}$ единичные векторы, а ${{{\mathbf{e}}}_{\zeta }} = r\nabla \zeta $. Тогда
должна быть (зависящей от времени) константой на ${{S}_{{pl}}}$, а(41)
$\frac{1}{{2\pi }}\oint\limits_{pl} {\psi \frac{{\nabla G}}{{{{r}^{2}}}} \cdot d{{{\mathbf{S}}}_{{pl}}}} = - {{\eta }_{{pl}}}{{\psi }_{b}},$(42)
${{\psi }^{{pl}}} - {{\eta }_{{pl}}}(\psi - {{\psi }_{b}}) = 2\pi \oint\limits_{pl} {G{\mathbf{B}} \cdot d{{{\vec {\ell }}}_{{pl}}}} .$Это компактное соотношение дает ${{\psi }^{{pl}}}$ вне плазмы (при ${{\eta }_{{pl}}} = 0$) и
(43)
${{\psi }^{{ext}}} \equiv {{\psi }^{e}} + {{\psi }^{w}} = {{\psi }_{b}} - 2\pi \oint\limits_{pl} {G{\mathbf{B}} \cdot d{{{\vec {\ell }}}_{{pl}}}} $Хотя $G$ имеет особенность при $k \to 1$ (когда ${\mathbf{x}} \to {\mathbf{x}}{\kern 1pt} '$), а в (42) присутствует ступенчатая функция ${{\eta }_{{pl}}}$, правая часть (42) должна быть непрерывной функцией. Из (29) и (30) следует, что
(44)
$G = \frac{{rr{\kern 1pt} '}}{{4\pi }}\int\limits_0^{2\pi } {\frac{{\cos (\zeta - \zeta {\kern 1pt} ')}}{{\left| {{\mathbf{x}} - {\mathbf{x'}}} \right|}}d\zeta {\kern 1pt} '} .$Поэтому
(45)
$\oint\limits_{pl} {Gfd\ell _{{pl}}^{'}} = \frac{r}{{4\pi }}\oint\limits_{pl} {f\frac{{\cos (\zeta - \zeta {\kern 1pt} ')}}{{\left| {{\mathbf{x}} - {\mathbf{x}}{\kern 1pt} '} \right|}}dS_{{pl}}^{'}} ,$Отметим, что равенство (45) позволяет трансформировать (42) в
(46)
$A_{\zeta }^{{pl}} - {{\eta }_{{pl}}}\left( {{{A}_{\zeta }} - \frac{{{{\psi }_{b}}}}{{2\pi r}}} \right) = \frac{{{{\mu }_{0}}}}{{4\pi }}{{{\mathbf{e}}}_{\zeta }} \cdot \oint\limits_{pl} {\frac{{{{i}_{\zeta }}{\mathbf{e}}_{\zeta }^{'}}}{{\left| {{\mathbf{x}} - {\mathbf{x}}{\kern 1pt} '} \right|}}dS_{{pl}}^{'}} $(47)
${{\mu }_{0}}{{i}_{\zeta }} \equiv ({{{\mathbf{n}}}_{{pl}}} \times {\mathbf{B}}) \cdot {{{\mathbf{e}}}_{\zeta }}.$Это показывает, что магнитное поле поверхностного тока ${{i}_{\zeta }}{{{\mathbf{e}}}_{\zeta }}$ на границе плазмы совпадает с произведенным плазмой магнитным полем ${{{\mathbf{B}}}^{{pl}}}$ вне ${{S}_{{pl}}}$. Кроме того, ток $ - {{i}_{\zeta }}{{{\mathbf{e}}}_{\zeta }}$ создает внутри ${{S}_{{pl}}}$ внешнее полоидальное магнитное поле ${\mathbf{B}}_{p}^{{ext}}$, необходимое для поддержания данной тороидальной плазмы в равновесии.
Эта интерпретация предложена в [50] и стала с тех пор называться “принципом виртуального кожуха” [5, 24, 51–57]. С подстановкой ${{\mu }_{0}}{\mathbf{j}} = $ $ = {{{\mathbf{n}}}_{{pl}}} \times {\mathbf{B}}\delta ({\mathbf{x}} - {\mathbf{x}}{\kern 1pt} ')$ в (23) она справедлива для любой трехмерной тороидальной конфигурации при условии, что ${{{\mathbf{n}}}_{{pl}}} \cdot {\mathbf{B}} = 0$. Что касается математики, (46) и более общие электромагнитные соотношения, покрывающие (46), были известны значительно раньше (раздел 4.15 в [33], уравнение (2.10) в [58]); обобщение (46) на случай с ${{{\mathbf{n}}}_{{pl}}} \cdot {\mathbf{B}} \ne 0$ или с S, представляющей любую охватывающую плазму тороидальную поверхность в промежутке плазма–стенка,
(48)
$\begin{gathered} {{{\mathbf{B}}}^{{pl}}}({\mathbf{r}}) - {{\eta }_{{pl}}}{\mathbf{B}}({\mathbf{r}}) = \\ \, = \frac{1}{{4\pi }}\int\limits_S {\left\{ {({\mathbf{n}} \times {\mathbf{B}}) \times \frac{{{\mathbf{r}} - {{{\mathbf{r}}}_{s}}}}{{{{{\left| {{\mathbf{r}} - {{{\mathbf{r}}}_{s}}} \right|}}^{3}}}} + ({\mathbf{n}} \cdot {\mathbf{B}})\frac{{{\mathbf{r}} - {{{\mathbf{r}}}_{s}}}}{{{{{\left| {{\mathbf{r}} - {{{\mathbf{r}}}_{s}}} \right|}}^{3}}}}} \right\}dS} , \\ \end{gathered} $Уравнение (42) показывает, что только ${{S}_{{pl}}}$ и B на ${{S}_{{pl}}}$ определяют и поле ${{{\mathbf{B}}}^{{pl}}}$ вне ${{S}_{{pl}}}$, и поле ${\mathbf{B}}_{p}^{{ext}}$, необходимое для поддержания плазмы в равновесии, которое подчиняется (11). Это означает, в частности, идентичные магнитные поля вне ${{S}_{{pl}}}$ для плазменных конфигураций с одинаковыми ${{S}_{{pl}}}$ и B на ${{S}_{{pl}}}$. Такие конфигурации нельзя отличить по магнитным измерениям, независимо от различий в распределениях давления и тока. Это обсуждалось в [41], а примеры были представлены в [44, 45]. Здесь важным моментом является то, что мы строим выкладки на твердой математической основе, хорошо известной и проверенной в различных электромагнитных задачах.
4. СВЯЗЬ СО СТЕНКОЙ
Чтобы использовать (43), нам нужно уравнение для ${{\psi }^{w}} = 2\pi rA_{\zeta }^{w}$. Эта функция может быть выражена через тороидальную плотность тока $j_{\zeta }^{w}$ посредством равенства (24), дающего
для геометрически тонкой стенки с толщиной ${{d}_{w}}$, которая считается здесь константой, как в [1, 2, 4, 5] и в различных вычислительных моделях [7, 9, 15, 16, 59]. С $j_{\zeta }^{w}$, подчиняющимся (22), это превращается в(50)
${{\psi }^{w}} = - {{\tau }_{w}}\oint\limits_w {\frac{\sigma }{{{{\sigma }_{0}}}}\frac{{\dot {\psi }}}{{{{b}_{w}}r}}Gd{{\ell }_{w}}} ,$Первое соотношение для ${{\psi }^{w}}$ является общим, в то время как второе ограничено законом Ома (15) для стенки. Различие в физике не затрагивает математику для тех выражений для ${{\psi }^{w}}$, которые имеют вид, подобный правой части в (42).
Подстановка (31) превращает (50) в интегральное уравнение для ${{\psi }^{w}}$, где ${{\psi }^{{pl}}} + {{\psi }^{e}}$ – входной параметр. Оно могло бы быть решено стандартными методами без плазмы (при ${{\psi }^{{pl}}} = 0$), но присутствие функции ${{\psi }^{{pl}}}$, зависящей от неизвестной ${{\psi }^{w}}$, значительно усложняет задачу. Эта зависимость навязана равенством (38), которое требует
(51)
${{{\mathbf{\tau }}}_{{pl}}} \cdot \nabla ({{\psi }^{e}} + {{\psi }^{w}}) = - {{{\mathbf{\tau }}}_{{pl}}} \cdot \nabla {{\psi }^{{pl}}}$Это учитывалось в выкладках, приводящих к (42). Последнее на самом деле дает нам готовое решение (43) для ${{\psi }^{e}} + {{\psi }^{w}}$ внутри плазмы, при ${{\eta }_{{pl}}} = 1$. Чтобы согласовать его с (50), мы должны соответственно подстроить ${{S}_{{pl}}}$. Именно геометрия плазмы как “скрытая переменная” с практически мгновенной реакцией на любое изменение B отличает плазменную задачу от подобных с твердыми проводниками. Различие возникает из равенства (40), служащего граничным условием для B во внешней области и превращающего (36) в (42).
Уравнения (43) и (50) содержат ${{\psi }^{w}}$ в своих левых частях. Эта величина может быть устранена вычитанием. Тогда получаем в терминах полного B и ψ:
(52)
${{\psi }^{e}} = {{\psi }_{b}} - 2\pi \oint\limits_{pl} {G{\mathbf{B}} \cdot d{{{\vec {\ell }}}_{{pl}}}} + {{\tau }_{w}}\oint\limits_w {\frac{\sigma }{{{{\sigma }_{0}}}}\frac{{\dot {\psi }}}{{{{b}_{w}}r}}Gd{{\ell }_{w}}} ,$(53)
${{\psi }_{{gap}}} = {{\psi }^{e}} + 2\pi \oint\limits_{pl} {G{\mathbf{B}} \cdot d{{{\vec {\ell }}}_{{pl}}}} - {{\tau }_{w}}\oint\limits_w {\frac{\sigma }{{{{\sigma }_{0}}}}\frac{{\dot {\psi }}}{{{{b}_{w}}r}}Gd{{\ell }_{w}}} ,$Она также содержится в интегралах с $\dot {\psi }$ в (52) и (53). Присутствие $\dot {\psi }$ со вкладами от плазмы, стенки и всех токов снаружи требует более тщательного вычисления ψ, чем в традиционной теории равновесия.
До сих пор единственными предположениями были осевая симметрия и граничное условие (38), следствие уравнения равновесия (11). Поэтому (52), (53) и предыдущие уравнения (42), (43) и (50) для ${{\psi }^{{pl}}}$, ${{\psi }^{{ext}}}$ и ${{\psi }^{w}}$ могут использоваться с любой двумерной моделью токамака или равновесными кодами. Возможное применение этих уравнений продемонстрировано ниже аналитически для токамака с большим аспектным отношением.
5. СВЕДЕНИЕ К СТАНДАРТНЫМ МОДЕЛЯМ ТОКАМАКА В АНАЛИТИЧЕСКИХ ИССЛЕДОВАНИЯХ
Интегралы в (42), (43), (49) и (50) выглядят похоже, и этот факт облегчает их вычисления. Они аналитически выполнены ниже для круглой плазмы и стенки в приближении большого аспектного отношения, которое является составной частью традиционных моделей равновесия.
Пошаговая строгая редукция к уровням, позволяющим обозримые аналитические выкладки, описана в [32, 63], см. также элементы техники в [24, 48, 64] с расширениями и применениями к стеллараторам. Сначала мы используем приблизительное выражение [63]
(55)
$G \approx {{G}_{1}} = \frac{R}{{2\pi }}[{{\lambda }_{0}} - 2 - {{\delta }_{x}}({{\lambda }_{0}} - 1)],$(56)
${{\lambda }_{0}} \equiv \ln \frac{{8R}}{{\sqrt {{{{(x - x{\kern 1pt} ')}}^{2}} + {{{(z - z{\kern 1pt} ')}}^{2}}} }},$С этого момента мы рассматриваем круглую плазму с малым и большими радиусами b и ${{R}_{{pl}}}$ и “граничным условием” на поверхности плазмы ($\ell = b$), предписанным как
(59)
${\mathbf{B}} \cdot {{\tau }_{{pl}}} = {{B}_{J}}\left( {1 - \frac{b}{{{{R}_{{pl}}}}}\Lambda \cos \alpha } \right),$Тогда с (55) и (59) получаем из (42) вне плазмы ($\ell > b$, ${{\eta }_{{pl}}} = 0$):
с(64)
${{a}_{1}}(\ell ) \equiv \frac{{\Delta (\ell )}}{\ell } + \frac{\ell }{b}\frac{{B_{ \bot }^{{eq}}}}{{{{B}_{J}}}},$(65)
$\Delta (\ell ) \equiv \frac{{{{\ell }^{2}}}}{{2{{R}_{{pl}}}}}\left[ {\ln \frac{\ell }{b} + \left( {\Lambda + \frac{1}{2}} \right)\left( {1 - \frac{{{{b}^{2}}}}{{{{\ell }^{2}}}}} \right)} \right],$В этой модели уравнение (43) для области внутри плазмы ($\ell < b$) дает
(66)
${{\psi }^{{ext}}} = {{\psi }_{b}} - {{\psi }_{J}}\left[ {{{a}_{0}}(b) + \frac{\ell }{b}\frac{{B_{ \bot }^{{eq}}}}{{{{B}_{J}}}}\cos \alpha } \right]$Поле $B_{ \bot }^{{eq}}$ появилось в (66) как комбинация, заданная (1). Это хорошо известное [1, 2, 4, 5, 22–26] выражение воспроизводится здесь как побочный продукт ограничения (51). Согласно (17), (31) и (43) функция ${{\psi }^{{ext}}}$ определяет магнитное поле, создаваемое всеми токами, внешними по отношению к плазме (включая те, которые индуцированы в стенке):
Подстановка (66), где $\ell \cos \alpha = {{R}_{{pl}}} - r$, см. рис. 2, дает ${\mathbf{B}}_{p}^{{ext}} = ({{R}_{{pl}}}{\text{/}}r)B_{ \bot }^{{eq}}{{{\mathbf{e}}}_{z}}$. В то время как (1) связывает $B_{ \bot }^{{eq}}$ с параметрами плазмы, равенство (68) также демонстрирует, что
С $B_{ \bot }^{{eq}}$, найденным из (1), и известным $B_{ \bot }^{e}$, созданным управляемыми внешними токами, это соотношение описывает реакцию стенки в терминах $B_{ \bot }^{w}$.
Представленные выкладки гарантируют нам, что формула (66) справедлива внутри ${{S}_{{pl}}}$. Мы можем расширить ее на область, свободную от токов, вплоть до стенки, потому что ${{\psi }^{{ext}}}({\mathbf{r}},t)$ должна быть непрерывной функцией, удовлетворяющей тому же уравнению
внутри вакуумной камеры. Во всем пространстве величина ${{\psi }^{{ext}}}$ подчиняется уравнению (35) с $j_{\zeta }^{{ext}} = j_{\zeta }^{e} + j_{\zeta }^{w}$ в правой части и должна быть регулярной на бесконечности. Разность $x = {{\psi }_{1}} - {{\psi }_{2}}$ двух решений, если предполагается, что они существуют при том же самом $j_{\zeta }^{{ext}}$, всюду починяется однородному уравнению (70). Тогда(71)
$\nabla \cdot \frac{{x\nabla x}}{{{{r}^{2}}}} = \frac{{{{{\left| {\nabla x} \right|}}^{2}}}}{{{{r}^{2}}}},$Чтобы быть последовательными, мы должны добавить, что расширение (66) на более широкую область также требует, чтобы приближение большого аспектного отношения было приемлемым во всем объеме, ограниченном стенкой, и требует отсутствия сильно локализованных токов вблизи. В противном случае использование (55) и (59) не будет оправданным, и следует сохранять более высокие гармоники.
При этих предположениях получаем, объединяя (61) и (66):
(73)
${{\psi }_{{gap}}} = {{\psi }^{{ext}}} + {{\psi }^{{pl}}} = {{\psi }_{b}} + {{\psi }_{J}}\left[ {\ln \frac{b}{\ell } + \frac{{\Delta (\ell )}}{\ell }\cos \alpha } \right].$Запись в координатах $(\ell ,\alpha )$, связанных с центром плазмы, удобна для демонстрации исчезновения косинусного члена на границе плазмы ($\ell = b$).
Интеграл (50), входящий в (52) и (53), содержит ${{\psi }_{{gap}}}$ на стенке. В общем случае ${{S}_{{pl}}}$ и ${{S}_{w}}$ не являются коаксиальными из-за смещения плазменного шнура
относительно стенки. Вводя координаты $(\rho ,u)$ с $\rho = 0$ в центре поперечного сечения стенки, как показано на рис. 2, имеем и приблизительно последнее применимо в зазоре плазма–стенка при или при небольшом смещении плазмы, что естественно удовлетворяется до срыва для полноразмерной плазмы, надлежащим образом расположенной в вакуумной камере. Тогда (73) можно преобразовать в с и где функция $\Delta (\rho )$ дана (65) с $\ell \to \rho $.Похожие на приведенные здесь выражения для ψ вне плазмы можно найти, например, в [1, 4, 5, 22–26, 39, 48, 65]. Вместо того чтобы выбрать одно из них и приспособить его к нашей задаче, мы предоставили полную цепь выкладок с кульминацией на компактных формулах (78)–(80). Главной побудительной причиной к этому была необходимость в получении правильного и легко проверяемого результата, содержащего все релевантные величины (включая ${{\psi }_{b}}(t)$ и ${{\Delta }_{b}}$) со строгими определениями. Это вынужденный подход, потому что доступные формулы для ψ отличаются, и какой-то конкретный выбор неизбежно противоречит другим.
Иногда [5, 22, 24, 48, 65] функция $\psi $ задается как
в то время как в [23, 25, 39] для той же модели, иллюстрированной рис. 2. Здесь J – полный ток плазмы, ${{a}_{0}}(\ell )$ определено (63), а где $\Delta (\ell )$ задано равенством (65).Отчасти несоответствия в выражениях для ψ связаны с выбором полоидального угла ω (как наш α на рис. 2 или $\pi - \alpha $), но простая замена $\omega \to \pi - \omega $ не может примирить эти две версии с
появившимся в известных работах [1, 4] и воспроизведенным в [26]. Коэффициенты пропорциональности положительны в этих трех случаях. Поэтому последнее выражение для ψ сводится к виду (81) двумя одновременными заменами $\omega \to \pi - \omega $ и $J \to - J$. Именно эта операция предлагается после уравнения (4.2) в [5] для перехода к формулам в [4], хотя логика этого совета осталась там необъясненной.Отмеченные трудности и неопределенности возникают из-за отсутствия строгих определений полоидального угла и положительного направления тороидального тока. Они усугубляются использованием привычной терминологии, которая игнорирует различия между ω и $\pi - \omega $, J и –J. Кроме того, ситуация усложняется использованием нескольких наборов координат в выкладках, до четырех или даже до пяти, как в [5, 23, 26]. За громоздкими преобразованиями, затрагивающими главным образом косинусный член в ψ, трудно проследить, даже если все было бы математически совершенным и не было опечаток, а обозначения были четкими (в отличие, например, от a с пятью различными значениями в разд. 4.1 в [5]).
Чтобы избежать перекрестных сопоставлений, идентификации истинного значения символов и приводящих в замешательство подстановок типа предложенных в [5], здесь мы опираемся на подробные прямые выкладки из первых принципов с предположениями и упрощениями, вводимыми шаг за шагом, только когда это необходимо.
Здесь главная цель – замена (7), чтобы гарантировать надежное описание эволюционирующей плазмы, в особенности при $dJ{\text{/}}dt \ne 0$. Тогда мы должны сохранить ${{\psi }_{b}}(t)$ в (79), но знакомые выражения для ψ не содержат этой величины, см. уравнения (64) и (65) в [1], (32) в [4], (62a) в [39], (3.8.7) и его следствия в [25] и подобные в [22–24, 48, 65]. В (4.35) в [5] и в (16.137) в [26] она описана как константа, потому что $\nabla {{\psi }_{b}} = 0$, и ${{\psi }_{b}}$ не дает вклада в (17).
Наконец, нам нужна величина ${{\Delta }_{b}}$ в (80), которая также часто отсутствует в некоторых используемых формулах для ψ [4, 23, 25]. Это становится проблемой, если различие между двумя системами координат, показанных на рис. 2, не подчеркнуто или потеряно в других технических деталях.
В исходном состоянии положение плазмы и, следовательно, смещение ${{\Delta }_{b}}$ должны быть известны. Выяснение того, что происходит позже, лежит в фокусе нашего исследования. Как заключительный шаг к уравнению эволюции мы должны связать (50) и (78).
6. РЕШЕНИЯ ДЛЯ ψw
Подобие интегралов в (43) и (50) подразумевает, что ${{\psi }^{w}}$ внутри ${{S}_{w}}$ должно описываться той же формулой, что и (66) при ${{\psi }_{b}} = 0$ (потому что ${{\psi }_{b}}$ появляется в (43) из другого интеграла), но в переменных, возникающих из замен $d{{\ell }_{{pl}}} \to d{{\ell }_{w}}$, $(\ell ,\alpha ) \to (\rho ,u)$ и
(85)
${\mathbf{B}} \cdot {{\tau }_{{pl}}} \to {{\left. {\frac{{{{\tau }_{w}}\dot {\psi }}}{{2\pi {{b}_{w}}r}}} \right|}_{w}} = \frac{{{{\tau }_{w}}{{{\dot {\psi }}}_{{gap}}}({{b}_{w}},u)}}{{2\pi {{R}_{w}}{{b}_{w}}(1 - {{\varepsilon }_{w}}\cos u)}},$Тогда тот же цикл вычислений, как прежде с (43), но теперь начинающийся от (50), приводит к
с и где ${{a}_{0}}$ определено (63), в то время как(90)
$B_{ \bot }^{w} = \frac{{{{\tau }_{w}}}}{{4\pi {{b}_{w}}{{R}_{w}}}}\left[ {{{{\dot {\psi }}}_{1}}({{b}_{w}}) - {{\varepsilon }_{w}}{{{\dot {\psi }}}_{0}}({{b}_{w}})\left( {\ln \frac{{8{{R}_{w}}}}{{{{b}_{w}}}} - \frac{3}{2}} \right)} \right]$Последнее показывает, что
(91)
${{\psi }_{1}}({{b}_{w}}) = {{\psi }_{J}}\frac{{{{\Delta }_{{iw}}} - {{\Delta }_{b}}}}{{{{b}_{w}}}},$(92)
${{\Delta }_{{iw}}} \equiv \Delta ({{b}_{w}}) = \frac{{b_{w}^{2}}}{{2{{R}_{w}}}}\left[ {\ln \frac{{{{b}_{w}}}}{b} + \left( {\Lambda + \frac{1}{2}} \right)\left( {1 - \frac{{{{b}^{2}}}}{{b_{w}^{2}}}} \right)} \right],$Чтобы оставаться в рамках приближения с равенством (78) и учесть тороидальные эффекты, мы задаем плотность тока в стенке в виде
где ${{J}_{w}}$ – полный тороидальный ток в стенке, а– площадь тонкой стенки (${{d}_{w}} \ll {{b}_{w}}$) в поперечном сечении $\zeta = \operatorname{const} $. Тогда из (49), где интеграл похож на входящий в (43), если мы там делаем замену
для внутренней области ($\rho < {{b}_{w}}$) снова получим (87), но теперь с и(98)
$B_{ \bot }^{w} = \frac{{{{\mu }_{0}}}}{{4\pi {{b}_{w}}}}\left[ {{{\varepsilon }_{w}}{{J}_{w}}\left( {{\text{ln}}\frac{{8{{R}_{w}}}}{{{{b}_{w}}}} - \frac{1}{2}} \right) - J_{w}^{c}} \right]$Приравнивание (88) и (97) дает
Также из (90) с (98) и (99) следует, что
(100)
${{\mu }_{0}}(J_{w}^{c} - {{\varepsilon }_{w}}{{J}_{w}}){{R}_{w}} = - {{\tau }_{w}}{{\dot {\psi }}_{1}}({{b}_{w}}).$Эти два соотношения завершают цепь вычислений с (49) и (50). Для перепроверки их можно получить и непосредственно из (22).
7. УРАВНЕНИЯ ЭВОЛЮЦИИ В ТЕРМИНАХ ТОКОВ В СТЕНКЕ
Правые части (99) и (100) содержат компоненты Фурье полной функции ψ, которая совместно создана током в плазме, “активными” внешними проводниками и “пассивной” стенкой, см. (21) и (31). Соответственно
Здесь мы использовали (87) и (97) для вклада от стенки и выражение
(102)
$\frac{{{{\psi }^{{pl}}}}}{{{{\psi }_{J}}}} = {{a}_{0}}(\rho ) + [{{a}_{1}}(\rho ) - {{\Delta }_{b}}{\text{/}}\rho ]\cos u$(103)
${{L}_{w}} \equiv {{\mu }_{0}}{{R}_{w}}{{a}_{0}}({{b}_{w}}) = {{\mu }_{0}}{{R}_{w}}\left( {{\text{ln}}\frac{{8{{R}_{w}}}}{{{{b}_{w}}}} - 2} \right),$Используя (101), можно преобразовать (99) в
(106)
${{J}_{w}} = - \tau _{w}^{0}\frac{d}{{dt}}\left[ {J + {{J}_{w}} + \frac{{\psi _{0}^{e}({{b}_{w}},t)}}{{{{L}_{w}}}}} \right].$Здесь постоянная времени
(107)
$\tau _{w}^{0} \equiv {{\tau }_{w}}\frac{{{{L}_{w}}}}{{{{\mu }_{0}}{{R}_{w}}}} = {{\tau }_{w}}\left( {{\text{ln}}\frac{{8{{R}_{w}}}}{{{{b}_{w}}}} - 2} \right)$В [66] уравнение (106) было получено для “пустой” тороидальной камеры (без плазмы, $J = 0$). В настоящем виде, пригодном и для токамака с плазмой, подчиняющейся (11), это равенство было строго выведено в [63].
Электромагнитная природа уравнения (106) очевидна. Оно хорошо тем, что соотносит ${{J}_{w}}$ с током плазмы. Точно так же уравнение (100) с ${{\psi }^{{pl}}}$, найденное из (24), дало бы нам $J_{w}^{c}$ в терминах косинусной компоненты $j_{\zeta }^{{pl}}$, если бы плазма была заменена набором жестких колец, как это делалось в некоторых работах [67–75] по изучению последствий CQ. Здесь, напротив, мы принимаем во внимание легкую адаптируемость ${{{\mathbf{j}}}^{{pl}}}$ к ограничению равновесия (11). Будучи включенной в условие (51) на свободной границе, она приводит к взаимозависимости ${{\psi }^{{pl}}}$ и ${{\psi }^{{ext}}}$, описываемой противодействующими (когда они встречаются в $\psi = {{\psi }^{{pl}}} + {{\psi }^{{ext}}}$) вкладами $ \propto B_{ \bot }^{{eq}}$ в (61) и (66). Объединяя их следствия (69) и (80) с (98) и (100), мы получаем, соответственно,
(108)
$J_{w}^{c} = {{\varepsilon }_{w}}{{J}_{w}}\left( {{\text{ln}}\frac{{8{{R}_{w}}}}{{{{b}_{w}}}} - \frac{1}{2}} \right) - \frac{{4\pi {{b}_{w}}}}{{{{\mu }_{0}}}}(B_{ \bot }^{{eq}} - B_{ \bot }^{e})$(109)
$J_{w}^{c} - {{\varepsilon }_{w}}{{J}_{w}} = {{\tau }_{w}}\frac{d}{{dt}}\left( {J\frac{{{{\Delta }_{b}} - {{\Delta }_{{iw}}}}}{{{{b}_{w}}}}} \right),$Уравнение (108) дает величину $J_{w}^{c}$ в терминах поля $B_{ \bot }^{{eq}}$, определенного (1) или (69), поля $B_{ \bot }^{e}$, произведенного внешними источниками (за стенкой) и полным током в стенке ${{J}_{w}}$. Знание ${{J}_{w}}$ и $J_{w}^{c}$ может быть необходимым в вычислениях электромагнитных нагрузок на стенку во время срывов. Оно может быть также полезно в задачах магнитной диагностики.
Уравнение (108) было недавно получено в [63] и сравнено с подобным результатом в [66] для вакуумной камеры бетатрона ($J = p = 0$ и, соответственно, $B_{ \bot }^{{eq}} = 0$). Теперь мы делаем шаг к изучению плазменных эффектов. Он облегчается использованием дополнительного уравнения (109) для того же самого $J_{w}^{c}$, но дающего связь с положением плазмы со свободной границей, которое описывается смещением ${{\Delta }_{b}}$.
Подстановка (108) в (109) превращает это соотношение в
(110)
$\begin{gathered} {{\tau }_{w}}\frac{d}{{dt}}\left( {J\frac{{{{\Delta }_{b}} - {{\Delta }_{{iw}}}}}{{{{b}_{w}}}}} \right) = \\ \, = {{\varepsilon }_{w}}{{J}_{w}}\left( {{\text{ln}}\frac{{8{{R}_{w}}}}{{{{b}_{w}}}} - \frac{3}{2}} \right) - \frac{{4\pi {{b}_{w}}}}{{{{\mu }_{0}}}}(B_{ \bot }^{{eq}} - B_{ \bot }^{e}), \\ \end{gathered} $8. СРАВНЕНИЕ С ТЕОРИЕЙ ШАФРАНОВА
При $B_{ \bot }^{e} = 0$ уравнение (110) описывает смещение плазменного шнура наружу, когда ему противодействует только ток, индуцированный в резистивной стенке движением плазмы. То есть по существу описывает переходный короткий импульс с неизбежной потерей разряда в первых токамаках [3], прежде чем они были оборудованы системами управления равновесия [78]. Мы упоминаем эту давно забытую историю, потому что задача (с дополнительным ограничением ${{J}_{w}} = 0$, разрешающим только дипольный ток в стенке) была тщательно проанализирована В.Д. Шафрановым в [1] и позже в [2, 4, 5], что делает этот случай подходящим для сравнения.
При тех сильно ограничивающих предположениями ($B_{ \bot }^{e} = {{J}_{w}} = 0$), устраняющих два слагаемых в уравнении (110), последнее сводится к
(111)
$\begin{gathered} {{\tau }_{w}}\frac{d}{{dt}}\left( {J\frac{{{{\Delta }_{b}} - {{\Delta }_{{iw}}}}}{{{{b}_{w}}}}} \right) = - \frac{{4\pi {{b}_{w}}}}{{{{\mu }_{0}}}}B_{ \bot }^{{eq}} = \\ \, = J\frac{{{{b}_{w}}}}{{{{R}_{w}}}}\left( {{\text{ln}}\frac{{8{{R}_{w}}}}{b} + \Lambda - \frac{1}{2}} \right) \\ \end{gathered} $Насколько нам известно, это – первое независимое подтверждение результата Шафранова (7) с ${{t}_{{con}}}$, определенным (8). Здесь оно получено методом, отличающимся от использованных в [1] и [4, 5]. Приближение большого аспектного отношения и круглые формы ${{S}_{{pl}}}$ и ${{S}_{w}}$, введенные в разд. 5, те же самые, что и в [1], но никаких ограничений на $J(t)$ и $B_{ \bot }^{e}$ не было наложено на пути к (110). Это привело нас к установлению того факта, что уравнение для эволюции ${{\Delta }_{b}}$ должно содержать два дополнительных члена по сравнению с (7) и (111), а именно, с ${{J}_{w}}$ и $B_{ \bot }^{e}$ в (110).
Отсутствие $B_{ \bot }^{e}$ в (7) подразумевается формулировкой задачи в [1], но условие ${{J}_{w}} = 0$ не было там оговорено. Теперь отсутствие ${{J}_{w}}$ в том подходе становится очевидным, когда уравнение (64) в [1] сравнивается с нашим уравнением (101). Из (106) следует, что при ${{J}_{w}} = 0$ поведение тока плазмы полностью определяется величиной $\psi _{0}^{e}(t)$. Типичные медленные изменения $\psi _{0}^{e}(t)$ тогда требуют $dJ{\text{/}}dt = 0$. Последнее условие не было упомянуто в [1]. К тому же присутствие J в (7) с одним J под $d{\text{/}}dt$ сбивает с толку, как бы указывая на противоположное. Однако, как мы только что установили, уравнение (7) может быть справедливым только при $dJ{\text{/}}dt = 0$ (и при неприемлемом для обычных токамаков условии $B_{ \bot }^{e} = 0$). Мы можем также дополнить картину уравнениями (108) и (109), где следует положить ${{J}_{w}} = 0$, $B_{ \bot }^{e} = 0$, и $dJ{\text{/}}dt = 0$, чтобы согласовать их с (7).
Таким образом, уравнение (7) не позволяет анализ процессов с $dJ{\text{/}}dt \ne 0$, как в случаях с CQ, например. Вместо него мы предлагаем более общее уравнение (110), которое идеально подходит для этой цели. Его обоснованность может быть проверена, если проследить представленные выкладки.
Различие между результатами в [1] и здесь может быть легко оценено в пределе идеальной стенки, который является другой удобной точкой для сопоставления. При ${{\tau }_{w}} \to \infty $ и обязательном для обоих уравнений (7) и (111) условии $J = {\text{const}}$ они дают
с ${{\Delta }_{{iw}}}$, введенным равенством (92). Хотя (112) относится к не представляющим практического интереса (после прогресса в исследованиях на токамаках, которому способствовала формула Шафранова (1) для $B_{ \bot }^{{eq}}$) короткоживущим равновесным состояниям, это остается хорошо установленным теоретическим результатом [1, 2, 4, 5, 65], содержащимся в (7) и явно данным уравнением (48) в [1].Наши уравнения (106), (108) и (110) допускают $dJ{\text{/}}dt \ne 0$, что также производит ${{J}_{w}} \ne 0$. Из них немедленно следует, что при том же ${{\tau }_{w}} \to \infty $ получается
с намного более широким покрытием событий, чем дает (112). Простая оценка из (113) показывает, что, при $J = {{J}_{0}}{\text{/}}2$ величина ${{\Delta }_{b}} - {{\Delta }_{{iw}}}$ должна быть в два раза больше, чем получается из (112).С помощью (113) мы подтвердили, что (112) должно быть правильным при $dJ/dt = 0$ и ${{\tau }_{w}} \to \infty $, и продемонстрировали, что включение $dJ{\text{/}}dt \ne 0$ в (113) сильно влияет на результат. Добавим для сравнения, что уравнение (4.72) в [5] сводится в пределе идеальной стенки к ограничению
которое не может быть согласовано с (112) или с (113) для переходных процессов типа TQ с быстрым изменением ${{\Delta }_{{iw}}}$.Казалось бы, оба уравнения (112) и (114) должны представлять одну и ту же ситуацию, но даже в диапазоне их применимости, при $J = {\text{const}}$, их предсказания не совпадают: $\delta {{\Delta }_{b}} = \delta {{\Delta }_{{iw}}} \ne 0$ в (112), но $\delta {{\Delta }_{b}} = 0$ в (114). Это демонстрирует, что происходит, когда сделан неверный выбор из доступных представлений для ψ.
9. ЗАКЛЮЧЕНИЕ
Стандартная теория равновесия [1, 2, 4, 5, 22–26] на основе уравнения Грэда–Шафранова позволяет находить ${{\Delta }_{b}}$ при предписанных распределениях давления и тока плазмы и заданного $B_{ \bot }^{e} + B_{ \bot }^{w}$, которое должно быть равным $B_{ \bot }^{{eq}}$, определяющему положение плазмы по большому радиусу в токамаках. Начиная с публикации [1], решения были известны и подтверждены для двух случаев: с $B_{ \bot }^{{eq}} = B_{ \bot }^{e}$ (равновесие без стенки или статическое равновесие) и с $B_{ \bot }^{{eq}} = B_{ \bot }^{w}$, но с ${{J}_{w}} = 0$ или $dJ{\text{/}}dt = 0$. Уравнение (110) расширяет теорию, покрывая переходные процессы с эволюционирующими J и $B_{ \bot }^{{eq}}$ наряду с соответствующей реакцией резистивной стенки.
В.Д. Шафранов был первым рассмотревшим эффекты резистивной стенки на глобальную динамику плазмы в токамаках. В пионерских работах [1, 2] вопрос состоял в том, могла ли растягивающая сила, действующая на тороидальный плазменный шнур, быть подавлена из-за дипольного тока, индуцированного в стенке, и ответ был дан равенствами (7)–(9). Это был крайний случай с $B_{ \bot }^{{eq}} = B_{ \bot }^{w}$, потому что первоначально, когда соотношение (1) и стоящая за ним физика еще не были известны, первые токамаки оперировали при $B_{ \bot }^{e} = 0$ [3]. Рассмотрение было идеалистическим также и в том, что давление и ток плазмы считались постоянными по времени.
Теперь сценарии с $B_{ \bot }^{e} \ne B_{ \bot }^{{eq}}$ снова привлекают внимание, как представляющие нежелательные срывы с быстрыми изменениями параметров плазмы и, следовательно, величины $B_{ \bot }^{{eq}}$, в то время как созданное внешними токами поле $B_{ \bot }^{e}$ остается практически фиксированным. Прямые измерения показывают, что продолжительность CQ в токамаках ${{\tau }_{{cq}}}$ сопоставима с резистивными временами стенки ${{\tau }_{w}}$ [6, 7]. Это косвенно подтверждается экспериментальным наблюдением больших боковых [71, 79–83] или вертикальных [71, 79, 80, 83–85] сил на стенку в сочетании с теоретическим предсказанием, что такие силы должны исчезать в пределе идеальной стенки [13, 15], в то время как их максимумы должны ожидаться [16, 59, 86, 87] при эволюции с инкрементами γ вблизи $\gamma {{\tau }_{w}} = {\rm O}(1)$. Поэтому включение эффектов резистивной стенки в моделирование срывов становится необходимостью. Эта идея получает теперь растущую поддержку со стороны аналитических [87] и численных [15, 16, 59, 86] исследований.
Выведенные здесь уравнения позволят расширить развитую теорию равновесия плазмы на анализ естественных и/или намеренно вызванных срывов с электромагнитным взаимодействием плазма–стенка, зависящим от резистивной диссипации индуцированного тока. Этот шаг нужен, в частности, для улучшения качества предсказаний срывов для режимов, представляющих интерес для токамака ИТЭР [21].
Эта работа возникла в связи с недавними успешными применениями теории равновесия плазмы в задачах срывов. Автор глубоко признателен В.Д. Шафранову, который делился своими знаниями этой теории и оказывал всестороннюю поддержку в течение нескольких десятилетий, начиная с моих студенческих лет. Его руководство было твердым, но всегда добрым, анализ глубоким, советы полными и практичными. Идеи, методы и результаты В.Д. Шафранова по-прежнему остаются полезными и продуктивными даже далеко вне первоначально намеченной области применимости.
Автор также благодарен экспертам группы I-TPA по МГД-устойчивости плазмы за многочисленные полезные обсуждения, своим российским коллегам Ю.В. Грибову, Н.В. Иванову и С.В. Коновалову за постоянную поддержку.
Список литературы
Шафранов В.Д. // Атомная энергия. 1962. Т. 13. С. 521 [V. D. Shafranov, Journal of Nuclear Energy, Part C, 5 (1963), 251].
Шафранов В.Д. // Вопросы теории плазмы. Вып. 2 / Под ред. М.А. Леонтовича. М.: Госатомиздат, 1963. С. 92 [V.D. Shafranov, in Reviews of Plasma Physics, ed. by M.A. Leontovich (Consultants Bureau, New York, 1966), Vol. 2, p. 103].
Арцимович Л.А., Карташев К.Б. // Докл. АН СССР. 1962. Т. 146. С. 1305–1308 [L.A. Artsimovich and K.B. Kartashev, Soviet Phys. Doklady, 5, (1962)].
Mukhovatov V.S., Shafranov V.D. // Nucl. Fusion. 1971. V. 11. P. 605.
Захаров Л.Е., Шафранов В.Д. // Вопросы теории плазмы. Вып. 11 / Под ред. М.А. Леонтовича и Б.Б. Кадомцева. М.: Энергоиздат, 1982. С. 118 [L.E. Zakharov and V. D. Shafranov, Reviews of Plasma Physics, Vol. 11. Ed. by M.A. Leontovich and B.B. Kadomtsev. Consultants Bureau, New York, 1986].
Myers C.E., Eidietis N.W., Gerasimov S.N., Gerhardt S.P., Granetz R.S., Hender T.C., Pautasso G., JET Contributors. // Nucl. Fusion. 2018. V. 58. 016050.
Chu M.S., Okabayashi M. // Plasma Phys. Control. F-usion. 2010. V. 52. 123001.
Pustovitov V.D. // J. Plasma Phys. 2015. V. 81. 905810609.
Villone F., Ramogida G., Rubinacci G. // Fusion Eng. Des. 2015. V. 93. P. 57.
Li Xujing, Zakharov L.E., Galkin S.A. // Plasma Science and Technology. 2015. V. 17. P. 97.
Zakharov L.E., Li X. // Phys. Plasmas. 2015. V. 22. 062511.
Пустовитов В.Д. // Физика плазмы. 2015. Т. 41. С. 1029 [V. D. Pustovitov, Plasma Phys. Rep. 41, 952 (2015)].
Pustovitov V.D. // Nucl. Fusion. 2015. V. 55, 113032.
Khayrutdinov R.R., Lukash V.E., Pustovitov V.D. // Plasma Phys. Control. Fusion. 2016. V. 58. 115012.
Pustovitov V.D., Rubinacci G., Villone F. // Nucl. F-usion. 2017. V. 57. 126038.
Portone A. // Nucl. Fusion. 2019. V. 59. 024002.
Пустовитов В.Д. // Физика плазмы. 2016. Т. 42. С. 957 [V. D. Pustovitov, Plasma Phys. Rep. 42, 1005 (2016)].
Pustovitov V.D., Kiramov D.I. // Plasma Phys. Control. Fusion. 2018. V. 60. 045011.
ITER Physics Basis. Chap. 3: MHD stability, operational limits and disruptions // Nucl. Fusion. 1999. V. 39. P. 2251.
Riccardo V., Loarte A., JET EFDA contributors // Nucl. Fusion. 2005. V. 45. P. 1427.
Hender T.C., Wesley J.C., Bialek J., Bondeson A., Boo-zer A.H., Buttery R.J., Garofalo A., Goodman T.P., Granetz R.S., Gribov Y., Gruber O., Gryaznevich M., Giruzzi G., Guenter S., Hayashi N. et al. // Nucl. F-usion. 2007. V. 47. P. S128.
Freidberg J.P. Ideal MHD. New York: Plenum, 1987.
Миямото К. Основы физики плазмы и управляемого синтеза. М.: Физматлит, 2007 [K. Miyamoto, Fundamentals of Plasma Physics and Controlled Fusion. Revised edn. NIFS-PROC-48 (Toki, National Institute for Fusion Science, 2001)].
Pustovitov V.D. // Rev. Plasma Phys. V. 21 / Ed. by B.B. Kadomtsev and V.D. Shafranov. New York: Consultants Bureau, 2000. P. 1.
Wesson J. Tokamaks, 3rd ed. Oxford: Clarendon Press, 2004.
Goedbloed J.P., Keppens R., Poedts S. Advanced Magnetohydrodynamics; with Applications to Laboratory and Astrophysical Plasmas. Cambridge: Cambridge Univ. Press, 2010.
Pustovitov V.D. // Fusion Eng. Des. 2017. V. 117. P. 1.
Cohl H.S., Tohline J.E. // Astrophys. J. 1999. V. 527. P. 86.
Cohl H.S., Rau A.R.P., Tohline J.E., Browne D.S., Ca-zes J.E., Barnes E.I. // Phys. Rev. A. 2001. V. 64. 052509.
Selvaggi J.P., Salon S., Kwon O.-M., M. Chari V.K. // IEEE Trans. Magn. 2007. V. 43. P. 3833.
Selvaggi J., Salon S., M. Chari V.K. // J. Appl. Phys. 2008. V. 104. 033913.
Pustovitov V.D. // Phys. Plasmas. 2008. V. 15. 072501.
Stratton J.A. Electromagnetic Theory. New York: McGraw-Hill, 1941.
Wootton A.J. // Nucl. Fusion. 1979. V. 19. P. 987.
Swain D.W., Neilson G.H. // Nucl. Fusion. 1982. V. 22. P. 1015.
Lao L.L., St. John H., Stambaugh R.D., Kellman A.G., Pfeiffer W. // Nucl. Fusion. 1985. V. 25. P. 1611.
Кузнецов Ю.К., Пятов В.Н., Ясин И.В. // Физика плазмы. 1987. Т. 13. С. 139 [Yu.K. Kuznetsov, V.N. Pyatov and I.V. Yasin, Sov. J. Plasma Phys. 13 (1987) 75].
Lao L.L., Ferron J.R., Groebner R.J., Howl W., St. John H., Strait E.J., Taylor T.S. // Nucl. Fusion. 1990. V. 30. P. 1035.
Braams B.J. // Plasma Phys. Control. Fusion. 1991. V. 33. P. 715.
Friedberg J.P., Graf M., Niemszewski A., Schultz S., Shajii A. // Plasma Phys. Control. Fusion. 1993. V. 35. P. 1641.
Pustovitov V.D. // Nucl. Fusion. V. 41. P. 721 (2001).
Lao L.L., St. John H.E., Peng Q., Ferron J.R., Strait E.J., Taylor T.S., Meyer W.H., Zhang C., You K.I. // Fusion Sci. Technol. 2005. V. 48. P. 968.
Brix M., Hawkes N.C., Boboc A., Drozdov V., Shara-pov S.E., JET-EFDA Contributors // Rev. Sci. Instrum. 2008. V. 79. 10F325.
Demidov A.S., Savel’ev V.V. // Russian J. Mathematical Physics. 2010. V. 17. P. 56.
Zaitsev F.S., Kostomarov D.P., Suchkov E.P., Droz-dov V.V., Solano E.R., Murari A., Matejcik S., Haw-kes N.C., JET-EFDA Contributors // Nucl. Fusion. 2011. V. 51. 103044.
Fitzgerald M., Appel L.C., Hole M.J. // Nucl. Fusion. 2013. V. 53. 113040.
King J.D., Strait E.J., Lazerson S.A., Ferraro N.M., Logan N.C., Haskey S.R., Park J.-K., Hanson J.M., Lanctot M.J., Liu Yueqiang, Nazikian R., Okabayashi M., Paz-Soldan C., Shiraki D., Turnbull A.D. // Phys. Plasmas. 2015. V. 22. 072501.
Pustovitov V.D. // Nucl. Fusion. 1990. V. 30. P. 1523.
Pustovitov V.D. // Plasma Phys. Control. Fusion. 2008. V. 50. 105001.
Shafranov V.D., Zakharov L.E. // Nucl. Fusion. 1972. V. 12. P. 599.
Zakharov L.E. // Nucl. Fusion. 1973. V. 13. P. 595.
Strumberger E., Günter S., Merkel P., Schwarz E., Tichmann C., Zehrfeld H.-P. // Nucl. Fusion. 2002. V. 42. P. 827.
Hirshman S.P., Lazarus E.A., Hanson J.D., Knowlton S.F., Lao L.L. // Phys. Plasmas. 2004. V. 11. P. 595.
Lazerson S.A., Sakakibara S., Suzuki Y. // Plasma Phys. Control. Fusion. 2013. V. 55. 025014.
Li Xujing, Zakharov Leonid E., Drozdov Vladimir V. // Phys. Plasmas. 2014. V. 21. 012505.
Hanson J.D. // Plasma Phys. Control. Fusion. 2015. V. 57. 115006.
Sweeney R.M., Strait E.J. // Phys. Plasmas. 2019. V. 26. 012509.
Морозов А.И., Соловьев Л.С. // Вопросы теории плазмы. Вып. 2 / Под ред. М.А. Леонтовича. М.: Госатомиздат, 1963. С. 3 [A.I. Morozov, L.S. So-lov’ev, in: Reviews of Plasma Physics (edited by M.A. Leontovich), Consultants Bureau, New York (1966), Vol. 2, pp. 1–101].
Sovinec C.R., Bunkers K.J. // Plasma Phys. Control. Fusion. 2019. V. 61. 024003.
Reimerdes H., Hender T.C., Sababgh S.A., Bialek J.M., Chu M.S., Garofalo A.M., Gryaznevich M.P., Ho-well D.F., Jackson G.L., La Haye R.J., Liu Y.Q., Me-nard J.E., Navratil G.A., Okabayashi M., Pinches S.D., Sontag A.C., Strait E.J., Zhu W., Bigi M., de Baar M., de Vries P., Gates D.A., Gohil P., Groebner R.J., Mueller D., Raman R., Scoville J.T., Solomon W.M., the DIII-D Team, JET-EFDA Contributors and the NSTX Team // Phys. Plasmas. 2006. V. 13. 056107.
Dubrov M.L., Pustovitov V.D. // Plasma Phys. Control. Fusion. 2019. V. 61. 065018.
Yanovskiy V.V., Isernia N., Pustovitov V.D., Villone F., Abate D., Bettini P., Chen S.L., Havlicek J., Herrmann A., Hromadka J., Hron M., Imrisek M., Komm M., Paccagnella R., Panek R., Pautasso G., Peruzzo S., Sestak D., Teschke M., Zammuto I., the COMPASS team // Fusion Eng. Des. 2019. ???Будет известно позже. https://doi.org/10.1016/j.fusengdes.2019.03.185
Pustovitov V.D. // Phys. Plasmas. 2018. V. 25. 062510.
Пустовитов В.Д. // Физика плазмы. 1988. Т. 14. С. 1436 [V. D. Pustovitov, Sov. J. Plasma Phys. 14, 840 (1988)].
Pustovitov V.D. // J. Plasma Fusion Res. SERIES. 2004. V. 6. P. 550 (www.jspf.or.jp/JPFRS/PDF/Vol6/jpfrs2004_06-550.pdf)
Dialetis D., Len L.K., Golden J., Kapetanakos C.A. // J. Appl. Phys. 1991. V. 69. P. 1813.
Xu W., Liu X., Song Y., Li J., Lu M. // Fusion Eng. Des. 2013. V. 88. P. 1848.
Albanese R., Carpentieri B., Cavinato M., Minucci S., Palmaccio R., Portone A., Rubinacci G., Testoni P., Ventre S., Villone F. // Fusion Eng. Des. 2015. V. 94. P. 7.
Rozov V., Alekseev A. // Nucl. Fusion. 2015. V. 55. 083022.
Zhang Ming, Zhang Jun, Rao Bo, Li Xiaolong, Xu Wendi, Jian Xiang, Li Fuming, Chen Zhipeng, Yu Kexun, Pan Yuan // J. Fusion Energy. 2015. V. 34. P. 1411.
Gerasimov S.N., Abreu P., Baruzzo M., Drozdov V., Dvornova A., Havlicek J., Hender T.C., Hronova O., Kruezi U., Li X., Markovič T., Pánek R., Rubinacci G., Tsalas M., Ventre S., Villone F., Zakharov L.E., JET Contributors // Nucl. Fusion. 2015. V. 55. 113006.
Roccella R., Roccella M., Riccardo V., Chiocchio S., JET Contributors // Nucl. Fusion. 2016. V. 56. 106010.
Xu Weiwei, Liu Xufeng, Du Shuangsong, Song Yuntao // Fusion Eng. Des. 2017. V. 114. P. 131.
Ma Xuebin, Li Min, Liu Songlin // Fusion Eng. Des. 2018. V. 131. P. 21.
Chen S.L., Villone F., Sun Y.W., Xiao B.J. // Nucl. F-usion. 2018. V. 58. 076009.
Besshou S., Pustovitov V.D., Fujita N., Kondo K., Mizuuchi T., Nagasaki K., Nakasuga M., Obiki T., Okada H., Sano F., Zushi H. // Phys. Plasmas. 1998. V. 5. P. 481.
Sato Y., Yokoyama M., Wakatani M., Pustovitov V.D. // Nucl. Fusion. 2000. V. 40. 1627.
Artsimovich L.A. // Nucl. Fusion. 1972. V. 12. P. 215.
Noll P., Andrew P., Buzio M., Litunovski R., Raimondi T., Riccardo V., Verrecchia M., “Present understanding of electromagnetic behaviour during disruptions in JET,” in Proc. 19th Symposium on Fusion Technology, Lisbon / Ed. by C. Varandas and F. Serra Elsevier. Amsterdam, 1996. V. 1. P. 751, www.iop.org/Jet/fulltext/JETP96044.pdf p. 73.
Riccardo V., Walker S., Noll P. // Fusion Eng. Des. 2000. V. 47. P. 389.
Riccardo V., Walker S.P. // Plasma Phys. Control. Fusion. 2000. V. 42. P. 29.
Riccardo V., Andrew P.L., Kaye A.S., Noll P. // Fusion Sci. Technol. 2003. V. 43. P. 493.
Lehnen M., Arnoux G., Brezinsek S., Flanagan J., Gerasimov S.N., Hartmann N., Hender T.C., Huber A., Jachmich S., Kiptily V., Kruezi U., Matthews G.F., Morris J., Plyusnin V.V., Reux C., Riccardo V., Sieglin B., de Vries P.C., the JET EFDA Contributors // Nucl. Fusion. 2013. V. 53. 093007.
Riccardo V., Hender T.C., Lomas P.J., Alper B., Bolzonella T., de Vries P., Maddison G.P., the JET EFDA Contributors // Plasma Phys. Control. Fusion. 2004. V. 46. P. 925.
Pautasso G., Bernert M., Dibon M., Duval B., Dux R., Fable E., Fuchs J.C., Conway G.D., Giannone L., Gude A., Herrmann A., Hoelzl M., McCarthy P.J., Mlynek A., Maraschek M., Nardon E., Papp G., Potzel S., Rap-son C., Sieglin B., Suttrop W., Treutterer W., the ASDEX Upgrade Team and the EUROfusion MST1 Team // Plasma Phys. Control. Fusion. 2017. V. 59. 014046.
Strauss H.R., Paccagnella R., Breslau J. // Phys. Plasmas. 2010. V. 17. 082505.
Mironov D.V., Pustovitov V.D. // Phys. Plasmas. 2017. V. 24. 092508.
Дополнительные материалы отсутствуют.


