1. На главную
  2. Электронные версии
  3. Физика плазмы
  4. T. 45, № 12, 2019

Физика плазмы, 2019, T. 45, № 12, стр. 1065-1071

Уравнения равновесия плазмы в магнитном поле с трехмерными магнитными поверхностями

Е. А. Сорокина a, c, *, В. И. Ильгисонис b, c

a НИЦ “Курчатовский институт”
Москва, Россия

b Государственная корпорация по атомной энергии “Росатом”
Москва, Россия

c Российский университет дружбы народов
Москва, Россия

* E-mail: sorokina.ekaterina@gmail.com

Поступила в редакцию 23.05.2019
После доработки 21.06.2019
Принята к публикации 25.06.2019

Полный текст (PDF)

Аннотация

Получена система уравнений, описывающая статическое равновесие плазмы в магнитном поле с трехмерными магнитными поверхностями тороидальной топологии. В основу подхода положено смешанное представление для магнитного поля, аналогичное используемому при выводе классического уравнения Грэда–Шафранова, но модифицированное с учетом возможной осевой несимметрии магнитных поверхностей. Система состоит из трех дифференциальных уравнений на три скалярные функции, два из которых могут быть записаны в форме магнитных дифференциальных уравнений, а третье (баланс сил в направлении, перпендикулярном к поверхности) служит аналогом уравнения Грэда–Шафранова. Полученные уравнения допускают простой предельный переход к случаю осевой симметрии. Представлен пример решения типа вихря Хилла в предположении о “слабой” осевой несимметрии задачи. Статья посвящена памяти замечательного физика – Виталия Дмитриевича Шафранова, умевшего мыслить просто и очень точно.

1. ВВЕДЕНИЕ

Задача нахождения равновесных конфигураций плазмы в магнитном поле относится к числу первоочередных в иерархии проблем физики плазмы и ее приложений. Статическое равновесие плазмы в магнитном поле описывается уравнениями

(1)
$\nabla p = \frac{1}{{4\pi }}[\operatorname{rot} {\mathbf{B}} \times {\mathbf{B}}],$
(2)
${\text{div}}{\mathbf{B}} = 0,$
первое из которых характеризует баланс сил давления p и силы Ампера, а второе – соленоидальность магнитного поля B.

Область применимости уравнений (1), (2), имеющих характерный “магнитогидродинамический” вид, как известно, значительно шире рамок идеальной магнитной гидродинамики (МГД); подробную аргументацию этого см. в [1].

Векторное уравнение (1) эквивалентно трем скалярным, два из которых сводятся к условиям постоянства давления вдоль линий тока и магнитных силовых линий $(\operatorname{rot} {\mathbf{B}} \cdot \nabla p) = 0$, $({\mathbf{B}} \cdot \nabla p) = 0$. Применительно к задаче лабораторного удержания высокотемпературной плазмы особое значение имеют конфигурации со вложенными магнитными поверхностями, позволяющие (до какой-то степени) реализовать исходную идею Тамма и Сахарова о магнитной термоизоляции. В таких конфигурациях, совместив граничную магнитную поверхность со стенкой камеры, мы можем избежать баллистического выноса энергии частицами плазмы, свободно движущимися вдоль силовых линий магнитного поля, из основного объема плазмы на эту стенку, тогда как процессы тепло- и массопереноса поперек силовых линий магнитного поля значительно более медленные. И хотя характер этих процессов может отличаться от классических теплопроводности и диффузии, т.е. быть связанным с уровнем турбулентности плазмы в большей степени, чем со столкновениями частиц, все равно рассматривать эти различия имеет смысл, лишь обеспечив глобальный баланс сил, т.е. равновесие плазмы. Другими словами, иерархия процессов, определяющих в итоге характерное время удержания плазмы, такова: равновесие–устойчивость–процессы переноса. Именно поэтому велика заслуга В.Д. Шафранова, одним из первых построивших адекватную теорию равновесия плазмы для практических систем управляемого термоядерного синтеза.

Наиболее известными примерами таких систем, магнитные конфигурации которых представляют собой наборы вложенных поверхностей, являются установки типа “токамак” и “стелларатор”. Топологически магнитные поверхности в этих системах представляют собой замкнутые торы, хотя непосредственно (осесимметричными) торами можно назвать лишь поверхности токамака и то приближенно – из-за дискретности магнитных катушек тороидального поля.

Именно для осесимметричных систем со вложенными магнитными поверхностями $\Psi ({\mathbf{r}})$ = = const: $({\mathbf{B}} \cdot \nabla \Psi ) = 0$, где r – радиус-вектор, теория равновесия выглядит особенно изящно. Основным инструментом расчета осесимметричных равновесных магнитных конфигураций служит великое уравнение Грэда–Шафранова (УГШ), полученное В.Д. Шафрановым в 1957 г. [2] и независимо от него, но почти на год позже, Грэдом [3].

Находка В.Д. Шафранова, позволившая получить УГШ, состояла в использовании смешанного представления для магнитного поля

(3)
${\mathbf{B}} = [\nabla \Psi \times \nabla \varphi ] + F\nabla \varphi .$

Здесь функция $\Psi = \Psi (r,z)$, служащая меткой магнитной поверхности, обозначает полоидальный поток магнитного поля, $F = F(r,z)$ характеризует полоидальный ток внутри тороидальной поверхности с данным значением Ψ, а φ – тороидальный угол цилиндрической системы координат ${\mathbf{r}} = \{ r,\varphi ,z\} $, связанной с геометрическим центром тора. Представление (3) может быть получено из общего представления магнитного поля ${\mathbf{B}} = [\nabla \Psi \times \nabla {{\alpha }^{3}}] + $ $[\nabla \Phi \times \nabla {{\alpha }^{2}}]$ (Φ – тороидальный поток магнитного поля, ${{\alpha }^{2}}$, ${{\alpha }^{3}}$ – полоидальная и тороидальная угловые координаты соответственно) [4, 5] путем простого перехода от контравариантной записи второго слагаемого к ковариантной, однако условию соленоидальности оно удовлетворят только в рассматриваемом случае осевой симметрии системы. Представление (3) называется “смешанным”, поскольку оно содержит как ко-, так и контравариантную запись входящих компонент.

В случае осевой симметрии преимущества задания магнитного поля в форме (3) очевидны, поскольку она позволяет удовлетворить двум налагаемым на магнитное поле условиям автоматически: ${\text{div}}{\mathbf{B}} \equiv 0$ и $({\mathbf{B}} \cdot \nabla \Psi ) \equiv 0$. При этом три компоненты магнитного поля определяются двумя скалярными функциями $\Psi = \Psi (r,z)$ и $F = F(r,z)$. Искомые магнитные поверхности – это поверхности уровня функции Ψ: $\Psi (r,z) = {\text{const}}$. Последующая подстановка (3) в уравнение баланса сил (1) и его проецирование на тройку некомпланарных векторов $[\nabla \Psi \times \nabla \varphi ]$, $\nabla \varphi $, $\nabla \Psi $ приводят к заключению о том, что F и p – “поверхностные” функции, $p(r,z) = p(\Psi )$, $F(r,z) = F(\Psi )$, и к собственно УГШ как уравнению на Ψ:

(4)
$\Delta {\text{*}}\Psi + 4\pi {{r}^{2}}\frac{{dp(\Psi )}}{{d\Psi }} + F(\Psi )\frac{{dF(\Psi )}}{{d\Psi }} = 0,$
где

${{\Delta }^{*}} = {{r}^{2}}{\text{div}}\left( {\frac{\nabla }{{{{r}^{2}}}}} \right)$

– оператор Грэда–Шафранова, имеющий в случае осевой симметрии $\partial {\text{/}}\partial \varphi = 0$ вид

${{\Delta }^{*}} = \Delta _{0}^{*} \equiv r\frac{\partial }{{\partial r}}\left( {\frac{1}{r}\frac{\partial }{{\partial r}}} \right) + \frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}}.$

Уравнение второго порядка в частных производных (4) на функцию Ψ определяет магнитные поверхности в произвольной осесимметричной плазменной системе, находящейся в статическом равновесии в магнитном поле, формируемом как внешними токами, так и токами, текущими по самой плазме. Несмотря на кажущуюся простоту, уравнение (4) весьма нетривиально. Во-первых, оно нелинейное и допускает возможность бифуркаций равновесий [6–10], во-вторых, это уравнение эллиптического типа, и, значит, оно в большинстве разумных ситуаций имеет решение.

Уравнение (4) обычно решают относительно Ψ при заданных зависимостях $F(\Psi )$ и $p(\Psi )$, считая одну из поверхностей $\Psi = {\text{const}}$ граничной, т.е. поверхностью нулевого давления. Альтернативным способом расчета равновесия с использованием УГШ является задание потока Ψ на фиксированной граничной магнитной поверхности заданной формы. Разумеется, при этом гарантий вложенности системы магнитных поверхностей во всем объеме внутри граничной поверхности не существует.

Подход, придуманный В.Д. Шафрановым, с представлением магнитного поля в виде (3) оказался весьма и весьма плодотворным. Его можно использовать и для более сложных уравнений, включающих динамические величины, фактически, сводя сложные трехмерные векторные уравнения равновесия к единственному двумерному дифференциальному уравнению на скалярную функцию Ψ. Известны аналоги УГШ для описания динамического равновесия [8, 11–14], анизотропного равновесия [1, 15], в том числе с течениями [16–18], релятивистские УГШ [19, 20], УГШ для холловской и многокомпонентной МГД [21–23] и др. Широкий спектр различных астрофизических обобщений уравнения Грэда–Шафранова можно найти в обзоре [24].

Ключевым предположением при выводе УГШ помимо предположения о существовании магнитных поверхностей является условие осевой симметрии равновесия, которое существенно ограничивает класс рассматриваемых задач. Попытки формулировки трехмерных уравнений равновесия предпринимались неоднократно – см., например, [1, 25] – однако простой аналог классического осесимметричного УГШ, сохраняющий логику построения решений и допускающий прямой предельный переход к (4) при осевой симметрии, получен только для случая винтовой симметрии системы, фактически эквивалентного осесимметричному случаю при переобозначении угловых координат. В [26, 27] предложен вариант обобщения УГШ для описания несимметричных МГД-конфигураций, основанный на смешанном представлении магнитного поля с использованием так называемых “опорных” векторов вместо $\nabla \varphi $ в (3). Такой подход позволяет в рамках некоторых дополнительных предположений записать уравнение равновесия в относительно простой форме, перенеся всю трудность дальнейшего анализа на нахождение самих опорных векторов, не заданных заранее и в свою очередь зависящих от $\Psi ({\mathbf{r}})$. При этом полученные уравнения не являются необходимым условием равновесия.

В настоящей работе, следуя подходу В.Д. Шафранова со смешанным представлением для магнитного поля с заданным базисом, мы выводим уравнения трехмерного равновесия плазмы в магнитном поле с тороидальными магнитными поверхностями $\Psi (r,\varphi ,z)$: $({\mathbf{B}} \cdot \nabla \Psi ) = 0$. В трехмерном случае условие соленоидальности уже не удовлетворяется автоматически, и для его обеспечения в выражение для магнитного поля необходимо вводить дополнительную свободную функцию, калибрующую полоидальный поток. Оставшиеся уравнения, тем не менее, не теряют своей наглядности и демонстрируют простой предельный переход к осесимметричному случаю. Уравнение для F имеет вид магнитного дифференциального уравнения и характеризует неоднородность функции $r{{B}_{\varphi }}$ на трехмерной магнитной поверхности, а уравнение на Ψ служит аналогом УГШ в неосесимметричном случае. Полученная форма записи трехмерных уравнений равновесия представляется наиболее удобной, во-первых, потому, что она сохраняет логику классического УГШ, а во-вторых, позволяет находить решения для трехмерных магнитных поверхностей в виде функций обычных цилиндрических координат без привлечения аппарата криволинейных координат и техники выпрямления магнитных силовых линий. Пример такого решения представлен в статье для случая “слабой” осевой несимметрии магнитных поверхностей.

Работа построена следующим образом. В разд. 2 представлен вывод уравнений равновесия плазмы в системах с магнитными поверхностями общего положения, т.е. без предположения об осевой симметрии. В разд. 3 полученные уравнения упрощены для случая слабой неосесимметричности системы. В четвертом разделе построен простой пример решения упрощенных уравнений, демонстрирующий их разрешимость. Основные выводы статьи суммированы в Заключении.

2. ОСНОВНЫЕ УРАВНЕНИЯ

Согласно логике УГШ, для сведения задачи о равновесии плазмы в магнитном поле к скалярному уравнению, определяющему форму магнитных поверхностей в равновесной плазменной конфигурации, следует задать вид B через функцию поверхности Ψ. Условие замыкания токов выполняется автоматически в силу выражения ${\mathbf{j}} = c\operatorname{rot} {\mathbf{B}}{\text{/}}(4\pi )$ (j – плотность тока, c – скорость света).

Будем подразумевать, что силовые линии магнитного поля лежат на трехмерных магнитных поверхностях: $({\mathbf{B}} \cdot \nabla \Psi (r,\varphi ,z)) = 0$. При этом, как и в осесимметричном случае, проекция уравнения баланса сил (1) на направление магнитного поля дает постоянство давления p на магнитной поверхности, $p = p(\Psi )$.

Очевидно, что смешанное представление (3) не годится для описания трехмерной магнитной поверхности с $\partial \Psi {\text{/}}\partial \varphi \ne 0$. Модифицируем (3), добавляя слагаемое с произвольным множителем $\nu $ вдоль градиента Ψ,

(5)
${\mathbf{B}} = \gamma [\nabla \Psi \times \nabla \varphi ] + F\nabla \varphi + \nu \nabla \Psi .$

Мы также ввели свободный коэффициент γ перед векторным произведением $[\nabla \Psi \times \nabla \varphi ]$. Таким образом, представление (5) дает разложение вектора ${\mathbf{B}}$ по трем различным направлениям: $[\nabla \Psi \times \nabla \varphi ]$, $\nabla \varphi $, $\nabla \Psi $ – и, значит, выбранная запись описывает поле произвольной топологии и не ограничивает общности рассмотрения.

Далее используем условие существования магнитной поверхности Ψ. Из $({\mathbf{B}} \cdot \nabla \Psi ) = 0$ следует выражение для функции $\nu $

$\begin{gathered} \nu = - \alpha F,\quad {\text{где}}\quad \alpha = \tfrac{1}{{{{{\left| {\nabla \Psi } \right|}}^{2}}}}\tfrac{1}{{{{r}^{2}}}}\tfrac{{\partial \Psi }}{{\partial \varphi }}, \\ {{\left| {\nabla \Psi } \right|}^{2}} = \mathop {\left( {\tfrac{{\partial \Psi }}{{\partial r}}} \right)}\nolimits^2 + \mathop {\left( {\tfrac{{\partial \Psi }}{{\partial z}}} \right)}\nolimits^2 + \tfrac{1}{{{{r}^{2}}}}\mathop {\left( {\tfrac{{\partial \Psi }}{{\partial \varphi }}} \right)}\nolimits^2 . \\ \end{gathered} $

Таким образом, коэффициент при $\nabla \Psi $ в (5) пропорционален $\partial \Psi {\text{/}}\partial \varphi $ и в осесимметричном случае это слагаемое пропадает.

Итоговое выражение для магнитного поля

${\mathbf{B}} = \gamma [\nabla \Psi \times \nabla \varphi ] + F\nabla \varphi - \frac{F}{{{{{\left| {\nabla \Psi } \right|}}^{2}}}}\frac{1}{{{{r}^{2}}}}\frac{{\partial \Psi }}{{\partial \varphi }}\nabla \Psi $
содержит три свободные функции γ, F, Ψ, что на одну больше, чем в осесимметричном случае; при этом условие $({\mathbf{B}} \cdot \nabla \Psi ) = 0$ выполняется тождественно.

Функции γ, F, Ψ определяются тремя уравнениями: условием соленоидальности ${\text{div}}{\mathbf{B}} = 0$; условием того, что линии тока лежат на магнитных поверхностях, $(\operatorname{rot} {\mathbf{B}} \cdot \nabla \Psi ) = 0$; и проекцией уравнения баланса сил (1) на $\nabla \Psi $. Итоговую систему уравнений удобно переписать, используя функцию ${{F}^{ \star }} = F\left( {1 - \alpha \partial \Psi {\text{/}}\partial \varphi } \right)$, характеризующую тороидальную компоненту магнитного поля ${{B}_{\varphi }} = {{F}^{ \star }}{\text{/}}r$ и совпадающую с функцией полоидального тока в осесимметричном случае, а также вводя “осесимметричные” операторы $\Delta _{0}^{*}$, ${{\nabla }_{0}} = \nabla - \nabla \varphi (\partial {\text{/}}\partial \varphi )$ и квадрат напряженности магнитного поля ${{B}^{2}} = $ $ = ({{\gamma }^{2}}{{\left| {{{\nabla }_{0}}\Psi } \right|}^{2}} + F{{F}^{ \star }}){\text{/}}{{r}^{2}}$. Окончательно имеем

(6)
${\mathbf{B}} \cdot \nabla \frac{{\gamma {{{\left| {\nabla \Psi } \right|}}^{2}}}}{F} = [\nabla \Psi \times \nabla \varphi ] \cdot \nabla \left( {F + \frac{{{{\gamma }^{2}}{{{\left| {\nabla \Psi } \right|}}^{2}}}}{F}} \right),$
(7)
${\mathbf{B}} \cdot \nabla {{F}^{ \star }} = \frac{1}{2}\nabla \varphi \cdot \nabla \left( {8\pi p{{r}^{2}} + {{B}^{2}}{{r}^{2}}} \right),$
(8)
$\begin{gathered} {{\gamma }^{2}}\Delta _{0}^{*}\Psi + \gamma ({{\nabla }_{0}}\Psi \cdot \nabla \gamma ) + 4\pi {{r}^{2}}\frac{{dp}}{{d\Psi }} + \\ \, + \frac{F}{{{{{\left| {\nabla \Psi } \right|}}^{2}}}}({{\nabla }_{0}}\Psi \cdot \nabla F) + \frac{1}{{\alpha {{{\left| {\nabla \Psi } \right|}}^{2}}}} \times \\ \, \times \left( {{\mathbf{B}} \cdot \nabla \left( {F\alpha \frac{{\partial \Psi }}{{\partial \varphi }}} \right) - \frac{{{{F}^{2}}}}{2}\nabla \varphi \cdot \nabla \left( {\alpha \frac{{\partial \Psi }}{{\partial \varphi }}} \right)} \right) = 0. \\ \end{gathered} $

Мы пришли к системе из трех дифференциальных уравнений на три свободные функции γ, F (или ${{F}^{ \star }}$) и Ψ. Уравнения (6), (7) имеют вид магнитных дифференциальных уравнений (МДУ), т.е. уравнений типа $({\mathbf{B}} \cdot \nabla f) = s$, играющих важную роль в теории равновесия плазмы в магнитном поле [28–30]. Однако в отличие от традиционно рассматриваемых МДУ, источник s в правой части которых считается заданной функцией, правые части уравнений (6), (7) содержат неизвестные функции Ψ, F, γ, которые предстоит определить.

Из уравнения (7) в отсутствие осевой симметрии полного давления плазмы немедленно следует неоднородность функции ${{F}^{ \star }} = r{{B}_{\varphi }}$ на трехмерной магнитной поверхности: ${{F}^{ \star }} \ne {{F}^{ \star }}(\Psi )$. В вырожденном случае $F = 0$ (чисто полоидальное магнитное поле) вместо уравнения (6) из условия ${\text{div}}{\mathbf{B}} = 0$ имеем $\gamma = \gamma (\Psi ,\varphi )$, а из уравнения (7) следует осевая симметрия полного давления плазмы $\partial (p + {{B}^{2}}{\text{/}}8\pi ){\text{/}}\partial \varphi = 0$.

Для осесимметричной магнитной поверхности $\partial \Psi {\text{/}}\partial \varphi = 0$ уравнения (6)–(8) переходят в систему

$\begin{gathered} \nabla \gamma \cdot [\nabla \Psi \times \nabla \varphi ] + (\nabla F \cdot \nabla \varphi ) = 0, \\ \nabla F \cdot [\nabla \Psi \times \nabla \varphi ] - {{\left| {\nabla \Psi } \right|}^{2}}(\nabla \gamma \cdot \nabla \varphi ) = 0, \\ {{\gamma }^{2}}{{\Delta }^{*}}\Psi + \gamma (\nabla \gamma \cdot \nabla \Psi ) + 4\pi {{r}^{2}}\frac{{dp}}{{d\Psi }} + \\ \, + \frac{F}{{{{{\left| {\nabla \Psi } \right|}}^{2}}}}\left( {\nabla F \cdot \nabla \Psi } \right) = 0, \\ \end{gathered} $
которая сводится к УГШ при $F = F(\Psi )$, $\gamma = \gamma (\Psi )$.

3. СЛУЧАЙ СЛАБОЙ ОСЕВОЙ НЕСИММЕТРИИ

Упростим полученную систему (6)–(8) для случая слабой осевой несимметрии, когда искомая магнитная поверхность $\Psi (r,\varphi ,z)$ может быть представлена в виде комбинации осесимметричной составляющей и малой периодической по φ добавки:

$\Psi (r,\varphi ,z) = {{\Psi }_{0}}(r,z) + \varepsilon {{\Psi }_{1}}(r,\varphi ,z),\quad \varepsilon \ll 1.$

Подобная ситуация типична, например, для токамаков со слабой тороидальной гофрировкой магнитного поля, а также для ряда астрофизических объектов.

Выберем F и γ в виде

$\begin{gathered} F(r,\varphi ,z) = {{F}_{0}}(r,z) + \varepsilon {{F}_{1}}(r,\varphi ,z), \\ \gamma (r,\varphi ,z) = 1 + \varepsilon {{\gamma }_{1}}(r,\varphi ,z). \\ \end{gathered} $

В выбранном приближении ${{F}^{ \star }} \approx F$.

Подстановка выражений для F, γ, Ψ в уравнение (8) в нулевом порядке по $\varepsilon $ приводит к классическому УГШ для функции ${{\Psi }_{0}}$:

(9)
${{\Delta }^{*}}{{\Psi }_{0}} + 4\pi {{r}^{2}}\mathop {\left( {\frac{{dp}}{{d\Psi }}} \right)}\nolimits_0 + {{F}_{0}}\frac{{d{{F}_{0}}}}{{d{{\Psi }_{0}}}} = 0.$

Здесь и далее нижний индекс у $(dp{\text{/}}d\Psi )$ также означает порядок по ε. Уравнение (6) в нулевом порядке удовлетворятся тождественно, а из уравнения (7) следует, что ${{F}_{0}} = {{F}_{0}}({{\Psi }_{0}})$.

В первом порядке по $\varepsilon $ уравнения (6)–(8) можно переписать в виде

(10)
$\begin{gathered} \nabla {{\gamma }_{1}} \cdot [\nabla {{\Psi }_{0}} \times \nabla \varphi ] + (\nabla {{F}_{1}} \cdot \nabla \varphi ) - \\ \, - \frac{{{{F}_{0}}}}{{{{r}^{2}}{{{\left| {\nabla {{\Psi }_{0}}} \right|}}^{2}}}}\left( {\nabla {{\Psi }_{0}} \cdot \nabla \frac{{\partial {{\Psi }_{1}}}}{{\partial \varphi }}} \right) + \frac{1}{{{{r}^{2}}}}\frac{{\partial {{\Psi }_{1}}}}{{\partial \varphi }} \times \\ \, \times \left( {\frac{{{{F}_{0}}}}{{{{{\left| {\nabla {{\Psi }_{0}}} \right|}}^{4}}}}\left( {\nabla {{\Psi }_{0}} \cdot \nabla {{{\left| {\nabla {{\Psi }_{0}}} \right|}}^{2}}} \right)} \right. - \\ \,\left. { - \frac{{{{F}_{0}}}}{{{{{\left| {\nabla {{\Psi }_{0}}} \right|}}^{2}}}}{{\Delta }^{*}}{{\Psi }_{0}} - \frac{{d{{F}_{0}}}}{{d{{\Psi }_{0}}}}} \right) = 0, \\ \end{gathered} $
(11)
$\begin{gathered} \nabla {{F}_{1}} \cdot [\nabla {{\Psi }_{0}} \times \nabla \varphi ] - {{\left| {\nabla {{\Psi }_{0}}} \right|}^{2}}(\nabla {{\gamma }_{1}} \cdot \nabla \varphi ) - \\ - \;\frac{1}{{{{r}^{2}}}}\left( {\nabla {{\Psi }_{0}} \cdot \nabla \frac{{\partial {{\Psi }_{1}}}}{{\partial \varphi }}} \right) - \frac{{d{{F}_{0}}}}{{d{{\Psi }_{0}}}}\nabla {{\Psi }_{1}} \cdot [\nabla {{\Psi }_{0}} \times \nabla \varphi ] + \\ + \;\frac{1}{{{{r}^{2}}}}\frac{{\partial {{\Psi }_{1}}}}{{\partial \varphi }}{{\Delta }^{*}}{{\Psi }_{0}} = 0, \\ \end{gathered} $
(12)
$\begin{gathered} \Delta _{0}^{*}{{\Psi }_{1}} + 2{{\gamma }_{1}}{{\Delta }^{*}}{{\Psi }_{0}} + (\nabla {{\Psi }_{0}} \cdot \nabla {{\gamma }_{1}}) + \\ \; + 4\pi {{r}^{2}}\mathop {\left( {\frac{{dp}}{{d\Psi }}} \right)}\nolimits_1 + \frac{1}{{{{r}^{2}}}}\frac{{F_{0}^{2}}}{{{{{\left| {\nabla {{\Psi }_{0}}} \right|}}^{2}}}}\frac{{{{\partial }^{2}}{{\Psi }_{1}}}}{{\partial {{\varphi }^{2}}}} + \\ \; + \frac{{d{{F}_{0}}}}{{d{{\Psi }_{0}}}}\left( {{{F}_{1}} - \frac{{{{F}_{0}}}}{{{{{\left| {\nabla {{\Psi }_{0}}} \right|}}^{2}}}}(\nabla {{\Psi }_{0}} \cdot \nabla {{\Psi }_{1}})} \right) + \\ \; + \frac{{{{F}_{0}}}}{{{{{\left| {\nabla {{\Psi }_{0}}} \right|}}^{2}}}}\left( {(\nabla {{\Psi }_{0}} \cdot \nabla {{F}_{1}}) + 2\nabla \frac{{\partial {{\Psi }_{1}}}}{{\partial \varphi }} \cdot [\nabla {{\Psi }_{0}} \times \nabla \varphi ]} \right) + \\ \; + {{r}^{2}}{{F}_{0}}\frac{{\partial {{\Psi }_{1}}}}{{\partial \varphi }}\nabla \frac{1}{{{{r}^{2}}{{{\left| {\nabla {{\Psi }_{0}}} \right|}}^{2}}}} \cdot [\nabla {{\Psi }_{0}} \times \nabla \varphi ] = 0. \\ \end{gathered} $

Дальнейшая методика решения уравнений равновесия в случае слабой осевой несимметрии состоит в выборе “нулевого” (базового) решения для ${{\Psi }_{0}}$, удовлетворяющего (9), т.е. любого известного решения классического осесимметричного УГШ, и последующего расчета тороидальных гармоник функций ${{\gamma }_{1}}$, ${{F}_{1}}$, ${{\Psi }_{1}}$ из уравнений (10)–(12). В следующем разделе в качестве примера такая процедура проделана для конфигурации, аналогичной рассмотренной в [31] для осесимметричного случая.

4. ПРИМЕР РЕШЕНИЯ ТИПА ВИХРЯ ХИЛЛА

Рассмотрим в качестве базовой конфигурации решение осесимметричного УГШ (9) с ${{F}_{0}} = 0$, $dp{\text{/}}d\Psi = {\text{const}} = - A{\text{/}}(4\pi )$. Уравнение ${{\Delta }^{*}}{{\Psi }_{0}} = A{{r}^{2}}$ имеет решение

(13)
${{\Psi }_{0}} = {{\Psi }_{a}}\frac{{{{r}^{2}}}}{{{{R}^{4}}}}(2{{R}^{2}} - {{r}^{2}} - 4{{k}^{2}}{{z}^{2}}),$
описывающее при ${{\Psi }_{0}}{\text{/}}{{\Psi }_{a}} > 0$ ограниченные тороидальные конфигурации [31]: $p = 2{{\Psi }_{a}}(1 + $ $ + \;{{k}^{2}})\Psi {\text{/}}(\pi {{R}^{4}}) + {\text{const}}$.

Положив ${{F}_{0}} = 0$, будем искать решение системы (10)–(12) в виде ${{\Psi }_{1}} = {{\Psi }_{c}}(r,z)cos\varphi $, ${{F}_{1}} = $ $ = {{F}_{s}}(r,z)sin\varphi $, ${{\gamma }_{1}} = {{\gamma }_{c}}(r,z)cos\varphi $. Подстановка гармоник искомых функций в (10)–(12) приводит к двумерным – зависящим только от r и z – уравнениям:

(14)
${{r}^{2}}\nabla {{\gamma }_{c}} \cdot [\nabla {{\Psi }_{0}} \times \nabla \varphi ] + {{F}_{s}} = 0,$
$\begin{gathered} {{r}^{2}}\nabla {{F}_{s}} \cdot [\nabla {{\Psi }_{0}} \times \nabla \varphi ]\; + \;{\text{|}}\nabla {{\Psi }_{0}}{{{\text{|}}}^{2}}{{\gamma }_{c}} + \\ + \;\left( {\nabla {{\Psi }_{0}} \cdot \nabla {{\Psi }_{c}}} \right) - A{{r}^{2}}{{\Psi }_{c}} = 0, \\ \end{gathered} $
(16)
$\Delta _{0}^{*}{{\Psi }_{c}} + 2A{{r}^{2}}{{\gamma }_{c}} + (\nabla {{\gamma }_{c}} \cdot \nabla {{\Psi }_{0}}) = 0.$

При ${{F}_{s}} \ne 0$ уравнение (14) можно считать уравнением на ${{F}_{s}}$. Оставшиеся два уравнения – (15) для ${{\gamma }_{c}}$ и (16) для ${{\Psi }_{c}}$ – составляют систему зацепленных уравнений в частных производных второго порядка, причем уравнение (15) является уравнением параболического типа11, а (16), как и УГШ – эллиптического. Примером ее частного решения могут служить

${{F}_{s}} = - \frac{R}{r}\frac{{\partial {{\Psi }_{0}}}}{{\partial z}},\quad {{\gamma }_{c}} = \frac{R}{r},\quad {{\Psi }_{c}} = - R\frac{{\partial {{\Psi }_{0}}}}{{\partial r}}.$

Тогда выражение для магнитной поверхности имеет вид

(17)
$\begin{gathered} \Psi = \frac{{{{\Psi }_{a}}}}{{{{R}^{4}}}}\left( {2{{R}^{2}}{{r}^{2}} - {{r}^{4}} - 4{{k}^{2}}{{r}^{2}}{{z}^{2}}} \right. - \\ \left. { - \;4\varepsilon Rcos\varphi ({{R}^{2}}r - {{r}^{3}} - 2{{k}^{2}}{{z}^{2}}r)} \right). \\ \end{gathered} $

Отметим, что полученное приближенное решение дает “невязку” в уравнениях ${\text{div}}{\mathbf{B}} = 0$, $(\operatorname{rot} {\mathbf{B}} \cdot \nabla \Psi ) = 0$ и в проекции уравнения баланса сил на $\nabla \Psi $ порядка ${{\varepsilon }^{2}}$; при этом условие $({\mathbf{B}} \cdot \nabla \Psi ) = 0$ и продольный баланс сил выполняются точно.

Тороидальные сечения линий уровня функции (17) и трехмерный вид одной выделенной замкнутой магнитной поверхности представлены на рис. 1, 2 соответственно. Полученный пример решения уравнений (9)–(12) служит простейшим обобщением осесимметричного вихря Хилла, рассмотренного Шафрановым в [2]22.

Рис. 1.

Линии уровня функции Ψ (17) при ${{k}^{2}} = 1$, $\varepsilon = $ = 0.3 в тороидальных сечениях $\varphi = 0{\kern 1pt} --{\kern 1pt} \pi $ и $\varphi = $ $ = \pi {\text{/}}2{\kern 1pt} --{\kern 1pt} 3\pi {\text{/}}2$. Черным цветом показаны линии уровня $\Psi = 0$, пунктиром – линии уровня магнитной поверхности $\Psi = 0.2{{\Psi }_{a}}$, представленной на рис. 2.

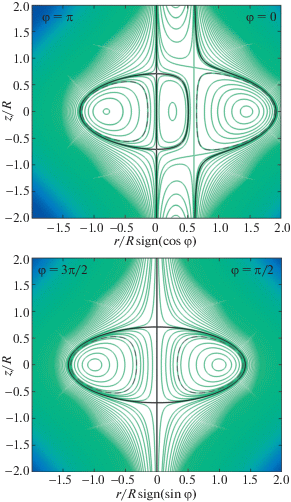
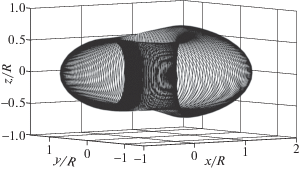
Рис. 2.

Магнитная поверхность $\Psi = 0.2{{\Psi }_{a}}$, описываемая выражением (17) при ${{k}^{2}} = 1$, $\varepsilon = 0,3$; $x = rcos\varphi $, $y = rsin\varphi $. Тороидальные сечения данной магнитной поверхности показаны на рис. 1 пунктирными линиями.

5. ЗАКЛЮЧЕНИЕ

Следуя подходу В.Д. Шафранова и используя смешанное представление для магнитного поля, мы получили уравнения (6)–(8), описывающие равновесную плазменную конфигурацию с трехмерными тороидальными магнитными поверхностями $\Psi = \Psi (r,\varphi ,z)$. Магнитное поле задается тремя взаимосвязанными функциями: функцией γ, калибрующей полоидальный поток, функцией ${{F}^{ \star }}$, задающей тороидальное магнитное поле, и меткой магнитной поверхности Ψ. В пределе осевой симметрии из уравнений на γ и ${{F}^{ \star }}$ следует, что $\gamma = \gamma (\Psi )$, $F = F(\Psi )$, а уравнение (8) переходит в УГШ. Таким образом, (8) следует рассматривать как аналог УГШ для неосесимметричной магнитной поверхности.

Отметим, что два из полученных уравнений – уравнения на γ и ${{F}^{ \star }}$ (6), (7) – записываются в форме МДУ. Последнее демонстрирует жесткую связь между вариацией функции ${{F}^{ \star }} = r{{B}_{\varphi }}$ на магнитной поверхности и тороидальной асимметрией полного давления плазмы в магнитном поле: ${\mathbf{B}} \cdot \nabla {{F}^{ \star }} = 4\pi \partial (p + {{B}^{2}}{\text{/8}}\pi ){\text{/}}\partial \varphi $. Отсюда, в частности, следует, что в трехмерном случае F не является функцией магнитной поверхности в отличие вырожденного случая осевой симметрии.

Работа частично поддержана грантом Российского фонда фундаментальных исследований № 18-29-21041.

Список литературы

  1. Шафранов В.Д., Захаров Л.Е. // Вопросы теории плазмы. Вып. 11 / Под общей ред. акад. М.А. Леонтовича и Б.Б. Кадомцева. М.: Энергоиздат, 1982. С. 118.

  2. Шафранов В.Д. // ЖЭТФ. 1957. Т. 33. С. 710.

  3. Grad H., Rubin H. // Proc. ${{2}^{{{\text{nd}}}}}$ United Nations Conf. Peaceful Uses of Atomic Energy, United Nations, Geneva, Switzerland, 1958. V. 31. P. 190.

  4. Boozer A.H. // Phys. Fluids. 1983. V. 26. P. 1288.

  5. Ильгисонис В.И., Сковорода А.А. // ЖЭТФ. 2010. Т. 137. С. 1018.

  6. Hsu J.Y., Chu M.S. // Phys. Fluids. 1987. V. 30. P. 1221.

  7. Lazzaro E., Shchepetov S.V. // Phys. Lett. A. 1990. V. 143. P. 393.

  8. Ильгисонис В.И., Поздняков Ю.И. // Физика плазмы. 2002. Т. 28. С. 99.

  9. Solano E.R. // Plasma Phys. Control. Fusion. 2004. V. 46. P. L7.

  10. Захаров Л.Е., Смоляков А.И., Субботин А.А. // Физика плазмы. 1990. Т. 16. С. 779–783.

  11. Hameiri E. // Phys. Fluids. 1983. V. 26. P. 230.

  12. Tasso H., Throumoulopoulos G.N. // Phys. Plasmas. 1998. V. 5. P. 2378.

  13. Goedbloed J.P., Belien A.J.C. // Phys. Plasmas. 2004. V. 11. P. 28.

  14. Guazzotto L., Betti R. // Phys. Plasmas. 2005. V. 12. P. 056107.

  15. Grad H. // Phys. Fluids. 1967. V. 210. P. 137.

  16. Iacono R., Bondeson A., Troyon F., Gruber R. // Phys. Fluids B. 1990. V. 2. P. 1794.

  17. Ilgisonis V.I. // Phys. Plasmas. 1996. V. 3. P. 4577.

  18. Ильгисонис В.И. Классические задачи физики горячей плазмы. М.: Изд. дом МЭИ, 2015. 326 с.

  19. Okamoto I. // MNRAS. 1975. V. 173. P. 357.

  20. Anderson M. // MNRAS. 1989. V. 239. P. 19.

  21. Steinhauer L.C. // Phys. Plasmas. 1999. V. 6. P. 2734.

  22. Ilgisonis V.I. // Plasma Phys. Control. Fusion. 2001. V. 43. P. 1255.

  23. Thyagaraja A., McClements K.G. // Phys. Plasmas. 2006. V. 13. P. 062502.

  24. Бескин В.С. Осесимметричные стационарные течения в астрофизике. М.: Физматлит, 2006. 384 с.

  25. Пустовитов В.Д., Шафранов В.Д. // Вопросы теории плазмы. Вып. 15 / Под ред. акад. Б.Б. Кадомцева. М.: Энергоатомиздат, 1987. С. 146.

  26. Дегтярев Л.М., Дроздов В.В., Михайлов М.И., Пустовитов В.Д., Шафранов В.Д. // Физика плазмы. 1985. Т. 11. С. 39.

  27. Грубер Р., Дегтярев Л.М., Купер А., Мартынов А.А., Медведев С.Ю., Шафранов В.Д. // Физика плазмы. 1996. Т. 22. С. 204.

  28. Соловьев Л.С., Шафранов В.Д. // Вопросы теории плазмы. Вып. 5 / Под ред. М.А. Леонтовича. М.: Атомиздат, 1967. С. 3.

  29. Kruskal M.D., Kulsrud R.M. // Phys. Fluids. 1958. V. 1. P. 265.

  30. Newcomb W.A. // Phys. Fluids. 1959. V. 2. P. 362.

  31. Шафранов В.Д. // Вопросы теории плазмы. Вып. 2 / Под ред. М.А. Леонтовича. М.: Госатомиздат, 1963. С. 92.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика плазмы

Архивы выпусков Информация о журнале Отправить рукопись в журнал