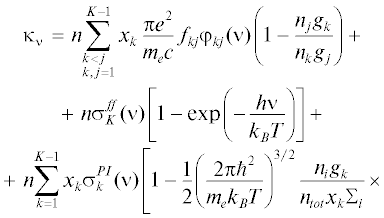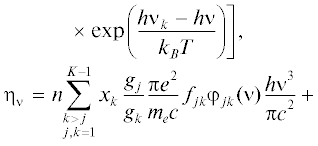Физика плазмы, 2019, T. 45, № 2, стр. 160-171

1. ВВЕДЕНИЕ

Исследования высокоскоростных потоков плазмы, генерируемых в различных плазменных установках, направлены на решение ряда актуальных задач. Дальнейшее использование потоков предполагает, в частности, согласованное взаимодействие с магнитным полем систем, в которые инжектируется плазма. Один из очевидных элементов систем – кольцевой проводник с током. Данная работа посвящена изучению взаимодействия потока плазмы с магнитным полем кольцевого токонесущего проводника на основе нестационарной МГД-модели и расчетов течений плазмы в трехкомпонентном магнитном поле.

Мощный инструмент для генерации высокоскоростных потоков плазмы представляет собой квазистационарный плазменный ускоритель (КСПУ). Эти ускорители были разработаны на основе идей и под научным руководством Алексея Ивановича Морозова [1, 2]. Реализация соответствующей государственной программы привела к созданию в конце 1980-х гг. ряда экспериментальных установок в различных научных центрах [3–6]. На установках КСПУ были достигнуты рекордные, до сих пор не превзойденные показатели по ускорению потока водородной плазмы до скоростей порядка 400 км/c [7, 8], что отвечает кинетической энергии ионов на уровне 1 кэВ.

Первоначально КСПУ создавались в качестве инжекторов для термоядерных ловушек [9]. Предполагая равнораспределение энергии по степеням свободы и равенство температуры электронной и ионной компонент в магнитных ловушках для удержания плазмы, получим, что необходимая кинетическая энергия ионов для последующей реакции синтеза должна быть более 30 кэВ для дейтерий-тритиевой смеси. Расчеты осесимметричных течений плазмы в канале КСПУ продемонстрировали [10], как можно достичь необходимой энергии при разумных разрядных токах в пределах 1 МА, используемых в реальных установках. Для этого необходимо уменьшить значение характерной концентрации на входе в плазменный ускоритель. В последние годы в рамках программы по управляемому термоядерному синтезу (УТС), в том числе в рамках проекта ITER, установки КСПУ использовались для изучения взаимодействия высокоскоростных потоков плазмы с различными материалами (см., например, [11–13]). Кроме того, с помощью плазменных ускорителей осуществлялась инжекция плазмы в ловушки Галатеи с левитирующими токонесущими кольцевыми проводниками. Данные ловушки также были предложены и обоснованы А.И. Морозовым (см., например, [14, 15]).

В настоящее время стало очевидно, что КСПУ это многофункциональные установки, предназначенные для термоядерных исследований и технологических приложений, включая сепарацию частиц по массе [16]. Соответствующие модификации КСПУ могут быть использованы в качестве мощных электрореактивных плазменных двигателей [17]. Расчеты, представленные в [10], показали, что тяга перспективных систем на основе К-СПУ пропорциональна кубу от разрядного тока $N\sim J_{d}^{3}$ и в зависимости от мощности атомного реактора на борту аппарата, используемого в космосе или атмосфере, может существенно превосходить тягу обычных ракетных двигателей. В современных стационарных плазменных двигателях (СПД) для разреженной плазмы, предложенных и разработанных под руководством А.И. Морозова [2, 17, 18], тяга весьма незначительная, порядка одного ньютона. Тем не менее СПД успешно используются для коррекции орбит космических аппаратов на протяжении нескольких десятилетий, и продолжаются работы по оптимизации данных двигателей, включая изучение протекающих в них процессов (см., например, [19–21]).

Исследования процессов в разреженной и плотной плазме, происходящих в различных установках, включая СПД, КСПУ и магнитные ловушки для удержания плазмы, проводятся на основе различных теоретических подходов, а также с помощью математического моделирования и расчетов. Этому посвящено большое количество монографий и оригинальных статей (см., например, [2, 22–39]).

Теоретические исследования, численное моделирование и анализ происходящих процессов внесли существенный вклад в разработку КСПУ [38–50]. В полноблочном варианте КСПУ представляет собой двухступенчатую установку. Первая ступень состоит из набора малых коаксиальных плазменных ускорителей, предназначенных для ионизации среды и предварительного ускорения плазмы. Для исследования процесса ионизации разработаны МГД-модели различного уровня сложности (см., например, [39, 42–44]), включая 3D-модель переноса излучения [45]. Вторая ступень, предназначенная для окончательного ускорения плазмы, является ускорителем большего размера, подключенного к независимой электрической цепи. Основной механизм ускорения плазмы в обеих ступенях обусловлен силой Ампера $({\mathbf{j}} \times {\mathbf{H}}){\text{/}}c$. В канале ускорителя ток в плазме j имеет преимущественно радиальное направление, а электрический ток, протекающий вдоль внутреннего электрода, генерирует азимутальное магнитное поле ${{H}_{\varphi }}$. Новое направление исследований связано с введением в установку КСПУ дополнительного продольного магнитного поля (см., например, [46–48]), которое позволяет нивелировать негативные приэлектродные процессы [49, 50].

Исследованию процессов в магнитных ловушках для удержания плазмы, в том числе их математическому моделированию и расчетам, также посвящено большое количество работ (см., например, [14, 15, 24, 26, 31, 51–54]). Элементы исследований, проводимых для различных магнитных ловушек, связаны, в частности, с изучением процесса проникновения потока плазмы через магнитный барьер (см., например, [55]), а также с изучением взаимодействия потока плазмы с магнитным полем кольцевых проводников с током. Существуют различные способы включения в модель и расчетную область кольцевых проводников. Ранее были рассмотрены упрощенные модели (см., например, [56]). В данной работе предложена более полная модель взаимодействия потока плазмы в КСПУ при наличии токов выноса с магнитным полем кольцевых токонесущих проводников. Проблемы взаимодействия потоков плазмы с магнитным полем представляют интерес для различных направлений исследований в физике плазмы и УТС, включая токамаки и стеллараторы.

2. УРАВНЕНИЯ РАДИАЦИОННОЙ МАГНИТНОЙ ГАЗОДИНАМИКИ

Теоретические и численные исследования процессов для достаточно плотной плазмы проводятся в рамках моделей магнитной газодинамики (см., например, [2, 22–28]). Численные МГД-модели для изучения процессов в КСПУ основаны на различных модификациях МГД-уравнений и разработаны для одножидкостной модели (см., например, [2, 10, 39–48]), а также двухжидкостной модели с учетом эффекта Холла [39, 49, 50]. В рамках радиационной магнитной газодинамики (РМГД) одновременно с МГД-задачей решается уравнение переноса излучения. С помощью РМГД-модели исследованы течения ионизующегося газа и перенос излучения в коаксиальном канале плазменного ускорителя, отвечающего первой ступени КСПУ (см., например, [45]).

В данной работе рассматривается двумерное осесимметричное течение плазмы в канале между двумя коаксиальными профилированными электродами и на выходе из второй ступени КСПУ, когда внутренний электрод короче внешнего, а продолжением внешней границы плазменного объема является изолятор. В задаче участвуют все три компоненты магнитного поля ${\mathbf{H}} = ({{H}_{z}},{{H}_{r}},{{H}_{\phi }})$ и скорости ${\mathbf{V}} = ({{V}_{z}},{{V}_{r}},{{V}_{\phi }})$ при наличии в канале ускорителя продольного магнитного поля, дополнительного к основному азимутальному полю, а также при наличии продольного поля, создаваемого кольцевым проводником с током на выходе из канала ускорителя. Плазму можно рассматривать как квазинейтральную среду ${{n}_{i}} = {{n}_{e}} = n$, учитывая ее параметры, представленные далее. Инерцией электронов (${{m}_{e}} \ll {{m}_{i}}$) и током смещения пренебрегаем. Эксперименты в КСПУ и оценки показывают также, что можно рассматривать случай однотемпературной смеси ${{T}_{i}} \approx {{T}_{e}} = T$. В рамках рассматриваемой одножидкостной модели (${{{\mathbf{V}}}_{e}} = {{{\mathbf{V}}}_{i}} = {\mathbf{V}}$) постановка задачи включает уравнения радиационной магнитной газодинамики с учетом конечной проводимости среды, теплопроводности и переноса излучения

Все переменные в системе уравнений (1) имеют обычный смысл. Величина $\sigma = {{e}^{2}}{{n}_{e}}{{\tau }_{e}}{\text{/}}{{m}_{e}}$ определяет электропроводность среды, вектор ${\mathbf{q}} = - \kappa \nabla T$ отвечает потоку тепла, обусловленному теплопроводностью, а W – плотность потока энергии излучения. Вязкостью компонент плазмы пренебрегаем в силу малости соответствующих диссипативных слагаемых.

Плотность потока энергии излучения W, а также плотность энергии излучения U определяются через интенсивность излучения ${{I}_{\nu }}\left( {{\mathbf{r}},\;{\mathbf{\Omega }}} \right)$ вдоль выбранного направления телесного угла Ω и для определенного участка спектра с частотой ν

В МГД-уравнениях плотность энергии излучения U можно не учитывать, так как она мала по сравнению с тепловой или внутренней энергией среды ($U \ll \rho \varepsilon $). Однако поток энергии излучения $W\sim cU$ может играть определенную роль в перераспределении энергии. Скорость распространения излучения существенно выше характерных скоростей плазмодинамических процессов. В этом случае поле излучения мгновенно подстраивается под распределение параметров потока, и можно ограничиться решением стационарного уравнения переноса излучения

для интенсивности излучения, отвечающей точке с координатой ${\mathbf{r}}$.

Коэффициент поглощения ${{\kappa }_{\nu }}\left( {\mathbf{r}} \right)$ и излучательная способность ${{\eta }_{\nu }}\left( {\mathbf{r}} \right)$ в уравнении (3) зависят от состояния среды, ее плотности и температуры, а также спектрального параметра $\nu $, связанного с энергией фотона $h\nu $ (см., например, [27, 30, 36, 57–60]). Для определения их значений необходимы в общем случае расчет спектра атома и вычисление населенностей состояний атомов, которые в предположении локального термодинамического равновесия определяются с помощью формулы Больцмана. Процессы испускания и поглощения света связаны с переходами электрона из одного энергетического состояния в другое. Соответственно коэффициент поглощения и излучательная способность складываются из трех частей, отвечающих поглощению и излучению в линиях, фотоионизации и фоторекомбинации, а также рассеянию.

Излучательная способность и коэффициент поглощения, поправленный на вынужденное излучение, вычисляются с помощью следующих соотношений:

где ${{x}_{k}}$ – относительная концентрация k-го состояния атома, ${{g}_{k}}$ – статистический вес k-го состояния атома, ${{f}_{{kj}}}$ – сила осцилляторов при переходе атома из k-го в j-е состояние, ${{\varphi }_{{kj}}}\left( \nu \right)$ – профиль линии соответствующего связанно-связанного перехода, $\sigma _{k}^{{PI}}(\nu )$ – сечение фотоионизации из k‑го состояния, $\sigma _{K}^{{ff}}(\nu )$ – сечение обратного тормозного поглощения, ${{n}_{{tot}}}$ – полная концентрация частиц. Суммирование в формулах проводится по всем состояниям, за исключением состояния $k = K$, отвечающего ионам с концентрацией ${{n}_{i}}$. Излучательная способность (4) отвечает количеству энергии частоты ν, самопроизвольно или спонтанно излучаемой в 1 см³ вещества за 1 с в единичном интервале частот.

Профиль линии, учитывающий разные по природе механизмы уширения, определяется по формуле Фойгта

где D – ширина Доплера, ${{\gamma }_{e}}$ – ширина, обусловленная взаимодействием атома с окружающими его ионами, электронами и излучением. Профиль линии Фойгта имеет вид колоколообразной кривой, характерная ширина которой соответствует времени жизни состояния. Взаимодействие с электронами является существенным фактором для характерных концентраций n ~ 10¹⁴–10¹⁷ см^–3 и температуры $T\sim 1$ эВ. В этом случае для вычисления величины ${{\gamma }_{e}}$ можно ограничиться уширением электронным ударом, используя следующую формулу [36, 59]: где ${{R}_{D}} = \sqrt {{{{{k}_{B}}T} \mathord{\left/ {\vphantom {{{{k}_{B}}T} {(4\pi {{e}^{2}}{{n}_{e}})}}} \right. \kern-0em} {(4\pi {{e}^{2}}{{n}_{e}})}}} $ – радиус Дебая, ${{R}_{W}} = $ $ = {{a}_{0}}\sqrt {{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}} \sqrt {I(k,j)} {{{{e}^{2}}} \mathord{\left/ {\vphantom {{{{e}^{2}}} {\left( {\hbar \left\langle {{{V}_{e}}} \right\rangle } \right)}}} \right. \kern-0em} {\left( {\hbar \left\langle {{{V}_{e}}} \right\rangle } \right)}}$ – радиус Вайскопфа, $I(k,j) = 0.5({{k}^{4}} + {{j}^{4}})$, ${{a}_{0}}$ – радиус Бора. Эффективная методика вычисления профиля Фойгта изложена в [60]. Расчет сечений связанно-свободных и свободно-свободных процессов осуществляется в приближении Крамерса [59] где ${{E}_{k}}$ – энергия ионизации, k – номер уровня, с которого происходит ионизация. Энергетический спектр атома водорода определяется по формуле ${{E}_{k}} = - {{{{Z}^{2}}{{e}^{2}}} \mathord{\left/ {\vphantom {{{{Z}^{2}}{{e}^{2}}} {(2{{a}_{0}}{{k}^{2}})}}} \right. \kern-0em} {(2{{a}_{0}}{{k}^{2}})}}$. Силы осцилляторов ${{f}_{{kj}}}$ для связанно-связанных переходов вычисляются с помощью известных квантовомеханических соотношений.

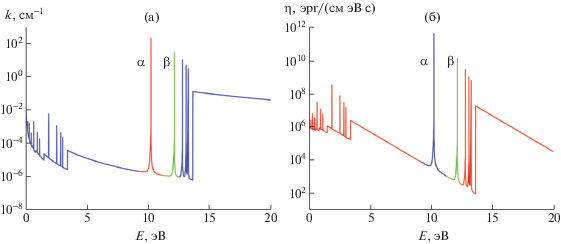
На рис. 1 представлен пример зависимости коэффициента поглощения и излучательной способности водородной плазмы от энергии излучения для концентрации $n = 1.4 \times {{10}^{{16}}}$ см^–3 и значения температуры T = 1 эВ. Излучательная способность, отвечающая единичному интервалу частот в соотношении (4), на рис. 1б отнесена к единичному интервалу энергии фотонов в 1 эВ. На рисунке отмечены α и β линии серии Лаймана. Ранее было показано [45], что эти линии переносят значительную долю энергии линейчатого спектра в потоках ионизующегося газа, поэтому профили этих линий посредством формулы (5) рассмотрены более детально, чем профили остальных линий. При этом на ширину линии приходится несколько спектральных групп, подробно описывающих форму ядра и крыльев линий. В то же время, линии в остальной части спектра описываются в рамках одной группы. Весь спектр в расчетах разбивается более чем на 300 спектральных групп. Коэффициент поглощения и излучательная способность рассчитаны в предположении равновесной заселенности уровней атома водорода. Значения коэффициентов соответствуют трем группам процессов перехода электрона из одного энергетического состояния в другое, включая связанно-связанные процессы, отвечающие поглощению и излучению в линиях. В данном примере излучательная способность и коэффициент поглощения построены с учетом более 10 уровней энергии. Каждый из рассмотренных процессов перехода электрона из одного энергетического состояния в другое вносит свой вклад в излучение и поглощение.

Для численного решения задачи с уравнениями (1)–(3) используются безразмерные переменные и параметры. Единицами измерения являются длина канала L, характерные значения концентрации или плотности ${{n}_{0}}$ (${{\rho }_{0}} = {{m}_{{\,i}}}{{n}_{0}}$), температуры ${{T}_{0}}$ и азимутальной составляющей магнитного поля на входе в канал ${{H}_{0}} = 2{{J}_{p}}{\text{/}}c{{R}_{0}}$, где ${{R}_{0}}$ – характерный радиус, ${{J}_{p}}$ – разрядный ток в системе. С помощью данных величин формируются единицы скорости ${{V}_{0}} = {{H}_{0}}{\text{/}}\sqrt {4\pi {{\rho }_{0}}} $, времени ${{t}_{0}} = L{\text{/}}{{V}_{0}}$, тока в плазме ${{j}_{0}} = c{{H}_{0}}{\text{/}}4\pi L$, а также единица измерения компоненты векторного потенциала ${{A}_{0}} = {{H}_{0}}L$, использованного в модели. Переход к безразмерному значению плотности потока энергии излучения W в (1) и (2) осуществляется с помощью следующей единицы измерения: ${{W}_{0}} = {{V}_{0}}H_{0}^{2}{\text{/}}4\pi $.

Система МГД-уравнений в безразмерных переменных содержит такие безразмерные параметры, как отношение характерного газового давления к магнитному $\beta = 8\pi {{P}_{0}}{\text{/}}H_{0}^{2}$ (${{P}_{0}} = 2k{{n}_{0}}{{T}_{0}}$) и магнитную вязкость $\nu = 1{\text{/}}{{\operatorname{Re} }_{m}} = {{c}^{2}}{\text{/}}4\pi L{{V}_{0}}\sigma $, которая обратно пропорциональна магнитному числу Рейнольдса, а также безразмерное значение коэффициента теплопроводности. Магнитное число Рейнольдса отвечает спитцеровской зависимости проводимости от температуры ${{\operatorname{Re} }_{m}} = {{\sigma }_{0}}{{T}^{{3/2}}}$, где величина ${{\sigma }_{0}}$ выражается через исходные размерные параметры и физические константы. Безразмерные параметры определяют законы подобия.

3. УРАВНЕНИЯ РМГД В ТЕРМИНАХ ВЕКТОРНОГО ПОТЕНЦИАЛА ПОЛЯ

Ранее проведенные исследования течений плазмы в КСПУ при наличии слабого дополнительного продольного магнитного поля показали, что продольное поле может изменить динамику плазмы в окрестности электродов, повлиять на приэлектродные процессы и связанные с ними негативные явления, не оказывая заметного влияния на процесс ускорения основного потока плазмы [46–50]. Дополнительное продольное магнитное поле в канале ускорителя может быть создано с помощью катушки Гельмгольца, которая представляет собой два одинаковых кольцевых витка, расположенных на расстоянии радиуса витка. Напряженность поля в такой системе катушек с током мало отличается в различных точках. Пример соответствующей экспериментальной реализации дополнительного продольного поля в КСПУ представлен в работе [61]. Иной способ создания продольного поля предложен в [6].

При наличии всех трех компонент магнитного поля важным фактором в МГД-моделях является сохранение свойства соленоидальности магнитного поля. В представленной численной модели осесимметричных течений плазмы используется векторный потенциал ${\mathbf{A}}$ магнитного поля так, что ${\mathbf{H}} = \nabla \times {\mathbf{A}}$. В осесимметричном случае ($\partial {\text{/}}\partial \varphi = 0$) имеем

где ${{A}_{\phi }}$ – азимутальная компонента векторного потенциала A. Соотношения (6) при условии аксиальной симметрии обеспечивают точное выполнение соотношения $\nabla \cdot {\mathbf{H}} = 0$. При этом систему уравнений (1) можно записать в безразмерном виде через ${{A}_{\phi }}$-компоненту векторного потенциала и ${{H}_{\phi }}$-компоненту магнитного поля где – азимутальный ток, ${{D}_{\phi }} = r\rho {{V}_{\phi }}$, $\varepsilon = \beta T{\text{/}}\left( {\gamma - 1} \right)$ и $P = \beta \rho T$. Уравнения (7) содержат семь независимых переменных ρ, T, ${{V}_{z}}$, ${{V}_{r}}$, ${{V}_{\phi }}$, ${{H}_{\phi }}$, ${{A}_{\phi }}$. Численное интегрирование уравнений ведется в области переменных $(z,\;r)$, соответствующей форме канала, схематично изображенного на рис. 2. Уравнения, включая безразмерные параметры, и условия на границах определяют динамику потока.

4. УСЛОВИЯ НА ГРАНИЦАХ И МЕТОДЫ РЕШЕНИЯ РМГД-ЗАДАЧИ

На входе в канал при $z = 0$ полагаем, что плазма подается с известными значениями плотности $\rho (r) = {{f}_{1}}(r)$ и температуры $T(r) = {{f}_{2}}(r)$. Можно не рассматривать уравнение электрической цепи, считая, что ток поддерживается постоянным и поступает в систему только через электроды, т. е. ${{j}_{z}} = 0$ при $z = 0$ и $\left| {r{{H}_{\phi }}} \right| = {{r}_{0}} = {\text{const}}$ (${{r}_{0}} = {{R}_{0}}{\text{/}}L$). Полагаем, что подача плазмы осуществляется вдоль определенного направления, например, вдоль координатных линий.

Данные граничные условия являются традиционными для численных моделей динамики плазмы в каналах в отсутствии продольного магнитного поля. При его наличии необходимы граничные условия для ${{V}_{\phi }}$ и ${{A}_{\phi }}$. Считаем, что при $z = 0$ плазма не вращается и азимутальная скорость равна нулю ${{V}_{\phi }} = 0$. Кроме того, зададим на входе ${{H}_{z}} \ne 0$. Следуя [46], воспользуемся уравнением радиального равновесия

В случае $r{{H}_{\phi }} = {\text{const}}$ и ${{V}_{\phi }} = 0$ из данного уравнения следует, что на входе в канал

Для холодной плазмы ($\beta = 0$) при $z = 0$ имеем ${{H}_{z}}(r) = H_{z}^{0} = {\text{const}}$. Интегрируя (6), найдем

В общем случае $\beta \ne 0$ необходимы дополнительные согласования граничных условий. Соотношение (8) отвечает равновесному в радиальном направлении потоку плазмы на входе. Это возможно, в частности, для двух очевидных способов подачи. Во-первых, традиционные в численных моделях условия на входе $\rho = 1$ и $T = 1$ при любом $\beta $ приводят в случае радиального равновесия к ${{H}_{z}}\left( {z = 0,\;r} \right) = H_{z}^{0} = {\text{const}}$ и соотношению (9). Во-вторых, если $\beta \ll 1$, возможна произвольная подача, в том числе в соответствии с аналитической моделью двумерных течений [46] в приближении плавно меняющегося канала [38]. При этом на входе имеем зависимость $\rho \left( {z = 0,r} \right) = r_{0}^{2}{\text{/}}{{r}^{2}}$, согласно которой плотность у внутреннего электрода существенно выше. Этот фактор учитывается в экспериментах и дает положительный эффект.

В данной работе граничные условия на электродах $r = {{r}_{{\;k}}}\left( z \right)$ и $r = {{r}_{{\,а }}}\left( z \right)$, образующих стенки канала ускорителя, предполагают их эквипотенциальность (${{E}_{\tau }} = 0$) и непроницаемость поверхности для плазмы (${{V}_{n}} = 0$). При наличии продольного магнитного поля необходимо дополнительное соотношение. В плазмодинамике равенство ${{H}_{n}} = 0$ дает типичное и естественное условие, связывающее компоненты магнитного поля на границе плазма–проводник. Оно приводит, в частности, к сохранению магнитного потока вдоль канала. Таким образом, на электродах выполнены следующие условия:

Равенство ${{H}_{n}} = 0$ на самом деле отвечает более точному соотношению ${{E}_{\phi }} = 0$, которое при ${{V}_{n}} = 0$ для классического закона Ома ${\mathbf{E}} = {\mathbf{j}}{\text{/}}\sigma - \left( {{\mathbf{V}} \times {\mathbf{H}}} \right){\text{/}}c$ приводит к зависимости ${{H}_{n}}\sim \nu {{j}_{\phi }}{\text{/}}{{V}_{z}}$, представленной в [47]. Для идеально проводящей плазмы, когда магнитная вязкость $\nu = 0$, из равенства ${{E}_{\phi }} = 0$ следует общепринятое условие ${{H}_{n}} = 0$. В представленных далее численных экспериментах $\nu \ll 1$ и ${{H}_{n}} = 0$.

На поверхности электродов с граничными условиями (10) соотношение ${{H}_{n}} = 0$ с учетом (6) означает, что функция магнитного потока постоянна $\psi = r{{A}_{\phi }} = {\text{const}}$, в том числе на поверхности внешнего электрода, который будем считать анодом.

В средней наиболее узкой части канала происходит переход скорости потока через скорость быстрой магнитозвуковой волны или скорость сигнала [2, 38], которая равна ${{C}_{s}} = \sqrt {C_{g}^{2} + C_{A}^{2}} $ в отсутствии продольного магнитного поля и при наличии единственной азимутальной компоненты поля, где $C_{g}^{2} = \gamma P{\text{/}}\rho $ и $C_{A}^{2} = {{H}^{2}}{\text{/}}4\pi \rho $. Соответственно, на выходе из канала ускорителя имеем сверхзвуковое течение плазмы.

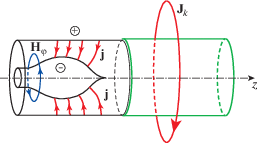
На рис. 2 схематично представлена геометрия области для численного исследования задачи с одним кольцевым проводником с током. Здесь изображены токи в плазме j, а также ток в кольцевом проводнике ${{J}_{k}}$. Проводник с током расположен вне расчетной области. Это позволяет избежать моделирования обтекания плазмой отдельного проводника, что является трудоемкой и не столь актуальной задачей. В данном случае основная цель исследований связана с ответом на ряд принципиальных вопросов и необходимостью изучения влияния магнитного поля кольца с током или внешнего магнитного поля на высокоскоростные потоки плазмы.

Изолятор на рис. 2 является продолжением внешнего цилиндрического электрода, ограничивая объем плазмы за профилированной частью ускорительного канала, и отвечает границе между плазмой и вакуумным магнитным полем, создаваемым кольцевым проводником с током. На поверхности изолятора с известными свойствами имеем следующие граничные условия:

Соответственно, на изоляторе значения азимутальной компоненты векторного потенциала ${{A}_{\phi }}$ и функции магнитного потока $\psi = r{{A}_{\phi }}$ заданы. Функция $A\left( z \right)$ вдоль изолятора вычисляется на основе решения задачи о внешнем магнитном поле. Функция ${{A}_{\phi }}\left( {z,\,r} \right)$ определяется с помощью известных соотношений (см, например, [23]). Для одного кольцевого проводника с током ${{J}_{k}}$ в безразмерных переменных азимутальная компонента векторного потенциала равна

где G и U – полные эллиптические интегралы 1-го и 2-го рода где ${{R}_{k}}$ – радиус кольца с током, ${{z}_{k}}$ – положение кольца с током в цилиндрической системе координат, для которой $z = 0$ отвечает входу в канал плазменного ускорителя. Соотношение (11) позволяет найти значение функции $A(z) = A_{\phi }^{k}(z,\,r = {{r}_{0}})$ на изоляторе, в данном случае цилиндрической поверхности, сопряженной с каналом ускорителя, или на границе расчетной области при $z > 1$.

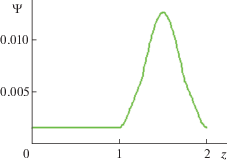
На рис. 3 представлено распределение функции магнитного потока $\psi = r{{A}_{\phi }}$, отвечающей азимутальной компоненте векторного потенциала, вдоль изолятора при $r = {{r}_{0}}$ для одного кольцевого проводника с током ${{J}_{k}} = 0.1{{J}_{P}}$. В данном случае кольцо с током расположено в плоскости $z = {{z}_{k}} = 1.5$, и его радиус равен ${{R}_{k}} = 1.5{{r}_{0}}$, где ${{r}_{0}} = {{R}_{0}}{\text{/}}L = 0.33$ и ${{R}_{0}}$ – радиус внешнего цилиндрического электрода, сопряженного с цилиндрической поверхностью изолятора в сечении $z = 1$.

В соответствии с экспериментальными данными течение плазмы в КСПУ обладает аксиальной симметрией. Численная модель двумерных осесимметричных течений плазмы предполагает расщепление по координатным направлениям и физическим факторам, учитывая смешанный тип МГД-уравнений.

Алгоритм численного решения уравнений (7) включает отображение исходной криволинейной области на прямоугольник в плоскости (y, z) с помощью соотношения

Для расчета гиперболической части МГД-уравнений используется разностная схема с коррекцией потоков [32]. Магнитная вязкость и теплопроводность учитываются с помощью метода потоковой прогонки [62]. Стационарные или квазистационарные течения рассчитываются методом установления в процессе численного решения исходной нестационарной МГД-задачи.

Для решения уравнения переноса излучения (3) используется метод длинных характеристик [30, 45, 58], который позволяет в деталях учесть геометрию канала ускорителя. Задача о переносе излучения с учетом интегральных соотношений (2) должна быть решена в трехмерной постановке для осесимметричного течения плазмы в канале ускорителя. Сетку для 3D-задачи о переносе излучения легко получить поворотом исходной сетки в плоскости переменных $(z,\;r)$ на 360° вокруг оси канала с заданным шагом. Интенсивность излучения должна быть определена по разным направлениям для дальнейшего вычисления интегральных значений плотности и потока энергии излучения в любом узле или ячейки сетки. С этой целью для каждого узла двумерной координатной сетки строится дополнительная угловая сетка по азимутальному и полярному углу. Разбиение полного телесного угла $\Omega = 4\pi $ на элементы угловой сетки производится методом, обеспечивающим равномерное распределение лучей по направлениям. Для каждого узла координатной сетки в расчетах используется до 440 лучей в угловой сетке.

В соответствии с методом длинных характеристик осуществляется трассировка лучей в трехмерной расчетной области, чтобы определить точки пересечения лучей с гранями ячеек трехмерной координатной сетки и места падения лучей на одну из границ исследуемого объема плазмы. Уравнение переноса излучения (3), которое необходимо решать вдоль любого заданного луча и для соответствующей частоты или энергии фотона, содержит коэффициент поглощения ${{\kappa }_{\nu }}$ и излучательную способность среды ${{\eta }_{\nu }}$. Эти коэффициенты зависят, в том числе от температуры и плотности среды, которые меняются вдоль луча. Полагаем, что в пределах отдельно взятой ячейки 3D-сетки коэффициент поглощения и излучательная способность постоянны. Они вычисляются по среднему значению плотности и температуры в центре ячейки.

Один из немаловажных факторов в расчетах переноса излучения связан с необходимостью учета теневых областей, которые возникают в процессе трассировки трехмерной расчетной области лучами, выходящими из любого узла координатной сетки. Невидимые теневые области исключаются из расчета потока энергии излучения для каждого узла координатной сетки.

Метод численного интегрирования уравнения переноса излучения изложен в [30, 45]. Решение уравнения (3) находится при условии, что интенсивность излучения равна нулю ${{I}_{0}} = 0$ для лучей, идущих от стенок канала, поскольку возможное излучение электродов не оказывает существенного влияния на радиационные характеристики плазмы внутри канала.

5. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ ЭКСПЕРИМЕНТОВ

В соплообразном канале ускорителя формируется трансзвуковое течение в процессе ускорения плазмы. При этом скорость потока переходит через скорость быстрой магнитозвуковой волны в средней наиболее узкой части канала. На выходе из канала образуется сверхзвуковой поток, схождение которого на оси системы приводит к возникновению конической ударной волны. Данный классический результат для компрессионных течений плазмы в отсутствии кольцевого проводника с током хорошо известен и представлен, например, в [10]. На конической ударной волне происходит резкое увеличение плотности и температуры. При этом в окрестности ударной волны наблюдается характерный излом линий потока плазмы и скачкообразное изменение направления скорости. Кроме того, в окрестности оси формируется область сжатия или компрессии с еще более высокими значениями концентрации и температуры.

Кольцевой проводник с током оказывает влияние на течение плазмы. На рис. 4 представлен установившийся поток плазмы в КСПУ, взаимодействующий с магнитным полем кольцевого проводника, по которому протекает указанный выше ток ${{J}_{k}} = 0.1{{J}_{P}}$. Изолятор, на котором задано значение ${{A}_{\phi }} = A\left( z \right)$ и $\psi = r{{A}_{\phi }}$ в соответствии с рис. 3, дополнительно выделен на внешней границе расчетной области при $1 < z < 2$ для всех представленных распределений МГД-величин. Расчет течения проведен при наличии дополнительного продольного поля в канале ускорителя и отвечает следующим параметрам задачи: $H_{z}^{0} = 0.03$, ${{n}_{0}} = {{10}^{{15}}}$ см^–3, ${{T}_{0}} = 2$ эВ, ${{J}_{P}} = 300$ кА, $L = 60$ см, ${{R}_{0}}\, = 20$ см, которые в рассматриваемом случае D‒T плазмы приводят к значениям ${{\sigma }_{0}} = 386$ и $\beta = 0.009$. При условии неравномерной подачи на входе в канал имеем $\rho \left( {z = 0,r} \right) = r_{0}^{2}{\text{/}}{{r}^{2}}$ и $T = {{\rho }^{{\gamma - 1}}}$. Масштаб векторов на рис. 4в и г определяется значениями ${{H}_{*}} = 0.1$ и ${{V}_{*}} = 1.5{{V}_{0}}$, где единица скорости равна ${{V}_{0}} = 1.3 \times $ × 10⁷ см/с, а в качестве единицы магнитного поля выступает характерное значение азимутальной компоненты ${{H}_{0}}$, определяемое разрядным током ${{J}_{P}}$.

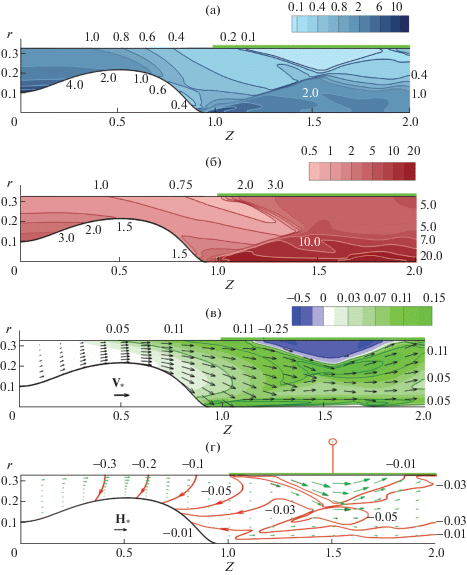
На рис. 4г видно, что магнитное поле, создаваемое кольцевым проводником с током, проникает в поток плазмы. Однако оно не проникает на всю глубину объема плазмы для использованных параметров и значения магнитной вязкости, характерных для экспериментов. Не наблюдается ожидавшийся ярко выраженный ударный переход, который мог бы сформироваться под действием магнитной преграды, создаваемой кольцом с током. Влияние магнитного поля кольцевого проводника с указанным током на исследуемый высокоскоростной поток плазмы наблюдается лишь во внешней области, периферийной по отношению к большей части основного потока. В окрестности внешней границы при значениях $1.25 < z < 1.75$ сильное магнитное поле выталкивает плазму, что приводит к значительному разрежению в соответствующей области, изображенной на рис. 4а. Слабое продольное магнитное поле в канале приводит к вращению, постоянно нарастающему вдоль канала. В указанной области сильного магнитного поля и разрежения плазмы наблюдается вращение в противоположном направлении так, что отдельные области в потоке вращаются в разные стороны согласно рис. 4в, на котором белый фон отвечает нулевым значениям азимутальной скорости вращения. Обтекание области сильного магнитного поля меняет прежнюю структуру течения, связанную с конической ударной волной, формирующейся в классическом компрессионном течении плазмы на выходе из канала ускорителя. В данном случае коническая ударная волна деформируется.

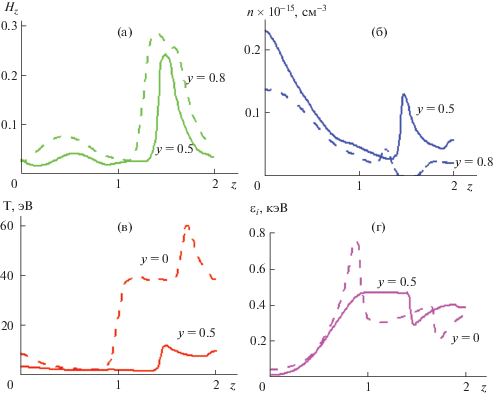
На рис. 5 для рассматриваемого варианта с одним кольцевым проводником с током ${{J}_{k}} = 0.1{{J}_{P}}$ представлены соответствующие одномерные графики зависимости некоторых МГД-переменных вдоль различных координатных линий, определяемых значением y в соотношении (12). Рис. 5а, отвечающий продольному магнитному полю ${{H}_{z}}$ для значений $y = 0.5$ (сплошная линия) и $y = 0.8$ (штриховая кривая), дополнительно иллюстрирует сужение области проникновения магнитного поля кольцевого проводника в поток плазмы по мере удаления от внешней границы, где продольное магнитное поле имеет максимальные значения. Сплошная кривая на рис. 5б соответствует распределению плотности при $y = 0.5$ и показывает ударный переход при $z \approx 1.5$ на конической ударной волне. В то же время штриховая кривая для $y = 0.8$ указывает на незначительное уплотнение плазмы перед областью сильного магнитного поля, создаваемого кольцом с током. Сплошные и штриховые кривые на рис. 5в и 5г для значений $y = 0.5$ и $y = 0$ соответственно показывают изменение температуры и энергии ионов в продольном направлении. Локальный максимум в распределении энергии ионов для $y = 0$ связан с ускорением плазмы в канале и ее торможением в компрессионной области на оси системы при $z \approx 1$. Скачкообразные изменения температуры и энергии ионов на сплошных кривых при $z \approx 1.5$ отвечают конической ударной волне. Обтекание области сильного магнитного поля и соответствующее схождение потока на оси системы при $z > 1.5$ приводят к частичной трансформации и преобразованию кинетической энергии в тепловую или внутреннюю энергию плазмы в окрестности оси системы. Следствием этой трансформации является локальный максимум в распределении температуры, наблюдаемый на рис. 4б для значений $z \approx 1.7$ в окрестности оси и на рис. 5в для штриховой кривой, отвечающей значению $y = 0$. Этому локальному максимуму температуры отвечает локальный минимум значений энергии ионов на оси системы при $y = 0$ и $z \approx 1.7$, изображенный на рис. 5г.

Увеличение тока в кольцевом проводнике приводит к тому, что более сильное магнитное поле проводника с током проникает в плазму на большую глубину. При этом температура существенно больше в окрестности оси при значениях $z \geqslant 1.5$, поскольку плазме приходится обтекать более обширную область с более сильным магнитным полем. Следствием обтекания этой обширной области является более глубокая деформация прежней структуры течения, связанной с конической ударной волной. Соответственно наблюдается более значительная трансформация кинетической энергии в тепловую энергию плазмы в окрестности оси системы при значениях $z\sim 1.5$.

Таким образом, выявлены основные закономерности процесса взаимодействия высокоскоростного потока достаточно плотной плазмы, генерируемой КСПУ, с магнитным полем кольцевого проводника или катушки с током. Проведенные численные эксперименты показывают, что небольшие по величине токи в кольцевом проводнике создают магнитное поле, которое не оказывает значительного влияния на большую часть высокоскоростного потока плазмы. При этом магнитное поле кольцевого проводника изолирует плазму от катушки с током.

На рис. 6 представлены распределение плотности энергии излучения U, точнее, линии уровня функции, отвечающей безразмерному значению cU, а также векторное поле, отвечающее плотности потока энергии излучения W. Поле излучения соответствует распределениям плотности и температуры, изображенным на рис. 4. Расчет переноса излучения проведен в условиях локального термодинамического равновесия с учетом соотношений (2)–(5). Безразмерная величина $\tilde {U}$, представленная на рис. 6, связана с плотностью энергии излучения U соотношением $\tilde {U} = {{10}^{6}}cU{\text{/}}{{W}_{0}}$, где единица плотности потока энергии излучения равна ${{W}_{0}} = {{V}_{0}}H_{0}^{2}{\text{/}}4\pi = 1.14 \times {{10}^{{13}}}$ эрг/см² ⋅ с для указанных выше исходных параметров ${{n}_{0}}$, ${{T}_{0}}$, ${{J}_{P}}$ и L. Масштаб векторов W определяется модулем вектора ${{W}_{*}} = {{10}^{{ - 6}}}{{W}_{0}}$, указанного на рисунке.

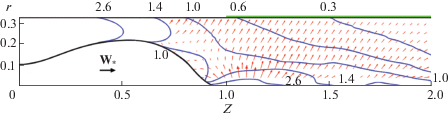
Видно, что плотность энергии излучения U имеет относительно большие значения в области компрессии. Поток энергии излучения W направлен во все стороны от области компрессии. Как и следовало ожидать, область компрессии является мощным источником излучения. Однако в рассматриваемом случае компрессионного течения плазмы основной вклад в общее поле излучения вносит рекомбинационный спектр.

Разработанная модель позволяет определить спектр излучения в направлении любого луча, выходящего из объема плазмы, в любом диапазоне частот. Учитывая возможные в перспективе сопоставления с экспериментальными данными, полученные результаты будут способствовать проведению комплексных расчетных и экспериментальных исследований, в том числе с использованием спектрометра на установках КСПУ, включая их приложения.

6. ЗАКЛЮЧЕНИЕ

Проведено исследование взаимодействия высокоскоростных потоков достаточно плотной плазмы с магнитным полем кольцевого проводника или катушки с током. Модель осесимметричных течений плазмы основана на модифицированной системе МГД-уравнений, представленных в терминах векторного потенциала магнитного поля. МГД-модель учитывает электропроводность и теплопроводность среды, а также перенос излучения. Показано, что небольшие по величине токи в кольцевом проводнике создают магнитное поле, которое не оказывает значительного влияния на основной поток, но изолирует его от катушки с током в результате образования слоя разреженной плазмы между кольцевым проводником и высокоскоростным потоком плазмы. Представленные исследования демонстрируют возможности использования КСПУ для инжекции потоков в магнитные ловушки для удержания плазмы. Кроме того, определены интегральные характеристики излучения в компрессионных течениях плазмы на выходе из ускорителя при условии воздействия на поток магнитного поля кольцевого токонесущего проводника.

Исследование выполнено за счет гранта Российского научного фонда (проект № 16-11-10278).