1. На главную
  2. Электронные версии
  3. Физика плазмы
  4. T. 45, № 2, 2019

Физика плазмы, 2019, T. 45, № 2, стр. 120-132

МГД-устойчивость и энергетический принцип без предположения о вложенности магнитных поверхностей двумерных равновесий

С. Ю. Медведев a, b, c, *, А. А. Мартынов a, b, **, В. В. Дроздов a, ***, А. А. Иванов a, ****, Ю. Ю. Пошехонов a, *****, С. В. Коновалов b, ******, Л. Виллард d, *******

a Институт прикладной математики им. М.В. Келдыша РАН
Москва, Россия

b Национальный исследовательский центр “Курчатовский институт”
Москва, Россия

c Национальный исследовательский ядерный университет “МИФИ”
Москва, Россия

d Швейцарский центр плазмы
Лозанна, Швейцария

* E-mail: medvedev@a5.kiam.ru
** E-mail: martynov@a5.kiam.ru
*** E-mail: vvdrozdov0712@gmail.com
**** E-mail: aai@a5.kiam.ru
***** E-mail: naida@a5.kiam.ru
****** E-mail: konovalov_sv@nrcki.ru
******* E-mail: laurent.villard@epfl.ch

Поступила в редакцию 13.06.2018
После доработки 24.07.2018
Принята к публикации 02.08.2018

Полный текст (PDF)

Аннотация

Отказ от предположения о вложенных магнитных поверхностях в плазме токамака расширяет область исследований и открывает новые подходы, как для теоретической, так и экспериментальной физики плазмы. Компьютерный код для расчетов идеальный МГД-устойчивости KINX был разработан для исследования дублетной плазмы с двумя магнитными осями с использованием блочно-структурных сеток в каждой подобласти с вложенными магнитными поверхностями. Затем был разработан код MHD_NX на неструктурных сетках для расчетов устойчивости двумерных равновесий с произвольной топологией магнитных поверхностей. Изучение равновесия и устойчивости равновесных конфигураций с обращением плотности тороидального тока и осесимметричными n = 0 островами, которые связаны с внутренним транспортным барьером и низкой плотностью тока у магнитной оси, а также c работой в режиме переменного тока в токамаках, приводит к более общим вопросам МГД-устойчивости двумерных решений уравнения равновесия Грэда–Шафранова с островами при других типах симметрии – цепочки островов в винтовой симметрии и цилиндрически симметричных m = 0 островов в конфигурациях с обращением продольного поля. Для всех типов двумерных островных конфигураций были обнаружены новые идеально неустойчивые моды. Энергетический принцип с МГД совместимыми граничными условиями на разомкнутых линиях магнитного поля необходим для самосогласованного исследования устойчивости диверторных конфигураций токамака с конечной плотностью тока на сепаратрисе с учетом плазмы за сепаратрисой. Разработан ряд кодов для расчетов равновесия и устойчивости плазмы с учетом влияния токов за сепаратрисой, которые готовы к интеграции с другими кодами моделирования краевой плазмы.

1. ВВЕДЕНИЕ

Задача детального исследования структур, образуемых магнитными силовыми линиями, или морфологии магнитного поля, была поставлена в работах А.И. Морозова. Следуя [1], магнитные системы для удержания плазмы могут быть условно разделены на две группы: а) системы, в которых требуемая геометрия поля создается в основном токами, текущими в плазме (пинчи, токамаки); б) системы, в которых магнитное поле определяется внешними токами, а собственным полем токов, текущих в плазме, можно пренебречь (стеллараторы, ловушки с магнитными пробками). Конфигурации с внутренними сепаратрисами, включая магнитные острова, обычны для трехмерных стеллараторов [2] и для других альтернативных концепций удержания плазмы, как Галатеи [3] с внутренними проводниками.

Настоящая работа посвящена в основном исследованию устойчивости плазмы токамаков с внутренними сепаратрисами при учете собственного поля токов в плазме. Таковыми, в частности, являются дублетные конфигурации токамака с двумя магнитными осями [4], которые рассматривались в качестве возможности увеличения вытянутости плазмы. Фактически, дублет является примером n = 0 островов в осесимметричной равновесной конфигурации. Другим примером островов n = 0 является конфигурация со знакопеременной плотностью тока, имеющая прямое отношение к работе токамака в режиме переменного тока (AC) [5]. Квазистационарные режимы с переменным током плазмы в токамаках основываются на существовании равновесных конфигураций с полным нулевым тороидальным током [6, 7]. Не исключено появление n = 0 островов и в режимах c Сurrent Hole. Эти режимы плазмы в токамаке с почти нулевым или отрицательным тороидальным током в центральной области обладают хорошими свойствами удержания плазмы и могут быть естественным образом достигнуты при высоком давлении и большой доле неиндукционного бутстреп-тока при стационарной работе реактора [8]. В обоих случаях предположение о плотности тока переменного знака приводит к появлению системы осесимметричных магнитных островов в равновесных конфигурациях. Наконец, перезамыкание магнитных поверхностей в плазме с конечным сопротивлением из-за развития неустойчивости тиринг-мод также приводит к появлению магнитных островов. Даже если оставаться в рамках двумерной равновесной модели (обобщенное уравнение Грэда–Шафранова при наличии осевой, плоской иливинтовой симметрии), для оценки устойчивости соответствующих конфигураций без вложенных магнитных поверхностей нужны МГД-коды нового поколения. Другая важная область применения таких кодов – это изучение свойств стандартных равновесных конфигураций в токамаках с дивертором (и вложенными магнитными поверхностями внутри сепаратрисы), где учет токов в плазме за сепаратрисой, в области с разомкнутыми линиями магнитного поля (SOL), приводит к изменению пределов по равновесию и устойчивости.

На основе метода конечных элементов с векторными базисными функциями разработана новая версия компьютерного кода MHD_NX [9] длярасчета устойчивости равновесных конфигураций с магнитными островами и произвольной топологией магнитных поверхностей на неструктурных сетках со смешанными треугольными и четырехугольными ячейками. Вопрос об устойчивости таких конфигураций с большим разнообразием топологий магнитных островов представляет собой сложную для численного решения задачу. В частности, использование структурированных сеток с узлами, лежащими на магнитных поверхностях, не представляется возможным. Энергетический принцип с МГД-совместимыми граничными условиями на разомкнутых линиях магнитного поля необходим для самосогласованного исследования устойчивости диверторных конфигураций токамака с конечной плотностью тока на сепаратрисе с учетом плазмы за сепаратрисой. Разработаны коды для расчета равновесия и устойчивости плазмы с учетом влияния токов в SOL, которые готовы к интеграции с другими кодами для моделирования краевой плазмы [10].

В разд. 2 приведена формулировка энергетического принципа для равновесий без вложенных магнитных поверхностей, на основе которого разработаны численные методы исследования устойчивости. В разд. 3 приводятся примеры неустойчивостей, возникающих из-за наличия магнитных островов. Раздел 4 посвящен пределам устойчивости диверторной плазмы с учетом конечной плотности тока на сепаратрисе и в SOL.

2. ЭНЕРГЕТИЧЕСКИЙ ПРИНЦИП БЕЗ ПРЕДПОЛОЖЕНИЯ О ВЛОЖЕННОСТИ МАГНИТНЫХ ПОВЕРХНОСТЕЙ

Существует два возможных подхода к исследованию устойчивости равновесных конфигураций без вложенных магнитных поверхностей. Если топология поверхностей не изменяется и существует несколько подобластей с вложенными поверхностями, как это имеет место в дублетах, то можно использовать формулировку стандартного энергетического принципа, основанного на проекциях смещения плазмы на направления, связанные с магнитным полем, как в коде KINX [4]. Использование магнитных проекций необходимо для явного учета анизотропии МГД-уравнений (в функционал возмущенной потенциальной энергии входит радиальная производная только от нормального к магнитным поверхностям смещения), что позволяет хорошо аппроксимировать спектр соответствующего эллиптического некомпактного оператора. Для анализа устойчивости равновесий с магнитными островами предлагается использовать вариационную формулировку задачи устойчивости (энергетический принцип) $\delta ({{W}_{F}} + {{W}_{S}} + {{W}_{V}} - {{\omega }^{2}}K) = 0$ [11, 12] на основе функционалов возмущений потенциальной и кинетической энергии, выраженных через возмущение электрического поля ${\mathbf{E}} = i\omega {\mathbf{e}}$, ${\mathbf{e}} = - {\mathbf{\xi }} \times {\mathbf{B}}$ [9], где ξ – вектор смещения плазмы от положения равновесия, B – равновесное магнитное поле, и предполагается экспоненциальная зависимость от времени $\exp (i\omega t)$. Тогда стандартные выражения для функционалов энергии (предполагая, что равновесная граница плазмы является магнитной поверхностью и, кроме того, показатель адиабаты $\Gamma = 0$) принимают вид

(1)
$\begin{gathered} {{W}_{F}} = \frac{1}{2}\int\limits_{{{V}_{p}}} {\left\{ {{{{\left| {\nabla \times {\mathbf{e}}} \right|}}^{2}} - \frac{{{\mathbf{j}} \cdot {\mathbf{B}}}}{{{{B}^{2}}}}{\mathbf{e}} \cdot \nabla \times {\mathbf{e}} + } \right.} \\ + \;\left. {\frac{{{\mathbf{j}} \cdot {\mathbf{e}}}}{{{{B}^{2}}}}\left[ {2{\mathbf{B}} \cdot \nabla \times {\mathbf{e}} - {\mathbf{t}} \cdot {\mathbf{e}}} \right]} \right\}dV, \\ K = \frac{1}{2}\int\limits_{{{V}_{p}}} {\rho {{{\left| {\mathbf{e}} \right|}}^{2}}{\text{/}}{{B}^{2}}} dV,\quad {\mathbf{t}} = {\mathbf{j}} + {{B}^{2}}\nabla \left( {\frac{1}{{{{B}^{2}}}}} \right) \times {\mathbf{B}}, \\ \end{gathered} $
где ${\mathbf{j}} = \nabla \times {\mathbf{B}}$ – плотность тока, ρ – массовая плотность, ${{V}_{p}}$ – объем плазмы. В идеальной МГД требование отсутствия компоненты вдоль равновесного магнитного поля ${\mathbf{e}} \cdot \;{\mathbf{B}} = 0$ замыкает формулировку задачи устойчивости. Естественным образом учитывается также наличие вакуумной прослойки между плазмой и проводящей стенкой со следующим выражением для возмущения потенциальной энергии в объеме вакуума ${{V}_{v}}$:
(2)
${{W}_{V}} = \frac{1}{2}{{\int\limits_{{{V}_{v}}} {\left| {\nabla \times {\mathbf{e}}} \right|} }^{2}}dV,$
где возмущенное магнитное поле $\delta {{{\mathbf{B}}}_{v}} = - \nabla \times {\mathbf{е }}$, и с требованием непрерывности тангенциальной составляющей e через границу плазмы в предположении отсутствия равновесного поверхностного тока, т. е. непрерывности равновесного магнитного поля через границу плазма–вакуум (при этом также обнуляется интеграл по этой границе, ${{W}_{S}} = 0$, см. Приложение). На идеально проводящей стенке ставится условие ${\mathbf{e}} \times {\mathbf{n}} = 0$.

Энергетический принцип (1), (2) может быть обобщен и на случай равновесных конфигураций с плазмой за сепаратрисой, которая ограничивается диверторными пластинами. В области разомкнутых линий равновесного магнитного поля граничные условия на диверторных пластинах для задачи идеальной МГД-устойчивости выглядят следующим образом:

(3)
${{{\mathbf{\xi }}}_{ \bot }} \cdot {\mathbf{n}} = 0,\quad {\mathbf{\xi }} \cdot {\mathbf{B}}{\text{/}}B = 0\quad {\text{и л и }}\quad {\mathbf{e}} \cdot {\mathbf{B}} \times {\mathbf{n}} = 0,$
где n – нормаль к диверторным пластинам. К такому простому виду приводятся следующие граничные условия на границе дебаевского слоя (sheath boundary conditions) [13]: ${\mathbf{v}} = {{{\mathbf{v}}}_{ \bot }} + {{v}_{{||}}}{\mathbf{B}}{\text{/}}B$, ${{{\mathbf{v}}}_{ \bot }} \cdot {\mathbf{n}} = 0$, ${{v}_{{||}}} = {{c}_{s}}$, где ${{c}_{s}}$ – скорость звука, при низких бета и при альфвеновской скорости, намного превышающей скорость звука ${{v}_{A}} \gg {{c}_{s}}$. Формулировка вариационного принципа с граничными условиями (3) совпадает со стандартным вариационным принципом с точностью до одного несимметричного слагаемого ${{W}_{d}}$, которое нужно добавить к функционалу ${{W}_{F}} + {{W}_{V}}$ из (1),
(4)
${{W}_{d}} = \frac{1}{2}\int\limits_{{{S}_{d}}} {{\mathbf{e}} \cdot \delta {{{\mathbf{j}}}_{s}}dS} ,$
где $\delta {{{\mathbf{j}}}_{s}} = {\mathbf{n}} \times \left\langle {\delta {\mathbf{B}}} \right\rangle $ – возмущенный поверхностный ток на диверторных пластинах ${{S}_{d}}$ (см. Приложение). Предполагая отсутствие возмущенных поверхностных токов на диверторных пластинах (например, из-за зазоров в тороидальном направлении), получаем вариационную формулировку с единственным отличием, связанным с постановкой особых условий на разомкнутых магнитных поверхностях, где для равновесного магнитного поля ${\mathbf{B}} \cdot {\mathbf{n}} \ne 0$. Чувствительность результата расчета устойчивости относительно граничных условий (3) можно проверить, поставив еще более сильное условие на диверторных пластинах (line-tying condition): $\xi = 0$, что приводит к ${{W}_{d}} = 0$. Оказывается, что отличие инкремента идеальной неустойчивости МГД при использовании условия $\xi = 0$ от результата с условием (3) довольно мало для кинк-баллонных мод, локализованных на внешней стороне плазмы. В коде устойчивости MHD_NX постановка граничных условий (3) на диверторных пластинах вполне естественна: требование ${\mathbf{e}} \cdot {\mathbf{B}} = 0$ заменяется условием ${\mathbf{e}} \cdot {\mathbf{B}} \times {\mathbf{n}} = 0$.

Чтобы расширить область применения кода, для неизвестного возмущения электрического поля ${\mathbf{e}}$ используются общегеометрические проекции, не связанные с равновесным магнитным полем. Для аппроксимации задачи устойчивости на неструктурированных сетках используется метод конечных элементов с векторными базисными функциями для проекции вектора e на плоскость постоянного тороидального угла, а также стандартные конечные элементы для проекции на тороидальное направление

(5)
$\begin{gathered} {\mathbf{e}} = {{{\mathbf{e}}}_{{pol}}} + {{e}_{\phi }}\nabla \phi : \\ {{{\mathbf{e}}}_{{pol}}} = \{ {{W}_{{mn}}} = {{W}_{m}}\nabla {{W}_{n}} - {{W}_{n}}\nabla {{W}_{m}}\} ,\quad {{e}_{\phi }} = \{ {{W}_{i}}\} , \\ \end{gathered} $
где ${{W}_{i}}$ – скалярные двумерные кусочно-линейные базисные функции для каждого i-го узла сетки, а ${{W}_{{mn}}}$ – векторные базисные функции для каждого ребра сетки. Выражения (5) естественно обобщаются на случай четырехугольных ячеек. При этом необходимым требованием для аппроксимации является выполнение тождества $\int {\nabla \times {\mathbf{e}}} \cdot d{\mathbf{S}} = \oint {{\mathbf{e}} \cdot d{\mathbf{l}}} $ по площади каждой ячейки. Условие непрерывности тангенциального электрического поля на границе плазма–вакуум $\left\langle {{\mathbf{e}} \times {\mathbf{n}}} \right\rangle = 0$ является естественным для этого варианта метода конечных элементов. Для того чтобы обеспечить выполнение условия ${\mathbf{e}} \cdot {\mathbf{B}} = 0$, используются множители Лагранжа на некотором подмножестве ребер или в узлах неструктурной сетки. Таким образом, задача сводится к решению задачи на собственные значения с седловой точкой, что, в частности, требует введения регуляризации для получения устойчивого треугольного LU разложения разреженных матриц со стандартным переупорядочением неизвестных.

3. УСЛОВИЯ ИДЕАЛЬНОЙ МГД-УСТОЙЧИВОСТИ ОСТРОВОВ В ПЛАЗМЕ ТОКАМАКА И ПИНЧА С ОБРАЩЕННЫМ ПОЛЕМ В ДВУМЕРНЫХ МОДЕЛЯХ

Структура равновесного поля с магнитными островами может быть описана уравнением Грэда–Шафранова для трех типов симметрии: осевой, плоской и винтовой. Это позволяет исследовать устойчивость равновесий с островами при помощи двумерных кодов устойчивости.

3.1. Осевая симметрия в координатах (R, ϕ, Z) для тороидальных конфигураций

Первым естественным объектом для изучения устойчивости равновесий с осесимметричными магнитными островами являются собственные функции оператора равновесного уравнения Грэда–Шафранова. В случае бессилового равновесия с нулевым давлением имеем следующую задачу на собственные значения:

(6)
$\nabla \cdot \left( {\nabla \psi {\text{/}}{{R}^{2}}} \right) = - {{j}_{\phi }}{\text{/}}R,\quad R{{j}_{\phi }} = \lambda \psi ,$
с граничным условием $\psi = 0$ на границе плазмы. На рис. 1 показаны линии уровня для первых 12 собственных функций оператора (6) для круглого сечения границы тороидальной плазмы, каждая из которых представляет собой равновесную конфигурацию. Кроме старшей собственной функции, которая соответствует равновесию с вложенными магнитными поверхностями, остальные собственные функции являются равновесиями с островами, их можно разделить на два класса: равновесия с центральными островами, когда сепаратриса острова находится внутри плазмы (функции с номерами 6, 9, 10), и дипольные или мультипольные равновесия с сепаратрисой на границе плазмы. Все конфигурации с центральными островами идеально неустойчивы относительно осесимметричных возмущений даже при условии закрепленной границы, отвечающей идеально проводящей стенке на границе плазмы [14]. На рис. 2 показана структура неустойчивой моды с тороидальным волновым числом n = 0 для такого равновесия. Характер неустойчивого смещения плазмы соответствует опрокидыванию острова в полоидальном направлении (так называемая тилт-мода). Инкременты такой неустойчивости пропорциональны полоидальной альфвеновской частоте $\omega _{{Ap}}^{2} = {{({{\psi }_{{\max }}} - {{\psi }_{{\min }}})}^{2}}{\text{/}}({{a}^{4}}{{R}^{2}}\rho ) \approx $ $ \approx B_{p}^{2}{\text{/}}({{\mu }_{0}}{{a}^{2}}\rho )$; плотность плазмы $\rho $ предполагается постоянной. Дипольные равновесия для вытянутого сечения плазмы также неустойчивы, и инкремент неустойчивости возрастает с вытянутостью сечения плазмы.

Рис. 1.

Линии уровня для функций полоидального потока, которые являются решениями спектральной задачи для оператора Грэда–Шафранова. Круглое сечение тороидальной плазмы с большим радиусом 3 м и малым радиусом 1 м.

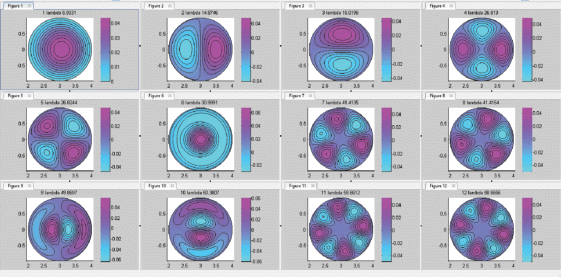
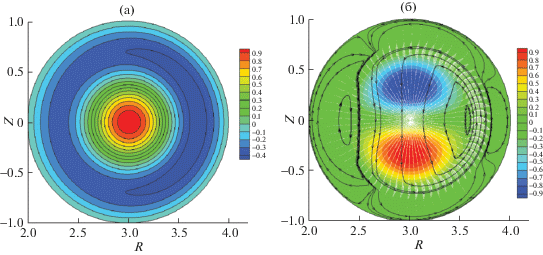
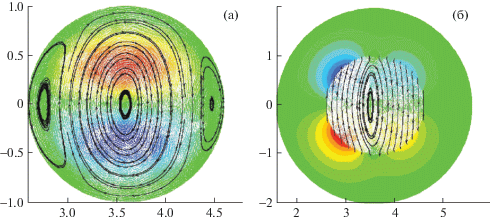
Рис. 2.

Линии уровня для функции полоидального потока (а); линии тока на плоскости $\varphi = {\text{const}}$ и линии уровня тороидального возмущенного электрического поля для неустойчивого смещения плазмы, отвечающего осесимметричной моде с тороидальным числом n = 0, для равновесной конфигурации с центральным островом m = 1 (б), ${{\omega }^{2}}{\text{/}}\omega _{{Ap}}^{2} = - 0.27$.

Однако в более широком, чем (6), классе конфигураций существуют дипольные равновесия, которые стабилизируются при наличии проводящей стенки, находящейся на конечном расстоянии от границы плазмы. Это, в частности, равновесные конфигурации с нулевым полным током плазмы, которые могут быть получены с использованием тороидальной плотности тока, основанной на линейных функциях полоидального потока [6]. Было исследовано влияние профилей и формы плазмы на существование и устойчивость таких конфигураций [15]. В частности, в классе, описываемом линейным уравнением равновесия Грэда–Шафранова, были найдены равновесия с нулевым полным током плазмы, устойчивые относительно идеальных мод n = 0 с проводящей стенкой на конечном расстоянии от границы плазмы.

На рис. 3 показаны линии уровня для функции полоидального потока и тороидальной плотности тока, отвечающие следующему виду правой части уравнения Грэда–Шафранова:

(7)
$R{{j}_{\phi }} = {{R}^{2}}p' + ff',\quad p' = - {{A}_{1}},\quad ff' = {{A}_{2}} + {{\alpha }^{2}}\psi .$
Рис. 3.

Линии уровня для функции полоидального потока и тороидальной плотности тока для равновесия с нулевым полным тороидальным током при ${{A}_{1}} = - 0.0064$, ${{A}_{2}} = - 0.0832$, $\,{{\alpha }^{2}} = 23.464$.

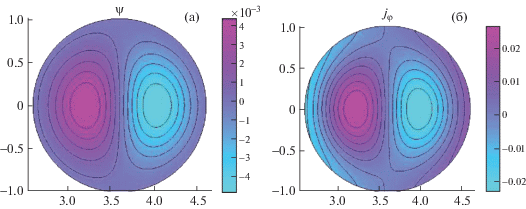
Аспектное отношение выбрано равным R/a = 3.6, что соответствует токамаку CT-6B [6]. Оставляя неизменными параметры A1 и A2, но меняя значение ${{\alpha }^{2}}$, можно найти другое равновесие с нулевым полным током, представленное на рис. 4.

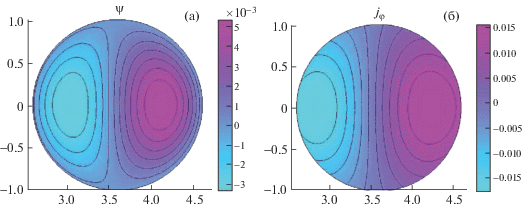
Рис. 4.

Линии уровня для функции полоидального потока и тороидальной плотности тока для равновесия с нулевым полным тороидальным током при ${{A}_{1}} = - 0.0064$, ${{A}_{2}} = - 0.0832$, $\,{{\alpha }^{2}} = 6.943$.

При помощи кода MHD_NX была рассчитана устойчивость равновесий с нулевым полным током относительно осесимметричной моды n = 0. Равновесие с большим значением параметра ${{\alpha }^{2}} = $ $ = 23.464$ неустойчиво даже с закрепленной границей (рис. 5а). Тип смещения соответствует тилт-моде. Равновесие с меньшим ${{\alpha }^{2}} = 6.943$ стабилизируется проводящей стенкой на конечном расстоянии от плазмы ${{a}_{w}}{\text{/}}a = 1.4$ (рис. 5б).

Рис. 5.

Линии тока для неустойчивого осесимметричного смещения плазмы и линии уровня для тороидальной проекции возмущенного электрического поля: неустойчивость с закрепленной границей для равновесия на рис. 3, ${{\omega }^{2}}{\text{/}}_{{Ap}}^{2} = - 7.04$ (а); неустойчивость с проводящей стенкой на расстоянии ${{a}_{w}}{\text{/}}a = 2$ от плазмы для равновесия на рис. 4, ${{\omega }^{2}}{\text{/}}\omega _{{Ap}}^{2} = - 1.16$ (б).

3.2. Осевая симметрия в координатах (r, θ, z) как двумерная деформация одномерного цилиндра

При помощи кода MHD_NX изучена устойчивость аксиально-симметричных магнитных островов с модой $m = 0$ в случае цилиндрической симметрии для периодической по z плазмы с продольным магнитным полем, которое может обращаться в нуль внутри плазмы, что моделирует конфигурацию с обращенным тороидальным магнитным полем [16]. Наличие двумерной деформации границы равновесной плазмы приводит к изменению топологии магнитных поверхностей и образованию цепочки островов (рис. 6). Исследуется устойчивость бессиловых равновесий с плотностью тока ${\mathbf{j}} = \lambda {\mathbf{B}}$ и заданной границей плазмы, на которую наложена осцилляция вокруг одномерного цилиндра: ${{r}_{b}}(z) = a - d\cos (2\pi z{\text{/}}{{z}_{p}})$ с параметрами d, zp, которые определяют размер магнитного острова по координатам r и z при наличии обращения тороидального поля в плазме. Размер по z: $0 \leqslant z \leqslant p{{z}_{p}}$, соответствует цепочке из p островов, радиус эквивалентного тора R = = $p{{z}_{p}}{\text{/}}(2\pi )$. Далее используются величины $a = 1,$ $d = 0.05,$ ${{z}_{p}} = 2.$ Осесимметричное равновесие с островами описывается уравнением Грэда–Шафранова для функции продольного потока с условием периодичности по координате z для топологически цилиндрической плазмы с магнитным полем ${\mathbf{B}} = \nabla \psi \times \nabla \theta + f\nabla \theta $. При возмущении границы цилиндра цепочка $m = 0$ островов появляется на месте обращения продольного магнитного поля ${{B}_{z}}(r)$ в цилиндрически симметричном равновесном поле ${{B}_{z}}(r) = {{J}_{0}}(\lambda r)$, ${{B}_{\theta }}(r) = {{J}_{1}}(\lambda r)$ при $\lambda r{\text{ }} > {\text{ }}2.4$. При этом потоковая функция задается выражением ${{\psi }_{{cyl}}}(r) = r{{J}_{1}}(\lambda r){\text{/}}\lambda $. Граничное значение ${{\psi }_{{cyl}}}(а )$ используется в качестве условия Дирихле для двумерной функции потока, удовлетворяющей уравнению Грэда–Шафранова

(8)
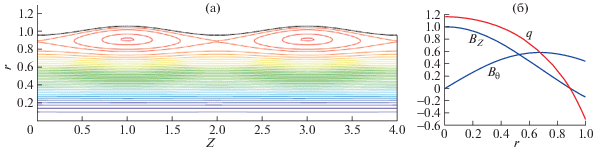
$\begin{gathered} - {{r}^{2}}\nabla \cdot \left( {\frac{{\nabla \psi }}{{{{r}^{2}}}}} \right) = {{r}^{2}}p' + ff', \\ \psi (r,z) = {{\psi }_{{cyl}}}(a),\quad r = {{r}_{b}}(z), \\ \end{gathered} $
Рис. 6.

Магнитные поверхности в плазме с обращением продольного магнитного поля и возмущенной границей (а); распределения компонент магнитного поля и фактора запаса устойчивости для соответствующего равновесия с цилиндрической симметрией (б).

с правой частью $p' \equiv dp{\text{/}}d\psi = 0$, $f = \lambda \psi $. Увеличение λ смещает острова от поверхности вглубь плазмы: λa = 2.7 на рис. 6. Отношение величин фактора запаса устойчивости $q = (r{{B}_{z}}){\text{/}}(R{{B}_{\theta }}) = $ $ = (2\pi rd\psi {\text{/}}dr){\text{/}}(fp{{z}_{p}})$ на границе плазмы и магнитной оси изменяется от ${{q}_{a}}{\text{/}}{{q}_{0}} = - 0.14$ при $\lambda a$ = 2.5 до ${{q}_{a}}{\text{/}}{{q}_{0}} = - 2.26$ при $\lambda a$ = 3.3. Величина фактора запаса устойчивости на магнитной оси ${{q}_{0}} = $ $ = 4\pi a{\text{/}}(\lambda p{{z}_{p}})$.

Были произведены необходимые изменения в коде MHD_NX для расчета устойчивости плазмы в цилиндрической топологии: изменены условия регулярности на оси симметрии и добавлена возможность использования условий периодичности. Появление островов приводит к новому типу неустойчивости моды $m = 0$, представленной на рис. 7. Такая неустойчивость не возникает ни в результате обращения поля в цилиндрически симметричной плазме, ни в случае двумерной деформации границы без островов. Инкремент неустойчивости островной моды $m = 0$ нечувствителен к значению фактора запаса устойчивости q на границе плазмы, но зависит от положения магнитной поверхности, на которой происходит обращение поля (т.е. $q = 0$): максимальные инкременты соответствуют обращению поля вблизи границы плазмы.

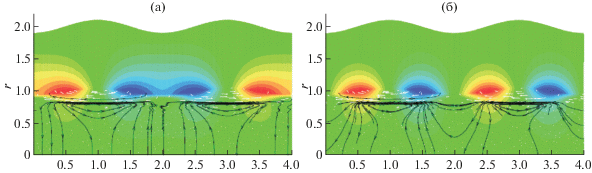
Рис. 7.

Островная мода $m = 0$со свободной границей (положение стенки на расстоянии ${{a}_{w}}{\text{/}}a = 2$ от плазмы) для равновесия на рис. 6. Показаны линии тока для неустойчивого смещения плазмы и линии уровня для полоидальной проекции возмущенного электрического поля; наиболее неустойчивая мода с периодом вдоль продольной оси z равным двум периодам равновесной конфигурации, ${{\omega }^{2}}{\text{/}}\omega _{A}^{2} = - 0.64$ (а); вторая неустойчивая мода с периодом равновесной конфигурации, ${{\omega }^{2}}{\text{/}}\omega _{A}^{2} = - 0.36$, альфвеновская частота $\omega _{A}^{2} = {{({{\psi }_{{{\text{max}}}}} - {{\psi }_{{{\text{min}}}}})}^{2}}{\text{/}}({{a}^{6}}\rho )$ (б).

3.3. Винтовая симметрия в координатах (ρ, θh, z)

Для моделирования островов в плазме с винтовой симметрией также можно рассмотреть цилиндрически симметричное равновесие с периодом по оси z равным ${{L}_{z}} = 2\pi R$, которое соответствует токамаку с большим аспектным отношением $R{\text{/}}a,$ $0 \leqslant r \leqslant a$ [17, 18]. Винтовое возмущение границы плазмы приводит к появлению цепочек винтовых магнитных островов на месте рациональных магнитных поверхностей $q = m{\text{/}}n$, если шаг магнитной линии на такой поверхности совпадает с шагом винтового возмущения. Для того чтобы периодичность системы с островами не нарушалась, необходимо наложить дополнительные условия вращательной симметрии на винтовое возмущение границы в полярных координатах на плоскости $z = {\text{const}}$: $(u,v) = (\rho \cos {{\theta }_{h}},\rho \sin {{\theta }_{h}})$, ${{\theta }_{h}} = \theta - \kappa z$ с шагом винта $2\pi {\text{/}}\kappa $, поскольку шаг винтовой линии магнитного поля на резонансной поверхности равен $2\pi Rq$ [17]. Если возмущение границы в винтовых координатах имеет период $2\pi {\text{/}}m$, то период равновесной конфигурации будет $2\pi R{\text{/}}n$. В то же время, любые возмущения границы, включая винтовую пространственную ось, допустимы для резонансных поверхностей $q = 1{\text{/}}n$.

Магнитное поле с винтовой симметрией можно записать в виде

(9)
${\mathbf{B}} = (\nabla {{\psi }_{h}} \times {{{\mathbf{e}}}_{3}} + f{{{\mathbf{e}}}_{3}}){\text{/}}{{g}_{{33}}}$

в криволинейных координатах $({{x}^{1}},{{x}^{2}},{{x}^{3}}) = (u,v,z)$ с соответствующими контравариантными ${{{\mathbf{e}}}_{k}} = $ $ = \partial {\mathbf{r}}{\text{/}}\partial {{x}^{k}}$, ${{g}_{{ik}}} = {{{\mathbf{e}}}_{i}} \cdot {{{\mathbf{e}}}_{k}}$ и ковариантными векторами ${{{\mathbf{e}}}^{k}} = \nabla {{x}^{k}}$. Обобщенное уравнение Грэда–Шафранова для винтового ${{\psi }_{h}}$ потока (на единицу длины по z) принимает следующий вид:

(10)
$ - \sum\limits_{i,k = 1}^2 {\frac{\partial }{{\partial {{x}^{i}}}}} \left( {\frac{{{{G}_{{ik}}}}}{{{{g}_{{33}}}}}\frac{{\partial {{\psi }_{h}}}}{{\partial {{x}^{k}}}}} \right) = p' + \frac{{ff'}}{{{{g}_{{33}}}}} - \frac{{2\kappa f}}{{g_{{33}}^{2}}},$
со следующими элементами метрического тензора

(11)
$\begin{gathered} {{G}_{{11}}} = 1 + {{\kappa }^{2}}{{v}^{2}},\quad {{G}_{{12}}} = - {{\kappa }^{2}}uv, \\ {{G}_{{22}}} = 1 + {{\kappa }^{2}}{{u}^{2}},\quad {{g}_{{33}}} = 1 + {{\kappa }^{2}}({{u}^{2}} + {{v}^{2}}). \\ \end{gathered} $

Используем линейную зависимость продольной компоненты плотности тока ${{j}_{3}} = ff' + {{g}_{{33}}}p'$ от ${{\psi }_{h}}$ для бессиловой конфигурации $p'$ = 0: ${{j}_{3}} = $ $ = \alpha {{\psi }_{h}}{\text{/}}{{a}^{2}} + A$, где а – малый радиус плазмы, а коэффициенты α и A подбираются для получения равновесий с островами. Такую задачу легко решить в приближении $f = {\text{const}}$, что приводит к линейному уравнению относительно ${{\psi }_{h}}$. Более того, винтовое равновесие с островами можно получить как суперпозицию цилиндрически симметричного решения ${{\psi }_{h}}(\rho )$, которое удовлетворяет неоднородному уравнению (10), и винтовой собственной функции с собственным числом α, удовлетворяющей однородному уравнению без слагаемого $ - 2\kappa f{\text{/}}g_{{33}}^{2}$ и при А = 0. Если у цилиндрически симметричного решения ${{\psi }_{h}}(\rho )$ существует локальный экстремум в плазме для выбранного собственного числа α, что соответствует наличию резонансного значения $q = 1{\text{/}}(R\kappa )$ в плазме, то сумма неоднородного и однородного решений даст равновесие с островами без всякого возмущения цилиндрической границы. При этом ширину острова можно менять, изменяя амплитуду вклада однородного решения (далее эта амплитуда обозначается Н с такой нормировкой собственной функции, что ее максимум совпадает с максимумом цилиндрически симметричного решения).

В коде устойчивости MHD_NX метрический тензор (11) может быть задан так, чтобы охватить все три типа представленных двумерных равновесий с тороидальной, цилиндрической и винтовой симметрией. Расчеты устойчивости для равновесных конфигураций с параметрами $R = 1$, $a = 0.1$, $f = 1$, $q\sim 1$, которые соответствуют токамаку с большим аспектным отношением и сильным продольным полем, показали, что зависимость от параметра $R\kappa $ достаточно слаба, по крайней мере для мод ${{e}^{{i{{n}_{h}}z}}}$ с продольным волновым числом ${{n}_{h}} = 0$. Поэтому расчеты внутренних неустойчивостей (в предположении идеально проводящей стенки на границе плазмы) можно проводить предполагая $R\kappa $ = 1, что соответствует наличию резонансной поверхности $q = 1$ в плазме. Отметим, что волновое число ${{n}_{h}}$ для цилиндрически симметричного равновесия следующим образом связано с волновыми числами в исходных координатах ($r,\theta ,z$): ${{n}_{h}} = n{\text{/}}R - m\kappa $.

Винтовые равновесия с резонансными магнитными островами оказываются сильно неустойчивыми относительно мод ${{n}_{h}} = 0$ (рис. 8). Инкременты, нормированные на винтовую альфвеновскую частоту $\omega _{{Ah}}^{2} = {{({{\psi }_{{h,{\text{max}}}}} - {{\psi }_{{h,{\text{min}}}}})}^{2}}{\text{/}}({{a}^{4}}{{\rho }_{p}})$, где ${{\rho }_{p}} = {\text{const}}$ – массовая плотность плазмы, растут с увеличением ширины острова.

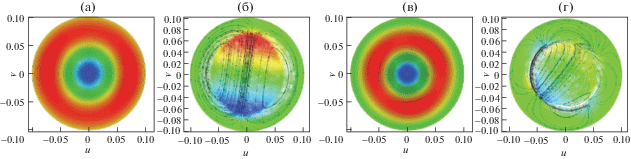
Рис. 8.

Линии уровня винтового потока ${{\psi }_{h}}$ для равновесия с резонансными островами m = 2, параметры равновесия: $\alpha $ = 26.5, A = 2.1, H = 0.04 (а); структура неустойчивого смещения плазмы с ${{n}_{h}}$= 0: линии уровня возмущенного продольного электрического поля и линии тока в плоскости z = const, $\omega _{{}}^{2}{\text{/}}\omega _{{Ah}}^{2} = - 0.87$ (б); линии уровня винтового потока ${{\psi }_{h}}$ для равновесия с резонансными островами m = 3, параметры равновесия: $\alpha $ = 41, A = 1.75, H = 0.04 (в); структура неустойчивого смещения плазмы с ${{n}_{h}}$ = 0, $\omega _{{}}^{2}{\text{/}}\omega _{{Ah}}^{2} = - 0.51$ (г).

4. УСЛОВИЯ УСТОЙЧИВОСТИ ОСЕСИММЕТРИЧНЫХ И ВИНТОВЫХ МОД В ТОКАМАКАХ ПРИ КОНЕЧНОЙ ПЛОТНОСТИ ТОКА НА СЕПАРАТРИСЕ И ПРИ НАЛИЧИИ ПЛАЗМЫ ЗА СЕПАРАТРИСОЙ

При помощи программных кодов для расчета равновесия и устойчивости CAXE-SOL, KINX-SOL, а также кода MHD_NX для численного анализа устойчивости на неструктурных сетках, было продолжено исследование устойчивости плазмы токамаков с ненулевой плотностью тока на сепаратрисе.

Конечная плотность тока на сепаратрисе может приводить к неустойчивости осесимметричной моды n = 0 в токамаках с дивертором [19]. Значение плотности тока вблизи сепаратрисы, вызывающее неустойчивость “пилинг” моды, локализованной около Х-точек, зависит от близости сепаратрисы к конфигурации с двумя Х-точками, лежащими на одной магнитной поверхности. Однако и любое равновесие с одной Х‑точкой на границе плазмы будет неустойчиво для фиксированной границы плазмы и при достаточно большой плотности тока на сепаратрисе. В случае непрерывной через сепаратрису плотности тока это несовместимо со стандартной конфигурацией дивертора в равновесии со свободной границей.

Равновесные диверторные конфигурации с двумя Х-точками на сепаратрисе легко становятся неустойчивыми относительно осесимметричной моды, как только плотность тока в X-точках становится конечной; логично назвать эту неустойчивость пилинг-модой n = 0. Несмотря на кажущуюся локализованную природу моды, равновесные свойства основного объема плазмы, а не только величина плотности тока у границы, играют роль в определении условий устойчивости. Для оценки осесимметричной устойчивости основной плазмы применимо обычное правило: чем ниже внутренняя индуктивность плазмы, что соответствует более плоскому профилю тока, тем лучше устойчивость. Противоположная зависимость наблюдается в случае с большой плотностью тока на сепаратрисе: чем выше плотность тока на границе, что соответствует более низкому значению внутренней индуктивности li, тем хуже устойчивость пилинг-моды n = 0.

Возможна ли неустойчивость пилинг-моды n = 0 в плазме, ограниченной сепаратрисой с одной Х-точкой, отвечающей стандартной конфигурации диверторной плазмы в токамаке JET и проекте ИТЭР? Для ответа на эти вопросы были проведены расчеты устойчивости по коду KINX для конфигураций, подобных плазме токамака JET с однонулевым (SN) и двухнулевым (DN) диверторами. DN конфигурация, которая, однако, не обладает зеркальной симметрией относительно экваториальной плоскости тора, аппроксимируется аналитической формой сепаратрисы с углом 90 градусов в X-точках (рис. 9а). Для исходной SN конфигурации идеальная мода n = 0 устойчива уже при наличии далекой проводящей стенки, находящейся на расстоянии ${{a}_{w}}{\text{/}}a = 2$ от плазмы (${{a}_{w}}{\text{/}}a$ – отношение малых радиусов стенки и плазмы), и только мода, возникающая из-за конечной проводимости стенки (RWM–resistive wall mode), неустойчива при ${{a}_{w}}{\text{/}}a = 1.3$ (рис. 9в, 10а). Отметим, что расчеты инкрементов RWM были проведены только при помощи кода KINX [4] без учета плазмы с разомкнутыми магнитными поверхностями за сепаратрисой. В отличие от SN, конфигурация DN остается идеально неустойчивой с инкрементом, пропорциональным обратному полоидальному альфвеновскому времени, даже для близко расположенной стенки. Несмотря на то, что смещение магнитных поверхностей сильно локализовано вблизи X-точек (рис. 10б), доминирующие полоидальные гармоники m = 1,2 для нормальной к магнитным поверхностям компоненты плазменного смещения $\xi \cdot \nabla \psi $ распространяются на весь объем плазмы (рис. 10в).

Рис. 9.

Сепаратриса с двумя Х-точками (штриховая линия) и исходное сечение плазмы с линиями уровня локального шира линий магнитного поля (а); профили плазмы (б); гармоники ${\mathbf{\xi }} \cdot \nabla \psi $ в потоковых координатах с выпрямленными линиями магнитного поля для глобальной n = 0 моды при наличии резистивной стенки на расстоянии aw/a = 1.3 от плазмы; инкремент моды с учетом конечной проводимости резистивной стенки 70 с−1 (в предположении стальной стенки толщиной 6 см) (в).

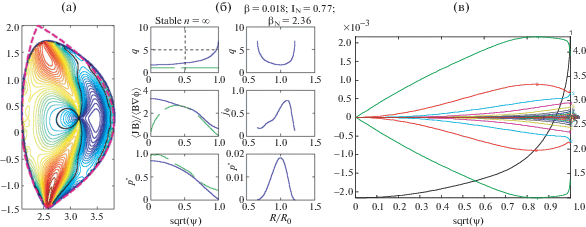
Рис. 10.

Линии уровня смещения плазмы, нормального к магнитным поверхностям, для глобальной моды n = 0 с учетом конечной проводимости резистивной стенки в исходном равновесии с одной Х-точкой, стенка на расстоянии aw/a = 1.3 от плазмы показана толстой черной линией (а); линии уровня нормального смещения плазмы для пилинг-моды n = 0 в равновесии с двумя Х-точками на сепаратрисе (б); гармоники ${\mathbf{\xi }} \cdot \nabla \psi $ в потоковых координатах с выпрямленными линиями магнитного поля для пилинг-моды n = 0 с инкрементом $\gamma {\text{/}}{{\gamma }_{A}} = 3.2 \times {{10}^{{ - 3}}}$ (в).

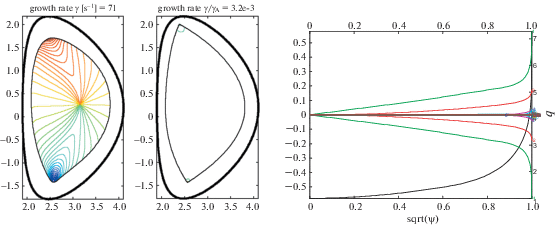
Расстояние до вторичной X-точки менялось в серии равновесий, полученных из DN-конфигурации с фиксированной нижней частью поперечного сечения плазмы с X-точкой и с верхней частью, “срезанной” по магнитной поверхности с заданным отношением полоидального потока внутри сепаратрисы ${{\psi }_{b}}{\text{/}}{{\psi }_{{sx}}}$. Для того чтобы смоделировать скиновый ток, к исходному профилю продольного тока была добавлена функция, принимающая максимальные значения на границе плазмы. Величина скиновой плотности тока характеризуется безразмерной величиной ${{J}_{{||}}}{\text{/}}\left\langle J \right\rangle $ на границе плазмы, где ${{J}_{{||}}}$ – значение плотности тока, параллельного магнитному полю, а $\left\langle J \right\rangle $ – осредненная по сечению плазмы плотность тороидального тока. Оказалось, что для конфигурации, которая соответствует ${{\psi }_{b}}{\text{/}}{{\psi }_{{sx}}} = 0.999$ и граница которой расположена близко к вторичной Х-точке, пилинг-мода n = 0 дестабилизируется при разумной величине скиновой плотности параллельного тока ${{J}_{{||}}}{\text{/}}\left\langle J \right\rangle = 1.2$ для положения проводящей стенки aw/a = 1.3. Для другой формы верхней части конфигурации с ${{\psi }_{b}}{\text{/}}{{\psi }_{{sx}}} = 0.9$, что ближе к исходному SN равновесию, соответствующее значение в 2.5 раза выше и предельная величина равна ${{J}_{{||}}}{\text{/}}\left\langle J \right\rangle = 3$ для положения стенки aw/a = 1.3. Как следствие, соответствующее равновесие со свободной границей будет иметь сильно деформированные магнитные поверхности вблизи X-точки, а также очень острый угол между ветвями X-точки с конечной плотностью тока за сепаратрисой. Реализация таких равновесий в эксперименте маловероятна. Исходные профили для ${{J}_{{||}}}{\text{/}}\left\langle J \right\rangle = 0.5$ представлены на рис. 9б.

С помощью программного кода CAXE-SOL было рассчитано равновесие для конфигурации SN, близкой к ИТЭР с током плазмы 15MA, для дальнейшего исследования влияния плазмы за сепаратрисой в области SOL на устойчивость конфигурации. Исходная функция полоидального потока была модифицирована так, чтобы придвинуть внешнюю сепаратрису ближе к границе плазмы, тем самым вызвав неустойчивость пилинг-моды n = 0 при большой плотности тока на границе в исходных профилях. Расчеты по коду MHD_NX показали, что пилинг-мода может быть стабилизирована относительно широким слоем проводящей плазмы в SOL с толщиной, равной примерно половине расстояния между внешней и внутренней сепаратрисами, или идеальной стенкой куполообразной формы, расположенной близко к X-точке, в дополнение к идеально проводящей стенке на внешней границе области [19]. На рис. 11б и 11в показана структура моды вблизи границы устойчивости для обоих случаев.

Рис. 11.

Линии уровня плотности тороидального тока в конфигурации типа ИТЭР, окруженной вакуумной областью (треугольная сетка), вставки показывают область между сепаратрисами – темный слой с нулевой плотностью тока, ограниченный внешней границей SOL (черная линия) со стороны вакуумной области с треугольной сеткой (а); смещение плазмы для моды, близкой к границе устойчивости, с линиями тока в плазме и SOL вокруг Х-точки и линиями уровня возмущенного тороидального электрического поля: случай с проводящей плазмой в SOL (б); случай с дополнительной идеальной проводящей стенкой (кривая снизу от Х-точки) (в).

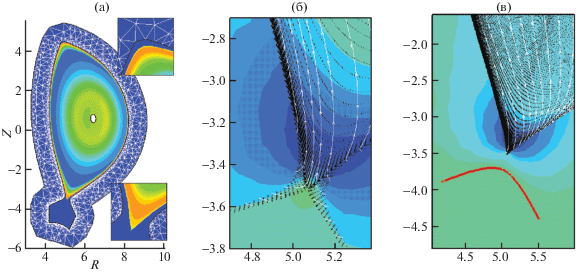
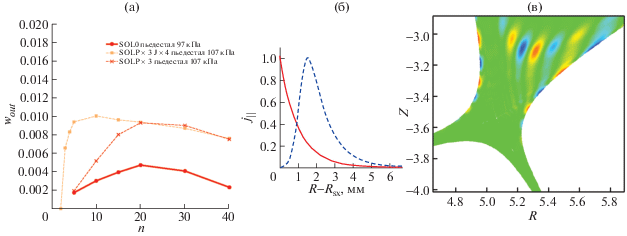
Коды для расчета равновесия и идеальной устойчивости с учетом плазмы за сепаратрисой CAXE-SOL и KINX-SOL были применены к анализу идеальной устойчивости пилинг-баллонных мод (PB) плазмы ИТЭР [20]. Для плазмы с полным током 15MA были исследованы пределы идеальной МГД-устойчивости в зависимости от ширины проводящей плазмы в SOL, используя те же профили с конечной параллельной плотностью тока на сепаратрисе, что и в [10]. Исходные профили градиента давления и плотности параллельного тока на пьедестале (на пределе устойчивости к PB модам) были увеличены в 1.25 раза, чтобы сделать исходную конфигурацию неустойчивой. На рис. 12 показаны предельные значения ширины проводящей плазмы в SOL (измеренной в экваториальной плоскости на внешнем обводе) в зависимости от тороидального волнового числа и для различных профилей. Предположим сначала, что в SOL находится бестоковая проводящая плазма с изменяющейся шириной ${{w}_{{out}}}$. Из рис. 12а видно, что около 5 мм проводящей плазмы в SOL может привести к увеличению высоты пьедестала на 25% из-за стабилизации внешних РВ-мод с различными волновыми числами n (обозначение легенды: SOL0). Высота пьедестала может быть увеличена и за счет конечного градиента давления в SOL. При малой ширине SOL в ИТЭР (~1 мм) градиент давления очень высок и его максимальное значение вне сепаратрисы в несколько раз больше значения на пьедестале внутри сепаратрисы [21]. Мы используем равновесие с градиентом давления, который испытывает разрыв на сепаратрисе и со стороны SOL равен утроенному значению со стороны основной плазмы с экспоненциальным спадом на ширине 1 мм, но с нулевой осредненной по магнитным поверхностям плотностью тока ${{j}_{{||}}}$, параллельной магнитному полю. Это дает дополнительный прирост высоты пьедестала, и устойчивость PB-мод достигается при ширине проводящей плазмы в SOL примерно равной 1 см (рис. 12а, обозначение: SOLPx3). Заметим, что наличие большой параллельной плотности тока в узком SOL с максимумом на сепаратрисе приводит к сильному уменьшению угла Х‑точки сепаратрисы, и только путем смещения максимума от сепаратрисы могут быть построены равновесные конфигурации со значениями полоидального тока выше 100 кА для плазмы ИТЭР [10]. Поэтому для исследования влияния конечного параллельного тока в SOL на устойчивость внешних винтовых мод был использован профиль параллельного тока с положением максимума, сдвинутым от сепаратрисы в SOL (рис. 12б). Достаточно большая плотность тока в SOL (в 4 раза превышающая его значение на сепаратрисе со стороны плазмы) приводит к дестабилизации мод со значениями тороидального волнового числа $n < 15$ (рис. 12а, обозначение SOLP × × 3J × 4, рис. 12в). При этом величина полоидального тока в SOL 60 кА, а тороидального 300 кА.

Рис. 12.

Критическая ширина проводящей плазмы вне сепаратрисы для устойчивости PB-мод с различными тороидальными волновыми числами; различные профили плазмы в SOL, в легенде приведены значения давления на вершине пьедестала в кПа (а); нормированные на максимальное значение профили${{j}_{{||}}}$: экспоненциальный с длиной спада 1 мм (сплошная линия) и сдвинутый от сепаратрисы (штриховая линия) в экваториальной плоскости на внешнем обводе SOL (б); линии уровня нормального смещения плазмы для моды n = 5 для случая с большой параллельной плотностью тока в SOL, ${{w}_{{out}}}$ = 5 мм (в).

5. ЗАКЛЮЧЕНИЕ

Большое разнообразие двумерных равновесий в токамаке без вложенных магнитных поверхностей представляет теоретический и экспериментальный интерес. Для исследования устойчивости таких конфигураций предлагается использовать модифицированный энергетический принцип, основанный на общегеометрических проекциях возмущенного электрического поля с дополнительным требованием нулевой компоненты, параллельной равновесному магнитному полю, в идеальной МГД. Такой энергетический принцип может быть обобщен на случай разомкнутых магнитных поверхностей при использовании МГД совместимых граничных условий на границе дебаевского слоя перед диверторными пластинами в токамаке. На основе обобщенного энергетического принципа разработаны коды идеальной МГД-устойчивости с использованием неструктурных сеток для конфигураций с произвольной топологией магнитных поверхностей, в том числе и с разомкнутыми магнитными поверхностями. Расчеты устойчивости двумерных равновесных конфигураций с магнитными островами были проведены для случаев осевой и винтовой симметрии. Обнаружены новые виды идеальных МГД-неустойчивостей, связанных с наличием островов в плазме токамака и пинча с обращенным полем. Исследование устойчивости равновесий с магнитными островами в двумерной постановке должно быть продолжено, в частности, на более широком классе профилей плотности тока в окрестности острова. Проведены систематические исследования влияния плазмы с конечной плотностью тока за сепаратрисой на МГД-устойчивость плазмы токамака. Показано влияние токов в SOL на пределы устойчивости винтовых мод, локализованных у края плазмы, которые приводят к развитию ELM (Edge Localized Modes). Набор кодов равновесия и устойчивости для плазмы с дивертороми с учетом конечной плотности тока в SOL готов к интеграции с другими кодами для моделирования краевой плазмы. Исследовано влияние конечной плотности тока на сепаратрисе на устойчивость осесимметричных мод $n = 0$ со свободной границей, в том числе, с учетом идеально проводящей плазмы за сепаратрисой.

Работа выполнена при поддержке Российского научного фонда (грант № 16-11-10278).

ПРИЛОЖЕНИЕ

Следуя классической работе [11], где сформулирован энергетический принцип для задачи идеальной МГД-устойчивости, покажем, как преобразуются части функционала потенциальной энергии в случае, когда граница ${{S}_{p}}$ между плазмой и вакуумом включает диверторные пластины ${{S}_{d}}$. Для этого установим связь между векторами смещения ${\mathbf{\xi }}$ и возмущения электрического поля ${\mathbf{e}}$. Из общего условия на границе плазмы и вакуума ${\mathbf{n}} \times \left\langle {\mathbf{E}} \right\rangle = {\mathbf{n}} \cdot {\mathbf{v}}\left\langle {\mathbf{B}} \right\rangle $ ([11], уравнение (2.10)) для идеально проводящей плазмы следует

(A1)
${\mathbf{n}} \times {{{\mathbf{e}}}_{v}} = - {\mathbf{n}} \times ({\mathbf{\xi }} \times {{{\mathbf{B}}}_{v}}){\text{,}}$
где индекс $v$ обозначает величины со стороны вакуума. На части границы ${{S}_{p}}{\backslash }{{S}_{d}}$, совпадающей с равновесной магнитной поверхностью, из (А1) следует ${\mathbf{n}} \times {{{\mathbf{e}}}_{v}} = ({\mathbf{n}} \cdot {\mathbf{\xi }}){{{\mathbf{B}}}_{v}}$. На диверторных пластинах ${{S}_{d}}$ имеем граничное условие ${\mathbf{n}} \cdot {\mathbf{\xi }} = 0$ (3) и соотношение (А1). С учетом этих связей и линеаризованного условия непрерывности полного давления (2.32) на ${{S}_{p}}{\backslash }{{S}_{d}}$ поверхностный член (3.14) из [11] можно записать в виде
(A2)
$\begin{gathered} W - {{W}_{F}} = - \frac{1}{2}\int\limits_{{{S}_{p}}} {\left\{ {{\mathbf{n}} \times ({\mathbf{\xi }} \times {\mathbf{B}}) \cdot \delta {\mathbf{B}} + } \right.} \\ + \;\left. {({\mathbf{n}} \cdot {\mathbf{\xi }})(\Gamma p\nabla \cdot {\mathbf{\xi }} + {\mathbf{\xi }} \cdot \nabla p)} \right\}dS = \\ = \;{{W}_{S}} - \frac{1}{2}\int\limits_{{{S}_{p}}\backslash {{S}_{d}}} {{\mathbf{n}} \times {{{\mathbf{e}}}_{v}} \cdot \nabla \times {{{\mathbf{e}}}_{v}}dS} + \\ + \;\frac{1}{2}\int\limits_{{{S}_{d}}} {{\mathbf{n}} \times {{{\mathbf{e}}}_{v}} \cdot \delta {\mathbf{B}}dS} + \frac{1}{2}\int\limits_{{{S}_{d}}} {({\mathbf{n}} \cdot \left\langle {\mathbf{B}} \right\rangle )({\mathbf{\xi }} \cdot \delta {\mathbf{B}})dS} , \\ \end{gathered} $
где ${{W}_{S}} = \frac{1}{2}\int_{{{S}_{p}}} {{{{({\mathbf{n}} \cdot {\mathbf{\xi }})}}^{2}}{\mathbf{n}} \cdot \left\langle {\nabla (p + {{B}^{2}}{\text{/}}2)} \right\rangle dS} ,$ а угловые скобки означают скачок соответствующей величины на границе, например $\left\langle {\mathbf{B}} \right\rangle = {{{\mathbf{B}}}_{v}} - {{{\mathbf{B}}}_{p}}$. Последнее слагаемое в (А2) обнуляется из-за предположения о непрерывности нормальной компоненты магнитного поля через тонкие диверторные пластины. Следующие с конца два слагаемых из (А2) после использования формулы Гаусса–Остроградского и с учетом $\delta {{{\mathbf{B}}}_{v}} = - \nabla \times {{{\mathbf{е }}}_{v}}$, $\nabla \times \delta {{{\mathbf{B}}}_{v}} = 0$ в вакууме дают
(A3)
$\begin{gathered} - \frac{1}{2}\int\limits_{{{S}_{p}}} {{\mathbf{n}} \times {{{\mathbf{e}}}_{v}} \cdot \nabla \times {{{\mathbf{e}}}_{v}}dS} + \\ + \;\frac{1}{2}\int\limits_{{{S}_{d}}} {{\mathbf{n}} \times {{{\mathbf{e}}}_{v}} \cdot (\delta {\mathbf{B}} + \nabla \times {{{\mathbf{e}}}_{v}})dS} = {{W}_{V}} + {{W}_{d}}, \\ {{W}_{V}} = \frac{1}{2}{{\int\limits_{{{V}_{v}}} {\left| {\nabla \times {{{\mathbf{e}}}_{v}}} \right|} }^{2}}dV, \\ {{W}_{d}} = \frac{1}{2}\int\limits_{{{S}_{d}}} {{{{\mathbf{e}}}_{v}} \cdot {\mathbf{n}} \times \left\langle {\delta {\mathbf{B}}} \right\rangle dS} , \\ \end{gathered} $
что совпадает с выражениями (2) и (4). В случае отсутствия равновесного поверхностного тока интеграл ${{W}_{S}}$ обнуляется, а соотношение (A1) сводится к непрерывности тангенциальной компоненты $\left\langle {{\mathbf{e}} \times {\mathbf{n}}} \right\rangle = 0$.

Список литературы

  1. Морозов А.И., Соловьев Л.С. // Вопросы теории плазмы. Вып. 2 / Ред. М.А. Леонтовича. М.: Госатомиздат, 1963. С. 3.

  2. Pustovitov V.D. // Nucl. Fusion. 1990. V. 30. P. 1079.

  3. Brushlinskii K.V., Goldich A.S. // Differential Equations. 2016.V. 52. P. 845.

  4. Degtyarev L., Martynov A., Medvedev S., Troyon F., Villard L., Gruber R. // Computer Phys. Commun. 1997. V. 103. P. 10.

  5. Martynov A.A., Medvedev S.Yu., Villard L. // Phys. Rev. Lett. 2003. V. 91. P. 85004.

  6. Hu Y. // Phys. Plasmas. 2008. V. 15. P. 022505.

  7. Guo W., Wang S., Li J. // Plasma Sci. Technol. 2010. V. 12. P. 657.

  8. Fujita T. // Nucl. Fusion. 2010. V. 50. P. 113001.

  9. Medvedev S.Yu., Martynov A.A., Villard L. // 35th EPS Conf. Plasma Physics, Hersonissos, Greece. ECA. 2008. V. 32D. P2.063.

  10. Medvedev S.Yu., Martynov A.A., Drozdov V.V., Iva-nov A.A., Poshekhonov Yu.Yu. // Plasma Phys. Control. Fusion. 2017. V. 59. P. 025018.

  11. Bernstein I.B., Frieman E.A., Kruskal M.D., Kuls-rud R.M. // Proc. Roy. Soc. London. 1958. V. A244. P. 17.

  12. Кадомцев Б.Б. // Вопросы теории плазмы. Вып. 2 / Под ред. М.А. Леонтовича. М.: Госатомиздат, 1963. С. 132.

  13. Strauss H.R. // Phys. Plasmas. 2014. V. 21. P. 032506.

  14. Medvedev S.Yu., Martynov A.A., Villard L. // 33rd EPS Conf. Plasma Phys. Rome, Italy. ECA. 2006. V. 30I. P1.167.

  15. Medvedev S.Yu., Martynov A.A., Villard L. // 34th EPS Conf. Plasma Physics, Warsaw, Poland. ECA. 2007. V. 31F. P4.087.

  16. Medvedev S.Yu., Martynov A.A., Villard L. // 36th EPS Conf. Plasma Physics, Sofia, Bulgaria. ECA. 2009. V. 33E. P1.130.

  17. Medvedev S.Yu., Martynov A.A., Villard L. // 41st EPS Conf. Plasma Physics, Berlin, Germany. ECA. 2014. V. 38F. P4.042.

  18. Medvedev S.Yu., Martynov A.A., Villard L. // 39th EPS Conf. 16th Int. Congress on Plasma Physics, Stockholm, Sweden. ECA. 2012. V. 36F. P1.082.

  19. Medvedev S.Yu., Martynov A.A., Villard L. // 40th EPS Conf. Plasma Physics, Espoo, Finland. ECA. 2013. V. 37D. P5.145.

  20. Martynov A.A., Medvedev S.Yu. // 44th EPS Conf. Plasma Physics, Belfast, Northern Ireland, UK. ECA. 2017. V. 41. P4.135.

  21. Medvedev S.Yu., Martynov A.A., Drozdov V.V., Iva-nov A.A., Poshekhonov Yu.Yu., Konovalov S.V., Villard L. // 44th EPS Conf. Plasma Physics, Belfast, Northern Ireland, UK. ECA. 2017. V. 41. O4.125.

  22. Loarte A., Liu F., Huysmans G.T.A., Kukushkin A.S., Pitts R.A. // J. Nucl. Materials. 2014. V. 463. P. 401.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика плазмы

Архивы выпусков Информация о журнале Отправить рукопись в журнал