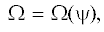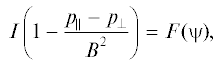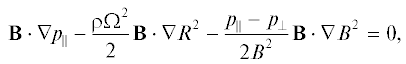Физика плазмы, 2019, T. 45, № 3, стр. 195-212

1. ВВЕДЕНИЕ

В современных установках с магнитным удержанием (в токамаках, стеллараторах) широко используются различные методы мощного дополнительного нагрева плазмы, такие как нагрев инжектируемыми пучками нейтральных частиц, ионно-циклотронный резонансный нагрев (ИЦРН), электронно-циклотронный резонансный нагрев (ЭЦРН). Таким образом достигаются высокие температуры плазмы, ${{T}_{i}} \geqslant 10$ кэВ, при которых существенно падает частота кулоновских столкновений частиц плазмы. Из-за этого скорость инжекции дополнительной энергии в параллельные или перпендикулярные по отношению к магнитному полю движения частиц может превышать скорость столкновительной изотропизации температуры плазмы. Поэтому зачастую мощный дополнительный нагрев плазмы приводит к сильной анизотропии ее давления (см., например, [1]). Сильную анизотропию давления плазмы наблюдали как в более ранних экспериментах [2–5], так и в некоторых современных установках [6–10].

Как и можно было ожидать, тангенциальная инжекция мощных пучков нейтральных частиц приводит к тому, что продольное давление плазмы ${{p}_{\parallel }}$ превосходит ее поперечное давление ${{p}_{ \bot }}$, ${{p}_{\parallel }} > {{p}_{ \bot }}$. Такая анизотропия зафиксирована в экспериментах на стеллараторах CHS и LHD. В стеллараторе CHS при тангенциальной инжекции нейтральных пучков достигалось отношение давлений ${{p}_{\parallel }}{\text{/}}{{p}_{ \bot }} = 3$ [5]. Позднее аналогичный уровень анизотропии наблюдался в разрядах с низкой плотностью плазмы и мощной инжецией пучков нейтральных частиц в стеллараторе LHD [7–9].

Анизотропия давления плазмы фиксировалась и в экспериментах на современных токамаках. Так, например, анализ данных диагностик на токамаках JET и Tore Supra при мощном дополнительном нагреве плазмы выявил большую разницу между продольным и поперечным давлениями: отношение ${{p}_{ \bot }}{\text{/}}{{p}_{\parallel }}$ доходило до 3 в некоторых разрядах на JET с инжекцией пучков нейтральных частиц и с волнами на резонансной ионно-циклотронной частоте (ion cyclotron resonance frequency waves, ICRF) [4] и ${{p}_{ \bot }}{\text{/}}{{p}_{\parallel }}$ до 2 в разрядах на Tore Supra c мощным нагревом ICRF волнами [6]. Также высокая степень анизотропии ${{p}_{ \bot }}{\text{/}}{{p}_{\parallel }} \simeq 1.7$ была обнаружена в сферическом токамаке MAST в разрядах с нагревом пучками нейтральных частиц [10].

Очень часто дополнительный нагрев плазмы сопровождается вращением плазмы. Скорости тороидального вращения плазмы достигают величин порядка ионно-звуковой скорости и измерялись на многих установках (см., например, экспериментальные обзоры [11–13]).

В свете сказанного выше представляется полезным исследовать совместное влияние эффектов, обусловленных анизотропией давления плазмы и ее тороидального вращения на низкочастотные МГД-возмущения, такие как зональные течения, геодезические акустические моды (ГАМ), низкочастотные альфвеновские моды, которые, в соответствии с современными представлениями, оказывают существенное влияние на функционирование современных токамаков. При исследовании упомянутых низкочастотных явлений в токамаках полезным оказывается анализ непрерывных МГД-спектров. В частности, такой анализ представляется полезным с точки зрения получения информации о щелях в непрерывном спектре, в которых могут существовать собственные альфвеновские моды (TAE, BAE, BAAE и т.п.), возбуждаемые высокоэнергичными частицами. Для изотропной плазмы в состоянии статического равновесия в рамках стандартной идеальной МГД такие спектры были впервые получены в работе Худблуда [14]. В дальнейшем анализ МГД-спектров был обобщен на случай равновесий с вращением плазмы. В многочисленных работах [15–24] исследовалось влияние различных аспектов, связанных с вращением, на МГД-спектры плазмы с изотропным давлением. В нашей недавней работе [25] мы обобщили анализ низкочастотного непрерывного акустико-альфвеновского спектра, под которым понимают спектр, образующийся в результате тороидального зацепления альфвеновских и низкочастотных магнитозвуковых мод [26], на случай статических равновесий плазмы с анизотропией давления. В качестве основы нашего анализа была использована хорошо известная МГД-модель Чу–Голдбергера–Лоу (ЧГЛ) [27], в которой термодинамическое состояние плазмы описывается двумя адиабатами. В настоящей работе, оставаясь в рамках ЧГЛ-модели, мы учитываем эффекты равновесного тороидального вращения плазмы.

Статья построена следующим образом. В разд. 2 мы приводим исходные МГД-уравнения ЧГЛ-модели, в которых учитывается эффект анизотропии давления, обсуждаем равновесие плазмы с тороидальным вращением и представляем линеаризованные уравнения возмущений такого равновесия, выраженные через лагранжевы смещения. В разд. 3 мы упрощаем уравнения возмущений плазмы применительно к возмущениям, сильно локализованным на магнитных поверхностях, и выводим систему уравнений, определяющих низкочастотный непрерывный МГД-спектр тороидально-вращающейся плазмы с анизотропным давлением. В разд. 4 мы применяем эти уравнения для аналитического исследования непрерывного МГД-спектра тороидально-вращающейся плазмы с низким анизотропным давлением, $({{p}_{\parallel }},{{p}_{ \bot }}){\text{/}}{{B}^{2}} \simeq {{\epsilon }^{2}}$, для максимально упрощенной модели токамака с большим аспектным отношением, $\epsilon = a{\text{/}}{{R}_{0}} \ll 1$, и круглыми концентрическими магнитными поверхностями (a и ${{R}_{0}}$ – малый и большой радиусы токамака, B – величина равновесного магнитного поля). Мы получаем и исследуем аналитически и численно дисперсионные уравнения как для возмущений в виде зональных течений с $(m,n) = 0$, так и для более общих электромагнитных возмущений с $(m,n) \ne 0$, где m и n – тороидальное и полоидальное волновые числа. Мы также выводим общее условие неустойчивости мод непрерывного спектра, обусловленной стратификацией плазмы по полоидальному углу на магнитных поверхностях из-за эффектов анизотропии давления и вращения. В разд. 5 мы суммируем и обсуждаем полученные в работе результаты. В Приложении представлен альтернативный вывод дисперсионного уравнения для зональных течений, основанный на предположении об их электростатичности и тороидальной симметрии.

2. ИСХОДНЫЕ УРАВНЕНИЯ: РАВНОВЕСИЕ И УРАВНЕНИЯ ДЛЯ ТОРОИДАЛЬНЫХ СОБСТВЕННЫХ МОД

При описании бесстолкновительной вращающейся плазмы с анизотропным давлением исходим из хорошо известной одножидкостной модели Чу–Голдбергера–Лоу [27]

Здесь ρ – массовая плотность плазмы, v – ее скорость, B – магнитное поле, нормированное таким образом, чтобы избавиться от множителя $1{\text{/}}4\pi $ в правой части уравнения (2), ${\mathbf{j}} = \nabla \times {\mathbf{B}}$, а $d{\text{/}}dt = $ $ = \partial {\text{/}}\partial t + {\mathbf{v}} \cdot \nabla $ – конвективная производная. Компоненты тензора давления P имеют вид

Продольное и поперечное давления удовлетворяют уравнениям так называемых ЧГЛ-адиабат

Используя явное выражение для градиента тензора давления (5), удобно и полезно переписать уравнение движения плазмы (2) в виде [28, 29]

Записанное в таком виде уравнение упрощает дальнейший анализ.

Далее мы будем полагать, что все физические величины представляются в виде суммы равновесной величины и ее малого возмущения, отмеченного штрихом: $f \to f + f{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{'}}$, ${\mathbf{f}} \to {\mathbf{f}} + {\mathbf{f}}{\kern 1pt} {\kern 1pt} {\text{'}}$.

2.1. Равновесие плазмы

Будем искать общее осесимметричное равновесие тороидально-вращающейся плазмы, удовлетворяющее уравнениям (1), (3), (6)–(8), в которых полагаем $\partial {\text{/}}\partial t = 0$. Используем цилиндрическую систему координат $\{ R,Z,\varphi \} $ с центром на основной оси тора, где R – расстояние от оси, Z – расстояние вдоль оси, а φ – угловая координата, от которой, в силу предположения об осевой симметрии, равновесные величины не зависят, $\partial {\text{/}}\partial \varphi = 0$. Равновесные магнитное поле и скорость плазмы могут быть представлены в виде

$\begin{gathered} {\mathbf{B}} = I(R,Z)\nabla \varphi + \nabla \varphi \times \nabla \psi (R,Z), \\ {\mathbf{v}} = {{R}^{2}}\Omega (R,Z)\nabla \varphi , \\ \end{gathered} $

где Ω – угловая скорость тороидального вращения, I – функция, определяющая полоидальный ток, а ψ – полоидальный магнитный поток. Тогда общее осесимметричное стационарное решение вышеуказанных уравнений описывается уравнениями (см., например, [29, 30])

(9)

(10)

(11)

(12)

$\begin{gathered} \nabla \cdot \left\{ {\left( {1 - \frac{{{{p}_{\parallel }} - {{p}_{ \bot }}}}{{{{B}^{2}}}}} \right)\frac{{\nabla \psi }}{{{{R}^{2}}}}} \right\} + \frac{{\nabla \psi \cdot \nabla {{p}_{\parallel }}}}{{{{{\left| {\nabla \psi } \right|}}^{2}}}} + \frac{I}{{{{R}^{2}}}}\frac{{dF}}{{d\psi }} - \\ - \;\frac{{{{p}_{\parallel }} - {{p}_{ \bot }}}}{{{{B}^{2}}}}\frac{{\nabla \psi \cdot \nabla ({{B}^{2}}{\text{/}}2)}}{{{{{\left| {\nabla \psi } \right|}}^{2}}}} - \frac{{\rho {{\Omega }^{2}}}}{2}\frac{{\nabla \psi \cdot \nabla {{R}^{2}}}}{{{{{\left| {\nabla \psi } \right|}}^{2}}}} = 0. \\ \end{gathered} $

Здесь $\Omega (\psi )$ и $F(\psi )$ – произвольные функции полоидального магнитного потока. Постоянство угловой тороидальной скорости Ω на магнитных поверхностях (9) следует из условия вмороженности магнитного поля в плазму (3). Уравнение (10) соответствует тороидальной проекции (вдоль $\nabla \varphi $) уравнения (8) и описывает влияние анизотропии давления плазмы на функцию I, определяющую полоидальный ток. Оно показывает, что равновесный полоидальный ток I в плазме низкого давления ${{\beta }_{{\parallel , \bot }}} \equiv {{p}_{{\parallel , \bot }}}{\text{/}}{{B}^{2}} \ll 1$, а также в плазме со слабой анизотропией давления, ${{\beta }_{\parallel }} - {{\beta }_{ \bot }} \ll 1$, практически постоянен на магнитной поверхности (с точностью до членов порядка ${{\beta }_{\parallel }} - {{\beta }_{ \bot }}$). Уравнение (11) описывает равновесие плазмы вдоль магнитного поля ${\mathbf{B}}$. Наконец, уравнение (12) представляет собой обобщение уравнения Грэда–Шафранова и соответствует балансу сил в направлении поперек магнитных поверхностей токамака.

Важно отметить, что как и при статическом равновесии при осесимметричном равновесии с чисто тороидальным вращением плазмы уравнение непрерывности (1) и уравнение поперечной ЧГЛ-адиабаты (7) удовлетворяются произвольными функциями $\rho = \rho (R,Z)$, ${{p}_{ \bot }} = {{p}_{ \bot }}(R,Z)$, которые не определяются уравнениями равновесия в модели ЧГЛ. Продольное давление плазмы ${{p}_{\parallel }}$ определяется условием продольного равновесия (11), и равновесное уравнение продольной ЧГЛ-адиабаты (6) удовлетворяется автоматически. При исследовании МГД-волн и неустойчивостей целесообразно использовать вместо цилиндрической системы координат $\{ R,Z,\varphi \} $ потоковую систему координат с выпрямленными силовыми линиями $\{ \psi ,\vartheta ,\varphi \} $, где $\vartheta $ – полоидальный угол. Будем предполагать, что для токамаков с большим аспектным отношением поперечное давление и массовая плотность плазмы слабо зависят от полоидального угла $\vartheta $, так что ${{p}_{ \bot }} = {{p}_{{0 \bot }}}(\psi ) + \epsilon {{p}_{{1 \bot }}}(\psi ,\vartheta )$ и $\rho = {{\rho }_{0}}(\psi ) + \epsilon {{\rho }_{1}}(\psi ,\vartheta )$.

3. УРАВНЕНИЯ НИЗКОЧАСТОТНОГО НЕПРЕРЫВНОГО МГД-СПЕКТРА

Упростим линеаризованные уравнения для мод возмущений плазмы, сильно локализованных вблизи выделенной магнитной поверхности $\psi = {{\psi }_{0}}$. Для таких мод предполагается, что производная собственных функций поперек магнитной поверхности, $\nabla \psi \cdot \nabla {\text{/}}\left| {\nabla \psi } \right|$, значительно превышает их производные вдоль двух других направлений, а также градиенты равновесных физических величин $1{\text{/}}L$

При выводе соответствующих уравнений непрерывного спектра мы будем следовать подходу, изложенному в работах [16, 23].

Производная поперек магнитной поверхности в явном виде входит только в уравнение (20), описывающее возмущенное движение плазмы перпендикулярно магнитной поверхности, и неявно (через $\nabla \cdot \xi $) – в выражения, определяющие $\rho '$, $p_{\parallel }^{'}$, $p_{ \bot }^{'}$ и ${{Q}_{\parallel }}$. В случае низкочастотных мод члены с нормальной производной не могут быть компенсированы другими членами в уравнении (20), и таким образом, оно может быть удовлетворено только при выполнении равенства

Подставляя соответствующие выражения $p_{ \bot }^{'}$ и ${{Q}_{\parallel }}$ из уравнений (14) и (21) в уравнение (22) и интегрируя полученное уравнение по $\psi $, получаем

С другой стороны, используя разложение $\xi $ из (17), находим

Тогда из уравнений (23) и (24) следует, что они могут быть удовлетворены только при выполнении условия

Выражения для компонент возмущенного магнитного поля также упрощаются и принимают вид

Подставляем выражения (25) и (26) в уравнения (18) и (19) и окончательно получаем следующую систему уравнений, определяющую непрерывный спектр колебаний тороидально-вращающейся плазмы с анизотропным давлением

Эта система уравнений не содержит производных смещений плазмы по отношению к ψ, а только их производные по полоидальному углу $\vartheta $ (через оператор ${\mathbf{B}} \cdot \nabla $). Она может рассматриваться как аналог соответствующей системы уравнений, полученной в работе ван дер Холста, Белиена и Худблуда [16] в рамках стандартной МГД-модели. В системе отсчета, вращающейся с плазмой, эта система уравнений описывает тороидальное зацепление медленных магнитозвуковых и альфвеновских возмущений, обусловленное кривизной магнитных силовых линий, эффектами из-за анизотропии давления плазмы, центробежными и кориолисовыми эффектами. Сдвинутые на доплеровскую величину частоты $\bar {\omega } = \omega + n\Omega $ могут рассматриваться как собственные значения регулярной задачи на собственные значения, описываемой уравнениями (27) и (28).

При выводе данной системы уравнений было сделано всего лишь два предположения – о сильной локализации возмущений поперек магнитных поверхностей и об их низкочастотности по сравнению с частотой быстрого магнитного звука. При этом не делалось никаких дополнительных предположений, касающихся геометрии магнитных силовых линий и давления плазмы. В общем случае полученная система уравнений может являться основой для численных расчетов низкочастотных МГД-спектров тороидально-вращающейся плазмы с анизотропным давлением в осесимметричных системах магнитного удержания.

Уравнения (27), (28) существенно упрощаются в предельном случае токамаков с малым обратным аспектным отношением $\epsilon \ll 1$, низким давлением плазмы и ее сравнительно медленным (по сравнению с альфвеновской скоростью) вращением, такими, что $({{\beta }_{\parallel }},{{\beta }_{ \bot }}) \simeq {{\epsilon }^{2}}$, ${{\Omega }^{2}}R_{0}^{2} \lesssim ({{p}_{\parallel }},{{p}_{ \bot }}){\text{/}}\rho $. Тогда, разлагая уравнения (27) и (28) по степеням малого параметра $\epsilon $ и сохраняя главные члены разложения, приходим к следующим уравнениям:

Мы учли, что при указанных предположениях полоидальный ток можно считать постоянным на магнитной поверхности, $I \approx F(\psi )$. Эти уравнения будут использованы ниже при анализе непрерывных спектров зональных течений и акустико-альфвеновских спектров в токамаках.

4. НЕПРЕРЫВНЫЙ МГД-СПЕКТР В ТОКАМАКАХ С БОЛЬШИМ АСПЕКТНЫМ ОТНОШЕНИЕМ И НИЗКИМ ДАВЛЕНИЕМ ПЛАЗМЫ

Применим уравнения (29) и (30) для исследования низкочастотного непрерывного МГД-спектра в токамаках с низким давлением плазмы и малым обратным аспектным отношением $a{\text{/}}{{R}_{0}} \ll 1$. Для простоты мы предполагаем, что магнитные поверхности токамака являются концентрическими и круглыми. Тогда они могут быть описаны следующими выражениями:

Полоидальный угол $\vartheta $ выбран таким образом, что магнитные силовые линии являются прямыми на плоскости $(\vartheta ,\varphi )$, а коэффициент запаса устойчивости токамака q является функцией магнитной поверхности, $q = q(r)$. Из равновесного баланса сил вдоль магнитного поля (11) следует, что осциллирующая по полоидальному углу часть продольного давления ${{p}_{\parallel }}$ пропорциональна $cos\vartheta $. Мы также предполагаем, что для рассматриваемой конфигурации осциллирующие по $\vartheta $ части поперечного давления ${{p}_{ \bot }}$ и массовой плотности ρ также малы как $\epsilon $ и содержат лишь члены пропорциональные $cos\vartheta $ и $sin\vartheta $.

4.2. Зональные течения и ГАМ

Под зональными течениями понимают тороидально- и полоидально-симметричные возмущения с $(m,n) = 0$, и поэтому для них $k = 0$. Тогда дисперсионное уравнение (34) упрощается и принимает вид

(35)

${{\omega }^{4}} - \left( {\omega _{G}^{2} + \frac{{c_{\parallel }^{2}}}{{{{q}^{2}}R_{0}^{2}}}} \right){{\omega }^{2}} + \frac{{c_{\parallel }^{4}G}}{{{{q}^{2}}R_{0}^{4}}} = 0,$

где

$\begin{gathered} G = \frac{\tau }{6}\left\langle {\frac{\partial }{{\partial \vartheta }}ln\left( {\frac{1}{{{{B}^{2}}}}} \right)\frac{\partial }{{\partial \vartheta }}ln\left( {\frac{{{{s}_{ \bot }}}}{{s_{\parallel }^{{1/3}}}}} \right)} \right\rangle - \\ - \;\frac{{{{M}^{2}}}}{2}\left\langle {\frac{\partial }{{\partial \vartheta }}ln{{R}^{2}}\frac{\partial }{{\partial \vartheta }}lns_{\parallel }^{{1/3}}} \right\rangle . \\ \end{gathered} $

Чтобы записать уравнение (35) в этом виде мы использовали тождество

(36)

$\frac{\partial }{{\partial \vartheta }}ln\left( {\frac{{\rho s_{\parallel }^{{1/3}}}}{{{{B}^{2}}}}} \right) \equiv \frac{1}{2}\left( {1 + \frac{\tau }{3}} \right)\frac{\partial }{{\partial \vartheta }}ln\left( {\frac{1}{{{{B}^{2}}}}} \right) + \frac{{{{M}^{2}}}}{2}\frac{\partial }{{\partial \vartheta }}ln{{R}^{2}},$

которое следует из уравнения равновесного баланса сил вдоль магнитного поля (11). Используя это тождество, можно показать, что дискриминант квадратного уравнения относительно ${{\omega }^{2}}$ положителен, и поэтому его решения являются либо осциллирующими во времени (при ${{\omega }^{2}} > 0$), либо апериодически растущими или затухающими, ${\text{Re}}\omega = 0$ (при ${{\omega }^{2}} < 0$). Тогда из уравнения (35) следует, что зональные течения устойчивы для таких равновесий, в которых

(37)

$\begin{gathered} \int\limits_0^{2\pi } \left\{ {\frac{\tau }{3}\frac{\partial }{{\partial \vartheta }}ln\left( {\frac{1}{{{{B}^{2}}}}} \right)\left[ {\frac{\partial }{{\partial \vartheta }}ln\left( {\frac{{{{s}_{ \bot }}}}{{s_{\parallel }^{{1/3}}}}} \right)} \right]} \right. - \\ \left. { - \;{{M}^{2}}\frac{\partial }{{\partial \vartheta }}ln{{R}^{2}}\frac{\partial }{{\partial \vartheta }}lns_{\parallel }^{{1/3}}} \right\}d\vartheta \geqslant 0. \\ \end{gathered} $

Отметим, что рассматриваемые в этом разделе зональные течения являются электростатическими возмущениями, и их дисперсионное уравнение может быть получено иным способом, изначально основанным на предположении об их электростатичности и представленным в Приложении.

Используя уравнения (11), (31), (32) и определения энтропийных функций ${{s}_{\parallel }}$ и ${{s}_{ \bot }}$, в явном виде вычисляем усредненные по полоидальному углу величины и представляем дисперсионное уравнение (35) в виде

(38)

${{\omega }^{4}} - A{{\omega }^{2}} + C = 0,$

где

$\begin{gathered} A = \left[ {\frac{1}{2} + \frac{{2\tau }}{3} + \frac{\tau }{3}{{\lambda }_{ \bot }} + \left( {\frac{7}{2} + {{\lambda }_{\rho }}} \right){{M}^{2}} + \frac{1}{{{{q}^{2}}}}} \right]\frac{{c_{\parallel }^{2}}}{{R_{0}^{2}}}, \\ C = \left\{ {\frac{\tau }{3}\left( {1 + {{\lambda }_{ \bot }} - \frac{\tau }{6}} \right) + \left( {\frac{1}{2} + {{\lambda }_{\rho }} - \frac{\tau }{3}} \right){{M}^{2}}\mathop - \limits_{_{{_{{_{{_{{}}}}}}}}} } \right. \\ \end{gathered} $

(39)

$ - \;\left. {\frac{{{{M}^{4}}}}{2}} \right\}\frac{{c_{\parallel }^{4}}}{{{{q}^{2}}R_{0}^{4}}},$

$\begin{gathered} {{\lambda }_{ \bot }} = \frac{{\left\langle {(\partial ln{{p}_{ \bot }}{\text{/}}\partial \vartheta )(\partial ln(1{\text{/}}{{B}^{2}}){\text{/}}\partial \vartheta )} \right\rangle }}{{\left\langle {\mathop {\left( {\partial ln(1{\text{/}}{{B}^{2}}){\text{/}}\partial \vartheta } \right)}\nolimits^2 } \right\rangle }}, \\ {{\lambda }_{\rho }} = \frac{{\left\langle {(\partial ln\rho {\text{/}}\partial \vartheta )(\partial ln{{R}^{2}}{\text{/}}\partial \vartheta )} \right\rangle }}{{\left\langle {\mathop {\left( {\partial ln{{R}^{2}}{\text{/}}\partial \vartheta } \right)}\nolimits^2 } \right\rangle }}. \\ \end{gathered} $

Дисперсионное уравнение (38) описывает две ветви зональных течений – низкочастотные зональные течения с частотой ${{\omega }^{2}} = A{\text{/}}2 - \sqrt {{{A}^{2}}{\text{/}}4 - C} $, и высокочастотные зональные течения с частотой ${{\omega }^{2}} = A{\text{/}}2 + \sqrt {{{A}^{2}}{\text{/}}4 - C} $. Низкочастотную ветвь зональных течений обычно коротко называют просто зональными течениями (ЗТ), а высокочастотную – ГАМ, поскольку в отсутствие вращения и анизотропии давления эта ветвь обусловлена геодезической кривизной магнитных силовых линий.

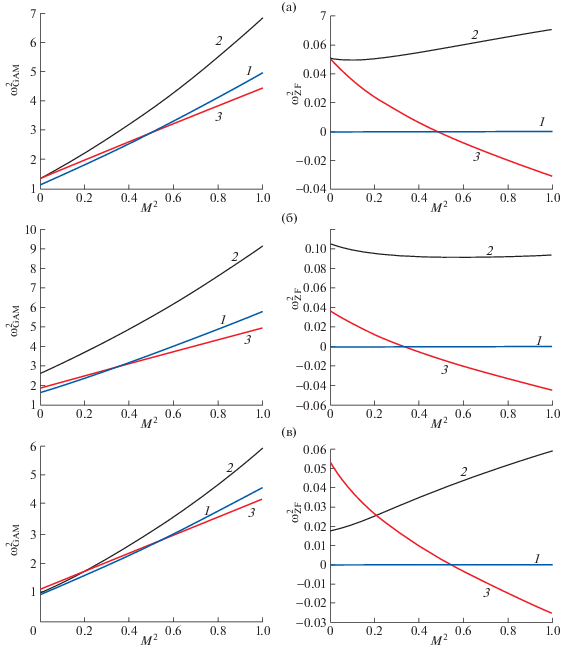
Высокочастотные зональные течения (или ГАМ) в диапазоне частот от 15 до 25 кГц наблюдаются во многих современных токамаках и стеллараторах (см., например, обзоры [31, 32]). Значительно более трудной экспериментальной задачей является идентификация низкочастотных (стационарных) зональных течений. Тем не менее соответствующие свидетельства их существования были получены в экспериментах на компактной винтовой системе (CHS) [33] и на токамаках HT-7 [34] и DIII-D [35, 36]. В этих экспериментах были обнаружены полоидально- и тороидально-симметричные возмущения электростатического потенциала плазмы в диапазоне частот 0.5–2 кГц. Обычно конечные частоты стационарных зональных течений связывают с их взаимодействием с мелкомасштабной турбулентностью плазмы. Как показывают уже грубые оценки при $q = 2{\kern 1pt} - {\kern 1pt} 3$ и ${{M}^{2}} \lesssim 1$ (см., например, рис. 1), из представленной нами теории следует, что частота таких зональных течений примерно в десять раз ниже частоты ГАМ. Эти оценки согласуются с экспериментальными данными, и, таким образом, нельзя исключить, что конечность частоты низкочастотных зональных течений может быть обусловлена тороидальным вращением и анизотропией давления плазмы.

Рис. 1.

Зависимости собственных частот ГАМ (${{\omega }_{{GAM}}}$) и ЗТ (${{\omega }_{{ZF}}}$) от квадрата числа Маха ${{M}^{2}}$ для различных равновесий: 1 – равновесие с ${{s}_{\parallel }} = {{s}_{\parallel }}(\psi )$, ${{s}_{ \bot }} = {{s}_{ \bot }}(\psi )$; 2 – гирокинетическое равновесие (43); 3 – равновесие с ${{p}_{\parallel }} + {{p}_{ \bot }} = P(\psi )$, $\rho = \rho (\psi )$. Вычисления проведены при $q = 2$ для различных отношений поперечного и продольного давлений τ: $\tau = 1$ (а); $\tau = 2$ (б); $\tau = 1{\text{/}}2$ (в). Собственные частоты нормированы на величину ${{c}_{\parallel }}{\text{/}}{{R}_{0}}$.

Можно легко показать, что ГАМ всегда устойчивы. Что касается ЗТ, то они неустойчивы для таких равновесий, что

(40)

$\frac{\tau }{3}\left( {1 + {{\lambda }_{ \bot }} - \frac{\tau }{6}} \right) + \left( {\frac{1}{2} + {{\lambda }_{\rho }} - \frac{\tau }{3}} \right){{M}^{2}} - \frac{{{{M}^{4}}}}{2} < 0.$

Из уравнений (38) и (40) следует, что спектр зональных течений и критерий их устойчивости существенным образом зависят от стратификации по полоидальному углу как поперечного равновесного давления плазмы, так и ее массовой плотности – ${{\lambda }_{ \bot }}$ и ${{\lambda }_{\rho }}$. В модели ЧГЛ оба указанных коэффициента не определяются из условия равновесия плазмы, и для их выбора требуются дополнительные аргументы или предположения.

При наличии медленного равновесного полоидального вращения плазмы из уравнений (6) и (7) следует, что функции продольной и поперечной энтропий должны быть однородными на магнитных поверхностях, ${{s}_{\parallel }} = {{s}_{\parallel }}(\psi )$, ${{s}_{ \bot }} = {{s}_{ \bot }}(\psi )$. Для такого равновесия ${{\lambda }_{\rho }} = {{M}^{2}}{\text{/}}2 + \tau {\text{/}}6 - 1{\text{/}}2$, ${{\lambda }_{ \bot }} = {{\lambda }_{\rho }} - 1{\text{/}}2$, и из дисперсионного уравнения следует, что частота ЗТ равна нулю, $\omega = 0$, а частота ГАМ определяется выражением

(41)

${{\omega }^{2}} = \left[ {\frac{1}{2} + \frac{\tau }{3} + \frac{{{{\tau }^{2}}}}{{18}} + \left( {3 + \frac{\tau }{3}} \right){{M}^{2}} + \frac{{{{M}^{4}}}}{2} + \frac{1}{{{{q}^{2}}}}} \right]\frac{{c_{\parallel }^{2}}}{{R_{0}^{2}}}.$

Таким образом, частота ГАМ растет с увеличением как скорости тороидального вращения, так и отношения поперечного давления плазмы к ее продольному давлению $\tau = {{p}_{ \bot }}{\text{/}}{{p}_{\parallel }}$.

Для часто используемого при описании анизотропной плазмы равновесия с постоянством суммарного давления плазмы на магнитных поверхностях, ${{p}_{\parallel }} + {{p}_{ \bot }} = P(\psi )$ получаем ${{\lambda }_{ \bot }} = $ $ = (1 - \tau ){\text{/}}2\tau - 3{{M}^{2}}{\text{/}}2\tau $. При этом величина ${{\lambda }_{\rho }}$ по-прежнему не определена и может быть произвольной. Для такого класса равновесий частоты зональных течений описываются дисперсионным уравнением

(42)

$\begin{gathered} {{\omega }^{4}} - \left[ {\frac{2}{3} + \frac{\tau }{2} + (3 + {{\lambda }_{\rho }}){{M}^{2}} + \frac{1}{{{{q}^{2}}}}} \right]\frac{{c_{\parallel }^{2}}}{{R_{0}^{2}}}{{\omega }^{2}} + \\ + \;\left\{ {\frac{1}{6}\left( {1 + \tau - \frac{{{{\tau }^{2}}}}{3}} \right) + \left( {{{\lambda }_{\rho }} - \frac{\tau }{3}} \right){{M}^{2}} - \frac{{{{M}^{4}}}}{2}} \right\}\frac{{c_{\parallel }^{4}}}{{{{q}^{2}}R_{0}^{4}}} = 0. \\ \end{gathered} $

Если дополнительно предположить, что магнитные поверхности являются изохорическими, $\rho = \rho (\psi )$, то в этом случае ${{\lambda }_{\rho }} = 0$, и тороидальное вращение плазмы является дестабилизирующим фактором. При таких скоростях вращения, что

${{M}^{2}} > \frac{1}{3}\left( {\sqrt {3(1 + \tau )} - \tau } \right)$

низкочастотное ЗТ апериодически неустойчиво. Ранее в рамках стандартной идеальной МГД-модели подобный дестабилизирующий эффект тороидального вращения на зональные течения для равновесия с изотропным давлением плазмы и изохорическими магнитными поверхностями был предсказан в работах [21, 24].

В недавней работе [37] зональные течения в тороидально-вращающейся плазме токамаков исследовались в рамках гирокинетического подхода. В рамках такого подхода ранее для двухтемпературных максвелловских функций распределения с использованием дрейфового приближения были получены уравнения равновесного состояния в виде (см., например, [30])

(43)

${{p}_{\parallel }} = \rho {{T}_{\parallel }}(\psi ),\quad {{p}_{ \bot }} = \rho {{T}_{ \bot }}(B,\psi ) = \frac{{\rho {{T}_{\parallel }}(\psi )B}}{{B - {{B}_{0}}(\psi )}}.$

Учитывая условие равновесия плазмы вдоль магнитного поля (11), находим, что для такого гирокинетического равновесия ${{\lambda }_{\rho }} = (\tau - 1){\text{/}}2 + 3{{M}^{2}}{\text{/}}2,$ ${{\lambda }_{ \bot }} = \tau - 1 + 3{{M}^{2}}{\text{/}}2$. В этом случае дисперсионное уравнение (38) записывается в виде

(44)

$\begin{gathered} {{\omega }^{4}} - \left[ {\frac{1}{2} + \frac{\tau }{3} + \frac{{{{\tau }^{2}}}}{3} + (3 + \tau ){{M}^{2}} + \frac{3}{2}{{M}^{4}} + \frac{1}{{{{q}^{2}}}}} \right] \times \\ \times \;\frac{{c_{\parallel }^{2}}}{{R_{0}^{2}}}{{\omega }^{2}} + \left( {\frac{{5{{\tau }^{2}}}}{{18}} + \frac{{2\tau }}{3}{{M}^{2}} + {{M}^{4}}} \right)\frac{{c_{\parallel }^{4}}}{{{{q}^{2}}R_{0}^{4}}} = 0. \\ \end{gathered} $

Из данного уравнения следует, что для обсуждаемого равновесия обе ветви зональных течений устойчивы. В предельном случае ${{q}^{2}} \gg 1$ частота ГАМ определяется выражением

(45)

$\omega _{{GAM}}^{2} = \left( {\frac{1}{2} + \frac{\tau }{3} + \frac{{{{\tau }^{2}}}}{3} + (3 + \tau ){{M}^{2}} + \frac{3}{2}{{M}^{4}}} \right)\frac{{c_{\parallel }^{2}}}{{R_{0}^{2}}}.$

Это выражение идентично частоте ГАМ, найденной в работе [37] и описываемой выражением (29) этой работы, если в нем перейти к пределу холодных электронов, ${{T}_{e}}{\text{/}}{{T}_{\parallel }} \to 0$. Таким образом, модель ЧГЛ обеспечивает вполне точное описание движений плазмы поперек магнитного поля. В то же время, хорошо известно, что оно не дает столь же точного описания движений плазмы вдоль магнитного поля. Поэтому следует с предосторожностью относиться к полученным эффектам, связанным с продольным движением плазмы. Строго говоря, их описание требует кинетического рассмотрения.

На рис. 1 представлены зависимости частот ЗТ и ГАМ от числа Маха M для приведенных выше равновесий плазмы при различных значениях параметра τ.

4.3. Общий акустико-альфвеновский спектр при $(m,n) \ne 0$

В общем случае при $(m,n) \ne 0$ после усреднения в нем соответствующих коэффициентов по полоидальному углу дисперсионное уравнение (34) принимает вид

(46)

$\begin{gathered} {{{\bar {\omega }}}^{2}} - {{k}^{2}}v_{A}^{2} - \frac{{c_{\parallel }^{2}}}{{R_{0}^{2}}}\left[ {\frac{1}{2} + \frac{{2\tau }}{3} + \frac{\tau }{3}{{\lambda }_{ \bot }} + \left( {\frac{7}{2} + {{\lambda }_{\rho }}} \right){{M}^{2}}} \right] - \\ - \;\frac{{c_{\parallel }^{2}}}{{R_{0}^{2}}}\frac{{{{g}_{1}}k_{ + }^{2}c_{\parallel }^{2} + {{g}_{2}}\bar {\omega }{{k}_{ + }}{{c}_{\parallel }}}}{{{{{\bar {\omega }}}^{2}} - k_{ + }^{2}c_{\parallel }^{2}}} - \frac{{c_{\parallel }^{2}}}{{R_{0}^{2}}}\frac{{{{g}_{1}}k_{ - }^{2}c_{\parallel }^{2} + {{g}_{2}}\bar {\omega }{{k}_{ - }}{{c}_{\parallel }}}}{{{{{\bar {\omega }}}^{2}} - k_{ - }^{2}c_{\parallel }^{2}}} = 0. \\ \end{gathered} $

Здесь

${{g}_{1}} = \frac{1}{4}\mathop {\left( {1 + \frac{\tau }{3} + {{M}^{2}}} \right)}\nolimits^2 + {{M}^{2}},\quad {{g}_{2}} = M\left( {1 + \frac{\tau }{3} + {{M}^{2}}} \right).$

Отметим, что дисперсионное уравнение инвариантно относительно преобразований $\bar {\omega } \to \bar {\omega },$ $k \to - k,$ $M \to - M$ и $\bar {\omega } \to - \bar {\omega },$ $k \to - k,$ $M \to M$.

Из этого уравнения следует, что сильное тороидальное зацепление альфвеновских и медленных звуковых возмущений имеет место только для мод, локализованных вблизи резонансной магнитной поверхности $r = {{r}_{s}}$, $m - nq({{r}_{s}}) = 0$. При локализации возмущений вдали от $r = {{r}_{s}}$ решения уравнения (46) в системе отсчета, вращающейся с плазмой, приближаются к частотам альфвеновских волн с полоидальным волновым числом m, ${{\bar {\omega }}^{2}} \to {{k}^{2}}v_{A}^{2}$, и к частотам медленных звуковых волн с полоидальными числами $m + 1$ и $m - 1$, ${{\bar {\omega }}^{2}} \to k_{ \pm }^{2}c_{\parallel }^{2}$.

Для мод, локализованных в области вблизи рациональной магнитной поверхности $r = {{r}_{s}}$, такой, где $k{{v}_{A}} \lesssim {{c}_{\parallel }}{\text{/}}{{R}_{0}}$, но при этом $k \ll 1{\text{/}}q{{R}_{0}}$, дисперсионное уравнение (46) можно переписать в виде

$\left( {{{{\bar {\omega }}}^{2}} - \frac{{c_{\parallel }^{2}}}{{{{q}^{2}}R_{0}^{2}}}} \right)\left( {{{{\bar {\omega }}}^{4}} - U{{{\bar {\omega }}}^{2}} + W} \right) + \ldots = 0,$

где

$U = \left( {\tfrac{1}{2} + \tfrac{{2\tau }}{3} + \tfrac{\tau }{3}{{\lambda }_{ \bot }} + \left( {\tfrac{7}{2} + {{\lambda }_{\rho }}} \right){{M}^{2}} + \tfrac{1}{{{{q}^{2}}}}} \right)\tfrac{{c_{\parallel }^{2}}}{{R_{0}^{2}}} + {{k}^{2}}v_{A}^{2},$

$\begin{gathered} W = \tfrac{{c_{\parallel }^{2}}}{{{{q}^{2}}R_{0}^{2}}}\left\{ {\left[ {\tfrac{\tau }{3}\left( {1 + {{\lambda }_{ \bot }} - \tfrac{\tau }{6}} \right) + \left( {\tfrac{1}{2} + {{\lambda }_{\rho }} - \tfrac{\tau }{3}} \right){{M}^{2}}\mathop - \limits_{}^{} } \right.} \right. \\ \left. {\left. { - \;\tfrac{{{{M}^{4}}}}{2}} \right]\tfrac{{c_{\parallel }^{2}}}{{R_{0}^{2}}} + {{k}^{2}}v_{A}^{2}} \right\}, \\ \end{gathered} $

а $ \ldots $ означают члены, пропорциональные ${{k}^{2}}c_{\parallel }^{2}$. Это дисперсионное уравнение описывает шесть ветвей возмущений плазмы, характеризуемых частотами

$\begin{gathered} {{{\bar {\omega }}}_{{1,2}}} = \pm {{\omega }_{ + }},\quad {{{\bar {\omega }}}_{{3,4}}} = \pm {{\omega }_{ - }}, \\ {{{\bar {\omega }}}_{{5,6}}} = \pm \frac{{{{c}_{\parallel }}}}{{q{{R}_{0}}}}\left[ {1 + O({{k}^{2}}R_{0}^{2})} \right], \\ \end{gathered} $

где

$\omega _{ \pm }^{2} = \frac{1}{2}\left( {U \pm \sqrt {{{U}^{2}} - 4W} } \right).$

Очевидно, что для мод, локализованных строго на рациональной поверхности $r = {{r}_{s}}$, частоты $\bar {\omega }$ первых четырех ветвей возмущений описываются тем же самым дисперсионным уравнением (38), что и частоты зональных течений.

Для мод, локализованных вдали от рациональной поверхности, для которых ${{k}^{2}} \gg ({{\beta }_{ \bot }},{{\beta }_{\parallel }}){\text{/}}R_{0}^{2}$, частоты мод, описываемых вблизи $r = {{r}_{s}}$ как ${{\bar {\omega }}_{{1,2}}}$, приближаются к альфвеновским частотам, ${{\bar {\omega }}_{{1,2}}} \to $ $ \to \pm k{{v}_{A}}$. Частоты других четырех ветвей, соответствующих ${{\bar {\omega }}_{{3,4}}}$ и ${{\bar {\omega }}_{{5,6}}}$, приближаются к частотам звуковых волн, причем

${{\bar {\omega }}_{{3,4}}} \to \pm \left| {\left| k \right| - \frac{1}{{q{{R}_{0}}}}} \right|{{c}_{\parallel }},\quad {{\bar {\omega }}_{{5,6}}} \to \pm \left| {\left| k \right| + \frac{1}{{q{{R}_{0}}}}} \right|{{c}_{\parallel }}.$

Для монотонно растущего профиля коэффициента запаса устойчивости q, $q'(r) > 0$, продольный волновой вектор k положителен в области $r < {{r}_{s}}$, $k(r) > 0$, и отрицателен – в области $r > {{r}_{s}}$, $k(r) < 0$. Тогда при $r < {{r}_{s}}$ частоты мод, описываемых ${{\bar {\omega }}_{{3,4}}}$, асимптотически приближаются к звуковым волнам с волновыми числами $(m - 1,\;n)$, ${{\bar {\omega }}_{{3,4}}} \to \pm {{k}_{ - }}{{c}_{\parallel }}$, а при $r > {{r}_{s}}$ – к частотам звуковых волн с волновыми числами $(m + 1,n)$, ${{\bar {\omega }}_{{3,4}}} \to \pm {{k}_{ + }}{{c}_{\parallel }}$. Наоборот, ${{\bar {\omega }}_{{5,6}}} \to \pm {{k}_{ + }}{{c}_{\parallel }}$ при $r < {{r}_{s}}$, и ${{\bar {\omega }}_{{5,6}}} \to \pm {{k}_{ - }}{{c}_{\parallel }}$ при $r > {{r}_{s}}$. Заметим, что для мод с локализацией вдали от рациональной поверхности $r = {{r}_{s}}$ на любом радиусе $\left| {{{{\bar {\omega }}}_{{5,6}}}} \right| > \left| {{{{\bar {\omega }}}_{{3,4}}}} \right|$.

Обусловленные эффектом Кориолиса члены, пропорциональные ${{g}_{2}}$ в дисперсионном уравнении (46), приводят к асимметрии МГД-спектра относительно продольного волнового числа $k$ (в отличие от МГД-спектра плазмы в отсутствие тороидального вращения). Эта асимметрия наиболее ярко выражена при $\left| k \right| \lesssim ({{c}_{\parallel }}{\text{/}}{{v}_{A}})R_{0}^{{ - 1}}$.

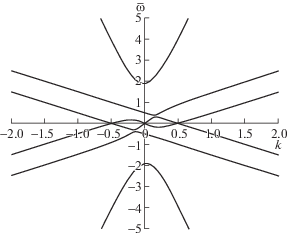
Низкочастотный акустико-альфвеновский спектр для равновесия плазмы с ${{s}_{\parallel }} = {{s}_{\parallel }}(\psi )$ и ${{s}_{ \bot }} = {{s}_{ \bot }}(\psi )$ схематически представлен на рис. 2. Предполагается, что полоидальное и тороидальное волновые числа являются большими, $(m,n) \gg 1$. Продольная компонента волнового вектора k изменяется из-за радиальной зависимости коэффициента запаса устойчивости q (вблизи $q = 2$), а остальные физические величины в уравнении (46) предполагаются независимыми от радиуса r.

Рис. 2.

Акустико-альфвеновский спектр для равновесия с ${{s}_{\parallel }} = {{s}_{\parallel }}(\psi )$ и ${{s}_{ \bot }} = {{s}_{ \bot }}(\psi )$. Здесь $\tau = 2$, ${{M}^{2}} = 0.5$, $q \approx 2$, $c_{\parallel }^{2}{\text{/}}v_{A}^{2} = 1{\text{/}}50$. Собственная частота $\bar {\omega }$ нормирована на величину ${{c}_{\parallel }}{\text{/}}{{R}_{0}}$, а продольный волновой вектор k – на величину $1{\text{/}}{{R}_{0}}$.

Для равновесий плазмы, для которых выполняется условие (40), собственные частоты ${{\bar {\omega }}_{3}}$ и ${{\bar {\omega }}_{4}}$ в окрестности рациональной магнитной поверхности $r = {{r}_{s}}$ становятся комплексными, и, таким образом, МГД-спектр неустойчив. Неустойчивость является апериодической для мод, локализованных строго на рациональной магнитной поверхности $r = {{r}_{s}}$, для которых $k = 0$. При $k \ne 0$ неустойчивая мода обладает ненулевой действительной частью собственной частоты $\bar {\omega }$, ${\text{Re}}\bar {\omega } \ne 0$, и, таким образом, является осциллирующей.

Неустойчивый спектр существенным образом зависит от направления скорости тороидального вращения. При $\Omega > 0$ частота ${{\bar {\omega }}_{3}}$, которая положительна при $k < - {{k}_{0}}$, пересекает ось $\bar {\omega } = 0$ при $k = - {{k}_{0}}$, где

${{k}_{0}} = \frac{1}{{{{R}_{0}}}}\frac{{{{c}_{\parallel }}}}{{{{v}_{A}}}}\mathop {\left[ {\frac{{{{M}^{4}}}}{2} - \left( {\frac{1}{2} + {{\lambda }_{\rho }} - \frac{\tau }{3}} \right){{M}^{2}} - \frac{\tau }{3}\left( {1 + {{\lambda }_{ \bot }} - \frac{\tau }{6}} \right)} \right]}\nolimits^{1/2} .$

При дальнейшем увеличении k частоты ${{\bar {\omega }}_{3}}$ и ${{\bar {\omega }}_{4}}$ становятся равными друг другу в некоторой точке $k(r) = - {{k}_{*}} < 0,$ ${{k}_{*}} < {{k}_{0}}$. При этом ${{\bar {\omega }}_{3}}( - {{k}_{*}}) = $ $ = {{\bar {\omega }}_{4}}( - {{k}_{*}}) < 0$. Эта точка $k = - {{k}_{*}}$ определяет границу неустойчивости, которая имеет место при $k > - {{k}_{*}}$. Действительные части этих собственных частот растут по мере увеличения величины k, и на рациональной поверхности при $k = 0$ становятся равными нулю, ${\text{Re}}{{\bar {\omega }}_{{3,4}}}(0) = 0$. При дальнейшем росте k в область положительных значений действительные части собственных частот становятся положительными, ${\text{Re}}{{\bar {\omega }}_{{3,4}}} > 0$, и неустойчивость стабилизируется при $k = {{k}_{*}}$. В этой точке имеет место равенство соответствующих собственных частот, ${{\bar {\omega }}_{3}}({{k}_{*}}) = {{\bar {\omega }}_{4}}({{k}_{*}}) > 0$. При $k > {{k}_{*}}$ частота ${{\bar {\omega }}_{4}}$ является убывающей функцией k и пересекает ось $\bar {\omega } = 0$ при $k = {{k}_{0}}$, становясь отрицательной в области, в которой $k > {{k}_{0}}$.

Зеркальная картина относительно $k = 0$ (или же рациональной магнитной поверхности) имеет место в случае вращения плазмы в противоположном направлении, т.е. при $\Omega < 0$. В этом случае действительные части собственных частот ${{\bar {\omega }}_{3}}$ и ${{\bar {\omega }}_{4}}$ положительны при $ - {{k}_{0}} < k < 0$ и отрицательны при $0 < k < {{k}_{0}}$. Таким образом, при $\left| k \right| < {{k}_{0}}$ ($k \ne 0$) продольные фазовые скорости таких возмущений во вращающейся с плазмой системе координат, ${{v}_{{ph}}} = {\text{Re}}{{\bar {\omega }}_{{3,4}}}{\text{/}}k$, имеют тот же знак, что и угловая скорость вращения плазмы, $\Omega {{v}_{{ph}}} > 0$.

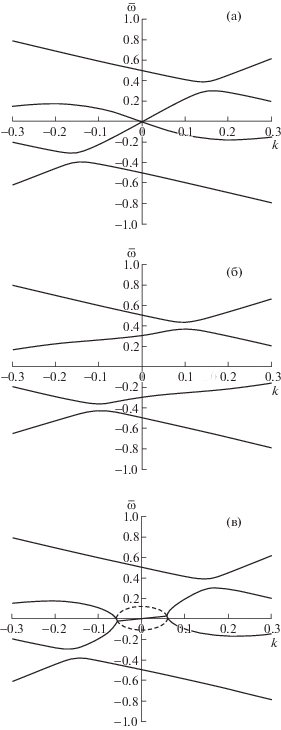
На рис. 3 изображена низкочастотная часть акустико-альфвеновского спектра в окрестности рациональной магнитной поверхности. Для типичных устойчивых равновесий (рис. 3а, б) и неустойчивого равновесия (рис. 3в) показаны только четыре низкочастотные ветви возмущений, частоты которых стремятся к величинам $ \pm {{\omega }_{ - }}$ и $ \pm {{c}_{\parallel }}{\text{/}}q{{R}_{0}}$ при $k \to 0$. В частности, на рис. 3а в области малых $\left| k \right|$ в более крупном масштабе представлена низкочастотная часть спектра, изображенного выше на рис. 2.

Рис. 3.

Низкочастотная часть акустико-альфвеновского спектра вблизи рациональной магнитной поверхности для различных равновесий плазмы: ${{s}_{\parallel }} = {{s}_{\parallel }}(\psi )$, ${{s}_{ \bot }} = {{s}_{ \bot }}(\psi )$ (а); гирокинетическое равновесие (43) (б); ${{p}_{\parallel }} + {{p}_{ \bot }} = P(\psi )$, $\rho = \rho (\psi )$ (в). Здесь $\tau = 2$, ${{M}^{2}} = 0.5$, $q \approx 2$, $c_{\parallel }^{2}{\text{/}}v_{A}^{2} = 1{\text{/}}50$; частота нормирована на величину ${{c}_{\parallel }}{\text{/}}{{R}_{0}}$, продольный волновой вектор k – на $1{\text{/}}{{R}_{0}}$. Сплошные е линии показывают действительные части частоты $\bar {\omega }$; штриховые линии – мнимые части $\bar {\omega }$.

5. ОСНОВНЫЕ РЕЗУЛЬТАТЫ И ЗАКЛЮЧЕНИЕ

В настоящей работе представлено исследование низкочастотного МГД-спектра тороидально-вращающейся плазмы с анизотропным давлением в осесимметричных тороидальных системах магнитного удержания. Проведенный анализ базируется на идеальной МГД-модели Чу–Голдбергера–Лоу, в которой термодинамическое равновесие плазмы описывается посредством двух адиабат. Для самого общего равновесия тороидально-вращающейся плазмы с анизотропным давлением, удовлетворяющего уравнениям ЧГЛ, получена система двух дифференциальных уравнений второго порядка относительно полоидального угла $\vartheta $ (27) и (28), описывающая низкочастотные моды, сильно локализованные на магнитных поверхностях. Она описывает тороидальное зацепление медленных магнитозвуковых и альфвеновских возмущений, обусловленное эффектами кривизны магнитного поля, анизотропии давления плазмы, центробежными и кориолисовыми эффектами. В систему уравнений входят две составляющие лагранжевого смещения элемента плазмы, лежащие на магнитной поверхности – параллельная силовым линиям равновесного магнитного поля, ζ, и перпендикулярная по отношению к ним η. Эта система уравнений обобщает уравнения, ранее полученные в работе [25], с учетом эффектов равновесного тороидального вращения плазмы. Полученные нами уравнения также могут рассматриваться как аналог уравнений ван дер Холста и др. [16] применительно к тороидально-вращающейся плазме с анизотропным давлением.

В качестве иллюстрации упрощенный вариант полученных уравнений применен для детального анализа МГД-спектра тороидально-вращающейся плазмы с анизотропным низким давлением $({{\beta }_{\parallel }},{{\beta }_{ \bot }}) \sim {{\epsilon }^{2}}$ в токамаке с большим аспектным отношением, $\epsilon = a{\text{/}}{{R}_{0}} \ll 1$, и круглыми магнитными поверхностями. Используя малость обратного аспектного отношения, $\epsilon \ll 1$, при исследовании непрерывного низкочастотного акустико-альфвеновского спектра нами было использовано трехмодовое приближение, в котором учтены только основная гармоника лагранжевого смещения плазмы поперек магнитного поля η с полоидальным волновым числом m и сателлитные гармоники продольного смещения ζ с полоидальными волновыми числами $m \pm 1$. В такой постановке задачи аналитически получено общее дисперсионное уравнение для описания непрерывного МГД-спектра (34).

Для полоидально и тороидально симметричных мод с $(m,n) = 0$ показано существование двух ветвей зональных течений. Такие возмущения с точностью до эффектов порядка ${{\beta }_{\parallel }},\;{{\beta }_{ \bot }}$ являются электростатическими. Показано, что условие их устойчивости и их частоты сильно зависят от стратификации по полоидальному углу равновесных поперечного давления и массовой плотности плазмы на магнитных поверхностях. Получено условие устойчивости зональных течений (37), которое включает в себя кривизну магнитных силовых линий, эффекты тороидального вращения и полоидальную стратификацию продольной и поперечной энтропийных функций. Низкочастотное зональное течение или просто ЗТ имеет конвективную природу и связано с полоидальной стратификацией продольной и поперечной энтропийных функций на магнитных поверхностях. Показано также, что высокочастотные зональные течения (или ГАМ) всегда устойчивы, а низкочастотные зональные течения ЗТ неустойчивы для класса равновесий, описываемого неравенством (40).

В настоящее время нет экспериментальных данных о распределении плотности и давления плазмы по полоидальному углу на магнитных поверхностях токамака. В этой связи не представляется возможным прямое сравнение теоретических предсказаний с результатами эксперимента. Существуют только численные реконструкции разрядов на основе моделей, учитывающих анизотропию давления плазмы. Например, в недавней работе [38] с использованием кода HELENA+ATF в конфигурации типа токамака MAST для гирокинетического равновесия, описываемого уравнением (43), было показано, что ${{p}_{ \bot }}$ может изменяться в полоидальном направлении на величину до 20%.

Для электромагнитных возмущений с $(m,n) \ne 0$ и локализованных строго на рациональной магнитной поверхности $m - nq({{r}_{s}}) = 0$ дисперсионное уравнение (46) совпадает с дисперсионным уравнением зональных течений. При локализации возмущений в окрестности рациональной поверхности $r = {{r}_{s}}$ оно описывает шесть ветвей колебаний. На рациональной поверхности частоты четырех из этих ветвей равны частотам зональных течений. Частоты оставшихся двух ветвей равны частотам сателлитных звуковых волн с полоидальными волновыми числами $m \pm 1$, ${{\bar {\omega }}_{{5,6}}} = \pm {{c}_{\parallel }}{\text{/}}q{{R}_{0}}$. Для мод, локализованных в области вдали от рациональной поверхности, где доминируют альфвеновские эффекты, тороидальное зацепление мод является слабым, и решения дисперсионного уравнения стремятся к частотам альфвеновских волн с волновыми числами $(m,n)$ и частотам сателлитных звуковых волн с волновыми числами $(m \pm 1,n)$.

В случае равновесий с неустойчивой полоидальной стратификацией плазмы, описываемых условием (40), четыре ветви колебаний с наивысшими по абсолютной величине частотами являются устойчивыми. При этом одна из мод с самыми низкими собственными частотами ${{\bar {\omega }}_{{3,4}}}$, переходящими на рациональной магнитной поверхности в собственные частоты низкочастотных зональных течений, неустойчива в окрестности рациональной поверхности при $\left| k \right| < {{k}_{*}} \simeq ({{c}_{\parallel }}{\text{/}}{{v}_{A}})R_{0}^{{ - 1}}$, а другая мода затухает. При $\left| k \right| \geqslant {{k}_{*}}$ неустойчивость подавляется посредством натяжения магнитных силовых линий (альфвеновским эффектом). При локализации моды строго на рациональной магнитной поверхности при $r = {{r}_{s}}$ неустойчивость является апериодической во вращающейся системе координат, ${\text{Re}}{{\bar {\omega }}_{{3,4}}} = 0$. Неустойчивые моды, локализованные в окрестности рациональной поверхности, так, что $\left| k \right| < {{k}_{*}},$ $k \ne 0$, имеют конечную частоту, ${\text{Re}}\bar {\omega } \ne 0$, и являются осциллирующими. Их продольная фазовая скорость во вращающейся системе координат ${{v}_{{ph}}}$ имеет тот же знак, что и угловая скорость тороидального вращения Ω.

Согласно экспериментальным данным, полученным на токамаке Т-10, в разрядах с мощным дополнительным нагревом плазмы [39] частота возмущений, ассоциируемых с ГАМ, быстро нарастает в процессе дополнительного нагрева и впоследствии существенно медленнее релаксирует к некоторому новому значению, которое превышает частоту ГАМ до включения дополнительного нагрева. Можно предполагать, что такое поведение частоты может быть обусловлено анизотропизацией плазмы при дополнительном нагреве с последующей столкновительной изотропизацией давления, которые приводят к изменению частоты ГАМ в соответствии с выражением для высокочастотного корня уравнения (38). Безусловно, эта предварительная гипотеза требует тщательной проверки.

Работа частично поддержана грантом Российского научного фонда (проект № 14-22-00193), при финансовой поддержке которого  получены результаты, приведенные в разделе 4.2, и грантом Российского фонда фундаментальных исследований № 18-29-21041. Публикация подготовлена при поддержке Программы РУДН “5-100”.

ПРИЛОЖЕНИЕ

АЛЬТЕРНАТИВНЫЙ ВЫВОД ДИСПЕРСИОННОГО УРАВНЕНИЯ ЗОНАЛЬНЫХ ТЕЧЕНИЙ

Считаем, что возмущения являются осесимметричными и электростатическими, зависят от времени как $exp( - i\omega t)$, от полоидального магнитного потока ψ, а также являются периодическими функциями полоидального угла $\vartheta $ (с периодом $2\pi $). В рамках модели ЧГЛ такие возмущения описываются системой уравнений

Здесь $\Phi '$ – возмущенный электростатический потенциал. Из уравнения (A3) следует, что ${\mathbf{B}} \cdot \nabla \Phi ' = 0$, так что $\Phi ' = \Phi '(\psi )$ и возмущение скорости плазмы лежит строго на магнитной поверхности, ${\mathbf{v}}'\; \cdot \nabla \psi = 0$, и представляется в виде

Из уравнения (A1) следует, что баланс возмущенных сил вдоль магнитного поля описывается уравнением

Возмущение плотности тока представляем в виде разложения

Подставляя это разложение в уравнение (A6) и учитывая осевую симметрию рассматриваемых возмущений, получаем

Оператор ${\mathbf{B}} \cdot \nabla $ для осесимметричного равновесия и осесимметричных возмущений представляется в виде

Из уравнения (A2) находим

С учетом выражения для возмущенной скорости ${\mathbf{v}}'$ (A7), получаем

Подставляем выражение (A13) в уравнение (A12) и, интегрируя по частям, а также пренебрегая полоидальными осцилляциями I, считая $I \approx I(\psi )$, окончательно приходим к уравнению

Замкнутая система уравнений (A8), (A9), (A14) описывает возмущения тороидально-вращающейся плазмы в виде зональных течений.

Далее, в качестве иллюстрации мы применим эту систему уравнений для вывода дисперсионного уравнения зональных течений при тех же предположениях, что и в разд. 4. Тогда уравнения (A8), (A9) упрощаются и с необходимой точностью принимают вид

Исключая возмущение продольного давления плазмы, выражаем величину U, определяющую продольную возмущенную скорость, через возмущенный электростатический потенциал $\Phi '$

Умножаем уравнение (A14) на $ - i\omega $ и подставляем в него выражения для возмущений продольного и поперечного давлений (A15). В результате оно принимает вид

Из уравнения (A16) следует, что $U = {{U}^{{(1)}}} + {{U}^{{(2)}}}$, где

Производим усреднение члена с ${{\Lambda }_{1}}$ по полоидальному углу, учитывая, что $J \approx J(r)$, $I \approx RB$, ${{\left| {\nabla \psi } \right|}^{2}}{\text{/}}{{B}^{2}} \approx {{r}^{2}}{\text{/}}{{q}^{2}}$. В результате получаем

Что касается вклада двух членов, связанных с продольным движением плазмы, то при интегрировании по полоидальному углу $\vartheta $ вклад в член пропорциональный ${{\Lambda }_{2}}$ дает только ${{U}^{{(2)}}}$, а вклад в связанный с силой Кориолиса член, пропорциональный ${{\Lambda }_{3}}$ – только ${{U}^{{(1)}}}$. Интегрируя по $\vartheta $, получаем

При усреднении по полоидальному углу члена, пропорционального ${{\Lambda }_{2}}$ в уравнение (A19), было использовано тождество (36).

Подставляя выражения (A18)–(A19) в уравне-ние (A17), получаем дисперсионное уравнение зональных течений в анизотропной тороидально-вращающейся плазме

Это уравнение можно переписать в виде, эквивалентном дисперсионному уравнению (35).