Физика плазмы, 2019, T. 45, № 7, стр. 657-671

МГД-волны и неустойчивости в двухкомпонентной анизотропной плазме

Н. С. Джалилов^a, С. Ш. Гусейнов^a, *

^a Шамахинская астрофизическая обсерватория НАН Азербайджана
Шемахы, Пиркули, Азербайджан

Поступила в редакцию 22.10.2018
После доработки 17.12.2018
Принята к публикации 20.12.2018

DOI: 10.1134/S0367292119060040

Аннотация

На основе 16-моментных МГД-уравнений переноса рассмотрено распространение линейных волн в анизотропной однородной космической плазме. Получено общее дисперсионное уравнение с учетом двух компонентов плазмы (электроны и протоны) и теплового потока вдоль магнитного поля. Полученное дисперсионное уравнение является обобщением ранее исследованных случаев, когда плазма являлась ионной. Более подробно анализирован случай, когда эффекты, связанные с тепловым потоком игнорируются. В пределе продольного распространения дана классификация волновых мод, которые полностью соответствуют известным модам из низкочастотной кинетической физики бесстолкновительной плазмы. Проанализированы шланговые и зеркальные неустойчивости. Показано, что учет электронов меняет инкременты и условия возникновения неустойчивостей.

1. ВВЕДЕНИЕ

В связи с тем, что измеряемые параметры сильноразреженной космической замагниченной плазмы (например, солнечный и звездные ветры, короны звезд, звездные диски, ионосфера и магнитосферы планет, межзвездная среда) являются макроскопическими, то МГД-описание такой плазмы является более уместным. Вывод замкнутых МГД-уравнений для бесстолкновительной плазмы имеет свои трудности. Основная трудность связана с прерыванием цепочек бесконечных уравнений для моментов функций распределения. Это требует дополнительного физического обоснования, а также конкретного вида функций распределения частиц по скоростям. Классическими примерами таких уравнений, описывающих плазму как жидкость, являются ЧГЛ [1] и 16-ти моментные уравнения переноса [2, 3], выведенные для би-максвелловской плазмы при нулевом радиусе ларморовского вращения. Главным преимуществом 16-ти моментных МГД-уравнений переноса по сравнению с ЧГЛ-уравнениями является то, что эти уравнения учитывают тепловой поток вдоль магнитного поля. В отличие от ЧГЛ-уравнений 16-моментные уравнения дают правильное выражение критерия возникновения зеркальной неустойчивости, совпадающее с низкочастотным кинетическим результатом [4, 5]. МГД-описания плазмы по сравнению с кинетикой имеет существенный недостаток, заключающийся в том, что рассматриваются малые волновые числа, $k < {{\omega }_{{pp}}}{\text{/}}c$ (${{\omega }_{{pp}}}$ – протонная плазменная частота, $c$ – скорость света). В ряде работ были выполнены оценки модификаций МГД-неустойчивостей при учете конечной длины ларморовского радиуса (см., например, [6, 7]).

В предыдущих работах мы развивали теорию МГД-неустойчивостей на основе 16-моментных уравнений [4, 5, 8, 9]. В этих работах результаты были получены для ионной плазмы. Роль электронов сводилась только к поддержанию квазинейтральности плазмы. Строго говоря, игнорирование вкладов электронной компоненты плазмы требует условие ${{T}_{e}} \ll {{T}_{p}}$, которое в реальности встречается очень редко. Здесь мы обобщаем теорию линейных МГД-неустойчивостей с учетом электронной компоненты и ее анизотропии, исследуются пороги шланговых и зеркальной неустойчивостей в электронно-протонной анизотропной плазме.

2. МГД-УРАВНЕНИЯ ПЕРЕНОСА В АНИЗОТРОПНОЙ ПЛАЗМЕ

Для кинетического описания динамических явлений в плазме, состоящей из электронов и ионов, обычно применяются эволюционные уравнения функций распределения ${{f}_{\alpha }}({\mathbf{u}};{\mathbf{r}};t)$ каждого сорта $\alpha = \{ e,i\} $ частиц – уравнения Больцмана–Власова. Если учитывается влияние электромагнитного поля, то к этим уравнениям добавляются уравнения Максвелла. Интересующие нас макроскопические параметры плазмы (плотность, макроскопическая скорость течения, давления, тепловой поток) определяются как интегральные моменты функций распределения в трехмерном пространстве микроскопических скоростей u. В движущейся системе отсчета эти моменты представляются как

$n = \int {f({\mathbf{u}};{\mathbf{r}};t){{d}^{3}}{\mathbf{u}}} ,\quad n{\mathbf{v}} = \int {{\mathbf{u}}f({\mathbf{u}};{\mathbf{r}};t){{d}^{3}}{\mathbf{u}}} ,$

$\begin{gathered} p = m\int {{{{\left| {{\mathbf{u}} - {\mathbf{v}}} \right|}}^{2}}f({\mathbf{u}};{\mathbf{r}};t){{d}^{3}}{\mathbf{u}}} , \\ {{p}_{\parallel }} = m\int {{{{[({\mathbf{u}} - {\mathbf{v}}) \cdot {\mathbf{b}}]}}^{2}}f({\mathbf{u}};{\mathbf{r}};t){{d}^{3}}{\mathbf{u}}} , \\ \end{gathered} $

$\begin{gathered} {{S}_{\parallel }} = (m{\text{/}}2)\int {{{{[({\mathbf{u}} - {\mathbf{v}}) \cdot {\mathbf{b}}]}}^{3}}f({\mathbf{u}};{\mathbf{r}};t){{d}^{3}}{\mathbf{u}}} , \\ {{S}_{B}} = (m{\text{/}}2)\int {[({\mathbf{u}} - {\mathbf{v}}) \cdot {\mathbf{b}}]{{{\left| {{\mathbf{u}} - {\mathbf{v}}} \right|}}^{2}}f({\mathbf{u}};{\mathbf{r}};t){{d}^{3}}{\mathbf{u}}} , \\ \end{gathered} $

где b – единичный вектор вдоль магнитного поля, среднее полное давление $p = (2{{p}_{ \bot }} + {{p}_{\parallel }}){\text{/}}3$ определяется поперечными ${{p}_{ \bot }}$ и продольными ${{p}_{\parallel }}$ давлениями, полный продольный поток тепла ${{S}_{B}} = $ $ = {{S}_{ \bot }} + {{S}_{\parallel }}$ определяется как сумма продольных потоков тепла, вызванных поперечными (${{S}_{ \bot }}$) и продольными (${{S}_{\parallel }}$) тепловыми движениями.

Количество этих интегральных моментов может быть сколь угодно большим, и они все выражаются друг через друга. Цепочка уравнений, описывающих эти моменты (уравнения переноса), также может быть бесконечной. Требуются дополнительные физически обоснованные условия разрыва цепочки уравнений. В случае плотной плазмы, когда функции распределения частиц равновесной столкновительной плазмы близки к максвелловской, эти цепочки уравнений легко прерываются. В результате получаются обычные МГД-уравнения для изотропной плазмы. Однако в случае редких столкновений и в присутствии сильного магнитного поля функции распределения частиц не описываются максвелловским распределением, и возникает трудность прерывания цепочки моментных уравнений для неравновесной плазмы. В этом случае решение кинетического уравнения для каждого сорта частиц обычно ищется в виде разложения вокруг заданной функции распределения с анизотропными температурами относительно направления внешнего магнитного поля. Если эту функцию считать би-максвелловской функцией (простейший вид для анизотропной плазмы), то при очень малых ларморовских радиусах обращения частиц вокруг силовых линий магнитного поля $\left( {{{r}_{B}} \to 0} \right)$ получается система 16-ти моментных уравнений [2, 3]. В общепринятых обозначениях эти уравнения представляются как

(1)

$\frac{{d{{\rho }_{\alpha }}}}{{dt}} + {{\rho }_{\alpha }}\nabla \cdot {\mathbf{v}} = 0,$

(2)

$\begin{gathered} \rho \frac{{d{\mathbf{v}}}}{{dt}} + \frac{1}{{4\pi }}{\mathbf{B}} \times \left( {\nabla \times {\mathbf{B}}} \right) + \\ + \;\sum\limits_\alpha \left[ {\nabla {{p}_{{\alpha \bot }}} + \left( {{\mathbf{B}} \cdot \nabla } \right)\left( {\frac{{{{p}_{{\alpha \parallel }}} - {{p}_{{\alpha \bot }}}}}{{{{B}^{2}}}}{\mathbf{B}}} \right)} \right] = 0, \\ \end{gathered} $

(3)

$\begin{gathered} B{{p}_{{\alpha \parallel }}}\frac{d}{{dt}}ln\left( {\frac{{{{B}^{2}}{{p}_{{\alpha \parallel }}}}}{{{{n}^{3}}}}} \right) + {\mathbf{B}} \cdot \nabla {{S}_{{\alpha \parallel }}} + \\ + \;2\left( {{{S}_{{\alpha \bot }}} - \frac{1}{2}{{S}_{{\alpha \parallel }}}} \right){\mathbf{B}} \cdot \nabla lnB = 0, \\ \end{gathered} $

(4)

$B{{p}_{{\alpha \bot }}}\frac{d}{{dt}}ln\left( {\frac{{{{p}_{{\alpha \bot }}}}}{{Bn}}} \right) + {\mathbf{B}} \cdot \nabla {{S}_{{\alpha \bot }}} - 2{{S}_{{\alpha \bot }}}{\mathbf{B}} \cdot \nabla lnB = 0,$

(5)

$B{{S}_{{\alpha \parallel }}}\frac{d}{{dt}}ln\left( {\frac{{{{B}^{3}}{{S}_{{\alpha \parallel }}}}}{{2{{n}^{4}}}}} \right) + \frac{{3{{p}_{{\alpha \parallel }}}}}{{{{m}_{\alpha }}}}{\mathbf{B}} \cdot \nabla \left( {\frac{{{{p}_{{\alpha \parallel }}}}}{n}} \right) = 0,$

(6)

$\begin{gathered} B{{S}_{{\alpha \bot }}}\frac{d}{{dt}}ln\left( {\frac{{{{S}_{{\alpha \bot }}}}}{{{{n}^{2}}}}} \right) + \frac{{{{p}_{{\alpha \parallel }}}}}{{{{m}_{\alpha }}}}{\mathbf{B}} \cdot \nabla \left( {\frac{{{{p}_{{\alpha \bot }}}}}{n}} \right) - \\ - \;\frac{{\left( {{{p}_{{\alpha \parallel }}} - {{p}_{{\alpha \bot }}}} \right){{p}_{{\alpha \bot }}}}}{{n{{m}_{\alpha }}}}{\mathbf{B}} \cdot \nabla lnB = 0, \\ \end{gathered} $

(7)

$\frac{{d{\mathbf{B}}}}{{dt}} + {\mathbf{B}}\nabla \cdot {\mathbf{v}} - \left( {{\mathbf{B}} \cdot \nabla } \right){\mathbf{v}} = 0,\quad \nabla \cdot {\mathbf{B}} = 0.$

При выводе этих уравнений считается, что плазма является квазинейтральной, ${{n}_{e}} \approx {{n}_{i}} = n$, а массовые скорости ее компонентов близки, ${{{\mathbf{v}}}_{{\mathbf{e}}}} \approx {{{\mathbf{v}}}_{{\mathbf{i}}}} = {\mathbf{v}}$. Здесь $d{\text{/}}dt = \partial {\text{/}}\partial t + {\mathbf{v}} \cdot \nabla $, ${{\rho }_{\alpha }} = n{{m}_{\alpha }}$ и ${{S}_{{\alpha \parallel }}}$ и ${{S}_{{\alpha \bot }}}$ – тепловые потоки вдоль магнитного поля, вызванные продольными и поперечными тепловыми движениями частиц сорта α. Если пренебречь этими потоками, ${{S}_{{\alpha \parallel }}} = 0$, ${{S}_{{\alpha \bot }}} = 0$, то получим законы изменения продольных и поперечных тепловых энергий вдоль траектории элемента жидкости (левые части уравнений (3) и (4)). Эта пара уравнений (так называемые “двойные адиабаты”) и уравнения (1), (2) и (7) образуют замкнутую систему уравнений, известную как ЧГЛ-уравнения [1]. Однако если воспользоваться ЧГЛ-уравнениями, то остаются не удовлетворенными уравнения (5) и (6). Это является следствием того, что при выводе ЧГЛ-уравнений без всяких обоснований были опущены третьи моменты функции распределения, т. е. тепловые потоки не учитывались. Приведенные здесь уравнения (1)–(7) содержат тепловые потоки и являются более полными уравнениями. ЧГЛ-уравнения не следуют из этих уравнений как частный случай.

При выводе 16-моментных уравнений сохранены моменты до третьего ранга (тепловые потоки) [3]. Как было показано, в этом случае в уравнения для моментов 3-го ранга входят моменты 4‑го ранга как неизвестные, которые должны подчиняться условиям Шварца. Далее все физические переменные, в том числе функция распределения частиц, разлагаются в ряд по малому ларморовскому радиусу. Для нулевого порядка уравнений предполагается, что зависимость функций распределения частиц от u должна быть в виде $m{{\left| {{\mathbf{u}} - {\mathbf{v}}} \right|}^{2}}{\text{/}}2$ (т. е. как энергия в системе координат, связанной с жидкостью) и от питч-угла как $sin\lambda = ({\mathbf{u}} - {\mathbf{v}}) \cdot {\mathbf{B}}{\text{/}}(\left| {{\mathbf{u}} - {\mathbf{v}}} \right|B)$. При этом допускается, что функции распределения частиц в нулевом порядке не зависят от гирофазы. Перечисленные условия являются основными требованиями к функциям распределения частиц при выводе замкнутой системы МГД-уравнений. Хотя такой вид функции распределения теряет некоторые тонкости кинетических эффектов, но они позволяют прервать ряд цепочек моментных уравнений. Функциональный вид функций распределений может быть различным: би-максвелловская, каппа и т.д. Для каждого конкретного вида этих функций получаемые конечные уравнения будут разными. В простейшем случае би-максвелловского распределения с двумя температурами

$\begin{gathered} {{f}_{0}}(\left| {{\mathbf{u}} - {\mathbf{v}}} \right|\lambda ;{\mathbf{r}};t) = {{\left( {\frac{m}{{2\pi }}} \right)}^{{3/2}}}\frac{{{{n}^{{5/2}}}}}{{{{p}_{ \bot }}p_{\parallel }^{{1/2}}}} \times \\ \times \;exp\left[ { - \frac{{mn{{{\left| {{\mathbf{u}} - {\mathbf{v}}} \right|}}^{2}}}}{2}\left( {\frac{{co{{s}^{2}}\lambda }}{{{{p}_{ \bot }}}} + \frac{{si{{n}^{2}}\lambda }}{{{{p}_{\parallel }}}}} \right)} \right] \\ \end{gathered} $

моменты 4-го ранга, входящие в уравнения 3-го ранга, выражаются моментами более низкого ранга. Это позволяет замыкать системы моментных уравнений. Отметим, что неравновесная плазма с пучком заряженных частиц, движущихся вдоль направления магнитного поля и вращающихся вокруг него, или двухпотоковая система может описываться подобными функциями распределения частиц.

3. ВЫВОД ДИСПЕРСИОННОГО УРАВНЕНИЯ

Для простоты рассмотрим случай, когда невозмущенное состояние плазмы однородно и стационарно: все величины ${{{\mathbf{v}}}_{0}}$, ${{\rho }_{0}}$, ${{p}_{{\parallel 0}}}$, ${{p}_{{ \bot 0}}}$, ${{{\mathbf{B}}}_{0}}$, ${{S}_{{\parallel 0}}}$ и ${{S}_{{ \bot 0}}}$ для частиц сорта α не зависят от координат и времени. Уравнения (1)–(7) автоматически удовлетворяют этим условиям с ненулевыми тепловыми потоками. Рассмотрим малые возмущения физических величин относительно равновесного состояния. Например, давление представим в виде $p = {{p}_{0}} + p'\left( {r,t} \right)$, где $p'\left( {r,t} \right) \sim expi\left( {{\mathbf{k}} \cdot {\mathbf{r}} - {{\omega }_{0}}t} \right)$ и $\left| {p'} \right| \ll {{p}_{0}}$. Здесь ${{\omega }_{0}} = \omega + \left( {{{{\mathbf{v}}}_{0}} \cdot {\mathbf{k}}} \right)$ является частотой колебаний в движущей совместно с плазмой системе координат, k – волновой вектор колебаний. Исключив из уравнений возмущения тепловых потоков

(8)

$\begin{gathered} S_{{\alpha \bot }}^{'} = \frac{{{{k}_{\parallel }}{{p}_{{\alpha \parallel 0}}}{{p}_{{\alpha \bot 0}}}}}{{\omega {{\rho }_{{\alpha 0}}}}}\left( {\frac{{p_{{\alpha \bot }}^{'}}}{{{{p}_{{\alpha \bot 0}}}}} - \frac{{\rho _{\alpha }^{'}}}{{{{\rho }_{{\alpha 0}}}}} - \frac{{{{p}_{{\alpha \parallel 0}}} - {{p}_{{\alpha \bot 0}}}}}{{{{p}_{{\alpha \parallel 0}}}}}\frac{{B'}}{{{{B}_{0}}}}} \right) + \\ + \;2{{S}_{{\alpha \bot 0}}}\frac{{\rho _{\alpha }^{'}}}{{{{\rho }_{{\alpha 0}}}}}, \\ \end{gathered} $

(9)

$S_{{\alpha \parallel }}^{'} = \frac{{3p_{{\alpha \parallel 0}}^{2}{{k}_{\parallel }}}}{{\omega {{\rho }_{{\alpha 0}}}}}\left( {\frac{{p_{{\alpha \parallel }}^{'}}}{{{{p}_{{\alpha \parallel 0}}}}} - \frac{{\rho _{\alpha }^{'}}}{{{{\rho }_{{\alpha 0}}}}}} \right) - {{S}_{{\alpha \parallel 0}}}\left( {3\frac{{B'}}{{{{B}_{0}}}} - 4\frac{{\rho _{\alpha }^{'}}}{{{{\rho }_{{\alpha 0}}}}}} \right),$

получим систему уравнений для возмущенного состояния

(10)

$\rho _{\alpha }^{'}\omega - {{\rho }_{{\alpha 0}}}\left( {{{k}_{x}}v_{x}^{'} + {{k}_{y}}v_{y}^{'} + {{k}_{z}}v_{z}^{'}} \right) = 0,$

(11)

$\begin{gathered} {{a}_{{\alpha 0}}}\frac{{p_{{\alpha \bot }}^{'}}}{{{{p}_{{\alpha \bot 0}}}}} = {{a}_{{\alpha 1}}}\frac{{B'}}{{{{B}_{0}}}} + {{a}_{{\alpha 2}}}\frac{{\rho _{\alpha }^{'}}}{{{{\rho }_{{\alpha 0}}}}}; \\ {{b}_{{\alpha 0}}}\frac{{p_{{\alpha \parallel }}^{'}}}{{{{p}_{{\alpha \parallel 0}}}}} = {{b}_{{\alpha 1}}}\frac{{B'}}{{{{B}_{0}}}} + {{b}_{{\alpha 2}}}\frac{{\rho _{\alpha }^{'}}}{{h{{o}_{{\alpha 0}}}}}, \\ \end{gathered} $

(12)

$\begin{gathered} \omega {{\rho }_{0}}{\mathbf{v}}' + \frac{1}{{4\pi }}\left( {{\mathbf{k}} \cdot {{{\mathbf{B}}}_{0}}} \right){\mathbf{B}}{\text{'}} - \frac{1}{{4\pi }}{{B}_{0}}B'{\mathbf{k}} - \\ - \;\sum\limits_\alpha \,\left[ {{\mathbf{k}}p_{{\alpha \bot }}^{'} + \frac{{{{p}_{{\alpha \parallel 0}}} - {{p}_{{\alpha \bot 0}}}}}{{B_{0}^{2}}}\mathop {}\limits_{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}^{^{{^{{}}}}} } \right. \times \\ \times \;\left( {{\mathbf{k}} \cdot {{{\mathbf{B}}}_{0}}} \right)\left. {\left( {{\mathbf{B}}{\text{'}} - 2\frac{{B'}}{{{{B}_{0}}}}{{{\mathbf{B}}}_{0}} + \frac{{p_{{\alpha \parallel }}^{'} - p_{{\alpha \bot }}^{'}}}{{{{p}_{{\alpha \parallel 0}}} - {{p}_{{\alpha \bot 0}}}}}{{{\mathbf{B}}}_{0}}} \right)} \right] = 0, \\ \end{gathered} $

(13)

$\omega {\mathbf{B}}{\text{'}} - {{{\mathbf{B}}}_{0}}\left( {{\mathbf{k}} \cdot {\mathbf{v}}} \right) + \left( {{{{\mathbf{B}}}_{0}} \cdot {\mathbf{k}}} \right){\mathbf{v}} = 0,\quad \left( {{\mathbf{k}} \cdot {\mathbf{B}}'} \right) = 0,$

где

(14)

$\begin{gathered} {{a}_{{\alpha 0}}} = 1 - \eta _{\alpha }^{2},\quad {{a}_{{\alpha 1}}} = 1 - 2{{\gamma }_{\alpha }}{{\eta }_{\alpha }} - {{{\bar {\varphi }}}_{\alpha }}\eta _{\alpha }^{2}, \\ {{a}_{{\alpha 2}}} = 1 + 2{{\gamma }_{\alpha }}{{\eta }_{\alpha }} - \eta _{\alpha }^{2}, \\ {{b}_{{\alpha 0}}} = 1 - 3\eta _{\alpha }^{2},\quad {{b}_{{\alpha 1}}} = 2{{\gamma }_{\alpha }}{{\eta }_{\alpha }}\left( {{{\varphi }_{\alpha }} - 2} \right) - 2, \\ {{b}_{{\alpha 2}}} = 3 + 4{{\gamma }_{\alpha }}{{\eta }_{\alpha }} - 3\eta _{\alpha }^{2}. \\ \end{gathered} $

Здесь для основного невозмущенного состояния были введены обозначения (нулевые индексы опущены)

(15)

$\begin{gathered} {{\rho }_{\alpha }} = n{{m}_{\alpha }},\quad {{\varphi }_{\alpha }} = \frac{{{{p}_{{\alpha \bot }}}}}{{{{p}_{{\alpha \parallel }}}}},\quad {{{\bar {\varphi }}}_{\alpha }} = 1 - {{\varphi }_{\alpha }},\quad c_{{\alpha \parallel }}^{2} = \frac{{{{p}_{{\alpha \parallel }}}}}{{{{\rho }_{\alpha }}}}, \\ c_{{\alpha \bot }}^{2} = \frac{{{{p}_{{\alpha \bot }}}}}{{{{\rho }_{\alpha }}}},\quad {{\eta }_{\alpha }} \equiv \frac{{{{c}_{{\alpha \parallel }}}{{k}_{\parallel }}}}{\omega } = \frac{{{{c}_{{\alpha \parallel }}}k}}{\omega }cos\theta , \\ \end{gathered} $

где θ – угол между векторами k и ${{{\mathbf{B}}}_{0}}$, ${{k}_{\parallel }} = {{{\mathbf{B}}}_{0}} \cdot {\mathbf{k}}{\text{/}}{{B}_{0}}$. Безразмерные величины, характеризующие тепловые потоки, ${{\bar {S}}_{{\alpha \parallel }}} = {{S}_{{\alpha \parallel }}}{\text{/}}({{p}_{{\alpha \parallel }}}{{c}_{{\alpha \parallel }}})$, ${{\bar {S}}_{{\alpha \bot }}} = {{S}_{{\alpha \bot }}}{\text{/}}({{p}_{{\alpha \bot }}}{{c}_{{\alpha \parallel }}})$ в реальных ситуациях различаются. Однако, здесь для простоты считаем, что ${{\bar {S}}_{{\alpha \parallel }}} = {{\bar {S}}_{{\alpha \bot }}} = {{\gamma }_{\alpha }}.$ Примем, что $\rho = \sum {{{\rho }_{\alpha }}} $ и

$\begin{gathered} l = {{l}_{1}} = co{{s}^{2}}\theta ,\quad {{l}_{2}} = si{{n}^{2}}\theta , \\ c_{A}^{2} \equiv \frac{{{{B}^{2}}}}{{4\pi \rho }},\quad {{\beta }_{\alpha }} = \frac{{{{B}^{2}}}}{{4\pi {{p}_{{\alpha \parallel }}}}}, \\ \end{gathered} $

${{p}_{{\alpha \parallel }}} = \frac{1}{2}{{n}_{e}}{{k}_{B}}{{T}_{{\alpha \parallel }}},\quad {{p}_{{\alpha \bot }}} = \frac{1}{2}{{n}_{e}}{{k}_{B}}{{T}_{{\alpha \bot }}},\quad \Omega \equiv \frac{{{{c}_{{i\parallel }}}}}{{{{c}_{{e\parallel }}}}} = \frac{\psi }{{\sqrt {{{\Lambda }_{e}}} }},$

(16)

${{\Lambda }_{\alpha }} = \frac{{{{m}_{i}} + {{m}_{e}}}}{{{{m}_{\alpha }}}} \approx \frac{{{{m}_{i}}}}{{{{m}_{\alpha }}}},\quad {{p}_{{i\parallel }}} = {{\Lambda }_{e}}{{\Omega }^{2}}{{p}_{{e\parallel }}},$

${{\Lambda }_{e}} = {{\kappa }^{2}} \approx 1836,$

$\begin{gathered} {{\psi }^{2}} = \frac{{{{p}_{{i\parallel }}}}}{{{{p}_{{e\parallel }}}}} = \frac{{{{T}_{{i\parallel }}}}}{{{{T}_{{e\parallel }}}}} = \frac{1}{{{{\tau }_{\parallel }}}},\quad c_{{s \bot }}^{2} \equiv \left( {\sum\limits_\alpha \,{{p}_{{\alpha \bot }}}} \right){\text{/}}\rho , \\ c_{{s\parallel }}^{2} \equiv \left( {\sum\limits_\alpha \,{{p}_{{\alpha \parallel }}}} \right){\text{/}}\rho . \\ \end{gathered} $

Допустив, не нарушая общности постановки задачи, что в плоской декартовой системе координат

(17)

$\begin{gathered} {\mathbf{k}} = \left( {k,0,0} \right),\quad {{{\mathbf{B}}}_{0}} = \left( {{{B}_{{0x}}},0,{{B}_{{0z}}}} \right), \\ {{B}_{{0x}}} = {{B}_{0}}cos\theta ,\quad {{B}_{{0z}}} = {{B}_{0}}sin\theta \\ \end{gathered} $

и исключив $\rho _{\alpha }^{'}$, $p_{{\alpha \bot }}^{'}$ и $p_{{\alpha \parallel }}^{'}$, получим

(18)

$\frac{{{\mathbf{B}}'}}{B} - \frac{{\mathbf{B}}}{B}\frac{{\left( {{\mathbf{k}} \cdot {\mathbf{v}}} \right)}}{\omega } + \frac{{{{k}_{\parallel }}}}{\omega }{\mathbf{v}} = 0,$

$\begin{gathered} \frac{1}{{{{\eta }_{i}}}}\frac{{\mathbf{v}}}{{{{c}_{{i\parallel }}}}} - {{\varphi }_{i}}\frac{{\mathbf{k}}}{{{{k}_{\parallel }}}}\left( {\frac{{{{a}_{{i1}}}}}{{{{a}_{{i0}}}}}\frac{{B'}}{B} + \frac{{{{a}_{{i2}}}}}{{{{a}_{{i0}}}}}\frac{{\left( {{\mathbf{k}} \cdot {\mathbf{v}}} \right)}}{\omega } + \frac{{\left( {{\mathbf{B}} \cdot {\mathbf{B}}'} \right)}}{{4\pi {{p}_{{i \bot }}}}}} \right) + \\ + \;\frac{{{\mathbf{B}}'}}{B}\left( {{{\beta }_{i}} - {{{\bar {\varphi }}}_{i}}} \right) - \frac{{\mathbf{B}}}{B}\left[ {\left( {\frac{{{{b}_{{i1}}}}}{{{{b}_{{i0}}}}} - {{\varphi }_{i}}\frac{{{{a}_{{i1}}}}}{{{{a}_{{i0}}}}} - 2{{{\bar {\varphi }}}_{i}}} \right)\frac{{B'}}{B} + } \right. \\ \end{gathered} $

(19)

$\begin{gathered} + \;\left. {\left( {\frac{{{{b}_{{i2}}}}}{{{{b}_{{i0}}}}} - {{\varphi }_{i}}\frac{{{{a}_{{i2}}}}}{{{{a}_{{i0}}}}}} \right)\frac{{\left( {{\mathbf{k}} \cdot {\mathbf{v}}} \right)}}{\omega }} \right] - \\ - \;{{\tau }_{\parallel }}\left[ {{{\varphi }_{e}}\frac{{\mathbf{k}}}{{{{k}_{\parallel }}}}\left( {\frac{{{{a}_{{e1}}}}}{{{{a}_{{e0}}}}}\frac{{B'}}{B} + \frac{{{{a}_{{e2}}}}}{{{{a}_{{e0}}}}}\frac{{\left( {{\mathbf{k}} \cdot {\mathbf{v}}} \right)}}{\omega }} \right) + \frac{{{\mathbf{B}}'}}{B}{{{\bar {\varphi }}}_{e}} + } \right. \\ \end{gathered} $

$\begin{gathered} + \;\frac{{\mathbf{B}}}{B}\left[ {\left( {\frac{{{{b}_{{e1}}}}}{{{{b}_{{e0}}}}} - {{\varphi }_{e}}\frac{{{{a}_{{e1}}}}}{{{{a}_{{e0}}}}} - 2{{{\bar {\varphi }}}_{e}}} \right)\frac{{B'}}{B} + } \right. \\ \left. {\left. { + \;\left( {\frac{{{{b}_{{e2}}}}}{{{{b}_{{e0}}}}} - {{\varphi }_{e}}\frac{{{{a}_{{e2}}}}}{{{{a}_{{e0}}}}}} \right)\frac{{\left( {{\mathbf{k}} \cdot {\mathbf{v}}} \right)}}{\omega }} \right]} \right] = 0, \\ \end{gathered} $

$y$-компонента этой системы сводится к

(20)

$\begin{gathered} \frac{{B_{y}^{'}}}{B} + {{\eta }_{i}}\frac{{{{v}_{y}}}}{{{{c}_{{i\parallel }}}}} + \frac{{B_{y}^{'}}}{B} + {{\eta }_{e}}\frac{{{{v}_{y}}}}{{{{c}_{{e\parallel }}}}} = 0, \\ {{p}_{{i\parallel }}}\frac{1}{{{{\eta }_{i}}}}\frac{{{{v}_{y}}}}{{{{c}_{{i\parallel }}}}} + {{p}_{{i\parallel }}}\left( {{{\beta }_{i}} - {{{\bar {\varphi }}}_{i}}} \right)\frac{{B_{y}^{'}}}{B} - {{p}_{{e\parallel }}}{{{\bar {\varphi }}}_{e}}\frac{{B_{y}^{'}}}{B} = 0, \\ \end{gathered} $

откуда легко получается дисперсионное уравнение для несжимаемых мод:

(21)

$\sum\limits_\alpha \,\frac{{\eta _{\alpha }^{2}}}{{{{\Lambda }_{\alpha }}}}\left( {\frac{1}{2}{{\beta }_{\alpha }} + {{\varphi }_{\alpha }} - 1} \right) = 1,$

из которого следует, что

(22)

$\frac{{{{\omega }^{2}}}}{{c_{{i\parallel }}^{2}{{k}^{2}}}} = l\left( {{{\beta }_{i}} + {{\varphi }_{i}} - 1 + \frac{{{{\varphi }_{e}} - 1}}{{{{\psi }^{2}}}}} \right).$

В размерных величинах это соответствует известному результату

(23)

${{\omega }^{2}} = c_{A}^{2}k_{\parallel }^{2}\left( {1 - 4\pi \sum\limits_\alpha \,\frac{{{{p}_{{\alpha \parallel }}} - {{p}_{{\alpha \bot }}}}}{{{{B}^{2}}}}} \right).$

Это является прототипом дисперсионного уравнения альфвеновских колебаний в изотропной плазме. При выполнении

(24)

${{\beta }_{i}} + {{\varphi }_{i}} + {{\varphi }_{e}}{\text{/}}{{\psi }^{2}} < 1 + 1{\text{/}}{{\psi }^{2}}$

альфвеновские моды становятся неустойчивыми, возникает шланговая неустойчивость. В двух случаях инкремент шланговой неустойчивости переходит к известному случаю: при ${{\psi }^{2}} \gg 1$ (холодные электроны, ${{T}_{{e\parallel }}} \ll {{T}_{{i\parallel }}}$) и при изотропных электронах, ${{\varphi }_{e}} = 1$. Если электронный компонент плазмы анизотропный, ${{\varphi }_{e}} \ne 1$, то при ${{\varphi }_{e}} > 1\;({{T}_{{e \bot }}} > {{T}_{{e\parallel }}})$ шланговая неустойчивость подавляется, а при обратном случае, ${{\varphi }_{e}} < 1\;({{T}_{{e \bot }}} < {{T}_{{e\parallel }}})$, наоборот, неустойчивость усиливается.

Другие x и z компоненты системы уравнений (18)–(19) имеют вид

${{q}_{{i1}}}\frac{{{{v}_{x}}}}{{{{c}_{{i\parallel }}}}} - {{q}_{{i2}}}\operatorname{tg} \theta \frac{{B_{z}^{'}}}{B} + {{\tau }_{\parallel }}{{q}_{{e1}}}\frac{{{{v}_{x}}}}{{{{c}_{{e\parallel }}}}} - {{\tau }_{\parallel }}{{q}_{{e2}}}\operatorname{tg} \theta \frac{{B_{z}^{'}}}{B} = 0,$

(25)

$\frac{{B_{z}^{'}}}{B} - {{\eta }_{\alpha }}\operatorname{tg} \theta \frac{{{{v}_{x}}}}{{{{c}_{{\alpha \parallel }}}}} + {{\eta }_{\alpha }}\frac{{{{v}_{z}}}}{{{{c}_{{\alpha \parallel }}}}} = 0,$

$\frac{1}{{{{\eta }_{i}}}}\frac{{{{v}_{z}}}}{{{{c}_{{i\parallel }}}}} - {{q}_{{i3}}}\operatorname{tg} \theta \frac{{{{v}_{x}}}}{{{{c}_{{i\parallel }}}}} + {{q}_{{i4}}}\frac{{B_{z}^{'}}}{B} - {{\tau }_{\parallel }}{{q}_{{e3}}}\operatorname{tg} \theta \frac{{{{v}_{x}}}}{{{{c}_{{e\parallel }}}}} + {{\tau }_{\parallel }}{{q}_{{e4}}}\frac{{B_{z}^{'}}}{B} = 0,$

где

${{q}_{{i4}}} = {{\beta }_{i}} - {{\bar {\varphi }}_{i}} - {{l}_{2}}{{q}_{{i0}}},\quad {{q}_{{e4}}} = - {{\bar {\varphi }}_{e}} - {{l}_{2}}{{q}_{{e0}}},$

${{q}_{{i2}}} = {{\varphi }_{i}}\frac{{{{a}_{{i1}}}}}{{{{a}_{{i0}}}}} + {{\beta }_{i}} + {{l}_{1}}{{q}_{{i0}}},\quad {{q}_{{e2}}} = {{\varphi }_{e}}\frac{{{{a}_{{e1}}}}}{{{{a}_{{e0}}}}} + {{l}_{1}}{{q}_{{e0}}},$

(26)

${{q}_{{i1}}} = \frac{1}{{{{\eta }_{i}}}} - {{\eta }_{i}}\frac{{{{\varphi }_{i}}}}{{{{l}_{1}}}}\frac{{{{a}_{{i2}}}}}{{{{a}_{{i0}}}}} - {{q}_{{i3}}},\quad {{q}_{{e1}}} = - {{\eta }_{e}}\frac{{{{\varphi }_{e}}}}{{{{l}_{1}}}}\frac{{{{a}_{{e2}}}}}{{{{a}_{{e0}}}}} - {{q}_{{e3}}},$

${{q}_{{i3}}} = {{\eta }_{i}}\left( {\frac{{{{b}_{{i2}}}}}{{{{b}_{{i0}}}}} - {{\varphi }_{i}}\frac{{{{a}_{{i2}}}}}{{{{a}_{{i0}}}}}} \right),\quad {{q}_{{e3}}} = {{\eta }_{e}}\left( {\frac{{{{b}_{{e2}}}}}{{{{b}_{{e0}}}}} - {{\varphi }_{e}}\frac{{{{a}_{{e2}}}}}{{{{a}_{{e0}}}}}} \right),$

${{q}_{{i0}}} = \frac{{{{b}_{{i1}}}}}{{{{b}_{{i0}}}}} - {{\varphi }_{i}}\frac{{{{a}_{{i1}}}}}{{{{a}_{{i0}}}}} - 2{{\bar {\varphi }}_{i}},\quad {{q}_{{e0}}} = \frac{{{{b}_{{e1}}}}}{{{{b}_{{e0}}}}} - {{\varphi }_{e}}\frac{{{{a}_{{e1}}}}}{{{{a}_{{e0}}}}} - 2{{\bar {\varphi }}_{e}}.$

Детерминант этой системы дает дисперсионное уравнение для сжимаемых мод:

(27)

$\begin{gathered} \sum\limits_\alpha \,{{l}_{1}}\frac{{{{\eta }_{\alpha }}{{q}_{{\alpha 1}}}}}{{{{\Lambda }_{\alpha }}}}\left( {1 - \sum\limits_\alpha \,\frac{{\eta _{\alpha }^{2}{{q}_{{\alpha 4}}}}}{{{{\Lambda }_{\alpha }}}}} \right) - \\ - \;\sum\limits_\alpha \,{{l}_{2}}\frac{{\eta _{\alpha }^{2}{{q}_{{\alpha 2}}}}}{{{{\Lambda }_{\alpha }}}}\left( {1 - \sum\limits_\alpha \,\frac{{{{\eta }_{\alpha }}{{q}_{{\alpha 3}}}}}{{{{\Lambda }_{\alpha }}}}} \right) = 0 \\ \end{gathered} $

Учитывая, что ${{\eta }_{i}} = \Omega {{\eta }_{e}}$, $c_{{e\parallel }}^{2}{{\rho }_{e}} = {{p}_{{i\parallel }}}{\text{/}}({{\Lambda }_{e}}{{\Omega }^{2}})$ дисперсионное уравнение для сжимаемых мод (27) представляется в виде

(28)

$\left( {{{x}^{2}} - 1} \right)\left( {{{x}^{2}} - 3} \right)\left( {{{\Omega }^{2}}{{x}^{2}} - 3} \right)\left( {{{\Omega }^{2}}{{x}^{2}} - 1} \right)Z = 0,$

где $x = 1{\text{/}}{{\eta }_{i}}$. Легко можно доказать, что корни множителей $({{x}^{2}} - 1)({{x}^{2}} - 3)$$({{\Omega }^{2}}{{x}^{2}} - 3)({{\Omega }^{2}}{{x}^{2}} - 1)$ являются ложными (см. (11)). Последний множитель $Z = 0$ в (28) является дисперсионным уравнением для сжимаемых мод. Это полиномиальное уравнение 12-го порядка для нормированной фазовой скорости $x = \omega {\text{/}}{{k}_{\parallel }}{{c}_{{i\parallel }}}$

(29)

$\begin{gathered} {{U}_{{12}}}{{x}^{{12}}} + {{U}_{{10}}}{{x}^{{10}}} + {{U}_{8}}{{x}^{8}} + {{U}_{6}}{{x}^{6}} + {{U}_{4}}{{x}^{4}} + \\ + \;{{U}_{2}}{{x}^{2}} + {{U}_{0}} + {{\gamma }_{\alpha }}\left[ {{{U}_{9}}{{x}^{9}} + {{U}_{7}}{{x}^{7}} + {{U}_{5}}{{x}^{5}} + } \right. \\ \left. { + \;{{U}_{3}}{{x}^{3}} + {{U}_{1}}x} \right] = 0, \\ \end{gathered} $

которое является общим дисперсионным уравнением сжимаемых волновых мод в однородной бесконечной анизотропной замагниченной двухкомпонентной плазме. Здесь учтены тепловые потоки вдоль магнитного поля, переносимые частицами сорта α. Коэффициенты уравнения ${{U}_{{0 - 12}}}$ являются сложными действительными функциями параметров задачи, которые были получены в работе [10]. Эти коэффициенты приведены в Приложении.

В частном случае, при переходе к однокомпонентной ионной плазме $\psi \to \infty $ общее дисперсионное уравнение (29) переходит в

(30)

$\begin{gathered} {{C}_{8}}{{x}^{8}} + {{C}_{6}}{{x}^{6}} + {{C}_{4}}{{x}^{4}} + {{C}_{2}}{{x}^{2}} + {{C}_{0}} + \\ + \;{{\gamma }_{i}}\left[ {{{C}_{5}}{{x}^{5}} + {{C}_{3}}{{x}^{3}} + {{C}_{1}}x} \right] = 0, \\ \end{gathered} $

которое точно совпадает с результатами работы [4].

В общем случае уравнение (29) сложное. Оно включает в себя эффекты анизотропии как ионного, так и электронного компонентов. Взаимодействие ионных и электронных колебаний усложняется присутствием тепловых потоков вдоль магнитного поля в обоих компонентах.

4. ВОЛНЫ В БЕСПОТОКОВОМ РЕЖИМЕ

Для идентификации волновых мод исключим эффекты, связанные с тепловыми потоками. Пусть ${{\gamma }_{\alpha }} = 0$. Для простоты обозначим $t = {{x}^{2}}$, $v_{{ph}}^{2} \equiv {{\omega }^{2}}{\text{/}}c_{{i\parallel }}^{2}{{k}^{2}} = lt$. Тогда уравнение (29) представляется в виде

(31)

${{U}_{{12}}}{{t}^{6}} + {{U}_{{10}}}{{t}^{5}} + {{U}_{8}}{{t}^{4}} + {{U}_{6}}{{t}^{3}} + {{U}_{4}}{{t}^{2}} + {{U}_{2}}t + {{U}_{0}} = 0.$

4.1. Параллельное распространение волн

В случае параллельного распространения волн относительного магнитного поля, $l = 1$, уравнение (31) удается представить в виде множителей

(32)

$\begin{gathered} \left( {t - 1} \right)\left( { - {{\psi }^{2}}t + {{\kappa }^{2}}} \right) \times \\ \times \;\left( {{{\psi }^{2}}t - {{\psi }^{2}}{{\beta }_{i}} - {{\psi }^{2}}{{\varphi }_{i}} + {{\psi }^{2}} - {{\varphi }_{e}} + 1} \right)\bar {Z} = 0, \\ \end{gathered} $

где

(33)

$\begin{gathered} \bar {Z} \equiv - {{\psi }^{4}}{{t}^{3}} + 3{{\kappa }^{2}}{{\psi }^{2}}{{t}^{2}} + 6{{\psi }^{4}}{{t}^{2}} - 18{{\kappa }^{2}}{{\psi }^{2}}t - \\ - \;3{{\psi }^{4}}t + 9{{\kappa }^{2}}{{\psi }^{2}} + 3{{\psi }^{2}}{{t}^{2}} - 3{{\kappa }^{2}}t - 9{{\psi }^{2}}t + 9{{\kappa }^{2}}. \\ \end{gathered} $

В (32) первое решение $t = 1$ соответствует медленным ионно-акустическим модам $(SIA)$, для которых ${{\omega }^{2}} = c_{{i\parallel }}^{2}k_{\parallel }^{2}$. Второй множитель $\left( { - {{\psi }^{2}}t + {{\kappa }^{2}}} \right) = 0$ соответствует медленным электронно-акустическим модам $(SEA)$, для которых ${{\omega }^{2}} = c_{{e\parallel }}^{2}k_{\parallel }^{2}$. Третий множитель в (32) ${{\psi }^{2}}t - {{\psi }^{2}}{{\beta }_{i}} - {{\psi }^{2}}{{\varphi }_{i}} + {{\psi }^{2}} - {{\varphi }_{e}} + 1 = $ $ = 0$ описывает ускоренные магнитозвуковые моды $(FMS)$, для которых ${{\omega }^{2}} = c_{{i\parallel }}^{2}k_{\parallel }^{2}{\text{(}}{{\varphi }_{i}}{{\psi }^{2}} + {{\beta }_{i}}{{\psi }^{2}} - $ $ - \;{{\psi }^{2}} + {{\varphi }_{e}} - 1){\text{/}}{{\psi }^{2}}$, которую можно представить в виде ${{\omega }^{2}} = c_{A}^{2}k_{\parallel }^{2}$$\left( {1 - 4\pi \sum\nolimits_\alpha {\frac{{{{p}_{{\alpha \parallel }}} - {{p}_{{\alpha \bot }}}}}{{{{B}^{2}}}}} } \right)$. Ускоренные магнитозвуковые моды при параллельном распространении становятся несжимаемыми, и дисперсионное уравнение совпадает с уравнением для альфвеновских волн (23).

Четвертый множитель в (32) $\bar {Z} = 0$ это кубическое уравнение. Сложных точных формул для решения кубического уравнения здесь приводить не будем. Воспользуемся разложением по малому параметру $1{\text{/}}{{\kappa }^{2}} = \epsilon \ll 1$. Пусть ${{\psi }^{2}} = \mu $, тогда

(34)

$\begin{gathered} \bar {Z} \equiv - \epsilon \mu t\left[ {\mu {{t}^{2}} - 3\left( {2\mu + 1} \right)t + 3\left( {\mu + 3} \right)} \right] + \\ + \;3\left[ {\mu {{t}^{2}} - \left( {6\mu + 1} \right)t + 3\left( {\mu + 1} \right)} \right] = 0. \\ \end{gathered} $

При $\epsilon \to 0$ получим

(35)

${{t}_{{1,2}}} = \frac{{6\mu + 1 \pm \sqrt {\mathop {\left( {6\mu + 1} \right)}\nolimits^2 - 12\left( {\mu + 1} \right)\mu } }}{{2\mu }},$

или

(36)

${{\omega }^{2}} = \frac{{6 + {{\tau }_{\parallel }} \pm \sqrt {24 + \tau _{\parallel }^{2}} }}{2}c_{{i\parallel }}^{2}k_{\parallel }^{2}.$

Здесь первое решение (верхний знак) описывает медленные звуковые моды $(SS)$. Это решение можно представить в виде

(37)

${{\omega }^{2}} = \frac{{6 + {{\tau }_{\parallel }} + \sqrt {24 + \tau _{\parallel }^{2}} }}{{2\left( {1 + {{\tau }_{\parallel }}} \right)}}c_{{s\parallel }}^{2}k_{\parallel }^{2}.$

При ${{\tau }_{\parallel }} \to 1$ (изотермическая плазма) ${{\omega }^{2}} = 3c_{{s\parallel }}^{2}k_{\parallel }^{2}$, а при ${{\tau }_{\parallel }} \to \infty $ (холодные ионы) ${{\omega }^{2}} = c_{{s\parallel }}^{2}k_{\parallel }^{2}$. Второе решение (нижний знак) описывает быстрые ионно-акустические моды $(FIA)$

(38)

${{\omega }^{2}} = \frac{{6 + {{\tau }_{\parallel }} - \sqrt {24 + \tau _{\parallel }^{2}} }}{2}c_{{i\parallel }}^{2}k_{\parallel }^{2}.$

При ${{\tau }_{\parallel }} \to 1$ (изотермическая плазма) ${{\omega }^{2}} = c_{{i\parallel }}^{2}k_{\parallel }^{2}$, а при ${{\tau }_{\parallel }} \to \infty $ (холодные ионы) ${{\omega }^{2}} = 3c_{{i\parallel }}^{2}k_{\parallel }^{2}$.

Третье решение (34)

(39)

${{t}_{3}} \approx \frac{1}{\epsilon }\frac{3}{\mu } = \frac{{3{{\kappa }^{2}}}}{{{{\psi }^{2}}}},$

что соответствует быстрым электронно-акустическим модам $(FEA)$, ${{\omega }^{2}} = 3c_{{e\parallel }}^{2}k_{\parallel }^{2}$.

Таким образом, в беспотоковом режиме при параллельном распространении общее дисперсионное уравнение (29) переходит в (32), которое описывает шесть мод: быстрые магнитозвуковые, медленные звуковые, быстрые/медленные ионно-акустические и быстрые/медленные электронно-акустические моды. Из них только быстрые магнитозвуковые волны могут стать неустойчивыми при выполнении условий развития шланговой неустойчивости (24).

4.2. Перпендикулярное распространение волн

При квазиперпендикулярном распространении волн $(l \to 0)$ из дисперсионного уравнения (31) для медленных звуковых волн получим

(40)

${{\omega }^{2}} = {{k}^{2}}\left( {c_{A}^{2} + 2c_{{s \bot }}^{2}} \right),$

которое является устойчивым. Для остальных мод колебаний ${{\omega }^{2}} \sim l \to 0$.

4.3. Наклонное распространение волн

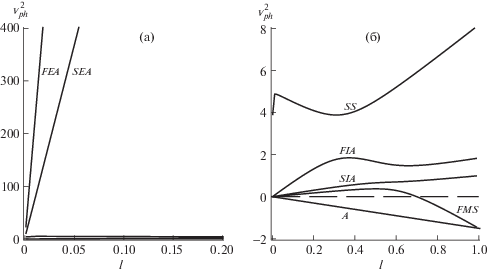
В общем случае, когда волны распространяются под произвольным углом $0 < l < 1$, дисперсионное уравнение (31) решается численно. Коэффициенты этого уравнения являются действительными функциями пяти параметров: l – параметр угла распространения волны относительно направления магнитного поля, ${{\beta }_{i}}$ – параметр интенсивности магнитного поля, ψ – степень неизотермичности плазмы, ${{\varphi }_{e}}$ и ${{\varphi }_{i}}$ – степени анизотропии электронной и ионной составляющих плазмы. При выборе набора параметров выделим два характерных случая, когда шланговая неустойчивость возникает (условие (24) выполняется), и когда шланговая неустойчивость не возникает (условие (24) не выполняется). На рис. 1 показана зависимость нормированного квадрата фазовой скорости $v_{{ph}}^{2}$ от l. На кривых указаны названия волновых мод, полученных в предыдущем разделе для продольного распространения. Если $v_{{ph}}^{2} < 0$, то возникает неустойчивость. При заданных на рис. 1 параметрах альфвеновские волны (A) для всех углов становятся неустойчивыми (шланговая неустойчивость), а быстрые магнитозвуковые моды (FMS) становятся неустойчивыми только при квазипродольном распространении (вторая шланговая неустойчивость). Порог неустойчивости FMS-мод определяется условием ${{U}_{0}}(l,\psi ,{{\beta }_{i}},{{\varphi }_{e}},{{\varphi }_{i}}) = 0$, где функция ${{U}_{0}}$ определена в [10]. Для устойчивых мод фазовые скорости располагаются в следующем порядке: $A < FMS < SIA < FIA < SS < SEA < FEA$.

Рис. 1.

Зависимость квадрата фазовой скорости распространения волн от параметра угла распространения $l = co{{s}^{2}}\theta $ в случае возникновения шланговой неустойчивости, когда выполняется условие (24): ${{\varphi }_{e}} = {{\varphi }_{i}} = 0.5$, ${{\beta }_{i}} = 1$, $\psi = 0.5$. Неустойчивость возникает, если $v_{{ph}}^{2} < 0$. Неустойчивыми становятся альфвеновские (A) и быстрые магнитозвуковые (FMS) моды. (a) – электронные акустические волны, (б) – все остальные волновые ветви.

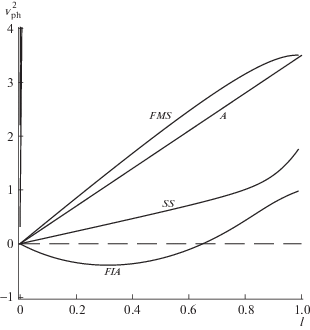
При другом наборе параметров, когда условие шланговой неустойчивости (24) не выполняется, может возникать зеркальная неустойчивость при больших углах распространения. Такой пример показан на рис. 2, где на ветке быстрых ион-акустик мод (FIA) развивается зеркальная неустойчивость. Для зеркальной неустойчивости также существует порог.

Рис. 2.

Зависимость квадрата фазовой скорости распространения волн от параметра угла распространения $l = co{{s}^{2}}\theta $ в случае, когда шланговая неустойчивость не возникает (условие (24) не выполняется): ${{\varphi }_{e}} = {{\varphi }_{i}} = 1.5$, ${{\beta }_{i}} = 1$, $\psi = 0.5$. В этом случае возможна зеркальная неустойчивость, которая развивается у быстрых ионно-акустических (FIA) мод при квазипоперечном распространении.

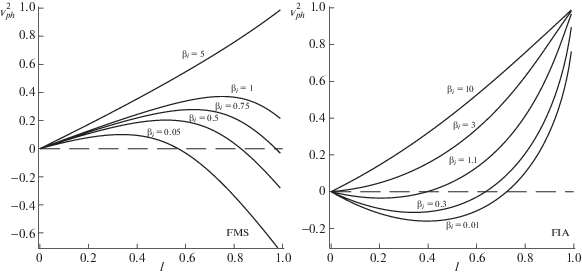
Увеличение интенсивности магнитного поля (${{\beta }_{i}} \sim {{B}^{2}}$) подавляет рассматриваемые неустойчивости. Это видно из примеров, показанных на рис. 3.

Рис. 3.

Влияние магнитного поля (параметр ${{\beta }_{i}}$) на условие возникновения неустойчивости. Слева: кривые зависимости квадрата фазовой скорости от угла распространения волн FMS-мод (вторая шланговая неустойчивость) при значениях параметров ${{\varphi }_{e}} = 0.5$, ${{\varphi }_{i}} = 0.7$, $\psi = 1$, справа: FIA-мод (зеркальная неустойчивость) при ${{\varphi }_{e}} = 1.2$, ${{\varphi }_{i}} = 1.5$, $\psi = 0.7$.

5. КРИТЕРИИ ВОЗНИКНОВЕНИЯ НЕУСТОЙЧИВОСТИ

Как видно из общего дисперсионного уравнения (29) при отсутствии теплового потока $({{\gamma }_{\alpha }} = 0)$ вблизи порога неустойчивости

(41)

${{x}^{2}} \approx - \frac{{{{U}_{0}}}}{{{{U}_{2}}}}.$

Здесь функции ${{U}_{0}} = {{U}_{0}}({{\varphi }_{i}},{{\varphi }_{e}},\psi ,{{\beta }_{i}},l)$ и ${{U}_{2}} = $ $ = {{U}_{2}}({{\varphi }_{i}},{{\varphi }_{e}},\psi ,{{\beta }_{i}},l)$ определены в [10]. Критерий возникновения неустойчивости в общем виде определяется как ${{U}_{0}}{\text{/}}{{U}_{2}} > 0$. Учитывая, что для наклонных волн функции ${{U}_{0}}$ и ${{U}_{2}}$ являются линейными функциями параметра $l = co{{s}^{2}}\theta $, то ${{x}^{2}} \approx - (a + bl){\text{/}}(c + dl)$, где a, b, c, d легко определяются из выражений для ${{U}_{0}}$ и ${{U}_{2}}$:

(42)

$\begin{gathered} a = - 18{{\kappa }^{4}}{{\psi }^{4}}\varphi _{i}^{2} + 9{{\kappa }^{4}}{{\psi }^{4}}{{\beta }_{i}} + 18{{\kappa }^{4}}{{\psi }^{4}}{{\varphi }_{i}} - \\ - \;9{{\kappa }^{4}}{{\psi }^{2}}\varphi _{e}^{2} - 18{{\kappa }^{4}}{{\psi }^{2}}{{\varphi }_{e}}{{\varphi }_{i}} - 9{{\kappa }^{4}}{{\psi }^{2}}\varphi _{i}^{2} + 9{{\kappa }^{4}}{{\psi }^{2}}{{\beta }_{i}} + \\ + \;18{{\kappa }^{4}}{{\psi }^{2}}{{\varphi }_{e}} + 18{{\kappa }^{4}}{{\psi }^{2}}{{\varphi }_{i}} - 18{{\kappa }^{4}}\varphi _{e}^{2} + 18{{\kappa }^{4}}{{\varphi }_{e}}, \\ \end{gathered} $

(43)

$\begin{gathered} b = 18{{\kappa }^{4}}{{\psi }^{4}}\varphi _{i}^{2} - 9{{\kappa }^{4}}{{\psi }^{4}}{{\varphi }_{i}} - 9{{\kappa }^{4}}{{\psi }^{4}} + 9{{\kappa }^{4}}{{\psi }^{2}}\varphi _{e}^{2} + \\ + \;18{{\kappa }^{4}}{{\psi }^{2}}{{\varphi }_{e}}{{\varphi }_{i}} + 9{{\kappa }^{4}}{{\psi }^{2}}\varphi _{i}^{2} - 9{{\kappa }^{4}}{{\psi }^{2}}{{\varphi }_{e}} - \\ - \;9{{\kappa }^{4}}{{\psi }^{2}}{{\varphi }_{i}} - 18{{\kappa }^{4}}{{\psi }^{2}} + 18{{\kappa }^{4}}\varphi _{e}^{2} - 9{{\kappa }^{4}}{{\varphi }_{e}} - 9{{\kappa }^{4}}, \\ \end{gathered} $

$\begin{gathered} c = 30{{\kappa }^{4}}{{\psi }^{4}}\varphi _{i}^{2} + 24{{\kappa }^{2}}{{\psi }^{6}}\varphi _{i}^{2} - 27{{\kappa }^{4}}{{\psi }^{4}}{{\beta }_{i}} - \\ - \;54{{\kappa }^{4}}{{\psi }^{4}}{{\varphi }_{i}} - 12{{\kappa }^{2}}{{\psi }^{6}}{{\beta }_{i}} - 24{{\kappa }^{2}}{{\psi }^{6}}{{\varphi }_{i}} + \\ + \;27{{\kappa }^{4}}{{\psi }^{2}}\varphi _{e}^{2} + 24{{\kappa }^{4}}{{\psi }^{2}}{{\varphi }_{e}}{{\varphi }_{i}} + 3{{\kappa }^{4}}{{\psi }^{2}}\varphi _{i}^{2} + \\ \end{gathered} $

(44)

$ + \;3{{\kappa }^{2}}{{\psi }^{4}}\varphi _{e}^{2} + 24{{\kappa }^{2}}{{\psi }^{4}}{{\varphi }_{e}}{{\varphi }_{i}} + 18{{\kappa }^{2}}{{\psi }^{4}}\varphi _{i}^{2} - $

$\begin{gathered} - \;12{{\kappa }^{4}}{{\psi }^{2}}{{\beta }_{i}} - 54{{\kappa }^{4}}{{\psi }^{2}}{{\varphi }_{e}} - 24{{\kappa }^{4}}{{\psi }^{2}}{{\varphi }_{i}} - \\ - \;18{{\kappa }^{2}}{{\psi }^{4}}{{\beta }_{i}} - 24{{\kappa }^{2}}{{\psi }^{4}}{{\varphi }_{e}} - 36{{\kappa }^{2}}{{\psi }^{4}}{{\varphi }_{i}} + \\ + \;24{{\kappa }^{4}}\varphi _{e}^{2} + 21{{\kappa }^{2}}{{\psi }^{2}}\varphi _{e}^{2} - 24{{\kappa }^{4}}{{\varphi }_{e}} - 36{{\kappa }^{2}}{{\psi }^{2}}{{\varphi }_{e}}, \\ \end{gathered} $

$\begin{gathered} d = - 30{{\kappa }^{4}}{{\psi }^{4}}\varphi _{i}^{2} - 24{{\kappa }^{2}}{{\psi }^{6}}\varphi _{i}^{2} + 27{{\kappa }^{4}}{{\psi }^{4}}{{\varphi }_{i}} + \\ + \;12{{\kappa }^{2}}{{\psi }^{6}}{{\varphi }_{i}} + 18{{\kappa }^{4}}{{\psi }^{4}} - 27{{\kappa }^{4}}{{\psi }^{2}}\varphi _{e}^{2} - \\ - \;24{{\kappa }^{4}}{{\psi }^{2}}{{\varphi }_{e}}{{\varphi }_{i}} - 3{{\kappa }^{4}}{{\psi }^{2}}\varphi _{i}^{2} + 12{{\kappa }^{2}}{{\psi }^{6}} - \\ \end{gathered} $

(45)

$\begin{gathered} - \;3{{\kappa }^{2}}{{\psi }^{4}}\varphi _{e}^{2} - 24{{\kappa }^{2}}{{\psi }^{4}}{{\varphi }_{e}}{{\varphi }_{i}} - 18{{\kappa }^{2}}{{\psi }^{4}}\varphi _{i}^{2} + \\ + \;27{{\kappa }^{4}}{{\psi }^{2}}{{\varphi }_{e}} + 12{{\kappa }^{4}}{{\psi }^{2}}{{\varphi }_{i}} + 12{{\kappa }^{2}}{{\psi }^{4}}{{\varphi }_{e}} + \\ \end{gathered} $

$\begin{gathered} + \;18{{\kappa }^{2}}{{\psi }^{4}}{{\varphi }_{i}} + 30{{\kappa }^{4}}{{\psi }^{2}} - 24{{\kappa }^{4}}\varphi _{e}^{2} + 30{{\kappa }^{2}}{{\psi }^{4}} - \\ - \;21{{\kappa }^{2}}{{\psi }^{2}}\varphi _{e}^{2} + 12{{\kappa }^{4}}{{\varphi }_{e}} + 18{{\kappa }^{2}}{{\psi }^{2}}{{\varphi }_{e}} + \\ + \;12{{\kappa }^{4}} + 18{{\kappa }^{2}}{{\psi }^{2}}. \\ \end{gathered} $

В простейшем случае, когда протоны и электроны одинаково анизотропны, ${{\varphi }_{i}} = {{\varphi }_{e}} = \varphi $, в квазипоперечном пределе $l \to 0$ получим

(46)

${{x}^{2}} \approx - \frac{{3\left( {{{\psi }^{2}} + 1} \right)\left[ {{{\psi }^{2}}\left( {2{{\varphi }^{2}} - 2\varphi - {{\beta }_{i}}} \right) + 2{{\varphi }^{2}} - 2\varphi } \right]}}{{16{{\varphi }^{3}}{{\beta }_{i}}\left( {\varphi - 1} \right){\text{/}}\mathop {\left( {2{{\varphi }^{2}} - 2\varphi - {{\beta }_{i}}} \right)}\nolimits^2 }},$

а условие возникновения зеркальной неустойчивости принимает форму

(47)

$\frac{{{{\psi }^{2}}\left( {2{{\varphi }^{2}} - 2\varphi - {{\beta }_{i}}} \right) + 2\varphi \left( {\varphi - 1} \right)}}{{\varphi - 1}} > 0.$

Если $\varphi < 1$, то это условие выполняется всегда. Если же $\varphi > 1$, должно быть ${{\psi }^{2}}\left[ {2\varphi \left( {\varphi - 1} \right) - {{\beta }_{i}}} \right] + $ $ + \;2\varphi \left( {\varphi - 1} \right) > 0$. Это условие при $\psi \to \infty $ (ионная плазма) переходит в ${{\varphi }^{2}} > \varphi + {{\beta }_{i}}{\text{/}}2$ или $p_{ \bot }^{2}{\text{/}}{{p}_{\parallel }} > $ $ > {{p}_{ \bot }} + {{p}_{m}}$, которое является классическим условием возникновения зеркальной неустойчивости [4]. Здесь ${{p}_{m}}$ – магнитное давление. При $\psi \to 1$ (${{T}_{{e\parallel }}} = {{T}_{{i\parallel }}}$ – изотермическая плазма) верно неравенство ${{\varphi }^{2}} > \varphi + {{\beta }_{i}}{\text{/}}4$. Для горячих электронов $(\psi \to 0)$ условие (47) выполняется во всех случаях.

В более общем случае ${{\varphi }_{i}} \ne {{\varphi }_{e}}$ и наклонного распространения ($l > 0$) порог неустойчивости соответствует критическому углу распространения волны ${{l}_{c}} = - a{\text{/}}b$, или

(48)

${{l}_{c}} = - \frac{{{{\mu }^{2}}\left[ {{{\beta }_{i}} + 2{{\varphi }_{i}}\left( {1 - {{\varphi }_{i}}} \right)} \right] - \mu \left[ {\left( {{{\varphi }_{i}} + {{\varphi }_{e}}} \right)\left( {{{\varphi }_{i}} + {{\varphi }_{e}} - 2} \right) - {{\beta }_{i}}} \right] - 2{{\varphi }_{e}}\left( {{{\varphi }_{e}} - 1} \right)}}{{{{\mu }^{2}}\left( {2{{\varphi }_{i}} + 1} \right)\left( {{{\varphi }_{i}} - 1} \right) + \mu \left[ {\left( {{{\varphi }_{i}} + {{\varphi }_{e}}} \right)\left( {{{\varphi }_{i}} + {{\varphi }_{e}} - 1} \right) - 2} \right] + \left( {2{{\varphi }_{e}} + 1} \right)\left( {{{\varphi }_{e}} - 1} \right)}},$

где $\mu = {{\psi }^{2}}$. Мы можем легко определить градиент изменения функции ${{x}^{2}}(l)$ в критической точке $l = {{l}_{c}}$

(49)

$\mathop {\left. {\frac{{d{{x}^{2}}}}{{dl}}} \right|}\nolimits_{l = {{l}_{c}}} = - \frac{{{{b}^{2}}}}{{cb - da}} = L.$

Как было показано выше, зеркальная неустойчивость возникает при малых $l < {{l}_{c}}$, когда $L > 0$, а вторая сжимаемая шланговая неустойчивость $(fh2)$ при больших $l > {{l}_{c}}$, когда $L < 0$.

Рассмотрим условия реализации критического угла распространения волны $0 \leqslant {{l}_{c}} \leqslant 1$ в зависимости от параметров плазмы ${{\varphi }_{i}}$, ${{\varphi }_{e}}$, ψ, ${{\beta }_{i}}$. Для этого представим ${{l}_{c}}$ как

(50)

${{l}_{c}} = \frac{{{{a}_{1}}{{\mu }^{2}} + {{b}_{1}}\mu + {{c}_{1}}}}{{{{a}_{2}}{{\mu }^{2}} + {{b}_{2}}\mu + {{c}_{2}}}} = \frac{{{{a}_{1}}}}{{{{a}_{2}}}}\frac{{\left( {\mu - {{\mu }_{1}}} \right)\left( {\mu - {{\mu }_{2}}} \right)}}{{\left( {\mu - \mathop {\bar {\mu }}\nolimits_1 } \right)\left( {\mu - \mathop {\bar {\mu }}\nolimits_2 } \right)}},$

где

$\begin{gathered} \bar {\varphi } = {{\varphi }_{i}} + {{\varphi }_{e}},\quad {{a}_{1}} = 2{{\varphi }_{i}}\left( {{{\varphi }_{i}} - 1} \right) - {{\beta }_{i}}, \\ {{b}_{1}} = \bar {\varphi }\left( {\bar {\varphi } - 2} \right) - {{\beta }_{i}},\quad {{c}_{1}} = 2{{\varphi }_{e}}\left( {{{\varphi }_{e}} - 1} \right), \\ \end{gathered} $

$\begin{gathered} {{a}_{2}} = \left( {2{{\varphi }_{i}} + 1} \right)\left( {{{\varphi }_{i}} - 1} \right),\quad {{b}_{2}} = \bar {\varphi }\left( {\bar {\varphi } - 1} \right) - 2, \\ {{c}_{2}} = \left( {2{{\varphi }_{e}} + 1} \right)\left( {{{\varphi }_{e}} - 1} \right), \\ \end{gathered} $

$\begin{gathered} {{\Delta }_{1}} = b_{1}^{2} - 4{{a}_{1}}{{c}_{1}},\quad {{\Delta }_{2}} = b_{2}^{2} - 4{{a}_{2}}{{c}_{2}}, \\ {{\mu }_{{1,2}}} = \frac{{ - {{b}_{1}} \pm \sqrt {{{\Delta }_{1}}} }}{{2{{a}_{1}}}},\quad \mathop {\bar {\mu }}\nolimits_{1,2} = \frac{{ - {{b}_{2}} \pm \sqrt {{{\Delta }_{2}}} }}{{2{{a}_{2}}}}. \\ \end{gathered} $

Из (50) следует, что ${{l}_{c}} \leqslant 1$ может выполняться в следующих условиях:

${{\varphi }_{e}} > 1,\quad {{\beta }_{i}} + {{\varphi }_{i}} < 1,\quad \mu \geqslant {{\mu }_{*}},$

(51)

${{\varphi }_{e}} < 1,\quad {{\beta }_{i}} + {{\varphi }_{i}} > 1,\quad \mu \leqslant {{\mu }_{*}},$

${{\varphi }_{e}} = 1,\quad {{\beta }_{i}} + {{\varphi }_{i}} \leqslant 1,\quad \mu > 0,$

где ${{\mu }_{*}} = (1 - {{\varphi }_{e}}){\text{/}}({{\beta }_{i}} + {{\varphi }_{i}} - 1).$ Для выяснения выполнения условия ${{l}_{c}} \geqslant 0$ необходимо различать два случая: ${{\varphi }_{e}} \ne 1$ (анизотропные электроны) и ${{\varphi }_{e}} = 1$ (изотропные электроны).

5.1. Анизотропные электроны

Здесь мы должны рассмотреть условия (51) отдельно.

1. Пусть ${{\varphi }_{e}} > 1$, ${{\beta }_{i}} + {{\varphi }_{i}} < 1$.

В этом случае ${{\varphi }_{i}} < 1$, и тогда ${{c}_{{1,2}}} > 0$, ${{a}_{{1,2}}} < 0$, ${{\Delta }_{{1,2}}} > 0$. Следовательно ${{\mu }_{1}} < 0$, ${{\mu }_{2}} > 0$, ${{\bar {\mu }}_{1}} < 0$, ${{\bar {\mu }}_{2}} > 0$. С учетом этого получаем, что

${{l}_{c}} = \left| {\frac{{{{a}_{1}}}}{{{{a}_{2}}}}} \right|\frac{{\mu + \left| {{{\mu }_{1}}} \right|}}{{\mu + \left| {{{{\bar {\mu }}}_{1}}} \right|}}\frac{{\mu - {{\mu }_{2}}}}{{\mu - \mathop {\bar {\mu }}\nolimits_2 }} > 0.$

Oтсюда получаем, что $\mu > max({{\mu }_{2}},{{\bar {\mu }}_{2}})$. Тогда для выполнения условия $0 \leqslant {{l}_{c}} \leqslant 1$ необходимо, чтобы (с учетом (51)) $\mu > max({{\mu }_{2}},{{\bar {\mu }}_{2}},{{\mu }_{*}})$. Это является условием возникновения наклонной шланговой неустойчивости $(fh2)$, для которой $L < 0$. Для зеркальной неустойчивости $L > 0$ должно быть $\mu < min({{\mu }_{2}},{{\bar {\mu }}_{2}})$.

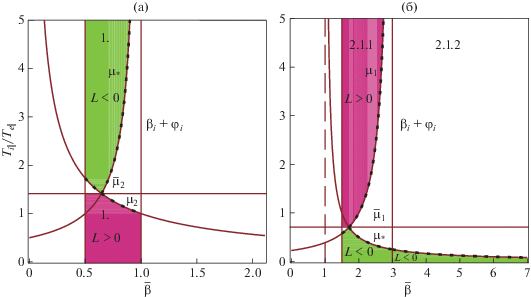
Найденные области неустойчивости показаны на рис. 4 при заданных ${{\varphi }_{e}} > 1$ и ${{\varphi }_{i}} < 1$. Обе неустойчивости (наклонные шланговые и зеркальные) возникают в области больших плазменных бета $\beta = 2{\text{/}}{{\beta }_{i}} > 1$. Для горячих ионов (${{\psi }^{2}} = {{T}_{{i\parallel }}}{\text{/}}{{T}_{{e\parallel }}} > 1$) доминирующей является шланговая неустойчивость ($L < 0$), а для горячих электронов (${{\psi }^{2}} < 1$) – зеркальная неустойчивость ($L > 0$).

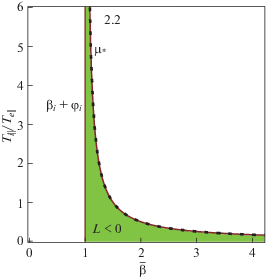
Рис. 4.

Области существования порога ($0 \leqslant {{l}_{c}} \leqslant 1$) наклонной шланговой ($L < 0$) и зеркальных ($L > 0$) неустойчивостей в анизотропной плазме при условиях: (a) ${{\varphi }_{e}} > 1$, $\bar {\beta } = {{\beta }_{i}} + {{\varphi }_{i}} < 1$, где ${{\varphi }_{e}} = 1.5$, ${{\varphi }_{i}} = 0.5$, зависимости ${{\psi }^{2}} = \mu $ от $\bar {\beta }$ в условиях $\mu > max({{\mu }_{2}},{{\bar {\mu }}_{2}},{{\mu }_{*}})$ (для $L < 0$) и $\mu < min({{\mu }_{2}},{{\bar {\mu }}_{2}})$ (для $L > 0$) определяют границы неустойчивостей; (б) для ${{\varphi }_{e}} < 1$, ${{\varphi }_{i}} > 1$, где ${{\varphi }_{e}} = 0.5$, ${{\varphi }_{i}} = 1.5$, зависимости ${{\psi }^{2}} = \mu $ от $\bar {\beta } = {{\beta }_{i}} + {{\varphi }_{i}}$ в условиях $\mu < min({{\mu }_{1}},{{\bar {\mu }}_{1}},{{\mu }_{*}})$ (для $L < 0$) и $\mu > max({{\mu }_{1}},{{\bar {\mu }}_{1}})$ (для $L > 0$) определяют границы неустойчивостей. На рисунках указаны пункты (1, 2.1.1 и 2.1.2) параграфа 4.1 основного текста, где приводятся формулы для определения границ областей.

2. Пусть ${{\varphi }_{e}} < 1$, ${{\beta }_{i}} + {{\varphi }_{i}} > 1$.

В этом случае ${{c}_{{1,2}}} < 0$ и рассмотрим два случая: ${{\varphi }_{i}} > 1$ и ${{\varphi }_{i}} < 1$.

2.1. Если ${{\varphi }_{i}} > 1$, тогда ${{a}_{2}} > 0$, ${{\Delta }_{2}} > 0$, и получим, что ${{\bar {\mu }}_{1}} > 0$ и ${{\bar {\mu }}_{2}} < 0$. Относительно значений ${{\beta }_{i}}$ возможны два варианта.

2.1.1. Если ${{\beta }_{i}} < 2{{\varphi }_{i}}\left( {{{\varphi }_{i}} - 1} \right)$, то ${{a}_{1}} > 0$, ${{\Delta }_{1}} > 0$ и ${{\mu }_{1}} > 0,$ ${{\mu }_{2}} < 0$. Тогда

${{l}_{c}} = \frac{{{{a}_{1}}}}{{{{a}_{2}}}}\frac{{\mu + \left| {{{\mu }_{2}}} \right|}}{{\mu + \left| {{{{\bar {\mu }}}_{2}}} \right|}}\frac{{\mu - {{\mu }_{1}}}}{{\mu - \mathop {\bar {\mu }}\nolimits_1 }} > 0,$

из которого с учетом (51) следует, что при $\mu > max({{\mu }_{1}},{{\bar {\mu }}_{1}})$ возникает зеркальная неустойчивость ($L > 0$), а при $\mu < min({{\mu }_{1}},{{\bar {\mu }}_{1}},{{\mu }_{*}})$ – вторая шланговая неустойчивость ($L < 0$).

2.1.2. В противоположном случае ${{\beta }_{i}} > $ $ > 2{{\varphi }_{i}}\left( {{{\varphi }_{i}} - 1} \right)$ параметр ${{a}_{1}} < 0$ и, следовательно, ${{\mu }_{1}} < 0,$ ${{\mu }_{2}} < 0$. Тогда

${{l}_{c}} = - \left| {\frac{{{{a}_{1}}}}{{{{a}_{2}}}}} \right|\frac{{(\mu + \left| {{{\mu }_{1}}} \right|)(\mu + \left| {{{\mu }_{2}}} \right|)}}{{\mu + \left| {{{{\bar {\mu }}}_{2}}} \right|}}\frac{1}{{\mu - {{{\bar {\mu }}}_{1}}}} > 0.$

Следовательно, в рассматриваемом случае возможна только вторая шланговая неустойчивость ($L < 0$), для которой $\mu < min({{\mu }_{*}},{{\bar {\mu }}_{1}})$.

Найденные области неустойчивости показаны на рис. 4 при заданных ${{\varphi }_{e}} < 1$ и ${{\varphi }_{i}} > 1$. Для горячих ионов (${{\psi }^{2}} = {{T}_{{i\parallel }}}{\text{/}}{{T}_{{e\parallel }}} > 1$) доминирующей является зеркальная неустойчивость ($L > 0$), а для горячих электронов (${{\psi }^{2}} < 1$) – вторая шланговая неустойчивость ($L < 0$). Как видно из рисунка, наклонные шланговые неустойчивости возможны в области малых плазменных бета $\beta = 2{\text{/}}{{\beta }_{i}} < 1$.

2.2. В случае ${{\varphi }_{i}} < 1$ получаем, что ${{a}_{1}} < 0,$ ${{b}_{1}} < 0$, ${{c}_{1}} < 0$, ${{\Delta }_{1}} > 0$ и, следовательно, ${{\mu }_{{1,2}}} < 0$, ${{a}_{2}} < 0$, ${{b}_{2}} < 0$, ${{c}_{2}} < 0$, ${{\Delta }_{2}} > 0$ и, следовательно, ${{\bar {\mu }}_{{1,2}}} < 0$. В этом случае условие ${{l}_{c}} > 0$ выполняется для любых μ, а условие ${{l}_{c}} \leqslant 1$ требует $\mu \leqslant {{\mu }_{*}}$, которое является условием возникновение второй шланговой неустойчивости, $L < 0$. Эта область для фиксированных ${{\varphi }_{i}} < 1$ и ${{\varphi }_{e}} < 1$ показана на рис. 5.

Рис. 5.

Области существования порога ($0 \leqslant {{l}_{c}} \leqslant 1$) наклонной шланговой ($L < 0$) неустойчивости в анизотропной плазме при условиях ${{\varphi }_{e}} < 1$, $\bar {\beta } = {{\beta }_{i}} + {{\varphi }_{i}} > 1$ и ${{\varphi }_{i}} < 1$. Здесь ${{\varphi }_{e}} = 0.5$, ${{\varphi }_{i}} = 0.5$. Зависимости ${{\psi }^{2}} = \mu $ от $\bar {\beta }$ в условиях $\mu \leqslant {{\mu }_{*}}$ определяют границы неустойчивости.

5.2. Изотропные электроны

В этом случае ${{\varphi }_{e}} = 1$ и

(52)

${{l}_{c}} = \frac{{2\mu {{\varphi }_{i}}\left( {1 - {{\varphi }_{i}}} \right) + {{\beta }_{i}}\left( {1 + \mu } \right) + \left( {1 + {{\varphi }_{i}}} \right)\left( {1 - {{\varphi }_{i}}} \right)}}{{\left( {1 - {{\varphi }_{i}}} \right)\left( {2\mu {{\varphi }_{i}} + \mu + {{\varphi }_{i}} + 2} \right)}}.$

Если ${{\varphi }_{i}} < 1$, условие ${{l}_{c}} > 0$ выполняется всегда, а для ${{l}_{c}} \leqslant 1$ необходимо выполнение ${{\beta }_{i}} + {{\varphi }_{i}} \leqslant 1$. При этом $L < 0$ и возникает вторая шланговая неустойчивость.

При ${{\varphi }_{i}} > 1$ условие ${{l}_{c}} \geqslant 0$ требует выполнения

${{\beta }_{i}} \leqslant \frac{{({{\varphi }_{i}} - 1)(1 + {{\varphi }_{i}} + 2\mu {{\varphi }_{i}})}}{{(1 + \mu )}},$

а ${{l}_{c}} \leqslant 1$ не выполняется.

5.3. Неустойчивости неизотермической анизотропной плазмы

Анализ критерия возникновения неустойчивостей показал, что влияние степени неизотермичности плазмы ${{\psi }^{2}} = {{T}_{{i\parallel }}}{\text{/}}{{T}_{{e\parallel }}}$ и степени анизотропности электронной компоненты ${{\varphi }_{e}} = {{T}_{{e \bot }}}{\text{/}}{{T}_{{e\parallel }}}$ являются существенными. В условиях слабостолкновительной космической плазмы эти параметры существенно отличаются от единицы. Например, в плазме солнечного ветра вблизи орбиты Земли в зависимости от плазменного бета ${{\beta }_{p}} = 2{\text{/}}{{\beta }_{i}}$ параметры анизотропии ${{\varphi }_{e}}$ и ${{\varphi }_{i}}$ имеют большой диапазон значений [11, 12]. Эти параметры отличаются для медленного и быстрого компонентов ветра, так как эти компоненты генерируются в различных физических условиях в атмосфере Солнца. На рис. 6 и 7 приведены примеры влияния этих параметров на условия возникновения неустойчивости. В приведенных примерах доминирующими являются моды с большими l, т. е. вторая шланговая неустойчивость. До узловой точки с ростом ${{\varphi }_{e}}$ неустойчивость подавляется, а после этой точки наоборот, с ростом ${{\varphi }_{e}}$ неустойчивость усиливается. Узловая точка определяется условием $b = 0$ в (43). Во всех случаях переход от условия ${{\varphi }_{i}} < 1$ к ${{\varphi }_{i}} > 1$ ослабевает неустойчивость.

Рис. 6.

Зависимость условий возникновения неустойчивости ($v_{{ph}}^{2} < 0$) неизотермической плазмы ($\psi \ne 1$) от степени анизотропии электронного компонента ${{\varphi }_{e}}$. В условиях плазмы медленного солнечного ветра $\psi = 0.48$: (a) случай ${{\beta }_{i}} + {{\varphi }_{i}} < 1$ (выбраны ${{\beta }_{i}} = 0.1$, ${{\varphi }_{i}} = 0.5$; (б) случай ${{\beta }_{i}} + {{\varphi }_{i}} > 1$ (выбраны ${{\beta }_{i}} = 0.1$, ${{\varphi }_{i}} = 1.5$). На кривых указаны значения параметра угла распространения волн $l = co{{s}^{2}}\theta $.

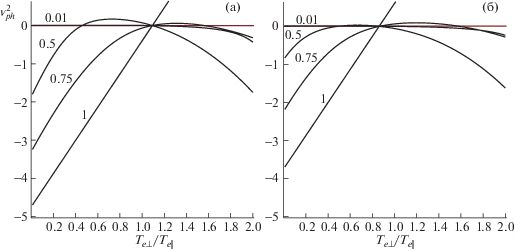
Рис. 7.

Зависимость условий возникновения неустойчивости ($v_{{ph}}^{2} < 0$) неизотермической плазмы ($\psi \ne 1$) от степени анизотропии электронного компонента ${{\varphi }_{e}}$. В условиях плазмы ускоренного солнечного ветра $\psi = 1.49$: (a) случай ${{\beta }_{i}} + {{\varphi }_{i}} < 1$ (выбраны ${{\beta }_{i}} = 0.1$, ${{\varphi }_{i}} = 0.5$; (б) случай ${{\beta }_{i}} + {{\varphi }_{i}} > 1$ (выбраны ${{\beta }_{i}} = 0.1$, ${{\varphi }_{i}} = 1.5$). На кривых указаны значения параметра угла распространения волн $l = co{{s}^{2}}\theta $.

6. ЗАКЛЮЧЕНИЕ

В предыдущих теоретических исследованиях МГД-неустойчивостей в анизотропной плазме, в основном как в ЧГЛ-, так и в 16-моментных приближениях роль электронов игнорировалась. Она сводилась только к обеспечению квазинейтральности плазмы. Однако в реальных космических условиях наблюдаемая плазма существенно неизотермична (${{T}_{e}} \ne {{T}_{i}}$) и анизотропна (${{T}_{ \bot }} \ne {{T}_{\parallel }}$) как для ионных, так и для электронных составляющих. Наша основная цель состояла в выяснении влияния присутствия электронного компонента на условия возникновения известных типов МГД‑неустойчивостей в анизотропной плазме. Для этого мы использовали 16-моментные МГД-уравнения переноса с учетом теплового потока в многокомпонентной би-максвелловской плазме. Показано, что учет электронов вводит в задачу новые параметры, связанные с неизотермичностью плазмы, анизотропностью электронного компонента и тепловым потоком за счет электронов. Для простоты, без учета тепловых потоков подробно изучалась роль электронного компонента для возникновения шланговых и зеркальных неустойчивостей. Оказалось, что в реально наблюдаемых областях параметров игнорировать электронную компоненту невозможно. Как критерии возникновения, так и степень неустойчивости существенно зависят от параметров ${{\psi }^{2}} = {{T}_{{i\parallel }}}{\text{/}}{{T}_{{e\parallel }}}$ и ${{\varphi }_{e}} = {{T}_{{e \bot }}}{\text{/}}{{T}_{{e\parallel }}}$.

В отсутствие теплового потока вдоль магнитного поля мы получили три вида МГД-неустойчивостей: несжимаемая параллельная шланговая, сжимаемая наклонная шланговая и сжимаемая зеркальная неустойчивость. Все неустойчивости имеют апериодичный характер, т. е. реальная часть частоты колебаний равна нулю, ${\text{Re}}(\omega ) = 0$. Это является, прежде всего, следствием игнорирования при выводе МГД-уравнений эффектов затухания Ландау. Кроме того, включение диссипативных эффектов (например, тепловых потоков, эффекты Холла и т. д.) будет стабилизировать неустойчивость, и неустойчивость станет колебательной. Главным недостатком полученных МГД-инкрементов неустойчивостей состоит в том, что эти инкременты являются линейными функциями волнового числа, ${\text{Im}}(\omega ) \sim k$. Это означает, что при очень малых масштабах ($k \to \infty $) получаются слишком большие инкременты неустойчивостей. Причина состоит в том, что используемые 16-моментные МГД-уравнения переноса справедливы при нулевом ларморовском радиусе.

Свойства рассматриваемых шланговых и зеркальных неустойчивостей хорошо известны из низкочастотной кинетической физики [13–16]. Влияние эффектов, связанных с конечностью ларморовского радиуса на пороги и инкременты кинетических неустойчивостей, а также их стабилизация широко обсуждается в литературе (см., например, [6, 17, 18]). Для длин волн порядка ионного ларморовского радиуса эффективная эластичность магнитных силовых линий существенно нарастает, что приводит к максимуму инкремента и к увеличению порога зеркальной неустойчивости [17]. При меньших длинах волны эффективное электрическое поле, действующее на ионы, уменьшается (из-за усреднения в результате ларморовского вращения). Это приводит к уменьшению инкремента в стороны коротких волн. В исследуемых случаях в основном предполагалось, что электроны изотропны и холодные. В более общем случае, когда электроны би-максвелловской плазмы не холодные и являются анизотропными, условия возникновения зеркальной неустойчивости существенно модифицируются [15, 19–23]. Было получены, что если электроны изотропны, то максимум инкремента зеркальной неустойчивости меньше, но с появлением анизотропии инкремент увеличивается. Влияние эффектов, связанных с конечностью ларморовского радиуса в присутствии анизотропных электронов рассматривались в работах [7, 24]. Получено, что эффекты ограничения развития неустойчивости конечностью ларморовских радиусов электронов и ионов существенно зависят от степени анизотропии температуры электронов.

Влияние конечности ларморовского радиуса на шланговую неустойчивость изучалось многими авторами (например, [6, 25–30]). Основной результат заключается в том, что при малых масштабах колебаний неустойчивость ограничивается.

Учет эффектов конечности ларморовского радиуса и диссипативных эффектов в жидкостном описании замагниченной бесстолкновительной плазмы очень сложно. В простейшем случае, когда тепловые потоки вдоль магнитного поля не учитываются, и выполняются двойные адиабаты (ЧГЛ-уравнения), такая попытка для шланговых мод сделана в работе [31]. В этой работе стабилизация шланговой неустойчивости при коротких волнах достигается включением холловского затухания и учетом конечности ионного ларморовского радиуса. Исследование неустойчивости бесстолкновительной замагниченной плазмы в жидкостном описании в более общем случае, когда учитываются тепловые потоки, конечный ларморовский радиус [32] и слабые столкновения между частицами [33] является слишком громоздкой, но важной задачей.

Полученные результаты могут быть использованы для интерпретации наблюдаемой низкочастотной крупномасштабной турбулентности в плазме солнечного и звездных ветров.

Авторы выражают благодарность рецензенту за полезные замечания и рекомендации, которые были учтены при доработке рукописи. Данная работа выполнена при финансовой поддержке Фонда развития науки при Президенте Азербайджанской Республики – Гранты № EIF-KETPL-2-2015-1(25)-56/11/1 и EIF-BGM-4-RFTF-1/2017-21/06/1 (совместный Российско-Азербайджанский грант).

Список литературы

Chew G.F., Goldberger M.L., Low F.E. // Proc. Roy. Soc. London. 1956. V. A236. P. 112.
Oraevskii V.N., Konikov Y.V., Chazanov G.V. Transport processes in anisotropic near-Earth plasma. M.: Nauka, 1985.
Ramos J.J. // Physics of Plasmas. 2003. V. 10. P. 3601.
Dzhalilov N.S., Kuznetsov V.D., Staude J. // Contrib. Plasma Phys. 2011. V. 51. P. 621.
Dzhalilov N.S., Kuznetsov V.D. // Plasma Phys. Rep. 2013. V. 39. P. 1026.
Hall A.N. // J. Plasma Phys. 1979. V. 21. P. 431.
Kuznetsov E.A., Passot T., Sulem P.L. // Phys. Plasmas. 2012. V. 19. P. 090701.
Kuznetsov V.D., Dzhalilov N.S. // Geomagnetism A-eronomy. 2014. V. 54. P. 886.
Dzhalilov N.S., Kuznetsov V.D., Staude J. // Astron. A-strophys. 2008. V. 489. P. 769.
Dzhalilov N.S., Huseynov S.Sh. // Azarbaijan Astronomical J. 2016. N. 1. P. 1.
Travnicek P., Stverak S., Maksimovic M. // J. Geophys. Res. 2008. V. 113. P. A03103.
Hellinger P., Travnicek P., Kasper J.C. // Geophys. Res. Lett. 2006. V. 33. P. L09101.
Rudakov L.I., Sagdeev R.Z. // Plasma Physics and the Problem of Controlled Thermonuclear Reactions. V. 3. N. Y.: Pergamon, 1958. P. 321.
Chandrasekhar S.A., Kaufman A.N., Watson K.M. // Proc. R. Soc. London. 1958. Ser. A. V. 245. P. 435.
Stix T.H. The Theory of Plasma Waves. N. Y.: McGraw-Hill, 1962.
Barnes A. // Phys. Fluids. 1966. V. 9. P. 1483.
Pokhotelov O.A., Sagdeev R.Z., Balikhin M.A., Treumann R.A. // J. Geophys. Res. 2004. V. 109. P. A09213.
Califano C., Hellinger P., Kuznetsov E., Passot T., Sulem P. L., Tra’vnicek P. M. // J. Geophys. Res. 2008. V. 113. P. A08219.
Pantellini F.G.E., Schwartz S.J. // J. Geophys. Res. 1995. V. 100. P. 3539.
Ge’not V., Schwartz S.J., Mazelle C., Balikhin M., Dunlop M., Bauer T.M. // J. Geophys. Res. 2001. V. 106. P. 21611.
Pokhotelov O.A., Balikhin M.A., Alleyne H. St-C.K., Onishchenko O.G. // J. Geophys. Res. 2000. V. 105. P. 2393.
Gary S.P., Karimabadi H. // J. Geophys. Res. 2006. V. 111. P. A11224.
Hellinger P. // Phys. Plasmas. 2007. V. 14. P. 082105.
Istomin Y.N., Pokhotelov O.A., Balikhin M.A. // Phys. Plasmas. 2009. V. 16. P. 122901.
Davidson R.C., Völk H.J. // Phys. Fluids. 1968. V. 11. P. 2259.
Achterberg A. // Monthly Notices Roy. Soc. 2013. V. 436. P. 705.
Hollweg J.V., Völk H.J. // J. Geophys. Res. 1970. V. 75. P. 5297.
Gary S.P., Madland C.D. // J. Geophys. Res. 1985. V. 90. P. 7607.
Yoon P.H., Wu C.S., de Assis A.S. // Phys. Fluids B. 1993. V. 5. P. 1971.
Li X., Habbal S.R. // J. Geophys. Res. 2000. V. A105. P. 27377.
Hunana P., Zank G. P. // Astrophys. J. 2017. V. 839. P. 13.
Ramos J. J. // Phys. Plasmas. 2005. V. 12. P. 052102.
Ramos J.J. // Phys. Plasmas. 2007. V. 14. P. 052506.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика плазмы

Архивы выпусков Информация о журнале Отправить рукопись в журнал