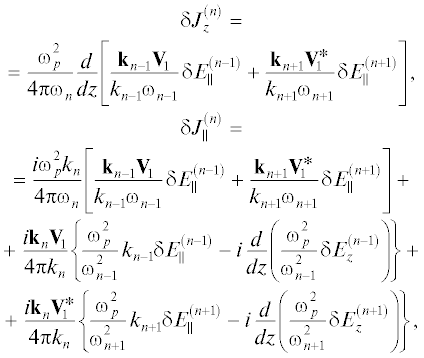Физика плазмы, 2019, T. 45, № 8, стр. 708-716

1. ВВЕДЕНИЕ

Интерес к поверхностным волнам связан как с их необычными физическими свойствами, так и c возможностью их использования для ряда практических приложений [1, 2]. Поверхностные электромагнитные волны (ПЭВ) могут применяться для диагностики поверхности, исследования свойств тонких пленок и границ раздела различных сред, изучения спектров поверхностных возбужденных состояний, передачи сигналов на большие расстояния. В рамках линейной теории дисперсионные свойства поверхностных волн и методы их возбуждения описаны достаточно подробно (см. [1, 2]). В последнее время возбуждение ПЭВ при воздействии на твердотельные мишени интенсивного лазерного излучения, когда важны нелинейные эффекты, наблюдалось в нескольких экспериментах [3–7]. Теория нелинейного возбуждения низкочастотных ПЭВ в плазме и проводящих средах под действием пондеромоторных сил лазерного излучения развита в публикациях [8–10]. Другой нелинейный механизм возбуждения ПЭВ связан с параметрическим воздействием мощного лазерного излучения на плазму и проводящие среды. Впервые теория параметрического возбуждения поверхностных волн при падении высокочастотного электромагнитного излучения на плазму с резкой границей при гидродинамическом описании была построена в [11]. Несколько позднее была развита кинетическая теория возбуждения поверхностных волн под действием высокочастотной волны накачки [12], что позволило вычислить не только инкремент, но и порог неустойчивости. Параметрический распад волны накачки на две ПЭВ обсуждался в публикации [13]. В отличие от работ [11–13], где рассматривалась плазма с концентрацией электронов, не превышающей критическую величину, в публикации [14] исследовано параметрическое возбуждение ПЭВ при воздействии излучения лазера на слой плотной плазмы. В работе [15] исследована роль плазмона, локализованного в узком приповерхностном слое, в распаде p-поляризованной волны накачки на две ПЭВ. Распад p-поляризованной электромагнитной волны на две ПЭВ рассмотрен в публикации [16], где вычислены инкременты и пороги неустойчивости. Однако следует отметить, что авторы публикации [16] ошибочно пренебрегли нелинейным поверхностным током, так как он дает такой же вклад в инкремент неустойчивости, как и пондеромоторная нелинейность.

Следует отметить, что в публикациях [11–14] раскачка поверхностных волн связана исключительно с учетом движения ионов, что справедливо для достаточно длинных лазерных импульсов. При воздействии фемтосекундных оптических импульсов движение ионов несущественно и рассмотренные ранее в [11–14] неустойчивости не успевают развиться. Поэтому в настоящей работе изучено параметрическое возбуждение ПЭВ, связанное только с движением электронов в электромагнитном поле. Рассмотрено наклонное падение s-поляризованной электромагнитной волны на полуограниченную плазму сверхкритической концентрации, приводящее к параметрическому возбуждению двух ПЭВ. Статья имеет следующую структуру: во 2 разд. найдено основное состояние и представлены уравнения и граничные условия для возмущений электромагнитного поля ПЭВ при гидродинамическом описании. В 3 разд. получено дисперсионное уравнение и найден инкремент неустойчивости, связанной с распадом волны накачки на две ПЭВ, который оказался пропорциональным первой степени напряженности электрического поля падающей волны. Проанализирована зависимость инкремента распадной неустойчивости от плотности электронов. Показано, что инкремент максимален в плазме с плотностью электронов, незначительно превышающей критическое значение. Исследована зависимость инкремента неустойчивости от угла падения лазерного излучения в околокритической и сверхкритической плазме. В четвертом разделе учтены соударения электронов и вычислен порог неустойчивости. Анализ зависимости порога неустойчивости от плотности электронов плазмы показал, что порог минимален в не очень плотной плазме, когда концентрация электронов близка к критическому значению. В заключение обсуждаются полученные результаты и приводятся оценки для характерных параметров современных лазерно-плазменных экспериментов.

2. ОСНОВНОЕ СОСТОЯНИЕ И УРАВНЕНИЯ ДЛЯ ВОЗМУЩЕНИЙ

Рассмотрим возбуждение ПЭВ под действием излучения лазера в полуограниченной плазме, занимающей полупространство $z > 0$. Для этого воспользуемся уравнениями Максвелла для электрического E и магнитного B полей и уравнениями бесстолкновительной гидродинамики для скорости v и плотности n электронов

где e, ${{m}_{e}}$ – заряд и масса электрона, c – скорость света, ${{N}_{{0e}}}$ – равновесная плотность электронов. Отметим, что уравнение для скорости движения электронов получено при учете равенства $\nabla \times {\mathbf{v}} + \left( {{e \mathord{\left/ {\vphantom {e {{{m}_{e}}c}}} \right. \kern-0em} {{{m}_{e}}c}}} \right){\mathbf{B}} = 0$, которое соответствует закону сохранения обобщенного вихря в бесстолкновительной плазме (см. [17]).

Пусть s-поляризованная электромагнитная волна с частотой ${{\omega }_{0}}$ и вектором напряженности электрического поля ${{{\mathbf{E}}}_{0}} = {{{\mathbf{e}}}_{y}}{{E}_{0}}$, ориентированным вдоль оси у, падает под углом α из вакуума на границу плотной плазмы, ${{\omega }_{0}} < {{\omega }_{p}}$, где ${{\omega }_{p}}$ – ленгмюровская частота электронов. Электрическое поле волны накачки в вакууме можно записать в следующем виде:

Рассмотрим устойчивость плазмы относительно возбуждения ПЭВ в поле волны (2.2). Для этого представим все физические величины в виде малых отклонений $\delta N$, $\delta {\mathbf{V}}$, $\delta {\mathbf{E}}$, $\delta {\mathbf{B}}$ от основного состояния ${{N}_{{0e}}} + {{N}_{L}}$, ${{{\mathbf{V}}}_{L}}$, ${{{\mathbf{E}}}_{L}}$, ${{{\mathbf{B}}}_{L}}$

Тогда для физических величин в основном состоянии имеем из (2.1) следующую систему уравнений:

Для малых отклонений от основного состояния справедливы следующие уравнения:

Так как инкремент неустойчивости оказывается пропорционален первой степени амплитуды падающей волны ${{E}_{0}}$, то для основного состояния ограничимся линейным приближением. Тогда в основном состоянии имеем следующие выражения для электрического поля в вакууме и в плазме

где $R = \frac{{\cos \alpha - i\left( {{c \mathord{\left/ {\vphantom {c {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}}} \right){{\kappa }_{L}}}}{{\cos \alpha + i\left( {{c \mathord{\left/ {\vphantom {c {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}}} \right){{\kappa }_{L}}}}$ – коэффициент отражения, величина ${{\kappa }_{L}} = \left( {{{{{\omega }_{0}}} \mathord{\left/ {\vphantom {{{{\omega }_{0}}} c}} \right. \kern-0em} c}} \right)\sqrt {{{{\sin }}^{2}}\alpha - \varepsilon \left( {{{\omega }_{0}}} \right)} $ характеризует глубину проникновения поля в сверхкритическую плазму, $\varepsilon \left( {{{\omega }_{0}}} \right) = 1 - {{\omega _{p}^{2}} \mathord{\left/ {\vphantom {{\omega _{p}^{2}} {\omega _{0}^{2}}}} \right. \kern-0em} {\omega _{0}^{2}}}$ – диэлектрическая проницаемость. Скорость электронов в плазме в поле (2.7) в соответствии с уравнениями (2.4) определяется следующим выражением: где ${{{\mathbf{V}}}_{1}} = \frac{{i{{{\mathbf{V}}}_{E}}\cos \alpha }}{{\cos \alpha + i(c{\text{/}}{{\omega }_{0}}){{\kappa }_{L}}}}\exp ( - {{\kappa }_{L}}z)$, ${{{\mathbf{V}}}_{E}} = $ $ = {{e{{{\mathbf{E}}}_{0}}} \mathord{\left/ {\vphantom {{e{{{\mathbf{E}}}_{0}}} {({{m}_{e}}{{\omega }_{0}})}}} \right. \kern-0em} {({{m}_{e}}{{\omega }_{0}})}}$.

Рассмотрим теперь малые отклонения от основного состояния (2.7), (2.8), которые описываются уравнениями (2.5). Будем использовать следующее разложение в ряд Фурье для возмущений электромагнитного поля и электрического тока

где ${\mathbf{\rho }} = x{{{\mathbf{e}}}_{x}} + y{{{\mathbf{e}}}_{y}}$, ${{{\mathbf{e}}}_{x}}$, ${{{\mathbf{e}}}_{y}}$ – базисные векторы декартовой системы координат. Ограничиваясь линейным приближением по амплитуде волны накачки, после несложных вычислений получим следующую систему уравнений для возмущений электромагнитного поля на частоте ${{\omega }_{n}} = \omega + n{{\omega }_{0}}$ с волновым вектором ${{{\mathbf{k}}}_{n}} = {\mathbf{k}} + n{{{\mathbf{k}}}_{0}}$, лежащим в плоскости $XOY$где ${{{\mathbf{k}}}_{0}} = {{{\mathbf{e}}}_{x}}\left( {{{{{\omega }_{0}}} \mathord{\left/ {\vphantom {{{{\omega }_{0}}} c}} \right. \kern-0em} c}} \right)\sin \alpha $, а выражение для возмущений электрического тока имеет вид

Представим электромагнитное поле и нелинейный ток $\delta {{{\mathbf{J}}}^{{\left( n \right)}}}$ в следующем виде:

Тогда из формул (2.10)_–(2.12) находим уравнения для компонент возмущений электромагнитного поля

где ${{\varepsilon }_{n}} = 1 - {{\omega _{p}^{2}} \mathord{\left/ {\vphantom {{\omega _{p}^{2}} {\omega _{n}^{2}}}} \right. \kern-0em} {\omega _{n}^{2}}}$, а составляющие нелинейного тока $\delta {{{\mathbf{J}}}^{{\left( n \right)}}}$ определяются следующими выражениями: где ${{{\mathbf{V}}}_{1}}$ – амплитуда скорости осцилляций электронов (2.8). Из системы уравнений (2.13) находим уравнение для возмущений магнитного поля

Граничные условия получаются интегрированием уравнений (2.13), (2.15) по тонкому переходному пограничному слою и имеют вид

где ${{\kappa }_{n}} = \sqrt {k_{n}^{2} - \left( {{{\omega _{n}^{2}} \mathord{\left/ {\vphantom {{\omega _{n}^{2}} {{{c}^{2}}}}} \right. \kern-0em} {{{c}^{2}}}}} \right){{\varepsilon }_{n}}} $, ${{\varepsilon }_{n}} = 1 - {{\omega _{p}^{2}} \mathord{\left/ {\vphantom {{\omega _{p}^{2}} {\omega _{n}^{2}}}} \right. \kern-0em} {\omega _{n}^{2}}}$ для $n = 1,2...$ и $\kappa = \sqrt {{{k}^{2}} - \left( {{{{{\omega }^{2}}} \mathord{\left/ {\vphantom {{{{\omega }^{2}}} {{{c}^{2}}}}} \right. \kern-0em} {{{c}^{2}}}}} \right)\varepsilon } $, $\varepsilon = 1 - {{\omega _{p}^{2}} \mathord{\left/ {\vphantom {{\omega _{p}^{2}} {{{\omega }^{2}}}}} \right. \kern-0em} {{{\omega }^{2}}}}$ для $n = 0$. Отметим в формуле (2.16) наличие скачка напряженности магнитного поля ПЭВ на границе плазмы, обусловленного возникновением нелинейного поверхностного тока.

3. ДИСПЕРСИОННОЕ УРАВНЕНИЕ И ИНКРЕМЕНТ НЕУСТОЙЧИВОСТИ

Представим компоненты электромагнитного поля во всем пространстве в следующем виде:

где ${{\kappa }_{{n,V}}} = \sqrt {k_{n}^{2} - {{\omega _{n}^{2}} \mathord{\left/ {\vphantom {{\omega _{n}^{2}} {{{c}^{2}}}}} \right. \kern-0em} {{{c}^{2}}}}} $ для $n = 1,2...$ и ${{\kappa }_{V}} = $ $ = \sqrt {{{k}^{2}} - {{{{\omega }^{2}}} \mathord{\left/ {\vphantom {{{{\omega }^{2}}} {{{c}^{2}}}}} \right. \kern-0em} {{{c}^{2}}}}} $ для $n = 0$, $\theta \left( z \right)$ – единичная ступенчатая функция Хевисайда, а неопределенные коэффициенты ${{A}_{n}}$, ${{B}_{n}}$, ${{B}_{{n,V}}}$ могут быть найдены из граничных условий (2.16). В формулах (3.1) учтено, что тангенциальная компонента электрического поля непрерывна на границе плазмы, а тангенциальная составляющая магнитного поля имеет скачок из-за наличия поверхностного тока (2.14).

Отметим, что в рассматриваемом нами случае полуограниченной плазмы собственными электромагнитными модами являются только поверхностные волны. Именно поэтому ниже нами рассматривается распадная неустойчивость с возбуждением двух поверхностных волн с номерами $n = 0,1$. Из (2.13)–(2.16) с учетом (3.1) находим следующее дисперсионное уравнение:

где функции $D\left( {\omega ,{\mathbf{k}}} \right)$, ${{D}_{1}}\left( {{{\omega }_{1}},{{{\mathbf{k}}}_{1}}} \right)$имеют вид и определяют дисперсионные свойства поверхностных волн с соответствующими частотами и волновыми числами. С учетом равенства ${{\left| {{\mathbf{k}}{{{\mathbf{V}}}_{1}}} \right|}^{2}} = $ $ = {{\left| {{{{\mathbf{k}}}_{1}}{{{\mathbf{V}}}_{1}}} \right|}^{2}} = \left( {{{\omega _{0}^{2}} \mathord{\left/ {\vphantom {{\omega _{0}^{2}} {\omega _{p}^{2}}}} \right. \kern-0em} {\omega _{p}^{2}}}} \right){{\left( {{\mathbf{k}}{{{\mathbf{V}}}_{E}}} \right)}^{2}}{{\cos }^{2}}\alpha $ уравнение (3.2) принимает вид

Решим дисперсионное уравнение (3.4), используя соотношения

Из формулы (3.4) при совместном выполнении условий $D\left( {\omega ,k} \right) = 0$, ${{D}_{1}}\left( {{{\omega }_{1}},{{k}_{1}}} \right) = 0$ находим выражение для инкремента неустойчивости

Для анализа инкремента (3.6) найдем решения дисперсионных уравнений $D\left( {\omega ,k} \right) = 0$, ${{D}_{1}}\left( {{{\omega }_{1}},{{k}_{1}}} \right) = 0$ и вычислим производные $\partial D\left( {\omega ,k} \right){\text{/}}\partial \omega $, $\partial {{D}_{1}}\left( {{{\omega }_{1}},{{k}_{1}}} \right){\text{/}}\partial {{\omega }_{1}}$. Решение уравнений $D\left( {\omega ,k} \right) = 0$, ${{D}_{1}}\left( {{{\omega }_{1}},{{k}_{1}}} \right) = 0$ имеет вид

С учетом формул (3.7) выражения для коэффициентов, κ, ${{\kappa }_{V}}$, ${{\kappa }_{1}}$, ${{\kappa }_{{1,V}}}$ приводятся к виду

Принимая во внимание формулы (3.8), находим производные от дисперсионных функций

Подставляя соотношения (3.9) в формулу (3.6), после несложных преобразований получаем

Если ввести обозначение θ для угла между векторами k и ${{{\mathbf{V}}}_{E}}$, ${{\left( {{\mathbf{k}}{{{\mathbf{V}}}_{E}}} \right)}^{2}} = {{k}^{2}}V_{E}^{2}{{\cos }^{2}}\theta $, где ${{V}_{E}} = $ $ = {{\left| e \right|{{E}_{0}}} \mathord{\left/ {\vphantom {{\left| e \right|{{E}_{0}}} {\left( {{{m}_{e}}{{\omega }_{0}}} \right)}}} \right. \kern-0em} {\left( {{{m}_{e}}{{\omega }_{0}}} \right)}}$, то выражение для инкремента принимает вид

При этом должны выполняться условия для возбуждения ПЭВ (3.7), которые можно представить в следующем виде, полагая $\omega = - \Omega $, ${{\omega }_{1}} = {{\omega }_{0}} - \Omega $:

Подставляя выражение для волнового числа k из первого соотношения в формуле (3.12) во второе получим уравнение для определения частоты Ω

Если ввести безразмерный параметр ${{a}^{2}} = {{\omega _{p}^{2}} \mathord{\left/ {\vphantom {{\omega _{p}^{2}} {\omega _{0}^{2}}}} \right. \kern-0em} {\omega _{0}^{2}}} > 1$ и безразмерную частоту $x = {\Omega \mathord{\left/ {\vphantom {\Omega {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}}$, то уравнение (3.13) принимает вид

Инкремент неустойчивости (3.11) в безразмерных переменных определяется следующим выражением:

где

Рассмотрим сначала нормальное падение лазерного излучения на границу плазмы. В этом случае $\alpha = 0$ и уравнение для безразмерной частоты (3.14) имеет вид

с решением $x = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$, откуда следует равенство $\,\Omega = {{\omega }_{1}} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}{{\omega }_{0}}$. Подставляя найденное решение в выражение (3.16), находим

Отсюда заключаем, что при нормальном падении электромагнитной волны параметрическое возбуждение поверхностных волн отсутствует.

Рассмотрим возможность возбуждения ПЭВ при наклонном падении. В общем виде для этого нужно найти решение уравнения (3.14) подставить его в формулу (3.16) и, анализируя угловую зависимость инкремента с целью определения максимума, найти оптимальные значения угла падения α и угла распространения возмущений θ.

Для очень плотной плазмы, когда выполнено условие ${{a}^{2}} \gg 1$, можно представить некоторые аналитические результаты. В этом случае решение уравнения (3.14) имеет вид

С учетом выражения для безразмерной частоты (3.19) формула (3.16) при условии ${{a}^{2}} \gg 1$ принимает вид

При малых углах падения ($\alpha \to 0$, $\sin \theta \gg \sin \alpha $) выражение (3.20) упрощается

В этом случае функция ${{G}^{2}}$ максимальна для угла распространения возмущений $\theta = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$

При скользящих углах падения, когда $\alpha \to {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$, выражение (3.20) принимает вид

Функция (3.23) имеет максимальное значение при $\theta = 0$

Глобальный максимум функции ${{G}^{2}}$ можно найти с помощью численного анализа выражения (3.20). В результате численных расчетов получаем следующее максимальное значение:

которое достигается для углов $\alpha \approx 33^\circ $, $\theta \approx 12^\circ $. При этом безразмерная частота в соответствии с (3.19) равна $x \approx 0.315$.

Численные расчеты по точным формулам (3.14), (3.16) для значения ${{a}^{2}} = 100$, углов $\alpha \approx 33^\circ $, $\theta \approx 13^\circ $ и безразмерной частоты $x \approx 0.314$ дают следующий результат для квадрата максимального безразмерного инкремента:

Сравнивая (3.26) с формулой (3.25), из которой при ${{a}^{2}} = 100$ следует $G_{{\max ,\max }}^{2} \approx 1.968 \times {{10}^{{ - 7}}}$, находим хорошее совпадение численных и аналитических результатов.

Рассмотрим теперь не очень плотную плазму. Пусть плотность плазмы в полтора раза превышает критическую величину ${{a}^{2}} = 1.5$. Численный анализ уравнения (3.14) совместно с формулой (3.16) показывает, что безразмерный инкремент (3.16) максимален для угла распространения поверхностной волны $\left( {\Omega ,{\mathbf{k}}} \right)$ $\theta \approx 16^\circ $ при падении волны накачки на границу плазмы под углом $\alpha \approx 39^\circ $ и имеет величину

для безразмерной частоты $x \approx 0.357$.

Из рассмотренных примеров следует, что чем больше плотность плазмы, тем меньше инкремент неустойчивости. С другой стороны, увеличивая плотность плазмы, можно возбуждать поверхностную волну с небольшим инкрементом неустойчивости, но на достаточно низкой частоте.

Для оценки инкремента неустойчивости рассмотрим незначительное превышение критической плотности, когда ${{a}^{2}} = 1.5$. В этом случае максимальный инкремент неустойчивости в соответствии с формулами (3.15), (3.27) имеет вид

При этом происходит возбуждение двух ПЭВ с частотами $\Omega \approx 0.357{{\omega }_{0}}$ и ${{\omega }_{1}} = {{\omega }_{0}} - \Omega \approx 0.643{{\omega }_{0}}$, которые находятся в инфракрасном диапазоне частот при воздействии оптического излучения. Волновые числа возбуждаемых волн определяются в соответствии с (3.7) соотношениями

Подставляя в формулы (3.29) ${{a}^{2}} = 1.5$, $x = 0.357$ находим величины волновых векторов

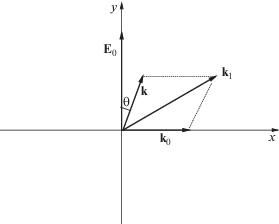
Таким образом, в рассматриваемом случае поверхностная волна $\left( {\Omega ,{\mathbf{k}}} \right)$ распространяется под углом $\theta \approx 16^\circ $ относительно электрического поля накачки, а поверхностная волна с более высокой частотой $\left( {{{\omega }_{1}},{{{\mathbf{k}}}_{1}}} \right)$ распространяется под углом $ \approx {\kern 1pt} 26^\circ $ относительно ${{{\mathbf{k}}}_{0}}$ или под углом $ \approx {\kern 1pt} 64^\circ $ по отношению к электрическому полю лазерного излучения. При этом угол между волновыми векторами k и ${{{\mathbf{k}}}_{1}}$ составляет величину $ \approx {\kern 1pt} 48^\circ $ (см. рисунок 1).

4. ПОРОГ НЕУСТОЙЧИВОСТИ

Рассмотрим теперь порог неустойчивости. Для этого следует учесть частоты соударений ν, ${{\nu }_{1}}$ электронов в выражениях для диэлектрической проницаемости. В случае редких столкновений, когда выполнены условия $\nu \ll \omega $, ${{\nu }_{1}} \ll {{\omega }_{1}}$, для диэлектрических проницаемостей имеем

При учете столкновений соотношения (3.5), (3.9) принимают вид

Тогда вместо (3.15) находим следующее уравнение для инкремента неустойчивости:

где введены обозначения

Решение уравнения (4.3) имеет вид

Порог неустойчивости находится из условия $\gamma \left( x \right) = 0$ и определяется соотношением

При значительном превышении порога, когда выполняется условие

из формулы (4.5) следует результат бесстолкновительной теории (3.15). Используя выражения (4.6) после несложных преобразований, получим следующее выражение для порога неустойчивости: где функция $W\left( x \right)$ имеет вид а безразмерная частота x определяется из уравнения (3.14).

Рассмотрим случай очень плотной плазмы, когда выполняется условие ${{a}^{2}} \gg 1$. Тогда с учетом формулы для безразмерной частоты (3.20) выражение (4.9) принимает вид

Численный анализ формулы (4.10) показывает, что минимальное значение функции W равное ${{W}_{{\max }}} \approx 21.8{{a}^{2}}$ реализуется для углов $\alpha \approx 39^\circ $, $\theta \approx 14^\circ $ и безразмерной частоты $x \approx 0.266$. Отсюда заключаем, что при условии ${{a}^{2}} \gg 1$ порог неустойчивости в соответствии с формулой (4.8) имеет очень большую величину.

Рассмотрим случай небольшого превышения плотностью электронов критического значения, когда ${{a}^{2}} = 1.5$. В этом случае численный анализ формулы (4.9) показывает, что минимальное значение функции ${{W}_{{\min }}} \approx 33.3$ достигается при следующих значениях безразмерной частоты, угла падения и угла распространения поверхностной волны: $x \approx 0.347$, $\alpha \approx 42^\circ $, $\theta \approx 15^\circ $. Отсюда следует, что пороговое значение амплитуды волны накачки для безразмерной плотности ${{a}^{2}} = 1.5$ имеет вид

Отметим, что параметры $x \approx 0.347$, $\alpha \approx 42^\circ $, $\theta \approx 15^\circ $, соответствующие порогу неустойчивости, несколько отличаются от параметров x ≈ $ \approx 0.357$, $\alpha \approx 39^\circ $, $\theta \approx 16^\circ $, отвечающих максимуму инкремента (3.27) при ${{a}^{2}} = 1.5$. Это связано, в отличие от объемных волн, со специфической зависимостью декрементов затухания поверхностных волн от частоты, которая описывается формулами (4.4).

5. ЗАКЛЮЧЕНИЕ

В настоящей работе исследовано параметрическое возбуждение поверхностных волн при наклонном падении s-поляризованной электромагнитной волны на полуограниченную плазму сверхкритической концентрации. Получено дисперсионное уравнение и вычислен инкремент неустойчивости, связанный с распадом волны накачки на две поверхностные электромагнитные волны, который оказался пропорциональным первой степени напряженности электрического поля волны накачки. Исследована зависимость инкремента неустойчивости от плотности электронов и угла падения. Показано, что инкремент имеет максимальное значение в плазме с концентрацией электронов, незначительно превышающей критическое значение. Вычислен порог неустойчивости, который определяется частотой соударений электронов и имеет минимальное значение в плазме с околокритической концентрацией.

Отметим, что важной особенностью настоящей работы является то, что в ней построена нелинейная теория возбуждения поверхностных плазмонов s-поляризованной электромагнитной волной накачки. В линейной теории возбуждение поверхностных волн происходит только при воздействии p-поляризованной накачки. Например, в оптике для возбуждения поверхностных волн применяются различные призмы для согласования падающего p-поляризованного электромагнитного излучения с поверхностными плазмонами. Как уже отмечалось выше, наиболее эффективное параметрическое нарастание ПЭВ происходит в случае, когда плотность электронов близка к критической величине. С ростом плотности плазмы инкремент неустойчивости падает. Отсюда следует, что рассмотренный в настоящей статье механизм возбуждения ПЭВ может быть реализован при воздействии лазерного излучения на малоплотные мишени (например, аэрогели с плотностью 1−100 мг/см²). При взаимодействии же лазерного излучения с твердотельными мишенями данный механизм видимо малоэффективен.

В заключение оценим величину инкремента неустойчивости для характерных параметров лазерно-плазменных экспериментов. Пусть лазерный импульс с длиной волны ${{\lambda }_{0}} = 1$ мкм (частота ${{\omega }_{0}} \approx 1.88 \times {{10}^{{15}}}$ с^–1), длительностью $\tau = 500$ фс и интенсивностью ${{I}_{L}} = {{10}^{{17}}}$ Вт/см² падает на границу плазмы, образующейся при ионизации твердотельной мишени, электроны которой имеют плотность ${{N}_{{0e}}} \approx 1.1 \times {{10}^{{23}}}$ см^–3 на два порядка больше критического значения. В этом случае инкремент, в соответствии с формулами (3.15), (3.25), имеет величину $\gamma \approx 1.2 \times {{10}^{{ - 5}}}{{\omega }_{0}}$, и неустойчивость за время длительности импульса не успевает развиться, так как коэффициент усиления $\Gamma = \gamma \tau \approx {{10}^{{ - 2}}}$ имеет малую величину. Если же использовать в качестве мишени аэрогель, который при ионизации имеет плотность электронов, близкую к критическому значению, то можно получить заметный эффект. Для плотности электронов ${{N}_{{0e}}} \approx 1.6 \times {{10}^{{21}}}$ см^–3 из формулы (3.28) находим $\gamma \approx {{10}^{{ - 2}}}{{\omega }_{0}}$. В этом случае коэффициент усиления имеет величину $\Gamma = \gamma \tau \approx 9.4$, и начальные затравочные значения амплитуд поверхностных волн вполне могут вырасти до заметных величин.

Работа выполнена при поддержке РФФИ (проект № 17-02-00648а.)