Физика плазмы, 2019, T. 45, № 8, стр. 745-754
Матричный алгоритм приближенного решения волновых уравнений в неоднородной магнитоактивной плазме
В. Г. Мизонова *
Нижегородский государственный технический университет им. Р.Е. Алексеева
Нижний Новгород, Россия
* E-mail: vermiz@mail.ru
Поступила в редакцию 24.10.2018
После доработки 28.12.2018
Принята к публикации 07.02.2019
Аннотация
Рассмотрена задача о распространении электромагнитной волны в плоскослоистой неоднородной магнитоактивной плазме. Предложен матричный алгоритм приближенного решения системы волновых уравнений. Суть алгоритма заключается в последовательном нахождении обусловленных неоднородностью среды поправок к локальным корням дисперсионного соотношения и локальным векторам поляризации. При этом система полевых уравнений сводится к системе линейных алгебраических уравнений. Предложенный алгоритм удобен для проведения численных расчетов. В отличие от классического приближения геометрической оптики рассмотренный алгоритм позволяет учесть слабый эффект линейного взаимодействия мод. Приведены примеры численных расчетов для коэффициента отражения по энергии свистовых волн, падающих на ионосферу сверху. Предложенный матричный алгоритм может быть полезен для нахождения коэффициентов отражения, коэффициентов линейной трансформации волн в плавно неоднородной ионосфере.
1. ВВЕДЕНИЕ
Несмотря на огромное количество существующих аналитических и численных методов описания распространения электромагнитных волн в неоднородных средах (см., например, [1–8]), классическая задача о нахождении приближенных решений волновых уравнений в неоднородных анизотропных средах до сих пор остается актуальной. Действительно, распространение монохроматической волны даже в сравнительно простом случае плоскослоистой среды с известным тензором диэлектрической проницаемости классически описывается системой четырех неразделяющихся в общем случае дифференциальных уравнений первого порядка [1, 4]. Точные аналитические решения такой системы в большинстве случаев либо неизвестны, либо не эффективны с практической точки зрения. Численные методы также могут быть связаны с большими вычислительными трудностями. Одной из основных проблем является расходимость решений волновых уравнений, обусловленная модами с большой по величине мнимой частью [4, 9, 10]. Различные подходы, улучшающие устойчивость численного решения волновых уравнений в ионосферной плазме, предложены в работах [5, 6, 9–11]. При этом удается получить устойчивое решение либо в частных случаях, например, при малых углах падения волны [6], либо на сравнительно небольших высотах (в пределах 250 км от поверхности Земли) [5, 9, 11].
Использование приближенных методов позволяет найти решение в тех случаях, где точные методы малоэффективны, а свойства среды достаточно медленно меняются на расстоянии. Например, на высотах более 100 км над поверхностью Земли характерный масштаб изменения ионосферных параметров составляет 100 км, что существенно превышает длины волн даже низкочастотных диапазонов. К классическим методам относится приближение геометрической оптики, известное в квантовой механике как ВКБ-метод [1, 12]. Приближение геометрической оптики эффективно, если свойства среды мало изменяются на расстояниях порядка длины волны. Условия применимости этого приближения нарушаются при малых показателях преломления среды (когда длина волны становится сравнимой с масштабом плазменной неоднородности), а также в случае близких показателей преломления двух волн. Кроме того, приближение геометрической оптики не учитывает возможности линейной трансформации мод. С практической точки зрения использование формул геометрической оптики при численном нахождении поля волны в анизотропных средах в общем случае наклонного падения (см., например, [1]) не всегда удобно из-за их математической громоздкости.
В данной работе развивается матричный подход к решению волновых уравнений в неоднородной анизотропной плазме. Исходная система четырех волновых уравнений представляется в матричной форме, сравнительно часто используемой для нахождения полей в плоскослоистых средах [4, 9, 13]. Представление поля волны через собственные значения и собственные векторы матрицы, вид которой определяется свойствами среды, применяется в работах [1, 13]. В работе [9] отмечается, что матричная форма записи волновых уравнений удобна для проведения численных расчетов. Предлагаемый в настоящей работе алгоритм позволяет найти приближенное решение волновых уравнений в плоскослоистой магнитоактивной холодной плазме. Суть алгоритма заключается в последовательном нахождении обусловленных плазменной неоднородностью поправок к корням дисперсионного соотношения и соответствующих им векторам поляризации. При этом система дифференциальных уравнений сводится к системе линейных алгебраических уравнений, что, во-первых, существенно упрощает расчеты, во-вторых, позволяет решить проблему численной расходимости решений. В качестве примера использования алгоритма приводятся результаты вычислений коэффициента отражения электромагнитных волн свистового диапазона от ионосферы сверху.
2. ИСХОДНЫЕ УРАВНЕНИЯ И ПОСТАНОВКА ЗАДАЧИ
Рассмотрим электромагнитную волну с частотой ω, распространяющуюся в плоскослоистой неоднородной магнитоактивной холодной плазме. Пусть концентрация заряженных частиц и их частоты столкновений изменяются вдоль оси z, магнитное поле ${{{\mathbf{B}}}_{0}}$ лежит в плоскости yz и составляет с осью z угол $\vartheta $. Представим поле волны в виде ${\mathbf{E}}(z)\exp \left( {i{{{\mathbf{k}}}_{ \bot }}{{{\mathbf{r}}}_{ \bot }} - i\omega t} \right)$, ${\mathbf{B}}(z)\exp \left( {i{{{\mathbf{k}}}_{ \bot }}{{{\mathbf{r}}}_{ \bot }} - i\omega t} \right)$, где ${{{\mathbf{k}}}_{ \bot }}$ – поперечная по отношению к оси z составляющая волнового вектора. Из уравнений Максвелла
(1)
$\begin{gathered} \nabla \times {\mathbf{B}} = - \frac{{i\omega }}{c}\hat {\varepsilon }{\mathbf{E}}, \\ \nabla \times {\mathbf{E}} = \frac{{i\omega }}{c}{\mathbf{B}} \\ \end{gathered} $Здесь
(3)
${\mathbf{F}} = \left( {\begin{array}{*{20}{c}} {{{E}_{x}}} \\ {{{E}_{y}}} \\ {{{B}_{x}}} \\ {{{B}_{y}}} \end{array}} \right),$(4)
$\begin{gathered} \hat {M} = \frac{{i\omega }}{c}\left( {\begin{array}{*{20}{c}} {{{n}_{x}}\frac{{ig\sin \vartheta }}{{{{\varepsilon }_{\vartheta }}}}}&{ - {{n}_{x}}\frac{{(\eta - \varepsilon )\sin 2\vartheta }}{{2{{\varepsilon }_{\vartheta }}}}}&{\frac{{{{n}_{x}}{{n}_{y}}}}{{{{\varepsilon }_{\vartheta }}}}}&{1 - \frac{{n_{x}^{2}}}{{{{\varepsilon }_{\vartheta }}}}} \\ {{{n}_{y}}\frac{{ig\sin \vartheta }}{{{{\varepsilon }_{\vartheta }}}}}&{ - {{n}_{y}}\frac{{(\eta - \varepsilon )\sin 2\vartheta }}{{2{{\varepsilon }_{\vartheta }}}}}&{\frac{{n_{y}^{2}}}{{{{\varepsilon }_{\vartheta }}}} - 1}&{ - \frac{{{{n}_{x}}{{n}_{y}}}}{{{{\varepsilon }_{\vartheta }}}}} \\ { - {{n}_{x}}{{n}_{y}} - \frac{{ig\eta \cos \vartheta }}{{{{\varepsilon }_{\vartheta }}}}}&{n_{x}^{2} - \frac{{\varepsilon \eta }}{{{{\varepsilon }_{\vartheta }}}}}&{ - {{n}_{y}}\frac{{(\eta - \varepsilon )\sin 2\vartheta }}{{2{{\varepsilon }_{\vartheta }}}}}&{{{n}_{x}}\frac{{(\eta - \varepsilon )\sin 2\vartheta }}{{2{{\varepsilon }_{\vartheta }}}}} \\ { - n_{y}^{2} + \varepsilon - \frac{{{{g}^{2}}{{{\sin }}^{2}}\vartheta }}{{{{\varepsilon }_{\vartheta }}}}}&{{{n}_{x}}{{n}_{y}} - \frac{{ig\eta \cos \vartheta }}{{{{\varepsilon }_{\vartheta }}}}}&{{{n}_{y}}\frac{{ig\sin \vartheta }}{{{{\varepsilon }_{\vartheta }}}}}&{ - {{n}_{x}}\frac{{ig\sin \vartheta }}{{{{\varepsilon }_{\vartheta }}}}} \end{array}} \right), \\ {{\varepsilon }_{\vartheta }} = \varepsilon {{\sin }^{2}}\vartheta + \eta {{\cos }^{2}}\vartheta ,\quad {{n}_{{x,y}}} = \frac{{{{k}_{{x,y}}}c}}{\omega }. \\ \end{gathered} $В выражениях (4) для “холодной” плазмы
(5)
$\begin{gathered} \varepsilon = 1 - \frac{{\omega _{{pe}}^{2}}}{{{{{(\omega + i{{\nu }_{e}})}}^{2}} - \omega _{{Be}}^{2}}}\frac{{\omega + i{{\nu }_{e}}}}{\omega } - \\ \, - \frac{{\omega _{{pi}}^{2}}}{{{{{(\omega + i{{\nu }_{i}})}}^{2}} - \omega _{{Bi}}^{2}}}\frac{{\omega + i{{\nu }_{i}}}}{\omega }, \\ \eta = 1 - \frac{{\omega _{{pe}}^{2}}}{{\omega \left( {\omega + i{{\nu }_{e}}} \right)}} - \frac{{\omega _{{pi}}^{2}}}{{\omega (\omega + i{{\nu }_{i}})}},{\text{ }} \\ g = - \frac{{\omega _{{pe}}^{2}{{\omega }_{{Be}}}}}{{\omega \left( {{{{(\omega + i{{\nu }_{e}})}}^{2}} - \omega _{{Be}}^{2}} \right)}} + \frac{{\omega _{{pi}}^{2}{{\omega }_{{Bi}}}}}{{\omega \left( {{{{(\omega + i{{\nu }_{i}})}}^{2}} - \omega _{{Bi}}^{2}} \right)}} \\ \end{gathered} $(6)
$\begin{gathered} {{E}_{z}} = - \left( {{{\left( {\eta - \varepsilon } \right)\sin \vartheta \cos \vartheta } \mathord{\left/ {\vphantom {{\left( {\eta - \varepsilon } \right)\sin \vartheta \cos \vartheta } {{{\varepsilon }_{\vartheta }}}}} \right. \kern-0em} {{{\varepsilon }_{\vartheta }}}}} \right){{E}_{y}} + \\ \, + \left( {ig\sin \vartheta {\text{/}}{{\varepsilon }_{\vartheta }}} \right){{E}_{x}} + \left( {{{n}_{y}}{{B}_{x}} - {{n}_{x}}{{B}_{y}}} \right){\text{/}}{{\varepsilon }_{\vartheta }}, \\ {{B}_{z}} = {{n}_{x}}{{E}_{y}} - {{n}_{y}}{{E}_{x}}. \\ \end{gathered} $Нахождение решения системы (2)–(4) в общем случае неоднородной среды связано со значительными математическими трудностями. Мы предположим, что свойства среды мало меняются на расстояниях порядка длины волны, и будем искать приближенное решение этих уравнений.
3. ОПИСАНИЕ МАТРИЧНОГО АЛГОРИТМА
Запишем сначала решение системы уравнений (2)–(4) для случая однородной среды
(7)
$\begin{gathered} {\mathbf{F}} = \sum\limits_{j = 1}^4 {{{{\mathbf{P}}}_{{0j}}}} {{A}_{{0j}}}\exp \left( {i{{\kappa }_{j}}z} \right) \equiv {{{\hat {P}}}_{0}}{{{\hat {D}}}_{{0\exp }}}{{{\mathbf{A}}}_{0}}, \\ {{A}_{{0j}}} = \operatorname{const} . \\ \end{gathered} $Здесь величины $i{{\kappa }_{j}} \equiv i{{k}_{{zj}}}$ являются собственными значениями (${{k}_{{zj}}}$ – корни дисперсионного соотношения), а векторы ${{{\mathbf{P}}}_{{0j}}}$ – собственными векторами матрицы $\hat {M}$ (4). Четыре вектор-столбца ${{{\mathbf{P}}}_{{0j}}}$
(8)
${{{\mathbf{P}}}_{{0j}}} = {{\left( {\begin{array}{*{20}{c}} {{{e}_{{0x}}}} \\ {{{e}_{{0y}}}} \\ {{{b}_{{0x}}}} \\ {{{b}_{{0y}}}} \end{array}} \right)}_{j}}$Из этого свойства следуют четность по ${{k}_{x}}$ ее собственных значений
а также соотношение, связывающее элементы матриц ${{\hat {P}}_{0}}$ и обратной ей матрицы $\hat {P}_{0}^{{ - 1}}$(11)
${{\beta }_{{0j}}}P{{_{0}^{{ - 1}}}_{{jk}}}( - {{k}_{x}}) = \,{{P}_{{0{\text{ }}5 - k{\text{ }}j}}}({{k}_{x}}).$Здесь коэффициент ${{\beta }_{{0j}}}$, в соответствии с равенством $\sum\nolimits_m {P{{{_{0}^{{ - 1}}}}_{{jm}}}} {{P}_{0}}_{{mk}} = {{\delta }_{{jk}}}$, определяется формулой
(12)
${{\beta }_{{0j}}}({{k}_{x}}) = \,{{\beta }_{{0j}}}( - {{k}_{x}}) = \sum\limits_m {{{P}_{0}}_{{5 - mj}}({{k}_{x}}){{P}_{0}}_{{mj}}( - {{k}_{x}})} .$Ниже векторы поляризации ${{{\mathbf{P}}}_{{0j}}}$ (столбцы матрицы ${{\hat {P}}_{0}}$) будем нормировать условием
(13)
$\begin{gathered} {{\beta }_{{0j}}} = \left( {{{e}_{{0x}}}{{b}_{{0y}}}( - {{k}_{x}}) + {{e}_{{0y}}}{{b}_{{0x}}}( - {{k}_{x}}) + } \right. \\ \, + {{\left. {{{e}_{{0x}}}( - {{k}_{x}}){{b}_{{0y}}} + {{e}_{{0y}}}( - {{k}_{x}}){{b}_{{0x}}}} \right)}_{j}} = 1. \\ \end{gathered} $В общем случае неоднородной среды представим решение системы уравнений (2)–(4) в аналогичном выражению (7) виде
(14)
$\begin{gathered} {\mathbf{F}} = \sum\limits_{j = 1}^4 {{{{\mathbf{P}}}_{j}}} (z){{A}_{j}}\exp \left( {\int\limits_0^z {i{{\chi }_{j}}} (z{\text{'}})dz{\text{'}}} \right) \equiv \hat {P}{{{\hat {D}}}_{{\exp }}}{\mathbf{A}}, \\ {{A}_{j}} = \operatorname{const} , \\ \end{gathered} $(15)
${{{\mathbf{P}}}_{j}} = {{\left( {\begin{array}{*{20}{c}} {{{e}_{x}}} \\ {{{e}_{y}}} \\ {{{b}_{x}}} \\ {{{b}_{y}}} \end{array}} \right)}_{j}},$(16)
$\begin{gathered} \left( {{{e}_{x}}{{b}_{y}}( - {{k}_{x}}) + {{e}_{y}}{{b}_{x}}( - {{k}_{x}}) + {{e}_{x}}b{{{( - {{k}_{x}})}}_{{0y}}} + } \right. \\ \, + {{\left. {{{e}_{y}}( - {{k}_{x}}){{b}_{x}}} \right)}_{j}} = 1. \\ \end{gathered} $Подставляя выражение (14) в уравнение (2), получаем
где $\hat {D}$ – диагональная матрица с элементами $i{{\chi }_{j}}$. Перепишем уравнение (17) в виде(18)
$\hat {P}\hat {D} = \left( {\hat {M} - \hat {P}{\text{'}}{{{\hat {P}}}^{{ - 1}}}} \right)\hat {P},$Тогда из уравнения (17) с учетом формулы (19) получаем уравнение на собственные значения и собственные векторы матрицы $\hat {M} - \hat {P}_{0}^{'}\hat {P}_{0}^{{ - 1}}$. Решая это уравнение, можно найти четыре z-проекции волновых векторов ${{\chi }_{{j(1)}}}$ и матрицу поляризаций ${{\hat {P}}_{1}}$ в первом приближении. Аналогично находятся z-проекции волновых векторов и матрицу поляризаций во втором и последующих приближениях. В результате получаем систему рекурентных уравнений
(20)
$\begin{gathered} {{{\hat {P}}}_{0}}{{{\hat {D}}}_{0}} = \hat {M}{{{\hat {P}}}_{0}}, \\ {{{\hat {P}}}_{1}}{{{\hat {D}}}_{1}} = \left( {\hat {M} - \hat {P}_{0}^{'}\hat {P}_{0}^{{ - 1}}} \right){{{\hat {P}}}_{1}}, \\ ... \\ {{{\hat {P}}}_{{n + 1}}}{{{\hat {D}}}_{{n + 1}}} = \left( {\hat {M} - \hat {P}_{n}^{'}\hat {P}_{n}^{{ - 1}}} \right){{{\hat {P}}}_{{n + 1}}}. \\ \end{gathered} $Отметим, что в некоторых случаях точное уравнение (17) и систему приближенных уравнений (20) удобнее записать для матрицы $\hat {\rho }$, связывающей поляризацию $\hat {P}$ и локальную поляризацию ${{\hat {P}}_{0}}$
Далее будем называть ее матрицей линейного взаимодействия мод. Условие нормировки матрицы линейного взаимодействия $\hat {\rho }$, в соответствии с формулами (11), (13), (16), (21), имеет вид
(22)
$\sum\limits_m {{{\rho }_{{mj}}}\left( {{{k}_{x}}} \right)} {{\rho }_{{mj}}}\left( { - {{k}_{x}}} \right) = 1.$В приближении однородной среды матрица $\hat {\rho }$ совпадает с единичной. В общем случае неоднородной среды точное уравнение (17) принимает вид
(23)
$\hat {\rho }'\, + \hat {\rho }\hat {D} = \left( {{{{\hat {D}}}_{0}} - \hat {t}} \right)\hat {\rho },$(24)
$\begin{gathered} {{{\hat {\rho }}}_{1}}{{{\hat {D}}}_{1}} = \left( {{{{\hat {D}}}_{0}} - \hat {t}} \right){{{\hat {\rho }}}_{1}}, \\ {{{\hat {\rho }}}_{2}}{{{\hat {D}}}_{2}} = \left( {{{{\hat {D}}}_{0}} - \hat {t} - \hat {\rho }_{1}^{{ - 1}}\hat {\rho }_{1}^{'}} \right){{{\hat {\rho }}}_{2}}, \\ ... \\ {{{\hat {\rho }}}_{{n + 1}}}{{{\hat {D}}}_{{n + 1}}} = \left( {{{{\hat {D}}}_{0}} - \hat {t} - \hat {\rho }_{n}^{{ - 1}}\hat {\rho }_{n}^{'}} \right){{{\hat {\rho }}}_{{n + 1}}}. \\ \end{gathered} $(26)
${{t}_{{jk}}} = \frac{{{{{\left( {\hat {P}_{0}^{{ - 1}}\hat {M}{\text{'}}{{{\hat {P}}}_{0}}} \right)}}_{{jk}}}}}{{i{{\kappa }_{k}} - i{{\kappa }_{j}}}}.$Из формул (11), (12) для элементов матрицы связи $\hat {t}$ (26) следует равенство
В частном случае распространения волны в плоскости, образованной магнитным полем и вертикальной осью z (при этом ${{k}_{x}} = 0$) диагональные элементы равны нулю, а недиагональные антисимметричны
По порядку величины коэффициенты связи равны
(29)
${{t}_{{jk}}} \sim \frac{{{{\kappa }_{{j,k}}}}}{{\Delta z\left( {{{\kappa }_{j}} - {{\kappa }_{k}}} \right)}}.$Таким образом, исходная система дифференциальных волновых уравнений (2)–(4) сводится к системе линейных алгебраических уравнений в виде (20) либо (24). Решение первых n уравнений систем (20) или (24) позволяет найти поле волны (14) в n-м приближении.
Выясним условия применимости уравнений (20) или (24).
4. УСЛОВИЕ ПРИМЕНИМОСТИ МАТРИЧНОГО АЛГОРИТМА
Условием применимости n-го уравнения систем (24) (и, соответственно, (20)) является относительная малость поправок $\hat {\rho }_{n}^{{ - 1}}\hat {\rho }_{n}^{'}$ в его правой части
(30a)
$\left| {{{{\left( {\hat {\rho }_{1}^{{ - 1}}\hat {\rho }_{1}^{'}} \right)}}_{{jk}}}} \right| \ll \left| {i{{\kappa }_{j}}{{\delta }_{{jk}}} - {{t}_{{jk}}}} \right|,$(30б)
$\left| {{{{\left( {\hat {\rho }_{2}^{{ - 1}}\hat {\rho }_{2}^{'}} \right)}}_{{jk}}}} \right| \ll \left| {i{{\kappa }_{j}}{{\delta }_{{jk}}} - {{t}_{{jk}}} - {{{\left( {\hat {\rho }_{1}^{{ - 1}}\hat {\rho }_{1}^{'}} \right)}}_{{jk}}}} \right|,$(30в)
$\left| {{{{\left( {\hat {\rho }_{{n + 1}}^{{ - 1}}\hat {\rho }_{{n + 1}}^{'}} \right)}}_{{jk}}}} \right| \ll \left| {i{{\kappa }_{j}}{{\delta }_{{jk}}} - {{t}_{{jk}}} - {{{\left( {\hat {\rho }_{n}^{{ - 1}}\hat {\rho }_{n}^{'}} \right)}}_{{jk}}}} \right|.$Неравенство (30а) является условием применимости первого приближения (24). Здесь коэффициенты связи можно оценить с помощью формулы (29), а элементы матриц ${{\hat {\rho }}_{1}}$ и ${{\left( {\hat {\rho }_{1}^{{ - 1}}\hat {\rho }_{1}^{'}} \right)}_{{jk}}}$ – с помощью первого уравнения системы (24). Для оценки предположим, что возможно линейное взаимодействие 1-й и 2-й волновых мод, а взаимодействие между остальными модами пренебрежимо мало. Тогда из первого уравнения (24) с учетом условия нормировки (22) для величин ${{\chi }_{{1,2}}}$ и элементов матрицы линейного взаимодействия мод ${{\rho }_{{jk}}},{\text{ }}j$, $k = 1,2$ получаем
(31)
$\begin{gathered} {{\chi }_{{1,2}}} = \frac{{{{{\tilde {\kappa }}}_{1}} + {{{\tilde {\kappa }}}_{2}} \pm \sqrt {\Delta {{{\tilde {\kappa }}}^{2}} - 4{{t}^{2}}} }}{2},\quad {{{\tilde {\kappa }}}_{j}} = {{\kappa }_{j}} - {{t}_{{jj}}}, \\ \Delta \tilde {\kappa } = {{{\tilde {\kappa }}}_{2}} - {{{\tilde {\kappa }}}_{1}},\quad t \sim {{t}_{{12}}} \sim {{t}_{{21}}}, \\ \end{gathered} $(32)
$\begin{gathered} {{\rho }_{{11}}} = {{\rho }_{{22}}} = \frac{1}{{\sqrt 2 }}\sqrt {1 + \frac{{\Delta \tilde {\kappa }}}{{\sqrt {\Delta {{{\tilde {\kappa }}}^{2}} - 4{{t}^{2}}} }}} , \\ {{\rho }_{{12}}} = - {{\rho }_{{21}}} = \frac{1}{{\sqrt 2 }}\sqrt {1 - \frac{{\Delta \tilde {\kappa }}}{{\sqrt {\Delta {{{\tilde {\kappa }}}^{2}} - 4{{t}^{2}}} }}} . \\ \end{gathered} $При этом
(33)
$\begin{gathered} {{\left( {\hat {\rho }_{1}^{{ - 1}}\hat {\rho }_{1}^{'}} \right)}_{{11}}} = {{\left( {\hat {\rho }_{1}^{{ - 1}}\hat {\rho }_{1}^{'}} \right)}_{{22}}} = 0, \\ {{\left( {\hat {\rho }_{1}^{{ - 1}}\hat {\rho }_{1}^{'}} \right)}_{{12}}} = {{\left( {\hat {\rho }_{1}^{{ - 1}}\hat {\rho }_{1}^{'}} \right)}_{{21}}} = \frac{{\Delta \tilde {\kappa }{\text{'}}t - t{\text{'}}\Delta \tilde {\kappa }}}{{\left( {\Delta {{{\tilde {\kappa }}}^{2}} + {{t}^{2}}} \right)}}. \\ \end{gathered} $Таким образом, условие (30а) применимости первого приближения матричного метода имеет вид
(34)
$\frac{{\left| {t{\text{'}}\Delta \kappa - \Delta \kappa {\text{'}}t} \right|}}{{\left( {\Delta {{\kappa }^{2}} + {{t}^{2}}} \right)}} \ll t.$Полагая в соответствии с формулой (29) $t \sim \kappa {\text{'/}}\Delta \kappa $, $\partial {\text{/}}\partial z \sim 1{\text{/}}\Delta z$, из неравенства (34) получаем
(35)
$\left| {\Delta \kappa } \right|\Delta z \ll {{\left| {\Delta \kappa } \right|}^{2}}\Delta {{z}^{2}} + {{\left| {\kappa {\text{/}}\Delta \kappa } \right|}^{2}}.$Оценочные формулы для второго приближения можно получить аналогичным образом, произведя в выражениях (31)–(33) замену
где(37)
$\Delta t = \frac{{\Delta \tilde {\kappa }{\text{'}}t - t{\text{'}}\Delta \tilde {\kappa }}}{{\left( {\Delta {{{\tilde {\kappa }}}^{2}} + {{t}^{2}}} \right)}} \ll t.$Тогда аналогично неравенству (34) получаем условие применимости второго приближения (второго уравнения (24))
(38)
$\frac{{\left| {\left( {t + \Delta t} \right){\text{'}}\Delta \kappa - \Delta \kappa {\text{'}}\left( {t + \Delta t} \right)} \right|}}{{\left( {\Delta {{\kappa }^{2}} + {{{\left( {t + \Delta t} \right)}}^{2}}} \right)}} \ll t,$(39)
$\frac{{\Delta t}}{t} \sim \frac{{\Delta \kappa \Delta z}}{{{{{\left( {\Delta \kappa \Delta z} \right)}}^{2}} + {{{\left( {\kappa {\text{/}}\Delta \kappa } \right)}}^{2}}}} \ll 1$Из оценочной формулы (39) следует, что приближенные уравнения (20), (24) могут применяться в двух случаях:
1) среда является плавно неоднородной, и все корни локального дисперсионного соотношения существенно различны
2) среда является резко неоднородной, и выполнены неравенства
(41)
$\left| {\Delta \kappa } \right|\Delta z \ll 1,\quad {{\left| {\frac{\kappa }{{\Delta \kappa }}} \right|}^{2}}.$Для “тестирования” матричного алгоритма в случаях плавно (40) и резко (41) неоднородных сред в Приложении рассмотрен сравнительно простой частный случай изотропной плазмы с показателем преломления $n(z)$. Приведены аналитические выражения для коэффициента отражения нормально падающей волны от верхней границы слоя ${{z}_{1}} \leqslant z \leqslant {{z}_{2}}$. При выполнении неравенства (40) полученная формула с точностью до малых величин порядка ${{\left( {1{\text{/}}\kappa \Delta z} \right)}^{2}}$ совпадает с известной интерполяционной формулой для случая слабого отражения [1, 2]. При выполнении неравенства (41) из формул матричного алгоритма следует формула Френеля.
В качестве другого примера использования матричного формализма и его связи с классическими подходами проанализируем случай плавно неоднородной магнитоактивной плазмы. Сравним решения, полученные в приближении геометрической оптики и с помощью формул матричного алгоритма.
5. О СВЯЗИ МАТРИЧНОГО АЛГОРИТМА С ПРИБЛИЖЕНИЕМ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
В нулевом приближении матричного метода решение системы уравнений (2)–(4) имеет вид (14), в котором значения ${{\chi }_{j}}\left( z \right)$ совпадают с локальными значениями вертикальных проекций волнового вектора ${{\kappa }_{j}}\left( z \right)$, а матрица поляризаций $\hat {P}$ совпадает с локальной матрицей поляризаций (при этом матрица линейной трансформации $\hat {\rho }$ равна единичной)
(42)
$\begin{gathered} {{\chi }_{j}} = {{\kappa }_{j}}, \\ \hat {\rho } = \hat {I}, \\ \hat {P} = {{{\hat {P}}}_{0}}. \\ \end{gathered} $Аналогично, в приближении геометрической оптики
(43)
$\begin{gathered} {{\chi }_{j}} = {{\kappa }_{j}} - {{t}_{{jj}}}, \\ \hat {\rho } = \hat {I}, \\ \hat {P} = {{{\hat {P}}}_{0}}. \\ \end{gathered} $Для дополнительного множителя $\exp \left( { - i\int {{{t}_{{jj}}}dz} } \right)$ в выражении (14) используют термин “additional memory” [4]. В частном случае распространения волны в плоскости, образованной магнитным полем и вертикальной осью z, и условии нормировки (13) значение ${{t}_{{jj}}} = {{\left( {\hat {P}_{0}^{{ - 1}}\hat {P}_{0}^{'}} \right)}_{{jj}}} = 0$ (см. формулу (28)). При этом множитель $\exp \left( { - i\int {{{t}_{{jj}}}dz} } \right)$ равен единице, и решения, полученные в нулевом приближении рассмотренного алгоритма и с помощью формул геометрической оптики, совпадают. Действительно, пусть компонента волнового вектора ${{k}_{x}} = 0$, и выполнено условие нормировки (13) ${{e}_{{0x}}}{{b}_{{0y}}} + {{e}_{{0y}}}{{b}_{{0x}}} = \operatorname{const} $. Учитывая, что
(44)
$\begin{gathered} {{b}_{{0x}}} = \frac{{{{k}_{y}}c}}{\omega }{{e}_{{0z}}} - \frac{{\kappa c}}{\omega }{{e}_{{0y}}}, \\ {{b}_{{0y}}} = \frac{{\kappa c}}{\omega }{{e}_{{0x}}}, \\ \end{gathered} $(45)
${{E}_{{x,y}}} = \sum\limits_j {{{A}_{{0j}}}} {{e}_{{0x,0y}}}\exp \left( {\int\limits_{{{z}_{0}}}^z {i{{\kappa }_{j}}dz{\text{'}}} } \right)$(46)
$\begin{gathered} {{E}_{x}} = K{{E}_{y}},\quad {{E}_{z}} = D{{E}_{y}}, \\ {{E}_{у }} = \sum\limits_{j = 1,2} {{{{\left( {\frac{{{\text{const}}}}{{\sqrt {{{\kappa }_{j}}\left( {{{K}^{2}} - 1} \right) + {{k}_{y}}D} }}} \right)}}_{j}} \times } \\ \, \times \exp \left( {i{{k}_{y}}y + \int\limits_{{{z}_{0}}}^z {i{{\kappa }_{j}}dz{\text{'}} - i\omega t} } \right). \\ \end{gathered} $Здесь суммирование ведется по распространяющимся волновым модам.
Отличие от нуля коэффициентов связи ${{t}_{{jk}}}$ и, следовательно, недиагональных элементов матрицы $\hat {\rho }$ свидетельствует о линейном взаимодействии мод между собой. В первом приближении матричного алгоритма, как видно из формул (32) и (33), значения ${{\chi }_{j}}$ и элементы матриц $\hat {\rho }$ и $\hat {P}$ отличаются от решений нулевого приближения (42) на малые величины порядка ${{\left( {\left| {\Delta \kappa } \right|\Delta z} \right)}^{{ - 2}}}$. Таким образом, использование матричного алгоритма, в отличие от приближения геометрической оптики, позволяет учесть слабый эффект линейного взаимодействия мод.
Отметим, что матричный алгоритм удобен прежде всего для проведения численных расчетов. На рис. 1, 2 приведен пример результатов вычислений коэффициента отражения свистовых волн по энергии от верхнего слоя дневной ионосферы. Выражение для коэффициента отражения в соответствии с формулами (П8)–(П10) Приложения имеет вид
(47)
$R = \frac{{\left| {{{S}_{{z2}}}} \right|}}{{\left| {{{S}_{{z1}}}} \right|}} = {{\left. {{{{\left| {r\left( {{{z}_{2}}} \right)} \right|}}^{2}}\frac{{\left| {P_{{(0)42}}^{*} - {{{{P}_{{(0)22}}}P_{{(0)32}}^{*}} \mathord{\left/ {\vphantom {{{{P}_{{(0)22}}}P_{{(0)32}}^{*}} {{{P}_{{(0)12}}}}}} \right. \kern-0em} {{{P}_{{(0)12}}}}}} \right|}}{{\left| {P_{{(0)41}}^{*} - {{{{P}_{{(0)21}}}P_{{(0)31}}^{*}} \mathord{\left/ {\vphantom {{{{P}_{{(0)21}}}P_{{(0)31}}^{*}} {{{P}_{{(0)11}}}}}} \right. \kern-0em} {{{P}_{{(0)11}}}}}} \right|}}} \right|}_{{z = {{z}_{2}}}}},$Рис. 1.
Высотные профили плазменной концентрации (а) и частот столкновений электронов (сплошная линия) и ионов (штриховая линия) (б) с нейтральными частицами.
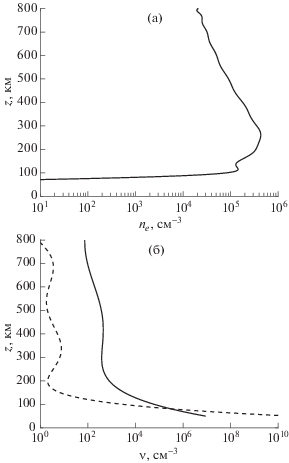
Рис. 2.
Коэффициенты отражения свистовых волн по энергии сверху от дневной ионосферы 120 км ≤ z ≤ 800 км, полученные матричным алгоритмом (сплошная линия) и в приближении геометрической оптики (штриховая линия).
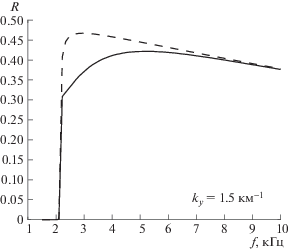
Частотные зависимости коэффициентов отражения по энергии R представлены на рис. 2. Сплошная линия соответствует результатам вычислений матричным методом (в первом приближении), штриховая получена с помощью уравнений геометрической оптики. При выбранных значениях поперечного волнового вектора и области решения волны с частотой ниже $ \leqslant {\kern 1pt} 2.1$ кГц не распространяются, и коэффициент отражения близок к нулю. Значения коэффициентов отражения, полученные для более высоких частот матричным алгоритмом, несколько ниже, чем аналогичные значения, вычисленные в приближении геометрической оптики. Это может быть связано с тем, что при вычислениях матричным алгоритмом учитывается слабый в плавно неоднородной ионосфере эффект линейной трансформации мод и, как следствие, “перекачка” части энергии распространяющихся мод в нераспространяющиеся. В соответствии с оценками (32), эффект линейной трансформации сильнее при более низких частотах свистовых волны. Поэтому с ростом частоты зависимости, полученные разными методами, становятся практически одинаковыми.
6. ОБСУЖДЕНИЕ И ВЫВОДЫ
Рассмотрена задача о распространении электромагнитной волны в плоскослоистой неоднородной холодной магнитоактивной плазме. Математически задача сводится к решению системы линейных однородных дифференциальных уравнений первого порядка для четырех поперечных компонент поля волны. Продольные компоненты поля волны выражаются через ее поперечные компоненты. Предложен приближенный алгоритм решения волновых уравнений в произвольном случае наклонного падения. Суть алгоритма заключается в последовательном нахождении обусловленных неоднородностью среды поправок к локальным корням дисперсионного соотношения и локальным векторам поляризации. При этом система дифференциальных уравнений сводится к системе алгебраических уравнений, что существенно упрощает как аналитическое, так и численное рассмотрения. Отметим, что предложенный алгоритм удобен прежде всего для проведения численных расчетов. В частности, переход от дифференциальных уравнений к алгебраическим позволяет избежать проблемы численной расходимости решений из-за больших декрементов затухания нераспространяющихся мод.
Выяснены условия применимости алгоритма. По проведенным оценкам, роль малого параметра в полученной системе рекурентных уравнений играет величина ${{\left| {\Delta \kappa } \right|\Delta z} \mathord{\left/ {\vphantom {{\left| {\Delta \kappa } \right|\Delta z} {\left( {{{{\left| {\Delta \kappa } \right|}}^{2}}\Delta {{z}^{2}} + {{{\left| {\kappa {\text{/}}\Delta \kappa } \right|}}^{2}}} \right)}}} \right. \kern-0em} {\left( {{{{\left| {\Delta \kappa } \right|}}^{2}}\Delta {{z}^{2}} + {{{\left| {\kappa {\text{/}}\Delta \kappa } \right|}}^{2}}} \right)}}$, где κ – характерное значение вертикальной проекции волнового вектора. Алгоритм эффективен, таким образом, если выполнено неравенство $\left| {\Delta \kappa } \right|\Delta z \ll {{\left| {\Delta \kappa } \right|}^{2}}\Delta {{z}^{2}} + {{\left| {\kappa {\text{/}}\Delta \kappa } \right|}^{2}}$. В частности, это неравенство выполняется в случае слабо неоднородной плазмы, т.е. если длины волн распространяющихся мод и декременты затухания нераспространяющихся мод малы по сравнению с масштабом плазменной неоднородности, и все локальные корни дисперсионного соотношения существенно различны $\left( {\left| {\Delta \kappa } \right|\Delta z \gg 1} \right)$. Отмеченные требования аналогичны условиям применимости приближения геометрической оптики. Показано, что при подходящем выборе условия нормировки для векторов поляризации нулевое приближение может давать такой же результат, что и геометрическая оптика. Поправки к локальным корням дисперсионного соотношения в слабо неоднородной среде имеют порядок ${{\left( {\left| {\Delta \kappa } \right|\Delta z} \right)}^{{ - 1}}}$или, в зависимости от выбора нормировки, ${{\left( {\left| {\Delta \kappa } \right|\Delta z} \right)}^{{ - 2}}}$. Коэффициенты связи, характеризующие эффект линейного взаимодействия мод, и соответственно поправки к локальным векторам поляризации имеют квадратичный по малому параметру порядок малости ${{\left( {\left| {\Delta \kappa } \right|\Delta z} \right)}^{{ - 2}}}$. В отличие от геометрооптического подхода, в рассмотренном методе учитываются вклад в поле волны всех четырех мод, в том числе нераспространяющихся, и слабый (в плавно неоднородной среде) эффект их линейного взаимодействия.
Алгоритм может применяться также в другом предельном случае сильно неоднородной плазмы. Эффект линейного взаимодействия мод в этом случае не является слабым, коэффициенты связи существенно превышают локальные корни дисперсионного соотношения. Алгоритм не эффективен в области, где изменяется характер распространения какой-либо из мод поля, в частности, в зоне отражения, либо в зоне трансформации волн в вакуумные электромагнитные. В этом случае необходимо точное решение системы волновых уравнений.
В качестве примера использования матричного алгоритма рассмотрена задача об отражении плоской монохроматической волны от слоя неоднородной плазмы. Получены (в Приложении) общие выражения, связывающие коэффициенты отражения волны на нижней и верхней границах слоя. Приведено аналитическое выражение для коэффициента отражения по амплитуде от слоя изотропной неоднородной плазмы при нормальном падении волны. В случае слабо неоднородной среды ${{n{\text{'}}с } \mathord{\left/ {\vphantom {{n{\text{'}}с } {{{n}^{2}}\omega }}} \right. \kern-0em} {{{n}^{2}}\omega }} \ll 1$, где n – показатель преломления, полученное выражение с точностью до малых величин порядка ${{\left( {1{\text{/}}\kappa \Delta z} \right)}^{2}}$, $\kappa = n\omega {\text{/}}c$ совпадает с известной приближенной формулой для случая слабого отражения [1, 2]. В другом предельном случае сильно неоднородной среды ${{n{\text{'}}с } \mathord{\left/ {\vphantom {{n{\text{'}}с } {{{n}^{2}}\omega }}} \right. \kern-0em} {{{n}^{2}}\omega }} \gg 1$ полученное выражение переходит в формулу Френеля.
Приведены примеры численных расчетов для коэффициента отражения по энергии свистовых волн, падающих на ионосферу сверху. Для расчетов были использованы высотные профили плазменной концентрации и частот столкновений электронов и ионов с нейтральными частицами, соответствующие типичным дневным условиям среднеширотной ионосферы. Область решения составляла от 120 до 800 км от поверхности Земли. Рассматривалось отражение сверху волн с частотами f от 1.5 до 10 кГц и с поперечной компонентой волнового вектора ${{k}_{ \bot }} = {\text{1}}{\text{.5}}$ км–1. При таком выборе диапазона частот f и значений ${{k}_{ \bot }}$ волны не доходят до земной поверхности, и для примера расчетов коэффициент отражения от нижней границы слоя принимался за единицу. Вычисления проводились матричным алгоритмом и с помощью формул геометрической оптики. Сравнение результатов показывает, что в первом случае значения коэффициента отражения оказываются несколько ниже. Это, вероятно, связано с эффектом линейной трансформации волн, при котором часть энергии перекачивается от распространяющихся мод к нераспространяющимся. С ростом частоты эффект линейной трансформации уменьшается, и коэффициенты отражения, полученные разными методами, становятся практически одинаковыми. Отметим, что для нахождения волновых полей и коэффициентов отражения в реальных ионосферных условиях эффективно комбинировать приближенный матричный формализм и полноволновой подход. Это позволит, с одной стороны, учесть сильную неоднородность плазменных параметров на высотах порядка ~100 км и ниже, с другой – получить численно стабильное решение волновых уравнений в протяженном слое ионосферы вплоть до ее верхней границы [11].
Принцип приближенного решения волновых уравнений рассмотрен для случая холодной магнитоактивной плазмы, однако полученный метод может быть обобщен на случай произвольной плоскослоистой анизотропной среды. В частности, матричный алгоритм поправок может быть полезен для численных расчетов коэффициентов отражения, коэффициентов линейной трансформации волн в плавно неоднородной ионосфере.
Список литературы
Гинзбург В.Л. Распространение электромагнитных волн в плазме. М.: Наука, 1967.
Бреховских Л.М. Волны в слоистых средах. Изд-во АН СССР, 1957.
Wait J.R. Electromagnetic waves in stratified media. 2nd ed. New York: Pergamon, 1970.
Budden K.G. The propagation of radio waves. Cambridge–London–New York: Cambridge Univ. Press, 1985.
Lehtinen N.G., Inan U.S. // J. Geophys. Res. 2008. V. 113. P. A06301.
Кузичев И.В., Шкляр Д.Р. // Физика плазмы. 2013. Т. 39. С. 891.
Лаптухов А.И., Чернов Г.П. // Физика плазмы. 2012. Т. 38. С. 613.
Лебедев Н.В., Руденко В.В. // Физика плазмы. 2015. Т. 41. С. 554.
Pitteway M.L.V., Jespersen J.L. // J. Atmos. Solar Terr. Phys. 1966. V. 28. P. 17.
Nygre’n T. // Planet. Space Sci. 1982. V. 30. P. 427.
Bespalov P.A., Mizonova V.G., Savina O.N. // J. Atmos. Solar Terr. Phys. 2018. V. 175. P. 40.
Фреман Н., Фреман П.У. ВКБ-приближение. М.: Мир, 1967.
Shklyar D.R., Parrot M., Titova E.E. // J. Geophys. Res. 2018. V. 123. P. 7077.
Bilitza D., Reinisch B. // Adv. Space Res. 2008. V. 42. P. 599.
Дополнительные материалы отсутствуют.


