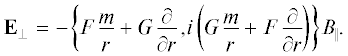Физика плазмы, 2019, T. 45, № 8, стр. 695-707
К теории ИЦР-нагрева по методу “магнитного берега”
А. В. Тимофеев a, *, Е. Д. Господчиков b, **
a Национальный исследовательский центр “Курчатовский институт”
Москва, Россия
b Институт прикладной физики РАН
Нижний Новгород, Россия
* E-mail: Timofeev_AV@nrcki.ru
** E-mail: egos@appl.sci-nnov.ru
Поступила в редакцию 12.03.2019
После доработки 25.03.2019
Принята к публикации 25.03.2019
Аннотация
В настоящее время интерес к ИЦР-нагреву по методу “магнитного берега” связан с экспериментами, проводимыми на космическом плазменном двигателе VASIMR. Данный метод предполагает возбуждение вне зоны ИЦР собственных альфвеновских колебаний плазменного столба или струи плазмы в случае двигателя. В настоящей работе показано, что при определенных условиях, которые характерны, например, для плазменных двигателей, основная часть электромагнитной энергии, закачиваемой в плазму, может перейти не к дискретному спектру собственных альфвеновских колебаний, а к непрерывному, образующему т.н. альфвеновский континуум. Вследствие явления альфвеновского резонанса колебания непрерывного спектра трансформируются в коротковолновые, отличающиеся от альфвеновских своей поляризацией (нижнегибридные). Эти колебания активно взаимодействуют с электронами, что вызывает их нагрев.
1. ВВЕДЕНИЕ
ИЦР-нагрев по методу “магнитного берега” предназначен для плазмы в магнитном поле, величина которого меняется в направлении вдоль поля [1]. Электромагнитные колебания левой циркулярной поляризации, электрический вектор которых вращается в ионную сторону (альфвеновские колебания, АК), должны возбуждаться в области сильного магнитного поля, превышающего резонансное значение. При приближении колебаний к зоне ИЦР их волновой вектор резко возрастает, фазовая и групповая скорости стремятся к нулю – колебания “останавливаются”. Поэтому, какова бы ни была интенсивность диссипативных процессов, колебания, в конце концов, поглотятся – отражение от зоны ИЦР отсутствует. Конфигурация магнитного поля, необходимая для “магнитного берега”, имеется в ряде космических плазменных двигателей. Однако ИЦР-нагрев для создания тяги используется лишь в двигателе VASIMR [2], причем способ нагрева нельзя отнести к “магнитному берегу”. Действительно, в VASIMR возбуждение электромагнитных колебаний происходит практически в зоне ИЦР, в то время как при нагреве по методу “магнитного берега” они должны возбуждаться вдали от этой зоны, на расстоянии, существенно превышающем длину волны. Хотя в настоящее время “магнитный берег” не нашел практического применения, возможность эффективного нагрева ионов, обещаемая этим методом, оправдывает его изучение.
В работе [3], которая, по-видимому, оказала большое влияние на концепцию двигателя -VASIMR, нагрев по методу магнитного берега рассматривался в одномерном приближении: учитывалась зависимость как основного магнитного поля, так и электромагнитного поля колебаний лишь от координаты вдоль основного поля. В линейном приближении по амплитуде колебаний был подтвержден вывод об их полном поглощении в зоне ИЦР. Было также показано, что нелинейные процессы могут приводить к частичному отражению от этой зоны. В [4] при анализе нагрева коротковолновыми – “квазиклассическими” – электромагнитными колебаниями принимались во внимание как продольная неоднородность магнитного поля, так и поперечная неоднородность плотности плазмы. Было найдено, что область локализации собственных АК при подходе к зоне ИЦР стягивается к центру плазменного шнура. При этом область непрозрачности, граничащая с вакуумом, расширяется. Это является одной из причин, вынуждающих возбуждать электромагнитные колебания вдали от зоны ИЦР. В [4] был также сделан вывод об одновременном возбуждении ВЧ-антенной не только АК, требуемых для реализации “магнитного берега”, но и нижнегибридных колебаний (НГК)11. Последние порождаются особенно интенсивно в результате явления альфвеновского резонанса (АР), см., например, [7]. АР возникает при локальном выполнении условия $\omega {\text{/}}{{k}_{{||}}} = {{V}_{A}}{{\left( {1 - {{{\left( {{\omega /}{{{\omega }}_{i}}} \right)}}^{2}}} \right)}^{{1/2}}}{\;}$, где $\quad{{V}_{A}} = B{\text{/}}{{\left( {4{\pi \rho }} \right)}^{{1/2}}}$ – альфвеновская скорость, ${{{\omega }}_{i}}$ ${\;}$ – ионная циклотронная частота, значок “параллельно” отмечает компоненту вектора вдоль основного магнитного поля.
В АК продольная компонента электрического поля мала, поэтому при их описании часто используется приближение ${{E}_{{||}}} = 0$. В этом приближении в области альфвеновского резонаса АК испытывают сильное поглощение и, как следствие, образуют т.н. альфвеновский континуум. Более полное описание с учетом ${{E}_{{||}}} \ne 0$ показывает, что при АР альфвеновские колебания трансформируются в нижнегибридные. В последних существенна продольная компонента электрического поля, поэтому они активно взаимодействуют с электронами, отдавая им свою энергию. В результате ВЧ-антенна может вкладывать энергию не в ионную компоненту плазмы в области ИЦР, а в электронную в области АР. Об этом свидетельствуют результаты работ [8, 9], где, как и в [3], использовалось одномерное приближение, однако учитывалась не продольная, а поперечная (радиальная) неоднородность плазмы.
Чтобы включить в рассмотрение как ИЦР, так и АР, необходимо наряду с продольной неоднородностью магнитного поля учесть и поперечную неоднородность плотности плазмы. Таким образом, последовательный анализ ИЦР-нагрева по методу магнитного берега должен быть двумерным. Однако в силу вытянутости плазменных шнуров вдоль магнитного поля возможны условия, при которых продольная неоднородность системы может учитываться параметрически, и для описания зависимости колебаний от продольной координаты может использоваться квазиклассическое приближение. Такой подход принят в настоящей работе при анализе собственных АК плазменного шнура, см. также [4]. Найдено, что при реальных значениях параметров, характерных для современных плазменных двигателей, на возбуждение собственных АК будет затрачиваться далеко не вся энергия, закачиваемая антенной в плазму. Ее значительную часть будет потреблять альфвеновский континуум. Альфвеновскому континууму соответствует непрерывный спектр упрощенного, за счет приближения ${{E}_{{||}}} = 0$, уравнения АК. Такой подход позволяет адекватно проанализировать собственные АК, и при определенных условиях в его рамках можно описать явление АР.
2. CОБСТВЕННЫЕ КОЛЕБАНИЯ
Согласно концепции “магнитного берега” АК, набегающие на зону ИЦР, полностью поглощаются. При использовании этого метода нагрева основная задача состоит в возбуждении собственных АК неоднородного столба плазмы. Чтобы составить представление об особенностях этого процесса, полезно $\quad$рассмотреть радиальную зависимость их поперечного показателя преломления (${{N}_{ \bot }} = {{k}_{ \bot }}c{\text{/}}\omega $) в неоднородном плазменном шнуре, находящемся в продольном магнитном поле. Полагая ${{E}_{z}} = 0$, для колебаний, характерная длина волны которых мала по сравнению с пространственными масштабами системы, в квазиклассическом приближении имеем, см., например, [5, 7],
(1)
$N_{ \bot }^{2} = \frac{{\left( {{{\varepsilon }_{{ - \quad}}} - N_{{||}}^{2}} \right)\quad\left( {{{\varepsilon }_{ + }} - N_{{||}}^{2}} \right)}}{{\left( {{{\varepsilon }_{ \bot }} - N_{{||}}^{2}} \right)}}$ ,Поперечный показатель преломления обращается в бесконечность при выполнении условия АР $N_{{||}}^{2} = {{\varepsilon }_{ \bot }}$. Точка АР является особой для дифференциального уравнения АК. Для регуляризации этого уравнения и (1) можно использовать правило обхода Ландау. Аналогичный результат достигается с учетом трения между ионами и нейтральными атомами, которые в малой концентрации обычно присутствуют в плазме. С этой целью в выражении для ${{\varepsilon }_{ \pm }}$ следует произвести замену $\omega \to \omega + i{{\nu }_{i}}$, где ${{\nu }_{i}}$ – частота соударений ионов с нейтралами; в дальнейшем считается ${{\nu }_{i}}{\text{/}}\omega = {{10}^{{ - 3}}}$.
Для определенности примем следующую зависимость концентрации плазмы от радиуса:
(2)
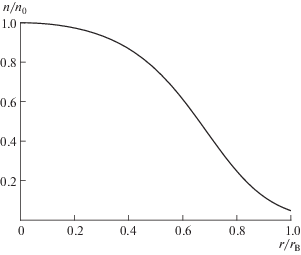
$n(r) = \left\{ \begin{gathered} {{n}_{0}}\left( {1 - {\text{th}}\left( {\frac{{{{r}^{2}} - r_{0}^{2}}}{{2{{r}_{0}}\Delta r}}} \right)} \right){{\left( {1 + {\text{th}}\left( {\frac{{{{r}_{0}}}}{{2\Delta {{r}_{0}}}}} \right)} \right)}^{{ - 1}}} \hfill \\ {\text{п р и }}\quad r < {{r}_{B}} \hfill \\ 0\quad {\text{п р и }}\quad r > {{r}_{B}}. \hfill \\ \end{gathered} \right.$В соответствии со стандартным способом организации эксперимента по ВЧ-нагреву плазмы в (2) считается, что в области $r = {{r}_{B}}$ расположена тонкая диэлектрическая стенка вакуумной камеры, на которой плотность плазмы испытывает скачок. Распределение (2) показано на рис. 1. При расчетах принималось ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{r} }_{B}} = 8$ см, ${{\hat {r}}_{0}} = 5{\;}$ см, $\Delta {{\hat {r}}_{0}} = 2.5$ см. Считалось, что ВЧ-антенна расположена при ${{\hat {r}}_{A}}$ = 8.5 см. Магнитное поле в месте нахождения антенны полагалось равным $B = $ = 3.3 кГс, частота ВЧ-поля $\omega = 1.25 \times {{10}^{7}}$ с–1. Величины размерности длины отмечены значком $\widehat {}$,чтобы отличать от безразмерных “длин”, используемых ниже ($r\omega {\text{/}}c \to r$). В случае, если параметры расчета отличаются от приведенных, их значения указываются в тексте или в подписи к рисунку, иллюстрирующему расчет.
Согласно (1) имеется две области прозрачности. Плазма прозрачна для АК при ${{\varepsilon }_{ \bot }}(r) < N_{{||}}^{2} < {{\varepsilon }_{ + }}(r)$ и для магнитозвуковых колебаний при ${{\varepsilon }_{ - }}\left( r \right) > N_{{||}}^{2}$, см. рис. 2. На части левой границы области прозрачности АК $\left( {N_{{||}}^{2} = {{\varepsilon }_{ \bot }}(r)} \right)$ их поперечный показатель преломления обращается в бесконечность – колебания испытывают АР, приводящий к интенсивному поглощению. Соответствующий интервал значений ${{N}_{{||}}}$ – $\varepsilon _{ \bot }^{{1/2}}\left( 0 \right) > N_{{||}}^{{}} > \varepsilon _{ \bot }^{{1/2}}\left( {{{r}_{B}}} \right)$ называют альфвеновским континуумом. Если в столбе плазмы существуют собственные АК, то их продольный показатель преломления должен лежать в области значений $N_{{||}}^{{}}$, исключающих АР $\left( {N_{{||}}^{2} > {{\varepsilon }_{ \bot }}\left( 0 \right)} \right)$.
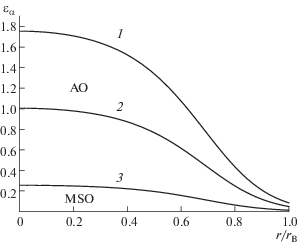
Рис. 2.
Области прозрачности альфвеновских ${{\varepsilon }_{ \bot }}(r) < N_{{||}}^{2} < {{\varepsilon }_{ + }}(r)$ и магнитозвуковых $N_{{||}}^{2} < {{\varepsilon }_{ - }}(r)$ $\quad$колебаний, $\alpha = + , \bot , - $. Кривая 1 – ${{\varepsilon }_{ + }}(r)$, 2 – ${{\varepsilon }_{ \bot }}(r),$ 3 – ${{\varepsilon }_{ - }}(r)$. ${{r}_{B}}$ – граница плазмы. ${{\omega }_{i}}{\text{/}}\omega $ = 1.26, ${{\omega }_{{pi}}} \gg \omega $$.$ AO – альфвеновские колебания, MSO – магнитозвуковые колебания.
В АК и МЗК продольная компонента электрического поля мала. В приближении ${{E}_{{||}}} = 0$ колебания аксиально- и азимутально-симметричного плазменного шнура описываются уравнением [4]
(3)
$\begin{gathered} \frac{1}{r}\frac{d}{{dr}}rF\frac{{d{{B}_{{||}}}}}{{dr}} - {{\left( {\frac{m}{r}} \right)}^{2}}F{{B}_{{||}}} + \frac{m}{r}\frac{{dG}}{{dr}}{{B}_{{||}}} + {{B}_{{||}}} = \\ = \;\frac{{4\pi }}{\omega }\frac{1}{{N_{{||}}^{2} - 1}}\frac{1}{r}\frac{d}{{dr}}r{{j}_{\theta }}\quad, \\ \end{gathered} $Однородное уравнение (3) используется в настоящей работе также для описания коротковолновых – квазиклассических – собственных АК, возбуждаемых при нагреве плазмы по методу “магнитного берега”. В этом случае в (3) продольный показатель преломления и величины $F,G$ параметрически зависят от координаты z, а возмущение продольного магнитного поля имеет вид ${{B}_{{||}}}\left( {{\mathbf{r}},t} \right) = b\left( r \right)f\left( z \right)$${\text{exp}}\left( {i\left( {m\theta + \int_{}^z {dz{{N}_{{||}}}} \left( z \right) - \omega t} \right)} \right)$. Амплитуда таких колебаний $f\left( z \right)$ находится с помощью уравнения баланса энергии, см. ниже.
Величины $F,G$, входящие в (3), удобно представить в виде [10]
Для этих величин справедливы соотношения
(4)
$\frac{{dF}}{{dN_{{||}}^{2}}} = {{F}^{2}} + {{G}^{2}},\quad\quad \frac{{dG}}{{dN_{{||}}^{2}}} = 2FG,$Хотя в антеннах, применяемых для ИЦР-нагрева, циркулируют как токи ${{j}_{\theta }}$, так и ${{j}_{z}}$, с АК в силу малой величины их продольного электрического поля взаимодействует преимущественно азимутальная компонента тока, что учтено в (3). Также учтено, что ВЧ-антенны располагаются вне плазмы. Рассматривается наиболее распространенная полуволновая винтовая антенна и используется аналитическая модель винтовых антенн, предложенная в [11]. В этой модели
(5)
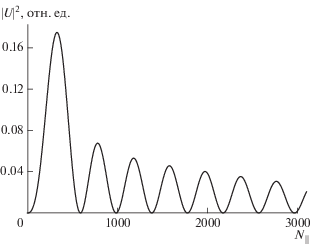
${{j}_{\theta }}\left( {r,z} \right) = \delta \left( {r - {{r}_{A}}} \right)V\left( {z;{{\theta }_{A}},{{L}_{A}},\alpha } \right),$Рис. 3.
Распределение тока в антенне по ${{N}_{{||}}}$ $\quad\left( {{{j}_{\theta }} \propto U} \right)$. $m = - 1$.
Электрическое поле колебаний выражается через магнитное:
В области $r > {{r}_{B}}$ для θ-компоненты электрического поля справедливо выражение
где при ${{r}_{B}} < r < {{r}_{A}}$ величина ${{B}_{{||}}}({\mathbf{r}},t) \sim b(r) = $ $ = {{C}_{1}}{{I}_{m}}(\rho ) + {{C}_{2}}{{K}_{m}}(\rho )$, и при ${{r}_{A}} < r$ – $b(r) = {{C}_{3}}{{K}_{m}}(\rho ),\quad$ ${{I}_{m}}$ – функция Бесселя мнимого аргумента, ${{K}_{m}}$ – функция Мак-Дональда, $\rho = r\sqrt {N_{{||}}^{2} - 1} $. Зависимость $b\left( r \right)$ в области плазмы $0 \leqslant r \leqslant {{r}_{B}}$ находится из решения однородного уравнения (3) при условиях непрерывности возмущений продольного магнитного поля и азимутальной компоненты электрического на границе плазмы с вакуумом.Чтобы проиллюстрировать существование как альфвеновского континуума, так и собственных АК, можно использовать зависимость энергии, закачиваемой ВЧ-антенной в плазму, от продольного показателя преломления $N_{{||}}^{{}}$ в простейшем случае однородного магнитного поля, рис. 4. На рисунке непрерывный спектр альфвеновского континуума занимает область $\varepsilon _{ \bot }^{{1/2}}\left( 0 \right) > N_{{||}}^{{}} > \varepsilon _{ \bot }^{{1/2}}\left( {{{r}_{B}}} \right),$ см. выше, а собственные АК выделяются в виде пиков. (Подробности – в следующем разделе.)
Рис. 4.
Распределение мощности, затрачиваемой антенной при ${{j}_{\theta }}\left( {{{N}_{{||}}}} \right) = {\text{const}}$. Плазма дейтерия, $m = $ –1. а) – ${{n}_{0}} = 3 \times {{10}^{{12}}}$ см–3, б) – $\quad{{n}_{0}} = 3 \times {{10}^{{13}}}$ см–3, в) – ${{n}_{0}} = 3 \times {{10}^{{14}}}$ см–3.
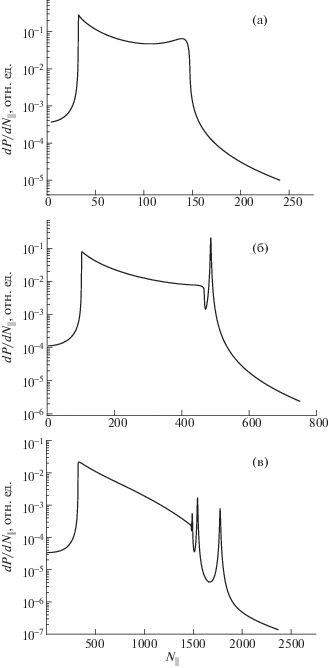
Рост амплитуды колебаний непрерывного спектра с уменьшением ${{N}_{{||}}}$ обусловлен двумя факторами. Во-первых, сокращается расстояние от ВЧ-антенны до области прозрачности АК, рис. 2. Во-вторых, сказывается индукционная природа электрических полей, генерируемых токовой антенной, что отражено в формулах (6), (7).
Рис. 4 получен при ${{j}_{\theta }}\left( {{{N}_{{||}}}} \right) = {\text{const}}.$ Он характеризует свойства плазмы как среды, поддерживающей АК. При их возбуждении реальной токовой антенной на зависимость спектральной плотности мощности, вкладываемой в плазму $dP{\text{/}}d{{N}_{{||}}}$, от ${{N}_{{||}}}$ влияет также геометрия антенны, определяющая распределение ${{j}_{\theta }}\left( {{{N}_{{||}}}} \right)$. Учет этого распределения модифицирует зависимости, показанные на рис. 4, см. рис. 5. Распределение ${{j}_{\theta }}\left( {{{N}_{{||}}}} \right)$ осциллирует, проходя через нулевое значение, рис. 4, что отражается на зависимости $dP{\text{/}}d{{N}_{{||}}}$ от ${{N}_{{||}}}$ на рис. 5.
Собственные моды исследовались с помощью однородного уравнения (3). В области $r > {{r}_{B}}$ полагалось $b\left( r \right) \propto {{K}_{m}}\left( \rho \right)$. Находился набор собственных значений $N_{{||;m,n}}^{\quad}\quad\left( {n = 0,1,2, \ldots } \right)\quad$, при которых однородное уравнение (3) имеет нетривиальное решение. Как следует из рис. 4, число собственных АК увеличивается с ростом плотности плазмы. Для каждой собственной моды имеется критическое значение плотности плазмы, ниже которого эта мода не существует. Зависимость собственных значений ${{N}_{{||,m,n}}}$ от концентрации плазмы на оси системы показывает, что на пороге возникновения моды собственное значение $N_{{||;m,n}}^{\quad}\quad\left( {n = 0,1,2, \ldots } \right)\quad$ близко к ${{N}_{{||,c\quad}}} = \varepsilon _{ \bot }^{{1/2}}\quad\left( 0 \right)\quad$. Приближенное равенство $N_{{||;m,n}}^{\quad} \approx {{N}_{{||,c\quad}}}$ сохраняется при небольшом превышении плотностью критического значения. Однако при дальнейшем росте плотности зависимость $N_{{||;m,n}}^{\quad}\left( {{{n}_{0}}} \right)\quad$ уходит в область значений, заметно больших ${{N}_{{||,c}}}\left( {{{n}_{0}}} \right)$. При этом ее место у кривой ${{N}_{{||,c}}}\left( {{{n}_{0}}} \right)$ занимает кривая $N_{{||;m,n + 1\quad}}^{\quad}\left( {{{n}_{0}}} \right)$ и т.д. В результате на рис. 6 зависимость ${{N}_{{||,c}}}\left( {{{n}_{0}}} \right)$ оказывается неотличимой от совокупности начальных участков кривых ${{N}_{{||;m,n}}}\left( {{{n}_{0}}} \right)$.
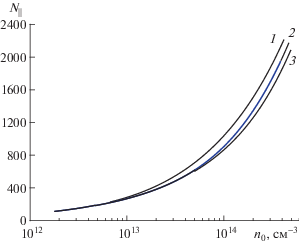
Рис. 6.
Зависимость собственных значений ${{N}_{{||}}}$ от плотности плазмы. $m = - 1.$ Кривая 1 – $n = 0$, 2 – $n = 1,$ 3 – n = 2.
Оценим по порядку величины плотность плазмы, при которой возникают собственные АК. Из квазиклассического дисперсионного соотношения (1) следует, что при ${{N}_{{||\quad}}} = \varepsilon _{ \bot }^{{1/2}}\quad\left( 0 \right)$ справедливо приближенное равенство ${{N}_{{||}}} \approx N_{ \bot }^{{}}.$ Характерный радиальный масштаб собственных АК не может превышать ${{r}_{0}}$, поэтому должно выполняться условие ${{r}_{0}}{{N}_{{||}}} \geqslant 1\quad$, из которого следует ${{\left( {\frac{{{{\omega }_{{pi}}}}}{{{{\omega }_{i}}}}r_{0}^{{}}} \right)}^{2}} \geqslant \frac{{\Delta {{\omega }_{i}}}}{{{{\omega }_{i}}}}$, где $\quad\Delta {{\omega }_{i}} = {{\omega }_{i}} - \omega .$
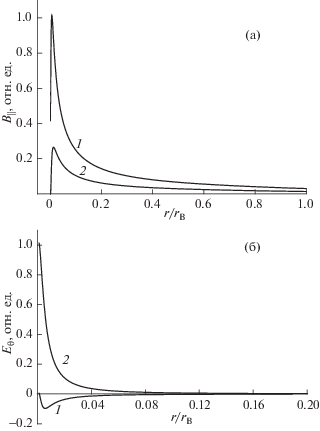
В настоящей работе радиальные собственные моды нумеруются по числу нулей зависимости ${{E}_{\theta }}\left( r \right)$, рис. 7а. У мод, рассматриваемых нами, с номером n совпадает число нулей функции ${{B}_{{||}}}\left( r \right)$, рис. 7б. Исключение составляет лишь мода $m = 1,\quad\;n = 0$, в которой функция ${{B}_{{||}}}\left( r \right)$ меняет знак в приграничной области. Заметим, что на рис. 7 не отображены радиальные зависимости Re${{E}_{\theta }}\left( r \right)$ и ${\text{Im}}{{B}_{{||}}}\left( r \right)$, которые пренебрежимо малы для собственных АК в плазме с малой диссипацией, см., однако, ниже.
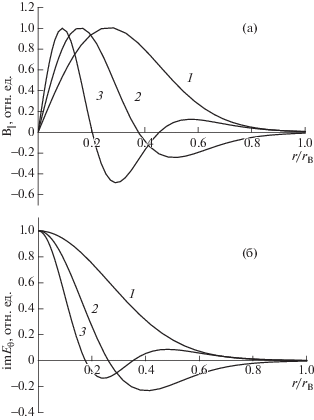
Рис. 7.
Радиальные профили электромагнитных полей собственных АК при $\quad{{n}_{0}} = 2 \times {{10}^{{14}}}$ см–3, $m = $ –1. Кривая 1 – $n = 0,$ ${{N}_{{||}}} = 1508;$ 2 – $n = 1,\quad$ ${{N}_{{||}}} = 1346;$ 3 – $n = 2,\quad$ ${{N}_{{||}}} = 1263$. а) – ${{B}_{{||}}}$; б) – ${\text{Im}}{{E}_{\theta }}$.
Собственные значения $N_{{||,k}}^{\quad}$ зависят не только от плотности, но и от магнитного поля, поэтому они меняются по мере приближения АК к зоне ИЦР. При совпадении с каким-то значением ${{N}_{{||}}}$ из широкого спектра ВЧ-полей антенны возможно возбуждение собственных колебаний. Для анализа этого процесса можно использовать уравнение баланса энергии (альтернативный вывод уравнения для амплитуды собственных АК изложен в Приложении)
где $S = \frac{\omega }{{4\pi }}{{N}_{{||}}}\int {rdr{{{\left| {{{E}_{ \bot }}} \right|}}^{2}}} $ = $\frac{\omega }{{4\pi }}{{N}_{{||}}}{{\left| {f\left( z \right)} \right|}^{2}}Q$, $Q = $ ${\kern 1pt} \int {rdr} {\kern 1pt} \left( {\left( {{{{\left| {\frac{{db}}{{dr}}} \right|}}^{2}}{\kern 1pt} + \,{{{\left| {\frac{m}{r}{\kern 1pt} b} \right|}}^{2}}\quad} \right){\kern 1pt} ({{F}^{2}}{\kern 1pt} + \,{{G}^{2}})} \right.\,\left. { + \,2{\kern 1pt} \frac{m}{r}{\kern 1pt} \left( {{{b}^{*}}{\kern 1pt} \frac{{db}}{{dr}}{\kern 1pt} + {\kern 1pt} b{\kern 1pt} \frac{{d{{b}^{*}}}}{{dr}}} \right){\kern 1pt} FG} \right){\kern 1pt} .$Напомним, что в работе используются безразмерные координаты, см. выше. Рассматривается одна из собственных мод, индексы n – радиальное волновое число и m – азимутальное для краткости опущены. Возмущение продольного магнитного поля берется в квазиклассическом виде, см. выше.Используя уравнение (8), получаем
(9)
$\begin{gathered} \frac{d}{{dz}}f = A{\text{exp}}\left( { - i\mathop \smallint \limits_{}^z dz{{N}_{{||}}}\left( z \right)} \right)\int {d{{N}_{{||,1}}}} \times \\ \times \;{\text{exp}}\left( {i{{N}_{{||,1}}}z} \right)U\left( {{{N}_{{||1}}};{{\theta }_{A}},{{L}_{A}},\alpha } \right). \\ \end{gathered} $Здесь введено обозначение A = $ = \frac{{{{r}_{A}}}}{{2\pi mQ\left( {N_{{||}}^{2} - 1} \right){{N}_{{||}}}}}\frac{{{{L}_{A}}}}{{\delta {{L}_{A}}}}{{\left. {\frac{{db}}{{dr}}} \right|}_{{r = {{r}_{A}}}}}\frac{\omega }{{{{c}^{2}}}}I.$
Нагрев методом магнитного берега должен производиться с помощью собственных АК, которые полностью поглощаются в зоне ИЦР. Их амплитуда определяется взаимодействием с током антенны. Ее конечное значение после прохождения области взаимодействия дается выражением ${{f}_{1}} = \mathop \smallint \limits_{ - \infty }^\infty dz\frac{d}{{dz}}f$. При плавном изменении магнитного поля, а вместе с ним и ${{N}_{{||}}}\left( z \right)$, интеграл, входящий в это выражение, может быть вычислен методом стационарной фазы. Он определяется окрестностью точки ${{z}_{S}}$, в которой ${{N}_{{||}}}\left( {{{z}_{S}}} \right) = {{N}_{{||,1}}}$,
(10)
$\begin{gathered} {{f}_{1}} = \left( {\frac{1}{{2\pi i}}\frac{{d{{N}_{{||}}}}}{{dz}}} \right)_{{z = {{z}_{S}}}}^{{ - \frac{1}{2}}}\int {d{{N}_{{||,1}}}A} \times \\ \times \;{\text{exp}}\left( {i{{N}_{{||,1}}}{{z}_{S}}\quad - i\mathop \smallint \limits_{}^{{{z}_{S}}} dz{{N}_{{||}}}\left( z \right)} \right)U\left( {{{N}_{{||1}}};{{\theta }_{A}},{{L}_{A}},\alpha } \right). \\ \end{gathered} $Такая процедура использовалась в [12] при анализе возбуждения геликонов в плазме в неоднородном магнитном поле.
Интеграл по $d{{N}_{{||,1}}}$ в (10) также вычисляется методом стационарной фазы. Точки стационарной фазы определяются условиями ${{z}_{S}}\left( {{{N}_{{||,1,s}}}} \right) = \pm {{L}_{A}}, \pm \alpha {{L}_{A}}$. При слабой неоднородности магнитного поля $\left( {{{L}_{A}} \ll {{L}_{B}}} \right)$ можно положить ${{N}_{{||,1,s}}} \approx {{N}_{{||}}}\left( z \right){\kern 1pt} {{|}_{{z = 0}}}$,
(11)
${{f}_{1}} \approx 2\pi AU\left( {{{N}_{{||}}}\left( 0 \right);{{\theta }_{A}},{{L}_{A}},\alpha } \right){\text{exp}}\Phi ,$Одно и то же условие позволяет использовать метод стационарной фазы при интегрировании по $dz$ и по $d{{N}_{{||,1}}}$:
(12)
$\frac{{\omega _{{}}^{{3/2}}}}{{{{\omega }_{{pi}}}\Delta \omega _{{i0}}^{{1/2}}}} \ll {{L}_{B}},$Результативно оказывается, что собственные моды подпитываются антенной в области $\left| z \right| \leqslant {{L}_{A}}$. За ее пределами мощность, уносимая собственной модой с радиальным номером n и азимутальным m дается выражением
Данное соотношение позволяет найти сопротивление, вносимое плазмой в электрическую цепь антенны, $R = 2S{\text{/}}{{I}^{2}}$.
Винтовые антенны возбуждают колебания с нечетными азимутальными числами m. Рис. 8 показывает, что при умеренных значениях плотности плазмы основной модой, определяющей
сопротивление, является наиболее крупномасштабная мода $m = - 1,\quad\;n = 0$, бегущая по азимуту в ионную сторону. Ее доминирование по сравнению с модой 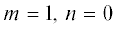 обусловлено влиянием дрейфа в скрещенных полях: постоянном магнитном и ВЧ азимутальном
электрическом. Дрейфовое движение учитывается в (3) слагаемым, пропорциональным
обусловлено влиянием дрейфа в скрещенных полях: постоянном магнитном и ВЧ азимутальном
электрическом. Дрейфовое движение учитывается в (3) слагаемым, пропорциональным 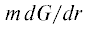 . Влияние дрейфа углубляет и расширяет эффективную потенциальную яму для АК. Она располагается
в центральной части плазменного столба, причем ее глубина в точке $r = 0$ неограниченно возрастает при ${{N}_{{||}}} \to \varepsilon _{ \bot }^{{1/2}}\left( 0 \right)$. Поэтому при критическом значении плотности плазмы, когда “яма” становится способной
удерживать АК, последние концентрируются к центру плазменного столба, см. рис. 9, что делает их связь с антенной довольно слабой, рис. 8.
. Влияние дрейфа углубляет и расширяет эффективную потенциальную яму для АК. Она располагается
в центральной части плазменного столба, причем ее глубина в точке $r = 0$ неограниченно возрастает при ${{N}_{{||}}} \to \varepsilon _{ \bot }^{{1/2}}\left( 0 \right)$. Поэтому при критическом значении плотности плазмы, когда “яма” становится способной
удерживать АК, последние концентрируются к центру плазменного столба, см. рис. 9, что делает их связь с антенной довольно слабой, рис. 8.
Рис. 8.
Зависимость “плазменной нагрузки” в цепи антенны, обусловленной возбуждением наиболее
крупномасштабных мод собственных АК, от плотности плазмы при ${{j}_{\theta }}\left( {{{N}_{{||}}}} \right) = {\text{const}}$. Кривая 1 – мода $m = - 1$, $n = 0$; 2 – $m = - 1$, $n = 1$; 3 – $m = 1\quad$, 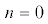 ; 4 – $m = - 3$, $n = 0$.
; 4 – $m = - 3$, $n = 0$.
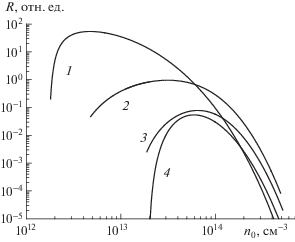
Рис. 9.
Радиальный профиль электромагнитных полей собственных АК при минимальном для существования основной моды $\left( {m = - 1,\quad\;n = 0\quad{\;}} \right)\quad$ значении плотности плазмы. ${{n}_{0}} = 1.8 \times {{10}^{{12}}}$ см–3, ${{N}_{{||}}} = 114.5$. а) – ${{B}_{{||}}}$ ; б) – ${\text{Im}}{{E}_{\theta }}$ (Re${{E}_{\theta }} = 0$).
Критическая плотность появления собственной моды определяется т.н. “условием падения на центр” [4]
Для основной моды АК m = –1 оно принимает вид
(13)
$\varepsilon _{ \bot }^{2}\left( 0 \right) = 2{{\left| {\frac{{d{{\varepsilon }_{ \bot }}}}{{d{{r}^{2}}}}} \right|}_{{r = 0}}}\frac{{{{\omega }_{i}}\Delta {{\omega }_{i}}}}{{{{\omega }^{2}}}}.$В режиме, близком к “падению на центр” (в рассматриваемом случае альфвеновскому резонансу в центре системы, см. ниже), даже слабое трение ионов о нейтралы оказывается существенным. Из-за его влияния действительные и мнимые части электромагнитных полей собственных АК оказываются сопоставимыми, ср. рис. 9 с рис. 7.
Рост плотности плазмы расширяет “яму”, усиливая связь с антенной. В результате “плазменная нагрузка” возрастает. Однако при существенном, на порядки величины, росте плотности плазмы определяющим становится возрастание собственных значений ${{N}_{{||}}}$, рис. 6. По этой причине ухудшается проникновение электромагнитных полей через барьер непрозрачности между антенной и областью, в которой могут распространяться АК. Одновременно в соответствии с (4), (5) уменьшается поперечное электрическое поле АК, посредством которого последние взаимодействуют с ВЧ-током антенны. Все это приводит к уменьшению “плазменной нагрузки”, см. рис. 8.
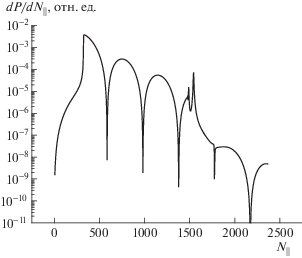
Рис. 10 иллюстрирует зависимость “плазменной нагрузки” в цепи антенны от плотности плазмы для основной моды АК $m = - 1$, $n = 0$. При расчете учитывалось распределение ${{j}_{\theta }}\left( {{{N}_{{||}}}} \right)$, см. (7). На фоне монотонного падения сопротивления с ростом плотности плазмы выделяется ряд резких провалов. Они происходят, когда собственное значение ${{N}_{{||}}}\left( {{{n}_{0}}} \right)$ проходит через нуль распределения ${{j}_{\theta }}\left( {{{N}_{{||}}}} \right)$.
Рис. 10.
Зависимость “плазменной нагрузки”, обусловленной возбуждением основной молы собственных
АК 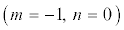 , от плотности плазмы.
, от плотности плазмы.
Для собственных значений ${{N}_{{||}}}$ справедливо приближенное равенство $N_{{||}}^{2} \approx \frac{{\omega _{{pi}}^{2}\left( 0 \right)}}{{{{\omega }_{i}}\Delta {{\omega }_{i}}}}$.
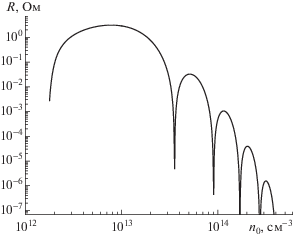
Согласно этому выражению увеличение (уменьшение) плотности плазмы оказывает на собственные АК такое же воздействие, как уменьшение (увеличение) ионной циклотронной частоты. Данная закономерность подтверждается рис. 11, который подобен зеркально отраженному рис. 10.
Рис. 11.
Зависимость “плазменной нагрузки”, обусловленной возбуждением основной молы собственных АК $\left( {m = - 1,\quad\;n = 0\quad{\;}} \right)$, от ионной циклотронной частоты в центре ВЧ-антенны. ${{n}_{0}} = 3.58 \times {{10}^{{13}}}$ см–3.
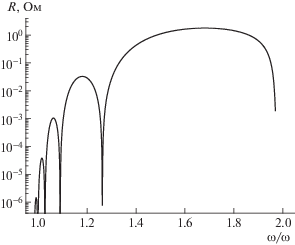
Приближение области возбуждения АК к зоне ИЦР (${{\omega }_{i}} \to \omega $) сопровождается увеличением собственных значений ${{N}_{{||}}}$. При этом, в подтверждение идеологии “магнитного берега”, эффективность возбуждения собственных АК падает. На другом краю области прозрачности максимальное значение ${{\omega }_{i}}$, как и минимальное значение плотности плазмы, определяется “условием падения на центр”, см. (13).
3. АЛЬФВЕНОВСКИЙ КОНТИНУУМ
АК, для которых при каком-то значении радиуса выполняется условие 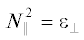 , испытывают альфвеновский резонанс, в окрестности которого они трансформируются в
нижнегибридные колебания. Если последние успевают поглотиться электронами за время
распространения от зоны АР до центра плазмы и обратно, то область значений продольной
фазовой скорости ${{V}_{{A\;\min }}} < \omega {\text{/}}{{k}_{{||}}} < {{V}_{{A\;\max }}}$ занимает непрерывный спектр возбуждения плазмы антенной – альфвеновский континуум.
АК с такими значениями продольной фазовой скорости в зоне АР полностью трансфрмируются
в НГК, отражение от этой зоны отсутствует.
, испытывают альфвеновский резонанс, в окрестности которого они трансформируются в
нижнегибридные колебания. Если последние успевают поглотиться электронами за время
распространения от зоны АР до центра плазмы и обратно, то область значений продольной
фазовой скорости ${{V}_{{A\;\min }}} < \omega {\text{/}}{{k}_{{||}}} < {{V}_{{A\;\max }}}$ занимает непрерывный спектр возбуждения плазмы антенной – альфвеновский континуум.
АК с такими значениями продольной фазовой скорости в зоне АР полностью трансфрмируются
в НГК, отражение от этой зоны отсутствует.
НГК характеризуются приближенным дисперсионным соотношением
(14)
$N_{ \bot }^{2} = {{\varepsilon }_{{||}}}\frac{{{{\varepsilon }_{ \bot }} - N_{{||}}^{2}}}{{{{\varepsilon }_{ \bot }}}},$Учитывая последнее соотношение, сводим условие существования альфвеновского континуума к виду
(15)
$\frac{{{{\omega }_{{pe}}}{{{\hat {r}}}_{0}}}}{c}{{\left( {\frac{\omega }{{{{k}_{{||}}}{{v}_{{Te}}}}}} \right)}^{2}} \gg 1,$При уменьшении поглощения НГК, когда нужно учитывать колебания, отраженные от центра плазменного шнура, альфвеновский континуум переходит в совокупность связанных АК и НГК – набор перекрытых, вследствие значительного поглощения, комбинированных собственных мод.
В точке АР уравнение (3), определяющее радиальную структуру АК, имеет особенность. При выполнении условия (15) влияние альфвеновского резонанса можно учесть, дополнив данное уравнение правилом обхода Ландау или, что эквивалентно, введя слабое трение о нейтралы, см. выше.
Влияние АР на АК можно рассматривать в одномерном приближении, не учитывая неоднородности магнитного поля, если до попадания в зону АР они сместятся вдоль магнитного поля на расстояние $\Delta z$, меньшее ${{L}_{B}}\Delta {{\omega }_{i}}{\text{/}}\omega $. Приближенную оценку смещения можно получить, рассматривая лучевые траектории АК, которые определяются уравнением
Движение АК по радиусу замедляется при подходе к зоне АР. Данная область дает основной вклад в смещение колебаний вдоль магнитного поля, в ней при ${{\omega }_{i}} \approx \omega $, имеем ${{\varepsilon }_{ + }} \approx 2{{\varepsilon }_{ \bot }}$, и следовательно,
В этом случае справедливо приближенное соотношение ${{\varepsilon }_{ \bot }} - N_{{||}}^{2} \approx N_{{||}}^{2}\left( {r - {{r}_{a}}} \right){\text{/}}{{r}_{0}}$, где ${{r}_{a}}$ – координата точки АР.
На границе зоны АР радиальная длина волны АК, определяемая условием $D = 0$, сравнивается с длиной волны НГК. Для оценки последней используем дисперсионное соотношение (14). В результате находим размер зоны АР $\Delta r \approx {{r}_{0}}{{\left( {{{\varepsilon }_{ \bot }}{\text{/}}{{\varepsilon }_{{||}}}} \right)}^{{1/2}}}$. Используя это выражение, получаем, что до попадания АК в зону АР они сместятся вдоль магнитного поля на расстояние порядка $\Delta z \approx $ $ \approx {{r}_{0}}{{\left( {{{\varepsilon }_{{||}}}{\text{/}}{{\varepsilon }_{ \bot }}} \right)}^{{1/4}}}$. Колебания не достигнут зоны ИЦР, так как до этого испытают АР, при выполнении условия
(16)
${{L}_{B}} \gg {{r}_{0}}{{\left( {\frac{{{{m}_{i}}}}{{{{m}_{e}}}}} \right)}^{{1/4}}}{{\left( {\frac{\omega }{{\Delta \omega }}} \right)}^{{3/4}}}{{\left( {\frac{{{{\omega }_{\quad}}}}{{{{k}_{{||}}}{{v}_{{Te}}}}}} \right)}^{2}}.$Если справедливо условие (16), то при описании альфвеновского континуума неоднородность магнитного поля оказывается несущественной, и радиальную структуру составляющих континуум АК можно анализировать с помощью уравнения (3), дополненного правилом обхода Ландау точки АР. Данное уравнение решалось численно. Однако при выполнении условий
становится возможным аналитическое решение. Так, если частота ВЧ-поля близка к ионной циклотронной $\left( {\Delta {{\omega }_{i}} \ll \omega } \right)$ и выполняется правое неравенство (16), то справедливо соотношение $dG{\text{/}}dr \approx - dF{\text{/}}dr$, и уравнение (3) можно представить в виде(18)
$\begin{gathered} \left( {\frac{d}{{dr}} + \frac{{m + 1}}{r}} \right)F\left( {\frac{d}{{dr}} - \frac{m}{r}} \right){{B}_{{||}}} + {{B}_{{||}}} = \\ \, = \frac{{4\pi }}{\omega }\frac{1}{{N_{{||}}^{2} - 1}}\frac{1}{r}\frac{d}{{dr}}r{{j}_{\theta }}. \\ \end{gathered} $Левое неравенство (17) позволяет пренебречь последним слагаемым в левой части данного уравнения. В этом случае в области $r < {{r}_{B}}$ его решение, описывающее колебания, бегущие по азимуту в ионную сторону ($m < 0$), имеет вид
При анализе колебаний, бегущих в электронную сторону $\left( {m > 0} \right)$, чтобы учесть влияние АР, необходимо включить в рассмотрение последнее слагаемое в левой части (17). Считая его малым и учитывая как поправку, получаем
(20)
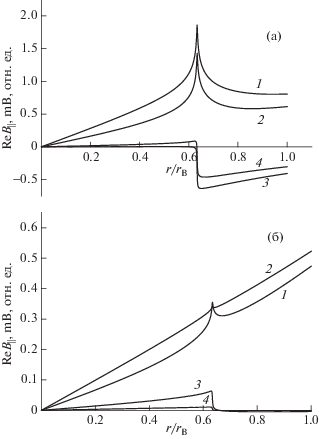
${{B}_{{||}}} \approx {{r}^{m}}\left( {1 - \mathop \smallint \limits_0^r \,dr\frac{r}{{2\left( {m + 1} \right)F}}} \right).$Рис. 12 показывает, что аналитические решения (19), (20) правильно отображают общий характер радиальной зависимости электромагнитных полей рассматриваемых колебаний, но при интересующих нас значениях параметров численные различия с решениями полного уравнения (3) могут быть значительными.
Рис. 12.
Радиальные профили ${{B}_{{||}}}$ АК непрерывного спектра при $m = - 1$, ${{N}_{{||}}} = 200$, ${{\omega }_{i}}{\text{/}}\omega = 1.26$, ${{\nu }_{i}}{\text{/}}\omega = {{10}^{{ - 3}}}$, ${{n}_{0}} = {{10}^{{13}}}$ см–3. Кривые 1 – профили $\operatorname{Re} {{B}_{{||}}}$, полученные численным решением (3), 2 – полученные аналитически; 3 – профили $\operatorname{Im} {{B}_{{||}}}$, полученные численным решением (3), 4 – полученные аналитически. а) – $m = - 1$; б) 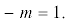
Формально для уравнения (3) наряду с точкой АР особыми являются также точки, в которых выполняется одно из условий ${{\varepsilon }_{ \pm }} = N_{{||}}^{2}$. Из выражений (19), (20), см. также [10], следует, что на самом деле сингулярной является лишь точка АР, в которой выполняется условие $\quad{{\varepsilon }_{ \bot }} = N_{{||}}^{2}$ $\left( {F = 0} \right)$.
Заметим, что решения (19), (20) непригодны для анализа собственных АК. Действительно, они справедливы, если ${{N}_{{||}}}{{r}_{0}} \ll 1$, в то время как для собственных АК выполняется условие $\quad{{N}_{{||}}}{{r}_{0}} \geqslant 1$, см. предыдущий раздел.
Выше при анализе ИЦР-нагрева по методу магнитного берега учитывались лишь колебания плазмы, бегущие от антенны к зоне ИЦР $\left( {{{k}_{{||}}} = {{N}_{{||}}}\omega {\text{/}}c > 0} \right)$. Между тем в альфвеновский континуум входят колебания с обоими знаками ${{k}_{{||}}},$ причем волны тока, бегущие по винтовой антенне, характеризуемые волновыми числами $\left( {m,{{k}_{{||}}}} \right)$ и $\left( { - m, - {{k}_{{||}}}} \right)$, имеют одинаковую амплитуду, будучи сдвинуты по фазе на π.
При выполнении условий, приведенных выше, мощность, закачиваемую в альфвеновский континуум, можно найти, считая магнитное поле однородным, равным значению в центре антенны
Зависимость плазменной нагрузки в цепи антенны от плотности плазмы изображена на рис. 13. На него также перенесена зависимость сопротивления, обусловленного возбуждением собственных колебаний, приведенная на рис. 10. Однако, в отличие от последнего, на рис. 13 на оси ординат используется не логарифмическая шкала, а линейная. Как видно из рисунка, альфвеновские колебания, бегущие навстречу друг другу по азимуту, наиболее эффективно возбуждаются при различающихся значениях плотности. Различие обусловлено гиротропией плазмы. В волновом уравнении (3) данному фактору обязано “дрейфовое слагаемое” $ \propto {\kern 1pt} m\,dG{\text{/}}dr$, см. выше. Его влияние способствует локализации колебаний с $m < 0$ в области неоднородности плотности и оказывает противоположное воздействие на колебания с $m > 0$. Воздействие максимально в области, где ${{\varepsilon }_{ + }}\left( r \right) \approx N_{{||}}^{2}$. Поэтому для колебаний с $m < 0$, бегущих по азимуту в сторону вращения ионов, выгодно, чтобы это условие выполнялось в области более плотной плазмы, см. рис. 14а, а для колебаний с $m > 0$ – на периферии плазменного шнура, или не выполнялось вообще, рис. 14б. Последнее возможно, поскольку в рассматриваемой модели плазмы ее плотность обрывается на границе ${\text{min}}\quad{{\varepsilon }_{ + }}\left( r \right) = {{\varepsilon }_{ + }}\left( {{{r}_{B}}} \right)$.
Рис. 13.
Зависимость сопротивления, вносимого в электрическую цепь ВЧ-антенны из-за возбуждения альфвеновского континуума и основной собственной моды $\left( {m = - 1,\quad\;n = 0\quad{\;}} \right)$: кривая 1 – вклад в сопротивление мод непрерывного спектра с $m = - 1$; 2 – вклад мод с $m = 1$; 3 – суммарное сопротивление; 4 – перенесена с рис. 8 (сопротивление, вызванное возбуждением основной собственной моды); 5 – расчет для мод $m = - 1$ с использованием аналитического решения (17).
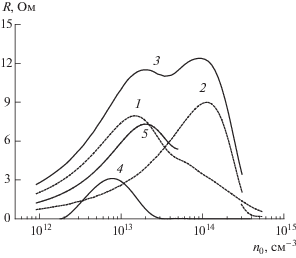
Рис. 14.
Радиальные профили электромагнитных полей$\quad\quad$АК непрерывного спектра, дающих наибольший вклад в сопротивление при значениях плотности
плазмы, соответствующих максимуму кривой 1 на рис. 13: а) – $m = - 1$, $\quad{{n}_{0}} = 1.445 \times {{10}^{{13}}}$ см–3, ${{N}_{{||}}} = 326.7$; б) – 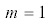 , ${{n}_{0}} = 1.176 \times {{10}^{{14}}}$ см–3, ${{N}_{{||}}} = - 205.0$.
, ${{n}_{0}} = 1.176 \times {{10}^{{14}}}$ см–3, ${{N}_{{||}}} = - 205.0$.
Колебания с $m > 0$ концентрируются к границе плазмы, поэтому уместен вопрос о влиянии величины скачка плотности на сопротивление, связанное с возбуждением этих мод. Расчеты с уменьшенным значением $\Delta {{r}_{0}} = 2$ см, при котором скачок плотности уменьшается примерно вдвое, приводят к уменьшению нагрузки в ее максимуме всего на 5%.
Согласно рис. 13 плазменная нагрузка максимальна в интервале значений плотности плазмы ${{n}_{0}} \approx {{10}^{{13}}}{\kern 1pt} - {\kern 1pt} {{10}^{{14}}}$ см–3. Снижение плотности плазмы сужает интервал значений ${{N}_{{||}}}$ колебаний непрерывного спектра. Уменьшение нагрузки в области большей плотности вызвано возрастанием барьера непрозрачности на периферии плазмы.
Учет высших азимутальных мод $\left( {m = \pm 3} \right)$ практически не влияет на результат в области максимума плазменной нагрузки, однако может быть существен в области больших значений плотности – на спаде “линии поглощения”.
Из условия (17) следует, что аналитические решения справедливы при не слишком больших значениях плотности плазмы, когда выполняется неравенство ${{r}_{0}}{{\omega }_{{pi}}}{\text{/}}\omega \ll 1$. Действительно, согласно рис. 13 использование выражения (19) позволяет составить общее представление о вкладе в плазменную нагрузку моды $m = - 1$ при ${{n}_{0}} \leqslant {{10}^{{13}}}$ см–3. Для мод с $m > 0$ основной вклад в нагрузку дает приграничная область, где решение волнового уравнения существенно отличается от выражения ${{B}_{{||}}} \approx {{r}^{m}}$, использованного при нахождении (20).
4. ЗАКЛЮЧЕНИЕ
ИЦР-нагрев плазмы методом “магнитного берега” предполагает возбуждение собственных альфвеновских колебаний плазменного столба в области, где значение магнитного поля превышает резонансное. Однако в неоднородном плазменном шнуре наряду с дискретным спектром собственных альфвеновских колебаний существует также их непрерывный спектр – альфвеновский континуум. Колебания, составляющие континуум, испытывают альфвеновский резонанс, трансформируясь в нижнегибридные. Последние обладают значительным продольным электрическим полем, что позволяет им активно взаимодействовать с электронами. Последовательный анализ интересующего нас способа нагрева плазмы должен быть двумерным, поскольку необходимо учитывать как продольную неоднородность основного магнитного поля, так и поперечную неоднородность плотности плазмы. В настоящей работе основное магнитное поле считается слабо неоднородным, что позволяет при описании структуры альфвеновских колебаний в направлении вдоль магнитного поля использовать квазиклассическое приближение. Найдено, что основная часть электромагнитной энергии, вводимой в плазму токовой антенной, может затрачиваться на возбуждение альфвеновского континуума и через явление альфвеновского резонанса пойдет на нагрев электронов.
Нагрев электронов обычно сопровождается ростом амбиполярного электрического потенциала, который в случае плазменного двигателя ускоряет ионы, выходящие из магнитного сопла. Однако на это затрачивается не вся энергия, вкладываемая в электронную компоненту плазмы. Часть ее остается у потока электронов, выходящих из сопла, а часть расходуется при взаимодействии с потоком газа в процессе его ионизации. Для создания тяги предпочтителен ИЦР-нагрев более массивных ионов. Действительно, энергия ларморовского вращения ионов, возрастающая при ИЦР-взаимодействии, практически полностью переходит в энергию продольного движения в магнитном сопле.
Работа поддержана грантом РФФИ, проект № 18-29-21002.
Список литературы
Стикс Т.Х. Теория плазменных волн. М.: Атомиздат, 1965.
Bering E.A., Diaz F.R., Squire J.P., Glover T.W., Car-ter M.D., McCaskill G.E., Longmier B.W., Bru-khard M.S., Chansery W.J., Jacobson V.T. // Phys. Plasmas. 2010. V. 17. 043509.
Breizman B.N., Arefiev A.V. // Phys. Plasmas. 2001. V. 8. P. 907.
Звонков А.В., Тимофеев А.В. // Физика плазмы. 1987. Т. 13. С. 282.
Лонгинов А.В., Степанов К.Н. В сб. Высокочастотный нагрев плазмы / Под ред. А.Г. Литвака. Горький, 1983. С. 105.
Piotrowicz P.A., Goulding R.H., Caneses J.F., Green D.L., Caughmen J.B.O., Lau C., Rapp J., Ruzic D.N. // Phys. Plasmas. 2019. V. 26. 033511.
Елфимов А.В., Киров А.Г., Сидоров В.П. В сб. Высокочастотный нагрев плазмы / Под ред. А.Г. Литвака. Горький, 1983. С. 211.
Тимофеев А.В. // Физика плазмы. 2014. Т. 40. С. 3.
Тимофеев А.В. // Физика плазмы. 2015. Т. 41. С. 946
Тимофеев А.В. Резонансные явления в колебаниях плазмы. М.: Физматлит, 2009.
Тимофеев А.В. // Физика плазмы. 2005. Т. 31. С.1087.
Тимофеев А.В. // Физика плазмы. 2002. Т. 28. С. 984.
Дополнительные материалы отсутствуют.