Физика плазмы, 2019, T. 45, № 9, стр. 804-824
Быстрое зажигание пучком протонов и горение цилиндрической оболочечной DT-мишени
А. А. Фролова a, К. В. Хищенко b, *, А. А. Чарахчьян a, **
a Вычислительный центр им. А.А. Дородницына ФИЦ ИУ РАН
Москва, Россия
b Объединенный институт высоких температур РАН
Москва, Россия
* E-mail: konst@ihed.ras.ru
** E-mail: chara@ccas.ru
Поступила в редакцию 06.10.2018
После доработки 23.03.2019
Принята к публикации 25.03.2019
Аннотация
Рассматривается краевое зажигание цилиндрической оболочечной мишени пучком протонов с небольшой массовой глубиной прогрева примерно 0.5 г/см2, для двух значений начальной плотности DT-горючего ${{\rho }_{0}} \approx 110$ и 22 г/см3 и заданных параметров пучка (интенсивности $J \sim {{\rho }_{0}}$ и времени действия $\Delta {{t}_{{{\text{pr}}}}} \sim \rho _{0}^{{ - 1}}$). Сравнением разных моделей теплопередачи через границу между горючим и оболочкой показано, что наличие сильного магнитного поля, зануляющего теплопередачу, но не влияющего на траектории движения α-частиц DT-реакции, уменьшает энергию зажигания всего примерно на 10%. Возникающая при зажигании нестационарная детонационная волна превращается в стационарную быструю безударную волну горения, в которой холодное горючее нагревается α-частицами. Параметры волны зависят от вложенной энергии. Движение волны сопровождается вылетом за пределы горючего α-частиц, которые уносят примерно половину их исходной мощности. Для одного из вариантов определен размер мишени H вдоль оси симметрии (${{\rho }_{0}}H \approx 10$ г/см2), для которого коэффициент усиления $G = 1250$. Получена приближенная формула, связывающая наклон профиля давления в стационарной волне со скоростью волны и мощностью нагрева единицы массы горючего вблизи точки начала волны. Показана применимость формул для сильной детонационной волны, связывающих давление и скорость в точке Чепмена–Жуге со скоростью волны.
1. ВВЕДЕНИЕ
Инерциальный управляемый термоядерный синтез предполагает зажигание небольшой части горючего с последующим распространением волны термоядерного горения на его остальную часть. Первой работой, в которой рассматривалась цилиндрическая оболочечная мишень, была, по-видимому, работа [1]. В середине мишени с DT-горючим (эквимолярная смесь дейтерия и трития) задавалась небольшая по оси симметрии горячая область с плотностью ${{\rho }_{0}}$, которая моделировала центральное зажигание мишени. Было показано, что для радиуса мишени R c условием ${{\rho }_{0}}R \geqslant 0.5$ г/см2 в мишени возникает стационарная детонационная волна вдоль оси симметрии. Было также показано, что с помощью расходящегося конического канала можно получить стационарную детонационную волну в цилиндрическом канале с условием ${{\rho }_{0}}R \gtrsim 0.35$ г/см2.
Настоящая работа основана на концепции быстрого зажигания [2, 3], предполагающей последовательное воздействие на мишень двух драйверов. Первый драйвер сжимает мишень до требуемой плотности горючего, а второй, зажигающий драйвер, быстро, по-возможности не меняя плотность, нагревает область внутри горючего, достаточную для образования волны термоядерного горения.
В литературе рассматриваются различные варианты зажигающего драйвера. Сходящаяся ударная волна [4, 5] и пучок высокоэнергичных ионов с ярко выраженным эффектом Брэгга [6] позволяют создать волну термоядерного горения, двигающуюся от центральной части горючего к периферии. В настоящей работе рассматривается пучок протонов, генерируемый поглощением лазерного излучения в окрестности точки с критической плотностью [7, 8], который дает так называемое краевое зажигание, когда волна термоядерного горения возникает вблизи границы горючего и движется внутрь.
Для быстрого зажигания сферических мишеней предполагалось создавать узкий канал для доставки энергии зажигающего драйвера к плотному ядру мишени (в настоящее время необходимость создания такого канала для пучков тяжелых частиц подвергается сомнению [9]). Применительно к такому каналу в ряде работ (см., например, [10, 11]) рассматривалась осесимметричная задача зажигания пучками протонов плоского полубесконечного слоя DT-горючего. В работе [12] показана возможность быстрого зажигания пучком быстрых электронов предварительно сжатой лазерным излучением сферической мишени. В работе [13] такая же возможность продемонстрирована применительно к несимметрично сжатым мишеням.
Работ по цилиндрическим мишеням в литературе намного меньше, чем по сферическим. Возможность уменьшить пороговую энергию зажигания с помощью нагрева небольшой части горючего на этапе его сжатия до того, как оно достигнет нужной плотности, изучалась в [14] применительно к цилиндрическим мишеням с более плотным DT-горючим в качестве оболочки.
Оболочечные цилиндрические мишени с предварительно сжатым DT горючим, облучаемые пучком тяжелых ионов, рассматривались в работах [15–17]. С помощью двумерного кода изучалось быстрое зажигание и распространение волн термоядерного горения. Определены параметры возникавшей стационарной детонационной волны и волны с радиационным механизмом распространения [17]. В работах [15, 16] начальная плотность горючего ${{\rho }_{0}} = 100$ г/см3, радиус цилиндра с горючим R выбирался из условия ${{\rho }_{0}}R = 0.5$ г/см2. В работе [17] расчеты проводились для разных значений ${{\rho }_{0}}$ и параметра ${{\rho }_{0}}R$.
Зажигание плоской мишени пучком протонов [18] и отражение детонационной волны от плоскости симметрии [19, 20] изучались в рамках квазиодномерной модели [18], позволяющей оценивать энергию зажигания на основе одномерных расчетов. Обнаружена возможность превращения волны медленного горения в пару детонационных волн, двигающихся в противоположных направлениях [19].
Как и в работах [15–17], в настоящей работе рассматривается мишень, состоящая из оболочки в форме цилиндрического слоя, внутри которого находится цилиндр с горючим, сжатым до заданной плотности ${{\rho }_{0}}$. На горючее со стороны торца цилиндра действует зажигающий драйвер, различие в котором определяет различие в задачах.
В настоящей работе зажигающим драйвером является моноэнергетический пучок протонов с энергией 1 MэВ. Радиус пучка R совпадает с радиусом цилиндра с горючим. Задается время действия пучка $\Delta {{t}_{{{\text{pr}}}}}$ и его максимальная интенсивность ${{J}_{0}}$. Интенсивность падающего пучка ${{J}_{b}} = {{J}_{0}}$ для радиальной координаты $0 \leqslant r \leqslant R$ и времени $t \leqslant \Delta {{t}_{{{\text{pr}}}}}$ (за исключением небольшого начального интервала времени $0.02\Delta {{t}_{{{\text{pr}}}}}$, где ${{J}_{b}} \propto t$). Расчет воздействия такого пучка на полностью ионизованное DT-горючее для некоторых выбранных значений J0 и $\Delta {{t}_{{{\text{pr}}}}}$ дает в момент прекращения действия пучка глубину прогрева горючего l, для которой $l{{\rho }_{0}} \approx 0.5$ г/см2 (далее для краткости массовая глубина прогрева), что достаточно для зажигания и примерно в 10 раз меньше массовой глубины прогрева пучком тяжелых ионов из работ [15–17]. Из-за такой разницы в глубине прогрева зажигающего драйвера задачи имеют существенно разный пространственный и временной масштаб. В частности, время действия пучка тяжелых ионов в работах [15–17] 200 пс для ${{\rho }_{0}}$ = = 100 г/см3, а в рассматриваемой задаче $\Delta {{t}_{{{\text{pr}}}}}$ = = 16 пс примерно для того же значения ${{\rho }_{0}}$.
Еще одно важное для зажигания мишени различие между пучками тяжелых ионов и протонов с энергией 1 MэВ связано с близостью области зажигания к свободной границе горючего, которая облучается пучком. Так как мишень зажигается примерно на глубине прогрева, зажигание пучком тяжелых ионов практически не зависит от наличия свободной границы. Это можно увидеть из приведенных в [16] результатов расчета. Когда детонационная волна уже сформировалась, примыкающая к ней волна разрежения еще не дошла до свободной границы. При зажигании пучком протонов с энергией 1 MэВ такая ситуация невозможна. Ранний выход волны разрежения на свободную границу усиливает ее воздействие на формирование детонационной волны.
Приведем результаты расчетов, демонстрирующие заметное влияние глубины прогрева горючего на область значений параметра ${{\rho }_{0}}R$, при которых мишень зажигается. Расчеты проводятся для трех пучков протонов с $l{{\rho }_{0}} \approx 0.5$, 1.5 и 2 г/см2 и тем же вложением энергии на единицу массы, что и в работах [15, 16]. Интенсивность пучка ${{J}_{0}} = 2.5 \times {{10}^{{19}}}$ Вт/см2 та же, что и в работах [15, 16], а время его действия $\Delta {{t}_{{{\text{pr}}}}}$ пропорционально массовой глубине прогрева и равно 200 пс для массовой глубины прогрева пучком тяжелых ионов $l{{\rho }_{0}} \approx 6$ г/см2 из работ [15, 16]. Для трех указанных выше значений параметра $l{{\rho }_{0}}$ получаются значения $\Delta {{t}_{{{\text{pr}}}}} \approx 16.7$, 50 и 66.7 пс. Серия расчетов для разных значений энергии протонов ${{e}_{{{\text{pr}}}}}$ позволяет подобрать нужные значения ${{e}_{{{\text{pr}}}}} = 1$, 20 и 30 МэВ, для которых массовая глубина прогрева в момент прекращения действия пучка примерно совпадает с тремя заданными значениями. Результаты следующие: для пучка с $l{{\rho }_{0}} \approx 0.5$ г/см2 мишень не зажигается даже при ${{\rho }_{0}}R = $ 2 г/см2, а для $l{{\rho }_{0}} \approx 1.5$ и 2 г/см2 пороговое значения ${{\rho }_{0}}R \approx $ ≈ 0.57 и 0.52 г/см2.
Таким образом, для зажигания пучком протонов с $l{{\rho }_{0}} \approx 0.5$ г/см2 энергия на единицу массы должна быть больше, чем в случае пучка тяжелых ионов. В настоящей работе эта энергия увеличена примерно вдвое: ${{J}_{0}} = 5 \times {{10}^{{19}}}$ Вт/см2, $\Delta {{t}_{{{\text{pr}}}}} = 16$ пс для начальной плотности ${{\rho }_{0}} \approx $ 110 г/см3. С ростом массовой глубины прогрева зажигание возможно для той же энергии пучка на единицу массы, что и в случае пучка тяжелых ионов, и с близким значением параметра ${{\rho }_{0}}R$.
В работе рассматриваются две задачи. Первая задача заключается в оценке влияния на пороговую энергию зажигания магнитного поля, достаточно сильного, чтобы воздействовать на электроны и существенно снизить отток тепла из горючего в оболочку [21], и в то же время недостаточно сильного, чтобы существенно повлиять на траектории движения нагревающих горючее α-частиц [22]. В этом случае эффект от воздействия магнитного поля можно приближенно описать, положив равным нулю тепловой поток на границе между оболочкой и горючим или, дополнительно, занулив проекцию теплового потока на нормаль к двум из четырех границ ячейки разностной сетки во всей расчетной области, которые ориентированы примерно вдоль осевого направления. Последний способ является разумным приближением задачи с нулевым тепловым потоком в радиальном направлении.
Помимо оболочки из золота в первой задаче рассматривается оболочка из гипотетического вещества, плотность которого после его сжатия до давления в предварительно сжатом горючем намного больше, чем плотность золотой оболочки после аналогичного сжатия, с целью оценить возможное уменьшение пороговой энергии зажигания при использовании такой оболочки.
Пороговая энергия зажигания обычно определяется как минимальная энергия пучка, необходимая для зажигания горючего заданной начальной плотности. Минимум ищется по параметрам пучка, таким как его интенсивность, длительность и площадь облучения, возможно при заданном законе распределения интенсивности по времени и расстоянию от центра пучка [10]. Так как в настоящей работе основной интерес связан не столько с самой пороговой энергией, сколько с ее относительным изменением при изменении условий задачи, мы используем более узкое определение, когда минимум ищется только по радиусу пучка (совпадающего с радиусом цилиндра с горючим), а параметры пучка ${{J}_{0}}$ и $\Delta {{t}_{{{\text{pr}}}}}$ полагаются заданными. Кроме того вводится определение задержки зажигания, которое позволяет вычислять минимальную энергию зажигания с заданной задержкой, отбрасывая тем самым режимы зажигания с большой задержкой по времени.
Первая задача рассматривается для двух значений начальной плотности горючего ${{\rho }_{0}} = 100{{\rho }_{a}}$ и $500{{\rho }_{a}}$, где ${{\rho }_{a}} \approx 0.22$ г/см3 – плотность горючего при атмосферном давлении и температуре 4 K. Параметры пучка для разных значений ${{\rho }_{0}}$ связаны известными соотношениями ${{J}_{0}} \propto {{\rho }_{0}}$, $\Delta {{t}_{{pr}}} \propto \rho _{0}^{{ - 1}}$, обеспечивающими близость нагрева горючего к изохорическому нагреву при изменении ${{\rho }_{0}}$ [10, 18]. Для случая ${{\rho }_{0}} = 500{{\rho }_{a}}$ значения параметров ${{J}_{0}}$, $\Delta {{t}_{{{\text{pr}}}}}$ приведены выше. Для ${{\rho }_{0}} = 100{{\rho }_{a}}$ значение ${{J}_{0}}$ получается тем же, что и в расчетах по квазиодномерной модели [18, 20], а параметр $\Delta {{t}_{{{\text{pr}}}}} = 80$ пс увеличен примерно в 1.5 раза (что в основном связано с различием в зависимости скорости DT-реакции от температуры ионов – формула из [23] в [18, 20] и формула из [24] в настоящей работе).
Толщина оболочки $\Delta R = 50$ и 250 мкм для ${{\rho }_{0}} = 500{{\rho }_{a}}$ и $100{{\rho }_{a}}$ соответствует условию ${{\rho }_{0}}\Delta R \approx $ ≈ 0.55 г/см2 и имеет тот же порядок величины, что и пороговые для зажигания мишени значения радиуса R. При увеличении указанных значений ΔR решение задачи не меняется.
Второй задачей настоящей работы, которая рассматривается только для ${{\rho }_{0}} = 500{{\rho }_{a}}$, является исследование выхода возникающей при зажигании нестационарной детонационной волны на стационарный режим. Расчет дал неожиданный результат: детонационная волна превращается в близкую к стационарной быструю безударную волну горения.
Основными механизмами распространения безударных волн термоядерного горения являются электронная теплопроводность и нелокальный нагрев заряженными продуктами термоядерных реакций. Такие волны рассматривались во многих работах. Приближенные формулы, основанные на анализе энергетического баланса, получены в работах [25–27] применительно к стационарным волнам и в работах [23, 28] применительно к нестационарным. Модели, основанные на полных уравнениях гидродинамики, применительно к нестационарным расходящимся волнам рассматривались в работах [29–31] (автомодельные решения) и, например, в работах [23, 31] (численное исследование).
Насколько известно авторам, единственной работой, где стационарная безударная волна горения получена как решение задачи на основе полных уравнений гидродинамики, является работа [32], в которой рассматривался вариант плоской задачи о точечном взрыве для двухтемпературной DT-плазмы с учетом локального нагрева $\alpha $-частицами и электронной теплопроводности. Отсутствие ударной волны в стационарном решении этой задачи скорее всего связано с ее спецификой (электронная температура в начальный момент времени бесконечна, а ионная температура равна нулю).
В настоящей работе математическая модель основана на уравнениях одножидкостной двухтемпературной гидродинамики с учетом электронной и ионной теплопроводности. Излучение плазмы (в диффузионном по телесному углу и многогрупповом по частоте приближении) и ее нагрев протонами и α-частицами DT-реакции учитывается только в горючем. Изучение эффекта дополнительного воздействия оболочки на горючее, вызванное нагревом оболочки выходящими из горючего излучением и α-частицами, выходит за рамки настоящей работы. Не учитывается также прогрев горючего на больших расстояниях от области горения высокоэнергичными нейтронами DT-реакции.
В работе [17] на основе одногруппового по частоте приближения уравнения переноса излучения обнаружен эффект сильного нагрева DT-горючего излучением, выходящим из золотой оболочки. Работы, подтверждающие этот эффект для моделей с более подробным учетом спектрального состава излучения, авторам неизвестны. В работе [16], где излучение описывается многогрупповым по частоте приближением, и нет информации об отсутствии учета излучения в оболочке, эффект радиационного воздействия оболочки на горючее не упоминается. Напомним также, что используемая в настоящей работе модель, не учитывающая излучения в оболочке, при увеличении глубины прогрева горючего пучком протонов дает зажигание мишени при той же интенсивности пучка и вложенной на единицу массы энергии, и примерно том же значении параметра ${{\rho }_{0}}R$, что и эти параметры горения мишени в работе [16].
Главное отличие математической модели от работ других авторов связано с переносом α-частиц, который обычно рассматривается в многогрупповом по скорости частицы и диффузионном по углу приближении нестационарного кинетического уравнения Фоккера–Планка с ограничением на величину потока, если она выходит за максимально возможное значение, имеющее физический смысл [33]. В настоящей работе используется известная задача Коши в пространстве скоростей [34] для стационарного однородного уравнения Фоккера–Планка, которое получается из соответствующего неоднородного уравнения при некоторых ограничениях на его вид.
2. ПОСТАНОВКА ЗАДАЧИ
Начальная плотность и другие термодинамические функции
Предполагается, что DT-смесь плотностью ${{\rho }_{0}}$ получена изоэнтропическим сжатием из нормального состояния (плотность ${{\rho }_{a}}$, атмосферное давление). Уравнение состояния DT-смеси получено (см. [19]) из широкодиапазонного полуэмпирического уравнения состояния водорода, основанного на модели [35]. Расчет дает давление DT-смеси ${{p}_{0}} \approx 2 \times {{10}^{4}}$ и 4 × 105 ГПа для ${{\rho }_{0}} = 100{{\rho }_{a}}$ и $500{{\rho }_{a}}$ соответственно.
Начальные термодинамические параметры оболочки определяются давлением ${{p}_{0}}$ [15] и предположением, что оболочка сжата изоэнтропически до этого давления из нормального состояния. Отношение $\delta = \rho _{0}^{{sh}}{\text{/}}{{\rho }_{0}}$, где $\rho _{0}^{{sh}}$ – начальная плотность оболочки, является важным параметром задачи. В приближении мгновенного нагрева горючего до давления $p \gg {{p}_{0}}$ (см. [36]) скорость границы раздела между горючим и оболочкой растет с уменьшением δ, увеличивая тем самым пороговую энергию зажигания.
Так как температура оболочки после изоэнтропического сжатия остается небольшой, изоэнтропа в плоскости $(\rho ,p)$ мало отличается от нулевой изотермы. Например, для золота (заряд ядра $Z = 79$, атомный вес $A = 197$) расчеты по изоэнтропе, построенной по уравнению состояния [37], и по нулевой изотерме для того же уравнения состояния дают практически совпадающие значения $\rho _{0}^{{sh}} \approx 100$ и 310 г/см3 для ${{\rho }_{0}} = 100{{\rho }_{a}}$ и $500{{\rho }_{a}}$ соответственно. Для тех же значений ${{\rho }_{0}}$ расчет по нулевой изотерме для уравнения состояния Томаса–Ферми с квантовыми и обменными поправками [38, 39] дает $\rho _{0}^{{sh}} \approx 95$ и 340 г/см3, отличающихся от приведенных выше значений для уравнения состояния [37] примерно на 5–10%.
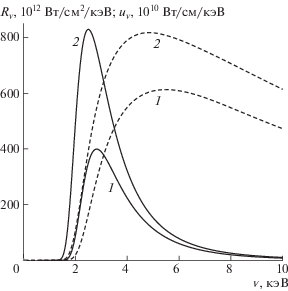
Модель Томаса–Ферми [39] определяет уравнение состояния и, в частности, нулевую изотерму любого вещества по значениям Z и A. Результат расчета параметра $\delta (Z)$ приведен на рис. 1а для элементов таблицы Менделеева с зарядом ядра $Z \leqslant 100$. За исключением небольших интервалов параметр $\delta (Z)$ растет вместе с Z для обоих значений ${{\rho }_{0}}$. Значение $\delta (Z)$ при ${{\rho }_{0}} = 500{{\rho }_{a}}$ заметно меньше, чем при ${{\rho }_{0}} = 100{{\rho }_{a}}$. На интервале $80 \leqslant Z \leqslant 100$ это различие заметно возрастает из-за существенного падения скорости роста $\delta _{Z}^{'}$ для ${{\rho }_{0}} = 500{{\rho }_{a}}$.
Рис. 1.
Отношение начальных плотностей оболочки и горючего как функция заряда ядра оболочки Z для элементов таблицы Менделеева (а) и для изотопов элементов с атомным весом золота (б) при ${{\rho }_{0}} = 100{{\rho }_{a}}$ (1) и $500{{\rho }_{a}}$ (2); точками отмечены значения для золота ($Z = 79$, $A = 197$).

Для обоих значений ${{\rho }_{0}}$ параметр δ намного меньше, чем для нормальных состояний горючего и оболочки (${{\rho }_{0}} = {{\rho }_{a}}$). Например, для золота, которое обычно рассматривается в качестве материала оболочки [15–17], $\delta \approx 3.1$ для ${{\rho }_{0}} = 500{{\rho }_{a}}$, 4.6 для ${{\rho }_{0}} = 100{{\rho }_{a}}$ и 86 для ${{\rho }_{0}} = {{\rho }_{a}}$ (плотность золота в нормальном состоянии примерно 19 г/см3). Последнее значение δ по порядку величины равно отношению атомных весов оболочки и горючего.
Возникает естественный вопрос, можно ли существенно увеличить параметр δ не ограничивая выбор вещества оболочки элементами таблицы Менделеева. На рис. 1б показана зависимость $\delta (Z)$ для ${{\rho }_{0}} = 100{{\rho }_{a}}$ и $500{{\rho }_{a}}$ для веществ с заданным атомным весом золота $A = 197$ на интервале $1 \leqslant Z \leqslant A - 1$, которые для определенности можно рассматривать как изотопы элементов таблицы Менделеева. Видно, что $\delta \approx 70$ при $Z = 1$ для обоих значений ${{\rho }_{0}}$ и быстро уменьшается с ростом Z. Таким образом, возможность существенно увеличить параметр δ формально существует, но для этого нужны экзотические вещества с большим атомным весом и малым зарядом ядра.
Чтобы оценить влияние параметра δ на величину пороговой энергии зажигания далее будет рассматриваться как оболочка из золота, так и гипотетическая оболочка из изотопа водорода с атомным весом золота, которую для краткости будем называть тяжелой оболочкой. Плотность золотой оболочки $\rho _{0}^{{sh}} \approx 95$ и 310 г/см3 для ${{\rho }_{0}} = 100{{\rho }_{a}}$ и $500{{\rho }_{a}}$ соответственно. Плотность тяжелой оболочки $\rho _{0}^{{sh}} \approx 70{{\rho }_{0}}$ для обоих значений ${{\rho }_{0}}$. Начальные температура и удельная внутренняя энергия определяется уравнением состояния Томаса–Ферми с квантовыми и обменными поправками [39], которое используется для замыкания уравнений гидродинамики в оболочке.
Расчетная область и граничные условия
Мишень и расчетная область в цилиндрических координатах z, r показаны на рис. 2. В начальный момент времени горючее имеет форму цилиндра радиусом R ($z \geqslant 0,\;r \leqslant R$), а оболочка является цилиндрическим слоем размером $\Delta R$ ($z \geqslant 0,\;R \leqslant r \leqslant R + \Delta R$). Перед цилиндром располагается дополнительная трапецевидная область, предназначенная для расчета горючего, вылетающего из мишени. Первоначально эта область заполнена DT-газом небольшой плотности и атмосферного давления.
Рис. 2.
Начальная конфигурация мишени и расчетной области в цилиндрических координатах z, r; Soft – граница с мягкими условиями, Free – свободная граница.
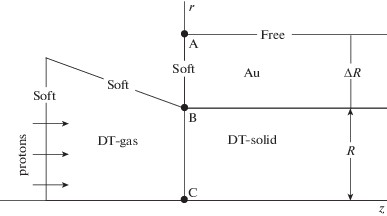
На рис. 2 указаны также типы условий на разных границах. На внешних границах дополнительной области (за исключением оси симметрии) ставятся мягкие условия (равенства нулю пространственных производных от неизвестных функций). Мягкие условия ставятся также на прямолинейной границе AB, совпадающей первоначально с торцевой поверхностью оболочки. Внешняя боковая граница оболочки является свободной границей с давлением 1 атм.
В дополнительной области не учитывается собственное излучение плазмы, что позволяет избежать не имеющих физический смысл решений уравнения диффузии излучения в оптически тонких средах. Граничное условие отсутствия падающего излучения для диффузионных уравнений ставится на линии BC.
В дополнительной области не учитывается также нагрев пучком протонов DT-газа, имеющего плотность меньше некоторой заданной величины. Это позволяет исключить из задачи нагрев и разлет DT-газа под действием пучка протонов.
Границы AB и BC лежат на неподвижной прямой линии, но точки A и B могут двигаться вдоль этой линии в соответствии с движением боковой границы оболочки и границы раздела между горючим и оболочкой.
Мягкие граничные условия позволяют исключить из рассмотрения вещество, вылетающее за границу расчетной области. В то же время границы с такими условиями могут отражать возмущения, идущие изнутри расчетной области, и тем самым искажать решение. Расчеты показывают, что мягкие условия в рассматриваемой задаче позволяют изучать зажигание мишени и распространение детонационной волны.
Основные уравнения и численный метод
Применительно к горючему уравнения одножидкостной двухтемпературной гидродинамики с учетом электронной и ионной теплопроводности, собственного излучения плазмы и ее нагрева протонами и α-частицами DT-реакции имеют вид
(3)
$\rho \frac{{d{{\varepsilon }_{e}}}}{{dt}} = - {{p}_{e}}\nabla \cdot {\mathbf{u}} - \nabla \cdot {{{\mathbf{q}}}_{{\mathbf{e}}}} + {{Q}_{{ei}}} + {{D}_{e}} + {{W}_{e}} + {{R}_{e}},$(4)
$\rho \frac{{d{{\varepsilon }_{i}}}}{{dt}} = - {{p}_{i}}\nabla \cdot {\mathbf{u}} - \nabla \cdot {{{\mathbf{q}}}_{{\mathbf{i}}}} - {{Q}_{{ei}}} + {{D}_{i}} + {{W}_{i}},$Оболочка описывается теми же уравнениями, но без последних слагаемых в уравнениях (3) и (4), учитывающих излучение и нагрев надтепловыми частицами.
Уравнения состояния для уравнений (1)–(4) определяются однотемпературными уравнениями состояния $p = p(\rho ,T)$, $\varepsilon = \varepsilon (\rho ,T)$ и степенью ионизации ξ
(5)
$\begin{gathered} {{p}_{e}}(\rho ,{{T}_{e}}) = p(\rho ,{{T}_{e}})\xi {\text{/}}(1 + \xi ), \\ {{\varepsilon }_{e}}(\rho ,{{T}_{e}}) = \varepsilon (\rho ,{{T}_{e}})\xi {\text{/}}(1 + \xi ), \\ {{p}_{i}}(\rho ,{{T}_{i}}) = p(\rho ,{{T}_{i}}){\text{/}}(1 + \xi ), \\ {{\varepsilon }_{i}}(\rho ,{{T}_{i}}) = \varepsilon (\rho ,{{T}_{i}}){\text{/}}(1 + \xi ). \\ \end{gathered} $В DT-смеси полагается $\xi = 1$, а в оболочке используется формула для ξ из стандартной модели Томаса–Ферми [39].
Учитывается только первичная реакция синтеза ядер дейтерия и трития, в результате которой возникают α-частица c энергией 3.5 МэВ и нейтрон c энергией 14 МэВ, который предполагается вылетающим из горючего без взаимодействия с ним. Количество актов реакции синтеза в единице объема за единицу времени определяется известной формулой
(6)
$F = {{n}_{{\text{D}}}}{{n}_{{\text{T}}}}{{\left\langle {\sigma v} \right\rangle }_{{{\text{DT}}}}},$(7)
$\frac{{d{{n}_{D}}}}{{dt}} = - {{n}_{D}}\nabla \cdot {\mathbf{u}} - F,\quad {{n}_{T}} = {{n}_{D}}.$Дополнительное слагаемое в уравнении неразрывности (1), описывающее изменение состава плазмы из-за DT-реакции, как и соответствующее изменение в уравнениях состояния, не учитываются.
Перенос α-частиц описывается стационарным кинетическим уравнением в приближении Фоккера–Планка [34] относительно функции распределения $f({\mathbf{r}},v,\Omega )$, которая определяет $f({\mathbf{r}},v,\Omega )dvd\Omega $ как число частиц в единице объема вблизи точки r, имеющих модуль скорости в интервале $dv$ вблизи $v$ и направление в интервале телесного угла $d\Omega $ вблизи единичного вектора Ω. Помимо функции F задаются скорости торможения частицы (отрицательные по величине ускорения) на электронах ${{a}_{e}}({{T}_{e}},\rho ,v)$ и ионах ${{a}_{i}}({{T}_{i}},{{T}_{e}},\rho ,v)$, а также скорость термализации частицы ${{v}^{{{\text{th}}}}}({{T}_{i}})$. Для краткости записи заменим зависимость от термодинамических функций на зависимость от r, полагая заданными функции ${{a}_{{e,i}}}({\mathbf{r}},v)$, $F({\mathbf{r}})$, ${{v}^{{{\text{th}}}}}({\mathbf{r}})$.
Пусть все рождающиеся частицы имеют одинаковый модуль скорости ${{v}_{0}}$ и однородное распределение по телесному углу. Тогда, в отсутствие диффузии функции распределения в скоростном пространстве, неоднородное кинетическое уравнение сводится к следующей задаче Коши для однородного уравнения [34]
(8)
$\begin{gathered} v(\Omega \nabla )f + \frac{{\partial af}}{{\partial v}} = 0, \\ f({\mathbf{r}},{{v}_{0}},\Omega ) = - \frac{{F({\mathbf{r}})}}{{4\pi a({\mathbf{r}},{{v}_{0}})}},\quad a = {{a}_{e}} + {{a}_{i}}, \\ {{v}_{m}}({\mathbf{r}},\Omega ) = max({{v}^{{{\text{th}}}}}({\mathbf{r}}),\;{{v}_{b}}({\mathbf{r}},\Omega )) \leqslant v \leqslant {{v}_{0}}, \\ \end{gathered} $(9)
${{W}_{{e,i}}}({\mathbf{r}}) = - {{m}_{\alpha }}\int\limits_{(4\pi )} \,\int\limits_{{{v}_{m}}({\mathbf{r}},\Omega )}^{{{v}_{0}}} f({\mathbf{r}},v,\Omega ){{a}_{{e,i}}}({\mathbf{r}},v)vdvd\Omega ,$Нагрев DT-плазмы протонами описывается их торможением вдоль лучей $r = {\text{const}}$. Отрицательные ускорения ${{a}_{e}}$ и ${{a}_{i}}$ вычисляются по тем же формулам, как и в случае α-частиц, но с другими значениями заряда и атомного веса. Перенос излучения описывается многогрупповым по частоте ν и диффузионным по телесному углу приближением. Многогрупповое приближение строится делением интервала $0 < \nu < \infty $ на N групп ${{\nu }_{{l - 1}}} < \nu < {{\nu }_{l}}$, $l = 1, \ldots ,N$, ${{\nu }_{0}} = 0$, ${{\nu }_{N}} = \infty $. Как правило, расчеты проводились для $N = 50$, ${{\nu }_{{N - 1}}} \approx $ ≈ 26 кэВ. Контрольные расчеты с $N = 150$, ${{\nu }_{{N - 1}}} \approx 17$ кэВ не дали сколько-нибудь заметных отклонений.
Подробности моделей включая ссылки на работы с формулами для расчета коэффициентов уравнений приведены в [36, 43]. Там же приведены ссылки на предшествующие работы по разработке компьютерного кода, в основе которого лежит квазимонотонная схема второго порядка точности типа Годунова на подвижных регулярных сетках, состоящих только из выпуклых четырехугольных ячеек. Границей раздела горючего и оболочки является некоторая линия сетки, которая движется вместе с веществом.
Для случая ${{\rho }_{0}} = 500{{\rho }_{a}}$ расчет зажигания мишени проводится на сетке с шагом вдоль оси симметрии $h = 0.5$ мкм, что соответствует условию $h{{\rho }_{0}} \approx 5 \times {{10}^{{ - 3}}}$ г/см2. Контрольные расчеты на других сетках показывают, что уменьшение h приводит к небольшому уменьшению пороговой энергии зажигания. Расчет выхода детонационной волны на стационарный режим проводится на более грубой сетке с увеличенным в два раза шагом h, что связано с необходимостью значительного увеличения размера расчетной области. В радиальном направлении сетка имеет 40 интервалов в горючем и 60 интервалов в оболочке. Для случая ${{\rho }_{0}} = 100{{\rho }_{a}}$ размеры расчетной области и шаги сетки увеличиваются в 5 раз.
Для расчета уравнений (8), (9), описывающих нагрев плазмы α-частицами, используется обратный трековый метод [42]. В отличие от обычного прямого метода, выпускаемые из центра ячейки сетки лучи используются для расчета влетающих в ячейку, а не вылетающих из нее частиц. Угловая сетка состоит из 32 лучей.
Условия на границе раздела для уравнения теплопроводности
Рассматриваются три разных условия. Первое условие (C0) зануляет поток тепла через границу раздела: $q_{e}^{{(n)}} = q_{i}^{{(n)}} = 0$, $q_{e}^{{(n)}} = ({{{\mathbf{q}}}_{{\mathbf{e}}}} \cdot {\mathbf{n}})$, $q_{i}^{{(n)}} = ({{{\mathbf{q}}}_{{\mathbf{i}}}} \cdot {\mathbf{n}})$, где n – нормаль к границе раздела. Строго говоря, зануление ионного теплового потока здесь излишне, так как условие C0 должно моделировать наличие магнитного поля, достаточно сильного для подавления электронного теплового потока, и недостаточно сильного, чтобы воздействовать на тяжелые частицы. Но так как электронный поток намного больше ионного, дополнительный эффект от зануления последнего незначителен.
Вторым условием (C1) является непрерывность температуры и потока тепла на границе раздела. Так как это условие является естественным для уравнения теплопроводности, его можно не включать в математическую постановку задачи. Однако в расчетах, чтобы избежать необходимости использования слишком подробных сеток вблизи границы раздела, следует использовать специальную аппроксимацию потока тепла на границе раздела, которая получена аппроксимацией условий непрерывности температуры и потока тепла, и в случае одной пространственной переменной $x$ имеет вид [44]
(10)
$\begin{gathered} q = - \varkappa \frac{{dT}}{{dx}} \approx \bar {\varkappa }\frac{{{{T}_{1}} - {{T}_{2}}}}{{\Delta {{x}_{1}} + \Delta {{x}_{2}}}}, \\ \bar {\varkappa } = \frac{{\Delta {{x}_{1}} + \Delta {{x}_{2}}}}{{\Delta {{x}_{1}}{\text{/}}{{\varkappa }_{1}} + \Delta {{x}_{2}}{\text{/}}{{\varkappa }_{2}}}}, \\ \end{gathered} $Третье условие (C2) допускает наличие температурного скачка на границе раздела по аналогии с известным эффектом температурного скачка в молекулярном газе на границе с твердой стенкой. Воспользуемся следующей формулой, полученной из асимптотического анализа уравнения Больцмана [45],
(11)
${{T}_{g}} - {{T}_{w}} = \frac{{{{{(m\pi )}}^{{1/2}}}}}{{{{{(2k)}}^{{3/2}}}T_{g}^{{1/2}}{{n}_{g}}}}\frac{{2 - 0.287{{\alpha }_{e}}}}{{{{\alpha }_{e}}}}{{q}^{{(n)}}},$Применительно к уравнениям (3), (4) под газом будем понимать горючее, под стенкой – оболочку. Заменяя характеристики молекул соответствующими характеристиками компонент плазмы получим два условия для электронов и ионов и потребуем непрерывности тепловых потоков на границе раздела. Полученные таким образом условия являются условиями третьего рода для уравнений теплопроводности электронов и ионов на внутренней границе области.
3. ЗАЖИГАНИЕ
Вложенная в мишень энергия пучка протонов определяется формулой
где множитель 0.99 учитывает линейный рост интенсивности пучка от 0 до ${{J}_{0}}$ на небольшом начальном интервале времени $0.02\Delta {{t}_{{{\text{pr}}}}}$. Параметры ${{J}_{0}}$ и $\Delta {{t}_{{{\text{pr}}}}}$ полагаются заданными, а пороговая энергия зажигания или минимальная энергия зажигания с заданной задержкой (см. ниже) определяются как минимум (12) по радиусу R.На рис. 3 показана типичная картина течения в случае зажигания мишени. В горючем возникает нестационарная неплоская детонационная волна с примыкающей к ее фронту волной разрежения. Давление на фронте детонационной волны вблизи оси симметрии заметно больше, чем вблизи границы раздела горючего и оболочки. Как и в одномерных расчетах [20], имеется предвестник детонационной волны, вызванный прогревом горючего теплопроводностью, α-частицами и излучением.
Рис. 3.
Изобары (107 ГПа) в горючем (DT) и оболочке (Au); ${{\rho }_{0}}{\text{/}}{{\rho }_{a}} = 500$, $R = 59$ мкм, $t = 50$ пс, тепловое условие С1 на границе раздела, оболочка из золота; жирная линия – граница раздела, стрелкой отмечено локальное возмущение.
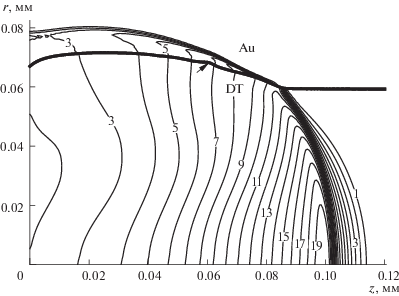
Внутрь оболочки идет ударная волна, которая порождает неустойчивость границы раздела. Стрелкой показано возникающее при формировании детонационной волны локальное возмущение границы раздела, амплитуда которого возрастает со временем вследствие неустойчивости.
Зажигание мишени связано с поведением детонационной волны, которое определяется двумя конкурирующими механизмами: нагревом α-частицами (горением) и воздействием примыкающей волны разрежения. Если превалирует горение, то детонационная волна усиливается, в частности, растет давление на фронте волны. В противном случае волна разрежения постепенно гасит детонационную волну.
Индикаторы и задержка зажигания
В качестве характеристики горения возьмем мощность нагрева горючего α-частицами как функцию относительного времени $\tau = t{\text{/}}\Delta {{t}_{{{\text{pr}}}}}$
где ${{W}_{e}}$ и ${{W}_{i}}$ – слагаемые в правых частях уравнений (3) и (4), интегрирование выполняется по всему объему горючего, $\Delta {{t}_{{{\text{pr}}}}}$ – время действия пучка протонов. В случае зажигания мишени функция $y(\tau )$ должна возрастать с увеличением τ при $\tau > 1$. В качестве параметра, характеризующего скорость возрастания функции $y(\tau )$, возьмем интервал относительного времени $\Delta \tau $ после прекращения действия пучка протонов, в течение которого мощность нагрева горючего удваивается и который будем называть задержкой зажигания.Дополнительно к обычной пороговой по R энергии зажигания, которая, вообще говоря, может достигаться при сколь угодно большом значении $\Delta \tau $, введем в рассмотрение минимальную энергию зажигания ${{E}_{ * }}$ с дополнительным ограничением
где $\Delta {{\tau }_{*}}$ – некоторое заданное значение задержки зажигания.Обезразмеривание функции $y(\tau )$ не меняет уравнения (14). Рассмотрим функцию
где в знаменателе стоит характерная мощность нагрева горючего пучком протонов.Для рассматриваемой задачи представляет интерес два способа изменения ее параметров: изменение радиуса R при неизменных значениях остальных параметров и изменение начальной плотности ${{\rho }_{0}}$, которое определяет изменение других параметров в соответствии со связями
Покажем, что для обоих способов изменения параметров значение $Y(1)$ меняется слабо. Это свойство позволяет во многих случаях сравнивать скорости роста разных функций $Y(\tau )$, отвечающих разным значениям параметров (или разным вариантам модели), с помощью визуального сравнения графиков функций при $\tau > 1$: чем выше расположена функция, тем больше скорость ее роста.
Рассмотрим вначале первый способ изменения параметров, когда меняется только радиус горючего R, совпадающий с радиусом пучка протонов. Так как интенсивность пучка не зависит от R, область нагрева при $t = \Delta {{t}_{{{\text{pr}}}}}$ близка к цилиндру радиуса R и высотой h, равной глубине прогрева горючего пучком протонов. Из уравнения (13) имеем $y(1) \approx \bar {W}h\pi {{R}^{2}}$, где $\bar {W}$ – осредненное по объему области нагрева значение функции ${{W}_{e}} + {{W}_{i}}$, которое слабо зависит от R. Подставляя это в (16), получим
В связи со вторым способом изменения параметров рассмотрим зависимость $Y(1)$ от ${{\rho }_{0}}$. Как известно (см. [10, 18]), изменение параметров по формулам (17) сохраняет изохоричность нагрева, а средняя температура нагретой плазмы $\bar {T}$ слабо зависит от ${{\rho }_{0}}$. Далее надо оценить зависимость $\bar {W}$ от ${{\rho }_{0}}$. Ограничимся рассмотрением наиболее простой модели нагрева плазмы α-частицами, когда вся энергия частицы поглощается в той же точке, где она родилась (модель локального нагрева) $W = F{{m}_{\alpha }}(v_{0}^{2} - {{({{v}^{{{\text{th}}}}})}^{2}}){\text{/}}2$. Как показано в [42], вдали от границ области уравнения (8), (9) переходят в модель локального нагрева, если коэффициенты уравнения (8) не зависят от r.
Как следует из формулы (6), $\bar {W} \sim \rho _{0}^{2}{{\left\langle {\sigma v} \right\rangle }_{{{\text{DT}}}}}(\bar {T})$, так как при $\tau = 1$ плотность нагретого горючего еще мало отличается от ${{\rho }_{0}}$. Подстановка этого выражения в (18) вместе с $h \propto \rho _{0}^{{ - 1}}$ и ${{J}_{0}} \propto {{\rho }_{0}}$ показывает, что $Y(1)$ в рамках сделанных предположений не зависит от ${{\rho }_{0}}$.
В качестве индикатора зажигания могут использоваться зависимости от времени разных характеристик, например, полного числа DT-реакций [16]. В данной задаче надежным индикатором зажигания является зависимость от времени максимального по пространственным переменным давления ${{P}_{{max}}}$. Как видно из рис. 3, максимум давления располагается вблизи фронта детонационной волны на оси симметрии. Поэтому функция ${{P}_{{max}}}(\tau )$, которая приведена рис. 4а для ${{\rho }_{0}} = 500{{\rho }_{a}}$ и нескольких значений R, начиная с некоторого момента времени (после второй точки излома кривых на рис. 4а) является также и максимальным давлением в детонационной волне.
Рис. 4.
Максимальное давление в горючем (а) и относительная мощность нагрева α-частицами (б) как функции относительного времени для $R = 64$ (1), 60 (2), 56 (3), 54 (4), 53.5 (5), 53 (6) и 52.5 мкм (6); ${{\rho }_{0}}{\text{/}}{{\rho }_{a}} = 500$, тепловое условие С1 на границе раздела, оболочка из золота.
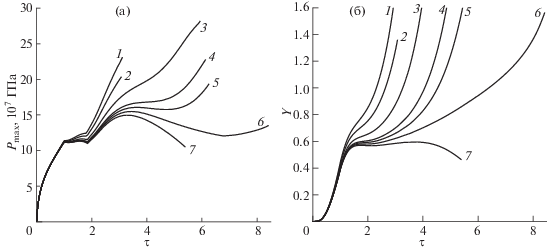
Давление в детонационной волне растет со временем для всех значений R, кроме самого маленького (52.5 мкм), либо монотонно (кривые 1–4), либо после некоторого интервала времени, где давление уменьшается (кривые 5 и 6). Так как при $R = 52.5$ мкм зажигания нет, пороговое значение радиуса ${{R}_{{{\text{ig}}}}} \approx 53$ мкм с точностью около 1%. Соответствующая пороговая по R энергия зажигания определяется формулой (12). Видно, что чем меньше вкладываемая в мишень энергия (которая пропорциональна ${{R}^{2}}$), тем медленнее растет давление в детонационной волне, а вблизи пороговой энергии зажигания рост давления может начинаться с большой задержкой по времени (см. кривую 6 на рис. 4а).
Для тех же значений R на рис. 4б приведена относительная мощность нагрева α-частицами $Y(\tau )$. Видно, что функция $Y(\tau )$ растет вместе с τ при зажигании и уменьшается начиная с некоторого значения τ при его отсутствии, являясь таким образом хорошим индикатором зажигания, дающим то же пороговое значение ${{R}_{{{\text{ig}}}}}$.
В таблице 1 приведены приближенные значения задержки зажигания Δτ, найденной из уравнения (14) для функций $Y(\tau )$ на рис. 4б. Как и следовало ожидать, Δτ быстро увеличивается при приближении радиуса R к своему пороговому значению.
Таблица 1.
Задержка зажигания $\Delta \tau $, определенная уравнением (14), для радиуса пучка протонов (и цилиндра с горючим) R (мкм); ${{\rho }_{0}}{\text{/}}{{\rho }_{a}} = 500$, условие C1
| R | 64 | 60 | 56 | 54 | 53.5 | 53 | 52.5 |
| Δτ | 1.1 | 1.3 | 1.8 | 2.5 | 2.8 | 3.8 | – |
Можно также предположить, что функция $\Delta \tau (R)$ является монотонной функцией R при заданных значениях остальных параметров задачи. Многочисленные расчеты с достаточно малым шагом по R подтверждают это предположение. В этом случае нахождение минимального радиуса ${{R}_{*}}$ с заданным максимально возможным значением задержки $\Delta {{\tau }_{ * }}$ сводится к нахождению единственного решения уравнения $\Delta \tau ({{R}_{*}}) = \Delta {{\tau }_{*}}$.
Сравнение энергии зажигания разных моделей
Далее будет изучаться горение мишеней с небольшой задержкой зажигания. Для определенности выбрано значение $\Delta {{\tau }_{*}} \approx 1.33$, отвечающее радиусу $R = 60$ мкм в табл. 1. Соответствующая энергия зажигания примерно на 30% больше пороговой энергии зажигания ${{E}_{{{\text{ig}}}}}$, соответствующей радиусу $R = 53$ мкм.
Рассматриваются следующие пять задач для двух значений ${{\rho }_{0}} = 500{{\rho }_{a}}$ и $100{{\rho }_{a}}$. Первые три задачи относятся к оболочке из золота (отношение плотности оболочки и горючего $\rho _{0}^{{sh}}{\text{/}}{{\rho }_{0}} \approx 3.1$ и 4.6 для ${{\rho }_{0}}{\text{/}}{{\rho }_{a}} = 500$ и 100 соответственно) и трем разным тепловым условиям на границе с горючим (см. раздел 2): отсутствие теплопередачи на границе, моделирующее наличие достаточно сильного магнитного поля (условие C0), непрерывность теплового потока и температуры (C1) и температурный скачок (C2). Рассматриваются также так называемая тяжелая оболочка ($\rho _{0}^{{sh}}{\text{/}}{{\rho }_{0}} \approx 70$ для обоих значений ${{\rho }_{0}}$, см. раздел 2) с тепловым условием С1 и задача с неподвижной теплоизолированной боковой границей горючего, которая является пределом рассматриваемой задачи с условием C0 при $\rho _{0}^{{sh}} \to \infty $.
На рис. 5 показаны кривые $Y(\tau )$ для разных задач с одной и той же небольшой относительной задержкой зажигания. Видно, что кривые, относящиеся к одному и тому же значению ${{\rho }_{0}}$, за исключением кривой для последней задачи с неподвижной теплоизолированной боковой границей горючего, близки друг к другу на всем показанном интервале изменения τ. Отличие кривой для последней задачи объясняется существенным уменьшением радиуса ${{R}_{*}}$ (примерно в два раза по сравнению с задачами для оболочки из золота), которое уменьшает значение $Y(1)$ из-за роста относительной доли энергии вылетающих из горючего частиц.
Рис. 5.
Функции $Y(\tau )$ с заданной относительной задержкой зажигания $\Delta {{\tau }_{*}} \approx 1.33$ для ${{\rho }_{0}}{\text{/}}{{\rho }_{a}} = 500$ (а) и 100 (б) с повтором одной функции на (а). Оболочка из золота: $ \bullet $ – условие C0, радиус ${{R}_{*}} \approx 58$ (а) и 264 мкм (б); △ – условие C1, ${{R}_{*}} \approx 60$ (а) и 268 мкм (б), приведена также на (а) в виде штрих-пунктирной линии; ⬜ – условие C2, ${{R}_{*}} \approx 61$ (а) и 279 мкм (б). Штриховая линия – тяжелая оболочка, условие C1, ${{R}_{*}} \approx 53$ (а) и 236 мкм (б); сплошная линия – неподвижная теплоизолированная боковая граница горючего, ${{R}_{*}} \approx 32$ (а) и 138 мкм (б).
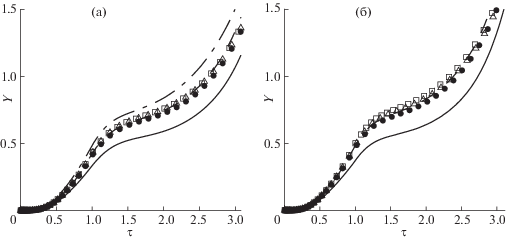
На рис. 5а, помимо кривых для ${{\rho }_{0}} = 500{{\rho }_{a}}$, приведена кривая для одной из задач с ${{\rho }_{0}} = 100{{\rho }_{a}}$ (штрих-пунктирная линия, тепловое условие C1, оболочка из золота). По сравнению с кривыми для одного и того же значения ${{\rho }_{0}}$, кривые для разных значений ${{\rho }_{0}}$ (и одинаковой относительной задержкой зажигания) отличаются заметно.
Возникает естественный вопрос, что будет, если изменить определение задержки зажигания (14), заменив двукратное увеличение мощности нагрева α-частицами после прекращения действия пучка протонов на, например, трехкратное. Если исключить из рассмотрения последнюю задачу, то кривые для ${{\rho }_{0}} = 500{{\rho }_{a}}$ изменятся незначительно, так как значение задержки определяется одной из этих кривых. Мало изменится и соответствующее каждой кривой значение ${{R}_{*}}$.
Для кривых с ${{\rho }_{0}} = 100{{\rho }_{a}}$ такое простое рассуждение не годится, так как задержки, определяемые этими кривыми, могут существенно отличаться от заданного значения. Тем не менее расчет дает незначительное изменение кривых и соответствующих значений ${{R}_{*}}$ при указанном выше изменении определения задержки зажигания (14). Например, значение ${{R}_{*}}$ для задачи с условием C1 и оболочкой из золота при ${{\rho }_{0}} = 100{{\rho }_{a}}$ (штрих-пунктирная линия на рис. 5а) меняется менее, чем на 1%. Это подтверждает обоснованность выбора относительной задержки зажигания в качестве параметра, который позволяет сравнивать скорость зажигания мишеней с разными значениями ${{\rho }_{0}}$.
В табл. 2 для рассматриваемых задач приведены энергия зажигания ${{E}_{*}}$ и параметр ${{\rho }_{0}}{{R}_{*}}$, вычисленные по значениям ${{R}_{*}}$, найденным из решения уравнения $\Delta \tau ({{R}_{*}}) = \Delta {{\tau }_{*}} \approx 1.33$ и приведенным с точностью до 1 мкм в подписи к рис. 5.
Таблица 2.
Энергия зажигания ${{E}_{*}} = {{E}_{{{\text{pr}}}}}({{R}_{*}})$ (кДж) и параметр ${{\rho }_{0}}{{R}_{*}}$ (г/см2) для относительной задержки зажигания $\Delta {{\tau }_{ * }} \approx 1.33$ и двух значений ${{\rho }_{0}}$; С0, С1 и С2 – разные тепловые условия на границе раздела, оболочка из золота; HS – тяжелая оболочка, условие C1; UB – неподвижная теплоизолированная боковая граница горючего
| ${{\rho }_{0}}{\text{/}}{{\rho }_{a}}$ | C0 | C1 | C2 | HS | UB | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| ${{E}_{ * }}$ | ${{\rho }_{0}}{{R}_{ * }}$ | ${{E}_{ * }}$ | ${{\rho }_{0}}{{R}_{ * }}$ | ${{E}_{ * }}$ | ${{\rho }_{0}}{{R}_{ * }}$ | ${{E}_{{{\text{pr}}}}}$ | ${{\rho }_{0}}{{R}_{ * }}$ | ${{E}_{{{\text{pr}}}}}$ | ${{\rho }_{0}}{{R}_{ * }}$ | |
| 500 | 84 | 0.64 | 90 | 0.66 | 94 | 0.67 | 69 | 0.58 | 25 | 0.35 |
| 100 | 1730 | 0.58 | 1790 | 0.59 | 1930 | 0.61 | 1380 | 0.52 | 470 | 0.3 |
Отсутствие теплопередачи через границу раздела (условие C0), которое моделирует наличие сильного магнитного поля, уменьшает энергию зажигания примерно на 10%. Применение гипотетической тяжелой оболочки (изотоп водорода с атомным весом золота) уменьшает энергию зажигания примерно на 30%. Модель неподвижной боковой границы горючего занижает энергию зажигания примерно в 3.5 раза.
Так как сильное магнитное поле вдоль оси симметрии подавляет тепловой поток в радиальном направлении во всей мишени, а не только на границе раздела, проводился контрольный расчет с занулением проекции теплового потока на нормаль к двум из четырех границ ячейки разностной сетки во всей расчетной области, которые ориентированы примерно вдоль оси симметрии. Соответствующее значение ${{R}_{*}}$ отличается от полученного для условия C0 менее чем на 2%.
В задаче зажигания пучком протонов плоского полубесконечного слоя DT-горючего зависимость энергии зажигания ${{E}_{{{\text{ig}}}}}$ от начальной плотности горючего с высокой точностью имеет вид ${{E}_{{{\text{ig}}}}} \propto \rho _{0}^{\beta }$, $\beta = - 1.85$ [10]. Предположим, что для рассматриваемых задач имеет место аналогичная связь ${{E}_{*}} \propto \rho _{0}^{\beta }$, где постоянную β легко найти по двум значениям ${{E}_{*}}$ для двух значений ${{\rho }_{0}}$ в табл. 2. Для задач с условиями C1 и C2 имеем $\beta \approx - 1.86$ и –1.88 соответственно, что близко к приведенному в [10] значению. Соответствующая зависимость параметра ${{\rho }_{0}}{{R}_{*}}$ от ${{\rho }_{0}}$ следует из (12) и имеет вид ${{\rho }_{0}}{{R}_{*}} \propto \rho _{0}^{{{{\beta }_{1}}}}$, ${{\beta }_{1}} = 0.07$ и 0.06 для задач с условиями C1 и C2. Заметное завышение параметра ${{\rho }_{0}}{{R}_{*}}$ по сравнению с зажиганием пучком тяжелых ионов в работах [15, 16] связано с близостью области зажигания пучком протонов с энергией 1 МэВ к свободной границе (см. обсуждение этого вопроса во введении).
4. БЫСТРАЯ БЕЗУДАРНАЯ ВОЛНА ТЕРМОЯДЕРНОГО ГОРЕНИЯ
Рассмотрим выход детонационной волны на стационарный режим. Ограничимся случаем ${{\rho }_{0}} = 500{{\rho }_{a}}$, задачей с золотой оболочкой и условием непрерывности температуры и теплового потока на границе раздела. Если это не оговорено особо, рассматривается значение $R = 64$ мкм.
Расчетная область, необходимая для изучения выхода детонационной волны на стационарный режим, имеет значительно больший размер по оси симметрии, чем расчетная область для изучения зажигания мишени из предыдущего раздела. Для уменьшения объема вычислений представленные в настоящем разделе результаты получены на более грубой пространственной сетке с увеличенным в два раза шагом вдоль оси симметрии, что приводит к небольшому замедлению зажигания. Для получения той же задержки зажигания, что и в соответствующем расчете из предыдущего раздела для $R = 60$ мкм, для более грубой сетки необходимо взять $R \approx 63$ мкм, увеличив тем самым энергию пучка протонов.
Еще одна вычислительная трудность связана с неустойчивостью границы раздела горючего и оболочки, которая увеличивает со временем амплитуду локального возмущения границы, возникающего при формировании детонационной волны и показанной стрелкой на рис. 3. Это приводит к искривлению ячеек сетки и соответствующему падению шага по времени, что фактически останавливает расчет.
Расчет поздней стадии развития неустойчивости границы раздела двух веществ требует применения методов, не использующих явное выделение границы раздела в виде линии сетки, но допускающих наличие ячеек сетки, содержащих смесь обоих веществ. Применительно к рассматриваемой задаче используется другой подход. Вводится искусственное ограничение на угол наклона границы раздела к оси симметрии, которое приводит к нарушению закона сохранения массы вблизи участков границы с сильным искривлением. Однако в рассматриваемой задаче таким участком является небольшое по размеру локальное возмущение, угол наклона границы в котором попадает под искусственное ограничение, когда детонационная волна уже далеко отошла от этого возмущения.
Превращение детонационной волны в безударную волну горения
Как было указано выше со ссылкой на рис. 3, точка с максимальным по пространству давлением находится вблизи детонационной волны. То же самое относится и к максимальной по пространству плотности. Эти две величины, как и температуру ионов и электронов в точке с максимальным давлением, можно рассматривать как значения соответствующих функций в детонационной волне. Их зависимость от относительного времени $\tau = t{\text{/}}\Delta {{t}_{{{\text{pr}}}}}$ приведена на рис. 6. Видно, что все четыре величины со временем выходят на постоянные значения, что указывает на переход к стационарному режиму. Необычным является поведение плотности, которая со временем уменьшается.
Рис. 6.
Характеристики детонационной волны (максимальные по пространству давление p и плотность ρ, температура ионов Ti и электронов Te в точке с максимальным давлением) и максимальная по пространству радиационная температура Tr как функции относительного времени; $R = 64$ мкм.
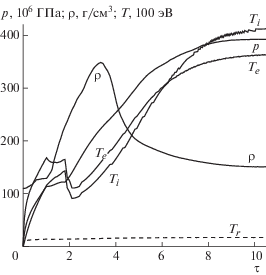
На рис. 6 показана также зависимость от τ максимальной по пространству радиационной температуры (${{T}_{r}} = {{({{c}_{l}}U{\text{/(}}4\sigma ))}^{{1/4}}}$, где ${{c}_{l}}$ – скорость звука, U – плотность энергии излучения, σ – постоянная Стефана–Больцмана), которая намного меньше температуры плазмы.
Причина существенного уменьшения плотности в детонационной волне на рис. 6 (степень сжатия падает с примерно 3 до примерно 1.4) показана на следующем рис. 7. В четыре последовательных момента времени приведены профили плотности, давления и z-компоненты скорости (взятой с обратным знаком, чтобы разгрузить верхнюю часть рисунка) вдоль оси симметрии. Видно, что происходит качественная перестройка структуры волны. В первый момент $\tau = 2.5$ структура типична для детонационной волны. Имеется ударная волна в виде узкой области, где происходит изменение функций от значений за волной до почти начальных значений. Во второй момент $\tau = 5$ виден предвестник ударной волны, где профили имеют заметно меньший наклон (небольшой предвестник такого типа можно увидеть уже в предыдущий момент $\tau = 2.5$). Окончательная структура стационарной волны видна в два последних момента $\tau = 7.5$ и 10. Ударная волна исчезает, а предвестник превращается в довольно большой по осевой координате интервал, где профили всех функций близки к линейным.
Рис. 7.
Профили плотности (ρ, сплошные линии), давления (p, штриховые) и взятой с обратным знаком z-компоненты скорости ($ - {{u}_{z}}$, штрих-пунктирные линии, показаны только участки с ${{u}_{z}} > 0$) вдоль оси симметрии в четыре момента относительного времени $\tau = 2.5$ (1), 5 (2), 7.5 (3) и 10 (4); R = 64 мкм.
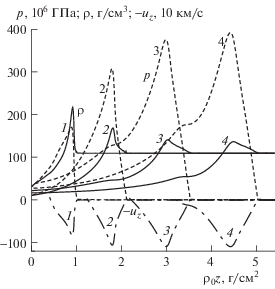
Скорость стационарной волны $D \approx 3350$ км/с определялась по траектории движения точки с максимальным давлением на оси симметрии. Максимальная массовая скорость вдоль оси симметрии навстречу холодному горючему примерно 1100 км/с.
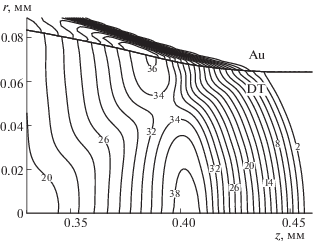
На рис. 8 приведено поле давления в последний из показанных на предыдущем рисунке моментов времени. Сравнивая это поле с полем давления на рис. 3 можно увидеть, что перестройка структуры произошла во всем горючем, а не только вблизи оси симметрии. Вместо ударной волны возникает непрерывная волна сжатия с близким к линейному профилем давления (расстояние между изобарами с постоянным шагом по давлению почти не меняется в волне сжатия), которая является также и волной термоядерного горения.
Рис. 8.
Изобары (107 ГПа) в горючем (DT) и оболочке (Au) при $t = 160$ пс ($\tau = 10$); $R = 64$ мкм.
Параметры стационарной волны зависят от вложенной энергии пучка протонов. В табл. 3 приведены значения максимального давления в волне для трех значений радиуса R и соответствующих значений энергии пучка протонов. Во всех трех случаях перед выходом на стационарный режим детонационная волна превращается в безударную волну термоядерного горения.
Таблица 3.
Максимальное давление в стационарной безударной детонационной волне ${{P}_{{max}}}$ (106 ГПа) и энергия пучка протонов ${{E}_{{{\text{pr}}}}}$ (кДж) для трех значений радиуса пучка протонов (и цилиндра с горючим) R (мкм)
| R | ${{E}_{{{\text{pr}}}}}$ | ${{P}_{{max}}}$ | R | ${{E}_{{{\text{pr}}}}}$ | ${{P}_{{max}}}$ | R | ${{E}_{{{\text{pr}}}}}$ | ${{P}_{{max}}}$ |
|---|---|---|---|---|---|---|---|---|
| 60 | 90 | 370 | 64 | 100 | 390 | 70 | 120 | 430 |
Интегральные характеристики
На рис. 9 для трех значений радиуса R приведены зависимости от относительного времени τ коэффициента потери мощности α-частиц (относительные потери мощности α-частиц из-за их вылета за границу горючего) и коэффициента усиления G (без учета затрат энергии на сжатие мишени). Видно, что при $\tau > 7$ примерно половина мощности α-частиц выносится за пределы горючего вылетающими частицами. Коэффициент усиления при $\tau = 10$ достигает значений примерно 350–500 в зависимости от значения R.
Рис. 9.
Коэффициент потери мощности α-частиц ${{k}_{\alpha }}$ и коэффициент усиления G как функции относительного времени для $R = 60$ мкм (штриховая линия), 64 мкм (сплошная) и 70 мкм (штрих-пунктирная).
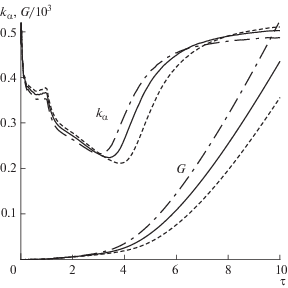
Так как производная $G_{\tau }^{'}$ выходит на примерно постоянное значение, зная скорость волны можно оценить, какого размера H вдоль оси симметрии должна быть мишень, чтобы значение G достигало заданного значения, в качестве которого было выбрано $G = 1250$. Для $R = 64$ мкм расчет дает $H \approx 0.9$ мм и, соответственно, ${{\rho }_{0}}H \approx $ 10 г/см2.
Коэффициент выгорания горючего в рассматриваемой задаче определяется на основе известного определения локального коэффициента выгорания [46, 47]. Определим число актов DT-реакции в единице объема ${{n}_{{\text{R}}}}$ уравнением
и начальным условием ${{n}_{{\text{R}}}} = 0$ при $t = 0$. В силу (7) сумма ${{n}_{{\text{R}}}} + {{n}_{{\text{D}}}}$ не зависит от числа актов DT-реакции. Коэффициент выгорания горючего определим формулойВ рассматриваемой задаче коэффициент выгорания ${{k}_{b}}$ немного растет со временем. Для момента времени $\tau = 10$ ($t = 160$ пс) и двух значений ${{B}_{{min}}} = $ 0.01 и 0.1, значения ${{k}_{b}} \approx 0.24$ и 0.26 соответственно. При $\tau = 15$ ($t = 240$ пс) и тех же значений ${{B}_{{min}}}$, коэффициент выгорания принимает значения ${{k}_{b}} \approx 0.31$ и 0.33.
Механизм распространения
Механизм распространения волны горения определяется тем физическим процессом, который нагревает холодное горючее до высокой температуры, необходимой для рождения в единицу времени достаточно большого числа α-частиц. Складывая уравнения (3) и (4) можно получить при $t > \Delta {{t}_{{{\text{pr}}}}}$ (когда ${{D}_{e}} = {{D}_{i}} = 0$)
(19)
$\frac{{d\varepsilon }}{{dt}} = {{F}_{g}} + {{F}_{h}} + {{F}_{\alpha }} + {{\rho }^{{ - 1}}}{{R}_{e}},$На рис. 10а приведены профили давления и указанных выше функций (последнее слагаемое в правой части (19), связанное с излучением, мало по сравнению с другими слагаемыми и поэтому не приводится). Точки профиля давления соответствуют серединам интервалов разностной сетки вдоль оси симметрии. Видно, что основным механизмом распространения волны является нагрев α-частицами, которые вылетают из горячей области и отдают значительную часть своей мощности холодному горючему в начале волны. Теплопроводный нагрев заметно уступает α-частицам в начале волны, а примерно с середины волны теплопроводность начинает охлаждать горючее. Нагрев гидродинамическим сжатием в безударной волне незначителен.
Рис. 10.
Профили вдоль оси симметрии давления (точки) и мощности нагрева (охлаждения) единицы массы горючего α-частицами (α, сплошная линия), теплопроводностью (h, штрих-пунктирная линия) и гидродинамическим сжатием или расширением (g, штриховая линия) при $t = 160$ пс для разных моделей нагрева α-частицами: уравнение Фоккера–Планка (а, $R = 64$ мкм) и модель локального нагрева (б, $R = 50$ мкм); знаком $\square $ отмечено значение производной $\varepsilon _{t}^{*}$, найденное из уравнения (24).
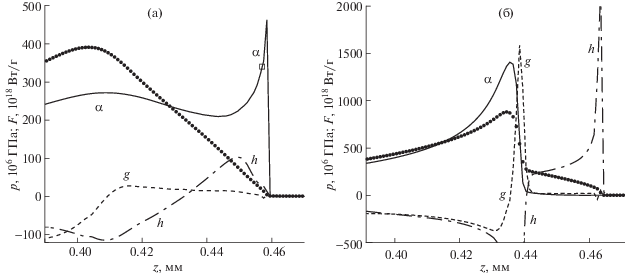
Для сравнения на рис. 10б приведены такие же профили в стационарной волне, полученной для модели локального нагрева α-частицами, которые отдают свою энергию в той же точке, где родились, и поэтому не могут являться механизмом распространения волны горения. Радиус R выбран так, чтобы в момент $t = 160$ пс волна находилась примерно там же, где и безударная волна для модели на основе уравнения Фоккера–Планка.
Превращения детонационной волны в безударную волну горения в этом случае не происходит. Стационарной волной горения является детонационная волна с небольшим предвестником того же типа, что и упомянутый выше предвестник при превращении детонационной волны в безударную волну горения на рис. 7, но с другим механизмом распространения (теплопроводность). Нагрев α-частицами начинается после гидродинамического нагрева в ударной волне.
Хотя теплопроводность не является основным механизмом распространения безударной волны на рис. 10а, для существования такой волны теплопроводность необходима. Расчет показывает, что если начиная с $t = 160$ пс “отключить” теплопроводность, то происходит обратное превращение безударной волны в детонационную волну с небольшим предвестником. Процесс превращения начинается с роста давления в левой на рис. 10а части волны из-за “отключения” теплопроводного охлаждения волны в этой части.
В работе [27] для значений параметра ${{\rho }_{0}}R = 0.5$ и 1 г/см2 приведены значения скорости стационарной волны, механизмом распространения которой является нелокальный нагрев α-частицами, вычисленные приближенно на основе анализа баланса энергии. Интерполяция в точку ${{\rho }_{0}}R = 0.7$ г/см2, которая соответствует параметрам мишени, дает значение $D \approx 1550$ км/с, что заметно меньше приведенного выше значения, полученного из настоящего расчета.
Профили гидродинамических функций
Предположим, что вблизи оси симметрии безударная волна термоядерного горения является одномерной и движется с постоянной скоростью D. Тогда профили давления, плотности и скорости вдоль оси симметрии должны удовлетворять известным уравнениям, которые следуют из одномерных аналогов стационарных уравнений непрерывности (1) и движения (2) в системе координат, двигающейся вместе с волной. Пусть $p(z)$, $\rho (z)$ и $u(z)$ – профили соответствующих функций в неподвижной системе координат в некоторый момент времени. В подвижной системе координат профили давления и плотности не изменятся, а профиль скорости примет вид $v(z) = u(z) - D$.
Связь между функциями $p(z)$, $\rho (z)$ и $v(z)$ задается теми же уравнениями, что и связь между параметрами за фронтом ударной волны
(20)
$\rho v = {{\rho }_{1}}{{v}_{1}},\quad p + \rho {{v}^{2}} = {{p}_{1}} + {{\rho }_{1}}v_{1}^{2},$Полагая ${{\rho }_{1}} = {{\rho }_{0}}$, ${{v}_{1}} = - D$ (${{u}_{1}} = 0$), ${{p}_{1}} = 0$, что соответствует началу волны, уравнения (20) приводятся к виду
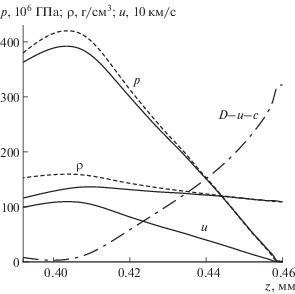
На рис. 11 приведены профили вдоль оси симметрии $p(z)$, $\rho (z)$ и $u(z)$ в безударной волне сжатия в последний из показанных на рис. 7 моментов времени, а также результат применения формул (21) и (22) к профилю $u(z)$. Видно, что профили $p(z)$ и $u(z)$ с хорошей точностью удовлетворяют формуле (21) почти во всей безударной волне сжатия.
Рис. 11.
Профили давления, плотности и скорости вдоль оси симметрии (сплошные линии), функции $p(u)$ и $\rho (u)$ (штриховые линии), полученные применением формул (21) и (22) к профилю скорости, и профиль функции $D{\kern 1pt} - {\kern 1pt} u{\kern 1pt} - {\kern 1pt} c$ (штрих-пунктирная линия); $t = 160$ пс ($\tau = 10$).
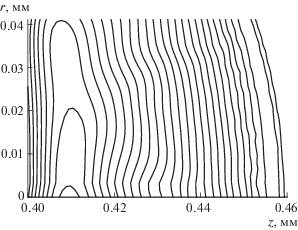
Функция (22) мало отличается от профиля $\rho (z)$ только на начальном участке волны, а при $z < 0.44$ мм отклонение становится заметным, хотя и не превосходит 20%. В значительной степени это отклонение объясняется нарушением одномерности поля плотности вблизи оси симметрии, показанного на рис. 12. Видно, что изолинии плотности (в отличие от изобар на рис. 8) не ортогональны оси симметрии и имеют волнообразный характер.
Рис. 12.
Изолинии плотности с постоянным шагом в безударной волне сжатия вблизи оси симметрии, $t = 160$ пс.
Простые геометрические соображения позволяют получить приближенную формулу, связывающую наклон профиля давления $\left| {{{p}_{z}}} \right|$ в стационарной волне со скоростью волны D и производной ${{\varepsilon }_{t}}$ вблизи точки начала волны. Пусть эта точка в некоторый момент времени t имеет координату $z = {{z}_{0}}$. В окрестности этой точки будем полагать $\rho = {{\rho }_{0}}$, а функции u, p и ε полагать малыми величинами, в отличие от производных от этих функций по z и t. За время $\Delta t$ точка начала волны сместится вдоль координаты z на $\Delta z = D\Delta t$. С другой стороны, если $\Delta t$ достаточно мало, давление в точке ${{z}_{0}}$ в момент $t + \Delta t$ равно ${{p}_{t}}\Delta t$. Тогда наклон профиля давления
Чтобы связать производную ${{p}_{t}}$ c производной ${{\varepsilon }_{t}}$ воспользуемся связью $p = \rho \varepsilon (\gamma - 1)$, $\gamma = 5{\text{/}}3$, которая с хорошей точностью выполняется в расчетных точках вдоль оси симметрии (в точке максимума профиля ${{F}_{\alpha }}$ на рис. 10а погрешность этой формулы 4%, а уже в следующей точке внутрь волны погрешность падает до 0.4%). Подставляя эту связь в (23) и отбрасывая $\varepsilon {{\rho }_{t}}$ из-за малости ε, окончательно получим
Так как вблизи точки начала волны в силу малости скорости u частная производная по t совпадает с полной производной, ${{\varepsilon }_{t}}$ в (24) является правой частью уравнения (19). Как видно из рис. 10а, вблизи точки начала волны с большой точностью ${{\varepsilon }_{t}} = {{F}_{\alpha }}$.
На рис. 10а на профиле функции ${{F}_{\alpha }}$ показано значение $\varepsilon _{t}^{*}$, полученное из формулы (24) по значению $\left| {{{p}_{z}}} \right|$, приближенно вычисленному по профилю давления на рис. 10а, и указанному выше значению скорости волны D. Видно, что $\varepsilon _{t}^{*}$ действительно соответствует координате z вблизи точки начала волны.
Максимальное значение ${{F}_{\alpha }}$ на рис. 10а заметно больше $\varepsilon _{t}^{*}$. Возникает вопрос, можно ли найти на профиле ${{F}_{\alpha }}(z)$ значение, близкое к $\varepsilon _{t}^{*}$, не прибегая к формуле (24). Оказывается, что для этого достаточно воспользоваться тем, что вблизи точки с максимальным значением ${{F}_{\alpha }}$ профиль $p(z)$ еще не сформировался. Надо перебирать точки профиля ${{F}_{\alpha }}(z)$, двигаясь справа налево на рис. 10а, и выбрать первую точку, в которой локальный наклон профиля $p(z)$ отличается от заданного не больше, чем на 10%. Найденное таким образом значение отличается от $\varepsilon _{t}^{*}$ примерно на 5%.
Условие Чепмена–Жуге
Вернемся к рис. 11, где показан профиль вдоль оси симметрии функции $D - u - c$, где c – скорость звука, которая вычисляется по значениям ρ, ${{T}_{e}}$, ${{T}_{i}}$ и уравнениям состояния (5). Видно, что эта функция имеет близкий к нулю минимум примерно там, где профили p, u и ρ имеют максимум. Это дает основание, как и в случае детонационных волн [48], воспользоваться условием Чепмена–Жуге
которое вместе с уравнениями (21), (22) дают три уравнения относительно четырех неизвестных: скорости волны D и значений p, ρ и u в точке Чепмена–Жуге. Для приведенных на рис. 11 профилей скорость звука с хорошей точностью определяется формулой $c = \sqrt {\gamma p{\text{/}}\rho } $, $\gamma = 5{\text{/}}3$. Тогда уравнения (21), (22), (25) дают следующие простые формулы(26)
$\begin{gathered} D = \sqrt {\frac{{p(\gamma + 1)}}{{{{\rho }_{0}}}}} ,\quad u = \sqrt {\frac{p}{{{{\rho }_{0}}(\gamma + 1)}}} , \\ \rho = {{\rho }_{0}}\frac{{\gamma + 1}}{\gamma }, \\ \end{gathered} $Возьмем p равным максимальному значению на соответствующем профиле рис. 11, вычислим значения D, u и ρ по формулам (26) и сравним их со скоростью волны $D = 3350$ км/с и максимальными значениями u и ρ на соответствующих профилях рис. 11. Значения D отличаются примерно на 9%, а значения u примерно на 6%, что можно объяснить погрешностью определения максимальных величин в двумерном расчете. Различие в значениях плотности (примерно 25%) намного больше, что связано с указанным выше нарушением одномерности поля плотности вблизи оси симметрии.
О роли излучения
В работах [15, 16], где рассматривалась аналогичная задача для пучка тяжелых ионов с глубиной прогрева 6 г/см2, перед детонационной волной возникал предвестник с плотностью горючего существенно меньше начальной плотности 100 г/см3. Этот эффект авторы объясняют нагревом предвестника излучением, идущим из области термоядерного горения.
Для зажигающего драйвера с небольшой глубиной прогрева, который рассматривается в настоящей работе, такого эффекта не возникает. Излучение быстро проникает во всю расчетную область перед волной горения и начинает сравнительно медленно поднимать там температуру. Вместе с температурой растет давление, а скорость горючего, из-за отсутствия больших градиентов давления, остается небольшой, что влечет за собой небольшие изменения плотности. Расчет без учета излучения дает примерно такую же стационарную безударную волну горения, что и с учетом излучения, с небольшим опережением по времени.
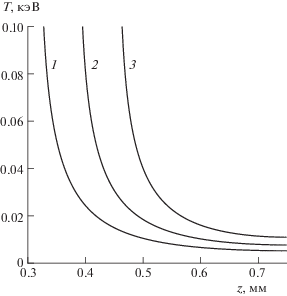
Анализ мощности нагрева горючего перед волной горения показывает, что при температуре примерно 0.1 кэВ и ниже основным механизмом нагрева является излучение. Приведем некоторые расчетные данные о температуре горючего и спектральном составе излучения в этой области.
На рис. 13 приведены профили температуры вдоль оси симметрии для области значений от 0.1 кэВ и ниже в три момента времени. Электронная и ионная температуры при таких значениях почти совпадают. Видно, что на большом расстоянии от волны температура слабо зависит от z и растет со временем, достигая при $t = 160$ пс значения примерно 0.01 кэВ. При приближении к волне горения производная $\partial T{\text{/}}\partial z$ плавно и достаточно быстро растет по абсолютной величине.
Рис. 13.
Низкотемпературные профили вдоль оси симметрии перед волной горения при $t = 120$ (1), 140 (2) и 160 пс (3).
Перейдем к спектральному составу излучения перед волной горения. Многогрупповая модель, которая используется для описания взаимодействия излучения с горючим, плохо приспособлена для наглядного описания спектрального состава, так как дает интегральные по частоте характеристики излучения в каждой группе. Представленные ниже зависимости получены решением диффузионного по телесному углу приближения стационарного уравнения переноса излучения
которое является исходным для многогрупповой модели и решается в некоторые моменты времени для очень подробного набора значений частоты ν. Здесь $\kappa (\nu ,\rho ,{{T}_{e}})$ – коэффициент тормозного поглощения с учетом индуцированного излучения [47], ${{u}_{\nu }}$ – спектральная плотность излучения, $B(\nu ,{{T}_{e}})$ – функция Планка, ${{R}_{\nu }}$ – спектральная плотность мощности нагрева излучением единицы объема горючего, которая определяет соответствующее слагаемое в правой части уравнения (3)На рис. 14 приведены функции ${{R}_{\nu }}(\nu )$ и ${{u}_{\nu }}(\nu )$ для двух моментов времени в точках на оси симметрии на примерно одинаковом расстоянии от положения волны горения. Обе функции растут по времени. Нагрев излучением определяется фотонами с частотой $\nu < 10$ кэВ несмотря на наличие значительно более энергичных фотонов (функция ${{u}_{\nu }}$ при $\nu = 30$ кэВ всего в четыре раза меньше своего максимального значения при $\nu \approx 5$ кэВ). Причиной является быстрое падение коэффициента тормозного поглощения с ростом ν ($\kappa \propto {{\nu }^{{ - 3}}}$).
Задача с искусственно завышенной начальной температурой
В настоящей работе не рассматривается нагрев горючего перед волной горения высокоэнергичными нейтронами DT-реакции. Чтобы оценить последствия такого нагрева, который может оказаться более значительным, чем нагрев излучением, выполнен расчет с искусственно завышенной до 1 кэВ начальной температурой горючего. Плотность горючего не меняется, а давление определяется уравнением состояния. Чтобы не допустить бокового разлета горючего до прихода волны горения, давление в оболочке полагается равным давлению в горючем, начальная плотность оболочки не меняется, а температура определяется уравнением состояния.
Из-за уноса энергии излучением происходит небольшое уменьшение со временем температуры перед волной горения. При $t = 160$ пс температура уменьшается до примерно 0.9 кэВ. Расчет показывает, что, по сравнению с основной рассмотренной задачей с температурой перед волной горения примерно 0.1 кэВ, увеличение этой температуры до 0.9 кэВ дает примерно такую же стационарную быструю безударную волну горения с немного уменьшенными значениями максимального давления и модуля наклона профиля давления.
5. ЗАКЛЮЧЕНИЕ
Применительно к краевому зажиганию цилиндрической оболочечной мишени пучком протонов с небольшой массовой глубиной прогрева примерно 0.5 г/см2, для двух значений начальной плотности ${{\rho }_{0}} = 500{{\rho }_{a}}$ и $100{{\rho }_{a}}$ (${{\rho }_{a}} \approx 0.22$ г/см3 – плотность горючего при атмосферном давлении) и заданных параметров пучка (интенсивности $J \sim {{\rho }_{0}}$ и времени действия $\Delta {{t}_{{{\text{pr}}}}} \sim \rho _{0}^{{ - 1}}$), рассмотрены три модели теплопередачи через границу между горючим и оболочкой.
Первой моделью является отсутствие теплопередачи, моделирующее наличие магнитного поля, достаточно сильного, чтобы воздействовать на электроны и существенно снизить отток тепла из горючего в оболочку (и недостаточно сильного, чтобы существенно повлиять на траектории движения нагревающих горючее α-частиц). Рассматривалось также некоторое приближение к задаче с нулевым потоком тепла в радиальном направлении, которая более адекватна теплопереносу при наличии сильного магнитного поля, чем задача с нулевым потоком тепла на границе раздела. Двумя другими моделями является обычное условие непрерывности температуры и теплового потока и некоторое условие температурного скачка, взятое из кинетической теории молекулярных газов и адаптированное к рассматриваемой задаче. Показано, что наличие сильного (в указанном выше смысле) магнитного поля уменьшает энергию зажигания всего примерно на 10%.
На основе равенства давления оболочки и горючего после изоэнтропического сжатия мишени до заданной плотности горючего изучается возможность выбора материала оболочки, имеющего максимальную плотность после сжатия $\rho _{0}^{{sh}}$, среди всех веществ с атомным весом золота $A$ и зарядом ядра $1 \leqslant Z \leqslant A - 1$. Показано, что $max\rho _{0}^{{sh}} = 70{{\rho }_{0}}$ достигается на изотопе водорода ($Z = 1$) для обоих значений ${{\rho }_{0}}$, в то время, как для золота $\rho _{0}^{{sh}}{\text{/}}{{\rho }_{0}} \approx 3$ и 4.5 для ${{\rho }_{0}} = 500{{\rho }_{a}}$ и $100{{\rho }_{a}}$ соответственно. По сравнению с золотой оболочкой такая гипотетическая тяжелая оболочка уменьшает энергию зажигания примерно на 30%.
По двум значениям предельного радиуса зажигания ${{R}_{ * }}({{\rho }_{0}})$ с заданной небольшой относительной задержкой зажигания получена приближенная формула ${{\rho }_{0}}{{R}_{ * }} \propto \rho _{0}^{{0.07}}$.
Изучен выход на стационарный режим возникающей при зажигании детонационной волны. Показано, что детонационная волна превращается в близкую к стационарной быструю безударную волну горения. Безударная волна возникает вначале в виде растущего со временем предвестника детонационной волны, а затем полностью ее заменяет. Основным механизмом распространения безударной волны является нагрев α-частицами.
Для модели локального нагрева горючего α‑частицами полного превращения детонационной волны в безударную волну горения не происходит. Безударная волна горения, механизмом распространения которой является теплопроводный нагрев, возникает только в виде предвестника детонационной волны.
Параметры волны зависят от вложенной энергии. Движение волны сопровождается вылетом за пределы горючего α-частиц, которые уносят примерно половину их исходной мощности. Коэффициент усиления G зависит от вложенной энергии и растет со временем, выходя на примерно постоянную скорость роста. Для одного из вариантов определена скорость волны $D \approx 3350$ км/с и размер мишени H вдоль оси симметрии (${{\rho }_{0}}H \approx 10$ г/см2), для которого $G = 1250$. Коэффициент выгорания горючего примерно 0.3 и немного растет со временем.
Профили давления, скорости и плотности вдоль оси симметрии в безударной волне горения близки к линейным, а два первых профиля с хорошей точностью удовлетворяют соотношению, вытекающему из одномерных стационарных уравнений непрерывности и движения в системе координат, связанной с волной. Другое соотношение, в которое входит профиль плотности, удовлетворяется значительно хуже, что связано с нарушением одномерности поля плотности вблизи оси симметрии.
Получена приближенная формула, связывающая наклон профиля давления в стационарной волне со скоростью волны и мощностью нагрева единицы массы горючего вблизи точки начала волны. Указан алгоритм, позволяющий найти на профиле мощности нагрева горючего точку, для которой точность выполнения формулы примерно 5%.
Показано, что к стационарной безударной волне горения с точностью меньше 10% применимы формулы для сильной детонационной волны, определяющие скорость волны и массовую скорость в точке Чепмена–Жуге по давлению в точке Чепмена–Жуге, если в качестве значений в точке Чепмена–Жуге брать максимальные значения на соответствующих профилях вдоль оси симметрии.
В отличие от работ [15, 16] с пучком тяжелых ионов в качестве зажигающего драйвера, прогрев излучением не приводит к появлению области пониженной плотности перед волной горения. Излучение быстро проникает во всю расчетную область перед волной горения и начинает сравнительно медленно поднимать там температуру. Температура непосредственно перед волной примерно 0.1 кэВ, а температура вдали от волны примерно 0.01 кэВ в конце расчета. Нагрев излучением определяется фотонами с частотой $\nu < 10$ кэВ.
Искусственное повышение температуры перед волной до 0.9 кэВ, которое можно рассматривать в качестве грубой модели прогрева горючего высокоэнергичными нейтронами DT-реакции, дает примерно такую же стационарную быструю безударную волну горения с немного уменьшенными значениями максимального давления и модуля наклона профиля давления.
Список литературы
Аврорин Е.Н., Бунатян А.А., Гаджиев А.Д., Мустафин К.А., Нурбаков А.Ш., Писарев В.Н., Феоктистов Л.П., Фролов В.Д., Шибаршов Л.И. // Физика плазмы. 1984. Т. 10. С. 514.
Basov N.G., Gus’kov S.Y., Feoktistov L.P. // J. Sov. Laser Research. 1992. V. 13. P. 396.
Tabak M., Hammer J., Glinsky M.E., Kruer W.L., Wilks S.C., Woodworth J., Campbell E.M., Perry M.D., Mason R.J. // Phys. Plasmas. 1994. V. 1. P. 1626.
Щербаков В.А. // Физика плазмы. 1983. Т. 9. С. 409.
Betti R., Zhou C.D., Anderson K.S., Perkins L.J., Theobald W., Solodov A.A. // Phys. Rev. Lett. 2007. V. 98. P. 155001.
Гуськов С.Ю., Змитренко Н.В., Ильин Д.В., Шерман В.Е. // ЖЭТФ. 2014. Т. 146. С. 1090.
Roth M., Cowan T.E., Key M.H., Hatchett S.P., Brown C., Fountain W., Johnson J., Pennington D.M., Snavely R.A., Wilks S.C., Yasuike K., Ruhl H., Pegoraro F., Bulanov S.V., Campbell E.M., Perry M.D., Powell H. // Phys. Rev. Lett. 2001. V. 86. P. 436.
Гуськов С.Ю. // Квант. электроника. 2001. Т. 31. С. 885.
Гуськов С.Ю., Змитренко Н.В., Ильин Д.В., Шер-ман В.Е. // Физика плазмы. 2015. Т. 41. С. 788.
Atzeni S. // Phys. Plasmas. 1999. V. 6. P. 3316.
Temporal M., Honrubia J.J., Atzeni S. // Phys. Plasmas. 2008. V. 15. P. 052702.
Atzeni S., Schiavi A., Bellei S. // Phys. Plasmas. 2007. V. 14. P. 052702.
Гуськов С.Ю., Демченко Н.Н., Змитренко Н.В., Кучугов П.А., Розанов В.Б., Степанов Р.В., Яхин Р.А. // Письма в ЖЭТФ. 2017. Т. 105. С. 381.
Caruso A., Strangio C. // Laser Part. Beams. 2001. V. 19. P. 295.
Basko M.M., Churazov M.D., Aksenov A.G. // Laser Part. Beams. 2002. V. 20. P. 411.
Vatulin V.V., Vinokurov O.A. // Laser Part. Beams. 2002. V. 20. P. 415.
Ramis R., Meyer-ter-Vehn J. // Laser Part. Beams. 2014. V. 32. P. 41.
Хищенко К.В., Чарахчьян А.А. // ВАНТ. Сер. Мат. моделирование физических процессов. 2015. Вып. 1. С. 3.
Charakhch’yan A.A., Khishchenko K.V. // Plasma Phys. Control. Fusion. 2013. V. 55. P. 105011.
Хищенко К.В., Чарахчьян А.А. // Физика плазмы. 2015. Т. 41. С. 240.
Пашинин П.П., Прохоров А.М. // ЖЭТФ. 1972. Т. 62. С. 189.
Kemp A.J., Basko M.M., Meyer-ter-Vehn J. // Nucl. -Fusion. 2003. V. 43. P. 16.
Бракнер К., Джорна С. Управляемый лазерный синтез. М.: Атомиздат, 1977.
Баско М.М. Препринт ИТЭФ № 87. М.: ИТЭФ, 1989.
Настоящий А.Ф., Шевченко Л.П. // Атомная энергия. 1972. Т. 32. С. 451.
Феоктистов Л.П. // УФН. 1998. Т. 168. С. 1247.
Феоктистов Л.П. Избранные труды. Снежинск: Изд-во РФЯЦ–ВНИИТФ, 2007. С. 13.
Аврорин Е.Н., Феоктистов Л.П., Шибаршов Л.И. // Физика плазмы. 1980. Т. 6. С. 965.
Gus’kov S.Yu, Krokhin O.N., Rozanov V.B. //Nucl. Fusion. 1976. V. 16. P. 957.
Гуськов С.Ю., Розанов В.Б. // Труды ФИАН. 1982. Т. 134. С. 153.
Гуськов С.Ю., Змитренко Н.В., Ильин Д.В., Левковский А.А., Розанов В.Б., Шерман В.Е. // ЖЭТФ. 1994. Т. 106. С. 1069.
Chu M.S. //Phys. Fluids. 1972. V. 15. P. 413.
Дюдерштадт Д., Мозес Г. Инерционный термоядерный синтез. М.: Энергоатомиздат, 1984.
Гуськов С.Ю., Розанов В.Б. // Труды ФИАН. 1982. Т. 134. С. 115.
Khishchenko K.V. // J. Phys.: Conf. Ser. 2008. V. 98. P. 032023.
Charakhch’yan A.A., Khishchenko K.V. // J. Phys.: Conf. Ser. 2016. V. 774. P. 012113.
Holzapfel W.B. // High Press. Res. 2010. V. 30. P. 372.
Калиткин Н.Н. //ЖЭТФ. 1960. Т. 38. С. 1534.
Калиткин Н.Н., Кузьмина Л.В. Препринт ИПМ АН СССР № 14. М.: ИПМ АН СССР, 1976.
Долголева Г. В., Забродина Е.А. Препринт ИПМ РАН № 68. M.: ИПМ РАН, 2014.
Fowler W.A., Caughlam G.R., Zimmerman B.A. // A-nnu. Rev. Astron. Astrophys. 1972. V. 18. P. 69.
Фролова А.А., Хищенко К.В., Чарахчьян А.А. // Журн. вычисл. матем. и матем. физ. 2016. Т. 36. С. 442.
Хищенко К.В., Чарахчьян А.А. // ВАНТ. Сер. Мат. моделирование физических процессов. 2016. Вып. 4. С. 51.
Федоренко Р.П. Введение в вычислительную физику. М.: МФТИ, 1994.
Коган М.Н. Динамика разреженного газа. М.: Наука, 1967.
Lindl J.D. // Phys. Plasmas. 1995. V. 2. P. 3933.
Баско М.М. Физические основы инерциального термоядерного синтеза. М.: МИФИ, 2009.
Зельдович Я.Б., Компанеец А.С. Теория детонации. М.: Гостехиздат, 1955.
Ландау Л.В., Лифшиц Е.М. Гидродинамика. М.: Наука, 1986.
Дополнительные материалы отсутствуют.