Физика плазмы, 2019, T. 45, № 9, стр. 848-864
Пылевые ионно-звуковые уединенные структуры на звуковой скорости в присутствии нетепловых электронов и изотермических позитронов
A. Paul a, A. Bandyopadhyay a, *, K. P. Das b
a Department of Mathematics, Jadavpur University
Kolkata, India
b Department of Applied Mathematics, University of Calcutta
Kolkata, India
* E-mail: abandyopadhyay1965@gmail.com
Поступила в редакцию 02.02.2018
После доработки 31.05.2018
Принята к публикации 31.05.2018
Аннотация
Метод псевдопотенциалов Сагдеева и теория, развитая в работе [J. Plasma Phys. 78, 565 (2012)], используются для изучения пылевых ионно-звуковых уединенных структур, движущихся со звуковой скоростью, в бесстолкновительной незамагниченной пылевой плазме, состоящей из отрицательно заряженных неподвижных пылевых частиц, адиабатических теплых ионов, нетепловых электронов и изотермических позитронов. Данная система допускает существование солитонов как с положительным, так и с отрицательным потенциалом со звуковой скоростью, но не допускает одновременное сосуществование уединенных структур противоположной полярности со звуковой скоростью. Система также допускает существование двойного слоя отрицательного потенциала на звуковой скорости, но не допускает существование двойного слоя положительного потенциала. Хотя система допускает существование суперсолитона положительного потенциала сосверхзвуковой скоростью, но на звуковой скорости не существует суперсолитонов любой полярности. Уединенные структуры исследуются с помощью составного пространства параметров и фазовых портретов динамической системы, описывающей нелинейное поведение пылевых ионно-звуковых волн на звуковых скоростях. В случае, когда в системе нет позитронов, существует двойной слой отрицательного потенциала и суперсолитон отрицательного потенциала со звуковой скоростью, и для этого случая с помощью фазовых портретов обсуждается механизм перехода суперсолитона в солитон после формирования двойного слоя на звуковой скорости. Различия между уединенными структурами на звуковой и на сверхзвуковой скорости анализируются с помощью фазовых портретов.
1. ВВЕДЕНИЕ
Исследования пылевых ионно-звуковых солитонов (DIA – dust ion acoustic) в четырехкомпонентной электронно-позитронно-ионно-пылевой (e-p-i-d) плазме в последние годы привлекают большое внимание, поскольку e-p-i-d-плазма может быть обнаружена во многих уголках космоса, например, вокруг пульсаров [1], вблизи поверхности нейтронных звезд [1, 2], в горячих пятнах на пылевых кольцах в центре галактики [3], в межзвездной среде [3–5], во внешних областях дисков аккреции вблизи нейтронных звезд и магнетаров [6], в Млечном пути [5], в магнитосфере и ионосфере Земли [7–9], в магнитосферах Юпитера [10] и Сатурна [11], а также в лабораторных условиях [1, 6]. Используя метод редуктивных возмущений, в статье [12] было исследовано нелинейное распространение ионных акустических (IA – ion acoustic) солитонов малых, но конечных амплитуд, и двойных слоев в бесстолкновительной незамагниченной e-p-i-d-плазме, состоящей из холодных ионов, отрицательно заряженных неподвижных частиц пыли и распределенных по Больцману электронов и позитронов. Используя метод псевдопотенциалов Бернулли, Дубинов и др. [6] разработали нелинейную теорию DIA-волн в бесстолкновительной незамагниченной четырехкомпонентной e-p-i-d-плазме, состоящей из теплых ионов, отрицательно заряженных включений неподвижной пыли, изотермических электронов и позитронов. Некоторые авторы [13–16] исследовали DIA уединенные структуры малой или произвольной амплитуды в различных e-p-i-d плазменных системах. Польи др. [17] исследовали существование различных DIA уединенных структур в бесстолкновительной незамагниченной четырехкомпонентной e-p-i-d-плазме, состоящей из отрицательно заряженных неподвижных частиц пыли, адиабатических теплых ионов, изотермически распределенных электронов и позитронов. Они подтвердили существование уединенных волн обеих полярностей, сосуществование уединенных волн обеих полярностей, существование двойных слоев обеих полярностей и существование солитонов положительного потенциала после образования двойного слоя положительного потенциала. Существование солитонов положительного потенциала после образования двойного слоя положительного потенциала подтверждает существование суперсолитонов положительного потенциала. Кроме того, в работе [18] рассмотрена e-p-i-d плазменная система, аналогичная системе, рассмотренной в [17], где вместо изотермических электронов рассматриваются нетепловые электроны с распределением Кернса [19]. В работе [18] DIA-солитоны детально исследовались с помощью качественно различных составных пространств параметров, были показаны условия существования различных солитонов, особое внимание уделялось существованию солитонов после образования двойного слоя одинаковой полярности. Недавно Поль и др. [20] детально рассмотрели формирование суперсолитона с помощью фазовых портретов динамической системы, описали нелинейное поведение DIA‑волн в четырехкомпонентной e-p-i-d-плазме, состоящей из нетепловых электронов и нетепловых позитронов. Они подробно обсудили переходные процессы различных уединенных структур, а именно: солитон → двойной слой → → суперсолитон → солитон после образования двойного слоя для возрастающих значений числа Маха.
В упомянутых выше работах DIA-солитоны рассматривались только на сверхзвуковых скоростях, т.е. для $U > {{C}_{D}}$, где U – скорость волнового пакета, а ${{C}_{D}}$ – линеаризованная скорость DIA‑волны длинноволнового возмущения плоской волны. Однако численные наблюдения [21–23] солитонов при скорости звука, т.е. для $U = {{C}_{D}}$, подтолкнули Дасаи др. [24] к развитию общей аналитической теории для существования солитонов на звуковых скоростях, т.е. для $U = {{C}_{D}} \Leftrightarrow $ $ \Leftrightarrow M = {{M}_{c}}$, где $M = U{\text{/}}{{C}_{D}}$ и ${{M}_{c}}$ – нижняя граница чисел Маха для существования солитонов, т.е. солитоны существуют при $M > {{M}_{c}}$. Фактически, в [24] было получено три важных результата, подтверждающих существование солитонов на звуковой скорости. Даси др. [24] исследовали пылевые звуковые (IA) солитоны со скоростью звука с помощью аналитической теории, развитой в этой же статье, ими также была предложена вычислительная схема для исследования условий существования солитонов на скорости звука. Позже они [25] рассмотрели DIA-солитоны на звуковой скорости в бесстолкновительной незамагниченной плазме, состоящей из отрицательно заряженных неподвижных пылевых частиц, адиабатических теплых ионов и нетепловых электронов с распределением Кернса. Было обнаружено, что система допускает существование солитонов отрицательного потенциала (NPSWs – the negative potential solitary waves), солитонов положительного потенциала (PPSWs – the positive potential solitary waves), двойного слоя положительного потенциала (NPDLs – negative potential double layers) и суперсолитонов отрицательного потенциала на звуковой скорости. Показаны также качественно различные области существования DIA уединенных структур на скорости звука. Некоторое время назад в [26] было проведено исследование существования IA- и DIA-солитонов на скорости звука и доказано существование NPDL и суперсолитона отрицательного потенциала на звуковой скорости.
В настоящей работе, следуя аналитическим методам и вычислительной схеме, разитым в работе [24], мы рассматриваем DIA уединенные структуры на звуковой скорости с помощью областей существования и фазовых портретов динамической системы, описывающей нелинейное поведение DIA-волн плазменной системе, рассмотренной в [18]. По сути, настоящая работа является продолжением опубликованной работы [18] по следующим направлениям.
1. Вместо DIA уединенных структур на сверхзвуковых скоростях ($U > {{C}_{D}} \Leftrightarrow M > {{M}_{c}}$), рассматриваются различные DIA уединенные структуры на звуковой скорости ($U = {{C}_{D}} \Leftrightarrow M = {{M}_{c}}$) в бесстолкновительной незамагниченной четырехкомпонентной e-p-i-d-плазме, состоящей из отрицательно заряженных неподвижных пылевых частиц, адиабатических теплых ионов, нетепловых электронов с распределением Кернса [19] и изотермических позитронов.
2. Впервые представлен анализ фазовых портретов динамических систем, соответствующих уединенным структурам со звуковой скоростью ($U = {{C}_{D}} \Leftrightarrow M = {{M}_{c}}$).
3. Фазовые портреты динамических систем, соответствующих различным солитонам демонстрируют четкое различие между солитонами со звуковой ($U = {{C}_{D}} \Leftrightarrow M = {{M}_{c}}$) и солитонами со сверхзвуковой скоростью ($U > {{C}_{D}} \Leftrightarrow M > {{M}_{c}}$).
4. Также рассмотрен случай отсутствия позитронов в системе. В этом случае возможно формирование NPSWs после формирования NPDL. Существование NPSWs после формирования NPDL подтверждает существование суперсолитонов отрицательного потенциала. Здесь также обсуждаются переходные процессы уединенных структур отрицательного потенциала на звуковых скоростях, а именно: солитон → двойной слой → суперсолитон → солитон после образования двойного слоя. Показано, что переходные процессы для различных уединенных структур на звуковых скоростях $U = {{C}_{D}} \Leftrightarrow M = {{M}_{c}}$ аналогичны переходным процессам для уединенных структур на сверхзвуковых скоростях ($U > {{C}_{D}} \Leftrightarrow M > {{M}_{c}}$).
2. ОСНОВНЫЕ УРАВНЕНИЯ И ИНТЕГРАЛ ЭНЕРГИИ
Рассматриваемая в данной работе плазменная система в точности соответствует системе из работы [18], следовательно, мы рассматриваем систему основных уравнений для описания условий существования DIA уединенных структур на звуковой скорости из работы [18]. Далее представлены основные уравнения, описывающие нелинейное поведение DIA-волн, распространяющихся вдоль оси x в бесстолкновительной незамагниченной мультикомпонентной пылевой плазменной системе, состоящей из адиабатических теплых ионов, отрицательно заряженных неподвижных пылевых частиц, электронов с нетепловым распределением и изотермических позитронов
(1)
$\frac{{\partial {{n}_{i}}}}{{\partial t}} + \frac{\partial }{{\partial x}}({{n}_{i}}{{u}_{i}}) = 0,$(2)
${{n}_{i}}{{m}_{i}}\left( {\frac{{\partial {{u}_{i}}}}{{\partial t}} + {{u}_{i}}\frac{{\partial {{u}_{i}}}}{{\partial x}}} \right) + \frac{{\partial {{p}_{i}}}}{{\partial x}} + {{n}_{i}}e\frac{{\partial \phi }}{{\partial x}} = 0,$(3)
$\frac{{\partial {{p}_{i}}}}{{\partial t}} + {{u}_{i}}\frac{{\partial {{p}_{i}}}}{{\partial x}} + \gamma {{p}_{i}}\frac{{\partial {{u}_{i}}}}{{\partial x}} = 0,$(4)
$\frac{{{{\partial }^{2}}\phi }}{{\partial {{x}^{2}}}} = - 4\pi e\left( {{{n}_{i}} - {{n}_{e}} + {{n}_{p}} - {{Z}_{d}}{{n}_{{d0}}}} \right).$Уравнения (1)–(4) должны быть дополнены следующими уравнениями для концентраций нетепловых электронов, изотермических позитронов и условием электронейтральности в невозмущенном состоянии
(5)
${{n}_{e}} = {{n}_{{e0}}}\left[ {1 - {{\beta }_{e}}\left( {\frac{{e\phi }}{{{{K}_{B}}{{T}_{e}}}}} \right) + {{\beta }_{e}}{{{\left( {\frac{{e\phi }}{{{{K}_{B}}{{T}_{e}}}}} \right)}}^{2}}} \right]{\text{exp}}\left[ {\frac{{e\phi }}{{{{K}_{B}}{{T}_{e}}}}} \right],$Здесь ${{n}_{i}}$, ${{n}_{e}}$, ${{n}_{p}}$, ${{u}_{i}}$, ${{p}_{i}}$, ϕ, x и t – концентрации ионов, электронов и позитронов, скорость ионной жидкости, давление ионной жидкости, электростатический потенциал, переменная пространства и времени соответственно. Концентрации ${{n}_{{e0}}}$, ${{n}_{{i0}}}$, ${{n}_{{p0}}}$ и ${{n}_{{d0}}}$ – равновесные концентрации электронов, ионов, позитронов, пылевых частиц соответственно, ${{K}_{B}}$ – постоянная Больцмана, $\gamma ( = 3)$ – показатель адиабаты, ${{Z}_{d}}$ – количество электронов, осевших на поверхности пылевой частицы, e – заряд электрона, ${{m}_{i}}$ – масса иона, ${{T}_{i}}$, ${{T}_{e}}$ и ${{T}_{p}}$ – средние температуры ионов, электронов и позитронов соответственно. Здесь ${{\beta }_{e}}$ – нетепловой параметр, связанный с моделью Кернса [19] для электронов, физически допустимые значения которого лежат в пределах $0 \leqslant {{\beta }_{e}} \leqslant 4{\text{/}}7 \approx 0.6$ [27].
Линейный закон дисперсии для DIA-волн в рассматриваемой плазменно-пылевой системе может быть представлен в виде
(8)
$\frac{\omega }{k} = {{C}_{D}}\sqrt {\frac{{1 + \frac{{\gamma {{\sigma }_{{ie}}}}}{{M_{s}^{2}}}{{k}^{2}}\lambda _{D}^{2}}}{{1 + {{k}^{2}}\lambda _{D}^{2}}}} ,$(10)
${{C}_{s}} = \sqrt {\frac{{{{K}_{B}}{{T}_{e}}}}{{{{m}_{i}}}}} ,\quad {{M}_{s}} = \sqrt {\gamma {{\sigma }_{{ie}}} + \frac{{(1 - p){{\sigma }_{{pe}}}}}{{p + \mu (1 - {{\beta }_{e}}){{\sigma }_{{pe}}}}}} ,$(11)
$\frac{1}{{\lambda _{D}^{2}}} = \frac{1}{{\lambda _{{Dp}}^{2}}} + \frac{{1 - {{\beta }_{e}}}}{{\lambda _{{De}}^{2}}},$(12)
$\lambda _{{Dp}}^{2} = \frac{{{{K}_{B}}{{T}_{p}}}}{{4\pi {{e}^{2}}{{n}_{{p0}}}}},\quad \lambda _{{De}}^{2} = \frac{{{{K}_{B}}{{T}_{e}}}}{{4\pi {{e}^{2}}{{n}_{{e0}}}}},$(13)
${{\sigma }_{{ie}}} = \frac{{{{T}_{i}}}}{{{{T}_{e}}}},\quad {{\sigma }_{{pe}}} = \frac{{{{T}_{p}}}}{{{{T}_{e}}}},\quad p = \frac{{{{n}_{{p0}}}}}{{{{n}_{0}}}},\quad \mu = \frac{{{{n}_{{e0}}}}}{{{{n}_{0}}}},$Для длинноволнового возмущения плоской волны, т.е. для $k \to 0$ из линейного дисперсионного уравнения (8) получаем
(15)
$\mathop {lim}\limits_{k \to 0} \frac{\omega }{k} = {{C}_{D}}\quad {\text{and}}\quad \mathop {lim}\limits_{k \to 0} \frac{{d\omega }}{{dk}} = {{C}_{D}}$В настоящей задаче, следуя Дубинову (2009) [28], пространственная координата обезразмерена на ${{\lambda }_{D}}$, а время обезразмерено на величину $\frac{{{{\lambda }_{D}}}}{{{{C}_{D}}}}$. Итак, мы используем следующую нормировку для зависимых и независимых переменных: ${{n}_{i}}$, ${{n}_{e}}$, ${{n}_{p}}$, ${{u}_{i}}$, ${{p}_{i}}$, ϕ, x и t нормированы соответственно на ${{n}_{0}}$ ($ = {\kern 1pt} {{n}_{{i0}}} + {{n}_{{p0}}} = {{n}_{{e0}}} + {{Z}_{d}}{{n}_{{d0}}}$), ${{n}_{0}}$, ${{n}_{0}}$, ${{C}_{D}}$ (линеаризованная скорость DIA-волны в рассматриваемой плазменной системе для длинноволнового плоского возмущения), ${{n}_{{i0}}}{{K}_{B}}{{T}_{i}}$, $\Phi = \frac{{{{K}_{B}}{{T}_{e}}}}{e}$, ${{\lambda }_{D}}$ (радиус Дебая для рассматриваемой плазменной системы) и ${{\lambda }_{D}}{\text{/}}{{C}_{D}}$.
Используя упомянутую выше нормировку для зависимых и независимых переменных, уравнения (1)–(6) могут быть переписаны в виде
(16)
$\frac{{\partial {{n}_{i}}}}{{\partial t}} + \frac{\partial }{{\partial x}}({{n}_{i}}{{u}_{i}}) = 0,$(17)
$M_{s}^{2}\left( {\frac{{\partial {{u}_{i}}}}{{\partial t}} + {{u}_{i}}\frac{{\partial {{u}_{i}}}}{{\partial x}}} \right) + \frac{{(1 - p){{\sigma }_{{ie}}}}}{{{{n}_{i}}}}\frac{{\partial {{p}_{i}}}}{{\partial x}} + \frac{{\partial \phi }}{{\partial x}} = 0,$(18)
$\frac{{\partial {{p}_{i}}}}{{\partial t}} + {{u}_{i}}\frac{{\partial {{p}_{i}}}}{{\partial x}} + \gamma {{p}_{i}}\frac{{\partial {{u}_{i}}}}{{\partial x}} = 0,$(19)
$\frac{{{{\partial }^{2}}\phi }}{{\partial {{x}^{2}}}} = - \frac{{M_{s}^{2} - \gamma {{\sigma }_{{ie}}}}}{{1 - p}}\left( {{{n}_{i}} - {{n}_{e}} + {{n}_{p}} - \frac{{{{Z}_{d}}{{n}_{{d0}}}}}{{{{n}_{0}}}}} \right).$Для исследования устойчивых DIA-солитонов произвольной амплитуды представим все зависимые переменные зависящими только от одной переменной $\xi = x - Mt$, где M – безразмерная скорость волнового пакета, нормированная на линеаризованную DIA-скорость (${{C}_{D}}$) для длинноволнового плоского возмущения.
Используя это преобразование и полагая граничные условия равными
(23)
$\begin{gathered} V(\phi ) = (M_{s}^{2} - 3{{\sigma }_{{ie}}})\left[ {{{V}_{i}} + \frac{p}{{1 - p}}{{\sigma }_{{pe}}}{{V}_{p}} - } \right. \\ \left. {\, - \frac{\mu }{{1 - p}}{{V}_{e}} - \frac{{1 - \mu }}{{1 - p}}{{V}_{d}}} \right], \\ \end{gathered} $(24)
$\begin{gathered} {{V}_{i}} = {{M}^{2}}M_{s}^{2} + {{\sigma }_{{ie}}} - \\ \, - {{N}_{i}}[{{M}^{2}}M_{s}^{2} + 3{{\sigma }_{{ie}}} - 2\phi - 2{{\sigma }_{{ie}}}N_{i}^{2}], \\ \end{gathered} $(25)
${{N}_{i}} = \frac{{{{n}_{i}}}}{{1 - p}} = \frac{{M{{M}_{s}}\sqrt 2 }}{{(\sqrt {{{\Phi }_{M}} - \phi } + \sqrt {{{\Psi }_{M}} - \phi } )}},$(26)
${{\Phi }_{M}} = \frac{1}{2}{{\left( {M{{M}_{s}} + \sqrt {3{{\sigma }_{{ie}}}} } \right)}^{2}},$(27)
${{\Psi }_{M}} = \frac{1}{2}{{\left( {M{{M}_{s}} - \sqrt {3{{\sigma }_{{ie}}}} } \right)}^{2}},$(28)
${{V}_{e}} = (1 + 3{{\beta }_{e}} - 3{{\beta }_{e}}\phi + {{\beta }_{e}}{{\phi }^{2}}){{e}^{\phi }} - (1 + 3{{\beta }_{e}}),$Интеграл энергии (22) можно интерпретировать как уравнение одномерного движения частицы единичной массы с координатой ϕ в момент времени ξ, движущейся со скоростью $d\phi {\text{/}}d\xi $ под действием силового поля $ - V'(\phi )$. Первое слагаемое в интеграле энергии (22) тогда играет роль кинетической энергии частицы единичной массы с координатой ϕ в момент времени ξ, а $V(\phi )$ – потенциальной энергии этой частицы в этот момент времени. Далее, согласно работе Р.З. Сагдеева [29], для существования решения уравнения (22) в виде солитона с положительным потенциалом (PPSW – positive potential solitary wave; солитон с отрицательным потенциалом – a negative potential solitary wave – NPSW) должны выполняться три условия:
1) $\phi = 0$ – это положение неустойчивого равновесия частицы единичной массы, связванной с интегралом энергии (22), т.е. $V(0) = V'(0) = 0$ и $V''(0) < 0$;
2) $V({{\phi }_{m}}) = 0$, $V'({{\phi }_{m}}) > 0$ ($V'({{\phi }_{m}}) < 0$) для ${{\phi }_{m}} > 0$ (${{\phi }_{m}} < 0$). Это условие соответствует осцилляциям частицы внутри интервала $min\{ 0,{{\phi }_{m}}\} < \phi < $ $ < max\{ 0,{{\phi }_{m}}\} $;
3) $V(\phi ) < 0$ для всех $0 < \phi < {{\phi }_{m}}$ (${{\phi }_{m}} < \phi < 0$). Это условие необходимо для того, чтобы определить интеграл энергии (22) в рамках интервала $min\{ 0,{{\phi }_{m}}\} < \phi < max\{ 0,{{\phi }_{m}}\} $. Для существования решения (22) в виде двойного слоя положительного (отрицательного) потенциала (PPDL(NPDL)), второе условие заменяется на $V({{\phi }_{m}}) = 0$, $V'({{\phi }_{m}}) = 0$, $V''({{\phi }_{m}}) < 0$ для ${{\phi }_{m}} > 0$ (${{\phi }_{m}} < 0)$. Это условие определяет, что частица не может отражаться назад от точки $\phi = {{\phi }_{m}}$ до точки $\phi = 0$.
Таким образом, необходимые условия существования солитонов и/или двойных слоев любой полярности подразумевают, что $\phi = 0$ является положением неустойчивого равновесия частицы единичной массы, связанной с интегралом энергии (22), т.е. $V''(0) < 0$ наряду с $V(0) = 0$ и $V'(0) = 0$. Другими словами, $\phi = 0$ может быть положением неустойчивого равновесия, если потенциальная энергия указанной частицы достигает своего максимума при $\phi = 0$. Теперь из условия $V''(0) < 0$ получаем $M > {{M}_{c}} = 1$, т.е. уединенные структуры (солитоны или/и двойные слои) начинают существовать чуть выше кривой $M = {{M}_{c}} = 1$. Условие $V''(0) > 0$ дает $M < {{M}_{c}} = 1$. Если $M < {{M}_{c}}$, потенциальная энергия указанной частицы достигает своего минимума при $\phi = 0$, и, следовательно, $\phi = 0$ – положение устойчивого равновесия частицы. В этом случае частица не может совершать колебания, даже если она слегка смещается от положения равновесия. Поэтому вопрос о существовании солитонов или двойных слоев любой полярности не возникает при $M < {{M}_{c}}$.
Рассмотрим теперь случай $V''(0) = 0 \Leftrightarrow M$ = = ${{M}_{c}} \Leftrightarrow V''({{M}_{c}},0) = 0$. Если $V''({{M}_{c}},0) = 0$ одновременно с $V'''({{M}_{c}},0) = 0$, то $\phi = 0$ – устойчивое или неустойчивое положение равновесия в зависимости от знака $V''''({{M}_{c}},0) > 0$ или $V''''({{M}_{c}},0) < 0$. Когда $V''''({{M}_{c}},0) < 0$, то уединенные структуры могут существовать при $M = {{M}_{c}}$, если другие условия неустойчивости уединенных структур удовлетворены. Для $V''''({{M}_{c}},0) > 0$ не существует уединенных структур при $M = {{M}_{c}}$. Однако при $V'''({{M}_{c}},0) \ne 0$ одновременно с $V({{M}_{c}},0) = $ $ = V'({{M}_{c}},0)$ = $V''({{M}_{c}},0) = 0$, следуя аналитической теории, развитой в работе [24], можно с легкостью изучать существование решений уравнения для интеграла энергии (22) в виде солитонов и/или двойных слоев для $M = {{M}_{c}}$.
Если $V(M,0) = V'(M,0)$ = $V''({{M}_{c}},0) = 0$, $V'''({{M}_{c}},0) < 0$ ($V'''({{M}_{c}},0) > 0$), $\partial V{\text{/}}\partial M < 0$ для всех $M > 0$ и для всех $\phi > 0$ ($\phi < 0$), Дас и др. [24] предложили следующие важные результаты для подтверждения существования уединенных структур на звуковой скорости.
Результат 1. Если существует хотя бы одно значение ${{M}_{0}}$ из M такое, что система допускает существование PPSWs (NPSWs) для всех ${{M}_{c}} < M < {{M}_{0}}$, то существует или PPSW (NPSW), или PPDL (NPDL) при $M = {{M}_{c}}$.
Результат 2. Если система допускает существование только NPSWs (PPSWs) для $M > {{M}_{c}}$, то не существует PPSW (NPSW) при $M = {{M}_{c}}$.
Результат 3. Невозможно одновременное существование уединенных структур противоположной полярности при $M = {{M}_{c}}$.
Согласно работе Даса и др. [24], решение в виде PPDL (NPDL) при $M = {{M}_{c}}$ возможно только тогда, когда существует решение в виде PPDL (NPDL) в любой правой окрестности ${{M}_{c}}$, т.е. PPDL (NPDL) решение при $M = {{M}_{c}}$ возможно только в случае, когда кривая $M = {{M}_{{PPDL}}}$ ($M = {{M}_{{NPDL}}}$) стремится пересечь $M = {{M}_{c}}$ в некоторой точке в области существования интеграла энергии, где каждая точка кривой $M = {{M}_{{PPDL}}}$ ($M = {{M}_{{NPDL}}}$) соответствует решению интеграла энергии в виде PPDL (NPDL) при ${{M}_{{PPDL}}} > {{M}_{c}}$ (${{M}_{{NPDL}}} > {{M}_{c}}$).
Из Результата 1, Результата 2 и Результата 3 следует, что существование уединенных структур при $M = {{M}_{c}}$ зависит от существования уединенных структур при $M > {{M}_{c}}$. В следующем разделе мы рассмотрим качественно различные области существования уединенных структур при $M > {{M}_{c}}$ для того, чтобы исследовать существование и полярность уединенных структур при $M = {{M}_{c}}$.
3. РАЗЛИЧНЫЕ ОБЛАСТИ СУЩЕСТВОВАНИЯ
Из обсуждения, приведенного в предыдущем разделе, следует, что для того, чтобы применить Результат 1, Результат 2 и Результат 3 [24] необходимо иметь определенные сведения о существовании и полярности уединенных структур в правой окрестности $M = {{M}_{c}}$. Продифференцировав V по M, получим следующее уравнение:
(30)
$\frac{{\partial V}}{{\partial M}} = - {{\left\{ {\sqrt {\frac{{M_{s}^{2}M(1 - p){{\sigma }_{{pe}}}}}{{p + \mu (1 - {{\beta }_{e}}){{\sigma }_{{pe}}}}}} \left( {\sqrt {{{N}_{i}}} - \frac{1}{{\sqrt {{{N}_{i}}} }}} \right)} \right\}}^{2}}.$Из уравнения (30) легко убедиться, что выполняются следующие условия:
Следовательно, все условия Результата 1, Результата 2 и Результата 3 выполняются при $V'''({{M}_{c}},0) \ne 0$. Итак, для обсуждения существования и полярности уединенных структур при $M = {{M}_{c}}$, необходимо изучить качественно различные области существования для $M > {{M}_{c}}$. Также необходимо определить знак $V'''({{M}_{c}},0)$.
Рисунки 1a–5a демонстрируют качественно различные области существования в зависимости от ${{\beta }_{e}}$. Эти рисунки показывают условия существования различных уединенных структур для $M > {{M}_{c}}$ при различных значениях p для $\mu = 0.2$ и ${{\sigma }_{{ie}}} = {{\sigma }_{{pe}}} = 0.9$. Кроме того, на рис. 1б–5б изображена зависимость $V'''({{M}_{c}},0)$ от ${{\beta }_{e}}$.
Рис. 1.
a) – Область существования в зависимости от ${{\beta }_{e}}$ для $p = 0.00001$, $\mu = 0.2$ и ${{\sigma }_{{ie}}} = {{\sigma }_{{pe}}} = 0.9$. Красным, пурпурным и синим цветами обозначены кривые $M = {{M}_{{NPDL}}}$, $M = {{M}_{c}}$ и $M = {{M}_{{{\text{max}}}}}$ соответственно; б) – зависимость $V'''({{M}_{c}},0)$ от ${{\beta }_{e}}$ для тех же значений параметров.
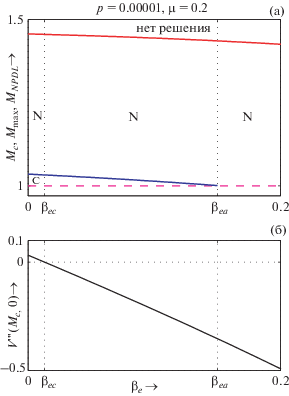
Хотя на рис. 1a представлена область существования различных уединенных структур для $p = 0.00001$, но качественно описаны области существования для любых p, лежащих в интервале $0 < p < 0.0008$ для любого физически допустимого значения ${{\beta }_{e}}$. Аналогично, рис. 2a, 3a и 4a дают результат для любых значений p, лежащих в интервалах $0.0008 \leqslant p < 0.034$, $0.034 \leqslant p < 0.065$ и $0.065 \leqslant p < 0.083$ соответственно. Наконец, рис. 5a дает область существования для $p > 0.083$.
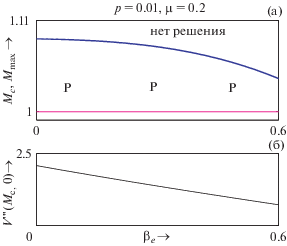
Рис. 2.
a) – Область существования в зависимости от ${{\beta }_{e}}$ для $p = 0.01$, $\mu = 0.2$ и ${{\sigma }_{{ie}}} = {{\sigma }_{{pe}}} = 0.9$. Красным, пурпурным и синим цветами обозначены кривые $M = {{M}_{{NPDL}}}$, $M = {{M}_{c}}$ и $M = {{M}_{{{\text{max}}}}}$ соответственно; б) – зависимость $V'''({{M}_{c}},0)$ от ${{\beta }_{e}}$ для тех же значений параметров.
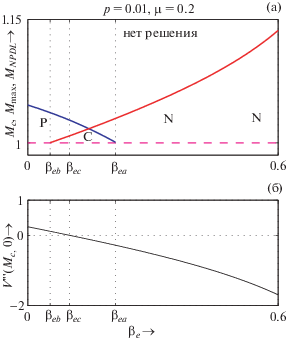
Рис. 3.
a) – Область существования в зависимости от ${{\beta }_{e}}$ для $p = 0.04$, $\mu = 0.2$ и ${{\sigma }_{{ie}}} = {{\sigma }_{{pe}}} = 0.9$. Красным, пурпурным, синим и черным цветами обозначены кривые $M = {{M}_{{NPDL}}}$, $M = {{M}_{c}}$, $M = {{M}_{{{\text{max}}}}}$ и $M = {{M}_{{NPDL}}}$ соответственно; б) – зависимость $V'''({{M}_{c}},0)$ от ${{\beta }_{e}}$ для тех же значений параметров.
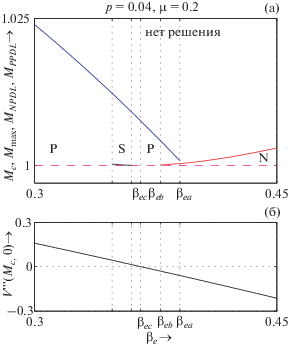
Рис. 4.
a) – Область существования в зависимости от ${{\beta }_{e}}$ для $p = 0.07$, $\mu = 0.2$ и ${{\sigma }_{{ie}}} = {{\sigma }_{{pe}}} = 0.9$. Пурпурным, синим и черным цветами обозначены кривые $M = {{M}_{c}}$, $M = {{M}_{{{\text{max}}}}}$ and $M = {{M}_{{NPDL}}}$ соответственно; б) – зависимость $V'''({{M}_{c}},0)$ от ${{\beta }_{e}}$ для тех же значений параметров.
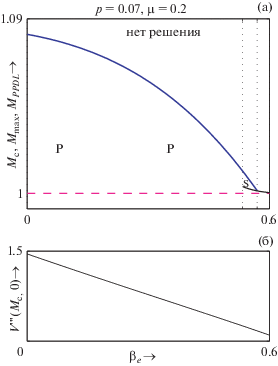
Рис. 5.
a) – Область существования в зависимости от ${{\beta }_{e}}$ для $p = 0.1$, $\mu = 0.2$ и ${{\sigma }_{{ie}}} = {{\sigma }_{{pe}}} = 0.9$. Пурпурным и синим цветами обозначены кривые $M = {{M}_{c}}$ и $M = {{M}_{{{\text{max}}}}}$ соответственно; б) – зависимость $V'''({{M}_{c}},0)$ от ${{\beta }_{e}}$ для тех же значений параметров.
На вышеупомянутых рисунках P, N, S, и C соответствуют областям существования PPSWs, NPSWs, PPSWs после формирования PPDL и области сосуществования PPSWs и NPSWs, соответственно. Здесь ${{M}_{{{\text{max}}}}}$ – это верхняя граница чисел Маха M, для которых существуют все уединенные структуры положительного потенциала. Следуя методике, разработанной в работах [30] и [31], легко убедиться, что ${{M}_{{{\text{max}}}}}$ – это наибольший положительный корень уравнения $V({{\Psi }_{M}}) = 0$, подчиняющийся условию $V({{\Psi }_{M}}) \geqslant 0$ для всех $M \leqslant {{M}_{{{\text{max}}}}}$. Другими словами, предполагается, что ${{M}_{{{\text{max}}}}}$ – это верхняя гарница M, при которой еще существуют все уединенные структуры положительного потенциала при стремлении ϕ к ${{\Psi }_{M}}$, т.е. когда концентрация ионов соответствует максимальному сжатию. Числа Маха $M = {{M}_{{PPDL}}}$ ($M = {{M}_{{NPDL}}}$) соответствуют решениям интеграла энергии (22) в виде PPDL (NPDL). В наших предыдущих работах [17, 18, 20], следуя методике, развитой в работах [30, 31], мы предложили численную схему для определния чисел Маха ${{M}_{{PPDL}}}$ (${{M}_{{NPDL}}}$), соответствующих решениям уравнения (22) в виде PPDL (NPDL) в некоторой точке пространства параметров.
Для исследования существования и полярности различных уединенных структур при $M > {{M}_{c}}$, мы определили следующие пороговые значения ${{\beta }_{e}}$:
${{\beta }_{{ea}}}$ : ${{\beta }_{{ea}}}$– пороговое значение ${{\beta }_{e}}$ такое, что Mmax (верхняя граница чисел Маха для существования уединенных структур положительноного потенциала) существует для всех $0 < {{\beta }_{e}} \leqslant {{\beta }_{{ea}}}$. Следовательно, ${{\beta }_{e}} = {{\beta }_{{ea}}}$ – верхняя граница ${{\beta }_{e}}$ для существования PPSWs.
${{\beta }_{{eb}}}$ : ${{\beta }_{{eb}}}$ – пороговое значение ${{\beta }_{e}}$ такое, что NPDL существует при ${{\beta }_{e}} \geqslant {{\beta }_{{eb}}}$, т.е. ${{\beta }_{e}} = {{\beta }_{{eb}}}$ – нижняя граница ${{\beta }_{e}}$ для существования решение в виде NPDL. Другими словами, для любого ${{\beta }_{e}} \geqslant {{\beta }_{{eb}}}$ существует последовательность NPSWs возрастающей амплитуды, которая сходится к NPDL при $M = {{M}_{{NPDL}}}$.
${{\beta }_{{ec}}}$ : ${{\beta }_{{ec}}}$ – значение ${{\beta }_{e}}$, при котором $V'''({{M}_{c}},0) = 0$.
Рисунки 1–5 представляют собой полное описание системы. Например, рассмотрим рис. 2. Из рис. 2a мы видим, что система допускает существование только PPSWs в правой окрестности кривой $M = {{M}_{c}}$ для $0 < {{\beta }_{e}} < {{\beta }_{{eb}}}$. NPDLs существуют при ${{\beta }_{e}} \geqslant {{\beta }_{{eb}}} = 0.054$ вдоль кривой $M = {{M}_{{NPDL}}}$, а сосуществование солитонов обоих полярностей наблюдалось в интервале ${{\beta }_{{eb}}} < {{\beta }_{e}} \leqslant {{\beta }_{{ea}}}$. При ${{\beta }_{e}} > {{\beta }_{{ea}}}$ в системе возможно существование только NPSWs в правой окрестности кривой $M = {{M}_{c}}$. Таким образом, из рис. 2a мы имеем полное представление о существовании и полярности уединенных структур в правой окрестности кривой $M = {{M}_{c}}$.
С другой стороны, рис. 2б показывает зависимость $V'''({{M}_{c}},0)$ от ${{\beta }_{e}}$.
Таким образом, используя Результат 1, Результат 2 и Результат 3, можно привести следующие выводы о существовании и полярности уединенных струтур вдоль кривой $M = {{M}_{c}}$.
1) При $0 \leqslant {{\beta }_{e}} < {{\beta }_{{eb}}}$ система допускает только PPSWs в правой окрестности $M = {{M}_{c}}$ и в заданном интервале ${{\beta }_{e}}$, мы имеем $V'''({{M}_{c}},0) > 0$. Итак, используя Результат 2, можно сделать вывод, что не существует уединенных структур при $M = {{M}_{c}}$ для ${{\beta }_{e}}$, лежащих в интервале $0 \leqslant {{\beta }_{e}} < {{\beta }_{{eb}}}$.
2) При ${{\beta }_{{eb}}} < {{\beta }_{e}} < {{\beta }_{{ec}}}$ система допускает одновременное существование PPSWs и NPSWs в правой окрестности $M = {{M}_{c}}$ и в интервале ${{\beta }_{e}}$, мы имеем $V'''({{M}_{c}},0) > 0$, что соответствует существованию NPSWs при $M = {{M}_{c}}$ для ${{\beta }_{{eb}}} < {{\beta }_{e}} < {{\beta }_{{ec}}}$ (Результат 1).
3) При ${{\beta }_{{ec}}} < {{\beta }_{e}} \leqslant {{\beta }_{{ea}}}$ система снова допускает одновременное существование PPSWs и NPSWs в правой окрестности $M = {{M}_{c}}$, но в этом интервале ${{\beta }_{e}}$, мы имеем $V'''({{M}_{c}},0) < 0$, что соответствует существованию PPSWs при $M = {{M}_{c}}$ в интервале ${{\beta }_{{ec}}} < {{\beta }_{e}} \leqslant {{\beta }_{{ea}}}$ (Результат 1).
4) Для ${{\beta }_{{ea}}} < {{\beta }_{e}} < 0.6$ система допускает существование NPSWs в правой окрестности $M = {{M}_{c}}$, но в этом интервале ${{\beta }_{e}}$, мы имеем $V'''({{M}_{c}},0) < 0$. Итак, можно заключить, что в интервале ${{\beta }_{{ea}}} < {{\beta }_{e}} < 0.6$ не существует уединенных структур на звуковой скорости (Результат 2).
5) Легко убедиться, что ${{\left. {V'''({{M}_{c}},0)} \right|}_{{{{\beta }_{e}} = {{\beta }_{{ec}}}}}} = 0$ и ${{\left. {V''''({{M}_{c}},0)} \right|}_{{{{\beta }_{e}} = {{\beta }_{{ec}}}}}} > 0$. Следовательно, потенциальная энергия псевдочастицы единичной массы, связанной с интегралом энергии (22), достигает минимального значения при $\phi = 0$ и ${{\beta }_{e}} = {{\beta }_{{ec}}}$, $M = {{M}_{c}}$ с $p = 0.01$, $\mu = 0.2$ и ${{\sigma }_{{ie}}} = {{\sigma }_{{pe}}} = 0.9$. В этом случае $\phi = 0$ является положением устойчивого равновесия частицы. Итак, невозможно привести частицу в колебательное движение, даже если частица слегка смещена из положения устойчивого равновесия и, следовательно, не возникает вопроса о существовании какой-либо уединенной структуры на звуковой скорости $U = {{C}_{D}} \Leftrightarrow M = {{M}_{c}}$ при ${{\beta }_{e}} = {{\beta }_{{ec}}}$.
6) Из рис. 2a видно, что кривая $M = {{M}_{{NPDL}}}$ стремится пересечь кривую $M = {{M}_{c}}$ в точке ${{\beta }_{e}} = {{\beta }_{{eb}}}$ в области существования при $p = 0.01$, $\mu = 0.2$ и ${{\sigma }_{{ie}}} = {{\sigma }_{{pe}}} = 0.9$, т.е. всегда существует NPDL решение в любой правой окрестности ${{M}_{c}}$. Следовательно, согласно [24], должно существовать NPDL решение при $M = {{M}_{c}}$ в точке ${{\beta }_{e}} = {{\beta }_{{eb}}}$ в области существования с $p = 0.01$, $\mu = 0.2$ и ${{\sigma }_{{ie}}} = {{\sigma }_{{pe}}} = 0.9$.
7) Не существует PPDL на звуковой скорости.
Таким образом, из рис. 1–5 мы видим, что для $p > 0$ существует пороговое значение ${{p}^{{(c)}}}$, такое, что для $0 < p \leqslant {{p}^{{(c)}}}$ система допускает существование NPSWs на звуковой скорости при $0 < {{\beta }_{e}} < {{\beta }_{{ec}}}$, в то время как при ${{\beta }_{{ec}}} < {{\beta }_{e}} \leqslant {{\beta }_{{ea}}}$ система допускает существование PPSWs на скорости звука. Опять же, существует пороговое значение ${{p}^{{(k)}}}$, такое, что для ${{p}^{{(c)}}} < p \leqslant {{p}^{{(k)}}}$ система допускает существование NPSWs на звуковой скорости для ${{\beta }_{{eb}}} < {{\beta }_{e}} < {{\beta }_{{ec}}}$, в то время как при ${{\beta }_{{ec}}} < {{\beta }_{e}} \leqslant {{\beta }_{{ea}}}$ система допускает существование PPSWs на звуковой скорости. Здесь мы видим, что для $M > {{M}_{c}}$ кривая $M = {{M}_{{NPDL}}}$ стремится пересечь кривую $M = {{M}_{c}}$ при ${{\beta }_{e}} = {{\beta }_{{eb}}}$ и, следовательно, имеется NPDL решение на звуковой скорости когда ${{\beta }_{e}}$ принимает значение ${{\beta }_{{eb}}}$. Для определенности мы изображаем $V(\phi )$ в зависимости от ϕ на рис. 6 на звуковой скорости для различных значений ${{\beta }_{e}}$, лежащих в интервале ${{\beta }_{{eb}}} \leqslant {{\beta }_{e}} < {{\beta }_{{ec}}}$. Из этого рисунка следует, что амплитуда NPSWs на скорости звука возрастает с ростом ${{\beta }_{e}}$ и эта последовательность NPSWs заканчивается NPDL при ${{\beta }_{e}} = {{\beta }_{{eb}}}$. На рис. 7 $V(\phi )$ представлено в зависимости от ϕ для различных значений ${{\beta }_{e}}$, лежащих в интервале ${{\beta }_{{ec}}} < {{\beta }_{e}} \leqslant {{\beta }_{{ea}}}$. Из этого рисунка следует, что амплитуда PPSWs при $M = {{M}_{c}}$ возрастает с ростом ${{\beta }_{e}}$, лежащих в интервале ${{\beta }_{{ec}}} < {{\beta }_{e}} \leqslant {{\beta }_{{ea}}}$, тогда как в точке ${{\beta }_{e}} = {{\beta }_{{ec}}}$ и NPSWs, и PPSWs коллапсируют. Легко убедиться, что потенциальная энергия системы достигает своего минимума при ${{\beta }_{e}} = {{\beta }_{{ec}}}$, т.е. при ${{\beta }_{e}} = {{\beta }_{{ec}}}$, $\phi = 0$ является положением устойчивого равновесия. Фактически в этой точке $V({{M}_{c}},0) = V'({{M}_{c}},0) = $ $ = V''({{M}_{c}},0) = V'''({{M}_{c}},0) = 0$, в то время как $V''''({{M}_{c}},0) > 0$. Следовательно, не возникает вопроса о существовании какой-либо уединенной структуры при ${{\beta }_{e}} = {{\beta }_{{ec}}}$. При дальнейшем росте p от $p = {{p}^{{(k)}}}$ существует пороговое значение ${{p}^{{(m)}}}$, такое, что для ${{p}^{{(k)}}} < p \leqslant {{p}^{{(m)}}}$ система допускает существование PPSWs на звуковой скорости для ${{\beta }_{{ec}}} < {{\beta }_{e}} < {{\beta }_{{eb}}}$, тогда как система не допускает существования уединенных структур отрицательного потенциала на звуковой скорости для допустимых значений ${{\beta }_{e}}$. Наконец, для $p > {{p}^{{(m)}}}$ система не допускает существования каких-либо уединенных структур при $M = {{M}_{c}}$. Из рис. 3 и 4 можно видеть, что система допускает существование PPDLs в правой окрестности $M = {{M}_{c}}$, но не допускает существования PPDLs при $M = {{M}_{c}}$. Следовательно, настоящая плазменная система не допускает существования какого-либо суперсолитона положительного потенциала на звуковой скорости. Опять же, поскольку не существует какого-либо солитона после формирования NPDL на звуковой скорости, не существует суперсолитона отрицательного потенциала на звуковой скорости для $p > 0$. Но в случае$p = 0$, т.е. если в системе нет позитронов, в [25] было обнаружено существование NPDLs и что более важно, существование суперсолитона отрицательного потенциала на звуковой скорости. Если мы положим $p = 0$ в настоящей работе, т.е. примем концентрацию позитронов равной нулю, то рассматриваемая плазменная система сведется к рассмотренной в [25].
Рис. 6.
$V(\phi )$ при $M = {{M}_{c}}$ для различных значений ${{\beta }_{e}}$ и при фиксированных значениях других параметров, значения которых приведены на рисунке.
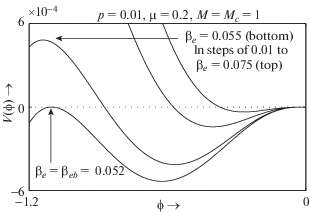
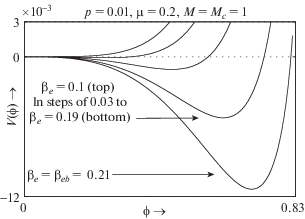
Рис. 7.
$V(\phi )$ при $M = {{M}_{c}}$ для различных значений ${{\beta }_{e}}$ и при фиксированных значениях других параметров, значения которых приведены на рисунке.
На рис. 8 представлена область существования относительно μ при $p = 0$ и ${{\sigma }_{{ie}}} = 0.9$. Эта область существования качественно совпадает с областью существования, изображенной на рис. 10 в работе [25]. На рис. 8 обозначение P соответствует области существования PPSWs при $M = {{M}_{c}}$, N соответствует области существования NPSWs при $M = {{M}_{c}}$, вдоль кривой ${{\beta }_{e}} = {{\beta }_{{eb}}}$ мы имеем NPDLs при $M = {{M}_{c}}$, NS представляет область существования NPSWs после формирования NPDL при $M = {{M}_{c}}$ и $V'''({{M}_{c}},0) = 0$ вдоль кривой ${{\beta }_{e}} = {{\beta }_{{ec}}}$. На этом рисунке показана область существования в зависимости от μ на скорости звука $U = {{C}_{D}} \Leftrightarrow M = {{M}_{c}}$ для $p = 0$ и ${{\sigma }_{{ie}}} = 0.9$.
Рис. 8.
Область существования в зависимости от $\mu $ при $M = {{M}_{c}}$ для различных значений параметров, значения которых приведены на рисунке.
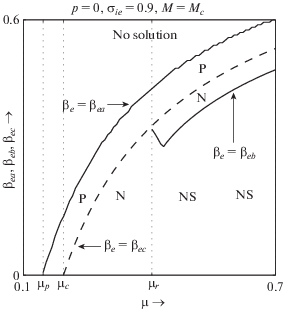
Рис. 9.
$V(\phi )$ (а) и фазовый портрет системы (33) (б) изображены на одинаковой $\phi ( = {\kern 1pt} {{\phi }_{1}})$-оси при $M = {{M}_{c}}$, $p = 0.01$, $\mu = 0.2$, ${{\beta }_{e}} = 0.07$ и ${{\sigma }_{{ie}}} = {{\sigma }_{{pe}}} = 0.9$.
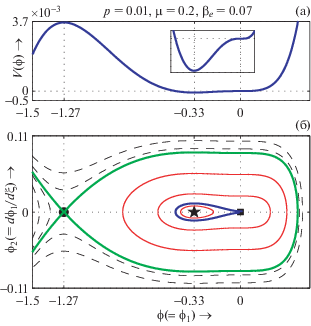
Рис. 10.
$V(\phi )$ (а) и фазовый портрет системы (33) (б) изображены на одинаковой $\phi ( = {\kern 1pt} {{\phi }_{1}})$-оси при $M = {{M}_{c}}$, $p = 0.01$, $\mu = 0.2$, ${{\beta }_{e}} = 0.15$ и ${{\sigma }_{{ie}}} = {{\sigma }_{{pe}}} = 0.9$.
Для описания рис. 8 мы определили следующие пороговые значения $\mu $:
${{\mu }_{p}}:{{\mu }_{p}}$ – пороговое значение μ такое, что ${{M}_{{{\text{max}}}}}$ не существует для любого допустимого значения ${{\beta }_{e}}$, если μ лежит в интервале $0 < \mu < {{\mu }_{p}}$, т.е. если $\mu \geqslant {{\mu }_{p}}$, то существует значение $\beta _{e}^{*}$ такое, что ${{M}_{{{\text{max}}}}}$ существует при ${{\beta }_{e}} = \beta _{e}^{*}$; более того, если $\beta _{e}^{*} > 0$, то ${{M}_{{{\text{max}}}}}$ существует для всех ${{\beta }_{e}}$, лежащих в интервале $0 \leqslant {{\beta }_{e}} < \beta _{e}^{*}$;
${{\mu }_{c}}:{{\mu }_{c}}$ – пороговое значение μ такое, что $V''({{M}_{c}},0) = 0$ и $V'''({{M}_{c}},0) = 0$ при $\mu = {{\mu }_{c}}$ и ${{\beta }_{e}} = {{\beta }_{{ec}}}$ для фиксированных значений ${{\sigma }_{{ie}}}$;
${{\mu }_{r}}:{{\mu }_{r}}$ – пороговое значение of μ такое, что для всех ${{\mu }_{r}} \leqslant {{\mu }_{T}}$ кривая $M = {{M}_{{NPDL}}}$ стремится к пересечению с кривой $M = {{M}_{c}}$ в точке ${{\beta }_{e}} = {{\beta }_{{eb}}}$;
${{\mu }_{T}}:{{\mu }_{T}}$ – физически допустимая верхняя граница μ.
Рисунок 8 ясно демонстрирует, что существует два типа NPSWs при $M = {{M}_{c}}$, если μ лежит в интервале ${{\mu }_{r}} < \mu < {{\mu }_{T}}$. Первый тип ограничен кривыми ${{\beta }_{e}} = {{\beta }_{{ec}}}$ и ${{\beta }_{e}} = {{\beta }_{{eb}}}$ и амплитуда этих NPSWs ограничена амплитудой NPDL на скорости звука. Второй тип NPSWs существует за кривой ${{\beta }_{e}} = {{\beta }_{{eb}}}$, т.е. после формирования NPDL при $M = {{M}_{c}}$. Амплитуда NPSWs после формирования двойного слоя при $M = {{M}_{c}}$ возрастает с уменьшением ${{\beta }_{e}}$ и достигает максимума при ${{\beta }_{e}} = 0$ и $M = {{M}_{c}}$. Кроме того, существует разрыв скачкообразного типа между амплитудой NPSWs на звуковой скорости непосредственно перед и после формирования NPDL при $M = {{M}_{c}}$ (см. рис. 16). Поскольку существование солитонов после образования двойного слоя подтверждает существование хотя бы одной последовательности суперсолитонов [20], то можно сделать вывод, что всякий раз, когда в системе не существует позитрона, она допускает существование суперсолитонов с отрицательным потенциалом на звуковой скорости. Следовательно, должен быть плавный переход уединенных структур при $M = {{M}_{c}}$, а именно, солитон → → двойной слой → суперсолитон → солитон. Этот переходный процесс впервые детально обсуждается в следующем разделе с помощью фазовых портретов динамической системы, соответствующей одиночным DIA-структурам на звуковой скорости.
4. ФАЗОВЫЕ ПОРТРЕТЫ РАЗЛИЧНЫХ УЕДИНЕННЫХ СТРУКТУР НА ЗВУКОВОЙ СКОРОСТИ
Прежде чем перейти к исследованию механизма перехода уединенных структур на звуковой скорости, необходимо описать фазовые портреты динамической системы, соответствующие различным уединенным структурам на звуковой скорости. Также необходимо провести четкое различие между уединенными структурами на звуковой скорости, т.е. при $M = {{M}_{c}}$, и уединенными структурами на сверхзвуковой скорости, т.е. для $M > {{M}_{c}}$.
Дифференцируя интеграл энергии (22) по переменной ϕ, получаем следующее дифференциальное уравнение:
Это уравнение эквивалентно следующей системе дифференциальных уравнений:
(33)
$\frac{{d{{\phi }_{1}}}}{{d\xi }} = {{\phi }_{2}} ,\quad \frac{{d{{\phi }_{2}}}}{{d\xi }} = - V'({{\phi }_{1}}) ,$Неподвижной точкой динамической системы (33) является ($\phi _{1}^{*}$, $\phi _{2}^{*}$), где $\phi _{2}^{*} = 0$ и $\phi _{1}^{*}$ задается уравнением
Это уравнение задает значение(я) $\phi _{1}^{*}$ как функцию физических параметров системы при числах Маха $M = {{M}_{c}} = 1$, т.е. $\phi _{1}^{*}$ является фуекцией p, μ, ${{\beta }_{e}}$, ${{\sigma }_{{ie}}}$ и ${{\sigma }_{{pe}}}$. Итак, можно записать
В настоящей работе мы принимаем ${{\sigma }_{{pe}}} = 0.9$, т.е. средние тепловые температуры позитронов почти такие же, как у электронов, и мы также считаем ${{\sigma }_{{ie}}} = 0.9$ (обычное приближение для пылевой плазмы ${{T}_{i}} \approx {{T}_{e}}$). Следовательно, для фиксированных значений p и μ уравнение (35) сводится к
Для определния ${{\beta }_{e}}$ мы уже изобразили области существования в зависимости от ${{\beta }_{e}}$ (см. рис. 1a–5a), из этих областей существования можно легко получить значение ${{\beta }_{e}}$, соответствующее желаемой уединенной структуре на звуковой скорости.
Для описания фазовых портретов уединенных структур при $M = {{M}_{c}}$ рассмотрим рис. 9–11. Здесь мы использовали области существования, аналогичные изображенным на рис. 2, для определения значения ${{\beta }_{e}}$, соответствующего существованию желаемой уединенной структуры на звуковой скорсоти. На рис. 9a–11a изображена зависимость $V(\phi )$. На нижней панели (рис. 9б–11б) каждого рисунка представлен фазовый портрет системы (33). При построении этих рисунков использовались значения параметров, отмеченные на них, при $p = 0.01$, $\mu = 0.2$ и ${{\sigma }_{{pe}}} = {{\sigma }_{{ie}}} = 0.9$. Кривая $V(\phi )$ и фазовый портрет изображены на одной и той же горизонтальной оси $\phi ( = {\kern 1pt} {{\phi }_{1}})$. Маленький сплошной квадрат соответствует точке перегиба в начале координат, маленький сплошной круг соответствует седловой точке, а маленькая сплошная звезда указывает точку равновесия, отличную от седловой точки, или точки перегиба системы (33). Нетрудно проверить, что каждая максимальная (минимальная) точка $V(\phi )$ соответствует седловой точке (точке равновесия, отличной от седловой точки) системы (33). Кроме того, маленький сплошной квадрат соответствует точке перегиба системы (33). Понятие точки перегиба при исследовании солитонов на скорости звука не является новым. В работе [24] уже упоминалось, что начало координат является точкой перегиба системы (33) для уединенных структур на звуковой скорости. Действительно, если $V(0) = V'(0) = 0$, $V''({{M}_{c}},0) = 0$ и $V'''({{M}_{c}},0) \ne 0$, точка $\phi = 0$ является точкой перегиба, которая отделяет выпуклую часть кривой $V({{M}_{c}},\phi )$ от ее вогнутой части. Согласно теоремам 3 и 4 из [24], точка (0, 0) всегда является точкой перегиба системы (33) для уединенных структур на звуковой скорости. Однако в случае сверхзвуковых уединенных структур ($M > {{M}_{c}}$) начало координат (0, 0) не является точкой перегиба системы (33). В этом (сверхзвуковом) случае начало координат (0, 0) всегда является седловой точкой системы (33). Этим определяется различие между уединенных структурами для $M > {{M}_{c}}$ и уединенных структурами при $M = {{M}_{c}}$.
Рис. 11.
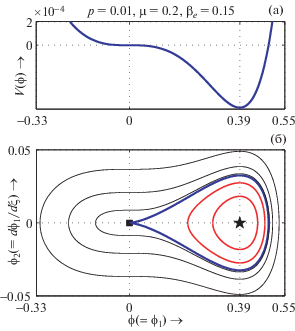
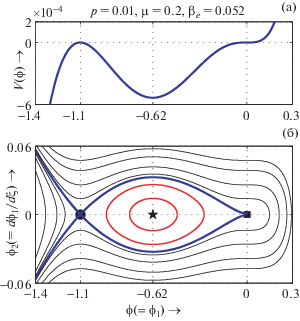
$V(\phi )$ (а) и фазовый портрет системы (33) (б) изображены на одинаковой $\phi ( = {\kern 1pt} {{\phi }_{1}})$-оси при $M = {{M}_{c}}$, $p = 0.01$, $\mu = 0.2$, ${{\beta }_{e}} = 0.052$ и ${{\sigma }_{{ie}}} = {{\sigma }_{{pe}}} = 0.9$.
Существует взаимно-однозначное соответствие между сепаратрисой фазового портрета, показанной жирной синей линией на нижней панели, с кривой $V(\varphi )$ в верхней панели. Фактически, это взаимно-однозначное соответствие между сепаратрисой фазового портрета и кривой $V(\varphi )$ подробно обсуждалось в работе [20] для сверхзвуковых уединенных структур. В этом разделе мы хотим обсудить фазовые портреты уединенных структур на звуковой скорости и процессы перехода: солитоны → двойные слои → суперсолитоны → солитоны после формирования двойного слоя на звуковой скорости, когда в системе нет позитронов. Для звукового случая, т.е. на звуковой скорости, сепаратриса, соответствующая уединенной структуре, начинается с точки перегиба (0, 0) и заканчивается в точке перегиба (0, 0). Это показывает, что если в положительном направлении ϕ-оси образуется сепаратриса, то невозможно создать другую сепаратрису в отрицательном направлении ϕ-оси, и, следовательно, сосуществование уединенных структур обеих полярностей невозможно при скорости звука. Это также не новый результат, потому что в работе [24] уже доказана следующая теорема: Теорема 5: Если $V(0) = V'(0) = 0$, $V''({{M}_{c}},0) = 0$ и $V'''({{M}_{c}},0) \ne 0$, невозможно сосуществование уединенных структур положительной и отрицательной полярности при $M = {{M}_{c}}$.Таким образом, анализ фазовых портретов подтверждает Результат-3 или Теорему-5. Сепаратриса, соответствующая уединенной структуре, показана жирной синей линией, тогда как другие сепаратрисы (если существуют) показаны зелеными линиями. Замкнутая кривая в окрестности точки равновесия (отличной от седловой точки или точки перегиба), содержащейся по меньшей мере в одной сепаратрисе, указывает на возможность периодического волнового решения в окрестности этой фиксированной точки.
Рисунок 9а показывает наличие NPSW при $M = {{M}_{c}}$, а рис. 9б описывает соответствующий фазовый портрет. Здесь мы видим, что система имеет точку перегиба в начале координат, точку равновесия в точке (–0.33, 0) и седло в точке (‒1.27, 0). Далее из рис. 9б мы видим, что есть две сепаратрисы: 1) сепаратриса (показанная жирной синей линией), которая начинается и заканчивается в начале координат, окружает неседловую неподвижную точку, и эта сепаратриса соответствует солитону отрицательного потенциала при $M = {{M}_{c}}$ и 2) сепаратриса (показанная жирной зеленой линией), которая проходит через седловую точку (–1.27, 0), и эта сепаратриса содержит сепаратрису (показанную жирной синей линией), которая начинается и заканчивается в начале координат. Между этими двумя сепаратрисами существует бесконечно много замкнутых кривых, и каждая из этих замкнутых кривых соответствует супернелинейной периодической волне. Таким образом, рис. 9б подтверждает существование супернелинейных периодических волн на звуковой скорости.
Рисунок 10а демонстрирует существование PPSW при $M = {{M}_{c}}$, а рис. 10б описывает соответствующий фазовый портрет. Здесь мы видим, что система имеет точку перегиба в начале координат, точку равновесия (0.39, 0), в которой нет седловой точки. Из рис. 10б мы видим, что существует только одна сепаратриса (показанная жирной синей линией), которая начинается и заканчивается в начале координат, охватывает неседловую неподвижную точку (0.39, 0), и, следовательно, эта сепаратриса соответствует солитону положительного потенциала при $M = {{M}_{c}}$.
Рисунок 11б представляет фазовый портрет NPDL на скорости звука, и этот рисунок показывает, что сепаратриса, соответствующая двойному слою на скорости звука, начинается и заканчивается в точке перегиба (0, 0) и проходит через седловую точку (–1.1, 0), окружая неседловую неподвижную точку (–0.62, 0). На рис. 11а представлена зависимость $V(\varphi )$ при скорости звука для заданных значений параметров, указанных на рисунке. Рисунки 11a и б вместе дают взаимно однозначное соответствие между сепаратрисой фазового портрета, изображенной жирной синей линией на нижней панели, с кривой $V(\phi )$ в верхней панели. Этот механизм работает для формирования PPSWs, а также для формирования N-PSWs на звуковой скорости.
Теперь мы можем обсудить процессы перехода уединенных структур, а именно: солитоны → → двойные слои → суперсолитоны → солитоны после формирования двойного слоя на звуковой скорости в системе без позитронов. В этом случае, т.е. для $p = 0$, мы рассматриваем область существования аналогично рис. 8, чтобы найти значения μ и ${{\beta }_{e}}$ для существования требуемой уединенной структуры на звуковой скорости. Взаимно однозначное соответствие между сепаратрисой фазового портрета с кривой $V(\phi )$и процессом перехода различных уединенных структур на звуковой скорости показано на рис. 12–17.
Рис. 12.
$V(\phi )$ (a) и фазовый портрет системы (33) (б) изображены на одинаковой $\phi ( = {\kern 1pt} {{\phi }_{1}})$-оси при $M = {{M}_{c}}$, $p = 0$, $\mu = 0.5$, ${{\beta }_{e}} = 0.372$ и ${{\sigma }_{{ie}}} = 0.9$.
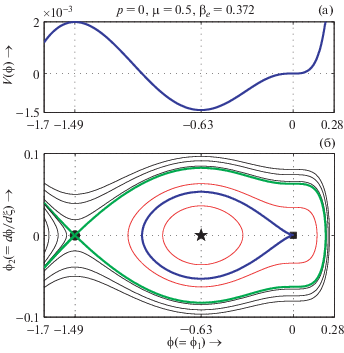
Рис. 13.
$V(\phi )$ (a) и фазовый портрет системы (33) (б) изображены на одинаковой $\phi ( = {\kern 1pt} {{\phi }_{1}})$-оси при $M = {{M}_{c}}$, $p = 0$, $\mu = 0.5$, ${{\beta }_{e}} = 0.36918$ и ${{\sigma }_{{ie}}} = 0.9$.
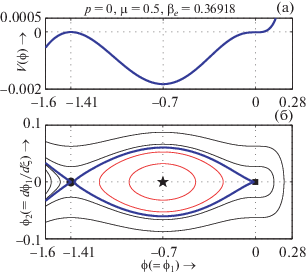
Рис. 14.
$V(\phi )$ (а) и фазовый портрет системы (33) (б) изображены на одинаковой $\phi ( = {\kern 1pt} {{\phi }_{1}})$-оси при $M = {{M}_{c}}$, $p = 0$, $\mu = 0.5$, ${{\beta }_{e}} = 0.36618$ и ${{\sigma }_{{ie}}} = 0.9$.
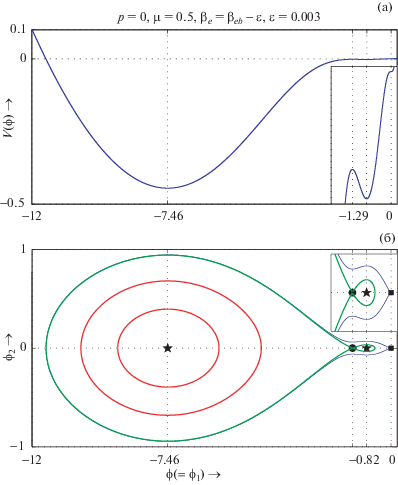
Рис. 15.
$V(\phi )$ (а) и фазовый портрет системы (33) (б) изображены на одинаковой $\phi ( = {\kern 1pt} {{\phi }_{1}})$-оси при $M = {{M}_{c}}$, $p = 0$, $\mu = 0.5$, ${{\beta }_{e}} = 0.26918$ и ${{\sigma }_{{ie}}} = 0.9$.
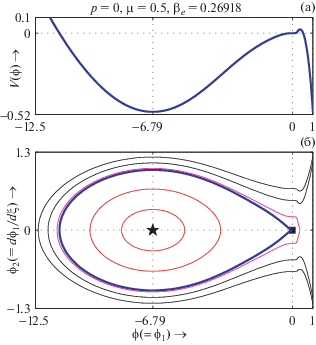
Рис. 16.
ϕ в зависимости от ξ при $M = {{M}_{c}}$ для ${{\beta }_{e}} = 0.26918$ (сплошная кривая) и ${{\beta }_{e}} = 0.372$ (штрихпунктирная кривая) при $p = 0$, $\mu = 0.5$ и ${{\sigma }_{{ie}}} = 0.9$.
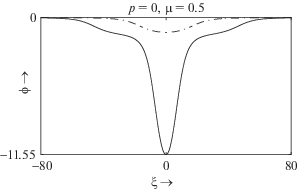
Рис. 17.
Точка перегиба (маленькие сплошные кубики), седловые точки (маленькие сплошные кружки) и точки равновесия, отличные от седловых точек (маленькие сплошные звезды) для системы (33), изображены на ϕ-оси при $M = {{M}_{c}}$ для различных значений ${{\beta }_{e}}$ при $p = 0$, $\mu = 0.5$ и ${{\sigma }_{{ie}}} = 0.9$.
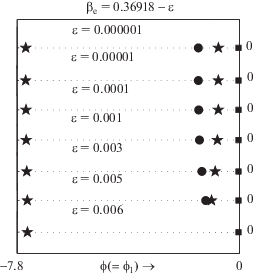
Рисунок 12a демонстрирует существование NPSW при $M = {{M}_{c}}$ до формирования NPDL, а рис. 12б описывает фазовый портрет динамической системы (33) при $M = {{M}_{c}}$ для значений параметров, отмеченных на рисунке. Здесь можно видеть, что у системы есть точка перегиба в начале координат, точка равновесия (–0.63, 0) и седло в точке (–1.49, 0). Кроме того, из рис. 12б следует, что существует две сепаратрисы: 1) сепаратриса (показанная жирной синей линией), которая начинается и заканчивается в начале координат, охватывает неседловую неподвижную точку, относится к солитону отрицательного потенциала при $M = {{M}_{c}}$; 2) эта синяя сепаратриса заключена в другую сепаратрису (показана жирной зеленой линией), которая проходит через седловую точку (–1.49, 0). Между этими двумя сепаратрисами существует бесконечно много замкнутых кривых, и каждая из этих замкнутых кривых соответствует супернелинейной периодической волне. Таким образом, рис. 12б подтверждает существование супернелинейных периодических волн на звуковой скорости.
На рис. 13б представлен фазовый портрет NPDL на звуковой скорости при ${{\beta }_{e}} = {{\beta }_{{eb}}} = 0.36918$, и из рисунка следует, что сепаратриса, соответсвующая решению в виде двойного слоя на звуковой скорости, начинается и заканчивается в точке перегиба (0, 0) и проходит через седловую точку (–1.41, 0), охватывая неседловую неподвижную точку (–0.7, 0). Теперь мы слегка уменьшим значение ${{\beta }_{e}}$ от ${{\beta }_{{eb}}}$ и изобразим рис. 14 для ${{\beta }_{e}} = {{\beta }_{{eb}}} - 0.003$. На рис. 14a построена зависимость $V(\phi )$, на которой участок от –2 до 0 показан в увеличенном масштабе во вставке, а на рис. 14б представлен фазовый портрет динамической системы (33) при $M = {{M}_{c}}$ для значений параметров, указанных на рисунке, причем участок от −2 до 0 показан в увеличенном масштабе во вставке. На рис. 14a показано, что $V(\phi )$ имеет два последовательных минимума при $\phi = - 0.81504 \approx - 0.82$ и $\phi = - 7.4622 \approx - 7.46$. Следовательно, фазовый портрет системы имеет две неседловые неподвижные точки, как показано на нижней панели рис. 14. Сепаратриса, соответствующая уединенной структуре, которая начинается и заканчивается в точке перегиба (0, 0), включает в себя одну ненулевую седловую точку $( - 1.2875,0) \approx ( - 1.29,0)$ и две неседловые неподвижные точки $( - 0.81504,0) \approx $ $ \approx ( - 0.82,0)$ и $( - 7.4622,0) \approx ( - 7.46,0)$. Из участка между −2 и 0, показанного в большем масштабе на вставке рис. 14б, можно убедиться, что эта сепаратриса также охватывает одну внутреннюю сепаратрису (показана зеленой линией), которая проходит через седловую точку $( - 1.2875,0) \approx ( - 1.29,0)$. Следовательно, согласно определению суперсолитона, эта сепаратриса связана с новым типом уединенной волны на скорости звука – суперсолитоном на скорости звука. Таким образом, рис. 14 подтверждает существование суперсолитонов отрицательного потенциала на звуковой скорости. Теперь мы еще сильнее уменьшим значение ${{\beta }_{e}}$ и изобразим рис. 15 для βe = βeb – 0.1 = = 0.26908. Из рис. 15б видно, что фазовый портрет качественно совпадает с фазовым портретом NPSW на скорости звука (см. рис. 12б). Однако существует скачкообразный разрыв между амплитудами солитонов до и после образования NPDL на звуковой скорости (см. рис. 16). Поэтому при уменьшении значений ${{\beta }_{e}}$ при ${{\beta }_{e}} < {{\beta }_{{eb}}}$ суперсолитоны отрицательного потенциала в конечном итоге сводятся к NPSWs после образования NPDL. Другими словами, должно быть критическое $\beta _{e}^{{(cr)}}$ значение ${{\beta }_{e}}$, такое, что система допускает существование суперсолитонов отрицательного потенциала на звуковой скорости, когда ${{\beta }_{e}}$ находится в пределах интервала ${{\beta }_{{eb}}} < {{\beta }_{e}} < \beta _{e}^{{(cr)}}$, и для ${{\beta }_{e}} > \beta _{e}^{{(cr)}}$ система допускает существование NPSW после формирования двойного слоя на звуковой скорости. Таким образом, существуют процессы перехода между уединенными структурами на звуковой скорости, а именно: солитон → двойной слой → суперсолитон → → солитон после формирования двойного слоя. Такие процессы перехода наблюдались в работе [20] для уединенных структур в случае сверхзвуковых волн, т.е. для $M > {{M}_{c}}$. Для понимания механизмов этих процессов перехода уединенных структур на звуковой скорости мы приводим начало координат (т.е. точку перегиба), седловую и другие точки равновесия системы (33) на $\phi ( = {\kern 1pt} {{\phi }_{1}})$-оси для уменьшающихся значений ${{\beta }_{e}}$, начиная от ${{\beta }_{e}} = {{\beta }_{{eb}}} - 0.000001$ на рис. 17. На этом рисунке показано, что при уменьшении значений ${{\beta }_{e}}$ расстояние между ненулевым седлом и ближайшей к нему неподвижной неседловой точкой уменьшается и, в конечном итоге, обе точки исчезают из системы. В итоге, система содержит только точку перегиба, т.е. начало координат, и ненулевую точку равновесия. Следовательно, сепаратриса, соответствующая уединенной структуре, начинается и заканчивается в начале координат, охватывает неподвижную неседловую точку, и мы имеем NPSW после формирования NPDL на звуковой скорости. Таким образом, мы видим, что механизмы перехода уединенных структур на скорости звука качественно такие же, как и процессы перехода уединенных структур для сверхзвуковых волн, представленные в работе [20].
5. ВЫВОДЫ
В настоящей работе мы исследовали условия существования различных DIA уединенных структур со скоростью звука в бесстолкновительной незамагниченной пылевой плазме, состоящей из отрицательно заряженных неподвижных частиц пыли, адиабатических теплых ионов, распределенных по Кернсу нетепловых электронов и изотермических позитронов, с помощью областей существования и фазовых портретов. Хотя в работе [18] доказано, что в сверхзвуковом случае в аналогичной системе возможно существование двойных слоев обоих полярностей суперсолитонов положительного потенциала, но на скорости звука в системе возможны только PPSWs, NPSWs и NPDL. Кроме того, в настоящей статье показано, что при $p = 0$ система допускает существование PPSW, NPSW, NPDL, NPSW после образования NPDL и суперсолитонов отрицательного потенциала на звуковой скорости. Эти результаты согласуются с результатами [25], где с целью исследования DIA уединенных структур со звуковой скоростью рассматривалась бесстолкновительная незамагниченная трехкомпонентная пылевая плазма, состоящая из отрицательно заряженных неподвижных частиц пыли, адиабатических теплых ионов и распределенных по Кернсу нетепловых электронов.
Впервые представлены фазовые портреты динамической системы, соответствующие DIA уединным структурам на звуковой скорости. Обнаружены следующие качественные различия между фазовыми портретами уединенных структур при $M = {{M}_{c}}$ и фазовыми портретами уединенных структур для $M > {{M}_{c}}$, которые обсуждались в работе [20].
1. В случае $M > {{M}_{c}}$ начало координат всегда является седловой точкой и сепаратриса, соответствующая уединенным структурам, проходит через начало координат. В случае же $M = {{M}_{c}}$, начало координат является точкой перегиба, а сепаратриса, соответствующая уединенным структурам, начинается и заканчивается в начале координат.
2. В случае $M > {{M}_{c}}$ фазовые портреты динамической системы, соответствующие DIA двойным слоям, имеют две седловые и две неседловые неподвижные точки, а в случае двойных слоев на звуковой скорости система имеет точку перегиба в начале координат, одну ненулевую седловую точку и одну неседловую неподвижную точку.
3. Из работ [32] и [20] для случая суперсолитонов при $M > {{M}_{c}}$ следует, что существует как минимум две сепаратрисы, и сепаратриса, проходящая через начало координат (седловую точку), охватывает другую. В случае звуковых DIA-волн, т.е. при $M = {{M}_{c}}$, мы имеем такое же определение суперсолитонов, т.е. для суперсолитонов на звуковой скорости существуют как минимум две сепаратрисы, а сепаратриса, которая начинается и заканчивается в начале координат (точке перегиба), охватывает другую.
С помощью фазовых портретов мы также объяснили процессы перехода уединенных структур на звуковой скорости для $p = 0$, а именно: солитон → двойной слой → суперсолитон → солитон для уменьшающихся значений ${{\beta }_{e}}$, невозможно объяснить процесс перехода уединенных структур, рассматривая только области существования или просто рисуя кривую $V(\phi )$. Это явление перехода на звуковой скорости происходит в соответствии с механизмом, описанным на рис. 17. Механизм перехода на звуковой скорости такой же, как и у сверхзвуковых уединенных структур, рассмотренный в работе [20].
Из этой работы можно сделать вывод, что образование двойного слоя также возможно на скорости звука. Согласно Альфвену [7], двойной слой состоит из двух противоположно заряженных параллельных слоев, приводящих к падению потенциала в слое и исчезновению электрического поля на каждой стороне слоя. Образование двойных слоев в плазменной системе выделяет количество энергии, ускоряющее заряженные частицы системы. Над ионосферой Земли в довольно узкой области наблюдалось ускорение электронов, и возможной причиной такого ускорения является образование нескольких двойных слоев в этой области [7]. Настоящая работа полезна для понимания механизмов образования двойного слоя на скорости звука.
Авторы выражают благодарность рецензенту за конструктивные замечания, способствовавшие улучшению статьи. Один из авторов (Ashesh Paul) благодарит за финансовую поддержку Департамент науки и техники правительства Индии, Программу стипендий INSPIRE.
Список литературы
Shukla P.K., Marklund M. // Phys. Scr. 2004. V. T113. P. 36.
Zel’dovich I.B., Novikov I.D. Relativistic Astrophysics, 2: The Structure and Evolution of the Universe. University of Chicago Press, 1971. V. 2.
Zurek W.H. Astrophys. J. 1985. V. 289. P. 603.
Higdon J.C., Lingenfelter R.E., Rothschild R.E. // Astrophys. J. 2009. V. 698. P. 350.
Shukla P.K. Phys. Scr. 2008. V. 77. P. 068201.
Dubinov A.E., Kolotkov D.Y., Sazonkin M.A. // Tech. Phys. 2012. V. 57. P. 585.
Alfvén H. Cosmic plasma. Taylor & Francis, 1981. V. 82.
Gusev A.A., Jayanthi U.B., Martin I.M., Pugacheva G.I., Spjeldik W.N. Braz. // J. Phys. 2000. V. 30. P. 590.
Gusev A.A., Jayanthi U.B., Martin I.M., Pugacheva G.I., Spjeldvik W.N. // J. Geophys. Res. 2001. V. 106. P. 26111.
Merlino R.L. // Plasma Phys. Appl. 2006. V. 81. P. 73.
Hor’anyi M., Hartquist T., Havnes O., Mendis D., Mor-fill G. // Rev. Geophys. 2004. V. 42. P. 1.
Ghosh S., Bharuthram R. // Astrophys. Space Sci. 2008. V. 314. P. 121.
El-Tantawy S.A., El-Bedwehy N.A., Moslem W.M. // Phys. Plasmas. 2011. V. 18. P. 052113.
El-Tantawy S.A., Moslem W.M. // Phys. Plasmas. 2011. V. 18. P. 112105.
Saini N.S., Chahal B.S., Bains A.S. // Astrophys. Space Sci. 2013. V. 347. P. 129.
Banerjee G., Maitra S. // Phys. Plasmas. 2016. V. 23. P. 123701.
Paul A., Das A., Bandyopadhyay A. // Plasma Phys. Rep. 2017. V. 43. P. 218.
Paul A., Bandyopadhyay A. // Astrophys. Space Sci. 2016. V. 361. P. 172.
Cairns R.A., Mamun A.A., Bingham R., Dendy R.O., Boström R., Shukla P.K., Nairn C.M.C. // Geophys. Res. Lett. 1995. V. 22. P. 2709.
Paul A., Bandyopadhyay A., Das K.P. // Phys. Plasmas. 2017. V. 24. P. 013707.
Baluku T.K., Hellberg M.A., Kourakis I., Saini N.S. // Phys. Plasmas. 2010. 17. P. 053702.
Baluku T.K., Hellberg M.A., Verheest F. // Europhys. Lett. 2010. V. 91. P. 15001.
Verheest F., Hellberg M.A. // Phys. Plasmas. 2010. V. 17. P. 023701.
Das A., Bandyopadhyay A., Das K.P. // J. Plasma Phys. 2012. V. 78. P. 565.
Das A., Bandyopadhyay A., Das K.P. “Existence of dust ion acoustic solitary wave and double layer solution at m = mc,” arXiv preprint arXiv:1110.5307(2011).
Verheest F., Hellberg M.A. // Phys. Plasmas. 2015. V. 22. P. 012301.
Verheest F., Pillay S.R. // Phys. Plasmas. 2008. V. 15. P. 013703.
Dubinov A.E. // Plasma Phys. Rep. 2009. V. 35. P. 991.
Sagdeev R.Z. Reviews of Plasma Physics, ed. M. A. Leontovich (New York, NY: Consultant Bureau, 1966), Vol. 4.
Das A., Bandyopadhyay A., Das K.P. // Phys. Plasmas. 2009. V. 16. P. 073703.
Das A., Bandyopadhyay A., Das K.P. // J. Plasma Phys. 2012. V. 78. P. 149.
Dubinov A.E., Kolotkov D.Y. // Plasma Phys. Rep. 2012. V. 38. P. 909.
Дополнительные материалы отсутствуют.
Инструменты
Физика плазмы


