Физика плазмы, 2019, T. 45, № 9, стр. 825-830

1. ВВЕДЕНИЕ

В типичных наземных лабораторных условиях ансамбль отрицательно заряженных пылевых частиц, помещенных в газоразрядную плазму, располагается на некоторой высоте над горизонтальным электродом. Равновесная высота левитации определяется балансом между силой земного тяготения и электрического отталкивания от электрода. Приэлектродная область характеризуется наличием потока ионов, направленного к электроду, скорость которого сопоставима со скоростью ионного звука. Подробнее эти и многие другие аспекты физики пылевой плазмы обсуждаются, например, в недавних монографиях [1–3].

С другой стороны, в условиях невесомости пылинки располагаются в объеме плазмы, где помимо электрических сил существенную роль играет сила ионного увлечения или трения, а сила тяжести роли не играет. Сила ионного увлечения возникает в результате двухмелкомасштабных процессов: рассеяния ионов в электрическом поле пылинки и поглощения ионов при прямых столкновениях с пылинкой. В результате происходит обмен импульсом между пылинкой и потоком ионов. Однако результаты численного моделирования (см., например, [4]) показывают, что в приэлектродной области сила ионного увлечения, действующая на отдельную пылинку, мала по сравнению с силой тяжести и силой электрического отталкивания от стенки, и в общем балансе сил ею можно пренебречь.

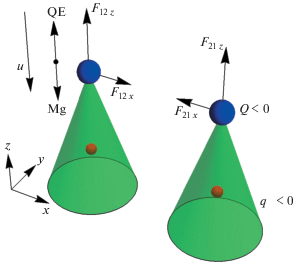
На рис. 1 схематически показаны силы, действующие на пылинку в пристеночном слое плазмы. Равновесная высота левитации ${{z}_{0}}$ отдельной пылинки определяется балансом сил $Mg + $ $ + \;QE({{z}_{0}}) = 0$, где M и Q – масса и заряд пылинки, g – ускорение свободного падения и $E(z)$ – электрическое поле в слое. Наличие потока ионов, показанного вектором u на рис. 1, приводит к сильной асимметрии электрического поля, создаваемого точечным зарядом. Благодаря черенковскому излучению внутри конусов Маха, затененных на рис. 1, возбуждается след ионно-звуковых колебаний, и электрическое поле пылинки представляет собой осциллирующую функцию координат. Вне конусов Маха электрическое поле обычно монотонно уменьшается по мере удаления от пылинки.

Сложная картина распределения поля вокруг точечного заряда в потоке плазмы исследовалась как аналитическими, так и численными методами для различных моделей плазмы (см. [1–3]). В общем случае потенциал поля $\phi ({\mathbf{r}})$ точечного заряда, расположенного в начале координат, симметричен относительно поворотов вокруг оси z, при этом $\phi ({\mathbf{r}}) = \phi (\rho ,z)$, где $\rho = \sqrt {{{x}^{2}} + {{y}^{2}}} $. Однако симметрия относительно отражений в плоскости $z = 0$ оказывается нарушенной, т.е. $\phi (\rho , - z) \ne $ $ \ne \phi (\rho ,z)$. В результате силы, действующие между пылинками, оказываются невзаимными (nonreciprocal) и для них не выполняется третий закон Ньютона. В частности, если две частицы расположены одна над другой вдоль потока ионов, взаимодействие между ними оказывается притягивающим, и они могут образовать связанный комплекс. Если же частицы расположены на одной высоте, они обычно отталкиваются друг от друга, но при некоторых условиях (например, [5–7]) может возникнуть притяжение.

Известно также, что электрическое поле, создаваемое отдельным зарядом, расположенным на определенной высоте, например, $z = 0$, имеет ненулевую вертикальную компоненту в плоскости $z = 0$, т.е. ${{E}_{z}}(\rho ,0)$ = $ - \partial \phi (\rho ,z){\text{/}}\partial z{{{\text{|}}}_{{z = 0}}} \ne 0$ (например, [8]). Благодаря этому возникают вертикальные компоненты сил, обозначенных как ${{F}_{{12z}}}$, ${{F}_{{21z}}}$ на рис. 1. Эти силы, в частности, приводят к развитию неустойчивости связанных мод (mode-coupling instability) однослойного плазменного кристалла, теоретически предсказанной в [9] и детально исследованной экспериментально [10].

В большинстве аналитических и численных исследований для описания динамики пылинок используется так называемая модель ионного фокуса. В рамках этой модели распределение электрического поля вокруг пылинки с зарядом Q аппроксимируется при помощи точечного безмассового виртуального заряда q противоположного знака, расположенного на фиксированном расстоянии ниже по течению (рис. 1). При этом считается, что заряд q не действует на расположенный выше по течению родительский заряд Q. Однако ионный фокус может оказывать влияние на соседние реальные пылинки, и силы ${{F}_{{12z}}}$, ${{F}_{{21z}}}$ не равны нулю. Часто ими пренебрегают или считают малыми (например, [9]). В целом, модель ионного фокуса в некоторых случаях позволяет получить качественно разумное описание динамики ансамбля пылевых частиц, однако ее точность остается неизвестной.

В настоящей статье более подробно исследуются силы, действующие между отдельными частицами, расположенными на одной высоте в пристеночном слое плазмы. Ниже показано, что вычисленные в рамках модели однородной плазмы вертикальные компоненты сил оказываются неожиданно большими, и в некоторых случаях сравнимыми с весом отдельной частицы. Поскольку возникновение подобной силы в конечном итоге обусловлено обменом импульсом с окружающей плазмой, и она существует только для нескольких частиц, мы называем ее коллективной силой ионного увлечения. В следующем разделе описана используемая в статье модель и приведены результаты расчетов сил между двумя частицами. В разд. 3 вычисляется коллективная сила ионного увлечения, действующая на гексагональную решетку пылевых частиц. Оценки характерных величин даны в заключительной части статьи.

2. ВЗАИМОДЕЙСТВИЕ МЕЖДУ ЧАСТИЦАМИ

В однородном потоке плазмы потенциал неподвижной заряженной частицы, расположенной в начале координат, дается выражением

где Q – заряд частицы и u – скорость потока. Здесь предполагается, что поток плазмы направлен в сторону $z \to - \infty $ (рис. 1). В дальнейшем все пространственные переменные нормализованы на характерную длину $\lambda = u{\text{/}}{{\omega }_{{pi}}}$, где ${{\omega }_{{pi}}}$ – ионная плазменная частота, а межчастичные силы нормализованы на ${{Q}^{2}}{\text{/}}{{\lambda }^{2}}$. В безразмерных переменных сила, действующая на другую частицу с тем же зарядом Q в точке r равна ${\mathbf{F}}({\mathbf{r}}) = - \nabla U({\mathbf{r}})$. Потенциальная функция $U({\mathbf{r}}) = U(\rho ,z)$ получается из (1) интегрированием по полярному углу

Предполагается, что плазма состоит из холодного потока ионов и максвелловских электронов с температурой ${{T}_{e}}$. В этом случае диэлектрическая проницаемость плазмы в безразмерных переменных имеет вид

где ν – частота столкновений ионов с нейтралами, считающаяся бесконечно малой. В выражении (3) $M = ({{n}_{e}}{\text{/}}{{n}_{i}})u\sqrt {{{m}_{i}}{\text{/}}{{T}_{e}}} $, где ${{n}_{{e,i}}}$ – равновесные плотности электронов и ионов и ${{m}_{i}}$ – масса ионов. В общем случае плазма в пристеночном слое не является нейтральной, т.е. ${{n}_{e}} \ne {{n}_{i}}$, однако при этом неоднородностью плазмы пренебрегается. Представляет интерес случай чисто ионного потока, когда влиянием электронов можно пренебречь и $M = 0$. Для квазинейтральной плазмы с ${{n}_{e}} = {{n}_{i}}$ параметр M совпадает с числом Маха потока, т.е. с отношением скорости u к скорости ионного звука.

Подынтегральное выражение в (2) как функция ${{k}_{z}}$ имеет четыре полюса. В пределе $\nu \to 0$ два из них комплексно сопряжены ${{k}_{z}} = \pm i{{q}_{1}}(k)$, а два других лежат вблизи действительной оси ${{k}_{z}} = \pm {{q}_{2}}(k) - i0$. В явном виде ${{q}_{{1,2}}}{{(k)}^{2}}$ = $( \pm \alpha (k) + \beta (k)){\text{/}}2$, где $\alpha (k) = $ $ = {{k}^{2}} + {{M}^{2}} - 1$ и $\beta (k) = \sqrt {\alpha {{{(k)}}^{2}} + 4{{k}^{2}}} $. Интеграл по ${{k}_{z}}$ в (2) легко вычисляется, и результирующий потенциал разбивается на сумму двух частей $U(\rho ,z)$ = $V(\rho ,z) + \theta ( - z)W(\rho ,z)$, где $\theta (z)$ – функция Хевисайда. Первый член

обусловлен комплексно-сопряженными полюсами ${{k}_{z}} = \pm i{{q}_{1}}(k)$, а второй возникает из-за действительных полюсов ${{k}_{z}} = $ $ = \pm {{q}_{2}}(k) - i0$. Четная функция z, определяемая интегралом (4) обычно рассматривается как экранированный кулоновский потенциал, а вторая часть (5) описывает след ионно-звуковых (или чисто ионных при $M = 0$) колебаний, формирующихся вниз по течению от точечного заряда.

Интегралы (4), (5) вычисляются численными методами, а различные предельные случаи подробно изучены в литературе. В общем случае выражение (2) представляет собой гладкую функцию при $\rho \ne 0$, $z \ne 0$. Вблизи начала координат $z \to 0$, $\rho \to 0$ полный потенциал приближается к кулоновскому $U(\rho ,z) \approx 1{\text{/}}\sqrt {{{z}^{2}} + {{\rho }^{2}}} $. Заметим, что в приближении холодных ионов в интеграле (5) появляется дополнительная сингулярность. Поскольку ${{q}_{2}}(k) \to 1$ при $k \to \infty $, выражение (5) логарифмически расходится при $\rho \to 0$. Эта расходимость сглаживается при учете конечной температуры ионов. В дальнейшем нас в основном интересует поведение потенциала при $z \approx 0$, $\rho > 0$, и использованных в (4), (5) выражений достаточно для целей настоящей статьи.

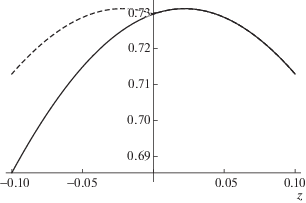
Хотя полный потенциал (2) представляет собой гладкую функцию координат при $z \approx 0$, производные интегралов (4), (5) разрывны при $z = 0$. Характерный пример показан на рис. 2, где сплошной линией изображена зависимость $U(\rho ,z)$ от z, а штриховой – четная функция (4). При $z > 0$ обе кривые совпадают, а разница при $z < 0$ связана со следом ионно-звуковых волн (5). Возбуждение следа приводит к сдвигу максимума $U(\rho ,z)$ при фиксированном значении ρ в сторону от плоскости $z = 0$, и производная потенциала $U{{,}_{z}}(\rho ,0) \ne 0$.

Предположим, что две частицы левитируют на одной высоте $z = {{z}_{1}}$ и расстояние между ними каким-то образом поддерживается постоянным. Например, этого можно добиться наложением дополнительного поля, удерживающего пылинки от разлета в горизонтальной плоскости. Отвлекаясь от пылевой плазмы, можно представить себе космический корабль удлиненной формы, у которого противоположные концы несут заряды одного знака, в потоке солнечного ветра¹¹.

Как показано на рис. 1, первая частица в этом случае толкает вторую вверх (или вниз), а вторая делает то же самое с первой в том же направлении. Вертикальные силы, действующие на каждую частицу ${{f}_{z}}(\rho ) = - U{{,}_{z}}(\rho ,0)$, равны и зависят от расстояния между частицами. При удалении частиц друг от друга эффект пропадает, поэтому мы называем их коллективными силами ионного увлечения. В отсутствие внешнего удерживающего потенциала подобные силы должны приводить к ускорению пары частиц, т.е.такой комплекс ведет себя как молекулярный мотор. Заметим, что в зависимости от параметров плазмы направление коллективной силы ионного увлечения может быть как положительным, так и отрицательным, а пара частиц может сдвигаться как вниз, так и вверх по течению.

В пристеночном слое плазмы дополнительную силу, удерживающую пылинки, можно приближенно записать как ${{F}_{{ext}}}(z)$ = $ - \omega _{0}^{2}(z - {{z}_{0}})$, где ${{z}_{0}}$ – равновесная высота левитации, а ${{\omega }_{0}}$ – частота колебаний отдельной пылинки. Вертикальные межчастичные силы приводят к смещению равновесной высоты левитации ${{z}_{1}}$ пары частиц, которую можно найти из соотношения ${{f}_{z}}(\rho ) - $ $ - \;\omega _{0}^{2}({{z}_{1}} - {{z}_{0}}) = 0$.

Поскольку потенциал $U(\rho ,z)$ непрерывен, его производную можно вычислять при помощи интеграла (4) в пределе $z \to + 0$. Для численных расчетов удобно вычесть кулоновский потенциал из (4) и записать результат в виде $V(\rho ,z)$ = = $1{\text{/}}\sqrt {{{\rho }^{2}} + {{z}^{2}}} + \delta V(\rho ,z)$, где

Тогда сила определяется хорошо сходящимся интегралом

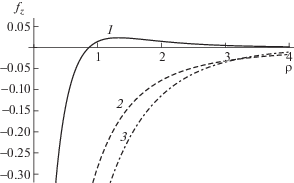
где $\chi (k)$ = ${{q}_{2}}(k){\text{/}}\beta (k)$. В частном случае чисто ионного потока $M = 0$, рассмотренного в [7], $\chi (k) = 1{\text{/}}(1 + {{k}^{2}})$, и функцию (6) можно записать в явном виде как ${{f}_{z}}(\rho ) = - {{K}_{0}}(\rho )$, где ${{K}_{0}}(\rho )$ – модифицированная функция Бесселя второго рода. При $M > 0$ интеграл (6) легко вычисляется стандартными численными методами.

Несколько примеров зависимости вертикальной компоненты силы от расстояния между частицами показаны на рис. 3. Насколько можно судить по результатам численных расчетов, в дозвуковом режиме ($M < 1$) сила (6) всегда параллельна потоку плазмы. В случае сверхзвукового потока ($M > 1$) при большом расстоянии между частицами направление силы становится антипараллельным потоку. Интересно, что горизонтальные компоненты силы (которые здесь не обсуждаются) всегда соответствуют отталкиванию при $M > 1$, тогда как при $M < 1$ может возникнуть притяжение.

3. ГЕКСАГОНАЛЬНАЯ РЕШЕТКА

Для большего числа пылинок коллективная сила ионного увлечения заметно увеличивается. Рассмотрим гексагональную решетку, составленную из частиц, левитирующих на одной высоте $z = {{z}_{1}}$, которая определяется полным балансом вертикальных сил. Координаты частиц в плоскости $xy$ равны ${{\rho }_{{{{n}_{1}},{{n}_{2}}}}} = a({{n}_{1}}{{{\mathbf{g}}}_{1}} + {{n}_{2}}{{{\mathbf{g}}}_{2}})$, где a – постоянная решетки и ${{n}_{{1,2}}}$ – целые числа. Единичные примитивные векторы решетки можно выбрать в виде ${{{\mathbf{g}}}_{1}} = (1,0)$, ${{{\mathbf{g}}}_{2}} = (1,\sqrt 3 ){\text{/}}2$. В силу симметрии решетки горизонтальный баланс сил обеспечен для произвольного аксиально-симметричного взаимодействия.

Вертикальные силы, действующие на каждую частицу, равны. Для пылинки с ${{n}_{1}} = {{n}_{2}} = 0$ сила обусловлена влиянием всех остальных частиц решетки и записывается в виде суммы

где ${{f}_{z}}(\rho )$ определяется интегралом (6).

Поскольку на больших расстояниях функция ${{f}_{z}}(\rho )$ экспоненциально уменьшается, сумма (7) быстро сходится. Для достаточно большой постоянной решетки (примерно, $a > 2$) разумная точность достигается при учете лишь шести ближайших соседей с ${{\rho }_{{{{n}_{1}},{{n}_{2}}}}} = a$ или $n_{1}^{2} + {{n}_{1}}{{n}_{2}} + n_{2}^{2} = 1$. В этом случае результат можно записать как ${{F}_{z}}(a) = 6{{f}_{z}}(a)$.

При уменьшении постоянной решетки необходим учет большего числа членов в сумме (7). Например, опытным путем было обнаружено, что при $a = 0.5$ относительная точность порядка 10^–2 достигается при учете всех точек решетки с ${{\rho }_{{{{n}_{1}},{{n}_{2}}}}} \leqslant 20a$. Это приводит к довольно сложной численной процедуре, требующей по меньшей мере 120 вычислений интеграла (6) для различных значений $\rho $. Расчеты существенно ускоряются при помощи следующего трюка, напоминающего метод Эвальда вычисления решеточных сумм (например, [11]).

Разделим функцию $\chi (k)$ в (6) на две части $\chi (k)$ = ${{\chi }_{1}}(k) + 1{\text{/}}({{k}^{2}} + {{\kappa }^{2}})$, где $\kappa > 0$ – вспомогательный параметр. Тогда сила, действующая на отдельную частицу, записывается в виде ${{f}_{z}}(\rho )$ = = ${{f}_{{1z}}}(\rho ) - {{K}_{0}}(\kappa \rho )$, где

Заметим, что функция ${{f}_{{1z}}}(\rho )$ регулярна при $\rho = 0$. Сумма (7) также разделяется на две части ${{F}_{z}}(a) = {{F}_{{1z}}}(a) + {{F}_{{2z}}}(a)$, где

Вторая сумма (10) быстро сходится и легко вычисляется с произвольной точностью. Выберем вспомогательный параметр κ так, чтобы ${{f}_{{1z}}}(0) = 0$. Поскольку интеграл (8) при $\rho = 0$ можно вычислить в явном виде, для этого нужно положить

Теперь можно добавить точку с индексом ${{n}_{1}} = {{n}_{2}} = 0$ в сумму (9) и при помощи формулы Пуассона (например, [11]) перейти к суммированию по обратной решетке

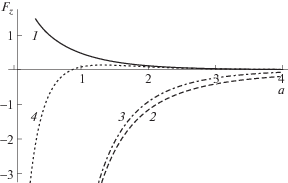
где ${{{\mathbf{b}}}_{{1,2}}}$ – примитивные векторы обратной решетки, определяемые соотношением ${{{\mathbf{g}}}_{i}} \cdot {{{\mathbf{b}}}_{j}} = {{\delta }_{{ij}}}2\pi {\text{/}}a$. Поскольку ${{\chi }_{1}}(k)$ представляет собой алгебраическую функцию и ${{\chi }_{1}}(k) \sim 1{\text{/}}{{k}^{4}}$ при $k \to \infty $, сумма (12) также легко вычисляется с произвольной точностью.

Несколько примеров зависимости коллективной силы ионного увлечения в расчете на одну частицу как функции постоянной решетки показаны на рис. 4. Для сравнения здесь также показана сила, полученная в приближении ближайших соседей (кривая 4). Хотя прямого доказательства не существует, по-видимому, в случае дозвукового или чисто ионного потока ($M < 1$) коллективная сила ионного увлечения всегда положительна (кривые 2, 3 на рис. 4), то есть направлена по течению. Для сверхзвукового потока ($M > 1$) сила направлена против течения (кривая 1 на рис. 4).

Асимптотическое поведение полной силы при малых межчастичных расстояниях можно оценить при помощи сумм (10, 12). Очевидно, что сумма (10) при $a \to 0$ расходится как ${{F}_{{2z}}}(a) \sim lna$, тогда как сумма (12) ведет себя более сингулярным образом: ${{F}_{{1z}}}(a) \sim {{\chi }_{1}}(0){\text{/}}{{a}^{2}}$. Таким образом, ${{F}_{z}}(a) \sim 1{\text{/}}{{a}^{2}}$ при $M > 1$ и ${{F}_{z}}(a) \sim - 1{\text{/}}{{a}^{2}}$ при $0 \leqslant M < 1$.

4. ЗАКЛЮЧЕНИЕ

Оценим характерную величину силы ионного увлечения. В этой статье использовался масштаб сил, равный ${{F}_{0}} = {{Q}^{2}}\omega _{{pi}}^{2}{\text{/}}{{u}^{2}}$. Естественный масштаб сил, действующих на частицу в пристеночном слое, определяется весом отдельной частицы $P = Mg$. Взяв, для примера, характерные значения $Q = {{10}^{4}}e$, $M = {{10}^{{ - 10}}}$ г, ${{n}_{i}} = {{10}^{{10}}}$ см^–3, ${{T}_{e}} = 2$ эВ для ионов аргона и скорости потока, равной скорости ионного звука, получаем, что ${{F}_{0}}{\text{/}}P \approx 2$. Таким образом, коллективная сила ионного увлечения по порядку величины может быть сравнима с весом отдельной частицы.

Как известно, при уменьшении межчастичного расстояния однослойный плазменный кристалл становится неустойчивым. Условия возникновения этой неустойчивости зависят от внешнего удерживающего потенциала, который обычно аппроксимируется параболической потенциальной ямой. Существует некоторое минимальное межчастичное расстояние, для которого рассмотренная здесь статическая картина становится неприменимой.

В действительности же удерживающий потенциал имеет конечную глубину, и возможен другой механизм разрушения однослойного плазменного кристалла. В дозвуковом потоке коллективная сила ионного увлечения может просто выбросить частицы из удерживающей потенциальной ямы. С другой стороны, эта сила облегчает существование кристалла в сверхзвуковом потоке.