Физика плазмы, 2019, T. 45, № 9, стр. 771-776
Влияние запертых электронов на потенциал плазмы в расширителе открытой ловушки
a Институт ядерной физики им. Г.И. Будкера СО РАН
Новосибирск, Россия
b Новосибирский государственный университет
Новосибирск, Россия
* E-mail: d.i.skovorodin@inp.nsk.su
Поступила в редакцию 21.06.2018
После доработки 22.04.2019
Принята к публикации 25.04.2019
Аннотация
Рассматривается влияние запертых между пробкой и дебаевским слоем электронов на распределение потенциала в расширителе открытой ловушки. Для вычисления функции распределения электронов в самосогласованном электростатическом потенциале разработана численная модель. Пролетные электроны рассматриваются как бесстолкновительные, а для вычисления функции распределения запертых электронов применяется баунс-усредненное кинетическое уравнение с интегралом столкновений Ландау. Получен самосогласованный профиль потенциала. Показано, что решение хорошо согласуется с полуаналитической моделью Д.Д. Рютова.
1. ВВЕДЕНИЕ
Осесимметричные пробочные ловушки пригодны для удержания плазмы с большим относительным давлением β [1], что делает их привлекательными в качестве источника нейтронов и, возможно, альтернативного реактора синтеза [2, 3]. Вопрос о перспективности открытых ловушек в качестве термоядерной системы связан, прежде всего, с возможностью ограничения потерь частиц и энергии вдоль магнитного поля. В последнее время предложены новые методы уменьшения скорости потерь плазмы из ловушек [4, 5]. Тем не менее, главным недостатком таких систем все еще являются продольные потери вдоль силовых линий магнитного поля, которые соединяют центральную часть ловушки с приемником плазмы.
Хотя условие амбиполярности потерь ограничивает поток электронов, поток тепла, который они переносят, определяет продольные потери энергии из ловушки [6]. Из-за разности скоростей потерь электронов и ионов через магнитную пробку плазма принимает положительный потенциал, возвращающий в ловушку большую часть электронов. Если холодные электроны, рожденные на приемнике плазмы, по какой-то причине не попадают в центральную часть ловушки, либо вторичная эмиссия вовсе отсутствует, величина потенциала в несколько раз превышает температуру электронов. Вообще говоря, вторичные электроны могут быть отражены магнитной пробкой обратно на стенку. Однако этому препятствует электрическое поле, которое удерживает горячие электроны в ловушке, но в то же время втягивает в нее холодные вторичные частицы. В случае, если приемник плазмы расположен в слабом магнитном поле, т.е. поток плазмы сильно расширяется за пробкой, распределение удерживающего потенциала между пробкой и стенкой оказывается нетривиальным [7]. В расширителе между пристеночным скачком потенциала в дебаевском слое и магнитной пробкой могут удерживаться запертые электроны. Их отрицательный объемный заряд приводит к частичному переносу скачка потенциала из пристеночного слоя в объем расширителя. Этот эффект является благоприятным по двум причинам. Во-первых, уменьшается опасность образования униполярных дуг на поверхности приемника плазмы. Во-вторых, чем меньше электрическое поле вблизи стенки, тем большая часть вторичных электронов отражается от пробки. Таким образом, профиль потенциала плазмы вдоль силовой линии между стенкой и пробкой определяет темп потерь тепла из ловушки по электронному каналу.
Cуществующая теория поведения электронов в расширителе основана на качественных оценках. В работе [7] рассмотрено распределение потенциала в случае, когда приемник плазмы может эмитировать бесконечный ток холодных электронов. Эта модель, по-видимому, далека от условий в современных ловушках, в которых поверхность приемника плазмы остается холодной. В работе Рютова [8] анализируется распределение потенциала в случае, когда вторичная эмиссия отсутствует. Эта модель основана на модельном предположении о характере функции распределения в области запертых электронов. Часть границы этой области является общей с областью пролетных электронов. Из-за столкновений функция распределения запертых частиц должна непрерывно сшиваться на границе с фазовой плотностью пролетных. В [8] предполагается, что в результате столкновений в области запертых частиц формируется “квазисферическая” функция распределения. При этом характерное значение этой функции распределения оценивается по порядку величины как значение функции распределения пролетных частиц при V ~ VTe (где V – скорость частиц, VTe – тепловая скорость электронов).
Недавно появились сведения о численной кинетической модели [9, 10], разработанной сотрудниками компании TriAlphaEnergy для анализа условий в диверторе FRC, который аналогичен расширителю открытой ловушки. Эта модель основана на прямом интегрировании полуторамерного кинетического уравнения с интегралом столкновений Ландау (в переменных продольная координата, продольная и поперечная скорости электронов). К сожалению, подробной публикации по результатам расчетов с использованием данной модели пока нет. В докладе [9] указано на то, что область удержания электронов в фазовом пространстве граничит не только с областью пролетных частиц, но и с незаполненной областью за границей удержания. Стационарная функция распределения запертых электронов устанавливается в результате столкновений и определяется балансом притока пролетных электронов и стока теряемых в результате рассеяния электронов. Поэтому предположение о том, что фазовая плотность запертых в расширителе электронов оказывается порядка фазовой плотности пролетных частиц, требует дополнительного обоснования.
Целью представляемой статьи является вычисление самосогласованного потенциала плазмы и функции распределения запертых электронов в расширителе открытой ловушки. Для вычисления функции распределения запертых электронов используется баунс-усредненное кинетическое уравнение. Во втором разделе работы описаны предположения, на которых основана разработанная численная модель. В третьем разделе анализируются результаты расчетов.
2. ЧИСЛЕННАЯ МОДЕЛЬ
В отсутствие вторичной эмиссии с приемника плазмы, электроны в расширителе можно условно разделить на три группы: пролетные (вылетают из пробки и попадают на стенку), возвратные (электроны, вылетающие из пробки и отражающиеся назад потенциальным барьером) и запертые. В условиях, характерных для перспективных термоядерных устройств на основе открытых ловушек, пролетные и возвратные электроны являются практически бесстолкновительными [8], однако именно благодаря рассеянию этих частиц заполняется область запертых электронов. При этом, при достаточно больших коэффициентах расширения (где Bm – магнитное поле в пробке, B(s) – поле в рассматриваемой точке, s – координата вдоль силовой линии) запертые электроны начинают играть существенную роль в обеспечении квазинейтральности плазмы. Таким образом, задача определения распределения потенциала вдоль силовой линии магнитного поля включает в себя рассмотрение кинетики электронов в самосогласованном электрическом поле.
В данной работе мы следуем предположениям, на которых основана модель [8]:
предполагается амбиполярность потерь вдоль магнитного поля;
рассматривается случай редких столкновений (это предположение обосновано в работе [7] для плазмы с характерными для открытых ловушек параметрами);
электроны подчиняются дрейфовому кинетическому уравнению;
в силу аксиальной симметрии задачи предполагается отсутствие влияния дрейфов поперек магнитного поля на функцию распределения;
для упрощения задачи считаем, что изменения скорости течения ионов пренебрежимо малы, т.е. (где ni – текущая плотность ионов, nim – плотность ионов в пробке);
функция распределения электронов, вылетающих из пробки в сторону расширителя, соответствует половине максвелловского распределения с температурой Te;
вторичная эмиссия электронов со стенки отсутствует.
Как было отмечено выше, задача об отыскании самосогласованного потенциала плазмы является нелинейной, так как требует вычисления функции распределения запертых электронов, которая в свою очередь зависит от распределения потенциала вдоль силовой линии. Для решения этой задачи была разработана итерационная схема, которая основана на следующей процедуре. Потенциал вычисляется исходя из условия квазинейтральности плазмы методом последовательных итераций. Для этого задается некоторый несамосогласованный профиль потенциала φk(s), для которого вычисляется плотность электронов nek. После этого вычисляется невязка между плотностью ионов ni (которая считается заданной) и плотностью электронов. При помощи этой невязки вычисляется потенциал для следующего шага φk+ 1 по формуле
(1)
${{\varphi }_{{k + 1}}}(s) = {{\varphi }_{k}}(s) + \alpha \cdot \frac{{{{n}_{{ek}}}(s) - {{n}_{i}}(s)}}{{{{n}_{i}}(s)}},$Для описания поведения потенциала в дебаевском скачке на стенке, вообще говоря, нужно решать уравнение Пуассона, так как плазма внутри слоя не является квазинейтральной. Далее будем рассматривать случай, в котором дебаевская длина существенно меньше, чем расстояние между пробкой и приемником плазмы. В этом случае ход потенциала внутри слоя не представляет интереса с точки зрения поиска функции распределения запертых электронов. Его роль сводится только к отражению частиц с маленькой продольной скоростью от стенки обратно в объем расширителя. Для учета отражения частиц достаточно знать только величину скачка ${\Delta \varphi }$. Величина скачка должна быть достаточной для поддержания амбиполярности потерь ионов и электронов на приемник плазмы. Она также подбирается во время итераций по формуле аналогичной (1), однако вместо невязки плотности электронов и ионов используется разность между потоками электронов и ионов.
Для вычисления плотности электронов в заданном потенциале нужно отыскать их функцию распределения. Стационарная функция распределения электронов, в указанных выше приближениях, подчиняется кинетическому уравнению
(2)
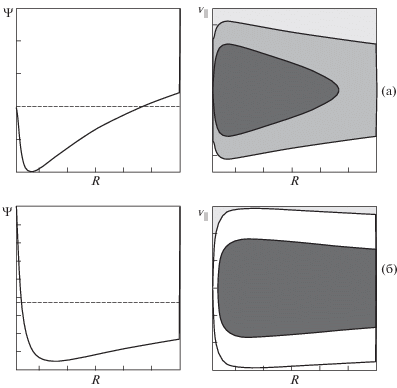
${{\left( {\frac{{\partial f}}{{\partial {\text{s}}}}} \right)}_{{{\varepsilon },{\mu } = {\text{const}}}}} = C\left( f \right),{\text{\;}}$Рис. 1.
Профиль эффективного потенциала (слева) и соответствующий фазовый портрет электронов при фиксированном μ (справа): а) – случай с отраженными электронами; б) – случай без отраженных электронов. Оттенками серого от светлого к темному показаны области, занятые соответственно пролетными, возвратными и запертыми электронами. Незакрашенная часть рисунка соответствует области фазового пространства, которая не заполнена электронами.
В работе [7] было показано, что если λ0 > R, электроны остаются слабостокновительными во всем объеме расширителя (R $~$– характерный размер расширителя, а λ0 – длина пробега электронов, определенная по параметрам плазмы в пробке). В этом случае уравнение (1) можно рассматривать для пролетных и возвратных частиц как бесстолкновительное, а для запертых применить процедуру усреднения по баунс-колебаниям. В таком приближении функция распределения пролетных и возвратных электронов переносится без изменений с границы (в пробке) вдоль траекторий частиц в фазовом пространстве. Процедура вычисления плотности этих частиц описана в работе [14].
Для отыскания функции распределения запертых электронов использована стандартная методика баунс-усреднения кинетического уравнения [15]
где интегрирование ведется вдоль замкнутой траектории запертых электронов в фазовом пространстве при постоянных энергии ε и магнитном моменте. Для ускорения расчетов используются потенциалы Трубникова, определенные по максвелловской функции распределения [12]. К уравнению (2) должны быть поставлены граничные условия на значения функции распределения на границе области удержания запертых частиц. Как было сказано выше, границу области удержания запертых электронов можно разбить на две части. При малых μ запертые электроны граничат с областью возвратных электронов. Их рассеяние приводит к заполнению области запертых электронов частицами. При больших μ запертые электроны граничат с незаполненной областью фазового пространства (рис. 1б). Через эту часть границы осуществляется сток запертых электронов. В результате этих процессов устанавливается стационарное распределение запертых электронов. Уравнение (2) решается при помощи разностной схемы на сетке в переменных ${{v}_{{||}}}$, μ и s. По вычисленной функции распределения определяется плотность запертых частиц, которая в сумме с плотностью пролетных и возвратных дает значение плотности электронов.3. РЕЗУЛЬТАТЫ РАСЧЕТОВ
Использование баунс-усреднения для решения кинетического уравнения оправдано малостью частоты столкновений. В этом пределе длина свободного пробега электронов превышает характерную длину области удержания запертых электронов в расширителе. Поэтому вид установившейся функции распределения этих электронов не зависит от самой длины свободного пробега. Так как между пробкой и приемником плазмы зависимость R(s) является взаимно-однозначной, было бы удобно использовать в качестве продольной координаты переменную R. Однако, несмотря на отсутствие зависимости решения от длины свободного пробега, оно зависит от профиля $B(s) = {{B}_{m}}{\text{/}}R(s)$. В данной работе расчеты проводились для двух видов профилей магнитного поля: “быстро” расширяющееся поле $B(s) = {{B}_{m}}{{e}^{{ - s/{{l}_{1}}}}}$ и “медленно” расширяющееся $B(s) = {{B}_{m}}{{(s{\text{/}}{{l}_{2}})}^{{1/3}}}$ ; здесь l1 и l2 – масштабы длины. Оказывается, что результаты расчетов: профиль потенциала плазмы φ(R) и величина дебаевского скачка на приемнике плазмы, – слабо отличаются для этих двух случаев. Далее показаны результаты для первого случая. В качестве продольной координаты на рисунках используется R.
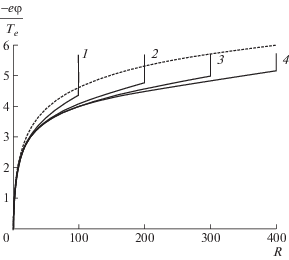
В модели, описанной в предыдущем разделе, были вычислены профили потенциала за пробкой ловушки для разных положений приемника плазмы Rw. В расчетах рассматривалась электронно-протонная плазма. На рис. 2 показан профиль потенциала плазмы вдоль силовой линии. Согласно модели [8], вблизи пробки функция электронов близка к больцмановской, что приводит к логарифмической зависимости потенциала от коэффициента расширения $\varphi = - ({{T}_{e}}{\text{/}}e)\ln R$. Заметное отличие профиля потенциала от логарифмической зависимости должно проявляться при значениях R порядка $\sqrt {{{m}_{i}}{\text{/}}{{m}_{e}}} \approx 40$. Как видно из рис. 2, результаты расчетов согласуются с моделью [8]. Уже при значении $R \approx 20$ наблюдается отличие хода потенциала от логарифмического профиля.
Рис. 2.
Профиль потенциала плазмы, нормированного на Te/(–e). Вертикальными линиями показан скачок потенциала в пристеночном слое. Линии 1, 2, 3 и 4 соответствуют положению приемника плазмы при коэффициенте расширения магнитного поля Rw 100, 200, 300 и 400 соответственно. Пунктир – логарифмический профиль, соответствующий больцмановскому распределению электронов.
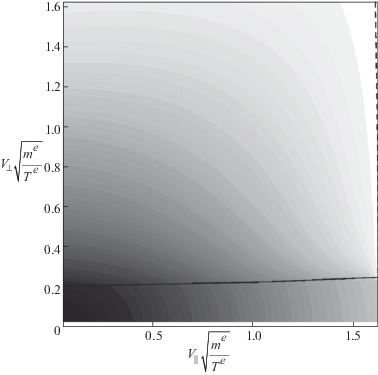
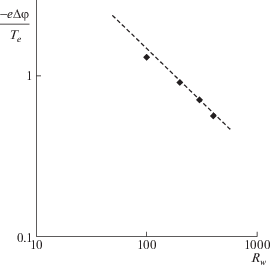
На рис. 3 приведена функция распределения электронов вблизи приемника плазмы в точке R = 99, рассчитанная для случая Rw = 100 (функция распределения пролетных частиц – максвелловская). Пролетные электроны диффундируют в область удержания через границу, показанную сплошной линией, а покидают ее через границу, показанную штриховой линией. В результате столкновений устанавливается баланс между притоком и стоком частиц из зоны удержания, которым определяется вид стационарной функции распределения. Видно, что хотя функция распределения далека от изотропной максвелловской, фазовая плотность в области удержания действительно оказывается порядка фазовой плотности пролетных частиц. С практической точки зрения наибольший интерес вызывает величина скачка потенциала в пристеночном слое. На рис. 4 точками показана рассчитанная величина скачка в зависимости от положения приемника плазмы Rw. Штриховой линией изображена зависимость вида
(4)
$\frac{{ - e{\Delta \varphi }}}{{{{T}_{e}}}} \approx \frac{{2.6}}{{R_{w}^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-0em} \!\lower0.7ex\hbox{$3$}}}}}}{{\left( {\frac{{{{m}_{i}}}}{{{{m}_{e}}}}} \right)}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0em} \!\lower0.7ex\hbox{$3$}}}}},$4. ЗАКЛЮЧЕНИЕ
Величина скачка потенциала в дебаевском слое на приемнике плазмы, имеющая большое значение в вопросе термоизоляции плазмы, определяется возможностью накопления запертых электронов за пробкой открытой ловушки. Стационарная функция распределения запертых электронов устанавливается в результате столкновений и определяется балансом притока пролетных электронов и стока теряемых в результате рассеяния электронов. Ранее для оценки величины скачка потенциала использовалась приближенная формула, предложенная в работе [8]. Она предполагает, что накопление запертых электронов происходит эффективнее, чем их потеря. В настоящей работе на основе строгих кинетических расчетов вычислена фазовая плотность запертых частиц и изучен ход профиля потенциала плазмы от пробки до приемника плазмы. Несмотря на то, что частью своей границы область удержания электронов соприкасается с незаполненной областью фазового пространства, оказывается возможным их эффективное накопление. Важно, что полученные результаты справедливы для широкого диапазона профилей спадания магнитного поля за пробкой ловушки.
Расчеты в целом подтверждают достаточно благоприятную зависимость скачка потенциала от коэффициента расширения, полученную в [8]. Однако точное значение оказывается приблизительно в 2.6 раза выше, что может стать достаточно существенным для практических расчетов. Хотя функция распределения электронов далека от максвелловской, ход профиля потенциала с приемлемой точностью можно описать, если предположить, что функция распределения запертых электронов больцмановская. Это обстоятельство в дальнейшем может существенно облегчить моделирование, так как избавляет от необходимости решать кинетическое уравнение при проведении приближенных расчетов.
Автор благодарен за полезные обсуждения А.Д. Беклемишеву.
Работа поддержана грантом РНФ № 18-72-10084.
Список литературы
Bagryansky P.A., Anikeev A.V., Beklemishev A.D., Do-nin A.S., Ivanov A.A., Korzhavina M.S., Kovalenko Yu.V., Kruglyakov E.P., Lizunov A.A., Maximov V.V., Murakhtin S.V., Prikhodko V.V., Pinzhenin E.I., Pushkareva A.N., Savkin V.Ya., Zaytsev K.V. // Fusion Sci. Tech. 2011. V. 59. № 1. P. 31.
Ivanov A.A., Prikhodko V.V. // Plasma Phys. Control. Fusion. 2013. V. 55. P. 1.
Beklemishev A.D. // AIP Conf. Proc. 2016. V. 1771. 030001.
Beklemishev A.D. // Phys. Plasmas. 2016. V. 23. 082506. https://doi.org/10.1063/1.4960129
Postupaev V.V., Sudnikov A.V., Beklemishev A.D., Iva-nov I.A. // Fusion Eng. Des. 2016. V. 106. P. 29.
Мирнов В.В., Рютов Д.Д. // Итоги науки и техники. Физика плазмы / Под ред. В.Д. Шафранова. Т. 8. М.: ВИНИТИ, 1988. С. 77.
Конкашбаев И.К., Ландман И.С., Улинич Ф.Р. // ЖЭТФ. 1978. Т. 74. С. 956. [I.K. Konkashbaev, I.S. Landman, F.R. Ulinich // JETP. 47, 501 (1978)].
Ryutov D.D. // Fusion Sci. Tech. 2005. V. 47. P. 148.
Yushmanov P., Gupta S., Barnes D., Dettrick S., Putvincki S. // Abstracts 11th Int. Conf. on Open Magnetic Systems for Plasma Confinement, Novosibirsk, 2016. P. 30.
Yushmanov P., Barnes D., Dettrick S., Gupta S., Ryutov D., Krasheninnikov S., Necas A., Putvinski S. // Abstracts APS Meeting, New Orlean, 2014. UP8.019.
Rosenbluth M.N., McDonald W., Judd D. // Phys. Rev. 1957. V. 107. P. 1.
Трубников Б.А. // ЖЭТФ. 1958. Т. 34. С. 1341.
Юшманов Е.Е. // ЖЭТФ. 1966. Т. 49. С. 588.
Skovorodin D.I., Beklemishev A.D. // AIP Conf. Proc. 2016. V. 1771. 030029.
Marx K.D. // Phys. Fluids. 1970. V. 13. P. 1355.
Дополнительные материалы отсутствуют.
Инструменты
Физика плазмы