Физика плазмы, 2020, T. 46, № 10, стр. 904-915

1. ВВЕДЕНИЕ

Электронный циклотронный резонансный (ЭЦР) нагрев плазмы микроволновым электромагнитным излучением является наиболее простым и естественным способом направленного энерговклада в электронную компоненту плазмы, удерживаемой в магнитной ловушке. Продемонстрированное на установке ГДЛ [1] повышение температуры электронов до 1 кэВ при ЭЦР‑нагреве излучением двух 54.5 ГГц/400 кВт гиротронов позволило за счет уменьшения частоты электрон-ионных соударений существенно увеличить время жизни энергичных ионов в ловушке [2, 3] и по-новому взглянуть на перспективы использования крупномасштабных прямых ловушек как объемных источников термоядерных нейтронов.

Однако использование прямых методов ЭЦР-нагрева, когда в плазме поглощаются волны, вводимые из вакуума, для перспективных аксиально-симметричных ловушек следующего поколения наталкивается на ряд ограничений. Дело в том, что одним из преимуществ аксиально-симметричной магнитной ловушки по сравнению с другими типами ловушек является более низкое магнитное поле в основном объеме ловушки. При этом всюду, кроме пробочного узла, выполняется неравенство

где ${{\omega }_{p}}$ и ${{\omega }_{B}}$ – электронные плазменная и циклотронная частоты, соответственно. Более того, в центральной части ловушки это неравенство становится сильным. Следовательно, для электромагнитных волн с частотой выше плазменной, которые могут проникать из вакуума в плазму, эффективное поглощение возможно только вблизи пробок, что технически очень неудобно.

Одним из путей, позволяющих обойти это ограничение, является нагрев электронов плазмы квази-электростатическими волнами [4], которые испытывают эффективное поглощение даже на высоких гармониках циклотронного резонанса и могут быть возбуждены в плазме за счет линейной трансформации электромагнитных волн в окрестности верхнего гибридного резонанса [5]

Для тороидальных магнитных ловушек такой процесс был предсказан теоретически [6, 7] и продемонстрирован экспериментально на целом ряде установок [8–10]. Эффективность нагрева при этом практически полностью определяется эффективностью трансформации обыкновенной волны в медленную необыкновенную в окрестности плазменного резонанса $\omega = {{\omega }_{p}}$. Исследованию такой трансформации посвящена настоящая работа. Эффективность трансформации в окрестности плазменного резонанса подробно изучалась в плоскослоистом приближении для различных вариантов одномерного распределения параметров плазмы [6, 7, 11–19], а также в неодномерном случае с учетом особенностей геометрии области трансформации, характерных для тороидальных магнитных ловушек [20–31]. При этом было показано, что геометрия области трансформации существенно влияет на эффективность трансформации.

Область трансформации в окрестности плазменного резонанса даже в крупномасштабной прямой ловушке не является одномерной, это связано с двумя обстоятельствами. Во-первых, масштабы изменения магнитного поля сравнимы с масштабами изменения концентрации плазмы, при этом их градиенты почти перпендикулярны (магнитное поле в основном меняется вдоль оси ловушки, а концентрация – поперек; во-вторых, поверхности постоянной концентрации имеют существенную кривизну, что может сильно влиять на эффективность трансформации. С другой стороны, геометрия области трансформации в аксиально-симметричной открытой магнитной ловушке существенно отличается от случая тороидальной магнитной ловушки. Наиболее существенное отличие связано с тем, что из-за распределения амбиполярного потенциала вдоль открытой магнитной ловушки концентрация плазмы меняется вдоль магнитного поля. Отметим, что наличие амбиполярного потенциала непосредственно связано с равенством потоков электронов и ионов через открытый конец магнитной ловушки [32]. Постоянство концентрации плазмы на магнитных поверхностях было существенным упрощающим фактором при определении эффективности трансформации в тороидальных магнитных ловушках [20–31].

В данной статье мы рассмотрим задачу о распределении электромагнитного поля в окрестности области трансформации в геометрии, отвечающей крупномасштабной аксиально симметричной прямой магнитной ловушке.

2. ВОЛНОВЫЕ УРАВНЕНИЯ В ОКРЕСТНОСТИ ОБЛАСТИ ПОЛЯРИЗАЦИОННОГО ВЫРОЖДЕНИЯ

Известно [33], что для волн, распространяющихся вдоль магнитного поля в однородной магнитоактивной плазме, при условии ${{\omega }_{p}} = \omega $ имеет место поляризационное вырождение. И как следствие, в неоднородной среде в окрестности этой точки возможна линейная трансформация нормальных волн. Рассмотрим уравнения, описывающие распределение электрического поля монохроматической волны в окрестности такой точки (точки трансформации) в плавнонеоднородной среде, параметры которой мало меняются на длине волны. Для этого рассмотрим волновое уравнение для электрического поля монохроматической волны ${\mathbf{E}} \propto \exp ( - i\omega \;t)$

где $\hat {\varepsilon }$ – тензор диэлектрической проницаемости холодной магнитоактивной плазмы, ${{k}_{0}} = {\omega \mathord{\left/ {\vphantom {\omega c}} \right. \kern-0em} c}$ – волновое число в вакууме. Выделим быстро осциллирующую часть, отвечающую структуре плоской волны, распространяющейся вдоль стационарного магнитного поля, и медленную огибающую:

Разделение на быстро осциллирующую часть и плавную огибающую выражается в виде неравенств

оно возможно, только если значение ${{\bar {N}}_{{||}}}$ удовлетворяет дисперсионному уравнению для продольного распространения волн в однородной среде при условии ${{\omega }_{p}} = \omega $где ${{Y}_{0}} = {{B}_{0}}{\text{/}}{{B}_{{res}}}$ – отношение модуля магнитного поля в точке трансформации к резонансному для данной частоты значению магнитного поля. Верхний знак отвечает распространению левополяризованных волн, нижний – правополяризованных. Отметим здесь, что мы не вполне строго определили точку трансформации, однако мы можем принять, что некоторая точка на поверхности ${{\omega }_{p}} = \omega $ была нами выбрана, например, исходя из распределения поля в падающем на область трансформации волновом пучке, и далее полагать, что такая точка нами определена, и производить разложение параметров среды в окрестности этой точки (см. подробнее [31]). При таком разложении будем считать, что параметры плазмы и магнитного поля мало меняются в исследуемой окрестности:

Здесь верхний знак также отвечает трансформации левополяризованных волн, а нижний – правополяризованных, ${{\varepsilon }_{ \pm }}$, ${{\varepsilon }_{{||}}}$ – элементы тензора диэлектрической проницаемости в стиксовом представлении

$X = {{n}_{e}}{\text{/}}{{n}_{{cr}}}$, $Y = B{\text{/}}{{B}_{{res}}}$, ${{n}_{{cr}}}$ – критическая концентрация плазмы, для которой плазменная частота оказывается равна частоте излучения ${{\omega }_{p}} = \omega $.

Учитывая неравенства (5), (7), получаем для стиксовых компонент поля (${{F}_{ \pm }} = ({{F}_{x}} \pm i{{F}_{y}}){\text{/}}\sqrt 2 $, ${{F}_{{||}}} = {{F}_{z}}$) систему уравнений

где введены дифференциальные операторы а система координат декартова, и ее ось z совпадает с направлением магнитного поля в точке трансформации. Отклонение магнитного поля от оси z в соседних точках определяется малыми параметрами: ${{\theta }_{x}} = {{B}_{x}}{\text{/}}{{B}_{0}}$, ${{\theta }_{y}} = {{B}_{y}}{\text{/}}{{B}_{0}}$. Условия (7) также позволяют сократить число неизвестных в уравнениях. Для трансформации левополяризованных волн, то есть при выполнении условия $\left| {{{\varepsilon }_{ + }} - \bar {N}_{{||}}^{2}} \right| \ll 1$, из второго уравнения (9) следует, что ${{F}_{ - }} \ll {{F}_{ + }}$, ${{F}_{{||}}}$, поэтому мы можем пренебречь ${{F}_{ - }}$ в третьем уравнении (9). Аналогично для правополяризованных волн из $\left| {{{\varepsilon }_{ - }} - \bar {N}_{{||}}^{2}} \right| \ll 1$ следует, что в третьем уравнении (9) можно пренебречь ${{F}_{ + }}$. В итоге, оставляя для случая левополяризованных волн только первое и третье уравнения, а для правополяризованных только второе и третье, перепишем систему (9) в следующем универсальном виде: где верхний знак соответствует трансформации левополяризованных волн ${{\varepsilon }_{ + }} = \bar {N}_{{||}}^{2}$, а нижний – правополяризованных ${{\varepsilon }_{ - }} = \bar {N}_{{||}}^{2}$.

Уравнения (11) описывают взаимодействие двух волн в окрестности точки трансформации. В ВКБ-приближении эта область является областью непрозрачности, разделяющей две области распространения волн. Соответственно уравнения (11) должны быть дополнены следующими граничными условиями: в одной области распространения волны задается распределение падающей на область трансформации волны, а в другой падающая на область трансформации волна отсутствует. Формально математически эти условия мы сформулируем в разд. 4.

Отметим, что трансформация правополяризованных волн возможна только при ${{Y}_{0}} > 1$ и не имеет прямого отношения к поставленной во Введении задаче возбуждения квазиэлектростатических бернштейновских волн для их последующего поглощения на гармониках циклотронной частоты. Однако генерируемые в условиях такой трансформации вистлеры сами могут эффективно поглощаться электронами плазмы, и для полноты описания мы рассмотрим и трансформацию правополяризованных волн.

3. МОДЕЛЬ СРЕДЫ В ОБЛАСТИ ТРАНСФОРМАЦИИ

Зададим распределения концентрации плазмы ${{n}_{e}}$ и компонент статического магнитного поля ${\mathbf{B}}$ в виде разложений в ряд Тейлора, воспользовавшись условиями (7).

Выражение для концентрации плазмы можно записать в виде

Здесь мы доопределили систему координат, введенную для системы (9), направив ось $x$ в сторону повышения концентрации, так чтобы вектор градиента концентрации лежал в плоскости $xz$, и добавили вспомогательную систему координат (${{x}_{\eta }} = x\cos \eta + z\sin \eta $, ${{z}_{\eta }} = z\cos \eta - x\sin \eta $), привязанную к направлению градиента концентрации (см. рис. 1). Введен угол $\eta $ – угол между нормалью к магнитному полю и градиентом концентрации. В самом разложении мы учли первые неисчезающие слагаемые вдоль и поперек градиента концентрации, кроме того учли аксиальную симметрию, которая эквивалентна симметрии относительно плоскости xz для коэффициентов нашего локального разложения.

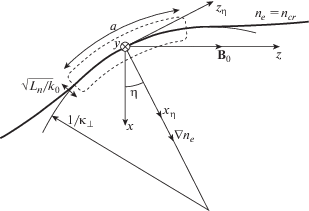
Коэффициенты разложения имеют следующий физический смысл. Величина ${{g}_{{||}}}$ – это нормированный градиент концентрации в точке разложения,

где ${{L}_{n}}$ – характерный масштаб изменения концентрации. Параметры η, ${{\kappa }_{y}},$ ${{\kappa }_{ \bot }}$ задают форму поверхности критической концентрации ${{\varepsilon }_{{||}}} = 0$, ${{\kappa }_{y}}$, ${{\kappa }_{ \bot }}$ – нормальные кривизны этой поверхности в ортогональных градиенту концентрации направлениях. При $\eta = 0$ градиент концентрации ортогонален магнитному полю, что соответствует случаю, рассмотренному в наших предыдущих работах [21, 22, 24, 26, 28–31], а при $\eta = \pi {\text{/}}2$ градиент концентрации параллелен магнитному полю.

Разложение для концентрации справедливо при выполнении условия плавной неоднородности $1{\text{/}}\sqrt {{{k}_{0}}{{L}_{n}}} \ll 1$ и условий ${{\kappa }_{y}}a$, ${{\kappa }_{ \bot }}a \ll 1$, где a – характерная ширина падающего пучка, определенная поперек градиента концентрации (см. рис. 1), то есть в тех случаях, когда ширина пучка мала по сравнению с кривизной поверхности постоянной концентрации. При этом отметим, что κ_y ~ $\sim \cos \eta {\text{/}}r$, где r – радиус плазменного шнура в рассматриваемой части ловушки, а ${{\kappa }_{ \bot }}$ может определяться как кривизной магнитной силовой линии в случае $\eta \ll {\text{1}}$, так и быть много больше этой величины в тех случаях, когда градиент концентрации составляет острый угол с магнитным полем.

Выражения для компонент магнитного поля принимают вид

Здесь $\nabla {{\theta }_{x}}$, $\nabla {{\theta }_{y}}$, $\nabla b$ – постоянные вектора, определяемые соответствующими градиентами, вычисленными в начале координат, величина b отвечает нормированному модулю магнитного поля $b = B{\text{/}}{{B}_{0}} \approx {{B}_{z}}{\text{/}}{{B}_{0}}$.

Для того чтобы уменьшить число свободных параметров, дополнительно учтем аксиальную симметрию магнитной конфигурации и уравнения Максвелла для стационарного магнитного поля. Аксиальная симметрия для коэффициентов нашего локального разложения эквивалентна симметрии относительно плоскости xz, откуда

где ${{\partial }_{x}},\;{{\partial }_{y}},\;{{\partial }_{z}}$ обозначают взятие производных по соответствующим координатам. Уравнения Максвелла дают соотношения

Здесь мы, считая плазму в ловушке стационарной, пренебрегли радиальным током и током, текущим вдоль оси ловушки, однако учли диамагнитный ток ${{J}_{d}}$, поскольку его влияние может быть существенно в установках, где давление плазмы сравнимо с давлением магнитного поля, $\beta \sim 1$. Для количественной оценки можно использовать соотношение $4\pi {{J}_{d}}{\text{/}}c{{B}_{0}}\sim 2\beta {\text{/}}{{L}_{n}}$, которое следует из условия равновесия плазмы $\nabla p = {{{\mathbf{J}} \times {\mathbf{B}}} \mathord{\left/ {\vphantom {{{\mathbf{J}} \times {\mathbf{B}}} c}} \right. \kern-0em} c}$. Учет соотношений (16), (17) позволяет переписать выражения (15) в виде

Учет условия $\nabla \cdot {\mathbf{B}} = 0$ сокращает в разложении (18) число независимых параметров, однако мы оставим в дальнейших выкладках все три величины ${{\partial }_{x}}{{\theta }_{x}},\,\,{{\partial }_{y}}{{\theta }_{y}},\,\,{{\partial }_{z}}b$, поскольку, как будет видно, они входят в них независимо. Для оценки параметров разложения (18) также можно использовать соотношение ${{\partial }_{x}}{{\theta }_{x}} \approx {{\partial }_{y}}{{\theta }_{y}} \approx {{ - {{\partial }_{z}}b} \mathord{\left/ {\vphantom {{ - {{\partial }_{z}}b} 2}} \right. \kern-0em} 2}$, справедливое для аксиально-симметричных ловушек, параметры магнитного поля которых слабо меняются на поперечном сечении плазменного шнура. Таким образом, для грубых оценок можно считать, что все коэффициенты в разложении (18) имеют сравнимый порядок величины, который мы определим как ${{L}_{B}} = 1{\text{/}}\sqrt {{{\partial }_{x}}{{b}^{2}} + {{\partial }_{z}}{{b}^{2}}} $, а условие справедливости разложения (18) имеет вид ${a \mathord{\left/ {\vphantom {a {{{L}_{B}}}}} \right. \kern-0em} {{{L}_{B}}}} \ll 1$.

Условия ${{\kappa }_{y}}a,$ ${{\kappa }_{ \bot }}a,$ ${a \mathord{\left/ {\vphantom {a {{{L}_{B}}}}} \right. \kern-0em} {{{L}_{B}}}} \ll 1$ накладывают ограничения на максимальный размер рассматриваемого волнового пучка. Это ограничение выглядит естественно для крупномасштабных ловушек, однако может нарушаться, если вводимое в ловушку поле представляет собой не квазиоптический волновой пучок, а комбинацию низших цилиндрических гармоник. В работе [30] использование специальной криволинейной системы координат позволило рассмотреть явление O–X-трансформации без подобных ограничений для частного случая классического токамака с большим аспектным отношением. Полученные при этом результаты мало отличались от результатов рассмотрения в рамках “локальной модели” [31]. Аналогичный рассмотренному в [30] подход может быть развит и для случая прямой ловушки, однако мы не считаем обсуждаемые ограничения слишком существенными, чтобы отказываться от простоты, связанной с рассмотрением локализованной области плазмы.

В итоге выделяем четыре малых параметра в наших уравнениях:

в дальнейшем будем удерживать первый порядок по каждому из них и отбрасывать второй порядок, а также любые их сочетания. При этом мы не накладываем никаких ограничений на взаимные соотношения малых параметров, поскольку слагаемые разного типа по-разному влияют на эффективность трансформации. Такой подход делает возможной ситуацию, когда одно или несколько учтенных слагаемых окажется за пределами точности нашего рассмотрения, однако это не будет проблемой, поскольку не внесет существенной ошибки при вычислении эффективности трансформации.

4. РЕШЕНИЕ СИСТЕМЫ УКОРОЧЕННЫХ ВОЛНОВЫХ УРАВНЕНИЙ

Используя соотношения (18), определим явную зависимость от координат для коэффициентов ${{\theta }_{x}}$ и ${{\theta }_{y}}$ в системе (11), а затем компенсируем соответствующие слагаемые при помощи замены

При этом система (11) перепишется в виде

Градиент суммы введенной таким образом фазы ${{\Phi }_{1}}$ и фазы быстро осциллирующей части (4) оказывается параллелен вектору магнитного поля: $\nabla \left( {{{k}_{0}}{{{\bar {N}}}_{{||}}}z + {{\Phi }_{1}}} \right)\,{\text{||}}\,{\mathbf{B}}$. Физический смысл замены (20) состоит в том, что мы уточняем распределение фазы у оптимальной моды и учитываем неоднородность продольного волнового числа вследствие неоднородности направления магнитного поля.

В правой части уравнений (21) учтем зависимость от координат диагональных элементов тензора диэлектрической проницаемости ${{\varepsilon }_{ \pm }}$ и ${{\varepsilon }_{{||}}}$ для выбранной нами модели среды (12), (18) и сформируем одинаковую зависимость от координат в правых частях уравнений системы. Для этого сделаем еще одну замену,

которая скорректирует коэффициенты перед линейными слагаемыми по x и z, и отбросим малые члены порядка ${{\kappa }_{y}}{{a}^{2}}{\text{/}}{{L}_{B}}$, ${{\kappa }_{ \bot }}{{a}^{2}}{\text{/}}{{L}_{B}}$, чтобы скорректировать коэффициенты перед квадратичными слагаемыми в первом уравнении. В результате имеем: где

Мы учли, что трансформация правополяризованных волн возможна только при ${{Y}_{0}} > 1$ (иначе $\bar {N}_{{||}}^{2} < 0$), и определили величины ${{g}_{ \pm }}$ так, чтобы они всегда оказывались положительными.

Отметим, что предельный переход $\eta \to {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ в выражении (22) является нетривиальным, поскольку при этом возникает особенность ${{\partial }_{x}}b\tan \eta \to \infty $. В дальнейших выкладках будем считать, что $\eta < {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$, а возможность и физический смысл такого предельного перехода отдельно рассмотрим после того, как получим выражение для коэффициента трансформации.

Далее введем новую криволинейную систему координат $x{\kern 1pt} ',\;y{\kern 1pt} ',\;z{\kern 1pt} '$, где

То есть мы принимаем метку поверхности постоянной концентрации $\left( {{{x}_{\eta }} - {{\kappa }_{y}}{{y}^{2}}{\text{/}}2 - {{\kappa }_{ \bot }}{{z}_{\eta }}^{2}{\text{/}}2} \right)$ за новую координату $x{\kern 1pt} '$, а остальные координаты сохраняем неизменными. Привязка координатных осей к градиенту концентрации и вектору магнитного поля упрощает в дальнейшем вид уравнений. Ортогональность системы координат нарушается, однако, как мы увидим далее, это не составляет проблемы. Отбросив малые слагаемые порядка ${{\kappa }_{y}}a{\text{/}}\sqrt {{{k}_{0}}{{L}_{n}}} $, ${{\kappa }_{ \bot }}a{\text{/}}\sqrt {{{k}_{0}}{{L}_{n}}} $, получим:

где операторы $\hat {D}_{ \pm }^{'}$ и $\hat {D}_{{||}}^{'}$ определены как

За счет условий ${{\kappa }_{y}}a{\text{/}}\sqrt {{{k}_{0}}{{L}_{n}}} $, ${{\kappa }_{ \bot }}a{\text{/}}\sqrt {{{k}_{0}}{{L}_{n}}} \ll 1$ члены, связанные с кривизной новой системы координат, не появляются в операторах пространственного дифференцирования. Однако кривизна поверхности постоянной концентрации оказывает влияние на эффективность трансформации: дело в том, что распределение поля в падающем волновом пучке задается на поверхности $x{\kern 1pt} ' = {\text{const}}$, и, следовательно, отличие поверхности постоянной фазы от этой поверхности будет приводить к дополнительной фазовой модуляции волнового поля в уравнениях (26). Схожий эффект имеет место и для тороидальных систем (см. [30, 31]).

После перехода в криволинейную систему координат мы исключили из уравнений зависимость коэффициентов от координат $z{\kern 1pt} '$ и $y{\kern 1pt} '$. Таким образом, задача трансформации волн в трехмерно неоднородной плазме аксиально симметричной прямой магнитной ловушки свелась математически к тем же уравнениям, что и в плоскослоистой среде с произвольным углом между магнитным полем и градиентом концентрации [13]. Воспользовавшись этим, переходим к фурье-представлению по $y{\kern 1pt} '$ и $z{\kern 1pt} '$

Как видно, преобразование производится для распределения поля на криволинейной поверхности $x{\kern 1pt} ' = {\text{const}}$, причем для преобразования по $z{\kern 1pt} '$ вводится нормировочный множитель $\cos \eta $ для компенсации наклона этой поверхности относительно оси z. Введенные таким образом коэффициенты ${{N}_{y}}$ и ${{N}_{ \bot }}$ характеризуют двумерный спектр пучка поперек градиента концентрации.

Затем вводим безразмерную координату $\xi $ и нормированные компоненты волнового поля

где имеет смысл характерного масштаба области трансформации. В результате система укороченных уравнений (26) перепишется в виде где

Тот факт, что укороченные уравнения удалось свести к одномерным, показывает, что случай O‒X-трансформации в аксиально-симметричной прямой ловушке качественно отличается от случая тороидальной магнитной системы, в котором аналогичные уравнения, полученные в работе [31], были существенно двумерными. Это связано с тем, что в тороидальных ловушках градиенты модуля магнитного поля, концентрации плазмы и внешнего магнитного поля в точке трансформации в общем случае образовывают базис в трехмерном пространстве, а в рассматриваем нами случае все эти три вектора всегда лежат в одной плоскости. В результате в прямой ловушке неодномерный характер области трансформации определяет оптимальную фазовую модуляцию волнового пучка, а в тороидальных ловушках неоднородность влияет также на оптимальное распределение амплитуды падающего пучка.

Компоненты электрического поля, выраженные через решение ${{A}_{ \pm }}$ и ${{A}_{{||}}}$ системы укороченных уравнений (31), суть

Здесь переменная $x{\kern 1pt} '$ есть функция от $x,\;y,\;z$, определяемая соотношением (25), а фаза

Для того чтобы определить граничные условия для системы (31), найдем поляризации волн, распространяющихся в положительном и отрицательном направлении на большом удалении от области трансформации, при $\left| \xi \right| \to \infty $. В этой области можно пренебречь константами ${{n}_{y}},\;{{n}_{ \bot }}$, и система (31) примет вид

Для этой системы уравнений можно написать общее решение, представляющее собой сумму двух ВКБ-волн,

где $\gamma = \delta - \sqrt {{{\delta }^{2}} \pm 1} $. Отметим, что при $\left| \delta \right| < 1$ величина γ становится комплексной, и ВКБ-моды ${{A}^{ + }}$ и ${{A}^{ - }}$ оказываются нераспространяющимися. Это означает, что в этом случае трансформация невозможна, а решения системы (31) представляют собой набор собственных мод специфического волноводного канала вблизи критической поверхности (см. [34]).

Для того чтобы ввести граничные условия, необходимо определить направления распространения для обеих мод. Для этого свяжем полученные из наших укороченных уравнений ВКБ-моды с нормальными волнами магнитоактивной плазмы, направления распространения которых известны. Рассмотрим решение дисперсионного уравнения для величины ${{N}_{\xi }}$, представляющей компоненту волнового вектора плоской волны, определенную следующим образом:

Дисперсионное уравнение решается в однородной среде, ось z направлена вдоль магнитного поля, как и ранее. Вблизи области трансформации введенная таким образом переменная ${{N}_{\xi }}$ должна совпадать с производной от фазы ВКБ-моды укороченной системы уравнений по соответствующей координате. Зависимость фазы от координаты $\xi $, характеризующей отстройку от критической поверхности, имеет вид

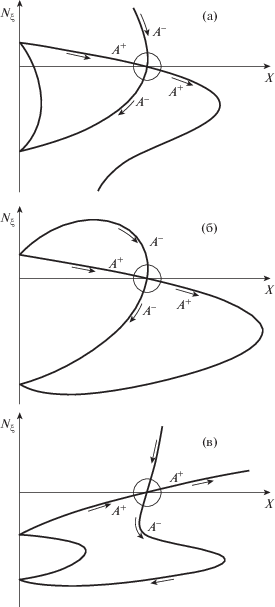
На рис. 2 показана зависимость ${{N}_{\xi }}$ от нормированной концентрации плазмы $X = {{{{n}_{e}}} \mathord{\left/ {\vphantom {{{{n}_{e}}} {{{n}_{{cr}}}}}} \right. \kern-0em} {{{n}_{{cr}}}}}$ для трех характерных случаев: трансформация левополяризованных волн при ${{Y}_{0}} < 1$ (рисунок а), трансформация левополяризованных волн при ${{Y}_{0}} > 1$ (б) и трансформация правополяризованных волн при ${{Y}_{0}} > 1$ (в). Графики приведены для случая $\eta \cdot {{\bar {N}}_{{||}}} > {{0}_{{||}}}$, в обратном случае они зеркально отражаются относительно горизонтальной оси, а направления распространения волн меняются на противоположные. Поскольку в области трансформации концентрация плазмы линейно зависит от координаты ξ, вблизи этой области тангенс угла наклона каждой из веток на рис. 2 будет пропорционален второй производной от фазы соответствующей ей моды ${{\partial }^{2}}{{\varphi }^{{ + , - }}}{\text{/}}\partial {{\xi }^{2}}$: $\gamma = \delta - \sqrt {{{\delta }^{2}} \pm 1} $ для ${{A}^{ + }}$ или $ \mp {1 \mathord{\left/ {\vphantom {1 \gamma }} \right. \kern-0em} \gamma } = \delta + \sqrt {{{\delta }^{2}} \pm 1} $ для ${{A}^{ - }}$. Такой простой анализ показывает, что мода ${{A}^{ + }}$ распространяется в положительном направлении координаты ξ из вакуума в плотную плазму, а мода ${{A}^{ - }}$ – наоборот, в отрицательном направлении координаты ξ, то есть из плотной плазмы в вакуум. Причем это справедливо как для левополяризованных, так и для правополяризованных волн при любых значениях нормированного магнитного поля ${{Y}_{0}} < 1$ и ${{Y}_{0}} > 1$, а также как для $\delta > 0$, так и для $\delta < 0$.

С учетом этого введем формально новые полевые переменные ${{A}^{ + }}(\xi )$ и ${{A}^{ - }}(\xi )$ с такими же поляризациями, как у мод ${{A}^{ + }}$ и ${{A}^{ - }}$:

и поставим граничные условия что соответствует волне, распространяющейся из вакуума, и отсутствию излучения, идущего из плотной плазмы. Начальная амплитуда и фаза падающей волны несущественны в силу линейности системы.

С учетом замены (39), а также соотношений $2\gamma \delta = \left( {{{\gamma }^{2}} \mp 1} \right)$ и $\left( {{{\gamma }^{2}} \pm 1} \right) = - 2\gamma \sqrt {{{\delta }^{2}} \pm 1} $ систему (31) можно переписать в виде

Левые части уравнений (41) описывают распространение прямой и отраженной волн, а правые задают их связь. Далее при помощи фазовой замены и сдвижки координат

можно упростить левую часть системы (41):

Решение системы (43) с граничными условиями (40) есть

Здесь ${{D}_{{i\nu }}}$ – функция параболического цилиндра c мнимым индексом, определяемым выражением

5. ВЫЧИСЛЕНИЕ ЭФФЕКТИВНОСТИ ТРАНСФОРМАЦИИ

Коэффициент трансформации определяется как отношение потоков энергии в падающей и прошедшей волне

Здесь ${{A}^{ + }}\left( { - {{\xi }_{0}},{{N}_{y}},{{N}_{ \bot }}} \right)$ представляет собой амплитуду волны вдали от области трансформации ${{\xi }_{0}} \gg 1$, а ${{A}^{ + }}\left( {{{\xi }_{0}},{{N}_{y}},{{N}_{ \bot }}} \right)$ – амплитуду прошедшей волны. Аналитическое выражение для коэффициента трансформации можно получить из решения (44) с учетом асимптотических свойств функции параболического цилиндра [22, 35]. Оно имеет вид

где

Для волнового пучка эффективность трансформации, также как и в плоскослоистом приближении [15], определяется ширинами двумерного фурье-спектра: область трансформации работает как фильтр, отражая фурье-гармоники, существенно отстоящие от оптимальной. Разница состоит в том, что в плоскослоистом приближении спектр распределения электрического поля E относится к плоскости ${{x}_{\eta }} = {\text{const}}$ [15], а полученный нами ответ зависит от спектра формального поля ${\mathbf{A}} = ({{A}_{ \pm }},{{A}_{{||}}})$, относящегося к криволинейной поверхности $x{\kern 1pt} ' = {\text{const}}$, и эти спектры естественно отличаются: как за счет отличия поверхностей ${{x}_{\eta }} = {\text{const}}$ и $x{\kern 1pt} ' = {\text{const}}$, так и за счет введенного в формулах (20), (22) фазового сдвига $\exp \left( {i{{k}_{0}}\Phi } \right)$, связывающего поля E и A.

Для того чтобы проиллюстрировать эту разницу, рассмотрим коэффициент трансформации волнового пучка, для которого задано распределение поля E на плоскости ${{x}_{\eta }} = - {{x}_{0}} = - {{\xi }_{0}}{{L}_{\nabla }}\sqrt {\cos \eta } $,

Для простоты будем считать, что коэффициент ${{N}_{{opt}}}$ соответствует оптимальному направлению распространения, т.е. отражение от поверхности отсечки связано только с конечными размерами пучка и неоптимальной фокусировкой. Тогда коэффициент трансформации, полученный интегрированием (47) по соответствующей спектральной плотности пучка, будет

Полученное выражение имеет ту же структуру, что и в плоскослоистом приближении. Коэффициент трансформации также определяется ширинами спектра пучка ${{k}_{y}}$ и ${{k}_{ \bot }}$. Однако эти спектральные ширины отвечают измененной фокусировке пучка (49): ${{K}_{y}} \to {{K}_{y}} + \delta {{K}_{y}}$, ${{K}_{ \bot }} \to {{K}_{ \bot }} + \delta {{K}_{ \bot }}$. Иными словами, переход к полю A в криволинейной системе координат сводится к изменению фокусировки пучка, а дальше уже работает обычное плоскослоистое приближение.

Рассмотрим, как получаются поправки к фокусировке $\delta {{K}_{y}},\,\,\delta {{K}_{ \bot }}$. Их можно представить как сумму частей, зависящих от неоднородности направления магнитного поля $\delta K_{y}^{{\mathbf{B}}},\,\,\delta K_{ \bot }^{{\mathbf{B}}}$ и от кривизны поверхности постоянной концентрации $\delta K_{y}^{{{{n}_{e}}}},\,\,\delta K_{ \bot }^{{{{n}_{e}}}}$:

Первая часть, связанная с неоднородностью направления магнитного поля, находится непосредственно из замен (20), (22), сделанных при переходе от электрического поля к полю ${\mathbf{A}}$:

Вторая часть зависит от разницы в распределении фазы между плоскостью ${{x}_{\eta }} = - {{x}_{0}}$ и криволинейной поверхностью $x{\kern 1pt} ' = - {{x}_{0}}$. Считая, что поверхности мало отличаются друг от друга, установим связь между этими распределениями. Такая связь может быть найдена из асимптотических свойств функций параболического цилиндра, но технически проще и физически понятнее найти ее, воспользовавшись приближением “прожекторной оптики”

где ${{k}_{0}}{{N}_{{{{x}_{\eta }}}}}$ – это проекция несущего волнового вектора пучка на ось ${{x}_{\eta }}$, рассчитанная в плоскости ${{x}_{\eta }} = - {{x}_{0}}$. Величина ${{N}_{{{{x}_{\eta }}}}}$ определяется из дисперсионного уравнения и может быть выражена через введенную ранее (37) величину ${{N}_{\xi }}$ для моды ${{A}^{ + }}$

Отсюда, используя соотношение $x{\kern 1pt} ' = {{x}_{\eta }} - $ ${{\kappa }_{y}}{{y}^{2}}{\text{/}}2 - {{\kappa }_{ \bot }}{{z}_{\eta }}^{2}{\text{/}}2$, можно получить выражения для коэффициентов $\delta K_{y}^{{{{n}_{e}}}},\,\,\delta K_{ \bot }^{{{{n}_{e}}}}$

Поскольку величина ${{N}_{{{{x}_{\eta }}}}}$ зависит от ${{x}_{0}}$, поправки $\delta K_{y}^{{{{n}_{e}}}},\,\,\delta K_{ \bot }^{{{{n}_{e}}}}$ также меняются для различных плоскостей ${{x}_{\eta }} = - {{x}_{0}}$, на которых мы можем задавать пучок. Очевидно, что это не влияет на итоговый ответ для коэффициента трансформации, поскольку такое изменение в точности отвечает изменению фокусировки самого пучка при распространении в неоднородной плазме, играющей роль своеобразной линзы. Эффекты неоднородности направления магнитного поля и кривизны поверхностей постоянной концентрации будут существенны, если соответствующие поправки к фокусировке достаточно велики.

Как уже отмечалось в работах [30, 31], поправки $\delta {{K}_{y}},\,\,\delta {{K}_{ \bot }}$ могут быть полностью компенсированы оптимальной фокусировкой: ${{K}_{y}} = - \delta {{K}_{y}},$ ${{K}_{ \bot }} = - \delta {{K}_{ \bot }}$, и в этом случае достигается наибольшая эффективность трансформации. В наилучшем случае трансформация может быть практически полной для широкого класса пучков, если пучок с оптимальной фокусировкой еще и достаточно широк по сравнению с ${{L}_{\nabla }}$, или выполнены неравенства

Отклонение от оптимальной фокусировки, напротив, существенно снижает эффективность трансформации. Максимально возможный коэффициент прохождения для заданных ${{K}_{y}},\,\,{{K}_{ \bot }}$ дается выражением

Причем, эффективность достигает этого значения только при оптимальных размерах пучка

и быстро падает при отходе от этого оптимума в обе стороны, то есть как для узких, так и для широких пучков.

Характерным масштабом в приведенных соотношениях выступает введенная ранее величина ${{L}_{\nabla }}$ с дополнительными безразмерными множителями $\sqrt {{{\mu }_{y}}} ,\,\,\sqrt {{{\mu }_{ \bot }}} $: чем больше соответствующие величины, тем уже спектральное окно эффективной трансформации, и, соответственно, строже ограничения на параметры пучка (57), нужные для прохождения через область непрозрачности.

В заключение раздела рассмотрим, как величины $\sqrt {{{\mu }_{y}}} {{L}_{\nabla }},\,\,\sqrt {{{\mu }_{ \bot }}} {{L}_{\nabla }}$, определяющие обратную ширину спектрального окна в направлениях $y$ и ${{z}_{\eta }}$ соответственно, зависят от выбора поляризации и угла $\eta $. Поскольку масштаб неоднородности магнитного поля ${{L}_{B}}$ обычно больше характерного масштаба изменения концентрации ${{L}_{n}}$, для качественного анализа можно считать магнитное поле однородным ${\mathbf{B}} = {\text{const}}$, что существенно упрощает выражения:

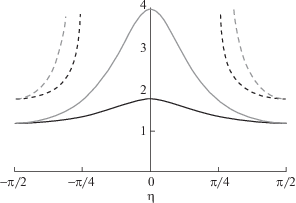
В этом приближении ${{L}_{\nabla }}$ не зависит от угла η и выбора поляризации. Таким образом, мы можем рассматривать только величины $\sqrt {{{\mu }_{y}}} ,\,\,\sqrt {{{\mu }_{ \bot }}} $. Их характерная зависимость от угла η для левополяризованных и правополяризованных волн изображена на рис. 3. Можно выделить некоторые особенности того, как выбор поляризации и неортогональность магнитного поля и градиента концентрации влияют на эффективность трансформации.

1. Трансформация для правополяризованных волн возможна только при достаточно больших значениях $\left| \eta \right|$, а также требует значительно более сильных ограничений на качество фокусировки и размер пучка для эффективной трансформации.

2. При этом, при сохранении всех прочих параметров, увеличение $\left| \eta \right|$ повышает коэффициент трансформации как для правополяризованных, так и для левополяризованных волн.

3. Ограничения на параметры пучка вдоль направления ${{z}_{\eta }}$ оказываются сильнее, чем вдоль $y$, при $\left| \eta \right| < {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$, но при $\left| \eta \right| \to {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ они становятся одинаковыми, поскольку при $\nabla {{n}_{e}}||{\mathbf{B}}$ направление ${{z}_{\eta }}$ престает быть выделенным относительно $y$.

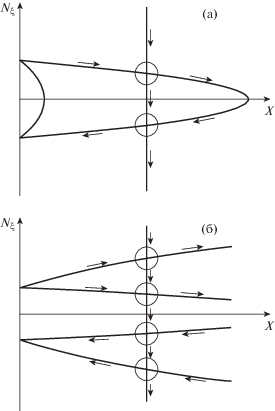
Можно видеть, что полученный ответ для коэффициента трансформации (50), (61) дает разумный результат в пределе $\left| \eta \right| \to {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$, несмотря на то, что часть предшествующих выкладок оказываются некорректными в случае строгого равенства $\eta = \pm {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$, так как в них при этом появляются особенности. Тем не менее, анализ дисперсионных соотношений при $\eta \approx {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ показывает, что полученный ответ не в полной мере корректен в этом случае. Как можно видеть из рис. 4, при $\eta \approx {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ появляются дополнительные точки трансформации: одна для случая ${{Y}_{0}} < 1$ и три для случая ${{Y}_{0}} > 1$, – влияния которых мы не учитываем в рамках нашей теории. Причем, как хорошо известно, в такой ситуации общий коэффициент трансформации определяется не только эффективностью каждой трансформации, но и набегом фазы [36]. Условие малости туннелирования с одной дисперсионной ветки на другую в этих дополнительных точках является условием применимости нашей “изолированной” теории. Оно имеет вид

Сам случай, когда градиент концентрации параллелен магнитному полю, требует отдельного рассмотрения. В плоскослоистом приближении такая задача будет сводится к задаче Баддена [36], на это указывает наличие нескольких взаимодействующих точек трансформации и общая структура дисперсионных кривых на рис. 4. Вне рамок плоскослоистого приближения сходную проблему рассматривали, например, в [37].

6. ЗАКЛЮЧЕНИЕ

Как было показано выше, задача линейной трансформации нормальных волн вблизи поверхности критической концентрации в геометрии, соответствующей крупномасштабной прямой аксиально-симметричной ловушке, существенно отличается от случая тороидальной магнитной ловушки. С одной стороны, геометрия области трансформации оказывается проще за счет того, что магнитное поле и градиенты концентрации и магнитного поля лежат в одной плоскости. Это позволило нам формально свести задачу к виду, аналогичному получаемому в плоскослоистой геометрии. С другой стороны, из-за того, что градиент концентрации может быть не ортогонален магнитному полю, возникает дополнительная область трансформации для правополяризованных волн.

Как следует из анализа, проведенного в разд. 5, основным эффектом, ограничивающим достижимую эффективность трансформации, является в данном случае кривизна магнитных поверхностей. При этом можно предложить два разных подхода к оптимизации эффективности трансформации (51). С одной стороны, в статье получены значения оптимальной фокусировки гауссового пучка ${{K}_{y}} = - \delta {{K}_{y}},$ ${{K}_{ \bot }} = - \delta {{K}_{ \bot }}$ (52), (53), (56), при которой эффективность трансформации достаточно широкого пучка близка к единице. Такой подход может быть применен только для крупномасштабных ловушек следующего поколения. К сожалению, характерные значения кривизны магнитных поверхностей для современных прямых ловушек приводят к очень жестким требованиям на фокусировку пучков левополяризованных волн, особенно если принять во внимание, что плазменный шнур для таких волн работает как дефокусирующая линза. С другой стороны, для неоптимальной фокусировки можно определить оптимальные размеры волнового пучка по двум поперечным координатам, при которых можно ожидать трансформации с эффективностью порядка 60%, если вводить излучение в центральном сечении установки.

Заметим, что в аксиально симметричных открытых ловушках достигается гораздо большее, чем в тороидальных, относительное давление плазмы. Это означает, что диамагнитные токи могут заметно менять конфигурацию магнитного поля системы, и их учет в формуле (17) будет принципиален для верного определения эффективности трансформации в области между точками разворота энергичных ионов.

Данная работа выполнена при поддержке гранта РФФИ № 18-42-520069 р а.