Физика плазмы, 2020, T. 46, № 11, стр. 977-984

1. ВВЕДЕНИЕ

Статья, в определенной степени, отражает состояние исследований по разработке одного из плазменных методов [1, 2] разделения многокомпонентных смесей, не имеющих газообразных соединений, пригодных для разделения кинетическим методом в центрифугах, на элементы или группы элементов – плазмооптического (ПОМС-Е) [3, 4]. Наиболее известными примерами смесей, требующих переработки, являются отработавшее ядерное топливо, литий-графитовые электроды и литийсодержащий электролит аккумуляторов, комплексы, содержащие редкоземельные элементы. Обращение к плазменным методам масс-сепарации (ПММС) связано с возможностью создания компенсированных по заряду ионных потоков и, следовательно, значительного увеличения наработки разделяемых элементов по сравнению с электромагнитным методом разделения (ЭММС) [5]. Конечно, строгого сравнения производительности ЭММС и ПММС проводить нельзя. По крайней мере, по двум причинам. Во-первых, задачи ЭММС – разделение изотопов; относительно же ПММС уже сложилось убеждение, что основное – это разделение на элементы, группы элементов или предварительное обогащение смеси по какому-либо элементу для последующей работы ЭММС. Во-вторых, производительность ЭММС – это уже более 75 лет контролируемый производственный показатель. Например, для промышленного ЭММС СУ-20 при обогащении изотопом кальций-48 от 0.187% до 87% накопление составляет 22 000 мА⋅час [6], что при энергии ионов кальция 30 кэВ, соответствует потоку отбора Φ_ЭММС ∼7 × × 10^–12 г/c. Единственная эмпирическая оценка производительности ПММС получена на прошедшем стадию опытных испытаний плазменном фильтре масс “Archimedes Demonstration Unit”, где во вращающейся плазме металлического натрия для легкой фракции радиоактивных отходов, инжектируемых в плазму, получена скорость отбора массы Φ_Arch ∼ 0.25 г/c [7]. Теоретическая оценка скорости отбора бинарной смеси 120 и 240 а.е.м. в новом варианте прямоточной плазменной центрифуги (ППЦ) из расширяющейся под действием вращающегося поперечного магнитного поля дипольной конфигурации плазменной струи дает Φ_ППЦ ∼ 2 × 10^–3 г/c [8]. Оценка производительности ПОМС-Е-сепаратора, приведенная в [3], сделана для плазменного ускорителя с суммарным ионным током 700 А (М = 100 а.е.м.) и составляет Φ_ПОМС ∼ 5 г/c.

Плазмооптический способ масс-сепарации включает этапы получения компенсированного по заряду аксиально-симметричного пучка ионов в плазменном ускорителе с замкнутым дрейфом электронов (УЗДП) и проведение его через область (элемент конструкции сепаратора), названную азимутатором, где создано поперечное к потоку ионов (радиальное) магнитное поле, в котором ионы приобретают азимутальную компоненту скорости. Далее в сепарирующем объеме, в котором создается стационарное радиальное электрическое поле и однородное постоянное продольное магнитное поле, замагничивающее электроны, но практически не влияющее на динамику ионов смеси, происходит разделение ионов в пространстве и собирание их на различные приемники. В настоящее время авторами данной статьи разрабатывается вариант ПОМС-Е-3 плазмооптического масс-сепаратора [4, 9–11], схема которого приведена на рис. 1. В качестве плазменного ускорителя здесь, в отличие от [3], используется УЗДП с анодным слоем (TAL – thruster with anodic layer) с проводящими удаленными стенками канала [12, 13]. Кроме того, азимутатор, являющийся частью магнитопровода, в ПОМС-Е-3 совмещен с катодом TAL, а приемники ионов выполнены протяженными, расположенными на определенных радиусах в сепарирующем пространстве и торце установки. Названная совокупность отличий обеспечила возможность использования в качестве источника компенсированного потока ионов УЗДП, в котором, нужно отметить, ионы имеют широкий спектр по энергии, что исключает возможность использования идеализированной схемы ПОМС-Е [3].

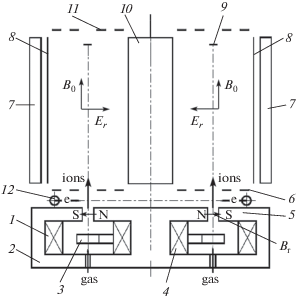
Рис. 1.

Схема макета плазмооптического масс-сепаратора ПОМС-Е-3: 1 – внешняя катушка магнитного поля TAL; 2 – магнитопровод; 3 – анод; 4 – внутренняя катушка; 5 – катод-азимутатор (1-5 – TAL); 6, 8, 10, 11 – система создания радиального электрического поля E_r в сепарирующем пространстве; 7 – катушка для создания продольного магнитного поля В₀ в сепарирующем пространстве; 8, 9, 10 – выполняют роль и приемников разделенных ионных компонент; 12 – источник электронов компенсации пространственного заряда ионов.

Для плазмооптической масс-сепарации эффективность метода, как и любого другого способа разделения, определяется степенью разделения и током ионов перерабатываемого пучка. При трехкомпонентном разделении в ПОМС-Е-3 степень разделения определяется, в основном, геометрией объема сепарации. Ионы центральной массы М₀, стартующие в точке R по радиусу, собираемые на торцевой приемник, не будут попадать на приемники ионов меньшей М₂ и большей М₁ масс, если они расположены на радиусах r₁ и r₂, таких, что ${{r}_{1}} = R - R\frac{{\delta M}}{{{{M}_{0}}}}$, ${{r}_{2}} = R + R\frac{{\delta M}}{{{{M}_{0}}}}$; δМ = (М₁– М₂)/2. Соответственно, $\frac{{\delta M}}{{{{M}_{0}}}} = \frac{{{{r}_{2}} - R}}{R} = $ $ = \frac{{R - {{r}_{1}}}}{R}$ [9].

Производительность источника плазмы ограничивается потерями в области с поперечным к потоку плазмы магнитным полем азимутатора, являющегося одним из основных элементов масс-сепаратора ПОМС-Е [3, 9–11]. Динамическое давление моноэнергетического плазменного потока 2n₀W₀, где n₀ и W₀ – плотность и энергия ионов, сравнивается с давлением магнитного поля азимутатора B²/8π при плотности ионов N_d = = B²/(16πW₀). Плотность ионов n₀ в экспериментах на макете плазмооптического масс-сепаратора ПОМС-Е-3 n₀ ≪ N_d, и отношение динамического давления к давлению магнитного поля β ≪ 1. Прохождение такого осесимметричного плазменного потока через магнитный барьер (МБ) за счет дрейфа при поляризации плазмы (возникновения электрического поля) в направлении, перпендикулярном магнитному полю и направлению движения [14–16], не реализуется, так как магнитное поле азимутатора радиальное, а поляризация по замкнутой угловой координате невозможна. Если плотность в плазменном потоке n₀ превышает величину N_q = B²/(8πmс²), то при поляризации вдоль скорости потока в отсутствие электронных столкновений плазма при движении в магнитном барьере сохраняет квазинейтральность и проникает в МБ на расстояние гибридного ларморовского радиуса ${{\rho }_{h}} = \sqrt {2{{W}_{0}}m{{c}^{2}}} {\text{/}}(eB)$ [17]; здесь m – масса электрона, c – скорость света. В случае, когда Q²= N_q/n₀ ≫ 1, что соответствует нашим экспериментам, электроны проникают в МБ на расстояние ρ_e = max(ρ_h /Q, ρ_e), а ионы – на расстояние ρ_i = ρ_hQ; здесь ρ_e = u_Te0/ω_Be, u_Te0– тепловая скорость электронов в плазменном потоке, ω_Be = = eB/(mс) – электронная циклотронная частота. Для экспериментов ρ_h ≈ 5 × 10^–2 см, N_q ≈ 5 × × 10¹¹ см^–3, Q ≈ 10², а ширина магнитного барьера Δ ≈ 1 см. Таким образом, в условиях эксперимента электроны не могут следовать вместе с ионами вглубь МБ; на ионы, можно считать, магнитное поле не влияет. Известно, что моноэнергетический поток ионов с энергией W₀ проходит через промежуток Δ, если n₀ ≤ N_B = (8/9)W₀/(πe²Δ²) [18]; в противном случае – он полностью отражается.

Теоретическое рассмотрение задачи о прохождении немоноэнергетических ионов с максимальной энергией W_m через МБ показало [19], что решение с частичным прохождением ионов есть во всем диапазоне изменения индукции В магнитного поля в азимутаторе, плотности n₀ и энергетического разброса в падающем пучке ионов. Плотность прошедших ионов в случае малого энергетического разброса при увеличении n₀ достигает максимума, равного N_B/2, и затем уменьшается, стремясь к некоторой конечной величине n_∞ = N_b/8 при дальнейшем увеличении плотности.

В работе [20] отмечалась критическая роль стенок канала в процессах переноса в газовых разрядах низкого давления с магнитным полем. В процессе численного моделирования методом частиц в ячейках обнаружены пристеночные слои электростатического потенциала, влияющие на динамику частиц. Найдено, что ток электронов, проходящих МБ, обратно пропорционален величине магнитного поля: I_e ∼ 1/B. Величина I_e монотонно уменьшалась с ростом длины барьера.

В частично ионизованной плазме, погруженной в магнитное поле, электроны поперек поля продвигаются в процессе классической диффузии при столкновениях с нейтралами, что заметно при высоких рабочих давлениях плазмообразующего газа, или из-за аномальной диффузии [21, 22]. В настоящей статье мы найдем распределение потенциала в плазме, движущейся в поле магнитного барьера, с учетом столкновений электронов с нейтралами. При этом учтем набор энергии электронами в электростатическом поле разделения зарядов и их уход на стенки при наличии потенциального барьера стенка–плазма, а также найдем максимальную плотность ионов в потоке, который преодолевает магнитный барьер.

2. ПОСТАНОВКА ЗАДАЧИ

Прохождение потоком плазмы МБ азимутатора ПОМС-Е-3 сопровождается возрастанием потенциала плазмы φ_pl. На рис. 2 даны зависимости однозначно связанного с потенциалом плазмы плавающего потенциала φ_fl ленгмюровского зонда в области МБ (в потоке плазмы из TAL, который применяется на ПОМС-Е-3).

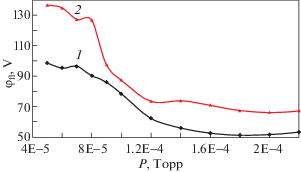
Рис. 2.

Плавающий потенциал: 1 – на входе в МБ азимутатора ПОМС-Е-3; 2 – в середине; разрядное напряжение TAL U_d = 680 В; индукция магнитного поля на аноде TAL B_an = 970 Гс; в МБ азимутатора поле B_az = 4270 Гс.

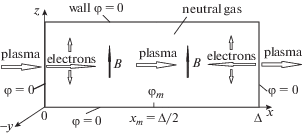
Для прояснения причин формирования потенциала и его влияния на прохождение потока плазмы рассмотрим стационарный процесс движения плазмы с β ≪ 1 в области с поперечным к потоку однородным магнитным полем, сосредоточенным на длине Δ вдоль оси x. Направим ось z вдоль магнитного поля (рис. 3). На рис. 2 (кри-вая 2) виден прирост потенциала внутри МБ по сравнению с областью E×B-разряда в плазменном ускорителе. Величина потенциала определяется степенью компенсации пространственного заряда ионного потока, которая возрастает с увеличением рабочего давления плазмообразующего газа.

Рис. 3.

Схема задачи.

Величина индукции магнитного поля B такая, что действием магнитного поля на ионы будем пренебрегать. Время t_Δ, за которое ионы проходят расстояние Δ, намного меньше, чем время между столкновениями ионов с нейтралами, с электронами и друг с другом, поэтому процессы столкновений ионов учитывать не будем. На входе в МБ в точке x = 0 моноэнергетичный поток ионов имеет скорость u₀, плотность n₀; энергия ионов ${{W}_{0}} = Mu_{0}^{2}{\text{/}}2$. Рассматривается случай замагниченных электронов, которые продвигаются в МБ за счет упругих столкновений с нейтралами. Этот процесс характеризуется средним временем τ_ea. Неупругие столкновения электронов – процессы возбуждения, ионизации и рекомбинации в МБ рассматривать не будем.

При движении потока в МБ из-за разделения зарядов формируется распределение потенциала φ(x) – потенциальный барьер высотой φ_m. Для выявления наиболее сильных эффектов будем рассматривать одномерную симметричную относительно центра МБ задачу при 0 ≤ x ≤ ∆/2, когда все величины зависят только от координаты x. На границах МБ поддерживается нулевой потенциал: φ(x = 0) = φ(x = ∆) = 0. С обеих границ к центру МБ вдоль оси x движутся одинаковые потоки электронов, обеспечиваемые, с одной стороны, плазменным ускорителем, с другой, плазменным источником электронов для компенсации пространственного заряда. В точках x = 0 и x = ∆ электроны имеют начальную температуру T₀, затем при движении в электрическом поле к центру МБ их наиболее вероятная энергия (температура) возрастает.

Перераспределение энергии между электронами происходит при электрон-электронных столкновениях. Будем считать, что время релаксации функции распределения электронов к максвелловской функции ${{\tau }_{{eem}}} \approx {{\tau }_{{ee}}} = \frac{{{{m}^{2}}u_{{Te}}^{3}}}{{\sqrt {12\pi } \Lambda {{n}_{e}}{{e}^{4}}}}$ [23], где τ_ee – среднее время между электрон-электронными столкновениями, n_e – плотность электронов, u_Te – тепловая скорость электронов, Λ – кулоновский логарифм.

В МБ при z = ±δ находятся проводящие стенки канала. Примем потенциал стенок равным нулю. Тогда разность потенциалов по оси z между областью потока и стенкой Δφ_z = φ(x) – φ(z = ±δ) = = φ(x). Будем учитывать уход на стенки некоторой части n_fast электронов: если электроны имеют энергию W > eφ(x) = eΔφ_z, то они за среднее время τ уходят вдоль z на стенки. Плотность n_fast электронов, энергия которых больше, чем eφ(x), определяется так: ${{n}_{{fast}}} = {{n}_{e}}{{e}^{{ - e\varphi (x)/kT(x)}}}$, где T(x) – температура электронов в точке траектории с координатой x. Тогда время ухода электронов на стенки можно определить из соотношения $\frac{{{{n}_{{fast}}}}}{{{{\tau }_{{eem}}}}} = $ $ = \frac{{{{n}_{e}}}}{{{{\tau }_{{eem}}}{{e}^{{e\varphi (x)/kT(x)}}}}}$ , и оно равно $\tau = {{\tau }_{{eem}}}{{e}^{{e\varphi (x)/kT(x)}}}$.

3. ДВИЖЕНИЕ ЭЛЕКТРОНОВ И ИОНОВ В ПОПЕРЕЧНОМ МАГНИТНОМ ПОЛЕ

На рис. 3 приведена схема МБ, используемая при теоретическом анализе задачи.

Уравнения динамики электронов имеют вид

Изменение энергии электронов при продвижении их в промежутке ∆ связано с переносом внутренней энергии, энергии направленного движения, работой сил давления и электрического поля. В стационарном режиме, с учетом ухода электронов на стенки, можно записать следующее уравнение:

Уравнение непрерывности потока электронов с учетом ухода электронов вдоль оси z имеет вид

Из (3), (4) можно получить

Пренебрегая инерцией электронов в уравнениях (1), (2), (5) и используя граничное условие φ(x = 0) = 0, получим выражения для скоростей и температуры электронов:

Уравнения (6)–(8) не содержат времени τ и соответствуют одномерной постановке задачи. Но учет потерь электронов из потенциальной ямы на стенки азимутатора заложен в уравнении (4).

Тепловая скорость электронов ${{u}_{{Te}}} = \sqrt {\frac{{2kT}}{m}} $ запишется так

Движение ионов в МБ описывается уравнениями сохранения энергии и потока: $M{{V}^{2}}{\text{/}}2 = $ $ = {{W}_{0}} - e\varphi $, ${{n}_{i}} = \frac{{{{n}_{0}}{{u}_{0}}}}{V}$, где V – скорость ионов вдоль оси x, M – масса иона, n_i – плотность ионов. Тогда распределение плотности ионов в МБ определяется по формуле

4. РАСПРЕДЕЛЕНИЕ ПОТЕНЦИАЛА

4.1. Квазинейтральный режим

Рассмотрим случай n₀ ≫ N_B, при котором электроны, продвигающиеся в МБ за счет столкновений с нейтралами, компенсируют заряд ионной компоненты, и на всей длине МБ осуществляется квазинейтральный режим течения с n_e = n_i = n. Полагаем, что для электронов выполняется условие ω_Be ≫ (τ_ea)^–1, при котором направленная скорость электронов (7) с учетом соотношений (8) и (10) будет определяться так:

(11)

${{u}_{x}} = \frac{{3e}}{{5m\omega _{{Be}}^{2}{{\tau }_{{ea}}}}}\frac{{d\varphi }}{{dx}}\left[ {1 - \frac{1}{{(1 - e\varphi {\text{/}}{{W}_{0}})}}\left( {\frac{{5k{{T}_{0}}}}{{6{{W}_{0}}}} + \frac{{e\varphi }}{{3{{W}_{0}}}}} \right)} \right],$

где ${{\tau }_{{ea}}} = 1{\text{/}}\left( {{{n}_{a}}{{\sigma }_{{ea}}}{{u}_{{Te}}}} \right)$ – время между упругими столкновениями электронов с нейтралами, n_a – плотность нейтралов, σ_ea – сечение упругих столкновений; считаем σ_ea = const.

Из (11) видно, что направленная скорость электронов становится равной нулю в точке, где потенциал становится равным некоторому критическому значению φ_cr, определяемому из формулы

(12)

$\frac{{e{{\varphi }_{{cr}}}}}{{{{W}_{0}}}} = \frac{3}{4} - \frac{{5k{{T}_{0}}}}{{8{{W}_{0}}}}.$

Введем безразмерные переменные $\psi = e\varphi {\text{/}}{{W}_{0}}$ – безразмерный потенциал и $\xi = x{\text{/}}\Delta $ – координату поперек поля. Объединяя (1), (4), (8), (9), (10) и (11), получим уравнение для определения потенциала в МБ

(13)

$G\frac{d}{{d\xi }}\left[ {f\left( \psi \right)\frac{{d\psi }}{{d\xi }}} \right] = - g(\psi ),$

где $G = \frac{1}{{5\Lambda \sqrt {4\pi } }}\frac{{{{n}_{a}}}}{{{{n}_{0}}}}\frac{{{{\sigma }_{{ea}}}}}{{{{\Delta }^{2}}}}\frac{{W_{0}^{3}}}{{{{e}^{4}}\omega _{{Be}}^{2}m}}$ – безразмерный критерий, который можно записать и как G = RN_B/n₀; здесь введен безразмерный параметр R = $ = \frac{9}{{80}}\sqrt {\frac{3}{\pi }} \frac{{{{n}_{a}}{{\sigma }_{{ea}}}W_{0}^{2}}}{{\Lambda {{e}^{2}}m\omega _{{Be}}^{2}}}$, который не зависит от плотности входного потока n₀, длины ∆ и в условиях эксперимента R ≫ 1.

В уравнении (13) функции g(ψ) и f(ψ) суть

(14)

$f\left( \psi \right) = \frac{{\left( {1 - 4{\text{/}}3\psi - 5{\text{/}}6\alpha } \right)}}{{{{{\left( {1 - \psi } \right)}}^{{3/2}}}}}\sqrt {\alpha + 2{\text{/}}5\psi } ;$

(15)

$g\left( \psi \right) = \frac{1}{{\left( {1 - \psi } \right){{{\left( {\alpha + 2{\text{/}}5\psi } \right)}}^{{3/2}}}}}\exp \left( { - \frac{\psi }{{\alpha + 2{\text{/}}5\psi }}} \right),$

где α = kT₀/W₀ ≪ 1; при численном моделировании (рис. 4, 6 ) принималось α = 0.006.

Вводя обозначение $z\left( \psi \right) = d\psi {\text{/}}d\xi $, приведем уравнение (13) к виду

(16)

$\frac{{d\left( {{{f}^{2}}{{z}^{2}}} \right)}}{{d\psi }} = - \frac{2}{G}gf.$

Уравнение (16) можно решить относительно $d\psi {\text{/}}d\xi $:

(17)

$\frac{{d\psi }}{{d\xi }} = \sqrt {\frac{2}{G}} \frac{1}{f}\sqrt {\int\limits_\psi ^{{{\psi }_{m}}} {g(p)f(p)dp} } .$

В решении (17) постоянную интегрирования мы нашли из условия симметрии распределения потенциала. В точке ξ = 1/2 потенциал ψ достигает максимума ψ(ξ = 0.5) = ψ_m, a производная ${{\left. {\frac{{d\psi }}{{d\xi }}} \right|}_{{0.5}}} = 0$. Интегрируя (17), для распределения потенциала вдоль МБ будем иметь

(18)

$\int\limits_0^\psi {\frac{{f(t)dt}}{{\sqrt {k({{\psi }_{m}}) - k(t)} }}} = \sqrt {\frac{2}{G}} \xi ,$

где обозначено

(19)

$\begin{gathered} k(t) = \int\limits_0^t {g(p)f(p)dp} = \\ \, = \int\limits_0^t {\frac{{\left( {1 - 4{\text{/}}3p - 5{\text{/}}6\alpha } \right)}}{{{{{\left( {1 - p} \right)}}^{{5/2}}}\left( {\alpha + 2{\text{/}}5p} \right)}}{{e}^{{ - \frac{p}{{\alpha + 2/5p}}}}}dp} . \\ \end{gathered} $

При ξ = 1/2 из (18) получим уравнение для определения значения максимального потенциала ψ_m:

(20)

$\int\limits_0^{{{\psi }_{m}}} {\frac{{f(t)dt}}{{\sqrt {k({{\psi }_{m}}) - k(t)} }}} = \frac{1}{{\sqrt {2G} }}.$

Для решения уравнения (20) на промежутке 0 ≤ t < 1 вычислялась функция k(t). Далее рассчитывалась функция

(21)

$s({{\psi }_{m}}) = \int\limits_0^{{{\psi }_{m}}} {\frac{{f(t)dt}}{{\sqrt {k({{\psi }_{m}}) - k(t)} }}} ,$

которая определена в области 0 ≤ ψ_m ≤ ψ_cr, где функция k(t) возрастает. Потенциал ψ_cr определяется в соответствии с соотношением (12).

Подынтегральное выражение в (21) при t = ψ_m стремится к бесконечности, но интеграл сходится, и его можно вычислить методом средних прямоугольников с рекуррентным уточнением. Интерполируя найденную функцию s(ψ_m) кубическими сплайнами, из уравнения (20) была определена зависимость величины максимального потенциала ψ_m от G (рис. 4a). Существует критическое значение G_cr, при котором максимум потенциала равен критическому значению ψ_cr, это ${{G}_{{cr}}} = 0.5{\text{/}}{{\left[ {s\left( {{{\psi }_{{cr}}}} \right)} \right]}^{2}}$.

Рис. 4.

а) – зависимость величины максимального потенциала ψ_m от критерия G; б) – распределение потенциала ψ для различных значений критерия G.

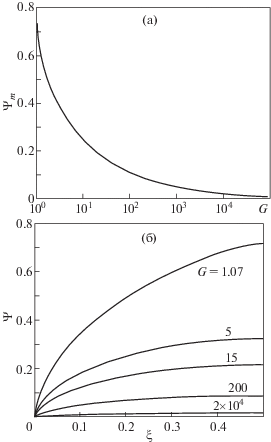
Численно вычисляя интеграл (21) при ψ_m = = ψ_cr = 0.74625, получим $s({{\psi }_{{cr}}})$ = 0.6844; тогда ${{G}_{{cr}}}$≈ 1.067. С помощью уравнения (18) было получено распределение потенциала в области 0 ≤ ξ ≤ 1 (рис. 4б). Максимальная плотность потока, при которой еще реализуется прохождение через МБ в квазинейтральном режиме, равна n_cr = = N_BR/G_cr, что в R раз превосходит величину N_B.

5. СРАВНЕНИЕ ТЕОРЕТИЧЕСКИХ РЕЗУЛЬТАТОВ С ДАННЫМИ ЭКСПЕРИМЕНТОВ

В макете плазмооптического масс-сепаратора ПОМС-Е-3 (рис. 1) в качестве источника плазмы использовался TAL, катод которого является и азимутатором с Δ = 6 × 10^–3 м. Необходимые для численных расчетов значения средней энергии W₀ и плотности ионов n извлекались из измеренных непосредственно на выходе из катода-азимутатора функций распределения ионов; плотность определялась как интеграл от функции распределения. Плавающий потенциал φ_fl в центре МБ находился по ВАХ ленгмюровского зонда. На рис. 5 демонстрируется сравнение ψ_m и φ_fl при изменении магнитного поля и рабочего давления. Как измеренный экспериментально, так и рассчитанный теоретически (Δ = 6 × 10^–3 м; W₀ = 500 эВ, n₀ = 10¹⁵ м^–3, σ_ea = 2 × 10^–20 м²) потенциалы растут примерно по одинаковому закону с увеличением магнитного поля. При P ≤ 8 × 10^–5 Торр в эксперименте φ_fl изменяется не более чем на 15%. Если давление продолжает возрастать, φ_fl падает значительно быстрее – эффективность компенсации электронами положительного заряда ионного потока возрастает. Поток квазинейтральной плазмы наблюдается при любых разрядных напряжениях U_d, но должно быть В_an ≥ 400 и B_az ≥ 1500 Гс; при меньших значениях индукции магнитного поля плавающий потенциал φ_fl ≈ const при росте Р.

Рис. 5.

Потенциал в МБ азимутатора: а) – как функция магнитного поля: кривая 1 – ψ_m = f(B) при Р = 9 × × 10^–5 Торр; 2 – экспериментально измеренный плавающий потенциал при U_d = 1160 В, В_an = 1000 Гс, B_az = 4270 Гс; б) – зависимость от давления: 1 – ψ_m = = f(Р) при B = 4000 Гс; 2 – φ_fl при U_d = 680 В, В_an = = 1000 Гс, B_az = 4270 Гс.

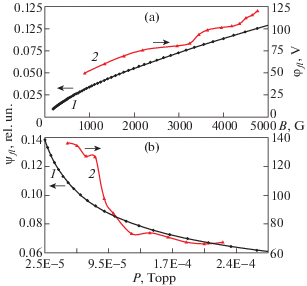
Надо отметить, что функция распределения ионов по энергии (с наиболее вероятной энергией W_0m) на входе в МБ в эксперименте изменялась в соответствии с динамикой режима горения разряда в TAL. Это обстоятельство, судя по кривой 2 на рис. 5a, заметного влияния на зависимость φ_fl = f(B) не оказывает.

На рис. 6 представлена максимально возможная плотность ионов как функция магнитного поля. Жирная горизонтальная линия отмечает границу бесстолкновительного режима N ≈ 1.7 × × 10²⁰ м^–3 для ионов при прохождении пути TAL + + МБ (l ≈ 1.5 × 10^–2 м), что является условием плазмооптической масс-сепарации. Данная граница получена из условия однократности столкновений ионов на пути l с учетом полного транспортного сечения (упругое рассеяние плюс перезарядка), которое, для оценки, взято для ионов аргона с W₀ = 400 эВ и равно σ_tr ≈ 3.9 × 10^–15 см² [24].

Рис. 6.

Зависимость максимальной плотности от величины магнитного поля в МБ: кривая 1 – P = 5 × × 10^–4 Торр; 2 – 10^–4 Торр; 3 – 5 × 10^–5 Торр; в области A – есть столкновения; B – столкновений нет. Расчет сделан при Δ = 6 × 10^–3 м, W₀ = 500 эВ, σ_ea = = 2 × 10^–20 м².

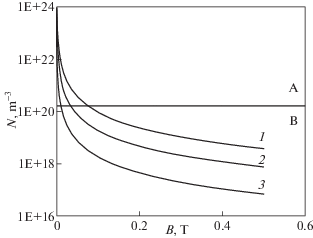
В экспериментах на ПОМС-Е-3 максимальная плотность на выходе МБ пока не превышает 10¹⁴ м^–3, что много меньше плотности, “разрешенной” для прохождения через МБ. Например, при В = 4000 Гс и Р = 10^–4 Торр плотность N ≈ ≈ 10¹⁸ м^–3. Максимальные плотности в прошедшем МБ потоке ионов (рис. 6) смогут обеспечить высокую производительность ПОМС.

6. ЗАКЛЮЧЕНИЕ

Характер движения потока плазмы в поперечном магнитном поле при диффузионном продвижении электронов определяется величинами плотностей ионов и нейтралов, индукцией магнитного поля, энергией ионов и длиной МБ. В работе сформирован информативный для проведения многопараметрического теоретического анализа безразмерный критерий G, который включает в себя все названные величины и ряд численных коэффициентов. Введен связанный с G безразмерный параметр R, который не зависит от плотности входного потока n₀ и от ∆, позволяющий выявить влияние на течение величины магнитного поля и энергии потока. Определено критическое значение G_cr ≈ 1.067. Если G ≥ G_cr, то движение плазмы в МБ происходит с сохранением квазинейтральности. Если G < G_cr, то существует промежуток в МБ, локализованный вблизи максимума потенциала, где движется только поток ионов. Именно в этом режиме достигается максимально возможная плотность ионов, прошедших через магнитный барьер. Найдена формула для максимальной плотности ионов, преодолевающих МВ, n_Δm≈ N_BR/G_cr, где N_B – величина максимальной плотности ионов, проходящих через МБ, полученная для случая, когда не учитывалось диффузионное проникновение электронов в МБ. Для условий эксперимента параметр R ≈ 200, и n_Δm на два порядка превышает величину N_B, достигая значения 2 × 10¹⁷ м^–3. Это означает, что для условий эксперимента значительных ограничений на производительность масс-сепарации, связанных с влиянием магнитного поля барьера, нет.

Зависимость φ_fl = f(B) экспериментально измеренного потенциала в МБ азимутатора ПОМС-Е-3 лежит в области G ≥ G_cr, что говорит о выполнении условия квазинейтральности. В эксперименте для этого нужно, чтобы B_az ≥ 1500 Гс. Плавающий потенциал, как и ψ_m, растет с увеличением B и уменьшается с Р. Данные факты говорят в пользу правильности основных положений предлагаемой теории прохождения потока плазмы через магнитный барьер масс-сепаратора.

Работа частично финансировалась в рамках проекта № 0667-2020-0037 Министерства науки и высшего образования РФ.