1. На главную
  2. Электронные версии
  3. Физика плазмы
  4. T. 46, № 12, 2020

Физика плазмы, 2020, T. 46, № 12, стр. 1125-1134

Спектральные характеристики для малоразмерных квазидвумерных кластеров

О. С. Ваулина a, b, *, Э. А. Саметов a, b, Е. А. Лисин a, b, И. И. Лисина a, b

a Объединенный институт высоких температур РАН
Москва, Россия

b Московский физико-технический институт (национальный исследовательский университет),
Московская обл., Долгопрудный, Россия

* E-mail: olga.vaulina@bk.ru

Поступила в редакцию 25.03.2020
После доработки 20.04.2020
Принята к публикации 27.04.2020

Полный текст (PDF)

Аннотация

Представлены результаты исследования спектральных характеристик стохастического движения заряженных частиц для квазидвумерных кластеров в электрическом поле ловушки. Рассмотрены характерные частоты частиц и способ их аналитического вычисления. Предложены аналитические соотношения для спектральной плотности смещений в малоразмерных кластерах, состоящих до семи заряженных частиц, взаимодействующих с попарным потенциалом. Полученные соотношения проверены путем численного моделирования задачи.

Ключевые слова: пылевая плазма, заряженные частицы

1. ВВЕДЕНИЕ

Исследование стохастического (теплового) движения взаимодействующих частиц представляет интерес в различных областях науки и техники [1–6].

Комплексная (пылевая) плазма представляет собой ионизованный газ, содержащий заряженные частицы вещества микронных размеров (пыль) [1–3]. Экспериментальные и теоретические исследования теплового движения заряженных пылевых частиц в газоразрядной плазме представлены в различных работах [7–13]. В обычных условиях в центре газоразрядных камер наблюдается некоторое превышение концентрации ионов плазмы над концентрацией ее электронной компоненты [14], что приводит к формированию эффективных ловушек для отрицательно заряженных частиц пыли [1, 2]. Лабораторные эксперименты с небольшим количеством пылевых частиц позволяют проводить исследования собственных и вынужденных колебаний частиц, изучать влияние различных внешних воздействий, а также разрабатывать новые методы диагностики [15–22].

Подробную информацию об особенностях теплового движения заряженных частиц можно получить путем анализа спектральной плотности их смещений и характерных частот колебаний. Информация о спектральной плотности тепловых смещений частиц в равновесных системах позволяет анализировать их температуру, коэффициенты трения и полный спектр частот их собственных колебаний. Это, в свою очередь, дает возможность оценить реакцию системы на кратковременные или периодические внешние возмущения, а также позволяет определить характер и тип потенциала взаимодействия между частицами среды [7–9, 23, 24].

Исследование взаимодействий между пылевыми частицами в комплексной плазме вызывает постоянный интерес [1–3]. За последние годы появилось немало работ, посвященных разработке экспериментальных методов определения потенциалов взаимодействия между пылевыми частицами в лабораторной плазме газовых разрядов [25–30]. Преимуществом обладают методы, основанные на решении обратной задачи Ланжевена [29], или на анализе корреляторов смещений и скоростей частиц [30]. В отличие от других, такие методы полностью учитывают диссипативные и случайные процессы. Тем не менее, и они могут давать некорректные результаты для частиц, колебания (смещения) которых искажены неучтенными регулярными и/или случайными внешними воздействиями [30].

В настоящее время задача о спектральной плотности смещений в системе взаимодействующих частиц детально рассмотрена только для двух случаев: 1) для двух заряженных частиц [31, 32]; 2) для малоразмерных цепочечных структур, состоящих из идентичных частиц с попарным взаимодействием [33]. В данной работе приводятся результаты исследования спектральных характеристик для частиц, взаимодействующих с произвольным попарным потенциалом, в малоразмерных квазидвумерных кластерах. Представленные результаты могут быть полезны для экспериментального анализа характера и типа потенциала взаимодействия между пылевыми частицами в плазме.

Отметим, что основное внимание в настоящей работе уделяется спектральным плотностям для кластеров в электрическом поле ловушки при вертикальных смещениях частиц ортогонально плоскости кластера. Теоретические расчеты некоторых частот колебаний для плоских кластеров с различным числом частиц были выполнены ранее в работах [34, 35]. Данные о характерных частотах заряженных частиц для случая бесконечной решетки представлены в работе [36].

2. ОСНОВНЫЕ СООТНОШЕНИЯ

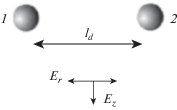
Рассмотрим равновесную систему, состоящую из N частиц массой Mi и зарядами Qi, взаимодействующих с произвольной формой потенциала в линейном электрическом поле ловушки с цилиндрической симметрией E(r, z) при радиальной составляющей ${{E}_{r}} = {{\beta }^{r}}r$ и вертикальной составляющей ${{E}_{z}} = E_{z}^{0} + {{b}^{z}}z$ (см. рис. 1). Здесь r ≡ (x2 + y2)1/2 – радиальная координата, z – вертикальная координата по оси z в направлении силы тяжести, β r = = β x ≡ β y и β z – величины градиентов электрического поля, а значение $E_{z}^{0}$ определяется балансом сил, действующих в системе.

Рис. 1.

Горизонтальная конфигурация двух заряженных частиц в электрическом поле ловушки E = E(z, r) с цилиндрической симметрией.

В предположении, что смещение, ξi, i-й частицы, где i = 1,2… N, от ее положения равновесия под действием некоторой случайной силы Fbi ограничено малыми отклонениями, систему линеаризованных уравнений движения в выбранном направлении (т.е. для каждой из степеней свободы: x, y, z) можно записать в общем виде

(1)
$\begin{gathered} {{M}_{i}}\frac{{d{{V}_{i}}^{{}}}}{{dt}} = - {{v}_{i}}{{M}_{i}}{{V}_{i}} - {{Q}_{i}}\beta {{\xi }_{i}} + \\ \, + \sum\limits_{j = 1,j \ne i}^N {{{b}_{{ji}}}({{\xi }_{i}} - {{\xi }_{j}}) + F_{{bi}}^{{}},} \\ \end{gathered} $
где νi – коэффициент трения i-й частицы за счет ее столкновений с нейтралами окружающего газа, $\beta = {{\beta }^{z}}$ для вертикальных смещений частиц по оси z, $\beta = {{\beta }^{r}}$ для смещений частиц в направлении оси x (или y), Vi = dξi/dt – скорость i-й частицы на одну степень свободы (x, y, z), Fbi – сила Ланжевена, являющаяся источником стохастической кинетической энергии частиц, а коэффициенты bij зависят от рассматриваемой степени свободы (x, y, z) для смещений частиц и от физики решаемой задачи (для попарного взаимодействия: bij ≡ bji).

Спектральная плотность, Gi, для случайных (тепловых) смещений частиц определяется как косинус-преобразование Фурье для корреляционной функции, описывающей зависимость среднеквадратичного отклонения этих частиц от их начального положения: ${{\left\langle {\xi _{i}^{2}} \right\rangle }_{t}} = {{\left\langle {{{{\left( {{{\xi }_{i}}(t){\text{ }}--{{\xi }_{i}}\left( 0 \right)} \right)}}^{2}}} \right\rangle }_{t}}$, где угловые скобки ${{\left\langle {...} \right\rangle }_{t}}$ обозначают усреднение по всем отрезкам времени равным t [40–42]. Основные гармоники частиц, ωi, и их коэффициенты трения, νi, можно получить путем решения характеристического уравнения для системы (1) при Fbi = 0 [40].

Спектральная плотность для одной заряженной частицы (N = 1) в ловушке описывается формулой для классического осциллятора [37–39]

(2)
${{G}_{1}}(\omega ) \equiv {{S}_{1}}(\omega ) = \frac{{2\nu T{\text{/}}M}}{{{{\omega }^{4}} + ({{\nu }^{2}} - 2\omega _{1}^{2}){{\omega }^{2}} + \omega _{1}^{4}}},$
где T – кинетическая температура частиц (удвоенная кинетическая энергия их стохастического движения на одну степень свободы), а $\omega _{1}^{2} = $ $ = {{(\omega _{t}^{{z(r)}})}^{2}} \equiv Q{{\beta }^{{z(r)}}}{\text{/}}M$ – характерная частота ловушки в радиальном и вертикальном направлениях.

В отдельных случаях, например, для цепочечных структур, состоящих из идентичных частиц с попарным взаимодействием (Mi ≡ M, Qi ≡ Q, νi ≡ ν), процедуру вычисления спектральной плотности для смещений каждой из частиц Gi(ω) (i = 1,2,.. N) можно свести к определению суперпозиции спектральных плотностей Sk = Sk(ω, ν, ωk) для отдельных гармоник системы с характерной частотой ωk [33]

(3)
${{G}_{i}}(\omega ) = \sum\limits_{k = 1}^N {{{A}_{k}}} \frac{{2\nu T{\text{/}}M}}{{{{\omega }^{4}} + ({{\nu }^{2}} - 2\omega _{k}^{2}){{\omega }^{2}} + \omega _{k}^{4}}} \equiv \sum\limits_{k = 1}^N {{{A}_{k}}} {{S}_{k}},$
где Ak – некоторые коэффициенты, а N – число частиц.

Задача о спектральных характеристиках двух частиц с произвольной формой потенциала взаимодействия подробно рассматривалась в различных работах [31–33]. В случае двух идентичных частиц с попарным взаимодействием G1(ω) ≡ ≡ G2(ω) = G(ω) имеет место

(4)
$G(\omega ) = \sum\limits_{i = 1}^2 {\frac{{2\nu T{\text{/}}M}}{{{{\omega }^{4}} + ({{\nu }^{2}} - 2\omega _{i}^{2}){{\omega }^{2}} + \omega _{i}^{4}}}} \equiv \sum\limits_{i = 1}^2 {\frac{1}{2}{{S}_{i}}} .$

Здесь характерные частоты, ω1(2), определяются соотношениями: $\omega _{1}^{2} = a--b$, $\omega _{2}^{2} = a + b$. В случае горизонтальной конфигурации частиц (рис. 1) для их радиальных смещений, ${{\xi }_{{1\left( 2 \right)}}} = \delta {{r}_{{1\left( 2 \right)}}}$: $a = $ $ = (Q{{\beta }^{r}} - F{\kern 1pt} '){\text{/}}M$ и $b = - F{\kern 1pt} '{\text{/}}M$, где $F{\kern 1pt} '$ – производная силы F взаимодействия между двумя частицами в радиальном направлении. Для вертикальных смещений, ${{\xi }_{{1\left( 2 \right)}}} = \delta {{z}_{{1\left( 2 \right)}}}$: $a = (Q{{\beta }^{z}} - F{\text{/}}l){\text{/}}M$, а b = F/lM, где l – расстояние между частицами. Для кулоновского взаимодействия: F = Q2/l2, $F{\kern 1pt} ' = $ $ = - 2{{Q}^{2}}{\text{/}}{{l}^{3}}$.

Уравнение баланса сил для горизонтальной конфигурации двух частиц имеет вид

(5)
${{\beta }^{r}}l = 2F,$
а устойчивость такой конфигурации нарушается при условии [41]

(6)
${{\beta }^{r}} > {{\beta }^{z}}.$

Отметим, что здесь под устойчивостью горизонтальной конфигурации двух частиц подразумевается их положение в горизонтальной (радиальной) плоскости ловушки.

Уравнения баланса сил и критерии устойчивости для малоразмерных систем (цепочечных структур и квазидвумерных кластеров при N = 3–5), состоящих из идентичных частиц с попарным взаимодействием, рассмотрены в работе [42]. В радиальной плоскости ловушки с цилиндрической симметрией частицы квазидвумерных кластеров при 2 ≤ N ≤ 7 вращаются относительно центра этих кластеров [41, 43, 44], т.е. дрейфуют с тепловой скоростью вдоль эквипотенциальных силовых линий внешнего электрического поля. (Здесь и далее термином “радиальная плоскость” мы обозначили плоскость [x, y] ловушки с цилиндрической симметрией, совпадающую с плоскостью кластера.) Данное обстоятельство затрудняет определение тепловых смещений частиц в радиальной плоскости (плоскости [x, y]) даже в условиях численного эксперимента. Вращение частиц в радиальной плоскости не оказывает влияния на величину их вертикальных смещений. Поэтому основное внимание в настоящей работе уделяется спектральным характеристикам частиц при их вертикальных смещениях, ортогональных плоскости квазидвумерных кластеров.

Спектральные характеристики частиц для системы (1) при Fbi = 0, такие как их характерные частоты, ωi, и спектральные плотности смещений, Gi, могут быть получены численно на основе существующих пакетов математического моделирования. Практически все современные программные пакеты имеют встроенные функции символьных вычислений и позволяют получить конечный результат в виде формул для ωi и Gi, которые являются математическими решениями задачи. Кроме того, такие формулы имеют весьма громоздкий вид и занимают, со всеми входящими в них коэффициентами, от двух (для N = 3) и более (при N >3) страниц текста. Таким образом, упомянутые соотношения являются малоэффективными для практического использования, включая анализ и/или обращение данных численных и лабораторных экспериментов.

Аналитические соотношения для характерных частот и спектральной плотности смещений для идентичных частиц (Mi ≡ M, Qi ≡ Q, νi ≡ ν), взаимодействующих с попарным потенциалом, в квазидвумерных кластерах (3 ≤ N ≤ 7) рассмотрены в следующих разделах данной работы.

3. СЛУЧАЙ ТРЕХ, ЧЕТЫРЕХ, ПЯТИ И СЕМИ ЧАСТИЦ

Рассмотрим спектральные характеристики для случая трех, четырех, пяти и семи идентичных частиц (Qi = Q, Мi = М, νi = ν), взаимодействующих с произвольной попарной силой Fij =F(lij) в линейном электрическом поле E(r, z) ловушки с цилиндрической симметрией (см. рис. 2); здесь i = 1, 2, … N, j = 1, 2, … N и i ≠ j. Критерии устойчивости таких систем представлены в работе [39]. В силу симметрии задачи относительно центра ловушки в таких системах, функции Gi(ω) ≡ G(ω) для частиц, которые имеют одинаковое расстояние от центра структуры (т.е. центра ловушки), см. рис. 2.

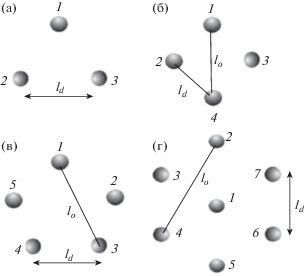
Рис. 2.

Квазидвумерные конфигурации трех (a), четырех (б), пяти (в) и семи (г) заряженных частиц в электрическом поле ловушки E = E(z, r) с цилиндрической симметрией.

Численное моделирование стохастических процессов выполнялось методом Ланжевена для идентичных частиц с равными массами зарядами и температурой. Техника моделирования подробно описана в работах [1–3]. Шаг интегрирования составлял от Δt ≅ (40 max[$\omega _{t}^{{z(r)}}$; ν])–1 до Δt ≅ ≅ (100 max[$\omega _{t}^{{z(r)}}$; ν])–1 в зависимости от начальных условий задачи. Время расчетов tc после установления равновесия в моделируемых системах варьировалось от ~103/min[$\omega _{t}^{{z(r)}}$; ν] до ~104/min[$\omega _{t}^{{z(r)}}$; ν]; здесь $\omega _{t}^{{z(r)}}$ = (Qβz(r)/M)1/2 – характерные частоты ловушки. Температура частиц в процессе моделирования не менялась, т.е. оставалась равной заданной Ti =$T_{t}^{0}$ ≡ T.

Вычисления спектральной плотности по результатам моделирования проводились на основе численных расчетов смещений x(t), y(t) и z(t) для отдельных частиц системы при помощи процедуры “N-D fast Fourier transform” в пакете прикладных программ MATLAB.

3.1. Три частицы

Обратимся к случаю трех частиц (N = 3), см. рис. 2а. В состоянии равновесия средние расстояния между частицами равны l12 = l23 = l31 ≡ ld, а уравнение баланса сил можно записать в виде

(7)
$Q{{\beta }^{r}}{{l}_{d}} = 3F,$
где F – сила взаимодействия между частицами (F12 = F23 = F13 ≡ F). А устойчивость горизонтальной конфигурации трех частиц нарушается при условии [42]

(8)
${{\beta }^{r}} > {{\beta }^{z}}.$

Для поиска спектральных характеристик выполним замену переменных в системе (1) для вертикальных смещений частиц (β = βz) при Fbi = 0: η1= ξ1 + ξ2 + ξ3; η2 = ξ1 – ξ3; η3 = 2ξ2 – (ξ1 + ξ3). (Здесь и далее, для вертикальных смещений частиц в кластере – ξi = δzi.) С учетом указанной замены переменных преобразуем систему уравнений движения (1) к виду

(9а)
$\frac{{{{d}^{2}}{{\eta }_{1}}}}{{d{{t}^{2}}}} = - \nu \frac{{d{{\eta }_{1}}}}{{dt}} - \frac{{Q{{\beta }^{z}}}}{M}{{\eta }_{1}},$
(9б)
$\frac{{{{d}^{2}}{{\eta }_{2}}}}{{d{{t}^{2}}}} = - \nu \frac{{d{{\eta }_{2}}}}{{dt}}--\left( {\frac{{Q{{\beta }^{z}}}}{M} + a + 2b} \right){{\eta }_{2}},$
(9в)
$\frac{{{{d}^{2}}{{\eta }_{3}}}}{{d{{t}^{2}}}} = - \nu \frac{{d{{\eta }_{3}}}}{{dt}}--\left( {\frac{{Q{{\beta }^{z}}}}{M} + 3a} \right){{\eta }_{3}}.$

Здесь для вертикальных смещений частиц: b ≡ a = = –F/Mld. Таким образом, данная система имеет две характерных частоты в вертикальном направлении: $\omega _{1}^{2} = Q{{\beta }^{z}}{\text{/}}M$; $\omega _{2}^{2} = Q{{\beta }^{z}}{\text{/}}M + 3а \equiv $ $ \equiv Q({{\beta }^{z}} - {{\beta }^{r}}){\text{/}}M$ (ω3 ≡ ω2).

Иллюстрация траекторий для трех частиц в радиальной плоскости цилиндрической ловушки, полученная в результате численного моделирования за время t = 40/ν, представлена на рис. 3 при коэффициенте трения ν = 2 с–1 и комнатной температуре Т = 0.027 эВ. Время полного оборота частицы вокруг центра ловушки ~240/ν. С ростом кинетической температуры частиц данное время будет уменьшаться как минимум на величину пропорциональную $\sqrt T $.

Рис. 3.

Иллюстрация траекторий для трех частиц в радиальной плоскости цилиндрической ловушки за время t = 40/ν при коэффициенте трения ν = 2 с–1 и температуре Т = 0.027 эВ.

Решение системы (9а)–(9в) для $\left\langle {\eta _{k}^{2}} \right\rangle $ с учетом $\left\langle {{{\xi }_{i}}{{\xi }_{j}}} \right\rangle = 0$ при i ≠ j позволяет получить для спектральной плотности смещений отдельных частиц Gi(ω) ≡ G(ω) (i = 1, 2, 3)

(10)
$G(\omega ) = \frac{{{{S}_{1}} + {\text{ }}2{{S}_{2}}}}{3},$
где Sk = Sk(ω, ν, ωk) – спектральная плотность классического осциллятора с частотой ωk; здесь k = 1, 2.

Напомним, что спектральная плотность для смещений ηk является Фурье-преобразованием функций ${{\left\langle {\eta _{k}^{2}} \right\rangle }_{t}}$, а величина ${{S}_{{\eta k}}} = {{D}_{k}}{{S}_{k}}$, где коэффициент Dk определяется суммарной температурой частиц, входящих в данный коррелятор. Так для η1 значение D1 = 3, для η2 – D2 = 2, а для η3 – D3 = 6.

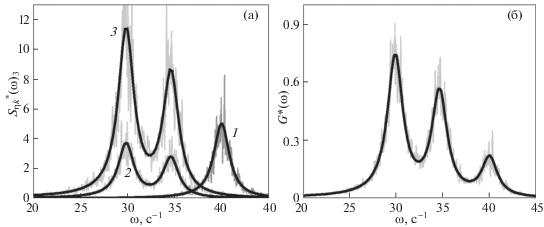
Нормированные спектральные плотности $S_{{\eta k}}^{*}$(ω) = Sηk(ω)/B и G*(ω) = G(ω)/B для системы из трех частиц с кулоновским взаимодействием представлены на рис. 4 при $\nu = 2$ с–1 и βz/βr = 4. Здесь и далее $B = 2Т{\text{/}}(\omega _{t}^{2}\nu М)$, где ${{\omega }_{t}} = \omega _{t}^{{z(r)}} \equiv {{(Q{{\beta }^{{z(r)}}}{\text{/}}M)}^{{1/2}}}$.

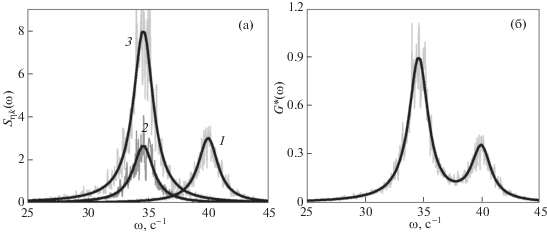
Рис. 4.

Функции $S_{{\eta k}}^{*}(\omega )$ (а) и G*(ω) (б) для вертикальных смещений частиц при ${{\beta }^{z}}{\text{/}}{{\beta }^{r}} = 4$, $\omega _{t}^{z} = 40$ с–1, $\omega _{t}^{r} = 20$ с–1 и ν = 2 с–1. Здесь: 1 – $S_{{\eta 1}}^{*} = 3S_{1}^{*}$; 2 – $S_{{\eta 2}}^{*} = 2S_{2}^{*}$; 3 – $S_{{\eta 3}}^{*} = 6S_{3}^{*}$. Черными линиями показаны аналитические решения задачи, серыми – результаты численного моделирования.

3.2. Четыре частицы

Уравнения баланса сил для горизонтальной конфигурации четырех частиц (рис. 2б) можно записать в виде

(11)
$Q{{\beta }^{r}} = \frac{{2F}}{{{{l}_{d}}}} + \frac{{2{{F}_{o}}}}{{{{l}_{o}}}},$
где ld – среднее расстояние между двумя соседними периферическими частицами, а ${{l}_{o}} = \sqrt 2 {{l}_{d}}$ – среднее расстояние между двумя противоположенными частицами, ${{F}_{{12}}} = {{F}_{{24}}} = {{F}_{{43}}} = {{F}_{{31}}} \equiv F$, F14 = F23 ≡ Fo. Для частиц с кулоновским взаимодействием: $F = {{Q}^{2}}{\text{/}}l_{d}^{2}$, ${{F}_{o}} = {{Q}^{2}}{\text{/}}l_{o}^{2}$. Устойчивость такой конфигурации нарушается при условии [42]

(12)
$Q{{\beta }^{z}} < 4F{\text{/}}{{l}_{d}}.$

Для поиска спектральных характеристик выполним замену переменных в системе (1) для вертикальных смещений частиц (β = βz) при Fbi = 0: η1 = ξ1 + ξ2 + ξ3 + ξ4; ${{\eta }_{2}} = ({{\xi }_{3}} + {{\xi }_{2}}) - ({{\xi }_{1}} + {{\xi }_{4}})$; ${{\eta }_{3}} = {{\xi }_{2}}--{{\xi }_{3}}$; ${{\eta }_{4}} = {{\xi }_{1}} - {{\xi }_{4}}$. Откуда получим

(13а)
$\frac{{{{d}^{2}}{{\eta }_{1}}}}{{d{{t}^{2}}}} = - \nu \frac{{d{{\eta }_{1}}}}{{dt}} - \frac{{Q{{\beta }^{z}}}}{M}{{\eta }_{1}},$
(13б)
$\frac{{{{d}^{2}}{{\eta }_{2}}}}{{d{{t}^{2}}}} = - \nu \frac{{d{{\eta }_{2}}}}{{dt}}--\left( {\frac{{Q{{\beta }^{z}}}}{M} + 4a} \right){{\eta }_{2}},$
(13в)
$\frac{{{{d}^{2}}{{\eta }_{3}}}}{{d{{t}^{2}}}} = - \nu \frac{{d{{\eta }_{3}}}}{{dt}}--\left( {\frac{{Q{{\beta }^{z}}}}{M} + 2a + 2b} \right){{\eta }_{3}},$
(13г)
$\frac{{{{d}^{2}}{{\eta }_{4}}}}{{d{{t}^{2}}}} = - \nu \frac{{d{{\eta }_{4}}}}{{dt}}--\left( {\frac{{Q{{\beta }^{z}}}}{M} + 2a + 2b} \right){{\eta }_{4}}.$

Здесь $a = - F{\text{/}}M{{l}_{d}}$, $b = - {{F}_{o}}{\text{/}}M{{l}_{o}}$. Рассматриваемая система имеет три характерных частоты в вертикальном направлении: $\omega _{1}^{2} = Q{{\beta }^{z}}{\text{/}}M$; $\omega _{2}^{2} = Q{{\beta }^{z}}{\text{/}}M + $ $ + \;4а$; $\omega _{3}^{2} = Q{{\beta }^{z}}{\text{/}}M + 2а + 2b$ (ω4 ≡ ω3).

Решение системы (13а)–(13г) позволяет получить для спектральной плотности смещений отдельных частиц Gi(ω) ≡ G(ω) (i = 1–4)

(14)
$G(\omega ) = \frac{{{{S}_{1}} + {{S}_{2}} + {\text{ }}2{{S}_{3}}}}{4},$
где Sk = Sk(ω, ν, ωk) – спектральная плотность осциллятора с частотой ωk; здесь k = 1, 2, 3.

Спектральная плотность для смещений ηk равна ${{S}_{{\eta k}}} = {{D}_{k}}{{S}_{k}}$, где коэффициент, Dk, определяется суммарной температурой частиц, входящих в соответствующий коррелятор. Так для η1 значение D1 = 4, для η2 – D2 = 4, а для η4 и η3 – D3(4) = 2.

Нормированные спектральные плотности $S_{{\eta k}}^{*}(\omega ) = {{S}_{{\eta k}}}(\omega ){\text{/}}B$ и G*(ω) = G(ω)/B для системы из четырех частиц с кулоновским взаимодействием показаны на рис. 5 при $\nu = 2$ с–1 и βz/βr = 4 для вертикальных смещений частиц.

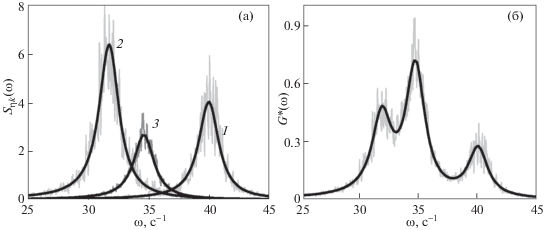
Рис. 5.

Функции $S_{{\eta k}}^{*}(\omega )$ (а) и G*(ω) (б) для вертикальных смещений частиц при ${{\beta }^{z}}{\text{/}}{{\beta }^{r}} = 4$, $\omega _{t}^{z} = 40$ с–1, $\omega _{t}^{r} = 20$ с–1 и ν = 2 с–1. Здесь: 1 – $S_{{\eta 1}}^{*} = 4S_{1}^{*}$; 2 – $S_{{\eta 2}}^{*} = 4S_{2}^{*}$; 3 – $S_{{\eta 3}}^{*} = 2S_{3}^{*}$. Черными линиями показаны аналитические решения задачи, серыми – результаты численного моделирования.

3.3. Пять частиц

Уравнение баланса сил для горизонтальной конфигурации пяти частиц (рис. 2в) позволяют получить величину $Q{{\beta }^{r}}$, используя математические соотношения для правильного пятиугольника и величину сил (F = F(ld); Fo = Fo(lo)), действующих между частицами

(15)
$Q{{\beta }^{r}}R = 2{{c}_{1}}F + 2{{c}_{2}}{{F}_{o}}.~$

Здесь ld – расстояние между двумя ближайшими частицами, ${{l}_{o}} = 2{{l}_{d}}\sin \theta $, где θ = 3π/10, R = $ = {{l}_{d}}{{(2{\text{/}}(5 - \sqrt 5 ))}^{{1/2}}}$, ${{c}_{1}} = \cos \theta $, а ${{c}_{2}} = {{с}_{3}}{{\left( {1 - {{с}_{3}}{\text{/}}4} \right)}^{{1/2}}}$, где с3 = (ld/lo)2. Для частиц с кулоновским взаимодействием $F = {{Q}^{2}}{\text{/}}l_{d}^{2}$, ${{F}_{o}} = {{Q}^{2}}{\text{/}}l_{o}^{2}$.

Для поиска спектральных характеристик выполним замену переменных в системе (1) для вертикальных смещений частиц (β = βz) при Fbi = 0: η1 = ξ1 + ξ2 + ξ3 + ξ4 + ξ5; ${{\eta }_{2}} = {{\xi }_{1}} - {{\xi }_{2}}$; ${{\eta }_{3}} = {{\xi }_{3}} - {{\xi }_{5}}$; ${{\eta }_{4}} = 2{{\xi }_{4}}--({{\xi }_{1}} + {{\xi }_{2}})$; ${{\eta }_{5}} = 2{{\xi }_{4}}--({{\xi }_{3}} + {{\xi }_{5}})$. Откуда получим

(16а)
$\frac{{{{d}^{2}}{{\eta }_{1}}}}{{d{{t}^{2}}}} = - \nu \frac{{d{{\eta }_{1}}}}{{dt}} - \frac{{Q{{\beta }^{z}}}}{M}{{\eta }_{1}},$
(16б)
$\frac{{{{d}^{2}}{{\eta }_{2}}}}{{d{{t}^{2}}}} = - \nu \frac{{d{{\eta }_{2}}}}{{dt}}--\left( {\frac{{Q{{\beta }^{z}}}}{M} + 3b + 2a} \right){{\eta }_{2}} - (a - b){{\eta }_{3}},$
(16в)
$\frac{{{{d}^{2}}{{\eta }_{3}}}}{{d{{t}^{2}}}} = - \nu \frac{{d{{\eta }_{3}}}}{{dt}}--\left( {\frac{{Q{{\beta }^{z}}}}{M} + 3a + 2b} \right){{\eta }_{3}} - (a - b){{\eta }_{2}},$
(16г)
$\frac{{{{d}^{2}}{{\eta }_{4}}}}{{d{{t}^{2}}}} = - \nu \frac{{d{{\eta }_{4}}}}{{dt}}--\left( {\frac{{Q{{\beta }^{z}}}}{M} + 3a + 2b} \right){{\eta }_{4}} - (a - b){{\eta }_{5}},$
(16д)
$\frac{{{{d}^{2}}{{\eta }_{5}}}}{{d{{t}^{2}}}} = - \nu \frac{{d{{\eta }_{5}}}}{{dt}}--\left( {\frac{{Q{{\beta }^{z}}}}{M} + 3b + 2a} \right){{\eta }_{5}} - (a - b){{\eta }_{4}}.$

Здесь a = –F/Mld, b = –Fo/Mlo. Рассматриваемая система имеет три характерных частоты в вертикальном направлении: $\omega _{1}^{2} = Q{{\beta }^{z}}{\text{/}}M$, $\omega _{2}^{2} = Q{{\beta }^{z}}{\text{/}}M + $ $\omega + 5(а + b){\text{/}}2{\text{ }} + d$, $\omega _{3}^{2} = Q{{\beta }^{z}}{\text{/}}M + 5(а + b){\text{/}}2 - d$, где $d = \sqrt 5 (b - a){\text{/}}2$ (ω4 ≡ ω2, ω5 ≡ ω3). Устойчивость горизонтальной конфигурации пяти частиц нарушается при условии [42]

(17)
$\frac{{Q{{\beta }^{z}}}}{M} < - \frac{{5(b + a)}}{2} + \frac{{\sqrt 5 (b - a)}}{2}.$

Решение системы (16а)–(16д) дает для спектральной плотности смещений частиц Gi(ω) ≡ G(ω) (i = 1–5)

(18)
$G(\omega ) = \frac{{{{S}_{1}} + {\text{ }}2{{S}_{2}} + {\text{ }}2{{S}_{3}}}}{5},$
где Sk = Sk(ω, ν, ωk) – спектральная плотность осциллятора с частотой ωk; здесь k = 1, 2, 3.

Спектральная плотность для смещений η1 равна Sη1 = D1S1, а для системы уравнений (16б), (16в) и системы уравнений (16г), (16д) имеют место следующие соотношения: ${{S}_{\eta }}_{2} + {{S}_{\eta }}_{3} = {{D}_{{2\left( 3 \right)}}}({{S}_{2}} + {{S}_{3}})$, ${{S}_{\eta }}_{4} + {{S}_{\eta }}_{5} = {{D}_{{4\left( 5 \right)}}}({{S}_{2}} + {{S}_{3}})$ [33]. Здесь коэффициенты Dk определяются суммарной температурой частиц, входящих в соответствующий коррелятор. Так для η1 значение D1 = 5, для η2 и η3 – D2(3) = 2, а для η4 и η5 – D4(5) = 6.

Нормированные спектральные плотности $S_{{\eta k}}^{*}(\omega ) = {{S}_{{\eta k}}}(\omega ){\text{/}}B$ и G*(ω) = G(ω)/B для системы из пяти частиц с кулоновским взаимодействием показаны на рис. 6 при $\nu = 2$ с–1 и βz/βr = 4.

Рис. 6.

Функции $S_{{\eta k}}^{*}(\omega )$ (а) и G*(ω) (б) для вертикальных смещений частиц при ${{\beta }^{z}}{\text{/}}{{\beta }^{r}} = 4$, $\omega _{t}^{z} = 40$ с–1, $\omega _{t}^{r} = 20$ с–1 и ν = 2 с–1. Здесь: 1 – $S_{{\eta 1}}^{*} = 5S_{1}^{*}$; 2 – $S_{{\eta 2}}^{*} + S_{{\eta 3}}^{*} = 2(S_{2}^{*} + S_{3}^{*})$; 3 – $S_{{\eta 4}}^{*} + S_{{\eta 5}}^{*} = 6(S_{2}^{*} + S_{3}^{*})$. Черными линиями показаны аналитические решения задачи, серыми – результаты численного моделирования.

3.4. Семь частиц

Уравнение баланса сил для горизонтальной конфигурации семи частиц (рис. 2г) можно записать в виде

(19)
$Q{{\beta }^{r}}{{l}_{d}} = 2F\left( {{{l}_{d}}} \right) + F{\kern 1pt} *\left( {2{{l}_{d}}} \right) + \sqrt 3 {{F}_{o}}\left( {{{l}_{o}}} \right).$

Здесь ld – среднее расстояние между двумя ближайшими частицами ${{l}_{o}} = \sqrt 3 {{l}_{d}}$. Для частиц с кулоновским взаимодействием $F = {{Q}^{2}}{\text{/}}l_{d}^{2}$, $F{\kern 1pt} * = {{Q}^{2}}{\text{/}}(4l_{d}^{2})$, ${{F}_{o}} = {{Q}^{2}}{\text{/}}l_{o}^{2}$.

Для поиска спектральных характеристик выполним замену переменных в системе (1) для вертикальных смещений частиц (β = βz) при Fbi = 0: ${{\eta }_{1}} = \sum\nolimits_{i = 1}^7 {{{\xi }_{i}}} $, ${{\eta }_{2}} = {{\xi }_{2}} - {{\xi }_{4}}$, ${{\eta }_{3}} = {{\xi }_{7}} - {{\xi }_{5}}$, ${{\eta }_{4}} = {{\xi }_{3}} + $ $ + \;{{\xi }_{5}} + {{\xi }_{7}}--({{\xi }_{2}} + {{\xi }_{4}} + {{\xi }_{6}})$. Откуда получим

(20а)
$\frac{{{{d}^{2}}{{\eta }_{1}}}}{{d{{t}^{2}}}} = - \nu \frac{{d{{\eta }_{1}}}}{{dt}} - \frac{{Q{{\beta }^{z}}}}{M}{{\eta }_{1}},$
(20б)
$\begin{gathered} \frac{{{{d}^{2}}{{\eta }_{2}}}}{{d{{t}^{2}}}} = - \nu \frac{{d{{\eta }_{2}}}}{{dt}}-- \\ \, - \left( {\frac{{Q{{\beta }^{z}}}}{M} + 3a + b + 3c} \right){{\eta }_{2}} + (a - b){{\eta }_{3}}, \\ \end{gathered} $
(20в)
$\begin{gathered} \frac{{{{d}^{2}}{{\eta }_{3}}}}{{d{{t}^{2}}}} = - \nu \frac{{d{{\eta }_{3}}}}{{dt}}-- \\ \, - \left( {\frac{{Q{{\beta }^{z}}}}{M} + 3a + b + 3c} \right){{\eta }_{3}} + (a - b){{\eta }_{2}}, \\ \end{gathered} $
(20г)
$\frac{{{{d}^{2}}{{\eta }_{4}}}}{{d{{t}^{2}}}} = - \nu \frac{{d{{\eta }_{4}}}}{{dt}}--\left( {\frac{{Q{{\beta }^{z}}}}{M} + 5a + 2b} \right){{\eta }_{4}},$
(20д)
$\frac{{{{d}^{2}}{{\xi }_{1}}}}{{d{{t}^{2}}}} = - \nu \frac{{d{{\xi }_{1}}}}{{dt}}--\left( {\frac{{Q{{\beta }^{z}}}}{M} + 7a} \right){{\xi }_{1}} + a{{\eta }_{1}}.$

Здесь $a = - F{\text{/}}M{{l}_{d}}$, $b = - F{\kern 1pt} *{\text{/}}2M{{l}_{d}}$, $с = - {{F}_{o}}{\text{/}}M{{l}_{o}}$. Рассматриваемая система имеет пять характерных частот в вертикальном направлении: $\omega _{1}^{2} = $ $ = \;\;Q{{\beta }^{z}}{\text{/}}M$, $\omega _{2}^{2}\;\, = \;\,Q{{\beta }^{z}}{\text{/}}M\;\, + \;\,2а\;\, + \;\,2b\;\, + \;\,3с$, $\omega _{3}^{2}\;\, = $ $ = Q{{\beta }^{z}}{\text{/}}M + 4а + 3с$, ${{\omega }_{4}} = Q{{\beta }^{z}}{\text{/}}M + 5a + 2b$, ${{\omega }_{5}} = $ $ = Q{{\beta }^{z}}{\text{/}}M + 7a$. Устойчивость горизонтальной конфигурации семи частиц нарушается при условии

(21)
$Q{{\beta }^{z}} < 7F{\text{/}}{{l}_{d}}.$

Решение системы (20а)–(20д) дает для спектральной плотности смещений частиц Gi(ω) ≡ ≡ G(ω) (i = 2–7) на оболочке кластера

(22)
$G(\omega ) = \frac{{{{S}_{1}} + {{S}_{5}}{\text{/}}6}}{7} + \frac{{2{{S}_{2}} + {\text{ }}2{{S}_{3}} + {{S}_{4}}}}{6},$
а для центральной частицы кластера

(23)
${{G}_{1}}(\omega ) = \frac{{{{S}_{1}} + {\text{ }}6{{S}_{5}}}}{7}.$

Здесь Sk = Sk(ω, ν, ωk) – спектральная плотность осциллятора с частотой ωk, где k = 1–5.

Спектральная плотность для смещений η1 равна ${{S}_{\eta }}_{1} = {{D}_{1}}{{S}_{1}}$, для смещений η4 – ${{S}_{\eta }}_{4} = {{D}_{4}}{{S}_{4}}$, а для системы уравнений (20б), (20в) имеет место следующее соотношение: ${{S}_{\eta }}_{2} + {{S}_{\eta }}_{3} = {{D}_{{2\left( 3 \right)}}}({{S}_{2}} + {{S}_{3}})$ [33]. Здесь коэффициенты, Dk, определяются суммарной температурой частиц, входящих в соответствующий коррелятор. Так для η1 значение ${{D}_{1}} = 7$, для η2 и η3 – D2(3) = 2, а для η4 – D4 = 6.

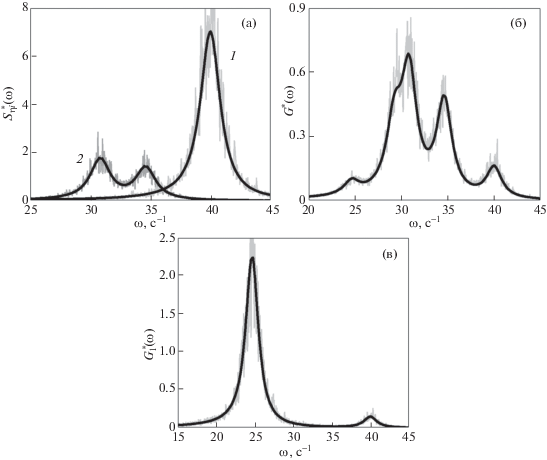
Нормированные спектральные плотности $S_{{\eta k}}^{*}(\omega ) = {{S}_{{\eta k}}}(\omega ){\text{/}}B$, G*(ω) = G(ω)/B и $G_{1}^{*}(\omega ) = $ $ = {{G}_{1}}(\omega ){\text{/}}B$ для системы из семи частиц с кулоновским взаимодействием показаны на рис. 7 при ν = 2 с–1 и βz/βr = 4.

Рис. 7.

Функции $S_{{\eta k}}^{*}(\omega )$ (а) и G*(ω) (б) и $G_{1}^{*}(\omega )$ (в) для вертикальных смещений частиц при ${{\beta }^{z}}{\text{/}}{{\beta }^{r}} = 4$, $\omega _{t}^{z} = 40$ с–1, $\omega _{t}^{r} = 20$ с–1 и ν = 2 с–1. Здесь: 1 – $S_{{\eta 1}}^{*} = 7S_{1}^{*}$; 2 – $S_{{\eta 2}}^{*} + S_{{\eta 3}}^{*} = 2(S_{2}^{*} + S_{3}^{*})$. Черными линиями показаны аналитические решения задачи, серыми – результаты численного моделирования.

3.5. Обсуждение результатов

Представленные аналитические соотношения для спектральной плотности вертикальных смещений частиц в квазидвумерных кластерах сравнивались с результатами определения спектральной плотности, полученными путем преобразования Фурье для решений системы (1) при Fbi = 0 при помощи пакета прикладных программ MATLAB. (Полученные аналитические соотношения полностью совпадают с вычислениями спектральной плотности для решений системы (1).)

Было получено, что для случая малых кластерных систем, состоящих из идентичных частиц с попарным взаимодействием, процедуру вычисления спектральной плотности для смещений каждой из частиц Gj(ω) ($j = 1,2, \ldots ,N$) можно свести определению суперпозиции спектральных плотностей Sk = Sk(ω, ν, ωk) для отдельных гармоник системы с характерной частотой ωk; здесь N – число частиц.

Для такой системы, коэффициент трения частиц ν и частоты ловушки ${{\omega }_{t}} = \omega _{t}^{{z(r)}} \equiv $ $ \equiv {{(Q{{\beta }^{{z(r)}}}{\kern 1pt} {\text{/}}M)}^{{1/2}}}$ (а соответственно, величина градиентов внешнего электрического поля, βz и βr) в реальном эксперименте легко определить из измерений спектральной плотности Sη1(ω) для суммарных смещений частиц, ${{\eta }_{1}} = \sum\nolimits_{i = 1}^N {{{\xi }_{i}}} $, которые пропорциональны смещению центра масс анализируемой системы. А, именно, ${{S}_{\eta }}_{1}(\omega ) = NS(\omega ,\nu ,\omega _{t}^{{z(r)}})$. Для определения других гармоник системы, ωk ≠ ≠ ωt, можно использовать как измерения спектральных плотностей для отдельных частиц Gj(ω), так и измерения спектральных плотностей для их взаимных смещений (${{\xi }_{i}} - {{\xi }_{j}}$); здесь $i = 1,2,...,N$, $j = {\text{ }}1,2,...,N$ и i ≠ j.

Добавим также, что измерение вертикальных смещений в квазидвумерных кластерах дает информацию о силах межчастичного взаимодействия Fij = F(lij), что, в свою очередь, позволяет получить информацию о потенциале взаимодействия между частицами системы. Расстояния между частицами, как в численных, так и в реальных экспериментах легко измеряется; и случае численного моделирования полностью соответствует аналитическим уравнениям баланса сил, см. (7), (11), (15), (19).

Еще раз напомним, что значение характерных частот ωk, частиц и спектральной плотности смещений Gj, в системе из N взаимодействующих частиц можно получить численно на основе существующих программных пакетов, см. раздел 2. Тем не менее применение аналитических соотношений существенно сокращает время необходимое для обращения экспериментальных данных.

4. ЗАКЛЮЧЕНИЕ

Представлены результаты аналитических и численных исследований спектральных характеристик стохастического движения для спектральной плотности вертикальных смещений частиц в малоразмерных квазидвумерных кластерах (смещений, ортогональных плоскости кластеров). Предложены соотношения для спектральной плотности вертикальных смещений частиц в таких системах. Рассмотрены характерные частоты частиц и способ их аналитического вычисления.

Результаты настоящей работы применимы для малых кластерных систем при любом типе попарных взаимодействий. Полученные результаты могут быть полезны для разработки новых методов диагностики физических свойств пылевой плазмы.

Данная работа была частично поддержана Российским фондом фундаментальных исследований (грант № 18-38-20175), а также программой Президиума РАН.

Список литературы

  1. Ваулина О.С., Петров О.Ф., Фортов В.Е., Храпак А.Г., Храпак С.А. Пылевая плазма (эксперимент и теория). М.: Физматлит, 2009.

  2. Complex and Dusty Plasmas / Eds. Fortov V.E. and Morfill G.E. CRC Press, 2010.

  3. Ivlev A., Morfill G., Lowen H., Royall C.P. Complex Plasmas and Colloidal Dispersions: Particle-Resolved Studies of Classical Liquids and Solids. Singapore: World Scientific, 2012.

  4. Photon Correlation and Light Beating Spectroscopy / Eds. H.Z. Cummins and E.R. Pike. N.Y.: Plenum, 1974.

  5. Balescu R. Equilibrium and Nonequilibrium Statistical Mechanics. Chichester: Wiley Interscience, 1975.

  6. Овчинников А.А., Тимашев С.Ф., Белый А.А. Кинетика диффузионно-контролируемых химических процессов. М.: Химия, 1986.

  7. Ваулина О.С., Адамович К.Г. // ЖЭТФ. 2008. Т. 133. С. 1091.

  8. Ваулина О.С., Адамович К.Г., Петров О.Ф., Фортов В.Е. // ЖЭТФ. 2008. Т. 134. С. 367.

  9. Lisin E.A., Timirkhanov R.A., Vaulina O.S., Petrov O.F., Fortov V.E. // New J. Phys. 2013. V. 15. P. 053004.

  10. Vaulina O.S., Lisin E.A. // Physics of plasmas 2009. V. 16. P. 113702.

  11. Фортов В.Е., Петров О.Ф., Ваулина О.С., Косс К.Г. // Письма в ЖЭТФ. 2013. Т. 97. С. 366.

  12. Hebner G.A., Riley M.E., Greenberg K.E. // Phys. Rev. E. 2002. V. 66. P. 046407.

  13. Vaulina O.S., Drangevski I.E. // Phys. Scripta. 2006. V. 73. P. 577.

  14. Райзер Ю.П. Физика газового разряда. М.: Наука, 1987.

  15. Juan W.-T., Huang Z.-H., Hsu J.-W., Lai Y.-J., I L. // Phys. Rev. E. 1998. V. 58. P. 6947.

  16. Ishihara O., Kamimura T., Hirose K.I., Sato N. // Phys. Rev. E. 2002. V. 66. P. 046406.

  17. Klindworth M., Melzer A., Piel A., Schweigert V.A. // Phys. Rev. B. 2000. V. 61. P. 8404.

  18. Melzer A., Klindworth M., Piel A. // Phys. Rev. Lett. 2001. V. 87. P. 115002.

  19. Ivlev A.V., Bartnick J., Heinen M., Du C.R., Nosenko V., Löwen H. // Physical Review X. 2015. V. 5. P. 011035.

  20. Ваулина О.С., Лисина И.И., Косс К.Г. // Физика плазмы 2013. Т. 39. С. 455.

  21. Lisina I.I., Vaulina O.S. // EPL. 2003. V. 103. P. 55002.

  22. Mukhopadhyay A.K., Goree J. // Phys. Rev. E. 2014. V. 90. P. 013102.

  23. Лисин Е.А., Ваулина О.С. // ЖЭТФ. 2012. Т. 142. С. 1077.

  24. Лисин Е.А., Ваулина О.С., Петров О.Ф. // ЖЭТФ. 2017. Т. 151. С. 791.

  25. Pieper J.B., Goree J. // Phys. Rev. Lett. 1996. V. 77. P. 3137.

  26. Homann A., Melzer A., Piel A. // Phys. Rev. E. 1996. V. 59. P. 3835.

  27. Qiao K., Ding Z., Kong J., Chen M., Matthews L.S., Hyde T.W. // arXiv:1810.07173. 2018.

  28. Yousefi R., Chen M., Matthews L.S., Hyde T.W. // ar-Xiv:1607.03177. 2016.

  29. Ваулина О.С., Лисин Е.А., Гавриков А.В., Петров О.Ф., Фортов В.Е. // ЖЭТФ. 2010. Т. 137. С. 751.

  30. Lisin E.A., Vaulina O.S., Petrov O.F. // Phys. Plasmas. 2018. V. 25. P. 013702.

  31. Саметов Э.А., Лисин Е.А., Ваулина О.С. // ЖЭТФ. 2020. Т. 157. С. 552.

  32. Саметов Э.А., Лисин Е.А., Ваулина О.С. // Вестник ОИВТ. 2019. Т. 2. С. 33.

  33. Ваулина О.С. // Физика плазмы. 2020. Т. 46. С. 1.

  34. Amiranashvili Sh., Gusein-zade N., Ignatov A. // Phys. Rev. A. 1999. V. 59. P. 3098.

  35. Amiranashvili Sh.G., Gusein-zade N.G., Tsytovich V.N. // Phys. Rev. E. 2001. V. 64. P. 016407.

  36. Игнатов А.М. // Физика плазмы. 2017. Т. 43. С. 560.

  37. Ваулина О.С., Саметов Э.А. // ЖЭТФ. 2018. Т. 154. С. 407.

  38. Климонтович Ю.Л. Статистическая физика. М.: Наука, 1982.

  39. Воронов А.А. Теория автоматического управления. Часть 2. М.: Высшая школа, 1986.

  40. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов. М.: Наука, 1986.

  41. Ваулина О.С., Адамович К.Г., Дранжевский И.Е. // Физика плазмы. 2005. Т. 31. С. 562.

  42. Ваулина О.С., Лисина И.И., Лисин Е.А. // Физика плазмы. 2018. Т. 44. С. 229.

  43. Lisina I.I., Vaulina O.S., Lisin E.A. // Phys. Rev. E. 2019. V. 99. P. 013207.

  44. Koss K.G., Petrov O.F., Myasnikov M.I., Statsenko K.B., Vasiliev M.M. // JETP. 2016. V. 123. P. 98.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика плазмы

Архивы выпусков Информация о журнале Отправить рукопись в журнал