Физика плазмы, 2020, T. 46, № 12, стр. 1094-1118
Особенности возбуждения электромагнитного поля в емкостном ВЧ-разряде I. Общие вопросы. Простая модель симметричного разряда
С. А. Двинин a, *, О. А. Синкевич b, **, З. А. Кодирзода c, Д. К. Солихов c, ***
a Московский государственный университет им. М.В. Ломоносова, Физический факультет
Москва, Россия
b Национальный исследовательский университет Московский энергетический институт
Москва, Россия
c Таджикский национальный университет, Физический факультет
Душанбе, Таджикистан
* E-mail: dvinin@phys.msu.ru
** E-mail: oleg.sinkevich@itf.mpei.ac.ru
*** E-mail: davlat56@mail.ru
Поступила в редакцию 10.02.2020
После доработки 12.05.2020
Принята к публикации 20.06.2020
Аннотация
Аналитически исследуются электродинамические свойства емкостного ВЧ-разряда низкого давления (частота столкновений электронов много меньше частоты поля) с электродами большой площади при возбуждении его электромагнитным полем частотой выше 13 МГц. Разряд поддерживается поверхностными волнами, распространяющимися вдоль границы, плазма–слой пространственного заряда–металл. При описании слоя пространственного заряда в рамках матричной модели, рассчитаны дисперсионные кривые для четной и нечетной поверхностных волн в трехслойной структуре: слой–плазма–слой, окруженной металлическими границами. Показано, что для корректного расчета импеданса разряда необходимо учитывать поле основной моды и квази-ТЕМ моды для малых плотностей электронов, а поверхностной волны – для высоких. Получено приближенное выражение для импеданса разряда, основанное на учтете только одной моды. Оно справедливо при малых плотностях электронов, когда поверхностные волны отсутствуют, и при высоких, если плотность превышает величину, определяющую существование геометрического резонанса, плазма–слой пространственного заряда.
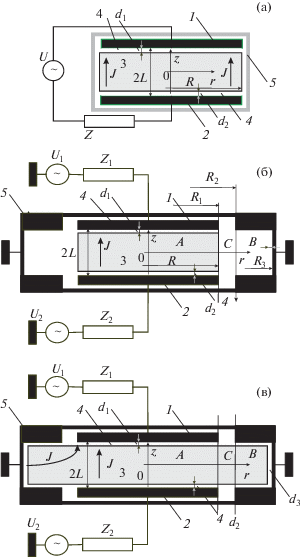
Высокочастотные емкостные разряды широко используются в научных исследованиях и технологических установках в течение последних 50 лет [1, 2]. Первые модели разряда [3, 4] рассматривали емкостной разряд как конденсатор со сложным заполнением диэлектрической средой. Поскольку в слоях пространственного заряда, формирующихся на границах плазмы с электродами, плотность электронов мала, диэлектрическая проницаемость слоев принималась равной единице. В свою очередь диэлектрическая проницаемость плазмы при высоких плотностях плазмы отрицательна [5, 6]. Поэтому уже на ранних стадиях исследований было теоретически и экспериментально показано, что при низких давлениях газа, когда частота столкновений электронов ν с нейтралами много меньше частоты ω электромагнитного поля, поддерживающего ионизацию, емкостные разряды обладают резонансными свойствами, связанными с компенсацией емкостного импеданса слоев пространственного заряда и индуктивного импеданса, вносимого плазмой [3]. Резонанс наблюдался при выполнении условия ${{\omega _{{Pe}}^{2}} \mathord{\left/ {\vphantom {{\omega _{{Pe}}^{2}} {{{\omega }^{2}}}}} \right. \kern-0em} {{{\omega }^{2}}}} = {{2L} \mathord{\left/ {\vphantom {{2L} {2\Delta }}} \right. \kern-0em} {2\Delta }}$, где ωPe – плазменная частота, соответствующая электронной плотности n в разряде, 2L – межэлектродное расстояние, Δ – толщина слоя пространственного заряда на границе плазмы и электродов. Было показано [7], что резонансный характер импеданса разряда приводит к появлению гистерезиса на вольтамперных характеристиках разряда. Эти расчеты были подтверждены экспериментально [5] в условиях, когда размер разряда был меньше глубины проникновения поля в плазму, поэтому потенциальное приближение, использовавшееся в модели [3], давало правильные результаты. Типичная схема возбуждения разряда в экспериментальных установках приведена на рис. 1а. Разряд поддерживается между двумя пластинчатыми электродами 1 и 2, к которым от генератора через согласующую цепь Z подводится ВЧ-напряжение U. Плазма 3 создается между электродами внутри диэлектрической вакуумной камеры 5 и отделена от них слоями пространственного заряда.
Рис. 1.
Типичные схемы экспериментальных установок: простая исследовательская разрядная камера (a), частично (б) и полностью заполненная (в) разрядные камеры: 1, 2 – электроды, 3 – плазма, 4 – слои пространственного заряда между плазмой и стенкой (электродами), 2L – межэлектродное расстояние, d1, d2, d3 – толщины слоев пространственного заряда.
Дальнейшее развитие экспериментальных и технологических установок [8], сопровождающееся увеличением как их размеров, так и плотности плазмы, привели к тому, что межэлектродное расстояние 2L и размеры электродов R стали превышать глубину скин-слоя ${{{{\Delta }_{S}} = c} \mathord{\left/ {\vphantom {{{{\Delta }_{S}} = c} {{{\omega }_{{Pe}}}}}} \right. \kern-0em} {{{\omega }_{{Pe}}}}}$. Стремление увеличить плотность электронов в плазме потребовало увеличения частоты поля, поддерживающего плазму. Фирмой Applied Materials запатентованы установки, работающие на частотах от 50 до 800 МГц [9]. Экспериментально начались исследования разряда при частотах до 160 МГц [10–14]. В то же время расчеты проводятся в более широком диапазоне вплоть до 300 МГц [11, 15–21]. В этих условиях потенциальное приближение, при котором не учитывается скин-эффект, а размеры системы предполагаются малыми по сравнению с длинами волн, которые могут в ней распространяться, становится недостаточным. Скин-эффект должен был привести к спаду амплитуды электромагнитного поля при удалении от боковой поверхности плазмы и в ряде работ была обнаружена сильная радиальная неоднородность плазмы [22–24]. Теория разряда в условиях сильного скин-эффекта была построена в работе [25]. Первое известное авторам утверждение, что в высокочастотном разряде могут распространяться электромагнитные волны, которые должны играть существенную роль в высокочастотных разрядах появилось в 1988 г. в работе сотрудников Applied Materials [26]. Позже распространение поверхностных волн в емкостных высокочастотных разрядах было отмечено в экспериментах на частотах от 13.56 до 81 МГц [8, 24].
По существу, условия необходимости учета электродинамических эффектов были сформулированы в работе [27]. Авторы [27] отметили, что осевая пространственная неоднородность поля, которая не учитывается в потенциальном приближении, имеет место при плотностях электронов в разряде выше 1010 см–3, (на частоте 13.56 МГц и более высоких). Появления резонансов, связанных с кратностью длины поверхностной волны размерам системы согласно [27], можно ожидать при частотах выше 70 МГц.
Этот вопрос будет рассмотрен более подробно в разделе 4 данной статьи.
Давление газа в экспериментальных и технологических установках с ВЧ-разрядом как правило определяется реализуемым технологическим процессом. В процессах нанесения покрытий оно лежит от долей Торра до нескольких Торр [1, 2]. Повышение давления дает возможность увеличить скорость роста пленки, однако затрудняет получение однородной плазмы вследствие ослабления процессов переноса. В установках плазмохимического и ионного травления часто используется давление 0.1 Торр [1]. Тем не менее во множестве установок используются более низкие давления – 0.04 Торр [13], 0.02 Торр [28], 0.015 Торр [12] или даже 0.005 и 0.001 Торр [29].
Теоретический анализ распределения поля в разряде при высоких плотностях электронов и большом размере электродов показал: а) возбуждаемое в разряде поле может быть представлено в виде суммы поверхностных волн, распространяющихся вдоль границы плазма–слой пространственного заряда–электрод [27, 30–32] и высших не распространяющихся мод [27, 33, 34], сосредоточенных вблизи боковой границы плазмы; б) наличие резких пространственных неоднородностей плазмы в разрядной камере. Глубина проникновения высших мод в плазму при большом расстоянии между электродами была близка к глубине скин-слоя с/ωPe.
Дальнейшие теоретические исследования [34, 35] показали, что кроме симметричной поверхностной волны в плазме могут распространяться и антисимметричные волны, магнитное поле которых у противоположных электродов противофазно. В этих расчетах толщина слоев у различных электродов считалась равной, а влияние высших не распространяющихся мод поля не учитывалось. Более детальный анализ разрядов, поддерживаемых поверхностными волнами, показал, что при больших размерах плазмы должны были наблюдаться резонансы токов и напряжений, когда поперечные размеры плазмы кратны целому числу полуволн поверхностной волны (для плоской геометрии).
Существование поверхностных волн в линейном режиме впервые было обнаружено в экспериментах по измерению импеданса стержневых антенн, помещенных в плазменную среду [36–39] в лабораторной и ионосферной плазме задолго до того, как возник вопрос об их существовании в ВЧ-разрядах. Найденные в экспериментах резонансы удалось объяснить, как следствие распространение волн вдоль слоя пространственного заряда, формирующегося между антенной и ионосферой. Модель, основанная на представлении слоя как диэлектрика с проницаемостью равной 1, была развита в работе [39]. Сравнение теории и эксперимента показало их удовлетворительное согласие. Экспериментально наличие таких волн в технологических установках подтверждено в работах [40, 41].
В последние годы появились теоретические работы, посвященные численному моделированию этих процессов в ВЧ технологических установках [42–44], где был обнаружен эффект спонтанного нарушения симметрии разряда. В технологических установках низкого давления на него обратили внимание сравнительно недавно [45], хотя аналогичный процесс в СВЧ-разрядах низкого давления известен более 35 лет [46, 47].
Поставленная задача является достаточно объемной и ее решение не может быть полностью изложено в одной статье. В данной части работы авторы анализируют систему собственных волн в разрядной камере, токи, протекающие через электроды емкостного ВЧ-разряда, и напряжения между электродами, возникающие при возбуждении этих волн. Рассматривается простейшая модель разряда, в которой плазма расположена между двумя электродами и ограничена с боков диэлектрической стенкой (рис. 1а). В простейшей модели разряда с возбуждением только одной электромагнитной моды, рассчитан импеданс ВЧ-разряда и проведена оценка пределов ее применимости. Кроме того, проведен расчет импеданса по феноменологическим формулам, учитывающим возбуждение поверхностной волны и высших не распространяющихся волн, причем амплитуды волн будут определены из условий соответствия полученных решений потенциальному приближению в предельных случаях (малые и большие плотности электронов), когда последнее оказывается справедливым.
В последующих работах из данного цикла будет сформулирована математически строгая модель разряда в цилиндрической разрядной камере, выполненной из металла. В них приведены уравнения, которым удовлетворяют амплитуды поверхностной волны и высших типов мод, и даны их приближенные аналитические решения. Во второй статье рассмотрен разряд, полностью заполняющий разрядную камеру (рис. 1б), при синфазном и противофазном возбуждении. Проведено сравнение импеданса разряда, рассчитанного по аналитическим формулам и полученного при математическом моделировании задачи с помощью пакета моделирования COMSOL Multiphysics®.
В третьей работе цикла проведен аналитический расчет амплитуд различных мод поля, возбужденных в разряде и импеданса разряда для случая частично заполненной плазмой разрядной камеры (рис. 1в). Полученные результаты также сопоставлены с результатами численного моделирования.
Расчеты проводились для частот поддерживающего плазму поля от 13.56 МГц до 1 ГГц. Нижняя частота является типичной для плазмохимических установок, разработанных до 2000 г. Возможность наблюдения волновых эффектов при этих условиях была отмечена в работах [8, 17, 18]. Со стороны высоких частот наибольшая частота, при которой проводились расчеты, была ограничена 1000 МГц. Увеличение частоты по сравнению с упоминавшимися выше работами связано с прогрессом в изготовлении мощных СВЧ-транзисторов, позволяющих в настоящий момент создать генераторы с частотой 1 ГГц мощностью до 1 кВт.
В ряде установок сегодня используется и частота 2.45 ГГц, однако требование получения однородности плазмы больших размеров вызывает необходимость использования специфических систем возбуждения (например, многощелевой антенны [48], эта задача авторами в данной работе не рассматривается).
1. СИСТЕМА УРАВНЕНИЙ. ГРАНИЧНЫЕ УСЛОВИЯ И ПРЕДСТАВЛЕНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
Геометрия исследуемых установок показана на рис. 1. На рис. 1а представлен способ возбуждения плазмы синфазным полем, на рис. 1б – противофазным. На рис. 1в – изображена схема типичной технологической установки. Радиус электрода считается равным R, а высота камеры и расстояние между электродами равной 2L. Между плазмой 3 и электродами формируются слои пространственного заряда [3, 5], толщины которых считаются равными d1 и d2. Толщину слоя пространственного заряда между плазмой и боковой стенкой вакуумной камеры будем считать равной d3. Напряжение на выходе высокочастотного генератора – U, внутреннее сопротивление – Z (соответственно U1 и U2, и Z1 и Z2 в случае двух генераторов, рис. 1б, в). Толщина слоев пространственного заряда зависит от плотности электронов в плазме и падения потенциала на слое, поэтому она может быть функцией радиальной (для d1 и d2) и осевой (для d3) координат. Размер слоев пространственного заряда определяется родом газа, температурой электронов и падением напряжения на слое. Обычно при расчете толщины слоя предполагают, что ток ионов определяется критерием Бома [49] и пренебрегают плотностью электронов в слое, так как она экспоненциально убывает с увеличением потенциала. При нахождении потенциала слоя плотность ионов считают постоянной (матричная модель слоя), либо считают убывающей вследствие ускорения ионов электрическим полем. В последнем случае потенциал слоя подчиняется закону 3/2 Чайлда–Ленгмюра [50, 51], а толщина слоя определяется формулой
(1)
$d = \frac{{{{2}^{{{5 \mathord{\left/ {\vphantom {5 4}} \right. \kern-0em} 4}}}}}}{3}\sqrt {\frac{{{{\varepsilon }_{0}}{{T}_{e}}}}{{{{n}_{e}}{{e}^{2}}}}} {{\left( {\frac{{e{{\phi }_{S}}}}{{{{T}_{e}}}}} \right)}^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}}}}.$В данном выражении использованы обозначения: e – элементарный электрический заряд, ε0 – диэлектрическая проницаемость вакуума, ne, Te – плотность (в м–3) и температура (в энергетических единицах) электронов, ϕS – потенциал слоя.
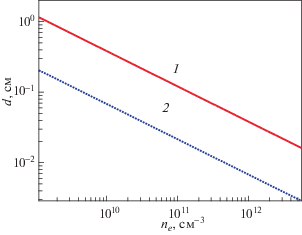
Разряды обычно используются в двух режимах: 1) режим минимальной энергии ионов (обычно реализуется в установках осаждения покрытий или химического травления); 2) режим физического распыления, для которого падение напряжения на слое стараются увеличить для увеличения коэффициента распыления. Например, в [29] в рабочем режиме смещение подложки относительно плазмы в зависимости от режима разряда изменялось в пределах 200–400 В. Аналогичные режимы часто используются при физическом травлении кремния и оксида кремния [1, 8]. Измерения напряжения на слое в разрядах при давлении аргона 0.015 Тор и ионном токе на стенку 0.03–0.3 мА/см2 (это примерно соответствует области плотностей электронов на границе плазмы и слоя от 5 × 108 до 1010 см–3) при частотах от 13.56 до 81.36 МГц в работах [12, 52] показали, что оно лежит в пределах от 30 до 200 В (напряжение увеличивается с ростом тока и уменьшением частоты). Зависимость толщины слоя от плотности электронов для аргона, рассчитанная по приведенной выше формуле, представлена на рис. 2 [53–56]. Плотность электронов на границе плазмы и слоя может быть существенно ниже, чем в центре вакуумной камеры, и этот эффект также должен учитываться при расчетах характеристик реального разряда.
Рис. 2.
Толщина слоя как функция плотности электронов в аргоновой плазме: 1 – напряжение на слое 300 В, 2 – напряжение на слое 30 В.
Альтернативный подход к расчету толщины слоев предложен Либерманом. Им в работах [1, 57, 58] в предположении малости тока смещения и питания разряда синусоидальным током была аналитически решена самосогласованная задача движения электронов в слое в бесстолкновительном и столкновительном режимах. При этом размер слоя оказывается близок к амплитуде колебаний электронов в слое. Такой подход обычно приводит к качественно другой зависимости толщины слоя от плотности электронов и его следует использовать при построении самосогласованной модели разряда. Попытки аналитического описания слоя пространственного заряда, сформулированные в [57, 58], получили дальнейшее развитие в [59]. В данной работе, посвященной исследованию исключительно электродинамических свойств разряда, размер слоя считается заданным.
Газовый разряд, в условиях когда длина свободного пробега электронов меньше характерных размеров разрядной камеры, описывается с помощью системы уравнений баланса частиц, баланса энергии электронов и уравнений Максвелла [60–62]. При описании электродинамических свойств плазмы движением ионов пренебрегается, поэтому как в плазме, так и в слоях пространственного заряда, частота поля должна быть много больше ионной ленгмюровской частоты ωLi, ${{\omega }^{2}} \gg \omega _{{Li}}^{2}$, где ${{\omega }_{{Li}}} = \sqrt {{{{{n}_{e}}{{e}^{2}}} \mathord{\left/ {\vphantom {{{{n}_{e}}{{e}^{2}}} {{{\varepsilon }_{0}}M}}} \right. \kern-0em} {{{\varepsilon }_{0}}M}}} $ = $210\sqrt {{{{{n}_{e}}({\text{с}}{{{\text{м}}}^{{ - 3}}})} \mathord{\left/ {\vphantom {{{{n}_{e}}({\text{с}}{{{\text{м}}}^{{ - 3}}})} A}} \right. \kern-0em} A}} $, ne – плотность электронов, e – элементарный электрический заряд, M – масса иона, А – атомный вес плазмообразующего газа в а. е. Для аргона и частоты генератора 13.56 МГц равенство частоты поля и ионной ленгмюровской частоты соответствует плотности электронов на границе плазмы и слоя 6.58 × 1012 см–3. Кроме того, существование поверхностных волн предполагает, что частота поля ω много больше частоты столкновений электронов, $~{{\omega }^{2}} \gg {{\nu }^{2}}$.
В данной работе при аналитическом анализе электродинамических свойств разряда, плотность электронов в плазме и их частота столкновений считаются заданными, а для расчета диэлектрической проницаемости используется приближение холодной плазмы. Это означает, что пренебрегается формированием пучков заряженных частиц в приграничной области плазмы вследствие аномального скин-эффекта [63], который может иметь место в индуктивном ВЧ-разряде, и стохастическим ускорением электронов в слое пространственного заряда [64], наблюдающимся при низких давлениях газа в емкостном разряде. Оба этих эффекта рассматриваются в приближении одномерно неоднородной плазмы, когда отсутствие радиальной неоднородности поля понижает размерность и сложность задачи, а также необходимый объем вычислений при численном моделировании.
Аномальный скин-эффект приводит к формированию неэкспоненциально убывающего хвоста (пучков) на функции распределения [65]), изменению глубины проникновения поля в плазму и пространственного распределения поглощаемой в плазме энергии [66, 67]. Возможно появление в пространстве областей, где электроны возвращают полю энергию, полученную в других областях [68–71]. В качестве одной из последних аналитических работ по этой проблеме упомянем работу [72].
Искажение функции распределения при взаимодействии со слоем пространственного заряда рассмотрено в работе [73], см. также обзор [74]. С точки зрения электродинамики, отвлекаясь от возможного искажения профиля плотности плазмы вследствие неоднородности ионизации, стохастическое поглощение энергии может быть описано введением эффективной частоты столкновений. Хотя величина самой частоты столкновений [75–77] и даже наличие стохастического поглощения при определенных пространственных профилях плазмы является предметом дискуссии [78, 79].
Рассматриваемые эффекты приводят к двум главным следствиям для разрядов в быстропеременном поле. В слабых полях наблюдается изменение импеданса [6] границы плазмы. Возникающее бесстолкновительное поглощение может быть описано с помощью эффективной частоты столкновений как в индуктивном [80, 81], так и емкостном [4] разрядах.
Энергия, необходимая для ионизации, набирается в данном случае электронами постепенно, в процессе диффузии электронов по оси энергий. При этом пространственно-временное распределение электронов по энергиям должно стать более однородным вследствие процессов переноса.
В режиме сильных полей необходимая для инициации неупругих процессов (возбуждения или ионизации) энергия может быть получена в процессе однократного нахождения частицы в области неоднородности (с учетом той энергии, которая у нее была), частоты этих процессов начинают зависеть от пространственной координаты и фазы ВЧ-поля. Эти эффекты были обнаружены [82–85] применительно к экспериментам и к численному моделированию нестационарных процессов в плазме методом частиц (в одномерной задаче).
При учете электродинамических эффектов и поддержания разряда поверхностной волной оба рассмотренных выше эффекта могут играть существенную роль. Они являются следствием нарушения адиабатичности движения электронов в неоднородном электрическом поле. Скин-эффект будет аномальным, если время пребывания электронов в скин-слое холодной плазмы оказывается меньше обратной частоты поля ${{\omega c} \mathord{\left/ {\vphantom {{\omega c} {\left( {{{\omega }_{{Le}}}{{V}_{{Te}}}} \right)}}} \right. \kern-0em} {\left( {{{\omega }_{{Le}}}{{V}_{{Te}}}} \right)}} < 1$ и меньше времени столкновений $\nu {c \mathord{\left/ {\vphantom {c {\left( {{{\omega }_{{Le}}}{{V}_{{Te}}}} \right)}}} \right. \kern-0em} {\left( {{{\omega }_{{Le}}}{{V}_{{Te}}}} \right)}} < 1$. Здесь ${{\omega }_{{Le}}} = \sqrt {{{{{n}_{e}}{{e}^{2}}} \mathord{\left/ {\vphantom {{{{n}_{e}}{{e}^{2}}} {{{\varepsilon }_{0}}m}}} \right. \kern-0em} {{{\varepsilon }_{0}}m}}} $ – ленгмюровская частота электронов, ${{V}_{{Te}}} = \sqrt {{{{{T}_{e}}} \mathord{\left/ {\vphantom {{{{T}_{e}}} m}} \right. \kern-0em} m}} $ – тепловая скорость электронов, m – их масса. В этом случае нельзя пользоваться выражением для диэлектрической проницаемости в приближении холодной плазмы [6]. Кроме изменения электродинамических свойств плазмы, уход в область аномального скин-эффекта означает обсужденное выше формирование в граничных областях плазмы на функции распределения пучков электронов, распространяющихся вдоль границы разряда.
При учете электродинамических явлений характерная длина изменения поля может быть разной в разных частях разряда. Поэтому могут быть области, в которых достаточно использовать гидродинамическое приближение, и области, где оно недостаточно и нужно учитывать нелокальные эффекты. Проведем соответствующие оценки.
Для высших мод характерная длина изменения поля есть L/N, где N – номер моды. Время пребывания электрона в области высшей моды τ = L/NVTe. Таким образом, нарушение адиабатичности движения электрона в поле высшей моды есть $\omega ,\nu < N{{{{V}_{{Te}}}} \mathord{\left/ {\vphantom {{{{V}_{{Te}}}} L}} \right. \kern-0em} L} \approx 2 \cdot N \times {{10}^{7}}$ с–1. Для L равной 4 см и тепловой скорости электронов 108 см/с, и первой моды получим, что частота поля должна быть меньше 3 МГц. Для высших мод граница по частотам будет увеличиваться с увеличением номера моды. Для поверхностной волны мы должны взять в качестве характерного размера длину волны λ0± (если она меньше глубины скин-слоя) или глубину скин-слоя в холодной плазме. Таким образом, условие имеет вид $\omega ,\nu < $ $ < {{V}_{{Te}}}\sqrt {{{{{4{{\pi }^{2}}} \mathord{\left/ {\vphantom {{4{{\pi }^{2}}} {\lambda _{{0 \pm }}^{2}}}} \right. \kern-0em} {\lambda _{{0 \pm }}^{2}}} + \omega _{{Pe}}^{2}} \mathord{\left/ {\vphantom {{{{4{{\pi }^{2}}} \mathord{\left/ {\vphantom {{4{{\pi }^{2}}} {\lambda _{{0 \pm }}^{2}}}} \right. \kern-0em} {\lambda _{{0 \pm }}^{2}}} + \omega _{{Pe}}^{2}} {{{c}^{2}}}}} \right. \kern-0em} {{{c}^{2}}}}} $. Если исходить из длины поверхностной волны и плотности электронов при том же значении тепловой скорости, получим $\omega ,\nu $ < $\sqrt {{{3.95 \times {{{10}}^{{17}}}} \mathord{\left/ {\vphantom {{3.95 \times {{{10}}^{{17}}}} {\lambda _{{0 \pm }}^{2}({\text{см}})}}} \right. \kern-0em} {\lambda _{{0 \pm }}^{2}({\text{см}})}} + 3.54 \times {{{10}}^{4}}{{n}_{e}}({\text{с}}{{{\text{м}}}^{{ - 3}}})} $. Для плотности электронов 1010 см–3 и длины поверхностной волны 30 см получим $\omega ,\nu < 3 \times {{10}^{7}}$ с–1. Таким образом, в рассматриваемых в данной статье условиях можно пользоваться приближением холодной плазмы, кроме, возможно, области, где большую амплитуду имеют высшие (3, 4 и выше) моды не распространяющихся волн. Тем не менее при низких частотах электромагнитного поля существуют области параметров разряда, когда необходимо учитывать как электродинамические, так и кинетические эффекты.
Таким образом существует широкий диапазон условий в разряде, когда можно ограничиться приближением холодной плазмы. Кинетическое приближение необходимо использовать только для высших мод плазмы выше пятой. Однако для этой моды будет несправедливым и рассмотрение слоя пространственного заряда в виде области пространства с диэлектрической проницаемостью, равной единице.
Обсудим кратко теперь возможное влияние неоднородности плазмы на рассматриваемые эффекты. Плотность плазмы у границы в реальном разряде меньше плотности в центре плазмы (а также и средней плотности по сечению), а распространение поверхностной волны определяется средней плотностью (при pL < 1, p – глубина проникновения поверхностной волны в плазму) или плотностью у границы плазмы (при pL > 1). Поэтому положение резонансов будет сдвигаться в область более низких значений плотности электронов. В целом неоднородность плазмы приводит к появлению следующих эффектов: 1) расширению области наблюдения рассматриваемых в статье эффектов на область более низких частот высокочастотного поля, меньших размеров плазмы или более высоких плотностей электронов в центре плазмы; 2) модификации свойств плазмы при плотностях, близких критической, в силу появления области резонансного усиления поля у границ. Влияние этого эффекта на импеданс СВЧ-разряда в волноводе экспериментально исследовалось в работе [86]. В данном цикле статей авторы пожертвовали возможностью учесть неоднородность плазмы при численном моделировании в пользу более корректного сравнения результатов численного и аналитического (хотя и приближенного) расчетов.
Уравнения Максвелла (в системе СИ) удобно записать так, чтобы выделить в явном виде волновое сопротивление вакуума ${{\rho }_{0}} = \sqrt {{{{{\mu }_{0}}} \mathord{\left/ {\vphantom {{{{\mu }_{0}}} {{{\varepsilon }_{0}}}}} \right. \kern-0em} {{{\varepsilon }_{0}}}}} $
(2)
$\left[ {\nabla \times {\mathbf{H}}} \right] + ik\sqrt {\frac{{{{\varepsilon }_{0}}}}{{{{\mu }_{0}}}}} \varepsilon {\mathbf{E}} = 0,\quad \left[ {\nabla \times {\mathbf{E}}} \right] - ik\sqrt {\frac{{{{\mu }_{0}}}}{{{{\varepsilon }_{0}}}}} {\mathbf{H}} = 0.$Здесь k = ω/c, $c = {{\left( {\sqrt {{{\varepsilon }_{0}}{{\mu }_{0}}} } \right)}^{{ - 1}}}$ – скорость света; ε0, µ0 – диэлектрическая и магнитная проницаемости вакуума, E(r), H(r) – комплексные напряженности электрического и магнитного полей, временная зависимость выбрана в виде exp(–iωt); ε – относительная диэлектрическая проницаемость среды. В слоях пространственного заряда будем считать $\varepsilon = 1$, в плазме $\varepsilon = {{\varepsilon }_{P}}$ = $1 - {{{{n}_{e}}} \mathord{\left/ {\vphantom {{{{n}_{e}}} {{{n}_{C}}\left( {1 + i{\nu \mathord{\left/ {\vphantom {\nu \omega }} \right. \kern-0em} \omega }} \right)}}} \right. \kern-0em} {{{n}_{C}}\left( {1 + i{\nu \mathord{\left/ {\vphantom {\nu \omega }} \right. \kern-0em} \omega }} \right)}}$. Поскольку основное внимание уделяется электродинамическим особенностям задачи, воспользуемся наиболее простой кинетической моделью плазмы. На стенках рабочей камеры тангенциальная составляющая электрического поля равнялась нулю
При плотностях электронов в плазме, превышающих удвоенную критическую, в соответствии с результатами [27, 33, 35] осевое и азимутальное электромагнитные поля в разрядной камере могут быть представлены в виде суммы собственных функций электромагнитных операторов (2), содержащих две поверхностных волны (слагаемые с коэффициентами A0±, постоянные распространения h0±, собственные функции $\{ {{{\mathbf{e}}}_{{0 \pm }}}({{h}_{{0 \pm }}}r,z),{{{\mathbf{h}}}_{{0 \pm }}}({{h}_{{0 \pm }}}r,z)\} $) и не распространяющиеся волны E- и H-типа (коэффициенты An± и Bn±, постоянные затухания $\tilde {h}_{{n \pm }}^{E}$ и $\tilde {h}_{{n \pm }}^{H}$, собственные функции $\{ {\mathbf{e}}_{{n \pm }}^{E}(\tilde {h}_{{n \pm }}^{E}r,z),{\mathbf{h}}_{{n \pm }}^{E}(\tilde {h}_{{n \pm }}^{E}r,z)\} $ и $\{ {\mathbf{e}}_{{n \pm }}^{H}(\tilde {h}_{{n \pm }}^{H}r,z),{\mathbf{h}}_{{n \pm }}^{H}(\tilde {h}_{{n \pm }}^{H}r,z)\} $) [60–62]
(4)
$\begin{gathered} \, + {{A}_{{0 - }}}\left( {\begin{array}{*{20}{c}} {{{{\mathbf{e}}}_{{0 - }}}\left( {{{h}_{{0 - }}}r,z} \right)} \\ {{{{\mathbf{h}}}_{{0 - }}}\left( {{{h}_{{0 - }}}r,z} \right)} \end{array}} \right)\exp \left( { - i\omega t} \right) + \\ \, + \sum\limits_{ \pm = + , - } {\sum\limits_{n = 1}^\infty {{{A}_{{n \pm }}}} } \left( {\begin{array}{*{20}{c}} {{\mathbf{e}}_{{n \pm }}^{E}\left( {\tilde {h}_{{n \pm }}^{E}r,z} \right)} \\ {{\mathbf{h}}_{{n \pm }}^{E}\left( {\tilde {h}_{{n \pm }}^{E}r,z} \right)} \end{array}} \right)\exp \left( { - i\omega t} \right) + \\ \end{gathered} $При меньших плотностях электронов (ne < 2nC) поверхностные волны отсутствуют. Однако все последующие формулы остаются справедливыми (при учете A0± = 0), только нужно принять во внимание, что первая четная мода при этих условиях представляет собой распространяющуюся (при ne < nC) квази-TEM волну (см. подробнее п. 4), нечетные распространяющиеся волны отсутствуют. При записи (4) в силу симметрии задачи мы ограничились только волнами без азимутальной зависимости (азимутальное волновое число m = 0). Расчет пространственного распределения полей собственных функций наиболее удобно проводить с помощью z-компонент электромагнитного поля, так как в однородной плазме уравнения для этих компонент сводятся к уравнениям Бесселя. В общем случае решение для поверхностных волн (и для квази-ТЕМ волны при ne < nC) может быть записано в виде
(5)
$\begin{gathered} {\mathbf{e}}_{{n \pm z}}^{E}(\tilde {h}_{{n \pm }}^{E}r,z)\exp ( - i\omega t) = \\ \, = {{{\mathbf{z}}}_{0}}{{I}_{0}}(\tilde {h}_{{n \pm }}^{E}r){{f}_{{n \pm }}}\left( z \right)\exp ( - i\omega t), \\ {\mathbf{h}}_{{n \pm z}}^{H}(r,z)\exp ( - i\omega t) = {{{\mathbf{z}}}_{0}}{{I}_{0}}(\tilde {h}_{{n \pm }}^{H}r){{g}_{{n \pm }}}(z)\exp ( - i\omega t). \\ \end{gathered} $В выражениях (4), (5) ${{{\mathbf{z}}}_{0}}$ – единичный орт, направленный вдоль оси z. Поперечные компоненты электромагнитного поля собственных функций могут быть рассчитаны через z-компоненты напряженностей электрического Ez и магнитного Hz полей по формулам [60, 61]
(6)
$\begin{gathered} {{{\mathbf{h}}}_{t}} = {{\left( {{{k}^{2}}\varepsilon + \frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}}} \right)}^{{ - 1}}}\left\{ {ik\sqrt {\frac{{{{\varepsilon }_{0}}}}{{{{\mu }_{0}}}}} \varepsilon \left[ {\nabla \times {{{\mathbf{e}}}_{z}}{{E}_{z}}} \right] + {{\nabla }_{t}}\frac{{\partial {{H}_{z}}}}{{\partial z}}} \right\}, \\ {{{\mathbf{e}}}_{t}} = {{\left( {{{k}^{2}}\varepsilon + \frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}}} \right)}^{{ - 1}}}\left\{ {{{\nabla }_{t}}\frac{{\partial {{E}_{z}}}}{{\partial z}} - ik\sqrt {\frac{{{{\mu }_{0}}}}{{{{\varepsilon }_{0}}}}} \left[ {\nabla \times {{{\mathbf{e}}}_{z}}{{H}_{z}}} \right]} \right\}. \\ \end{gathered} $При m = 0 E- и Н-моды возбуждаются независимо друг от друга даже при осевой неоднородности волноведущей структуры. В индуктивных ВЧ‑разрядах преобладают H-моды. Хотя полностью исключить Е-моды не удается, но их амплитуда обычно существенно ниже, чем амплитуда H-мод. Поэтому, если не изучаются комбинированные разряды, E-моды могут рассматриваться как паразитные. В емкостных ВЧ-разрядах в разрядных камерах, изображенных на рис. 1, H-моды не возбуждаются, поэтому далее мы ограничимся рассмотрением только волн Е-типа. Далее будем считать Bn± ≡ 0, а в формулах исключим верхний индекс E в обозначениях. Формулы для электромагнитных полей собственных функций, из которых легко определяются осевые зависимости $f\left( z \right),$ $g\left( z \right)$ приведены в Приложении 1, ${{\nabla }_{t}} = {{{\mathbf{r}}}_{0}}{\partial \mathord{\left/ {\vphantom {\partial {\partial r}}} \right. \kern-0em} {\partial r}} + {{\varphi }_{0}}{{r}^{{ - 1}}}{\partial \mathord{\left/ {\vphantom {\partial {\partial \varphi }}} \right. \kern-0em} {\partial \varphi }}$, ${{{\mathbf{r}}}_{0}},\;{{\varphi }_{0}}$ – единичные векторы вдоль радиальной и азимутальной осей координат. Расчет собственных значений будет проведен в следующем разделе. Выражения для поля поверхностной волны, высших мод и волноводных мод приведены в разделе 4.
Полученные формулы дают возможность провести расчет характеристик разряда. Если поле в разряде (r < R) представлено в виде собственных функций (4), то напряжение на разряде U(R) и токи верхнего ${{i}^{{\left( 1 \right)}}}$ и нижнего ${{i}^{{\left( 2 \right)}}}$ электродов в произвольной точке r цилиндрической поверхности при r < R могут быть представлены в виде
(7)
$\begin{gathered} {{i}^{{\left( 1 \right)}}}\left( r \right) = {{A}_{{0 + }}}i_{{0 + }}^{{\left( 1 \right)}}\left( r \right) + {{A}_{{0 - }}}i_{{0 - }}^{{\left( 1 \right)}}\left( r \right) + \\ \, + \sum\limits_{n = 1}^\infty {{{A}_{{n + }}}} i_{{n + }}^{{\left( 1 \right)}}\left( r \right) + \sum\limits_{n = 1}^\infty {{{A}_{{n - }}}} i_{{n - }}^{{\left( 1 \right)}}\left( r \right), \\ \end{gathered} $Определение тока разряда при использовании известных коэффициентов разложения в формуле (6) и токов ${{i}_{{n \pm }}}$, вносимых каждой из собственных волн, не так однозначно. В силу граничных условий для магнитного поля, ток каждой из волн, протекающий на электрод через цилиндрическую поверхность радиуса r, равен
(8)
$\begin{gathered} i_{{n \pm }}^{{\left( 1 \right)}}\left( r \right) = 2\pi r{{h}_{{\varphi n \pm }}}\left( {r,L} \right), \\ i_{{n \pm }}^{{\left( 2 \right)}}\left( r \right) = 2\pi r{{h}_{{\varphi n \pm }}}\left( {r, - L} \right). \\ \end{gathered} $При симметричном возбуждении разряда (нет тока на боковую стенку) $I = {{i}^{{\left( 2 \right)}}}\left( r \right) = {{i}^{{\left( 1 \right)}}}\left( r \right)$. Если размер электрода равен размеру плазмы, то импеданс разряда следует из формулы (7) с учетом поля высших мод, амплитуды которых необходимо будет рассчитать. Из (7), (8), опуская верхние индексы (1), (2), получим
(9)
$\frac{{U\left( r \right)}}{{I\left( r \right)}} \equiv Z\left( r \right) = \frac{{{{A}_{{0 + }}}{{U}_{ + }}\left( r \right) + {{A}_{{0 - }}}{{U}_{ - }}\left( r \right) + \sum\limits_{n = 1}^\infty {{{A}_{{n + }}}} {{U}_{{n + }}}\left( r \right) + \sum\limits_{n = 1}^\infty {{{A}_{{n - }}}} {{U}_{{n - }}}\left( r \right)}}{{{{A}_{{0 + }}}{{i}_{{0 + }}}\left( {r,L} \right) + {{A}_{{0 - }}}{{i}_{{0 - }}}\left( {r,L} \right) + \sum\limits_{n = 1}^\infty {{{A}_{{n + }}}} {{i}_{{n + }}}\left( {r,L} \right) + \sum\limits_{n = 1}^\infty {{{A}_{{n - }}}} {{U}_{{n - }}}\left( r \right)}},$Если размер электрода превышает размер плазмы, то при R > r поле можно представить в виде собственных волн пустого волновода, составленного их двух плоскостей. Поскольку на некотором расстоянии от плазмы высшие моды этого волновода затухают, то их амплитуды будут равны нулю, и ток внешней цепи, подводимый к электроду, будет определяться только полем волны ТЕМ, для которой токи верхнего и нижнего электрода будут равны. Этот ток может быть рассчитан по формуле
(10)
$\begin{gathered} {{I}_{{TEM}}}\left( r \right) = \frac{{2\pi r}}{{2L}}\left( {{{A}_{{0 + }}}\int\limits_{ - L}^L {{{h}_{{0 + }}}} \left( {r,z} \right)dz + } \right. \\ \left. {\, + \sum\limits_{n = 1}^\infty {{{A}_{{n + }}}} \int\limits_{ - L}^L {{{h}_{{n + }}}} \left( {r,z} \right)dz} \right). \\ \end{gathered} $Таким образом, импеданс разряда в данном случае будет определяться формулой
(11)
$\frac{{U\left( r \right)}}{{I\left( r \right)}} \equiv Z\left( r \right) = \frac{{{{A}_{{0 + }}}{{U}_{ + }}\left( r \right) + {{A}_{{0 - }}}{{U}_{ - }}\left( r \right) + \sum\limits_{n = 1}^\infty {{{A}_{{n + }}}} {{U}_{{n + }}}\left( r \right) + \sum\limits_{n = 1}^\infty {{{A}_{{n - }}}} {{U}_{{n - }}}\left( r \right)}}{{{{A}_{{0 + }}}{{{\tilde {i}}}_{{0 + }}}\left( {r,L} \right) + {{A}_{{0 - }}}{{{\tilde {i}}}_{{0 - }}}\left( {r,L} \right) + \sum\limits_{n = 1}^\infty {{{A}_{{n + }}}} {{{\tilde {i}}}_{{n + }}}\left( {r,L} \right) + \sum\limits_{n = 1}^\infty {{{A}_{{n - }}}} {{{\tilde {i}}}_{{n - }}}\left( r \right)}},$Резонанс токов соответствует обращению в нуль знаменателя (9), либо (11), а резонанс напряжений – числителя. Как следует из полученных формул, импеданс разряда в общем случае будет близок к волновому сопротивлению одной из мод только тогда, когда амплитуда одной из волн (например, поверхностной или первой не распространяющейся моды) преобладает. Для расчета амплитуды всех собственных волн необходимо решить уравнения для поля в разрядной камере. В статье II данного цикла будет проведено это решение для цилиндрической разрядной камеры полностью заполненной плазмой (рис. 1в), а в статье III – для камеры, частично заполненной плазмой (рис. 1б).
2. ДИСПЕРСИЯ ПОВЕРХНОСТНЫХ И НЕ РАСПРОСТРАНЯЮЩИХСЯ ВОЛН. ЧИСЛЕННЫЙ РАСЧЕТ И ПРИБЛИЖЕННЫЕ ВЫРАЖЕНИЯ
Дисперсионное уравнение для E-волн, которые поддерживают разряды емкостного типа в геометрии рис. 1 (см. Приложение 1), имеет вид
где(12)
$\begin{gathered} \left. {\mathop \times \limits_{_{{_{{_{{_{{}}}}}}}}} \;{\text{th}}\left( {\sqrt {{{h}^{2}} - {{k}^{2}}{{\varepsilon }_{P}}} {{L}_{2}}} \right){\text{th}}\left( {\sqrt {{{h}^{2}} - {{k}^{2}}{{\varepsilon }_{2}}} {{d}_{2}}} \right)} \right) + \\ \, + \left( {\frac{{{{\varepsilon }_{P}}\sqrt {{{h}^{2}} - {{k}^{2}}{{\varepsilon }_{2}}} }}{{{{\varepsilon }_{2}}\sqrt {{{h}^{2}} - {{k}^{2}}{{\varepsilon }_{P}}} }}{\text{th}}\left( {\sqrt {{{h}^{2}} - {{k}^{2}}{{\varepsilon }_{2}}} {{d}_{2}}} \right) + } \right. \\ \end{gathered} $(13)
$\, \times \left. {\operatorname{th} \left( {\sqrt {\frac{{{{{\tilde {p}}}^{2}}}}{{{{k}^{2}}}} - \left( {{{\varepsilon }_{2}} - {{\varepsilon }_{p}}} \right)} k{{d}_{2}}} \right)} \right) + $В приближении узких слоев пространственного заряда, которое обычно справедливо для поверхностных волн и нескольких не распространяющихся волн с малыми номерами, уравнение (13) может быть упрощено и сведено к виду
В давнейшем мы будем предполагать, что диэлектрические проницаемости слоев пространственного заряда равны, ε1 = ε2. Тогда последнее уравнение позволяет выразить диэлектрическую проницаемость как функцию $\tilde {p}$, (либо p)
(14)
$\varepsilon _{P}^{2} - {{\varepsilon }_{P}}\left( {{{\varepsilon }_{1}} - \frac{{{{{\tilde {p}}}^{2}}}}{{{{k}^{2}}}}} \right) - \frac{{\tilde {p}{{\varepsilon }_{1}}}}{{2{{k}^{2}}}}\left( {\frac{1}{{{{d}_{1}}}} + \frac{1}{{{{d}_{2}}}}} \right){{\tilde {Q}}_{{1,2}}} = 0,$(15)
$\begin{gathered} {{{\tilde {Q}}}_{{1,2}}} = \frac{1}{2}\left( {\mathop {\left( {\operatorname{th} \left( {\tilde {p}{{L}_{2}}} \right) + \operatorname{cth} \left( {\tilde {p}{{L}_{2}}} \right)} \right) \pm }\limits_{_{{_{{}}}}}^{^{{^{{}}}}} } \right. \\ \left. {\, \pm \sqrt {{{{\left( {\operatorname{th} \left( {\tilde {p}{{L}_{2}}} \right) - \operatorname{cth} \left( {\tilde {p}{{L}_{2}}} \right)} \right)}}^{2}} + 4{{{\left( {\frac{{{{d}_{1}} - {{d}_{2}}}}{{{{d}_{1}} + {{d}_{2}}}}} \right)}}^{2}}} } \right). \\ \end{gathered} $Поскольку согласно (15) существует два значения функции ${{\tilde {Q}}_{{1,2}}}$, для 4 корней уравнения (14) имеем
(16)
$\begin{gathered} {{\varepsilon }_{{P1,2,3,4}}} = \frac{1}{2}\left( {\mathop {\left( {{{\varepsilon }_{1}} - \frac{{{{{\tilde {p}}}^{2}}}}{{{{k}^{2}}}}} \right) \pm }\limits_{}^{} } \right. \\ \left. {\, \pm \sqrt {{{{\left( {{{\varepsilon }_{1}} - \frac{{{{{\tilde {p}}}^{2}}}}{{{{k}^{2}}}}} \right)}}^{2}} + \frac{{2\tilde {p}{{\varepsilon }_{1}}}}{{{{k}^{2}}}}\left( {\frac{1}{{{{d}_{1}}}} + \frac{1}{{{{d}_{2}}}}} \right){{{\tilde {Q}}}_{{1,2}}}} } \right). \\ \end{gathered} $При записи этих соотношений учтено ReεP < 1, поэтому для не распространяющихся мод физически реализуются только решения с отрицательным знаком перед корнем. Для поверхностных волн имеют смысл оба решения. Равенство нулю подкоренного выражения в уравнении (16) соответствует максимальной глубине проникновения поля поверхностной волны в плазму. Формулы (14)–(16) позволяют вычислить аналитически затухание волн в среде с поглощением с помощью теории возмущений
(17)
$\begin{gathered} \Delta \tilde {p} = 2{{\left( { - \frac{{2\tilde {p}}}{{{{k}^{2}}}} \pm \frac{{2\left( {{{\varepsilon }_{1}} - {{{\tilde {p}}}^{2}}{\text{/}}{{k}^{2}}} \right)(2\tilde {p}{\text{/}}{{k}^{2}}) + (2\tilde {p}{{\varepsilon }_{1}}/{{k}^{2}})\left( {d_{1}^{{ - 1}} + d_{2}^{{ - 1}}} \right)\left( {{{{\tilde {Q}}}_{{1,2}}} + \tilde {p}\Delta {{{\tilde {Q}}}_{{1,2}}}{\text{/}}\Delta \tilde {p}} \right)}}{{2\sqrt {{{{\left( {{{\varepsilon }_{1}} - {{{\tilde {p}}}^{2}}{\text{/}}{{k}^{2}}} \right)}}^{2}} + (2\tilde {p}{{\varepsilon }_{1}}/{{k}^{2}})\left( {d_{1}^{{ - 1}} + d_{2}^{{ - 1}}} \right){{{\tilde {Q}}}_{{1,2}}}} }}} \right)}^{{ - 1}}}\Delta {{\varepsilon }_{{P1,2,3,4}}}, \\ \frac{{\Delta {{{\tilde {Q}}}_{{1,2}}}}}{{\Delta \tilde {p}}} = \frac{1}{2}{{L}_{2}}\left( {\left( {\frac{1}{{{{{\cosh }}^{2}}\left( {\tilde {p}{{L}_{2}}} \right)}} - \frac{1}{{{{{\sinh }}^{2}}\left( {\tilde {p}{{L}_{2}}} \right)}}} \right) \pm \frac{{\left( {\operatorname{th} \left( {\tilde {p}{{L}_{2}}} \right) - \operatorname{cth} \left( {\tilde {p}{{L}_{2}}} \right)} \right)\left( {{{{\cosh }}^{{ - 2}}}\left( {\tilde {p}{{L}_{2}}} \right) + {{{\sinh }}^{{ - 2}}}\left( {\tilde {p}{{L}_{2}}} \right)} \right)}}{{\sqrt {{{{\left( {\operatorname{th} \left( {\tilde {p}{{L}_{2}}} \right) - \operatorname{cth} \left( {\tilde {p}{{L}_{2}}} \right)} \right)}}^{2}} + 4{{{\left( {({{d}_{1}} - {{d}_{2}})/({{d}_{1}} + {{d}_{2}})} \right)}}^{2}}} }}} \right). \\ \end{gathered} $Любопытно, что в точках ветвления (нули подкоренных выражений в (16)) поправка к поперечной постоянной распространения в плазме будет равна нулю. Это не означает тем не менее равенства нулю поправки к постоянной распространения волны h, так как ${{h}^{2}} = {{k}^{2}}{{\varepsilon }_{P}} - {{p}^{2}}$ и $\Delta h = {{\left( {{{k}^{2}}\Delta {{\varepsilon }_{P}} - 2p\Delta p} \right)} \mathord{\left/ {\vphantom {{\left( {{{k}^{2}}\Delta {{\varepsilon }_{P}} - 2p\Delta p} \right)} {2h}}} \right. \kern-0em} {2h}}$.
Квадрат постоянной распространения поверхностной волны (1) и не распространяющихся мод (2, 3, 4) для частоты 135.6 МГц и постоянной толщины слоев 3 мм приведена на рис. 3. Зависимости ${{{{h}^{2}}} \mathord{\left/ {\vphantom {{{{h}^{2}}} {{{k}^{2}}}}} \right. \kern-0em} {{{k}^{2}}}}\left( {{{n}_{e}}} \right)$ представляют собой границу между темной и светлой областями. Из рисунка следует, что поверхностные волны имеют длину волны существенно ниже, чем длина волны в вакууме [30]. На дисперсионных кривых можно выделить три характерных области. При высоких и при относительно низких плотностях электронов, когда плотность электронов близка к удвоенной критической, поверхностные волны у разных границ не взаимодействуют друг с другом. Их дисперсия может быть получена из уравнений (10), если приравнять выражение $\operatorname{th} \left( {\sqrt {{{h}^{2}} - {{k}^{2}}{{\varepsilon }_{P}}} {{L}_{2}}} \right)$ единице.
Рис. 3.
Квадрат безразмерной постоянной распространения h2/k2 поверхностных волн 1 и не распространяющихся волн 2, 3, 4 как функция плотности электронов в симметричном разряде. Зависимости представляют собой границу между темной и светлой областями; толщина слоев пространственного заряда – 3 мм; частота поля – 135.6 МГц; четная поверхностная волна (a), нечетная (б); толщина плазмы – 8 см.
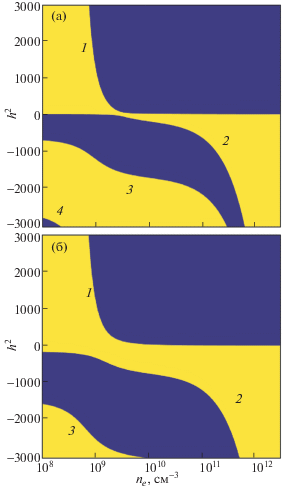
В области положительных диэлектрических проницаемостей существует четная распространяющаяся волна (при ne → 0 это волна типа ТЕМ), которая с ростом плотности электронов при ne > nC переходит в не распространяющуюся. Нечетные волны при типичных для ВЧ плазменных реакторов межэлектродных расстояниях всегда не распространяющиеся (кривые с h2 < 0).
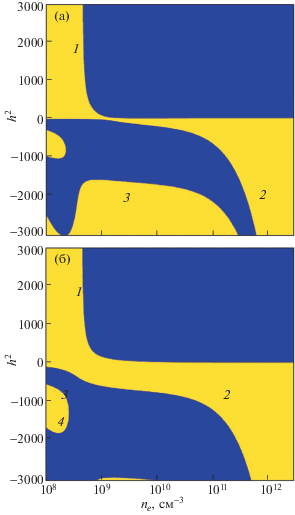
На рис. 4 приведены аналогичные кривые для плазмы, размеры слоев которой d1 = d2 = d на границе согласованы с плотностью электронов, и они убывают с ростом последней. Падение потенциала на слоях предполагалось равным 200 В, а размер плазменного столба 2L2 постоянным и равным 8 см. Межэлектродное расстояние представляло собой сумму размера плазмы и слоев пространственного заряда, поэтому увеличивалось с уменьшением плотности электронов. В силу изменения толщины слоев при малых плотностях плазмы замедление поверхностной волны в самосогласованном случае оказывается более слабым, а при высоких плотностях – более сильным. В тех случаях, когда размер слоя пропорционален радиусу Дебая, длина поверхностных волн в области высоких концентраций электронов перестает зависеть от плотности электронов (правая часть кривой рис. 4).
Рис. 4.
Квадрат безразмерной постоянной распространения h2/k2 поверхностных (1) и не распространяющихся волн (2, 3, 4) в симметричном разряде. Зависимости представляют собой границу между темной и светлой областями. Толщина слоев пространственного заряда соответствует напряжению на слоях 200 В. Ее изменение слоев в соответствии с плотностью плазмы, при постоянном размере плазмы предполагает уменьшение межэлектродного расстояния с ростом плотности электронов; четная (по магнитному Hφ и осевому Ez электрическому полям) поверхностная волна (a), нечетная (б); частота поля – 135.6 МГц; полутолщина плазмы L2 поддерживалась постоянной и равной 4 см.
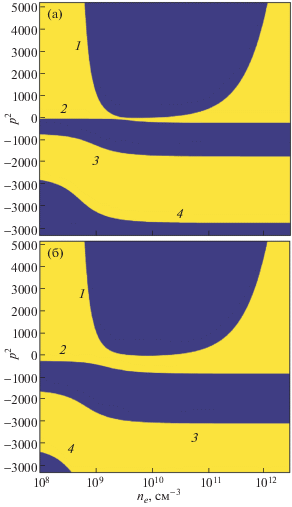
Для расчета импеданса разряда представляет интерес зависимость постоянной затухания волны в плазме $p = \sqrt {{{h}^{2}} - {{k}^{2}}{{\varepsilon }_{p}}} $ как функции плотности электронов. Пример таких зависимостей приведен на рис. 5. Из рисунка следует, что постоянные затухания четных и нечетных поверхностных волн близки, для волны квази-ТЕМ и не распространяющихся волн p2 < 0, т. е. эти волны присутствуют во всем сечении плазмы r = const.
Рис. 5.
Квадрат безразмерной постоянной затухания волны вдоль оси 0Z p2 в плазме для различных условий: четная волна (a), нечетная волна (б). Зависимости представляют собой границу между темной и светлой областями: 1 – поверхностная волна, 2, 3, 4 – не распространяющаяся волна. Условия расчета совпадают с данными рис. 3.
3. СТОЛКНОВИТЕЛЬНОЕ ЗАТУХАНИЕ ДЛЯ СОБСТВЕННЫХ ВОЛН
Приведенные на рис. 3–5 зависимости получены при отсутствии поглощения электромагнитного поля. В реальной плазме существуют столкновительные и бесстолкновительные механизмы поглощения электромагнитного поля [5]. В данной работе поглощение поля учитывается посредством эффективной частоты столкновений электронов [5, 6, 87, 88].
В бесстолкновительном случае длина поверхностных волн неограниченно убывает при ne → 2nC. В реальных условиях длина поверхностной волны в окрестности этой точки ограничивается параметром ω/ν [89]. Вдали нее учесть поглощение можно с помощью теории возмущений. Изменение постоянной распространения рассчитывается по стандартной формуле [5]
(18)
$\begin{gathered} h\left( {{{n}_{e}},{\nu \mathord{\left/ {\vphantom {\nu \omega }} \right. \kern-0em} \omega }} \right) = h\left( {{{n}_{e}},0} \right) - \\ \, - iD\left( {h,\varepsilon {}_{P}\left( {{{n}_{e}},{\nu \mathord{\left/ {\vphantom {\nu \omega }} \right. \kern-0em} \omega }} \right)} \right){{\left( {{{{\left. {\frac{{\partial D}}{{\partial \left( {{\nu \mathord{\left/ {\vphantom {\nu \omega }} \right. \kern-0em} \omega }} \right)}}} \right|}}_{{\nu = 0}}}} \right)}^{{ - 1}}}\frac{\nu }{\omega }, \\ \end{gathered} $Зависимости комплексных постоянных распространения для поверхностных и затухающих волн при малых частотах столкновений приведены на рис. 6а – четная волна, рис. 6б – нечетная, 1, 3, 5 – мнимые части постоянной распространения, 2, 4, 6 – действительные). Кривые 1, 2 соответствуют поверхностной волне, кривые 3–6 – высшим не распространяющимся модам. При докритических плотностях электронов первая не распространяющаяся четная мода (3, 4) переходит в квази-ТЕМ моду.
Рис. 6.
Зависимость действительной и мнимой частей постоянных распространения для поверхностных и затухающих волн при учете столкновений (d1 = d2 = = 0.3 см, 2L = 8 см); частота электромагнитного поля – 135.6 МГц; четная волна (a), нечетная волна (б).
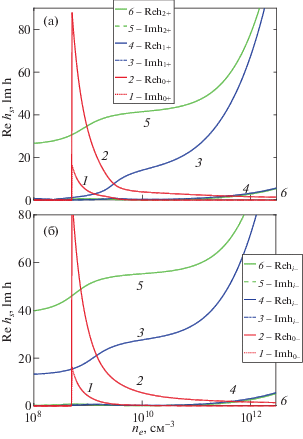
В точке ε = –1 в отсутствие поглощения постоянная распространения и ее производная обращаются в бесконечность, а сама точка будет существенно особой точкой комплексной функции h(ε). Поэтому методы теории возмущений, приводящие к формуле (18), в окрестности этой точки не применимы. В работе [89] получено, что при учете столкновений действительная часть постоянной распространения будет ограниченной. Коэффициент замедления поверхностной волны не может превышать величину ω/ν.
Для оценки постоянной распространения в условиях, когда указанными эффектами нельзя пренебречь, полезно использовать вариационные методы [90–92]. Для расчета характеристик поверхностных волн в условиях больших частот столкновений можно рекомендовать аналитические формулы, полученные в предположении малости толщин слоев пространственного заря-да [31].
Следует отметить, что предложенные методы могут быть использованы в тех случаях, когда фиксирована пространственная мода электромагнитной волны. Однако в точке εP = –1 происходит ветвление функций и обход в плоскости комплексной переменной вокруг данной точки приводит к переходу от одной ветви к другой. Исследование деталей поведения зависимостей h(ε) в окрестности особой точки является отдельной сложной математической задачей и выходит за рамки настоящей работы.
4. СТРУКТУРА ПОЛЯ ПОВЕРХНОСТНЫХ И ЗАТУХАЮЩИХ ВОЛН В СИММЕТРИЧНОМ РАЗРЯДЕ
Расчетные формулы для пространственного распределения поля представлены в табл. 1. Выражения для нераспространяющихся волн, следующие из формул табл. 1, приведены в табл. 2. Выражения для функций Q0, Q1, P0, P1 даны в Приложении II. Результаты детального расчета осевых распределений поля для всех качественно различных условий в плазме изображены на рис. 7. Магнитные поля нормированы таким образом, чтобы максимальное значение модуля функции было равно единице. На рис. 7a представлены распределения поля для малых концентраций электронов, ne = 108 см–3 < nC – квази-ТЕМ мода 1, и четная 3 и две нечетные 2, 4 затухающие моды. На рис. 7б (nC < ne = 3.16 × 108 см–3 < < 2nC) квази-ТЕМ волна 1 стала нераспространяющейся, так же как остальные моды (2, 3, 4). Пространственные распределения поля, казалось бы, пока не претерпели заметных изменений, однако производные магнитного поля на границе плазмы и слоя на рис. 7б уже имеют разные знаки, так как разные знаки имеет диэлектрическая проницаемость. Причем на границе плазмы и слоя наблюдается локальный минимум поля. Для собственных волн при ne < 2nC выполняется теорема Штурма, т.е. поле квази-ТЕМ волны не имеет перемен знака, поле первой затухающей моды 2 – одну перемену знака, поля второй 3 и третьей 4 затухающих мод – две и три перемены знака.
Таблица 1.
Распределение электромагнитных полей в плазме и слоях пространственного заряда для поверхностных E-волн
| Симметричная волна | Антисимметричная волна |
|---|---|
| Общие выражения для поля $\left\{ {\begin{array}{*{20}{c}} {{{e}_{{z + }}}} \\ {{{e}_{{r + }}}} \\ {{{h}_{{\varphi + }}}} \end{array}} \right\} = A\left( {\begin{array}{*{20}{c}} { - \sqrt {\frac{{{{\mu }_{0}}}}{{{{\varepsilon }_{0}}}}} \frac{{{{h}_{ + }}}}{{ik\varepsilon }}f\left( z \right){{P}_{0}}\left( {{{h}_{ + }}r} \right)} \\ {\sqrt {\frac{{{{\mu }_{0}}}}{{{{\varepsilon }_{0}}}}} \frac{1}{{ik{{\varepsilon }_{P}}}}\frac{{df\left( z \right)}}{{dz}}{{P}_{1}}\left( {{{h}_{ + }}r} \right)} \\ {f\left( z \right){{P}_{1}}\left( {{{h}_{ + }}r} \right)} \end{array}} \right)$ | |
| В слое $\left\{ {\begin{array}{*{20}{c}} {{{e}_{{z + }}}} \\ {{{e}_{{r + }}}} \\ {{{h}_{{\varphi + }}}} \end{array}} \right\} = A\left( {\begin{array}{*{20}{c}} { - \sqrt {\frac{{{{\mu }_{0}}}}{{{{\varepsilon }_{0}}}}} \frac{{{{h}_{ + }}}}{{ik}}\frac{{\operatorname{ch} \left( {\sqrt {h_{ + }^{2} - {{k}^{2}}{{\varepsilon }_{1}}} \left( {L + d - z} \right)} \right)}}{{\operatorname{ch} \left( {\sqrt {h_{ + }^{2} - {{k}^{2}}{{\varepsilon }_{1}}} {{d}_{1}}} \right)}}{{P}_{0}}\left( {{{h}_{ + }}r} \right)} \\ \begin{gathered} - \operatorname{th} \left( {\sqrt {h_{ + }^{2} - {{k}^{2}}{{\varepsilon }_{P}}} {{L}_{2}}} \right)\sqrt {\frac{{{{\mu }_{0}}}}{{{{\varepsilon }_{0}}}}} \frac{{\sqrt {h_{ + }^{2} - {{k}^{2}}{{\varepsilon }_{P}}} }}{{ik{{\varepsilon }_{P}}}} \times \hfill \\ \times \;\frac{{\operatorname{sh} \left( {\sqrt {h_{ + }^{2} - {{k}^{2}}{{\varepsilon }_{1}}} \left( {{{L}_{2}} + {{d}_{1}} - z} \right)} \right)}}{{\operatorname{sh} \left( {\sqrt {h_{ + }^{2} - {{k}^{2}}{{\varepsilon }_{1}}} {{d}_{1}}} \right)}}{{P}_{1}}\left( {{{h}_{ + }}r} \right) \hfill \\ \end{gathered} \\ {\frac{{\operatorname{ch} \left( {\sqrt {h_{ + }^{2} - {{k}^{2}}{{\varepsilon }_{1}}} \left( {{{L}_{2}} + {{d}_{1}} - z} \right)} \right)}}{{\operatorname{ch} \left( {\sqrt {h_{ + }^{2} - {{k}^{2}}{{\varepsilon }_{1}}} {{d}_{1}}} \right)}}{{P}_{1}}\left( {{{h}_{ + }}r} \right)} \end{array}} \right)$ | $\begin{gathered} \left\{ {\begin{array}{*{20}{c}} {{{e}_{{z - }}}} \\ {{{e}_{{r - }}}} \\ {{{h}_{{\varphi - }}}} \end{array}} \right\} = B \times \\ \times \left( {\begin{array}{*{20}{c}} { - \sqrt {\frac{{{{\mu }_{0}}}}{{{{\varepsilon }_{0}}}}} \frac{{{{h}_{ - }}}}{{ik}}\operatorname{th} \left( {\sqrt {h_{ - }^{2} - {{k}^{2}}{{\varepsilon }_{P}}} {{L}_{2}}} \right)\frac{{\operatorname{ch} \left( {\sqrt {h_{ - }^{2} - {{k}^{2}}{{\varepsilon }_{1}}} \left( {{{L}_{2}} + {{d}_{1}} - z} \right)} \right)}}{{\operatorname{ch} \left( {\sqrt {h_{ - }^{2} - {{k}^{2}}{{\varepsilon }_{1}}} {{d}_{1}}} \right)}}{{P}_{0}}\left( {{{h}_{ - }}r} \right)} \\ {\sqrt {\frac{{{{\mu }_{0}}}}{{{{\varepsilon }_{0}}}}} \frac{{\sqrt {h_{ - }^{2} - {{k}^{2}}{{\varepsilon }_{P}}} }}{{ik{{\varepsilon }_{P}}}}\frac{{\operatorname{sh} \left( {\sqrt {h_{ - }^{2} - {{k}^{2}}{{\varepsilon }_{1}}} \left( {{{L}_{2}} + {{d}_{1}} - z} \right)} \right)}}{{\operatorname{sh} \left( {\sqrt {h_{ - }^{2} - {{k}^{2}}{{\varepsilon }_{1}}} {{d}_{1}}} \right)}}{{P}_{1}}\left( {{{h}_{ - }}r} \right)} \\ {th\left( {\sqrt {h_{ - }^{2} - {{k}^{2}}{{\varepsilon }_{P}}} {{L}_{2}}} \right)\frac{{\operatorname{ch} \left( {\sqrt {h_{ - }^{2} - {{k}^{2}}{{\varepsilon }_{1}}} \left( {{{L}_{2}} + {{d}_{1}} - z} \right)} \right)}}{{\operatorname{ch} \left( {\sqrt {h_{ - }^{2} - {{k}^{2}}{{\varepsilon }_{1}}} {{d}_{1}}} \right)}}{{P}_{1}}\left( {{{h}_{ - }}r} \right)} \end{array}} \right) \\ \end{gathered} $ |
| В плазме $\left\{ {\begin{array}{*{20}{c}} {{{e}_{{z + }}}} \\ {{{e}_{{r + }}}} \\ {{{h}_{{\varphi + }}}} \end{array}} \right\} = A\left( {\begin{array}{*{20}{c}} { - \sqrt {\frac{{{{\mu }_{0}}}}{{{{\varepsilon }_{0}}}}} \frac{{{{h}_{ + }}}}{{ik{{\varepsilon }_{P}}}}\frac{{\operatorname{ch} \left( {\sqrt {h_{ + }^{2} - {{k}^{2}}{{\varepsilon }_{P}}} z} \right)}}{{\operatorname{ch} \left( {\sqrt {h_{ + }^{2} - {{k}^{2}}{{\varepsilon }_{P}}} {{L}_{P}}} \right)}}{{P}_{0}}\left( {{{h}_{ + }}r} \right)} \\ {\sqrt {\frac{{{{\mu }_{0}}}}{{{{\varepsilon }_{0}}}}} \frac{{\sqrt {h_{ + }^{2} - {{k}^{2}}{{\varepsilon }_{P}}} }}{{ik{{\varepsilon }_{P}}}}\frac{{\operatorname{sh} \left( {\sqrt {h_{ + }^{2} - {{k}^{2}}{{\varepsilon }_{P}}} z} \right)}}{{\operatorname{ch} \left( {\sqrt {h_{ + }^{2} - {{k}^{2}}{{\varepsilon }_{P}}} {{L}_{P}}} \right)}}{{P}_{1}}\left( {{{h}_{ + }}r} \right)} \\ {\frac{{\operatorname{ch} \left( {\sqrt {h_{ + }^{2} - {{k}^{2}}{{\varepsilon }_{2}}} z} \right)}}{{\operatorname{ch} \left( {\sqrt {h_{ + }^{2} - {{k}^{2}}{{\varepsilon }_{P}}} {{L}_{P}}} \right)}}{{P}_{1}}\left( {{{h}_{ + }}r} \right)} \end{array}} \right)$ | $\left\{ {\begin{array}{*{20}{c}} {{{e}_{{z - }}}} \\ {{{e}_{{r - }}}} \\ {{{h}_{{\varphi - }}}} \end{array}} \right\} = {{B}_{2}}\left( {\begin{array}{*{20}{c}} { - \sqrt {\frac{{{{\mu }_{0}}}}{{{{\varepsilon }_{0}}}}} \frac{{{{h}_{ - }}}}{{ik{{\varepsilon }_{P}}}}\frac{{\operatorname{sh} \left( {\sqrt {h_{ - }^{2} - {{k}^{2}}{{\varepsilon }_{P}}} z} \right)}}{{\operatorname{ch} \left( {\sqrt {h_{ - }^{2} - {{k}^{2}}{{\varepsilon }_{P}}} {{L}_{P}}} \right)}}{{P}_{0}}\left( {{{h}_{ - }}r} \right)} \\ {\sqrt {\frac{{{{\mu }_{0}}}}{{{{\varepsilon }_{0}}}}} \frac{{\sqrt {h_{ - }^{2} - {{k}^{2}}{{\varepsilon }_{P}}} }}{{ik{{\varepsilon }_{P}}}}\frac{{\operatorname{ch} \left( {\sqrt {h_{ - }^{2} - {{k}^{2}}{{\varepsilon }_{P}}} z} \right)}}{{\operatorname{ch} \left( {\sqrt {h_{ - }^{2} - {{k}^{2}}{{\varepsilon }_{P}}} {{L}_{P}}} \right)}}{{P}_{1}}\left( {{{h}_{ - }}r} \right)} \\ {\frac{{\operatorname{sh} \left( {\sqrt {h_{ - }^{2} - {{k}^{2}}{{\varepsilon }_{P}}} z} \right)}}{{\operatorname{ch} \left( {\sqrt {h_{ - }^{2} - {{k}^{2}}{{\varepsilon }_{P}}} {{L}_{P}}} \right)}}{{P}_{1}}\left( {{{h}_{ - }}r} \right)} \end{array}} \right)$ |
Таблица 2.
Распределение электромагнитных полей в плазме и слоях пространственного заряда для затухающих E-волн
| Симметричная волна | Антисимметричная волна |
|---|---|
| В слое | В слое |
| $\left\{ {\begin{array}{*{20}{c}} {{{e}_{{zn + }}}} \\ {{{e}_{{rn + }}}} \\ {{{h}_{{\varphi n + }}}} \end{array}} \right\} = \left( {\begin{array}{*{20}{c}} { - \sqrt {\frac{{{{\mu }_{0}}}}{{{{\varepsilon }_{0}}}}} \frac{{{{{\tilde {h}}}_{{n + }}}}}{{ik}}\frac{{\cos \left( {\sqrt {{{k}^{2}}{{\varepsilon }_{1}} + \tilde {h}_{{n + }}^{2}} \left( {L + d - z} \right)} \right)}}{{\cos \left( {\sqrt {{{k}^{2}}{{\varepsilon }_{1}} + \tilde {h}_{{n + }}^{2}} {{d}_{1}}} \right)}}{{Q}_{0}}\left( {{{{\tilde {h}}}_{{n + }}}r} \right)} \\ \begin{gathered} - \sqrt {\frac{{{{\mu }_{0}}}}{{{{\varepsilon }_{0}}}}} \frac{{\sqrt {{{k}^{2}}{{\varepsilon }_{P}} + \tilde {h}_{{n + }}^{2}} }}{{ik{{\varepsilon }_{P}}}}tg\left( {\sqrt {{{k}^{2}}{{\varepsilon }_{P}} + \tilde {h}_{{n + }}^{2}} {{L}_{2}}} \right) \times \hfill \\ \times \;\frac{{\sin \left( {\sqrt {{{k}^{2}}{{\varepsilon }_{1}} + \tilde {h}_{{n + }}^{2}} \left( {{{L}_{2}} + {{d}_{1}} - z} \right)} \right)}}{{\sin \left( {\sqrt {{{k}^{2}}{{\varepsilon }_{1}} + \tilde {h}_{{n + }}^{2}} {{d}_{1}}} \right)}}{{Q}_{1}}\left( {{{{\tilde {h}}}_{{n + }}}r} \right) \hfill \\ \end{gathered} \\ {\frac{{\cos \left( {\sqrt {{{k}^{2}}{{\varepsilon }_{1}} + \tilde {h}_{{n + }}^{2}} \left( {{{L}_{2}} + {{d}_{1}} - z} \right)} \right)}}{{\cos \left( {\sqrt {{{k}^{2}}{{\varepsilon }_{1}} + \tilde {h}_{{n + }}^{2}} {{d}_{1}}} \right)}}{{Q}_{1}}\left( {{{{\tilde {h}}}_{{n + }}}r} \right)} \end{array}} \right)$ | $\left\{ {\begin{array}{*{20}{c}} {{{e}_{{zn - }}}} \\ {{{e}_{{rn - }}}} \\ {{{h}_{{\varphi n - }}}} \end{array}} \right\} = \left( {\begin{array}{*{20}{c}} \begin{gathered} - \frac{{i{{{\tilde {h}}}_{{n - }}}}}{{ik}}\sqrt {\frac{{{{\mu }_{0}}}}{{{{\varepsilon }_{0}}}}} tg\left( {\sqrt {{{k}^{2}}{{\varepsilon }_{P}} + \tilde {h}_{{n - }}^{2}} {{L}_{2}}} \right) \times \hfill \\ \times \;\frac{{\cos \left( {\sqrt {{{k}^{2}}{{\varepsilon }_{1}} + \tilde {h}_{{n - }}^{2}} \left( {{{L}_{2}} + {{d}_{1}} - z} \right)} \right)}}{{\cos \left( {\sqrt {{{k}^{2}}{{\varepsilon }_{1}} + \tilde {h}_{{n - }}^{2}} {{d}_{1}}} \right)}}{{Q}_{0}}\left( {{{{\tilde {h}}}_{{n - }}}r} \right) \hfill \\ \end{gathered} \\ {\sqrt {\frac{{{{\mu }_{0}}}}{{{{\varepsilon }_{0}}}}} \frac{{\sqrt {{{k}^{2}}{{\varepsilon }_{P}} + \tilde {h}_{{n - }}^{2}} }}{{ik{{\varepsilon }_{P}}}}\frac{{\sin \left( {\sqrt {{{k}^{2}}{{\varepsilon }_{1}} + \tilde {h}_{{n - }}^{2}} \left( {{{L}_{2}} + {{d}_{1}} - z} \right)} \right)}}{{\sin \left( {\sqrt {{{k}^{2}}{{\varepsilon }_{1}} + \tilde {h}_{{n - }}^{2}} {{d}_{1}}} \right)}}{{Q}_{1}}\left( {{{{\tilde {h}}}_{{n - }}}r} \right)} \\ {tg\left( {\sqrt {{{k}^{2}}{{\varepsilon }_{P}} + \tilde {h}_{{n - }}^{2}} {{L}_{2}}} \right)\frac{{\cos \left( {\sqrt {{{k}^{2}}{{\varepsilon }_{1}} + \tilde {h}_{{n - }}^{2}} \left( {{{L}_{2}} + {{d}_{1}} - z} \right)} \right)}}{{\cos \left( {\sqrt {{{k}^{2}}{{\varepsilon }_{1}} + \tilde {h}_{{n - }}^{2}} {{d}_{1}}} \right)}}{{Q}_{1}}\left( {{{{\tilde {h}}}_{{n - }}}r} \right)} \end{array}} \right)$ |
| В плазме $\left\{ {\begin{array}{*{20}{c}} {{{e}_{{zn + }}}} \\ {{{e}_{{rn + }}}} \\ {{{h}_{{\varphi n + }}}} \end{array}} \right\} = \left( {\begin{array}{*{20}{c}} { - \sqrt {\frac{{{{\mu }_{0}}}}{{{{\varepsilon }_{0}}}}} \frac{{{{{\tilde {h}}}_{{n + }}}}}{{ik{{\varepsilon }_{P}}}}\frac{{\cos \left( {\sqrt {{{k}^{2}}{{\varepsilon }_{P}} + \tilde {h}_{{n + }}^{2}} z} \right)}}{{\cos \left( {\sqrt {{{k}^{2}}{{\varepsilon }_{P}} + \tilde {h}_{{n + }}^{2}} {{L}_{P}}} \right)}}{{Q}_{0}}\left( {{{{\tilde {h}}}_{{n + }}}r} \right)} \\ {\sqrt {\frac{{{{\mu }_{0}}}}{{{{\varepsilon }_{0}}}}} \frac{{\sqrt {{{k}^{2}}{{\varepsilon }_{P}} + \tilde {h}_{{n + }}^{2}} }}{{ik{{\varepsilon }_{P}}}}\frac{{\sin \left( {\sqrt {{{k}^{2}}{{\varepsilon }_{P}} + \tilde {h}_{{n + }}^{2}} z} \right)}}{{\cos \left( {\sqrt {{{k}^{2}}{{\varepsilon }_{P}} + \tilde {h}_{{n + }}^{2}} {{L}_{P}}} \right)}}{{Q}_{1}}\left( {{{{\tilde {h}}}_{{n + }}}r} \right)} \\ {\frac{{\cos \left( {\sqrt {{{k}^{2}}{{\varepsilon }_{P}} + \tilde {h}_{{n + }}^{2}} z} \right)}}{{\cos \left( {\sqrt {{{k}^{2}}{{\varepsilon }_{P}} + \tilde {h}_{{n + }}^{2}} {{L}_{P}}} \right)}}{{Q}_{1}}\left( {{{{\tilde {h}}}_{{n + }}}r} \right)} \end{array}} \right)$ | $\left\{ {\begin{array}{*{20}{c}} {{{e}_{{zn - }}}} \\ {{{e}_{{rn - }}}} \\ {{{h}_{{\varphi n - }}}} \end{array}} \right\} = \left( {\begin{array}{*{20}{c}} { - \sqrt {\frac{{{{\mu }_{0}}}}{{{{\varepsilon }_{0}}}}} \frac{{{{{\tilde {h}}}_{{n - }}}}}{{ik{{\varepsilon }_{P}}}}\frac{{\sin \left( {\sqrt {{{k}^{2}}{{\varepsilon }_{P}} + \tilde {h}_{{n - }}^{2}} z} \right)}}{{\cos \left( {\sqrt {{{k}^{2}}{{\varepsilon }_{P}} + \tilde {h}_{{n - }}^{2}} {{L}_{P}}} \right)}}{{Q}_{0}}\left( {{{{\tilde {h}}}_{{n - }}}r} \right)} \\ {\sqrt {\frac{{{{\mu }_{0}}}}{{{{\varepsilon }_{0}}}}} \frac{{\sqrt {{{k}^{2}}{{\varepsilon }_{P}} + \tilde {h}_{{n - }}^{2}} }}{{ik{{\varepsilon }_{P}}}}\frac{{\cos \left( {\sqrt {{{k}^{2}}{{\varepsilon }_{P}} + \tilde {h}_{{n - }}^{2}} z} \right)}}{{\cos \left( {\sqrt {{{k}^{2}}{{\varepsilon }_{P}} + \tilde {h}_{{n - }}^{2}} {{L}_{P}}} \right)}}{{Q}_{1}}\left( {{{{\tilde {h}}}_{{n - }}}r} \right)} \\ {\frac{{\sin \left( {\sqrt {{{k}^{2}}{{\varepsilon }_{P}} + \tilde {h}_{{n - }}^{2}} z} \right)}}{{\cos \left( {\sqrt {{{k}^{2}}{{\varepsilon }_{P}} + \tilde {h}_{{n - }}^{2}} {{L}_{P}}} \right)}}{{Q}_{1}}\left( {{{{\tilde {h}}}_{{n - }}}r} \right)} \end{array}} \right)$ |
Рис. 7.
Осевое распределение электромагнитных полей в плазме для квази-ТЕМ волны, поверхностной и затухающей волн. Частота поля 135.6 МГц, плотности электронов: 108 см–3 (а), 3.16 ⋅ 108 см–3 (б), 109 см–3 (в), 1010 см–3 (г), 1011 см–3 (д), 1012 см–3 (е).
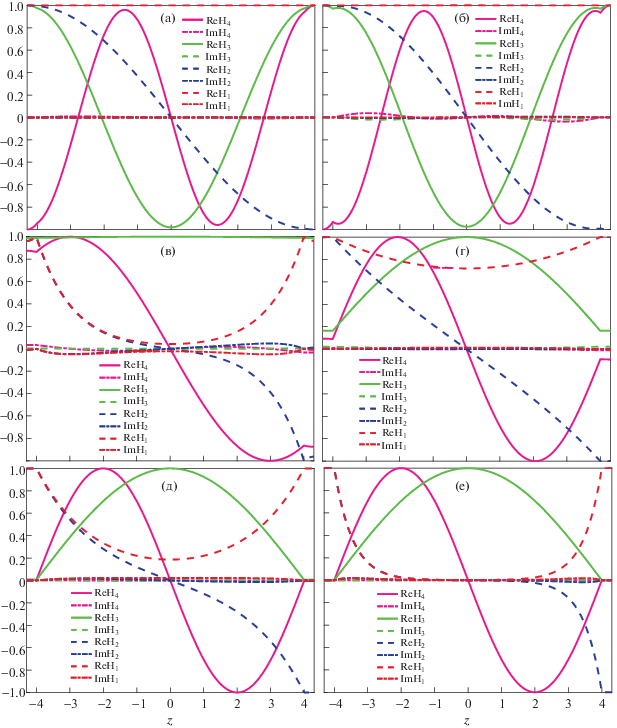
При плотностях электронов выше удвоенной критической (рис. 7в–е) происходит перестройка структуры поля собственных волн. На рисунках приведены поля четной 1 и нечетной 2 поверхностных волн, а также четной 3 и нечетной 4 затухающих волн. Обе четные волны не имеют перемен знака (следующая четная затухающая волна будет иметь две перемены знака), а обе нечетные – по одной перемене знака. Расчет показывает, что теорема Штурма выполняется только для затухающих волн. Производные магнитного поля на границе плазмы и слоя также имеют разные знаки, поэтому поле имеет на этой границе локальный максимум (для поверхностной волны) или локальный минимум. При плотности электронов, близкой к удвоенной критической (но выше нее, рис. 7в) глубина проникновения поверхностной волны в плазму мала, но магнитное поле первой четной затухающей моды (кривая 3) распределено в плазме почти равномерно, напоминая нам, что эта волна является продолжением квази-ТЕМ волны. При дальнейшем увеличении плотности электронов глубина проникновения поля обеих (четной и нечетной) поверхностных волн в плазму увеличивается в соответствии с рис. 5, поле затухающих волн на границе плазмы и слоя уменьшается, а конфигурация их поля начинает существенно отличаться от той, которая была при малых плотностях электронов. Последующий рост плотности электронов опять приводит теперь уже к монотонному уменьшению глубины проникновения обеих 1, 2 поверхностных волн в плазму. Магнитное поле высших мод, наоборот, сосредотачивается в плазме, как будто на границе плазмы и слоя поставлено граничное условие неидеального “магнитного проводника”, идеальность которого увеличивается по мере роста плотности электронов. Для не распространяющихся волн высокого порядка с характерным размером затухания волны близким к толщине слоя необходимо учитывать перемещение границы плазмы и слоя и рассматриваемая нами матричная модель слоя неприменима.
Данные расчеты демонстрируют: для поверхностных волн поле в окрестности слоя существенно выше среднего поля в плазме, радиальный перенос энергии к центру разряда происходит по слою пространственного заряда. Для затухающих мод поток энергии к центру разряда по плазме значительно больше, чем поток по слоям пространственного заряда.
Для поверхностных волн поле в слое существенно выше, чем поле в плазме (в особенности при высоких плотностях электронов, когда $\left| \varepsilon \right| \gg 1$) и можно было бы ожидать, что импеданс разряда, поддерживаемого поверхностными волнами, определяется прежде всего падением постоянного напряжения на слоях пространственного заряда. Для не распространяющихся волн магнитное поле, наоборот, сосредотачивается в плазме, поэтому вносимый этими модами импеданс должен быть индуктивным.
Из расчетов можно видеть, как изменяется пространственное распределение электромагнитного поля и его математическое описание при переходе от квазистатического описания к электродинамическому в простейшем варианте конденсатора с электродами радиуса R, заполненного плазмой (рис. 1а). В квазистатическом приближении электрическое и магнитное поля описываются независимо друг от друга. Потенциальное приближение означает радиальную однородность электрического поля и рост магнитного поля пропорционально радиусу. Вблизи ребер электродов наблюдаются так называемые краевые эффекты, т.е. искажения поля, связанные с необходимостью выполнения граничных условий на боковой границе плазмы. В квазистатическом приближении этими возмущениями, можно пренебречь при выполнении условий L, $R \gg {{d}_{1}}$, d2. Важно то, что в квазистатическом приближении возмущения электрического и магнитного поля можно рассчитывать независимо друг от друга. Связь их обеспечивается только через граничные условия.
Переход к электродинамическому описанию означает, что поля собственные функции электрического и магнитного поля оказываются связанными не только через граничные условия, но и непосредственно через уравнения Максвелла. При малых плотностях электронов ne< 2nC осевое распределение электрического поля квази-ТЕМ волны, которая представляет собой поле внутри плазменного конденсатора, слабо отличается от распределения, получаемого в квазистатическом приближении. Поэтому последнее можно использовать, если можно пренебречь радиальной неоднородностью поля, т.е. при выполнении условия $\left| {k\sqrt {{{\varepsilon }_{P}}} R} \right|$ = $\left| {k\left( {\sqrt {1 - {{\omega _{{Pe}}^{2}} \mathord{\left/ {\vphantom {{\omega _{{Pe}}^{2}} {\left( {{{\omega }^{2}}\left( {1 + {{i\nu } \mathord{\left/ {\vphantom {{i\nu } \omega }} \right. \kern-0em} \omega }} \right)} \right)}}} \right. \kern-0em} {\left( {{{\omega }^{2}}\left( {1 + {{i\nu } \mathord{\left/ {\vphantom {{i\nu } \omega }} \right. \kern-0em} \omega }} \right)} \right)}}} } \right)R} \right| \ll 1$. Условие пренебрежения возбуждением поля высших мод остается таким же, как в потенциальном приближении.
При росте плотности электронов свыше двух критических происходит полная перестройка системы собственных функций, появляются поверхностные волны, радиальный перенос энергии к центру разряда в которых происходит через слои пространственного заряда, и высшие типы поля, в которых основная передача энергии происходит не через слои, а через плазму. В силу того, что диэлектрическая проницаемость плазмы отрицательна, поле высших типов мод не может проникнуть в плазму в радиальном направлении больше, чем на глубину скин-слоя. Кроме того, как следует из рис. 7, осевое распределение электромагнитного поля в плазме также становится неоднородным. Поэтому, если подходить к описанию процесса проникновения поля строго, то квазистатическое приближение в этой области параметров не применимо.
Можно описать условия, при которых квазистатическое приближение дает приемлемые результаты. Так при $R \gg L$ поле всех высших мод, кроме первой, сосредоточено вблизи границ плазмы. При относительно малых плотностях электродов поле в центре плазмы будет представлено суммой поверхностной волны и первой высшей моды. Пренебрегая высшими модами, получим, что радиальное распределение плотности плазмы будет однородным при выполнении условий $\left| {{{h}_{{0 + }}}R} \right| < 1$ и $\left| {{{h}_{{1 + }}}R} \right| < 1$. Условие осевой однородности распределения поля в плазме имеет вид $\left| {{{p}_{{0 + }}}L} \right| < 1$. В силу того, что L < R условие осевой однородности поля первой высшей моды при выполнении предыдущих условий будет выполнено автоматически.
При высоких плотностях электронов первая высшая мода не будет проникать в плазму на расстояние больше глубины скин-слоя, поэтому в глубине положительного столба поле будет представлено только поверхностной волной. Это предполагает выполнение условий $\left| {{{h}_{{0 + }}}R} \right| < 1$ и $\left| {{{h}_{{1 + }}}R} \right| \gg 1$. Условие осевой однородности распределения поля в плазме имеет тот же вид, что и в предыдущем случае $\left| {{{p}_{{0 + }}}L} \right| < 1$.
Следует отметить, что приведенные в данном пункте условия касаются только получения однородного распределения поля в центральной части плазмы. Соотношение энергий, передаваемых в поверхностную волну и в высшие моды, зависит от геометрии области возбуждения поля в камере, и в зависимости от условий может быть реализована как преимущественная передача энергии в поверхностную волну, так и наоборот – в высшие моды поля.
5. ИМПЕДАНС РАЗРЯДА. ПРИБЛИЖЕННЫЕ МЕТОДЫ РАСЧЕТА
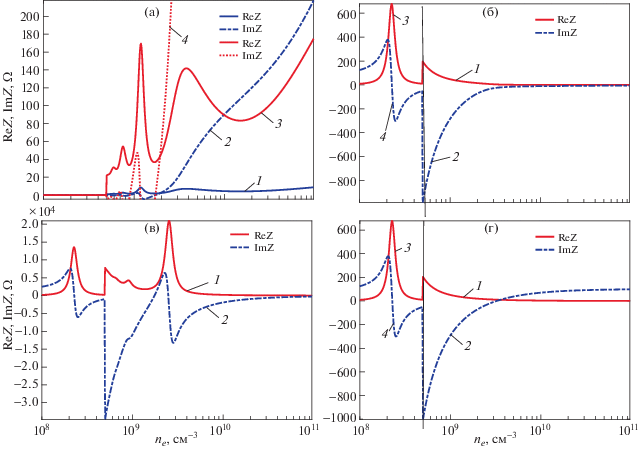
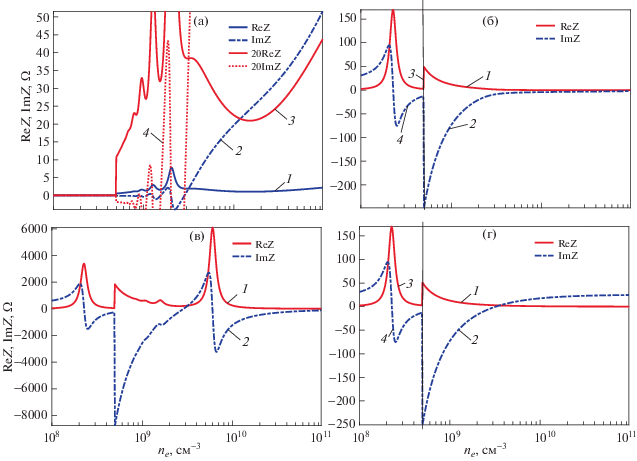
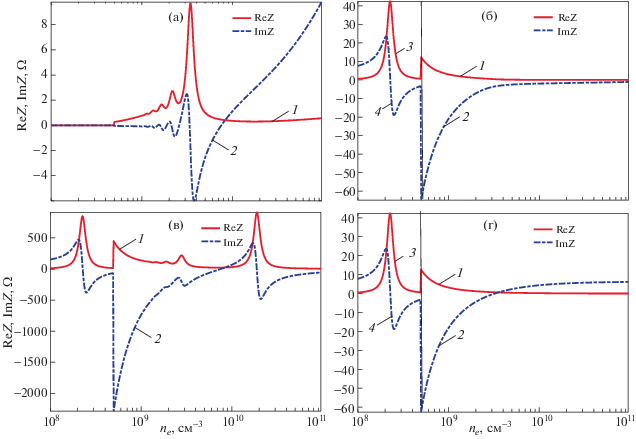
Общие выражения для импеданса разряда были приведены в разд. 1 (уравнения (9), (11)). Различные частные случаи расчета по этим формулам представлены на рис. 8–11. Наиболее простые приближенные выражения для импеданса учитывают только одну возбуждаемую моду. При больших плотностях плазмы (ne > 2nc) обычно предполагается, что возбуждается поверхностная волна [27, 33], при меньших плотностях это квази-ТЕМ волна или первая затухающая мода. В этом случае из (10) следует для поверхностной волны
(19)
$\begin{gathered} {{Z}_{{0 + }}} = \frac{{2L}}{{2\pi R}}i\rho \frac{{{{h}_{{0 + }}}}}{k}\left( {\frac{{\operatorname{th} \left( {\sqrt {h_{{0 + }}^{2} - {{k}^{2}}{{\varepsilon }_{P}}} {{L}_{2}}} \right)}}{{{{\varepsilon }_{P}}\sqrt {{{h_{{0 + }}^{2}} \mathord{\left/ {\vphantom {{h_{{0 + }}^{2}} {{{k}^{2}}}}} \right. \kern-0em} {{{k}^{2}}}} - {{\varepsilon }_{P}}} }} + } \right. \\ \, + \left. {\frac{{\operatorname{th} \left( {\sqrt {h_{{0 + }}^{2} - {{k}^{2}}{{\varepsilon }_{1}}} d} \right)}}{{{{\varepsilon }_{1}}\sqrt {{{h_{{0 + }}^{2}} \mathord{\left/ {\vphantom {{h_{{0 + }}^{2}} {{{k}^{2}}}}} \right. \kern-0em} {{{k}^{2}}}} - {{\varepsilon }_{1}}} }}} \right)\left( {\frac{{\operatorname{th} \left( {\sqrt {h_{{0 + }}^{2} - {{k}^{2}}{{\varepsilon }_{P}}} {{L}_{2}}} \right)}}{{\sqrt {{{h_{{0 + }}^{2}} \mathord{\left/ {\vphantom {{h_{{0 + }}^{2}} {{{k}^{2}}}}} \right. \kern-0em} {{{k}^{2}}}} - {{\varepsilon }_{P}}} }} + } \right. \\ \, + {{\left. {\frac{{\operatorname{th} \left( {\sqrt {h_{{0 + }}^{2} - {{k}^{2}}{{\varepsilon }_{1}}} d} \right)}}{{\sqrt {{{h_{{0 + }}^{2}} \mathord{\left/ {\vphantom {{h_{{0 + }}^{2}} {{{k}^{2}}}}} \right. \kern-0em} {{{k}^{2}}}} - {{\varepsilon }_{1}}} }}} \right)}^{{ - 1}}}\frac{{{{J}_{0}}\left( {{{h}_{{0 + }}}R} \right)}}{{{{J}_{1}}\left( {{{h}_{{0 + }}}R} \right)}} \\ \end{gathered} $(20)
$\begin{gathered} {{Z}_{{1 + }}} = - \frac{{{{{\tilde {h}}}_{{1 + }}}}}{k}i\rho \frac{{2L}}{{2\pi R}}\left( {\frac{{\operatorname{tg} \left( {\sqrt {{{k}^{2}}{{\varepsilon }_{P}} + \tilde {h}_{{1 + }}^{2}} {{L}_{2}}} \right)}}{{{{\varepsilon }_{P}}\sqrt {{{\varepsilon }_{P}} + {{\tilde {h}_{{1 + }}^{2}} \mathord{\left/ {\vphantom {{\tilde {h}_{{1 + }}^{2}} {{{k}^{2}}}}} \right. \kern-0em} {{{k}^{2}}}}} }} + } \right. \\ \, + \left. {\frac{{\operatorname{tg} \left( {\sqrt {{{k}^{2}}{{\varepsilon }_{1}} + \tilde {h}_{{1 + }}^{2}} d} \right)}}{{{{\varepsilon }_{1}}\sqrt {{{\varepsilon }_{1}} + {{\tilde {h}_{{1 + }}^{2}} \mathord{\left/ {\vphantom {{\tilde {h}_{{1 + }}^{2}} {{{k}^{2}}}}} \right. \kern-0em} {{{k}^{2}}}}} }}} \right)\left( {\frac{{\operatorname{tg} \left( {\sqrt {{{k}^{2}}{{\varepsilon }_{P}} + \tilde {h}_{{1 + }}^{2}} {{L}_{2}}} \right)}}{{\sqrt {{{\varepsilon }_{P}} + {{\tilde {h}_{{1 + }}^{2}} \mathord{\left/ {\vphantom {{\tilde {h}_{{1 + }}^{2}} {{{k}^{2}}}}} \right. \kern-0em} {{{k}^{2}}}}} }} + } \right. \\ \, + {{\left. {\frac{{\operatorname{tg} \left( {\sqrt {{{k}^{2}}{{\varepsilon }_{1}} + \tilde {h}_{{1 + }}^{2}} d} \right)}}{{\sqrt {{{\varepsilon }_{1}} + {{\tilde {h}_{{1 + }}^{2}} \mathord{\left/ {\vphantom {{\tilde {h}_{{1 + }}^{2}} {{{k}^{2}}}}} \right. \kern-0em} {{{k}^{2}}}}} }}} \right)}^{{ - 1}}}\frac{{{{I}_{0}}\left( {{{{\tilde {h}}}_{{1 + }}}R} \right)}}{{{{I}_{1}}\left( {{{{\tilde {h}}}_{{1 + }}}R} \right)}}. \\ \end{gathered} $Рис. 8.
Импеданс симметричного разряда, рассчитанный в различных приближениях: при учете только поверхностной волны (a), при учете только первой высшей моды (б), при учете поверхностной волны и первой высшей моды с амплитудами, полученными из условия соответствия расчету в квазистатическом приближении (в), расчет в квазистатическом приближении (г). Частота поля – 135.6 МГц, радиус разряда – 2 см, межэлектродное расстояние 2L = 8 см, размер слоев пространственного заряда – 0.3 см, отношение частоты столкновений к частоте поля ν/ω = 0.1. На рисунках б и г при плотностях ниже 5 × 108 см–3 масштаб кривых 3, 4 уменьшен в 20 раз. Кривые 3 и 4 на рис. 8a увеличены по масштабу в 20 раз.
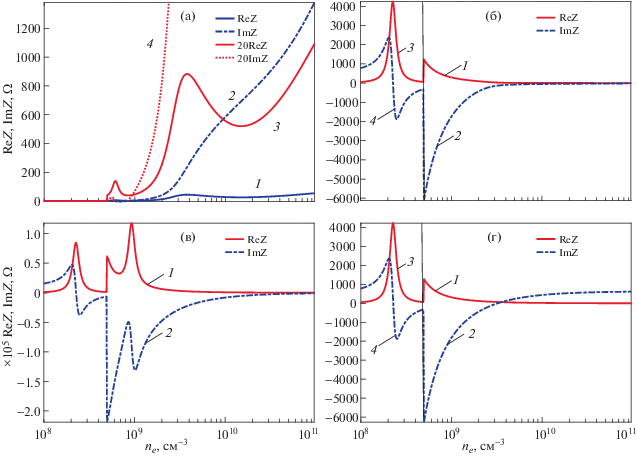
При записи последних формул предполагалось, что токи различных мод определяются соотношением (11). В случае (9), уравнения (19) и (20) принимают вид
Для малых размеров плазмы (${{h}_{{0 + }}}R < 2.4$) выражение (19) всегда дает емкостной импеданс, напротив, импеданс, вносимый не распространяющимися модами, (20) всегда индуктивный. Этот результат подтверждается численным расчетом по указанным формулам (панели а, б на рис. 8–11). Для коротких поверхностных волн коэффициент затухания велик (рис. 6), поэтому отражение поверхностной волны от центра плазменного столба незначительно и вносимый ими импеданс имеет активный характер. По мере увеличения плотности электронов коэффициент затухания уменьшается и существенную роль начинает играть реактивная составляющая, а затем, после нескольких колебаний, связанных с изменением соотношения длины поверхностной волны и радиуса плазмы, импеданс приобретает емкостной характер. Количество колебаний увеличивается с ростом радиуса разряда. Поскольку импеданс сильно изменяется с изменением плотности плазмы на рис. 8a–11а представлены отдельными кривыми также значения импеданса в увеличенном в 20 раз масштабе. Напротив, на рис. 8б, г–11б, d в области ne < 2nC, где распространение поверхностных волн отсутствует и сопротивление плазменного столба велико, значение импеданса уменьшено в 20 раз.
Сравнение показывает (рис. 8г–11г), что при пренебрежении полем поверхностной волны (ne < < 2nc) и учете только первой высшей моды результат близок к получаемому в потенциальном приближении, для которого
Для поверхностной волны близкий к этому результат получается при плотностях много выше плотности, при которой наблюдается геометрический резонанс плазма–слой пространственного заряда.
Детальные расчеты демонстрируют: приближенные выражения (19) и (20) не описывают поведение импеданса разряда в промежуточном диапазоне плотностей электронов и геометрический резонанс. Естественным уточнением модели было бы включение в расчет импеданса как поверхностной волны, так и хотя бы одной из высших мод. Подробный расчет импеданса весьма громоздок, поэтому в данной работе мы приведем феноменологическое выражение, предполагающее, что амплитуда первой высшей моды равна амплитуде поверхностной волны
Можно ожидать, что данное выражение будет давать правдоподобный результат для тонкого столба плазмы и для плотностей, при которых наблюдается резонанс плазма-слой и выше. Результаты расчетов приведены на рис. 8в–11в. Последняя формула, полученная из эвристических соображений, не может считаться справедливой при низких плотностях электронов в разряде. При плотностях ниже удвоенной критической на рис. 8в–11в учитывается только квази-ТЕМ мода, поэтому в этой области результаты совпадают с рис. 8б–11б. Поскольку перестройка системы собственных функций при ${{n}_{e}} > 2{{n}_{C}}$ в отсутствие столкновений по существу означает добавление новой собственной функции (поверхностной волны), при ${{n}_{e}} > 2{{n}_{C}}$ на рис. 8в–11в импеданс в окрестности этой точки в диапазоне плотностей $\Delta {{n}_{e}} \approx {{n}_{C}}{\nu \mathord{\left/ {\vphantom {\nu \omega }} \right. \kern-0em} \omega }$ испытывает резкий скачок. На рис. 8б–11б и 8г–11г импеданс изменяется плавно, а скачки на рисунках обусловлены изменением масштаба кривых.
Согласно расчетам, импеданс разряда при высоких плотностях плазмы приближается к квазистатическому, и в нем появляется геометрический резонанс плазма–слой пространственного заряда. Поскольку поле высших мод плохо проникает в плазму и вносимый ими индуктивный импеданс оказывается меньше, чем в квазистатическом приближении, плотности, при которых наблюдается геометрический резонанс, увеличиваются и для камеры большого радиуса (рис. 10в) он должен наблюдаться при плотностях вне диапазона, представленного на рисунке. В промежуточной области вносимый высшими модами индуктивный импеданс приводит к сдвигу плотностей электронов, при которых наблюдаются резонансы токов и напряжений, обусловленные нулями функций Бесселя на оси плотностей (рис. 8a и в–11a и в). Однако в этой области используемое нами предположение о равенстве амплитуд поверхностной волны и затухающей моды почти наверняка не работает. При увеличении радиуса плазмы число резонансов, связанных с кратностью размеров плазмы половине длины поверхностной волны (рис. 9а и г), увеличивается. Полученные выражения качественно правильно описывают импеданс разряда при высоких плотностях электронов, наличие геометрического резонанса плазма–слой. Возбуждение не распространяющейся волны существенно меняет положение резонансных точек на оси плотностей электронов.
Предлагаемый авторами подход к расчету импеданса разряда является приближенным и явно демонстрирует необходимость проведения дальнейших исследований.
Расчеты (рис. 8–11) показывают, что при εP = 0 наблюдается резонанс токов. Это происходит потому, что при этом ток проводимости в плазме полностью компенсируется током смещения и магнитное поле, а следовательно, и токи электродов отсутствуют. Подводящая линия при длине много меньше длины волны (рис. 1а–в) приводит к внесению дополнительной емкости, подключенной параллельно разряду. Ток через эту емкость протекает даже в том случае, если εP = 0. При резонансе токов общий ток в системе должен быть равен нулю и такой резонанс должен наблюдаться при плотности электронов выше критической, но ниже плотности, соответствующей геометрическому резонансу плазмы и слоя. Если эта дополнительная емкость равна С, то общий импеданс разряда и подводящей линии будет равен
Эта емкость может быть оценена как емкость цилиндрического конденсатора с размерами подводящей линии передачи. При радиусах электродов R, R + 1 см и высоте цилиндра 1 см, она составляла примерно 1, 5, 3, 6 и 12 пФ. При учете емкости подводящего кабеля она обычно составляет несколько десятков пФ. Наиболее ярко сдвиг резонанса в сторону больших плотностей заметен, если записать импеданс разряда в квазистатическом приближении
Из последней формулы следует, что, как правило, резонанс токов в реальном разряде наблюдается при отрицательной диэлектрической проницаемости.
ОСНОВНЫЕ РЕЗУЛЬТАТЫ РАБОТЫ
1. Проведенные аналитические расчеты поля в емкостном высокочастотном разряде c трехслойной структурой (слой пространственного заряда, плазма, слой пространственного заряда) окруженной металлическими электродами, показали, что для корректного расчета импеданса разряда необходимо учитывать как поверхностные, так и не распространяющиеся моды электромагнитного поля.
2. Показано, что высшие не распространяющиеся волны вносят существенный вклад. Именно они определяют те значения плотностей электронов, при которых наблюдаются резонансы. В геометрический резонанс системы плазма–слой пространственного заряда, когда размеры плазмы малы, в емкостной импеданс вносят вклад поверхностные волны, а индуктивный – высшие моды. При пренебрежении поверхностными волнами или высшими типами мод этот резонанс не проявляется в аналитических расчетах.
3. При больших размерах электродов и малых частотах столкновений (${\nu \mathord{\left/ {\vphantom {\nu \omega }} \right. \kern-0em} \omega } < {\lambda \mathord{\left/ {\vphantom {\lambda L}} \right. \kern-0em} L}$) возможно появление резонансов тока и резонансов напряжения. Эти резонансы обусловлены кратностью размеров разряда числу полуволн поверхностной волны. При расчете импеданса разряда нельзя ограничиться рассмотрением только поверхностных волн, поскольку высшие не распространяющиеся волны вносят существенный вклад в импеданс разряда и определяют те значения плотностей электронов, при которых наблюдаются резонансы.
4. Предложен феноменологический метод расчета импеданса разряда, основанный на соотношении значений амплитуд поверхностной и первой затухающей моды в потенциальном приближении. Метод удобен для определения условия возбуждения геометрического резонанса плазмы и слоя пространственного заряда. Он справедлив только при концентрациях электронов, превышающих плотности существования геометрического резонанса. Для меньших плотностей плазмы необходимы уточнения, основанные на прямых численных расчетах.
Список литературы
Lieberman M.A., Lichtenberg A.J. Principles of Plasma Discharges and Material Processing. N.-Y.: Wiley, 2005.
Ивановский Г.Ф., Петров В.И. Ионно-плазменная обработка материалов. М.: Радио и связь, 1986. 232 с.
Taillet J. // American J. Phys. 1969. V. 37. 423.
Годяк В. А. // Физика плазмы. 1976. Т. 2. С. 141.
Гинзбург В.Л. Распространение электромагнитных волн в плазме. М.: Наука, 1961.
Александров А.Ф., Богданкевич Л.С., Рухадзе А.А. Основы электродинамики плазмы. М.: Энергоатомиздат, 1976.
Leprince P., Mattieussent G., Allis W.P. // J. Appl. Phys. 1971. V. 42. P. 4.
Samukawa S., Hori M., Raul S., Tachibana K., Brugge-man P., Kroesen G., Whitehead J.C., Murphy A.B., Gutsol A.F., Starikovskaia S., Kortshagen U., Boeuf J.-P., Som-merer T.J., Kushner M.J., Czarnetzki U., Mason N. // J. Phys. D.: Appl. Phys. 2012. V. 45. P. 253001.
Collins K.S., Roderick C.A., Yang S.-L., Wang D.N.K., Maydan D. United States Patent No 5210466A, May 1993.
Schmidt H., Sansonnens L., Howling A.A., Hollenstein Ch., Elyaakoubi M., Schmitt J.P.M. // J. Appl. Phys. 2004. V. 95. P. 4559.
Kawamura E., Lieberman M.A., Graves D.B. // Plasma Sources Sci. Technol. 2014. V. 23. P. 064003.
Perret A., Chabert P., Booth O.-P., Jolly J., Gulion J., Auvray Ph. // Appl. Phys. Lett. 2003. V. 83. P. 243.
Ohiwa T., Hayashi H., Sakai I., Kolma A., Shinomiya E. // Japanese J. Appl. Phys. 2004. V. 43. P. 6413.
Goto H.H., Lome H.D., Ohmi T. // J. Vac. Sci. Technol. A. 1992. V. 10. P. 3048.
Chen Z., Rauf S., Collins K. // J. Appl. Phys. 2010. V. 108. P. 073301.
Sharma S., Sirse N., Sen A., Turner M.M., Ellingboe A.R. // Phys. Plasmas. 2019. V. 26. P. 103508.
Wilczek S., Trieschmann J., Schulze J., Schuengel E., Brinkmann R.P., Derzsi A., Korolov I., Donkó Z., Mussenbrock T. // Plasma Sources Sci. Technol. 2015. V. 24. P. 024002.
Wilczek S., Trieschmann J., Eremin D., Brinkmann R.P., Schulze J., Schuengel E., Derzsi A., Korolov I., Hartmann P., Donkó Z., Mussenbrock T. // Phys. Plasmas. 2016. V. 23. P. 063514.
Sharma S., Sirse N., Sen A., Turner M.M., Ellingboe A.R. // Phys. Plasmas. 2016. V. 23. P. 110701.
Kitamura T., Nakano N., Makabe T., Yamaguchi Y. // Plasma Sources Sci. Technol. 1993. V. 2. P. 40.
Segawa S., Kurihara M., Nakano N., Makabe T. // Japanese J. Appl. Phys. 1999. V. 38. P. 4416.
Park A.E., Cho B.U., Lee J. K. // IEEE Trans. Plasma Sci. 2003. V. 31. P. 628.
Perrin J., Schmitt J., Hollenstein C., Howling A., Sansonnes L. // Plasma Phys. Contr. Fusion. 2000. V. 42. P. B353.
Schmitt J., Elyaakoubu M., Sansonnes L. // Plasma Sources Sci. Technol. 2002. V. 11. P. A206.
Mussenbrock T., Hemke T., Ziegler D., Brinkman R.P., Klick M. // Plasma Sources Sci. Technol. 2008. V. 17. 025018.
Savas S.E., Plavidal R.W. // J. Vacuum Sci. Technol. A. 1988. V. 6 (3). P. 1775.
Liberman M.A., Booth J.P., Chabert P., Rax J.M., Tur-ner M.M. // Plasma Sources Sci. Technol. 2002. V. 11. P. 283.
Alshakami K.A., Daniels S. // AIP Advances. 2019. V. 9. P. 035047.
Hwang S.M., Garay AA., Lee W.I., Chung C.W. // Thin Solid Films. 2015. V. 587. P. 28.
Cooperberg D.J. // Phys. Plasmas. 1998. V. 5. P. 862.
Cooperberg D.J., Birdsall C.K. // Plasma Sources Sci. Technol. 1998. V. 7. P. 41.
Двинин С.А., Вологиров А.Г., Михеев В.B., Свиридкина В.С. // Физика плазмы. 2008. Т. 34. С. 746.
Chabert P. // J. Phys. D.: Appl. Phys. 2007. V. 40. P. R63.
Lee I., Graves D.B., Lieberman M.A. // Plasma Sources Sci. Technol. 2008. V. 17. P. 015018.
Sansonnens L., Howling A.A., Hollenstein Ch. // Plasma Sources Sci. Technol. 2006. V. 15. P. 302.
Bachinski M.P. // Radio Corp. of America Review. 1967. V. 28. P. 111.
Miller E.K. // Radio Sci. 1968. V. 3. P. 1175.
Schiff M.L., Fejer J.A. // Radio Sci. 1970. V. 5. P. 819.
Meyer P., Vernet N., Lassudrie-Duchesne P. // J. Appl. Phys. 1974. V. 45. P. 700.
Hebner G.A., Barnat E.V., Miller P.A., Paterson A.M. Holland J.P. // Plasma Source Sci. Technol. 2006. V. 15. P. 889.
Gekelman W., Barnes M., Vincena S., Pribyl P. // Phys. Rev. Lett. 2009. V. 103. P. 045003.
Sung D., Woo J., Lim K., Kim K., Volynets V., Kim G.-H. // J. Appl. Phys. 2009 V. 106. P. 023303.
Xu X., Zhao S.-X., Zhang Yu-Ru, Wang Y-N. // J. Appl. Phys. 2010. V. 108. P. 043308.
Eremin D., Hemke T., Brinkmann R.P., Mussenbrock T. // J. Phys. D: Appl. Phys. 2013. V. 46. P. 084017.
Kawamura E., Lieberman M.A., Lichtenberg A.J. // Phys. Plasmas. 2018. V. 25. P. 093517.
Двинин С.А., Довженко В.А., Солнцев Г.С. // Физика плазмы. 1982. Т. 8. С. 1228.
Двинин С.А., Постников С.А., Солнцев Г.С., Цветкова Л.И. // Физика плазмы. 1983. Т. 9. С. 1297.
Yasaka Y., Nozaki D., Koga K., Ando M., Yamamoto M. Coto N., Ishii N., Morimoto T. // Japan J. Appl. Phys. 1999. V. 38. P. 4309.
Bohm D. // The characteristics of electrical discharges in magnetic field. N.-Y.: Mc-Graw-Hill, 1949. P. 77.
Child C.D. // Phys. Rev. (Series I). 1911. V. 32. P. 492.
Langmuir I. // Phys. Rev. 1913. V. 2. P. 450.
Perret A., Chabert P., Jolly J., Booth J.P. // Appl. Phys. Lett. 2005. V. 86. P. 021501.
Langmuir I., Mott-Smith H.M. // Phys. Rev. 1926. V. 28. P. 727.
Чан П., Тэлбот Л., Турян К. Электрические зонды в неподвижной и движущейся плазме. М.: Мир, 1978. 201 с.
Laframboise J.G., Rubinstein J. // Phys. Fluids. 1976. V. 19. P. 1900.
Laframboise J.G. The theory of spherical and cylindrical probes in a collisionless, Maxwellian plasma at rest. University of Toronto Institute for Aerospace Studies (UTIAS) Report 100. 1966.
Lieberman M.A. // IEEE Trans. On Plasma Science. 1998. V. 16. P. 638.
Lieberman M.A. // IEEE Trans. Plasma Sci. 1989. V. 17. P. 338.
Czarnetzki U. // Phys. Rev. E. 2013. V. 88. P. 063101.
Никольский В.В., Никольская Т.А. Электродинамика и распространение радиоволн. М.: Наука, 1989. 543 с.
Фелсен Л., Маркувитц Н. Излучение и рассеяние волн. Т. 1. М.: Мир. 1978. 547 с.
Вайнштейн Л.А. Электромагнитные волны. М.: Радио и связь, 1990. 442 с.
Силин В.П., Рухадзе А.А. Электромагнитные свойства плазмы и плазмоподобных сред. М.: Атомиздат, 1961. 243 с.
Годяк В.А. // ЖТФ. 1972. V. 16. С. 1073.
Kaganovich I.D., Polomarov O.V., Theodosiou C.E. // Phys. Plasmas. 2004. V. 11. P. 2399.
Kaganovich I.D., Polomarov O.V., Theodosiou C.E. // IEEE Trans. Plasma Sci. 2006. V. 34. P. 696.
Polomarov O.V., Theodosiou C.E., Kaganovich I.D., Economou D.J., Ramamurthi B.N. // IEEE Trans. Plasma Sci. 2006. V. 34. P. 767.
Godyak V.A., Kolobov V.I. // Phys. Rev. Lett. 1997. V. 79. P. 4589.
Hagelaar G.J.M. // Plasma Sources Sci. Technol. 2008. V. 17. P. 025017.
Hagelaar G.J.M. // Phys. Rev. Lett. 2008. V. 100. P. 025001.
Ding Z.F., Sun B., Huo W.G. // Phys. Plasmas. 2015. V. 22. P. 063504.
Triesmachmann J., Mussenbrock T. // Plasma Sources Sci. Technol. 2017. V. 26. P. 024004.
Kaganovich I.D. // Phys. Rev. Lett. 2002. V. 89. P. 2065006.
Turner M.M. // J. Phys. D: Appl. Phys. 2009. V. 42. P. 194008.
Lafleur T., Chabert P. // Plasma Sources Sci. Technol. 2015. V. 24. P. 044002.
Lafleur T., Chabert P., Turner M.M., Booth J.P. // Plasma. Sources Sci. Technol. 2014. V. 23. P. 015016.
Lafleur T. // Plasma Sources Sci. Technol. 2016. V. 25. P. 013001.
Kaganovich I.D., Tsendin L.D. // IEEE Trans. Plasma Sci. 1992. V. 20. P. 86.
Kawamura E., Lieberman M.A. Lichtenberg A.J. // Phys. Plasmas. 2014. V. 21. P. 123505.
Vahedi V., Lieberman M.A., Dipiezo G., Rognlien T.D., Hewett D. // J. Appl. Phys. 1995. V. 78. P. 1446.
Shaing K.C. and Aydemir A.Y. // Physics of Plasmas. 1997. V. 4. P. 3163.
Ahr P., Schungel E., Schulze J., Tsankov Ts.V., Czarnetszki U. // Plasma. Sources Sci. Technol. 2015. V. 24. P. 044006.
Wegner Th., Kullig C., Melchener J. // Plasma. Sources Sci. Technol. 2015. V. 24. P. 044001.
Schulze J., Donkó Z., Lafleur T., Wilczek S., Brink-mann R.P. // Plasma. Sources Sci. Technol. 2018. V. 27. P. 055010.
Vass M., Wilczek S., Lafleur T., Brinkmann R.P., Don-kó Z., Schulze J. // Plasma. Sources Sci. Technol. 2020. V. 29. P. 026019.
Булкин П.С., Двинин С.А., Солнцев Г.С. // Вестник Московского ун-та. Сер. 3. 1982. Т. 23. С. 84.
Гуревич А.В., Шварцбург А.Б. Нелинейная теория распространения радиоволн в ионосфере. М.: Наука. ГРФМЛ. 1973. 272 с.
Шкаровский И., Джонстон Т., Бачинский М. Кинетика частиц в плазме. М.: Атомиздат, 1969. 396 с.
Cibin P.K. // Plasma Physics. 1980. V. 22. P. 609.
Никольский В.В. Вариационные методы для внутренних задач электродинамики. М.: Наука. 1967. С. 169.
Михлин С.Г. Вариационные методы в математической физике. М.: Наука, 1970. 512 с.
Пономарев В.Н., Солнцев Г.С. // ЖТФ. 1966. Т. 36. С. 1376.
Тихонов А.Н., Самарский А.А. Уравнения математической физики. М., Наука, 2004. 742 с.
Стреттон Дж.А. Теория электромагнетизма. М.: ГИТТЛ, 1948. 539 с.
Дополнительные материалы отсутствуют.