Физика плазмы, 2020, T. 46, № 3, стр. 257-263

1. ВВЕДЕНИЕ

В наши дни непрерывно растет научный интерес к электрон-позитрон-ионной плазме (e–p–i-плазма). Только в XXI в. было опубликовано более сотни статей, посвященных этой теме. Этот интерес объясняется существенным прогрессом в наблюдательной астрофизике, который привел к открытию и активному изучению таких необычных компактных объектов как магнитары, релятивистских струй, высвобождаемых из активных ядер галактик и т. п. Считается, что магнитосфера нейтронных звезд состоит из e–p–i-плазмы. Наличие позитронов и электронов обусловлено неустойчивостью в сверхсильном магнитном поле. Ионы появляются от внутренних источников, например, в результате испарения или сейсмических процессов на поверхности звезды, а также рождаются снаружи в процессе аккреции [1]. Множество примеров [2, 3] показали важность изучения нелинейных структур (ударных волн, солитонов и т.п.), имеющих место в e–p–i-плазме.

Магнитозвуковые солитоны – это фундаментальная мода в замагниченной плазме. Они распространяются перпендикулярно внешнему магнитному полю. Нелинейные магнитозвуковые волны интенсивно изучались, так как они играют огромную роль в нагреве частиц и их ускорении в космической и термоядерной плазме [4–8]. В работе [9] исследовались магнитозвуковые волны в плазме, распространяющиеся под углом к магнитному полю, которая моделировалась би-анизотропным распределением Кеирнса. В работе [10] исследовались низкочастотные магнитозвуковые волны в столкновительной плазме с положительными и отрицательными ионами одинаковой массы и электронами. Был проведен анализ нелинейного поведения магнитозвуковых солитонов и ударных структур произвольной амплитуды в спиновой квантовой плазме [11], показавший, что за диссипацию отвечает магнитная диффузия. В работе [12] исследовались двумерные цилиндрические быстрые магнитозвуковые солитоны в пылевой плазме, а в [13] были проведены параметрические исследования нелинейных наклонно распространяющихся магнитозвуковых волн в плазме с двумя видами ионов. Нелинейные магнитозвуковые волны в бесстолкновительной однородной замагниченной квантовой плазме были исследованы с помощью двухжидкостной квантовой магнитогидродинамической модели [14]. В [15] изучались быстрые магнитозвуковые солитоны, распространяющиеся под углом к магнитному полю в холодной бесстолкновительной плазме. Возбуждение и затухание нелинейных пылевых магнитозвуковых волн в диссипативной плазме было исследовано в [16]. В [17] было проведено исследование магнитозвуковых солитонов для электронных магнитогидродинамических уравнений. В [18] изучалось распространение двумерных цилиндрических быстрых магнитозвуковых солитонов в теплой пылевой плазме. В [19] изучались магнитозвуковые солитоны в плотной астрофизической e–p–i-плазме.

Следует указать, что, как правило, e–p–i-плазма замагничена и типичные цилиндрические структуры имеют ось симметрии, параллельную магнитному полю. Именно по этой причине целью многих работ является поиск решения в виде цилиндрических магнитозвуковых солитонов в e–p–i-плазме. Abdikian [20] провел иследование быстрых магнитозвуковых солитонов в вырожденной квантовой e–p–i-плазме [21], которое показало, что потенциал Бома оказывает основное влияние на периодические и солитонные структуры. Решения в форме цилиндрических магнитозвуковых солитонов сжатия и разрежения были получены в рамках трехкомпонентной электромагнитной газодинамической модели e–p–i-плазмы [1]. Цилиндрические магнитозвуковые солитоны в диссипативной горячей e–p–i-плазме были численно исследованы с помощью уравнения МКДВБ [22]. Тем не менее до сих пор с помощью приближенных аналитических решений уравнения МКДВБ не было достаточно изучено влияние цилиндрической симметрии на зависящие от времени магнитозвуковые солитоны с кинематической вязкостью. В настоящей статье мы исследуем этот вопрос. Во-первых, мы выводим уравнение МКДВБ для такой плазмы с помощью метода редуктивных возмущений, который отличается от приближения Сагдеевского потенциала [23]. Затем приводится приближенное аналитическое решение зависящего от времени уравнения МКДВБ. С помощью полученного решения демонстрируется влияние параметров на магнитозвуковые солитоны. Статья организована следующим образом. В разделе 2 приводятся основные уравнения. Влияние параметров обсуждается в разделе 3. В заключение основные выводы приводятся в разделе 4.

2. ОСНОВНЫЕ УРАВНЕНИЯ

Часто при исследовании e–p–i-плазмы используются основные уравнения без вязкости [24–26]. Тем не менее в настоящей статье мы рассматриваем трехжидкостную слабовязкую плазменную систему, состоящую из адиабатически горячих электронов, позитронов и однократно ионизированных ионов. Мы рассматриваем ион-ионные столкновения, приводящие к ионной кинематической вязкости. Мы исследуем цилиндрическую геометрию, в которой внешнее магнитное поле направлено вдоль направления z, т.е. ${{{\mathbf{B}}}_{{ext}}} = {{B}_{0}}{\mathbf{z}}$. Далее мы рассматриваем возмущения, распространяющиеся в радиальном направлении, и полагаем, что все переменные зависят только от радиальной координаты (т.е. $\partial {\text{/}}\partial \theta = \partial {\text{/}}\partial z = 0$). Нормализованные уравнения неразрывности и движения для трех жидкостей имеют вид

где, индекс $j = e,p,i$ относится к электронам, позитронам и ионам соответственно, параметр $\nu = 1$ соответствует цилиндрической геометрии, ${{\rho }_{j}} = $ $ = {{m}_{i}}{\text{/}}{{m}_{j}}$, ${{s}_{j}} = e{\text{/}}{{q}_{j}}$, ${{\sigma }_{j}} = {{T}_{{j0}}}{\text{/}}{{T}_{{e0}}}$; ${{n}_{{j0}}}({{n}_{j}})$ соответствует равновесной (возмущенной) концентрации, ${{\gamma }_{j}}$ – показатель адиабаты j-й компоненты, ${{v}_{{j\theta }}}({{v}_{{jr}}})$ – азимутальная (радиальная) компонента скорости соответственно. $\beta {\kern 1pt} ' = c_{s}^{2}{\text{/}}v_{A}^{2}$ (${{c}_{s}}$ – ионная звуковая скорость и ${{v}_{A}}$ – альфвеновская скорость в e–i-плазме) относится к параметру плазмы $\beta = 8\pi \Sigma {{n}_{{j0}}}{{T}_{{j0}}}{\text{/}}B_{0}^{2}$ как $\beta {\kern 1pt} ' = \chi {\text{/}}[2(1 + {{\delta }_{i}}{{\sigma }_{i}} + {{\delta }_{p}}{{\sigma }_{p}})]{\kern 1pt} {\kern 1pt} \beta $, где $\chi = {{\delta }_{i}} + \mu (1 + {{\delta }_{p}})$, ${{\delta }_{i}} = {{n}_{{i0}}}{\text{/}}{{n}_{{e0}}}$, ${{\delta }_{p}} = {{n}_{{p0}}}{\text{/}}{{n}_{{e0}}}$, $\mu = {{m}_{e}}{\text{/}}{{m}_{i}}$. В равновесии ${{\delta }_{p}} + {{\delta }_{i}} = 1$. ${{\tilde {\eta }}_{j}}$ – кинематическая вязкость j-й компоненты, нормализованная на $v_{A}^{2}{\text{/}}{{\omega }_{0}}$, где ${{\omega }_{0}} = {{({{\omega }_{{ci}}}{{\omega }_{{ce}}})}^{{1/2}}}$ – нижняя гибридная частота, которая является верхним пределом частоты для магнитозвуковых волн в e–i-плазме. ${{\omega }_{{cj}}} = e{{B}_{0}}{\text{/}}{{m}_{j}}c$ является циклотронной частотой j-й компоненты. Предположим, что возмущение компонент электромагнитного поля лежит в плоскости (r, θ), таким образом, ${\mathbf{E}} = $ $ = ({{E}_{r}},{{E}_{\theta }},0)$. Также предположим, что возмущенное и внешнее магнитные поля сонаправлены, так что B = (0, 0, B_z).

Уравнения Максвелла [27] для электрического и магнитного поля имеют вид

где символом Λ обозначено отношение $v_{A}^{2}{\text{/}}{{c}^{2}}$. Плотности нормализованы на соответствующие равновесные значения, скорости нормализованы на альфвеновскую скорость ${{v}_{A}}$, магнитное поле на внешнее постоянное поле ${{B}_{0}}$, электрическое поле на ${{v}_{A}}{{B}_{0}}{\text{/}}c$, время и пространственные переменные на нижнюю гибридную частоту ${{\omega }_{0}}$ и ${{v}_{A}}{\text{/}}{{\omega }_{0}}$, соответственно. В соответствии с двумя высоко- и низкочастотными моделями, здесь мы рассматриваем низкочастотную ветвь магнитозвуковых волн, для которой частота $\omega \to 0$, в то время как волновое число $k \to 0$.

Для вывода эволюционного уравнения, которое описывает динамику внутренних распространяющихся солитонных структур в дальнем поле, мы вводим растянутые независимые переменные $\xi = - {{\varepsilon }^{{1/2}}}(r + {{v}_{0}}t)$ и $\tau = {{\varepsilon }^{{3/2}}}t$, где ε – малый параметр и ${{v}_{0}}$ – линейная бездисперсионная фазовая скорость волны, отнесенная к ${{v}_{A}}$. В случае поперечного сжатия в сильном магнитном поле вязкость плазмы практически такая же, как в незамагниченном случае, и считается малой, т. е. $\mathop {\tilde {\eta }}\nolimits_j = {{\varepsilon }^{{1/2}}}{{\eta }_{j}}$. В уравнении (1) мы предположили, что компоненты адиабатически нагреты. Предположение об адиабатичности обосновано, так как изменение энтропии, связанное с генерацией тепла в результате вязкой диссипации, является эффектом более высокого порядка и здесь им можно пренебречь. Зависимые переменные раскладываются в ряд следующим образом [28–30]: ${{n}_{j}} = 1 + \varepsilon {{n}_{{j1}}} + $ $ + {\kern 1pt} \;{{\varepsilon }^{2}}{{n}_{{j2}}} + ...$, ${{v}_{{jr}}} = \varepsilon {{v}_{{jr1}}} + {{\varepsilon }^{2}}{{v}_{{jr2}}} + ...$, ${{v}_{{j\theta }}} = {{\varepsilon }^{{3/2}}}{{v}_{{j\theta 1}}} + $ $ + \;{{\varepsilon }^{{5/2}}}{{v}_{{j\theta 2}}} + ...$, ${{B}_{z}} = 1 + \varepsilon {{B}_{{z1}}} + {{\varepsilon }^{2}}{{B}_{{z2}}} + ...$, ${{E}_{{j\theta }}} = $ $ = {{\varepsilon }^{{3/2}}}{{E}_{{r1}}} + {{\varepsilon }^{{5/2}}}{{E}_{{r2}}} + ...$ и ${{E}_{\theta }} = \varepsilon {{E}_{{\theta 1}}} + {{\varepsilon }^{2}}{{E}_{{\theta 2}}} + ...$.

Подставляя разложения в (1) и (2), для низшей степени ε получим

Для более высоких степеней мы получаем эволюционное уравнение для ${{B}_{{z1}}}$, которое сводится к уравнению МКДВБ

где коэффициент нелинейной связи a, коэффициент дисперсии b и коэффициент c при члене, характеризующем вязкую диссипацию, имеют, соответственно, вид где,

В отсутствие c и h, т.е. при $c = 0$ и $h = 0$ ($\nu = 0$ для одномерной геометрии), уравнение (3) принимает вид хорошо известного уравнения Кортевега де Вриза (КДВ), которое имеет решение в виде уединенной волны:

где ${{B}_{{zm}}} = \sqrt {3M{\text{/}}a} $ и $W = \sqrt {b{\text{/}}M} $ – амплитуда и ширина солитона соответственно.

Для малых значений c и h предположим, что амплитуда, ширина и скорость магнитозвукового солитона зависят от τ, и приближенное решение уравнения (3) имеет вид

где амплитуда ${{B}_{{zm}}}(\tau ) = \sqrt {3M(\tau ){\text{/}}a} $, $W(\tau ) = \sqrt {b{\text{/}}M(\tau )} $ и скорость $M(\tau )$ должны быть определены.

Для уравнения КДВ хорошо известно, что

является сохраняющейся величиной. Используя (6), получим

Дифференцирование (7) по τ и использвание (3) и условий $\frac{{\partial {{\varphi }_{1}}}}{{\partial \xi }}$, $\frac{{{{\partial }^{3}}{{\varphi }_{1}}}}{{\partial {{\xi }^{3}}}} \to 0$ как $\xi \to \pm \infty $, дает

Подставляя (8) в (9), получим уравнение

которое является уравнением Бернулли, где $P = 4h{\text{/}}3$ и $Q = 4c{\text{/}}15b$. Положив $M(0) = {{M}_{0}}$ для $\tau = 0$, получим

Таким образом, форма медленной зависимости от времени магнитозвукового солитонного решения МКДВБ (3) определяется выражением (6). Амплитуда и ширина солитонов также определяются.

3. ВЛИЯНИЕ ПАРАМЕТРОВ

Рассматриваемая задача содержит множество параметров, которые влияют на структуру нелинейной волны: параметр $\beta {\kern 1pt} '$, который определяет параметр плазмы $\beta $, относительная позитрон-электронная плотность ${{\delta }_{p}}$, которая характеризует концентрацию позитронов в плазме, относительные температуры ${{\delta }_{i}}$ и ${{\delta }_{p}}$, три показателя адиабаты γ_j трех жидкостей и параметр Λ, три нормализованных коэффициента кинематической вязкости ${{\gamma }_{j}}$, которые характеризуют интенсивность диссипации. Для одинаковых температур и однократно ионизованных ионов разных типов, кинематические вязкости электронов и позитронов связаны с кинематической вязкостью ионов следующим образом: ${{\eta }_{{e,p}}} \approx {{\mu }^{{ - 1/2}}}\eta (\eta = {{\eta }_{i}})$, в этом случае коэффициент вязкой диссипации h принимает вид $[{{\delta }_{i}} + {{\mu }^{{1/2}}}(1 + {{\delta }_{p}})\eta ]$. Предположим, что все компоненты находятся в термодинамическом равновесии: ${{\delta }_{i}} = {{\delta }_{p}} = 1$. Далее предположим, что показатели адиабаты равны ${{\gamma }_{j}} = 5{\text{/}}3$. Утверждение, что ${{\gamma }_{j}} = 5{\text{/}}3$ также означает, что мы игнорируем эффекты разделения зарядов, которые становятся важными только в случаях высоких частот и коротких длин волн. Мы положили $\Lambda = 0$ (если обратное не оговорено особо), так как этот параметр очень мал для малой скорости, малой частоты и длинных волн, и дисперсии, обусловленной в основном инертностью электронов и позитронов. Тем не менее мы также кратко описываем эффекты малых, но конечных токов смещения (т.е. $\Lambda \ne 0$) для различных нелинейных структур. Три коэффициента a, b и c зависят от различных плазменных параметров ${{\delta }_{p}}$, $\tilde {\beta }$, η и Λ, которые влияют на амплитуду и ширину цилиндрических магнитозвуковых солитонов.

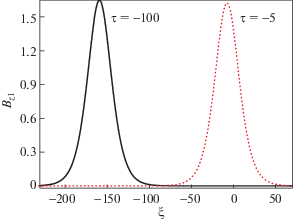
На рис. 1 показан цилиндрический магнитозвуковой солитон, эволюционирующий со временем, т.е. $\tau = - 100$ и $\tau = - 5$. Понятно, что магнитозвуковой солитон ослабляется с течением времени. Для выбранных нами параметров затухание медленное.

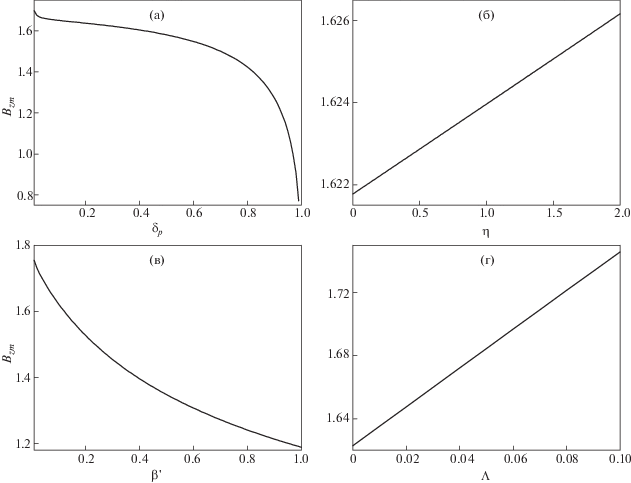
На рис. 2а показана зависимость амплитуды магнитозвукового солитона от относительной позитрон-электронной плотности ${{\delta }_{p}}$. Было найдено, что амплитуда солитона в цилиндрической геометрии уменьшается при увеличении ${{\delta }_{p}}$. Когда ${{\delta }_{p}}$ меньше 0.8, амплитуда снижается медленно, в противном случае амплитуда снижается быстро. На рис. 2б показана зависимость амплитуды магнитозвукового солитона от кинематической вязкости η. Было найдено, что с возрастанием вязких диссипативных эффектов, амплитуда солитона в цилиндрической геометрии возрастает, и диссипативные эффекты меньше влияют на амплитуду. На рис. 2в график амплитуды солитона представлен в зависимости от параметра $\eta $, который демонстрирует, что амплитуда уменьшается с увеличением $\beta {\kern 1pt} '$, и магнитозвуковой солитон имеет наибольшую амплитуду при $\beta {\kern 1pt} ' = 0$. На рис. 2г показана зависимость амплитуды солитона от параметра Λ. Заметно, что амплитуда магнитозвукового солитона увеличивается с увеличением Λ и достигает минимума, когда $\Lambda = 0$ при фиксированных остальных параметрах.

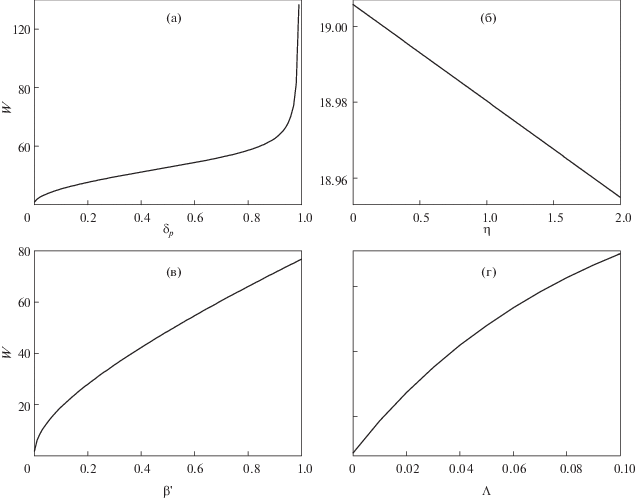
На рис. 3а показана зависимость ширины солитона от параметра $W(\tau )$ от относительной позитрон-электронной плотности ${{\delta }_{p}}$. Понятно, что когда ${{\delta }_{p}}$ возрастает, ширина солитона возрастает в цилиндрической геометрии. Когда ${{\delta }_{p}}$ меньше 0.8, амплитуда возрастает медленно, в противном случае быстрее. Магнитозвуковой солитон имеет наименьшую амплитуду при отсутствии позитронной плотности при фиксированных других параметрах. На рис. 3б показана зависимость ширины солитона от кинематических вязкостей η. Ясно, что при усилении вязких диссипативных эффектов ширина солитона в цилиндрической геометрии уменьшается, и диссипативные эффекты также оказывают меньшее влияние на ширину. На рис. 3в график ширины солитона в цилиндрической геометрии изображен в зависимости от параметра $\beta {\kern 1pt} '$ и демонстрирует рост ширины солитона с ростом параметра $\beta {\kern 1pt} '$. На рис. 3г показана зависимость ширины солитона от Λ, из которой следует, что ширина увеличивается с увеличением Λ.

Отметим, что согласно рис. 2 и рис. 3 изменение параметров ${{\delta }_{p}}$, η и $\beta {\kern 1pt} '$ противоположно влияет на изменения амплитуды и ширины, в то время как изменение параметра Λ отражается на амплитуде и ширине одинаковым образом.

4. ВЫВОДЫ

В данной статье мы исследовали цилиндрический магнитозвуковой солитон, распространяющийся в диссипативной горячей трехкомпонентной плазменной системе, состоящей из электронов, позитронов и ионов. Мы воспользовались методом редуктивных возмущений для вывода модифицированного уравнения КДВ-Бюргерса, которое описывает динамику нелинейных волн в дальнем поле, и получили солитонное решение этого уравнения. Мы анализируем влияние различных физических параметров, таких как параметр $\beta {\kern 1pt} '$, относительная позитрон-электронная плотность, кинематическая вязкость η и параметр Λ на магнитозвуковой солитон. Указанные параметры существенно влияют на нелинейную структуру магнитозвукового солитона в рассматриваемой плазме. Результаты работы могут быть применены к плазме с кинематической вязкостью как в лабораторных условиях, так и в условиях космического пространства (например, для магнитосферы нейтронных звезд).

Эта работа поддержана Проектом финансирования научных исследований молодых учителей Ланьчжоуского городского университета (no. LZCUQN2018-06), Проектом поддержки докторских исследовательских стартапов Ланьчжоуского городского университета (LZCU-BS2018-13) и Фондом талантов провинции Ганьсу.