1. На главную
  2. Электронные версии
  3. Физика плазмы
  4. T. 46, № 3, 2020

Физика плазмы, 2020, T. 46, № 3, стр. 195-205

Статистическая модель квазиконтинуума тяжелых ионов в горячей плазме

А. В. Демура a, Д. С. Леонтьев a, *, В. С. Лисица a, В. А. Шурыгин a

a Национальный исследовательский центр “Курчатовский институт”
Москва, Россия

* E-mail: leontievdmitiy@gmail.com

Поступила в редакцию 22.04.2019
После доработки 01.09.2019
Принята к публикации 26.09.2019

Полный текст (PDF)

Аннотация

Предложено статистическое описание формы спектров тяжелой примеси, соответствующих квазинепрерывному распределению излучения, называемому квазиконтинуумом, и наблюдаемых в токамаках и стеллараторах, в частности, для ионов вольфрама в области ∼2–7 нм. Метод основан на статистической плазменной модели атома, позволяющей выразить структуру квазиконтинуума через распределение электронной плотности многоэлектронных ионов. В качестве модельного распределения плотности использовано распределение Слэтера. Квазиконтинуум формируется огромным числом близко расположенных линий ионов различной степени ионизации, и его расчет сопряжен со значительными трудностями. Сравнение результатов статистического подхода с квантовыми поуровневыми кодами показывает, что такая модель правдоподобно описывает огибающие массива индивидуальных линий в спектре ионов. Статистическая модель атома является, в отличие от поуровневых кодов, достаточно простой и доступной для широкого круга пользователей. Проведено моделирование квазиконтинуума ионов вольфрама, золота, свинца и гадолиния, наблюдаемых в плазме термоядерных установок. Результаты находятся в достаточно хорошем соответствии с экспериментальными данными. Исследование квазиконтинуума вольфрама представляет интерес для диагностики плазмы, определения плотности этой примеси и ее транспорта в термоядерных установках.

Ключевые слова: излучения плазмы, тяжелые ионы, квазиконтинуум, статистическая теория, процессы в плазме

1. ВВЕДЕНИЕ

Важной задачей современных термоядерных исследований на токамаках является оптимизация планируемого квазистационарного режима с улучшенным удержанием плазмы в Н-моде [1–16]. Взаимодействие плазмы с конструкционными элементами камеры и дивертора, изготовленными из вольфрама, приводит к неизбежному его попаданию в разряд. Даже не самое большое накопление вольфрама в центре плазменного шнура в Н-моде [8, 12, 15] может вызывать потерю его устойчивости [12] из-за развития МГД-процессов, переход в L-моду, радиационный коллапс и срыв разряда. Для контроля этого процесса проводят как отдельные спектральные измерения плотности примеси вольфрама, так и мониторинг профилей плотности в сечении, что представляет значительный интерес для диагностики плазмы современных крупных токамаков и стеллараторов [1–19]. Однако наблюдаемые в плазме термоядерных установок спектры примеси вольфрама имеют сложную структуру [1–19], обусловленную множеством радиационных переходов ионов разной кратности. Массивы перекрывающихся спектральных линий всех наиболее представленных в сечении плазмы зарядовых состояний (ЗС) ионов вольфрама образуют квазинепрерывный спектр – “квазиконтинуум” в области длин волн ∼2–7 нм [1–19]. Как показывают оценки, число спектральных линий здесь может достигать порядка 104 [2].

Необходимый мониторинг плотности вольфрама реализуется в эксперименте на основе измерения и анализа: (i) интегральной эмиссии примеси рентгеновскими детекторами [11, 12]; (ii) интенсивности отдельных выделенных в спектре линий ионов вольфрама W45+ и W46+ [5–10]; (iii) интенсивности эмиссии в области квазиконтинуума [1–19]. Последние в настоящее время широко распространены из-за характерных четко отличимых и хорошо воспроизводимых особенностей этой области спектра, достаточной точности и надежности измерений. Однако из-за сложности процессов формирования квазиконтинуума связь его интенсивности с плотностью примеси представляет пока не вполне решенную проблему.

Квазиконтинуум наиболее представленных ионов вольфрама неоднократно наблюдался на токамаках ORMAK [1, 3], PLT [2, 3], ASDEX-Upgrade [6, 7, 9], JT60 [8, 10] и на стеллараторе LHD [17, 18]. На токамаке TEXT [4] были получены спектры таких тяжелых элементов, как вольфрам, золото и свинец. Кроме того, на стеллараторе LHD проводились исследования спектров циркония, молибдена, рутения, олова, ксенона, гафния, платины, золота, свинца, висмута и лантанидов с зарядом ядра в диапазоне 58–71 [18, 19]. Аналогичные закономерности наблюдались в спектрах Gd и Tb в лазерной плазме и в плазме вакуумной искры [20]. С ростом заряда ядра примеси и с ростом температуры область спектра, где наблюдается квазиконтинуум, смещается в сторону коротких длин волн (см. например, [19, 20]).

В настоящей работе для описания квазиконтинуума тяжелых элементов используется статистическая модель атома [21–28]. В [21–28] были уже получены универсальные статистические скоростные коэффициенты радиационно-столкновительных элементарных процессов в плазме, происходящих при участии тяжелых ионов, и продемонстрировано разумное согласие результатов с экспериментальными данными и поуровневыми вычислениями. Преимуществом статистической модели атома [21–28] являются также значительно меньшие затраты вычислительных ресурсов по сравнению с поуровневыми вычислениями (см., например, [17]).

Следует отличать статистическую модель атома [21–28], применяемую в настоящей работе, от других статистических моделей. Так, например, отметим статистический квазиклассический подход, развитый в работах [29–31] для описания полных радиационных потерь и основанный на водородоподобном приближении для уровней энергии внешних электронов и квазиклассическом движении электронов в центральном поле заряда ядра иона.

Описание формы квазиконтинуума тесно связано с общефизической проблемой спектрального распределения сил осцилляторов, сформулированной еще Фано и Купером [32]. Такое распределение определяется внутренней структурой многоэлектронных атомов (ионов), а плазма является фактором, выявляющим через ионизационное равновесие при данной температуре набор атомных структур, ответственных за образование наблюдаемого спектра. Квазиконтинуум отдельного иона, очевидно, формируется интенсивностями массива радиационных переходов, отвечающими распределению сил осцилляторов по энергетическому спектру. При этом вклад отдельного иона в распределение интенсивности квазиконтинуума можно находить различными методами: как путем поуровневых вычислений вероятностей всего массива переходов (см. [5–12, 17]), так и разбивая статистическое распределение электронной плотности Томаса–Ферми на “блоки”, отвечающие определенным значениям орбитальных моментов l и энергий – главных квантовых чисел n [27, 33, 34], и используя представления о связи энергетического спектра возбуждения массива атомных уровней и соответствующих сил осцилляторов с плазменными колебаниями электронов на определенной атомной оболочке [27, 28, 35]. В рамках последнего подхода [35], применяемого в настоящей работе и обсуждаемого также в [32], распределение сил осцилляторов по спектру целиком задается распределением электронной плотности в атоме. Важной особенностью такого распределения, независимо от выбираемой атомной модели, является наличие характерного максимума, определяющего обрыв наблюдаемых спектров в области больших частот. При этом конкретный вид распределения плотности можно также выбирать из различных моделей [27, 33–35]. Ниже используется распределение плотности по модели Слэтера [36], играющее важную роль в теории многоэлектронных атомов [37], с аппроксимацией вблизи ее максимума гауссовым распределением.

Наблюдаемый более 50 лет в различных экспериментах на токамаках и стеллараторах квазиконтинуум [1–15, 17–20] обладает, как отмечалось выше, важной качественной особенностью – “частотой отсечки”, то есть резко выделенным со стороны высоких частот или коротких длин волн краем спектра (см., например, [17]). В рамках статистической плазменной модели квазиконтинуума [21–28] эта особенность находит свое качественное объяснение: максимально возможные частоты в спектре излучения атома соответствуют наибольшим частотам “плазменных” колебаний его электронной оболочки. Это подтверждает правомерность применения статистической модели атома [21–28] к анализу квазиконтинуума. В этой связи любопытно добавить, что проявление коллективных свойств электронных конфигураций оболочек ионов тяжелых элементов [1–15, 17–20] в процессах фотопоглощения и фотоионизации было известно достаточно давно как в эксперименте, так и в квантовомеханической теории [38], и поэтому применение именно статистического подхода [21–28] к этой задаче вполне естественно и оправдано.

2. МОДЕЛИРОВАНИЕ КВАЗИКОНТИНУУМА МНОГОЭЛЕКТРОННЫХ ИОНОВ

Детальные поуровневые вычисления распределения интенсивности в спектрах вольфрама и других тяжелых элементов в термоядерной плазме очень трудоемки вследствие сложности многоэлектронной атомной структуры и наличия громадного числа близких спектральных переходов [17]. При этом многие авторы, например, считают, что квазиконтинуум формируется в основном за счет переходов с Δn = 0 [20], где n обозначает главное квантовое число атомного уровня. Например, подобные поуровневые расчеты проводились для условий стелларатора LHD [17]. Соответствующие этим расчетам экспериментальные спектры образованы большим числом радиационных переходов, включая спектральные линии всех представленных в зарядовом распределении ионов. При этом усреднение по аппаратной функции спектрометра в процессе измерений, приводит к дополнительному перекрытию наблюдаемых линий. Очевидно, что интерпретация таких экспериментальных данных очень сложна.

Наиболее адекватным физической постановке задачи является расчет “усредненных” спектров, представляющих собой огибающие множества линий в определенном спектральном диапазоне. Эти огибающие можно вычислить на основе статистической теории радиационно-столкновительных процессов с участием многоэлектронных ионов [21–28], позволяющей сравнительно быстро рассчитывать необходимые спектры в зависимости от параметров плазмы.

В статистическом подходе возбуждение ионов происходит налетающим потоком электронов плазмы [21–28]. Предполагается, что это возбуждение, как и излучение, носят коллективный характер и возникают на плазменных частотах, определяемых локальным распределением электронной плотности в атоме [35]

(1)
${{\omega }_{p}}(r) = \sqrt {\frac{{4\pi {{e}^{2}}n(r)}}{{{{m}_{e}}}}} ,$
где e – заряд электрона, me – его масса, n(r) – распределение электронной плотности.

Пользуясь правилом суммирования, соответствующие эффективные силы осцилляторов fij можно также связать с локальным распределением электронной плотности [21–28]: fij = 4πn(r)r2dr, с очевидной нормировкой на полное число электронов в атомной оболочке (в применении к рассматриваемой задаче) после интегрирования по радиусу. Таким образом, величины, рассчитываемые в рамках статистического метода, являются функционалами распределения плотности электронов в атоме, что позволяет добиться универсального описания разнообразных элементарных столкновительно-радиационных процессов для широкого ряда элементов.

Для описания спектральных свойств иона в рамках такого подхода необходимо распределение электронной плотности nnl(r) в его соответствующей валентной электронной оболочке (nl), где n – главное квантовое число, а l – орбитальное квантовое число оболочки. В качестве такого распределения электронной плотности в атомной оболочке используется аппроксимация Слэтера [36] (атомные единицы)

(2)
$n(r) \equiv {{n}_{{Sl}}}(r) = {{N}_{{Sl}}}{{r}^{{2k}}}{{e}^{{ - 2\gamma r}}},$
где нормировочная константа NSl определяется числом эквивалентных электронов, а постоянные γ и k задают энергию состояния и структуру волновой функции внешней оболочки иона.

Распределение электронной плотности (2) обладает максимумом, определяющим согласно (1) максимальное значение плазменной частоты, реализуемой в рассматриваемой атомной оболочке. При этом спектр излучения определяется из условия равенства излучаемой и плазменной частоты. При значении величины наблюдаемой частоты больше максимальной, спектр излучения согласно плазменной модели должен резко обрываться. Иначе говоря, структурной особенностью наблюдаемого квазиконтинуума [1–20] является достаточно резкий спад спектральной интенсивности при достижении частоты отсечки. Это свойство плазменной статистической модели подтверждает основную наблюдаемую закономерность, которая обнаруживается и в поуровневых расчетах [8, 17, 19].

Для выявления скейлинга частоты излучения ω от параметров слэтеровского распределения электронной плотности аппроксимируем его вблизи максимума в точке rmax=k/γ гауссовским профилем (G)

(3)
${{n}_{G}}(r) = \frac{{{{N}_{G}}}}{{{{{(2\pi )}}^{{3/2}}}\Delta {{r}^{3}}}}{{e}^{{ - \frac{{{{{(r - {{r}_{{\max }}})}}^{2}}}}{{2\Delta {{r}^{2}}}}}}} = {{n}_{{Sl}}}({{r}_{{\max }}}){{e}^{{ - \frac{{{{{(r - {{r}_{{\max }}})}}^{2}}}}{{2\Delta {{r}^{2}}}}}}},$
где NG – нормировочная постоянная для числа электронов на рассматриваемой оболочке, Δr – ширина гауссовского распределения. Величина Δr связана с параметрами этого распределения очевидным образом

(4)
${{n}_{{Sl}}}(r) \approx {{n}_{{Sl}}}({{r}_{{\max }}}){{e}^{{ - \frac{{|n_{{Sl}}^{{{\text{''}}}}({{r}_{{\max }}})|}}{{2n({{r}_{{\max }}})}}{{{(r - {{r}_{{\max }}})}}^{2}}}}},$
(5)
$\Delta r = \sqrt {\frac{{{{n}_{{Sl}}}({{r}_{{\max }}})}}{{{\text{|}}n_{{Sl}}^{{{\text{''}}}}({{r}_{{\max }}}){\text{|}}}}} = \frac{1}{\gamma }\sqrt {\frac{k}{2}} .$

Спектральное распределение удельных (на один ион) линейчатых радиационных потерь из объема dV на частоте перехода ω в интервале частот dω определяется общей формулой для мощности излучения [21–28]

(6)
$d{{Q}_{{ij}}}(\omega ) = a(\omega )\hbar \omega \cdot d\omega dV,$
где a(ω) – спектральный (безразмерный) коэффициент Эйнштейна для излучения, который выражается через сечение фотопоглощения [37],

(7)
$a(\omega ) = \frac{{{{\omega }^{2}}}}{{{{\pi }^{2}}{{c}^{2}}}}\sigma (\omega ).$

Взаимодействие электронов плазмы с атомами в [21–28] рассматривается в приближении эквивалентных фотонов Ферми [39], согласно которому электрическое поле эквивалентного потока фотонов определяется фурье-разложением электрического поля электрона, движущегося по классической траектории в поле возбуждаемого атома. Тогда сечение возбуждения связанных электронов в многоэлектронном ионе выражается через сечение фотопоглощения, для которого, в свою очередь, можно использовать упомянутую выше статистическую модель тяжелых атомов [21–28]. В итоге сечение фотопоглощения в статистической модели принимает вид [21–28, 35]

(8)
$\begin{gathered} \sigma (\omega ) = \frac{{2{{\pi }^{2}}{{e}^{2}}}}{{{{m}_{e}}c}}\int {{{d}^{3}}r\,n(r)\delta (\omega - {{\omega }_{p}}(r)) = } \\ \, = \frac{{2{{\pi }^{2}}{{e}^{2}}}}{{{{m}_{e}}c}}4\pi \sum\limits_{{{r}_{\omega }}} {r_{\omega }^{2}} {{\frac{{n({{r}_{\omega }})}}{{\left| {\frac{{d{{\omega }_{p}}(r)}}{{dr}}} \right|}}}_{{r = {{r}_{\omega }}}}}, \\ \end{gathered} $
(9)
$\omega = {{\omega }_{p}}({{r}_{\omega }}),$
где rω – корни уравнения (9). Рассмотрим уравнение (9) с плазменной частотой, определяемой гауссовским профилем плотности

(10)
$\begin{gathered} \omega = \sqrt {\frac{{4\pi {{e}^{2}}{{n}_{G}}({{r}_{\omega }})}}{m}} = \\ \, = {{\left( {\frac{{4\pi {{e}^{2}}{{N}_{G}}}}{{{{{(2\pi )}}^{{3/2}}}m\,\Delta {{r}^{3}}}}\exp \left[ { - \frac{{{{{({{r}_{\omega }} - {{r}_{{\max }}})}}^{2}}}}{{2\Delta {{r}^{2}}}}} \right]} \right)}^{{1/2}}}. \\ \end{gathered} $

Возведя в квадрат обе части уравнения, получим решения уравнения для эффективного радиуса, определяющего резонанс между плазменной и наблюдаемой частотами:

(11)
$\begin{gathered} r_{\omega }^{ \pm } = {{r}_{{\max }}} \pm 2\Delta r\sqrt {\left| {\ln x} \right|} , \\ x = \frac{\omega }{{\omega {\text{*}}}},\quad \omega {\text{*}} = \sqrt {\frac{{4\pi {{e}^{2}}{{N}_{G}}}}{{{{{(2\pi )}}^{{3/2}}}m\,\Delta {{r}^{3}}}}} . \\ \end{gathered} $

Величина ω* в (11) соответствует максимально возможной частоте спектра в (9)–(10), ввиду ограничения значений плотности атомных электронов. Отсюда следует, что в (11) величина x ≤ 1. Наличие максимальной возбуждаемой частоты перехода в ионе продемонстрировано на рис. 1, где представлены частоты, находящиеся в резонансе с плазменной частотой.

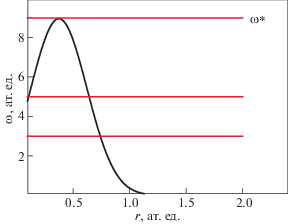
Рис. 1.

Схема резонансов между плазменной (сплошная кривая) и наблюдаемой частотой ω (горизонтальные линии). Наличие максимума плазменной частоты отвечает резкому обрыву спектра в области частот выше частоты отсечки ω*.

Имея в виду, что сечение фотопоглощения пропорционально силе осцилляторов [40], с учетом (4)–(11) его можно представить в виде

(12)
$\begin{gathered} \sigma (\omega ) = \frac{{4{{\pi }^{2}}}}{c}\omega \Delta {{r}^{2}}\left[ {\frac{{{{{({{r}_{{\max }}} + 2\Delta r\sqrt {\left| {\ln x} \right|} )}}^{2}}}}{{\left| {r_{\omega }^{ + } - {{r}_{{\max }}}} \right|}} + } \right. \\ \left. {\, + \frac{{{{{({{r}_{{\max }}} - 2\Delta r\sqrt {\left| {\ln x} \right|} )}}^{2}}}}{{\left| {r_{\omega }^{ - } - {{r}_{{\max }}}} \right|}}} \right] = \\ = \frac{{2{{\pi }^{2}}}}{c}\omega {{r}_{{\max }}}\left[ {\frac{{r_{{\max }}^{2} + 4\Delta {{r}^{2}}{\text{|}}\ln x{\text{|}}}}{{\gamma \Delta r\sqrt {{\text{|}}\ln x{\text{|}}} }}} \right]. \\ \end{gathered} $

Таким образом, структура сечения фотовозбуждения (12) вместе с поведением плазменной частоты, целиком определяют спектральную зависимость радиационных потерь в статистической плазменной модели [21–28].

Интересно сравнить результаты статистических расчетов распределений сил осцилляторов (или вероятностей радиационных переходов) по спектру с квантовыми. Результаты квантовых расчетов в работах [8, 10, 17, 19] представлены фактически в виде дельтаобразных распределений радиационных вероятностей переходов по длинам волн А(λ) для различных электронных конфигураций (см. рис. 2а и 2б). Для расчета такого распределения будем исходить из общего выражения для безразмерной вероятности радиационных переходов а(ω), имеющей в статистической модели вид (ср. [24])

(13)
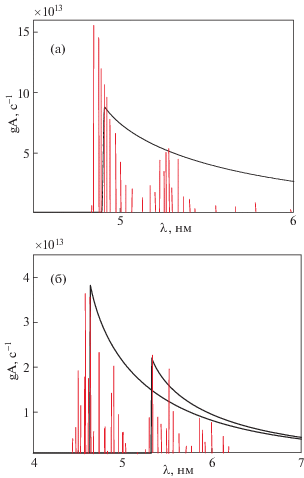
$\begin{gathered} a(\omega ) = \frac{{dA}}{{d\omega }} = \\ \, = \int\limits_0^r {dr{\text{'}}4\pi r{{{\text{'}}}^{2}}n(r{\text{'}})} \frac{{2{{\pi }^{2}}{{e}^{2}}}}{{mc}}\frac{{{{\omega }^{2}}}}{{{{\pi }^{2}}{{c}^{2}}}}\delta (\omega - {{\omega }_{p}}(r{\text{'}})). \\ \end{gathered} $
Рис. 2.

Сравнение статистических распределений коэффициентов Эйнштейна, умноженных на статистический вес с результатами квантовых расчетов, для W20+ (а) и W35+ (б). Для иона W20+ данные соответствуют переходу 4d104f 8–4d94f 9, а для иона W35+ – комбинации переходов 4p64d3–4p54d4 + 4p64d24f. Вертикальные линии – результаты поуровневых расчетов [17], а огибающие – результаты статистической модели (14).

Интегрируя (13) сначала по частоте с переменным верхним пределом (текущее ω), а затем по радиусу и преобразуя к шкале длин волн, приходим к выражению

(14)
$A(\lambda ) = \frac{{32{{\pi }^{2}}{{e}^{4}}}}{{{{m}^{2}}{{c}^{3}}}}\left[ {\int\limits_0^{r_{\lambda }^{ - }} {{{r}^{2}}{{n}^{2}}(r)dr} + \int\limits_{r_{\lambda }^{ + }}^\infty {{{r}^{2}}{{n}^{2}}(r)dr} } \right],$
где $r_{\lambda }^{ \pm } = {{r}_{{\max }}} \pm 2\Delta r\sqrt {\left| {\ln (\lambda {\text{*/}}\lambda )} \right|} $. Сравнение результатов статистических расчетов спектральных распределений вероятностей радиационных переходов с квантовыми представлено на рис. 2а,б, где приведены профили спектрального распределения коэффициентов Эйнштейна А(λ), полученные из (14) для ионов вольфрама W20+ и W35+ в плазменной модели атома и умноженные на статистический вес начального состояния g = = (2 j + 1). На этих рисунках показаны также положения спектральных линий с их вероятностями радиационных переходов, полученные на основе поуровневых расчетов [17]. Видно, что результаты статистического подхода являются огибающими массива индивидуальных спектральных линий для отдельного иона в соответствии с постановкой задачи в статистической модели. Видно, что массив переходов в ионе вольфрама W 20+ (рис. 2а), отвечающий переходам 4d104f 8–4d94f 9 из одной оболочки, описывается также одним распределением атомной электронной плотности типа (2), тогда как для иона W35+ необходим учет двух распределений плотности в соответствии с двумя массивами переходов 4p64d3 –4p54d4 + 4p64d24f. Таким образом, статистическая плазменная модель селективна по структуре электронных оболочек. Важно отметить, что сравнение расчетных данных демонстрирует хорошее соответствие как профилей огибающих, так и абсолютных значений вероятностей переходов (1013–1014 с–1). Удовлетворительное согласие результатов обоих расчетов указывает на достаточную реалистичность используемой плазменной модели.

Для сравнения с экспериментом спектральное распределение радиационных потерь сворачивалось с аппаратной функцией гауссовой формы, как и в работах [4, 8, 10, 17–19]. Используя (6) и (12), для спектральных линейчатых радиационных потерь из объема dV на частоте перехода ω и в интервале частот dω можно получить следующее выражение:

(15)
$\begin{gathered} dQ{{(\omega )}_{z}} = \frac{{2\hbar }}{{{{c}^{3}}}}{{\omega }^{3}}\int {d\omega {\text{'}}\omega {\text{'}}{{r}_{{\max }}}} \times \\ \, \times \left[ {\frac{{r_{{\max }}^{2} + 4\Delta {{r}^{2}}\left| {\ln (\omega {\text{'/}}\omega {\text{*}})} \right|}}{{\gamma \Delta r\sqrt {\left| {\ln (\omega {\text{'/}}\omega {\text{*}})} \right|} }}} \right]\frac{1}{{\sqrt {2\pi {{\delta }_{w}}} }}{{e}^{{ - \frac{{{{{(\omega - \omega {\text{'}})}}^{2}}}}{{2{{\delta }_{w}}}}}}}d\omega dV, \\ \end{gathered} $
где δW – квадрат полуширины аппаратной функции предполагаемого спектрометра. В настоящей работе величина δW в атомных единицах выбрана равной 0.02, чтобы отношение δW/ω2 соответствовало работе [4]. Это оказывается вполне достаточным для получения огибающих линий спектра в статистическом подходе. Расчеты для меньших значений δW демонстрируют малую чувствительность квазиконтинуума к величине δW. После перехода к шкале длин волн удельная мощность (на один ион с зарядом z) линейчатого излучения из единицы объема принимает вид

(16)
$\begin{gathered} dQ{{(\lambda )}_{z}} = \frac{{64{{\pi }^{5}}\hbar {{c}^{2}}}}{{\lambda {{{\text{*}}}^{4}}}}{{\left( {\frac{{\lambda {\text{*}}}}{\lambda }} \right)}^{5}}\left( {\int\limits_{\lambda {\text{*}}}^\infty {\frac{{d\lambda {\text{'}}}}{{\lambda {\text{'}}}}{{r}_{{\max }}}} \mathop \times \limits_{_{{_{{_{{_{{}}}}}}}}}^{^{{^{{}}}}} } \right. \\ \left. {\, \times \left[ {\frac{{r_{{\max }}^{2} + 4\Delta {{r}^{2}}\left| {\ln (\lambda {\text{*/}}\lambda {\kern 1pt} {\text{'}})} \right|}}{{\gamma \Delta r\sqrt {\left| {\ln (\lambda {\text{*/}}\lambda {\kern 1pt} {\text{'}})} \right|} }}} \right]\frac{1}{{\sqrt {2\pi {{\delta }_{\lambda }}} }}{{e}^{{ - \frac{{{{{(\lambda {\text{'}} - \lambda )}}^{2}}}}{{2{{\delta }_{\lambda }}}}}}}} \right)\frac{{d\lambda }}{{\lambda {\text{*}}}}dV. \\ \end{gathered} $

Полученную мощность удельных линейчатых спектральных радиационных потерь (16) следует усреднить по функции распределения примеси по зарядовым состояниям (ЗС), которую приближенно можно считать гауссовой

(17)
${{f}_{z}} = \frac{1}{{\sqrt {2\pi D} }}\exp \left[ { - \frac{{{{{(z - m)}}^{2}}}}{{2D}}} \right],$
где $m = \sum\nolimits_{z = 0}^Z {z{{f}_{z}}} \equiv \left\langle {{{Z}_{i}}} \right\rangle $ – средний заряд и D – дисперсия распределения по ЗС при данной температуре. Для расчета распределений по ЗС примесей тяжелых элементов в рамках статистической теории были рассчитаны отношения скорости ионизации [21–25] к скорости диэлектронной рекомбинации [27], и по этим данным построено распределение по ЗС при заданной температуре. Действительно, для многоэлектронных ионов тяжелых элементов при высоких температурах плазмы скорости диэлектронной рекомбинации оказываются заметно выше скоростей перезарядки на нейтральных атомах, концентрация которых в плазме относительно мала и, как правило, падает с ростом температуры. Поэтому только вклад диэлектронной рекомбинации определяет распределение по ЗС в этих случаях. Кроме того, в качестве сравнения для расчета равновесия по ЗС ионов вольфрама использовались данные работы [5], где средний заряд ионов оказывается больше, чем в статистической модели. Значения среднего заряда ионов в статистической модели при электронных температурах 800, 1500, 3000 и 5000 эВ следующие: 23, 28, 33 и 43, соответственно. В то время как согласно работам [5, 9] средние значения заряда ионов: 24, 30, 43 и 47. Как видно, при больших температурах различия между статистической моделью и пакетами квантовомеханических кодов [5, 9] возрастают. Эти пакеты включают расчеты как атомной кинетики в рамках радиационно-столкновительной модели, так и скоростных коэффициентов разнообразных столкновительно-радиационных процессов для разных ионов, а также расчеты равновесия по ЗС при заданной температуре [5, 9]. В используемые там скоростные коэффициенты вводились произвольные множители [5, 9] для подгонки под результаты сложных экспериментов на больших установках [5, 9]. Очевидно, что значения скоростных коэффициентов из [5, 9] могут заметно отличаться от значений, полученных из физических (“первых”) принципов. Поэтому отличие результатов статистической модели от [5, 9] не может рассматриваться как ее недостаток, так как по своему построению и результатам она может быть отнесена к расчетам из первых принципов в отличие от тех, которые используют практику применения подгоночных факторов для скоростных коэффициентов. Влияние среднего заряда на форму квазиконтинуума проиллюстрировано ниже на рис. 9.

Окончательный результат для суммарной мощности спектральных радиационных потерь принимает вид

(18)
$dQ{{(\lambda )}_{{{\text{tot}}}}} = \sum\limits_z {dQ{{{(\lambda )}}_{z}}} {{f}_{z}}.$

Для тестирования статистической модели наряду с ионами вольфрама были рассчитаны квазиконтинуумы ионов гадолиния, золота и свинца с близкими зарядовыми числами, наблюдаемыми в недавних экспериментах на стеллараторе LHD [17]. Отметим также, что такие спектры наблюдались в плазме вакуумной искры и лазерной плазме [20]. Полученные выше формулы статистической модели атома применены далее в разд. 3 к расчетам спектральных радиационных потерь в области квазиконтинуума 2–8 нм, который наблюдался в экспериментах на различных термоядерных установках.

3. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ

Параметры в электронном распределении -Слэтера (2) определялись следующим образом: степень k для каждого иона варьировалась так, чтобы обрыв по частоте (или длине волны) соответствовал пику наблюдаемого спектра для данного иона (данные для большинства ионов взяты из [17], рис. 2). Для остальных ионов вольфрама параметры подбирались исходя из того, что при различных температурах максимумы сохраняют свое положение. При этом, согласно поуровневым расчетам, с ростом заряда иона положение синтетического спектра смещается в область больших длин волн [8, 10]. Затравочным значением параметра k выбиралась величина орбитального момента данной оболочки, а затем оно корректировалось для наилучшего воспроизведения формы экспериментальных спектров. Параметр γ вычисляется по формуле

(19)
$\gamma = \sqrt {2mI} {\text{/}}\hbar ,$
где I – потенциал ионизации. Само значение I вычислялось по формулам статистической теории [21–28]. При этом нормировочная константа NSl выбрана так, чтобы интеграл по объему от распределения плотности был равен числу электронов на внешней (рассматриваемой) оболочке. В распределении Гаусса (3) нормировочная константа NG определена аналогично.

В таблице 1 представлены результаты расчетов параметров k, γ, NSl, NG для ионов вольфрама.

Таблица 1.
Zi Конфигурация внешней оболочки Число электронов k γ , ат. ед. NSl NG
4f оболочка
20 4d104f8 8 2.47 6.09 5.96 × 104 0.67
21 4d104f7 7 2.45 6.39 7.41 × 104 0.59
22 4d104f6 6 2.44 6.68 8.99 × 104 0.51
23 4d104f5 5 2.19 6.58 4.90 × 104 0.47
24 4d104f4 4 2.1 6.87 4.71 × 104 0.39
25 4d104f3 3 1.99 7.15 4.00 × 104 0.30
26 4d104f2 2 1.74 7.44 2.27 × 104 0.22
27 4d104f1 1 1.35 7.73 6.54 × 104 0.17
4d оболочка
28 4p64d10 10 3.89 8.03 3.64 × 106 0.57
29 4p64d9 9 3.89 8.33 4.85 × 106 0.51
30 4p64d8 8 3.91 8.63 6.49 × 106 0.45
31 4p64d7 7 3.91 8.94 8.23 × 106 0.39
32 4p64d6 6 3.86 9.25 9.69 × 106 0.34
33 4p64d5 5 3.77 9.57 1.03 × 107 0.29
34 4p64d4 4 3.62 9.89 9.53 × 106 0.24
35 4p64d3 3 3.38 10.22 6.91 × 105 0.19
36 4p64d2 2 3.00 10.55 3.27 × 106 0.14
37 4p64d1 1 2.01 10.89 2.64 × 105 0.10
4p оболочка
38 4s24p6 6 4.59 11.24 2.24 × 108 0.29
39 4s24p5 5 4.44 11.59 2.20 × 108 0.25
40 4s24p4 4 4.22 11.95 1.82 × 108 0.21
41 4s24p3 3 3.91 12.32 1.14 × 108 0.17
42 4s24p2 2 3.43 12.70 4.22 × 107 0.13
43 4s24p1 1 2.68 13.09 5.48 × 106 0.08
4s оболочка
44 3d104s2 2 4.58 13.49 6.79 × 108 0.10
45 3d94s1 1 3.63 13.90 7.89 × 107 0.06
3d оболочка
46 3p63d10 10 4.89 14.33 1.21 × 1010 0.46
47 3p63d9 9 4.94 14.76 1.75 × 1010 0.41
48 3p63d8 8 4.89 15.21 2.09 × 1010 0.37
49 3p63d7 7 4.82 15.68 2.36 × 1010 0.33
50 3p63d6 6 4.74 16.17 2.51 × 1010 0.29
51 3p63d5 5 4.63 16.67 2.47 × 1010 0.24
52 3p63d4 4 4.49 17.19 2.13 × 1010 0.20
53 3p63d3 3 4.37 17.74 1.75 × 1010 0.15

Для других элементов была проведена аналогичная процедура. Для золота и свинца использовались данные работы [4], для гадолиния – [19].

Результаты расчетов относительного распределения интенсивности в квазиконтинууме и сравнение с данными экспериментов на токамаках приведены ниже на рис. 3–8.

Рис. 3.

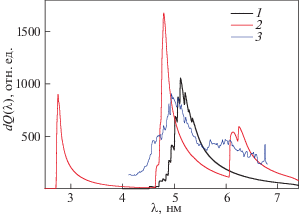
Спектральные распределения излучаемой мощности радиационных потерь гадолиния при температуре Тe = 2.2 кэВ. 1 – теоретические расчеты по формуле (16); 2 – экспериментальные данные LHD [19].

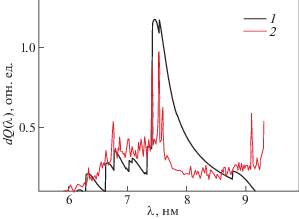
Рис. 4.

Спектральные распределения излучаемой мощности радиационных потерь вольфрама при температуре Тe = 800 эВ. 1 – теоретические расчеты по формуле (16) со средним зарядом, рассчитанным в статистической модели; 2 – теоретические расчеты по формуле (16) со средним зарядом, рассчитанным по данным работы [5]; 3 – экспериментальные данные TEXT [4].

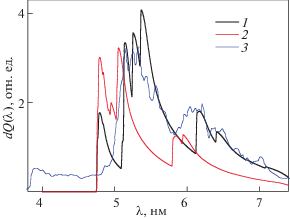
Рис. 5.

Спектральное распределение мощности радиационных потерь вольфрама при температуре Тe = = 1.5 кэВ. 1 – теоретические расчеты по формуле (16) со средним зарядом, рассчитанным в статистической модели; 2 – теоретические расчеты по формуле (16) со средним зарядом, рассчитанным по данным работы [5]; 3 – экспериментальные данные LHD [17].

Рис. 6.

То же, что на рис. 5, при температуре Тe = = 3 кэВ.

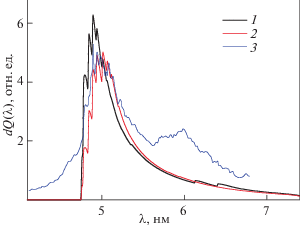
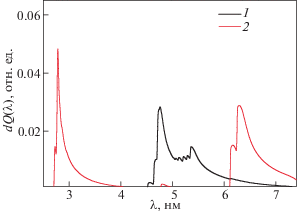
Рис. 7.

Спектральные распределения излучаемой мощности радиационных потерь золота при температуре Тe = 800 эВ. 1 – теоретические расчеты по формуле (16); 2 – экспериментальные данные TEXT [4].

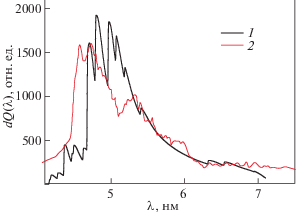
Рис. 8.

Спектральные распределения излучаемой мощности радиационных потерь свинца при температуре Тe = 800 эВ. 1 – теоретические расчеты по формуле (16); 2 – экспериментальные данные TEXT [4].

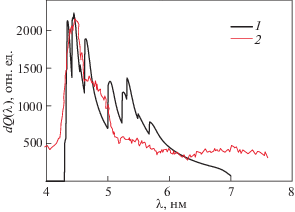
Рис. 9.

Спектральные распределения излучаемой мощности радиационных потерь вольфрама при температуре Тe = 5 кэВ. 1 – теоретические расчеты по формуле (16) со средним зарядом, рассчитанным в статистической модели; 2 – теоретические расчеты по формуле (16) со средним зарядом, рассчитанным по данным работы [5].

Как экспериментальные данные, так и результаты теоретических расчетов приведены к единому масштабу и представлены в относительных единицах на рис. 3–8. Видно, что формы экспериментальных и теоретических удельных линейчатых спектральных радиационных потерь, в которых использовалась статистическая модель для расчета распределения примеси по ЗС, удовлетворительно согласуются друг с другом, что позволяет утверждать, что статистический подход применим для описания спектральных потерь в области 2–8 нм, отвечающей наблюдаемому квазиконтинууму тяжелых ионов в токамаках и стеллараторах. Степень соответствия с экспериментом может заметно варьироваться: так, она относительно хорошая для рис. 4, 5, 7, 8, в то время как для рис. 3, 6 она ниже. Проблема состоит в моделировании электронной плотности сложных электронных конфигураций одним членом слэтеровского разложения, которое улавливает основные особенности спектров. Однако для описания деталей спектров различных электронных конфигураций одного члена может быть недостаточно.

Для спектральных удельных линейчатых радиационных потерь в условиях проектируемого токамака Т-15МД развитый метод дает результат, приведенный на рис. 9 для различных ионизационных равновесий (предполагается Тe = 5 кэВ). Как видно из рисунка, квазиконтинуум радиационных потерь вольфрама в статистической модели атома при температуре плазмы Тe = 5 кэВ должен наблюдаться в области 5–6 нм, в то время как результаты другого зарядового распределения [5, 9] приводят к другому распределению в более широкой области 2.5–7 нм.

4. ЗАКЛЮЧЕНИЕ

В данной работе проведены расчеты спектральных радиационных потерь в квазиконтинууме тяжелых ионов в плазме в рамках статистической модели атома [21–28]. Для описания распределения плотности электронов в ионе использовалось приближение Слэтера [36]. Получены усредненные огибающие спектров для ряда тяжелых элементов: гадолиния, вольфрама, золота и свинца при различных температурах. Сравнение результатов численных расчетов в статистической модели с данными квантовых поуровневых расчетов и с экспериментальными данными на термоядерных установках продемонстрировало удовлетворительное согласие. Кроме того, были получены результаты для распределения спектральных потерь на ионах вольфрама для токамака Т-15МД при типичных температурах порядка 5 кэВ.

Важно отметить, что статистическая модель атома [21–28], в отличие от поуровневых вычислений, качественным образом предсказывает возникновение “частот отсечки”, наблюдаемого квазиконтинуума, что можно рассматривать в качестве принципиального обоснования статистического подхода [21–28] для анализа квазиконтинуума. Однако следует заметить, что статистическая модель чувствительна к числу электронов на рассматриваемой оболочке, и, в случае небольшого их числа, результаты статистической модели по величине могут заметно отличаться от квантовых расчетов.

Полученные результаты представляют интерес для диагностики тяжелых примесных ионов, в частности вольфрама, в современных токамаках. Статистическая модель атома позволяет достичь экономии расчетного времени по сравнению с поуровневыми расчетами спектров, проводимыми на суперкомпьютерах, и разумно описывает основные закономерности наблюдаемых спектров. Важно отметить, что для интерпретации результатов эксперимента можно ориентироваться также на менее затратные измерения с малым спектральным разрешением в диапазоне 2–8 нм, позволяющие следить сразу за группой линий радиационных переходов в тяжелых ионах.

Следует отметить, что существует еще один статистический подход к описанию сложных спектров, в котором спектральные области типа квазиконтинуума именуются “массивом неразрешенных переходов” – Unresolved Transition Arrays (UTA) [41]. Этот метод, основанный на вычислении моментов от спектрального распределения, фактически требует знания всех атомных данных, используемых в квантовых поуровневых кодах, и в этом отношении его применение также является более трудоемким, чем статистической модели атома [21–28]. С другой стороны, в [17, 42] он применялся только для расчетов среднего положения массива и его эффективной полуширины, в то время как форма квазиконтинуума рассчитывалась с помощью поуровневых кодов и соответствующих реализаций радиационно-столкновительных моделей для вычисления распределения по ЗС. В [42] метод UTA подробно тестировался на предмет правильного описания массивов переходов с Δn = 0 при n = 4, 5. Как выяснили авторы [42], UTA не учитывает конфигурационное взаимодействие для правильного описания этих переходов. К тому же UTA не предсказывает частот отсечки квазиконтинуума. Поэтому описание квазиконтинуума в настоящей работе, основанное на статистической модели атома [21–28], является более наглядным и в определенной степени аналитическим результатом, доступным для широкого круга пользователей.

Таким образом, применение статистической модели атома позволяет для различных параметров плазмы достаточно быстро (по сравнению с другими возможными методами) рассчитывать форму квазиконтинуума многоэлектронных ионов вольфрама, которая, как следует из сравнения на рис. 4–6, удовлетворительно соответствует экспериментальным наблюдениям.

Список литературы

  1. Isler R.C., Neidigh R.V., Cowan R.D. // Phys. Lett. A. 1977. V. 63(3). P. 295. https://doi.org/10.1016/0375-9601(77)90908-2

  2. Hinnov E., Mattioli M. // Phys. Lett. A. 1978. V. 66(2). P. 109. https://doi.org/10.1016/0375-9601(78)90010-5

  3. Johnson B.M., Jones K.W., Cecchi J.L., Hinnov E., Kruse T.H. // Phys. Lett. A. 1979. V. 70. P. 320. https://doi.org/10.1016/0375-9601(79)90136-1

  4. Finkenthal M., Huang L.L., Lippmann S., Moos H.W., Mandelbaum P., Klapisch J.L. and the TEXT Group. // Phys. Lett. A. 1988. V. 127. P. 255. https://doi.org/10.1016/0375-9601(88)90691-3

  5. Asmussen K., Fournier K.B., Laming J.M., Neu R., Seely J.F., Dux R., Engelhardt W., Fuchs J.C. and the ASDEX Upgrade Team // Nucl. Fusion. 1998. V. 38. P. 967. https://doi.org/10.1088/0029-5515/38/7/302

  6. Pütterich T., Neu R., Biedermann C., Radtke R. and the ASDEX Upgrade Team // J. Phys. B: At. Mol. Opt. Phys. 2005. V. 38. P. 3071. https://doi.org/10.1088/0953-4075/38/16/017

  7. Pütterich T., Neu R., Dux R., Whiteford A.D., O’Mulla-ne M.G. and the ASDEX Upgrade Team // Plasma Phys. Control. Fusion. 2008. V. 50. 085016. https://doi.org/10.1088/0741-3335/50/8/085016

  8. Nakano T., Asakura N., Kubo H., Janagibayashi J., -Ueda Y. // Nucl. Fusion. 2009. V. 49. 1150024. https://doi.org/10.1088/0029-5515/49/11/115024

  9. Pütterich T., Neu R., Dux R., Whitefor A. D., O’Mullane M.G., Summers H.P. and the ASDEX Upgrade Team // Nucl. Fusion. 2010. V. 50. 025012. https://doi.org/10.1088/0029-5515/50/2/025012

  10. Yanagibayashi J., Nakano T., Iwamae A., Kubo H., Hasuo M., Itami K. // J. Phys. B: At. Mol. Opt. Phys. 2010. V. 43. 144013. https://doi.org/10.1088/0953-4075/43/14/144013

  11. Pütterich T., Dux R., Beurskens M.N.A., Bobkov V., Brezinsek S., Bucalossi J., Coenen J.W., Coffey I., Czarnecka A., Giroud C., Joffrin E., Lawson K.D., Lehnen M., de la Luna E., Mailloux J., Marsen S., Mayo-ral M.-L., Meigs A., Neu R., Rimini F., Sertoli M., Stamp M., van Rooij G. and JET EFDA Contributors // Proc. 24rd IAEA Fusion Energy Conf., San Diego, 2012. IAEA-CN-197. EX–P3.15.

  12. Pütterich T., Dux R., Neu R., Bernert M., Beurskens M.N.A., Bobkov V., Brezinsek S., Challis C., Coenen J.W., Cof-fey I., Czarnecka A., Giroud C., Jacquet P., Joffrin E., Kallenbach A., Lehnen M., Lerche E., de la Luna E., Marsen S., Matthews G., Mayoral M.-L., McDermott R.M., Meigs A., Mlynar J., Sertoli M., van Rooij G., the ASDEX Upgrade Team and JET EFDA Contributors // Plasma Phys. Control. Fusion. 2013. V. 55. 124036. https://doi.org/10.1088/0741-3335/55/12/124036

  13. Земцов И.А., Крупин В.А., Нургалиев М.Р., Ключников Л.А., Немец А.Р., Днестровский А.Ю., Сары-чев Д.В. // ВАНТ. Сер. Термоядерный синтез. 2017. Т. 40. Вып. 2. С. 29. https://doi.org/10.21517/0202-3822-2017-40-2-29-35

  14. Krupin V.A., Nurgaliev M.R., Klyuchnikov L.A., Ne-mets A.R., Zemtsov I.A., Dnestrovskij A.Yu., Sary-chev D.V., Lisitsa V.S., Shurygin V.A., Leontiev D.S., Borschegovskij A.A., Grashin S.A., Ryjakov D.V., Serge-ev D.S., Mustafin N.A., Trukhin V.M., Solomatin R.Yu., Tugarinov S.N., Naumenko N.N. // Nucl. Fusion. 2017. V. 57. 066041. https://doi.org/10.1088/1741-4326/aa69c5

  15. Zhang L., Morita S., Xu Z., Zhang P.F., Zang Q., Duan Y.M., Liu H.Q., Zhao H.L., Ding F., Ohishi T., Gao W., Huang J., Yang X.D., Chen Y.J., Wu Z.W., Xu P., Ding B.J., Hu C.D., Gong X.Z., Chen J.L., Hu L.Q., EAST Team // Nucl. Materials and Energy. 2017. V. 12. P. 774. https://doi.org/10.1016/j.nme.2017.01.009

  16. Krupin V.A., Klyuchnikov L.A., Nurgaliev M.R., Ne-mets A.R., Zemtsov I.A, Melnikov A.V., Myalton T.B., Sarychev D.V., Sergeev D.S., Sushkov A.V., Trukhin V.M., Tugarinov S.N., Naumenko N.N. // Plasma Phys. Control. Fusion. 2018. V. 60. 115003. https://doi.org/10.1088/1361-6587/aada6b

  17. Harte C.S., Suzuki C., Kato T., Sakaue H.A., Kato D., Sato K., Tamura N., Sudo S., D’Arcy R., Sokell E., White J., O’Sillivan G. // J. Phys. B: At. Mol. Opt. Phys. 2010. V. 43. 205004. https://doi.org/10.1088/0953-4075/43/20/205004

  18. Suzuki C., Murakami I., Koike F., Tamura N., Sa-kaue H.A., Morita S., Goto M., Kato D., Ohashi H., Higashiguchi T., Sudo S., O’Sullivan G. // Plasma Phys. Control. Fusion. 2017. V. 59. 014009. https://doi.org/10.1088/0741-3335/59/1/014009

  19. Suzuki C., Koike F., Murakami I., Tamura N., Sudo S. // Atoms. 2018. V. 6. P. 24. https://doi.org/10.3390/atoms6020024

  20. Churilov S.S., Kildiyarova R.R., Ryabtsev A.N., Sadovsky S.V. // Phys. Scr. 2009. V. 80. 045303. https://doi.org/10.1088/0031-8949/80/04/045303

  21. Демура А.В., Кадомцев М.Б., Лисица В.С., Шуры-гин В.А. // Письма ЖЭТФ. 2013. Т. 98. С. 886. https://doi.org/10.7868/S0370274X13240053

  22. Demura A.V., Kadomtsev M.B., Lisitsa V.S., Shury-gin V.A. // J. Phys. B: At. Mol. Opt. Phys. 2015. V. 48. 055701. https://doi.org/10.1088/0953-4075/48/5/055701

  23. Demura A.V., Kadomtsev M.B., Lisitsa V.S., Shury- gin V.A. // Письма ЖЭТФ. 2015. Т. 101(12). С. 90. https://doi.org/10.7868/S0370274X15020046

  24. Demura A.V., Kadomtsev M.B., Lisitsa V.S., Shury-gin V.A. // HEDP. 2015. V. 15. P. 49. https://doi.org/10.1016/j.hedp.2015.03.006

  25. Demura A.V., Kadomtsev M.B., Lisitsa V.S., Shury- gin V.A. // Atoms. 2015. V. 3. P. 162. https://doi.org/10.3390/atoms3020162

  26. Leontyev D.S., Lisitsa V.S. // Contrib. Plasma Phys. 2016. V. 56. P. 846. https://doi.org/10.1002/ctpp.201500075

  27. Демура А.В., Леонтьев Д.С., Лисица В.С., Шуры-гин А.В. // ЖЭТФ. 2017. Т. 152. С. 781.

  28. Демура А.В., Леонтьев Д.С., Лисица В.С., Шуры-гин А.В. // Письма ЖЭТФ. 2017. Т. 106. С. 417. https://doi.org/10.7868/S0370274X17190031

  29. Гаранин С.Ф., Палагина Е.М. // ЖЭТФ. 2004. Т. 125. С. 1258.

  30. Гаранин С.Ф., Палагина Е.М. // ЖЭТФ. 2007. Т. 131. С. 594.

  31. Гаранин С.Ф., Кравец Е.М., Мамышев В.И., Тока-рев В.А. // Физика плазмы. 2009. Т. 35. С. 744.

  32. Fano U., Cooper J.W. // Rev. Mod. Phys. 1968. V. 40. P. 441.

  33. Ферми Э. Научные труды. Том I. М.: Наука, 1971. С. 284.

  34. Мигдал А.Б., Крайнов В.П. Приближенные методы квантовой механики. М.: Наука, 1966.

  35. Brandt W., Lundquist S. // Phys. Rev. 1965 .V. 139. № 3A. P. 612. https://doi.org/10.1103/PhysRev.139.A612

  36. Slater J. C. // Phys. Rev. 1930. V. 36. P. 57. https://doi.org/10.1103/PhysRev.36.57

  37. Собельман И.И. Введение в теорию атомных спектров. М.: ГФМЛ, 1963.

  38. Амусья М.Я. // Изв. АН СССР. Сер. физич. 1981. Т. 45. С. 2242.

  39. Fermi E. // Zeitschrift für Physik. 1924. V. 29. P. 315. https://doi.org/10.1007/BF03184853

  40. Астапенко В.А. Взаимодействие излучения с атомами и наночастицами. Долгопрудный: Издательский дом Интеллект, 2010.

  41. Bauche J., Bauche-Arnoult C., Peyrusse O. Atomic Properties in hot plasmas. From levels to superconfigurations. Grenoble: Springer, 2015.

  42. Liu L., Kilbane D., Dunne P., Wang X., O’Sullivan G. // Atoms. 2017. V. 5. P. 20.

Инструменты

следующая статья выпуска содержание выпуска

Физика плазмы

Архивы выпусков Информация о журнале Отправить рукопись в журнал