1. На главную
  2. Электронные версии
  3. Физика плазмы
  4. T. 46, № 3, 2020

Физика плазмы, 2020, T. 46, № 3, стр. 206-212

Резонансный лазерно-модифицированный процесс тормозного излучения ультрарелятивистских электронов в поле ядра в лазерной плазме

А. Дубов a, *, В. В. Дубов a, **, С. П. Рощупкин a, ***

a Санкт-Петербургский политехнический университет Петра Великого, Кафедра теоретической физики
Санкт-Петербург, Россия

* E-mail: alexanderpolytech@gmail.com
** E-mail: dubov@spbstu.ru
*** E-mail: serg9rsp@gmail.com

Поступила в редакцию 28.08.2019
После доработки 18.09.2019
Принята к публикации 20.09.2019

Полный текст (PDF)

Аннотация

Рассматривается процесс резонансного лазерно-модифицированного тормозного излучения (ЛМТ) ультрарелятивистских электронов в окружении лазерной плазмы в поле ядра. В кинематике исследуемого эффекта выделяется возможность протекания процесса по двум каналам реакции. В первом канале электрон излучает спонтанный фотон и в последующем рассеивается на ядре, во втором – электрон изначально рассеивается на ядре, а затем излучает спонтанный фотон. Важно подчеркнуть, что в окружении лазерной плазмы виртуальный ультрарелятивистский электрон, находящийся в промежуточном состоянии, трансформируется в реальную частицу. Более того, процесс второго порядка по постоянной тонкой структуре функционально преобразовывается в два последовательных процесса первого рода (обособленный лазерно-стимулированный процесс Комптона и лазерно-модифицированный процесс рассеяния Мотта). Определены резонансные частоты спонтанного фотона для различных вариаций начальных параметров. Как результат, при анализе модификации резонансной частоты спонтанного фотона выделен специфический диапазон изменения для второй реакционной схемы, в котором выявлены три различных дискретных значения спонтанной частоты для угла вылета, что альтернативно однозначной зависимости в первой схеме. В дальнейшем, вычислено значение дифференциального сечения рассеяния и определено, что резонансное сечение рассеяния существенно превышает соответствующее сечения рассеяние для процесса, протекающего вне лазерной плазмы. Показано, что специализированные лаборатории импульсного лазерного излучения (SLAC, FAIR, XFEL, ELI, XCELS) экспериментально подтверждают результаты вычислений данного проекта.

Ключевые слова: ультрарелятивистский электрон, тормозное излучение, лазерная плазма, резонанс, процесс второго порядка, виртуальные частицы

1. ВСТУПЛЕНИЕ

Теоретическое изучение квантово электродинамических (КЭД) процессов в окружении лазерной плазмы представляет собой одну из наиболее важных областей, которые интенсивно развиваются в связи с использованием мощных установок лазерного излучения в прикладном и фундаментальном исследовании [1–5]. Основные результаты исследований были систематизированы в монографиях [6–9] и обзорах [10–13]. Важно подчеркнуть, что КЭД процессы высокого порядка по постоянной тонкой структуре в лазерной плазме (модифицированные лазерным полем КЭД эффекты) могут протекать по резонансному и нерезонансному каналам. Резонансы Олейника могут возникать в лазерной плазме [14, 15] вследствие того, что процессы низкого порядка по постоянной тонкой структуре (стимулированные лазерной плазмой КЭД взаимодействия) возможны в лазерной плазме [16]. Вероятность резонансного процесса КЭД процесса в лазерной плазме может значительно (на несколько порядков величины) превышать соответствующую вероятность процесса, протекающего без внешнего поля лазерной плазмы [17, 18].

Резонансы Олейника для спонтанного тормозного торможения электрона на ядре в поле плазмы были изучены только для одного из возможных каналов реакции, когда электрон сначала излучает спонтанный фотон, а затем рассеивается на ядре. Второй канал – когда электрон сначала рассеивается на ядре, а после излучает спонтанный фотон ранее не подвергался детальному анализу. Дополнительно, для первого канала в ультрарелятивистком случае были рассмотрены небольшие энергии рассеивающихся электронов, а также рассеяние данных частиц под большими углами, в то время как спонтанный фотон распространялся внутри небольшого углового конуса относительно направления импульса начального электрона [19, 20].

Настоящая работа разрабатывает теорию резонансного ЛМТ процесса ультрарелятивистcких высокоэнергичных электронов, в которых электрон рассеивается в кулоновском поле на малые углы в окружении лазерной плазмы. Статья представляет исследование для обоих каналов взаимодействия. В указанных условиях конечный электрон и спонтанный фотон распространяются в узком угловом конусе относительно импульса начального электрона. В задачах связанных с ЛМТ процессами в лазерной плазме используются два характеристических параметра. Классический релятивистcко-инвариантный параметр [21]

(1)
$\eta = \frac{eF\lambda }{{m{{c}^{2}}}},$
где e и m – заряд и масса электрона, F и $\lambda = c{\text{/}}\omega $ – напряженность поля и длина волны, ω – частота волны. Следующий параметр – квантовый мультифотонный параметр (параметр Бункина–Федорова) [8, 11, 19–22]
(2)
${{\gamma }_{i}} = \eta \frac{{m{{v}_{i}}c}}{{\hbar \omega }},$
где ${{v}_{i}}$ – скорость начального электрона. Для диапазона оптических частот ($\omega \sim {{10}^{{15}}}$ с–1) классический параметр $\eta \sim 1$ и $F \sim {{10}^{{10}}}{\kern 1pt} - {\kern 1pt} {{10}^{{11}}}$ В/см, а квантовый параметр ${{\gamma }_{i}} \sim 1$ для $F \sim ({{10}^{5}}{\kern 1pt} - {\kern 1pt} {{10}^{6}})(c{\text{/}}{{v}_{i}})$ В/см. В рамках представленного исследования

(3)
$\eta \ll 1.$

Данная работа использует релятивистcкую систему единиц $\hbar = c = 1$.

2. АМПЛИТУДА ПРОЦЕССА

В данной статье выбирается следующая структура 4-потенциала в присутствии внешней эллиптически поляризованной световой волны для характеристики взаимодействий внутри лазерной плазмы:

(4)
$\begin{gathered} A(\phi ) = \frac{F}{\omega }({{e}_{x}}cos\phi + \delta {{e}_{y}}sin\phi ), \\ \phi = kx = \omega (t - z), \\ \end{gathered} $
где δ – параметр эллиптичности, а $k = \omega n = $ $ = \omega (1,{\mathbf{n}})$ – 4-векторы поляризации и импульса фотона.

Работа изучает проблему спонтанного тормозного излучения (СТИ) в борновском приближении при рассеянии электронов на ядре в поле лазерной плазмы. Это процесс второго порядка по постоянной тонкой структуры и он может быть описан диаграммами Фейнмана (см. рис. 1). Амплитуду данного процесса после определенных вычислений можно представить в следующем виде (см., на пример, [23–25]):

(5)
${{S}_{{fi}}} = \sum\limits_{n = - \infty }^\infty \,{{S}_{l}},$
где парциальная амплитуда ($\left| l \right|$ – количество излученных и поглощенных фотонов) имеет вид

(6)
${{S}_{l}} = - i\frac{{8{{\pi }^{{5/2}}}Z{{e}^{3}}}}{{\sqrt {2\omega {\text{'}}{{{\tilde {E}}}_{i}}{{{\tilde {E}}}_{f}}} }}{{e}^{{i{{\varphi }_{{fi}}}}}}[\mathop {\overline u }\nolimits_f {{M}_{l}}{{u}_{i}}]\frac{{\delta ({{q}_{0}})}}{{{{{\mathbf{q}}}^{2}}}}.$
Рис. 1.

Диаграммы Фейнмана для ЛМТ процесса электрона на ядре в поле лазерной плазмы. Двойные входящие и выходящие линии отвечают функциям Волкова электрона в начальном и конечном состояниях, внутренняя линия соответствует функции Грина электрона в поле плоской волны. Волнистые линии отвечают 4-импульсам спонтанного фотона и “псевдофотона” отдачи ядра.

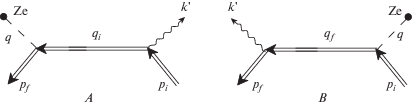
Здесь 4-импульс промежуточных электронов ${{q}_{{i,f}}}$ и переданный 4-импульс q определяются следующими выражениями:

(7)
${{q}_{i}} = {{\tilde {p}}_{i}} - k{\text{'}} + rk,\quad {{q}_{f}} = {{\tilde {p}}_{f}} + k{\text{'}} - rk,$
(8)
$q = {{\tilde {p}}_{f}} - {{\tilde {p}}_{i}} + k{\kern 1pt} '\; + lk,$
где $k{\text{'}} = \omega {\text{'}}(1,{\mathbf{n}}{\text{'}})$ – 4-импульс спонтанного фотона.

3. ПОЛЮСА АМПЛИТУДЫ

Дальнейшее исследование концентрируется на резонансах в лазерной плазме в условиях (3). В данном случае, при учете резонансных слагаемых амплитуды (6), (7) выполняются следующие условия (см. рис. 2):

(9)
$q_{i}^{2} = {{m}^{2}},$
(10)
$q_{f}^{2} = {{m}^{2}}.$
Рис. 2.

Лазерно-модифицированное резонансное спонтанное излучение электрона в поле ядра и лазерной плазмы.

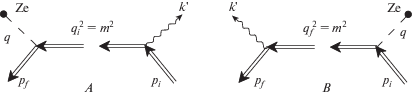
Резонансы (9) для первого слагаемого амплитуды (6), (7) (см. рис. 2, диаграмма A), когда электрон сначала излучает спонтанный фотон, а затем рассеивается на значительный угол на ядре были детально изучены для различных энергий электрона, с исключением случая когда спонтанный фотон излучается в узком конусе относительно импульса начального электрона очень большой ультрарелятивистcкой энергии. Резонансы (10) для второго слагаемого амплитуды (6), (7) (см. рис. 2, диаграмма B) когда электрон сначала рассеивается на ядре, а затем излучает спонтанный фотон (см. рис. 2) не были изучены ранее и являются предметом актуального исследования. Дальнейший анализ фокусируется на наиболее интересном случае ультрарелятивистcких энергий электронов и случае, когда спонтанный фотон и конечный электрон распространяются в узком угловом конусе относительно импульса начального электрона

(11)
${{E}_{{i,f}}} \gg m,$
(12)
$\theta _{{i,f}}^{'} \ll 1,\quad \theta = \measuredangle ({{{\mathbf{p}}}_{i}},{{{\mathbf{p}}}_{f}}) \ll 1,\quad \theta {\text{'}} \sim 1.$

С использованием нескольких вычислительных методов было получено выражение для резонансной частоты спонтанного фотона для канала A (см. рис. 2)

(13)
$\begin{gathered} x_{{(a)}}^{'}(\delta {\text{'}}_{i}^{2}) = \frac{{{{\varepsilon }_{i}}}}{{1 + {{\varepsilon }_{i}} + \delta {\text{'}}_{i}^{2}}},\quad x_{{(a)}}^{'} = \frac{{\omega _{{(a)}}^{'}}}{{{{E}_{i}}}}, \\ {{\varepsilon }_{i}} = \frac{{{{E}_{i}}}}{{{{E}_{*}}}},\quad {{E}_{*}} = \frac{{{{m}^{2}}}}{{4\omega si{{n}^{2}}(\theta {\text{'/}}2)}},\quad \delta _{i}^{'} = \frac{{{{E}_{i}}\theta _{i}^{'}}}{m}. \\ \end{gathered} $

Для канала B было получено кубическое выражение, которое после определенных выкладок может быть представлено в форме

(14)
$\begin{gathered} \delta {\text{'}}_{f}^{2}x{\text{'}}_{{(b)}}^{3} - 2\delta {\text{'}}_{f}^{2}x{\text{'}}_{{(b)}}^{2} + (1 + \delta {\text{'}}_{f}^{2} + {{\varepsilon }_{i}})x_{{(b)}}^{'} - {{\varepsilon }_{i}} = 0, \\ x_{{(b)}}^{'} = \frac{{\omega _{{(b)}}^{'}}}{{{{E}_{i}}}}, \\ \end{gathered} $
которое выделяет различные решения для разных интервалов значений параметра $\delta _{f}^{'} = {{E}_{i}}\theta _{f}^{'}{\text{/}}m$. Таким образом, для диапазона
(15)
$\delta {\text{'}}_{ - }^{2} < \delta {\text{'}}_{f}^{2} < \delta {\text{'}}_{ + }^{2},$
в котором
(16)
$\begin{gathered} \delta {\text{'}}_{ \pm }^{2} = 3(1 + {{\varepsilon }_{i}}) + \frac{1}{8}({{\varepsilon }_{i}} - 8)[({{\varepsilon }_{i}} + 4) \pm \sqrt {{{\varepsilon }_{i}}({{\varepsilon }_{i}} - 8)} ], \\ {{\varepsilon }_{i}} > 8 \\ \end{gathered} $
имеется три корня уравнения для резонансной частоты
(17)
$\begin{gathered} x_{{(b)1}}^{'} = \frac{2}{3} + d{\text{'}}cos\left( {\frac{{\varphi {\text{'}}}}{3}} \right), \\ x_{{(b)2}}^{'} = \frac{2}{3} + d{\text{'}}cos\left( {\frac{{\varphi {\text{'}}}}{3} + \frac{{2\pi }}{3}} \right), \\ x_{{(b)3}}^{'} = \frac{2}{3} + d{\text{'}}cos\left( {\frac{{\varphi {\text{'}}}}{3} + \frac{{4\pi }}{3}} \right), \\ \end{gathered} $
где $d{\text{'}} = d{\text{'}}({{\varepsilon }_{i}},\delta _{f}^{'})$, $cos(\varphi {\text{'}}) = cos(\varphi {\text{'}}({{\varepsilon }_{i}},\delta _{f}^{'}))$. Если параметр $\delta _{f}^{'}$ находится в области
(18)
$0 < \delta {\text{'}}_{f}^{2} \leqslant 3(1 + {{\varepsilon }_{i}}),\quad {\text{если}}\quad 0 < {{\varepsilon }_{i}} \leqslant 8$
(19)
$0 < \delta {\text{'}}_{f}^{2} \leqslant \delta {\text{'}}_{ - }^{2},\quad \delta {\text{'}}_{ + }^{2} \leqslant \delta {\text{'}}_{f}^{2} < \infty ,\quad {\text{если}}\quad {{\varepsilon }_{i}} > 8,$
тогда значение резонансной частоты спонтанного фотона определяется следующим выражением:
(20)
$x_{{(b)}}^{'} = \frac{2}{3} + ({{\alpha }_{ + }} + {{\alpha }_{ - }}),$
в котором

(21)
${{\alpha }_{ \pm }} = \mathop {\left( { - \frac{b}{2} \pm \sqrt Q } \right)}\nolimits^{1/3} ,\quad Q = \mathop {\left( {\frac{a}{3}} \right)}\nolimits^3 + \mathop {\left( {\frac{b}{2}} \right)}\nolimits^2 ,$
(22)
$\begin{gathered} a = \frac{1}{{3\delta {\text{'}}_{f}^{2}}}[3(1 + {{\varepsilon }_{i}}) - \delta {\text{'}}_{f}^{2}], \\ b = \frac{1}{{27\delta {\text{'}}_{f}^{2}}}[2(9 + \delta {\text{'}}_{f}^{2}) - 9{{\varepsilon }_{i}}]. \\ \end{gathered} $

Важно подчеркнуть, что в нерезонансном случае частота спонтанного фотона и энергия конечного электрона могут изменяться независимо в рамках закона сохранения энергии. При этом углы вылета спонтанного фотона не влияют на энергии этих частиц. В резонансном случае имеем принципиально другую ситуацию. В данном случае энергия спонтанного фотона и конечного электрона определяются из двух уравнений: закона сохранения энергии и резонансного уравнения. При этом, углы вылета спонтанного фотона относительно импульсов начального или конечного электронов определяют возможный энергетический спектр частиц для каналов A или B.

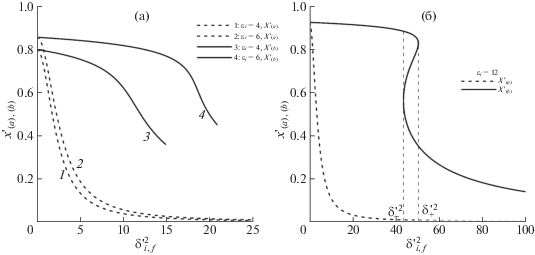
Рис. 3.

Зависимость резонансной частоты спонтанного фотона от его угла вылета: область значений параметра ${{\varepsilon }_{i}} \leqslant 8$ (a); область значений параметра ${{\varepsilon }_{i}} > 8$ $({{\varepsilon }_{i}} = 12)$ (б). Пунктирные линии отвечают резонансным частотам канала A $(x_{{(a)}}^{'}(\delta {\text{'}}_{i}^{2}))$, сплошные кривые отвечают резонансным частотам канала B $(x_{{(b)}}^{'}(\delta {\text{'}}_{f}^{2}))$.

4. РЕЗОНАНСНОЕ ДИФФЕРЕНЦИАЛЬНОЕ СЕЧЕНИЕ РАССЕЯНИЯ

Резонансное дифференциальное сечение рассеяния ЛМТ процесса для неполяризованных электронов и спонтанного фотона в лазерной плазме малой интенсивности (3) получается с помощью стандартной процедуры (см. [26]). После определенных выкладок резонансное дифференциальное сечение рассеяния ЛМТ процесса для канала A $(d{{\sigma }_{{(a)res}}})$ и B $(d{{\sigma }_{{(b)res}}})$ приобретает форму

(23)
$\begin{gathered} d{{\sigma }_{{(a)res}}} = \frac{{4{{\pi }^{2}}{{Z}^{2}}{{\eta }^{2}}\alpha r_{e}^{2}}}{{{{d}^{2}}(x_{{(a)}}^{'})}}\frac{{{{{(1 - x_{{(a)}}^{'})}}^{2}}D(x_{{(a)}}^{'})}}{{[{{{(\delta {\text{'}}_{i}^{2} - \delta {\text{'}}_{{(a)i}}^{2})}}^{2}} + \Gamma _{{{{\delta }_{i}}}}^{2}]}} \times \\ \, \times \frac{{dx_{{(a)}}^{'}}}{{x_{{(a)}}^{'}}}d\delta {\text{'}}_{i}^{2}d\delta {\text{'}}_{f}^{2}d{{\varphi }_{ - }}, \\ \end{gathered} $
(24)
$\begin{gathered} d{{\sigma }_{{(b)res}}} = \frac{{4{{\pi }^{2}}{{Z}^{2}}{{\eta }^{2}}\alpha r_{e}^{2}}}{{{{d}^{2}}(x_{{(b)}}^{'})}}\frac{{{{{(1 - x_{{(b)}}^{'})}}^{{ - 2}}}D(x_{{(b)}}^{'})}}{{[{{{(\delta {\text{'}}_{f}^{2} - \delta {\text{'}}_{{(b)f}}^{2})}}^{2}} + \Gamma _{{{{\delta }_{f}}}}^{2}]}} \times \\ \, \times \frac{{dx_{{(b)}}^{'}}}{{x_{{(b)}}^{'}}}d\delta {\text{'}}_{i}^{2}d\delta {\text{'}}_{f}^{2}d{{\varphi }_{ - }}, \\ \end{gathered} $
где ${{\varphi }_{ - }}$ – угол между $({\mathbf{k}}{\text{'}},{{{\mathbf{p}}}_{i}})$ и $({\mathbf{k}}{\text{'}},{{{\mathbf{p}}}_{f}})$; ${{\Gamma }_{{{{\delta }_{{i,f}}}}}}$ – угловая радиационная ширина резонанса для каналов A и B

(25)
$\begin{gathered} {{\Gamma }_{{{{\delta }_{i}}}}} = \frac{1}{4}\alpha {{\eta }^{2}}{{K}_{i}}\left( {\frac{{1 - x_{{(a)}}^{'}}}{{x_{{(a)}}^{'}}}} \right), \\ {{\Gamma }_{{{{\delta }_{f}}}}} = \frac{1}{4}\alpha {{\eta }^{2}}\frac{{{{K}_{i}}}}{{x_{{(b)}}^{'}(1 - x_{{(b)}}^{'})}}, \\ \end{gathered} $
(26)
${{K}_{i}} = \left( {1 - \frac{4}{{{{\varepsilon }_{i}}}} - \frac{8}{{\varepsilon _{i}^{2}}}} \right)ln(1 + {{\varepsilon }_{i}}) + \frac{1}{2} + \frac{8}{{{{\varepsilon }_{i}}}} - \frac{1}{{2{{{(1 + {{\varepsilon }_{i}})}}^{2}}}},$
(27)
$D(x{\text{'}}) = 1 + {{(1 - x{\text{'}})}^{2}} - \frac{{4x{\text{'}}}}{{{{\varepsilon }_{i}}}}\left( {1 - \frac{{x{\text{'}}}}{{{{\varepsilon }_{i}}(1 - x{\text{'}})}}} \right),$
(28)
$\begin{gathered} d(x{\text{'}}) = {{d}_{0}} + \\ \, + \mathop {\left( {\frac{m}{{2{{E}_{i}}}}} \right)}\nolimits^2 \left[ {d_{1}^{2}(x{\text{'}}) + \frac{{{{\varepsilon }_{i}}}}{{sin(\theta {\text{'/}}2)}}({{\varepsilon }_{i}} + {{d}_{1}}(x{\text{'}}))} \right], \\ \end{gathered} $
(29)
$\begin{gathered} {{d}_{0}} = \tilde {\delta }{\text{'}}_{f}^{2} + \delta _{i}^{2} - 2{{\delta }_{i}}\tilde {\delta }_{f}^{'}cos({{\varphi }_{ - }}), \\ {{d}_{1}}(x{\text{'}}) = (1 + \delta _{i}^{2}) - \frac{{(1 + \tilde {\delta }{\text{'}}_{f}^{2})}}{{(1 - x{\text{'}})}}, \\ \end{gathered} $
(30)
$\tilde {\delta }_{f}^{'} = (1 - x{\text{'}})\delta _{f}^{'},$
(31)
$\begin{gathered} d{{\sigma }_{0}} = \frac{1}{\pi }{{Z}^{2}}\alpha r_{e}^{2}{{(1 - x{\text{'}})}^{3}}\frac{{[{{D}_{0}}(x{\text{'}}) + {{{(m{\text{/}}{{E}_{i}})}}^{2}}{{D}_{1}}(x{\text{'}})]}}{{{{{[{{d}_{0}} + {{{(m{\text{/}}2{{E}_{i}})}}^{2}}d_{1}^{2}(x')]}}^{2}}}} \times \\ \, \times \frac{{dx{\text{'}}}}{{x{\text{'}}}}d\delta {\text{'}}_{i}^{2}d\delta {\text{'}}_{f}^{2}d{{\varphi }_{ - }}, \\ \end{gathered} $
(32)
$\begin{gathered} {{D}_{0}}(x{\text{'}}) = \frac{{\delta {\text{'}}_{i}^{2}}}{{{{{(1 + \delta {\text{'}}_{i}^{2})}}^{2}}}} + \frac{{\tilde {\delta }{\text{'}}_{f}^{2}}}{{{{{(1 + \tilde {\delta }{\text{'}}_{f}^{2})}}^{2}}}} + \frac{{x{{{\text{'}}}^{2}}}}{{2(1 - x{\text{'}})}} \times \\ \, \times \frac{{(\delta {\text{'}}_{i}^{2} + \tilde {\delta }{\text{'}}_{f}^{2})}}{{(1 + \delta {\text{'}}_{i}^{2})(1 + \tilde {\delta }{\text{'}}_{f}^{2})}} - \left[ {(1 - x{\text{'}}) + \frac{1}{{(1 - x{\text{'}})}}} \right] \times \\ \, \times \frac{{\delta _{i}^{'}\tilde {\delta }_{f}^{'}}}{{(1 + \delta {\text{'}}_{i}^{2})(1 + \tilde {\delta }{\text{'}}_{f}^{2})}}cos{{\varphi }_{ - }}. \\ \end{gathered} $

После интегрирования резонансного дифференциального сечения рассеяния $d{{\sigma }_{{(j)res}}}$, $j = a,b$, а также сечения рассеяния в отсутствии внешнего окружения из лазерной плазмы $d{{\sigma }_{0}}$, по азимутальному углу ${{\varphi }_{ - }}$ получаются следующие выражения:

(33)
$\begin{gathered} d{{\sigma }_{{(a)res}}} = 8{{\pi }^{3}}{{Z}^{2}}\alpha r_{e}^{2}{{\eta }^{2}}\frac{{\delta {\text{'}}_{i}^{2} + \tilde {\delta }{\text{'}}_{f}^{2}}}{{{{{[b(x_{{(a)}}^{'})G(x_{{(a)}}^{'})]}}^{{3/2}}}}} \times \\ \, \times \frac{{{{{(1 - x_{{(a)}}^{'})}}^{2}}D(x_{{(a)}}^{'})}}{{[{{{(\delta {\text{'}}_{i}^{2} - \delta {\text{'}}_{{(a)i}}^{2})}}^{2}} + \Gamma _{{{{\delta }_{i}}}}^{2}]}}\frac{{dx_{{(a)}}^{'}}}{{x_{{(a)}}^{'}}}d\delta {\text{'}}_{i}^{2}d\delta {\text{'}}_{f}^{2}, \\ \end{gathered} $
(34)
$\begin{gathered} d{{\sigma }_{{(b)res}}} = 8{{\pi }^{3}}{{Z}^{2}}\alpha r_{e}^{2}{{\eta }^{2}}\frac{{\delta {\text{'}}_{i}^{2} + \tilde {\delta }{\text{'}}_{f}^{2}}}{{{{{[b(x_{{(b)}}^{'})G(x_{{(b)}}^{'})]}}^{{3/2}}}}} \times \\ \, \times \frac{{{{{(1 - x_{{(b)}}^{'})}}^{{ - 2}}}D(x_{{(b)}}^{'})}}{{[{{{(\delta {\text{'}}_{f}^{2} - \delta {\text{'}}_{{(b)f}}^{2})}}^{2}} + \Gamma _{{{{\delta }_{f}}}}^{2}]}}\frac{{dx_{{(b)}}^{'}}}{{x_{{(b)}}^{'}}}d\delta {\text{'}}_{i}^{2}d\delta {\text{'}}_{f}^{2}, \\ \end{gathered} $
(35)
$\begin{gathered} d{{\sigma }_{0}} = \\ = 4{{Z}^{2}}\alpha r_{e}^{2}\frac{{{{{(1 - x{\text{'}})}}^{3}}}}{{{{{[b(x{\text{'}})]}}^{{3/2}}}}}(\delta {\text{'}}_{i}^{2} + \tilde {\delta }{\text{'}}_{f}^{2}){{D}_{2}}(x{\text{'}})\frac{{dx{\text{'}}}}{{x{\text{'}}}}d\delta {\text{'}}_{i}^{2}d\delta {\text{'}}_{f}^{2}, \\ \end{gathered} $
где

(36)
$G(x{\text{'}}) = 1 + \mathop {\left( {\frac{m}{{{{E}_{i}}}}} \right)}\nolimits^2 \frac{{{{\varepsilon }_{i}}(\delta {\text{'}}_{i}^{2} + \tilde {\delta }{\text{'}}_{f}^{2})}}{{2si{{n}^{2}}(\theta {\text{'/}}2)}}\frac{{[{{\varepsilon }_{i}} + {{d}_{1}}(x{\text{'}})]}}{{b(x{\text{'}})}},$
(37)
$b(x{\text{'}}) = {{(\delta {\text{'}}_{i}^{2} - \tilde {\delta }{\text{'}}_{f}^{2})}^{2}} + \frac{1}{2}\mathop {\left( {\frac{m}{{{{E}_{i}}}}} \right)}\nolimits^2 (\delta {\text{'}}_{i}^{2} + \tilde {\delta }{\text{'}}_{f}^{2})d_{1}^{2}(x{\text{'}}),$
(38)
${{D}_{2}}(x{\text{'}}) = D_{0}^{'}(x{\text{'}}) + {{(m{\text{/}}{{E}_{i}})}^{2}}D_{1}^{'}(x{\text{'}}),$
(39)
$\begin{gathered} D_{0}^{'}(x{\text{'}}) = \frac{{\delta {\text{'}}_{i}^{2}}}{{{{{(1 + \delta {\text{'}}_{i}^{2})}}^{2}}}} + \frac{{\tilde {\delta }{\text{'}}_{f}^{2}}}{{{{{(1 + \tilde {\delta }{\text{'}}_{f}^{2})}}^{2}}}} + \frac{{x{{{\text{'}}}^{2}}}}{{2(1 - x{\text{'}})}} \times \\ \, \times \frac{{(\delta {\text{'}}_{i}^{2} + \tilde {\delta }{\text{'}}_{f}^{2})}}{{(1 + \delta {\text{'}}_{i}^{2})(1 + \tilde {\delta }{\text{'}}_{f}^{2})}} - \left[ {(1 - x{\text{'}}) + \frac{1}{{(1 - x{\text{'}})}}} \right] \times \\ \, \times \frac{{2\delta _{i}^{'}\tilde {\delta }_{f}^{'}}}{{(1 + \delta {\text{'}}_{i}^{2})(1 + \tilde {\delta }{\text{'}}_{f}^{2})(\delta {\text{'}}_{i}^{2} + \tilde {\delta }{\text{'}}_{f}^{2})}}, \\ \end{gathered} $
(40)
$\begin{gathered} D_{1}^{'}(x{\text{'}}) = {{D}_{1}}(x{\text{'}}) + \left[ {(1 - x{\text{'}}) + \frac{1}{{(1 - x{\text{'}})}}} \right] \times \\ \, \times \frac{{d_{1}^{2}\delta _{i}^{'}\tilde {\delta }_{f}^{'}}}{{2(1 + \delta {\text{'}}_{i}^{2})(1 + \tilde {\delta }{\text{'}}_{f}^{2})(\delta {\text{'}}_{i}^{2} + \tilde {\delta }{\text{'}}_{f}^{2})}}. \\ \end{gathered} $

Резонансные знаменатели уравнений (33), (34) представляют характерную форму Брейта–Вигнера. Для $\delta {\text{'}}_{i}^{2} \to \delta {\text{'}}_{{(a)i}}^{2}$ (для канала A) и $\delta {\text{'}}_{f}^{2} \to \delta {\text{'}}_{{(b)f}}^{2}$ (для канала B) резонансные дифференциальные сечения достигают острого максимума. Форму-лы (33) и (34) в данном случае достигают максимальных значений (в единицах соответствующего дифференциального сечения рассеяния в отсутствие лазерной плазмы (35)) и приобретают вид

(41)
$R_{{(j)res}}^{{{\text{max}}}} = \frac{{d\sigma _{{(j)res}}^{{{\text{max}}}}}}{{d{{\sigma }_{0}}}} = {{f}_{0}}{{R}_{{(j)}}},\quad {{f}_{0}} = \frac{{32{{\pi }^{3}}}}{{{{\eta }^{2}}{{\alpha }^{2}}}},$
(42)
${{R}_{{(j)}}} = \frac{{x{\text{'}}_{{(j)}}^{2}}}{{{{{(1 - x_{{(j)}}^{'})}}^{3}}}}\frac{{D(x_{{(j)}}^{'})}}{{{{D}_{2}}(x_{{(j)}}^{'})}}\frac{{{{{[G(x_{{(j)}}^{'})]}}^{{ - 3/2}}}}}{{K_{i}^{2}}},\quad j = a,b.$

Выражения (41) и (42) определяют значения резонансного дифференциального сечения рассеяния ЛМТ эффекта (в единицах соответствующего дифференциального сечения рассеяния в отсутствии лазерной плазмы) для каналов A и B с одновременной регистрацией углов вылета конечного электрона и спонтанного фотона (параметров $\delta _{i}^{'}$ и $\delta _{f}^{'}$) и, дополнительно, уравнения определяют частоту спонтанного фотона. Рисунки 4 и 5 иллюстрируют принципиальные результаты для различных значений характеризующих параметров.

Рис. 4.

Зависимость резонансного дифференциального сечения ЛМТ процесса ультрарелятивистских электронов от параметра $\delta {\text{'}}_{i}^{2}$ для канала A (35), (41), (42) при фиксированных углах вылета конечного электрона (parameter $\delta {\text{'}}_{f}^{2}$): соответствует энергии электронов ${{E}_{i}} \approx 167$ ГэВ (a), соответствует энергии электронов ${{E}_{i}} \approx 250$ ГэВ (б).

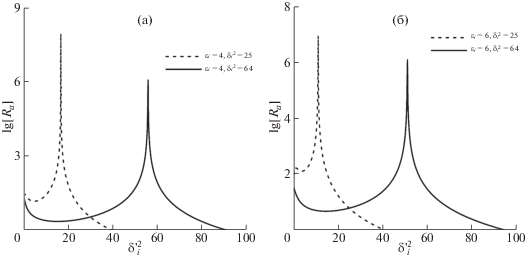
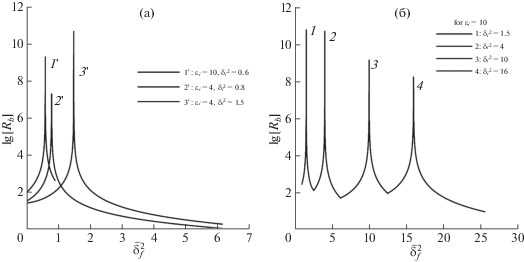
Рис. 5.

Зависимость резонансного дифференциального сечения ЛМТ процесса ультрарелятивистских электронов от параметра $\tilde {\delta }{\text{'}}_{f}^{2}$ для канала B (35), (41), (42) при фиксированных значениях параметра $\delta {\text{'}}_{i}^{2}$. Пики 2  ', 3 ' отвечают энергии электронов ${{E}_{i}} \approx 167$ ГэВ и изменению параметра $\mathop {\delta '}\nolimits_f^2 $ в интервале $0 \leqslant \delta {\text{'}}_{f}^{2} \leqslant 3(1 + {{\varepsilon }_{i}})$. Пик 1’ соответствует энергии электрона ${{E}_{i}} \approx 417$ ГэВ и изменению параметра $\delta {\text{'}}_{f}^{2}$ в интервале $0 < \delta {\text{'}}_{f}^{2} \leqslant \delta {\text{'}}_{ - }^{2}$. Пики 1, 2, 3 отвечают изменению параметра $\delta {\text{'}}_{f}^{2}$ в интервале $\delta {\text{'}}_{ - }^{2} \leqslant \delta {\text{'}}_{f}^{2} \leqslant \delta {\text{'}}_{ + }^{2}$ и трем возможным частотам (17), пик 4 отвечает изменению параметра $\delta {\text{'}}_{f}^{2}$ в интервале для $\delta {\text{'}}_{ + }^{2} < \delta {\text{'}}_{f}^{2}$ энергии электронов ${{E}_{i}} \approx 417$ ГэВ.

5. ВЫВОДЫ

Исследована резонансная кинематика лазерно-модифицированного процесса спонтанного торможения ультрарелятивистcких электронов на ядре в окружении поля лазерной плазмы. Статья выделяет три возможных диапазона, в которых отдельный угол вылета спонтанного фотона координирует три возможных дискретных значения для резонансной частоты спонтанного фотона. Представленный феномен имеет как фундаментальное, так и прикладное значение. Определено дифференциальное сечение рассеяния эффекта в лазерной плазме. Построенная модель определяет, что полученные дифференциальные сечения рассеяния превышают сечения рассеяния, вычисленные в отсутствии взаимодействий с внешней лазерной плазмой на 18–20 порядков величины. Можно утверждать, что специализированные лаборатории импульсного лазерного излучения (SLAC, FAIR, XFEL, ELI, XCELS) экспериментально подтверждают результаты вычислений данного проекта.

Список литературы

  1. Mourou G.A., Tajima T., Bulanov S.V. // Rev. Mod. Phys. 2006. V. 78. P. 309.

  2. Piazza A.Di., Müller C., Hatsagortsyan K.Z., Keitel C.H. // Rev. Mod. Phys. 2012. V. 84. P. 1177.

  3. Bagnoud V., Aurand B., Blazevic A., Borneis S., Bruske C., Ecker B., Eisenbarth U., Fils J., Frank A., Gaul E. et al. // Appl. Phys. B. 2010. V. 100. P. 137.

  4. Bula C., McDonald K.T., Prebys E.J., Bamber C., Boege S., Kotseroglou T., Melissinos A.C., Meyerhofer D.D., Ragg W., Burke D.L. et al. // Phys. Rev. Lett. 1996. V. 76. P. 3116.

  5. Kanya R., Morimoto Y., Yamanouchi K. // Phys. Rev. Lett. 2010. V. 105. P. 123202.

  6. Bunkin F.V., Fedorov M.V. // Zh. Eksp. Teor. Fiz. 1965. V. 49. P. 1215 [Sov. Phys. JETP. 1966. V. 22. P. 844].

  7. Oleinik V.P. // Zh. Eksp. Teor. Fiz. 1967. V. 52. P. 1049 [Sov. Phys. JETP. 1967. V. 25. P. 697].

  8. Oleinik V.P. // Zh. Eksp. Teor. Fiz. 1967. V. 53. P. 1997 [Sov. Phys. JETP. 1968. V. 26. P. 1132].

  9. Fedorov M.V. // An Electron in a Strong Light Field. Nauka, Moscow, 1991.

  10. Ritus V.I., Nikishov A.I. Trudy FIAN / Ed. by V.L. Ginz-burg. M., Nauka, 1979. V. 111.

  11. Ehlotzky F., Krajewska K., Kamiński J.Z. // Rep. Prog. Phys. 2009. V. 72. P. 046401.

  12. Roshchupkin S.P., Lebed’ A.A., Padusenko E.A. // Las. Phys. 2012. V. 22. P. 1513.

  13. Roshchupkin S.P. // Las. Phys. 1996. V. 6. P. 837.

  14. Roshchupkin S.P., Lebed’ A.A., Padusenko E.A., Voroshilo A.I. // Las. Phys. 2012. V. 22. P. 1113.

  15. Dondera M., Florescu V. // Radiat. Phys. Chem. 2006. V. 75. P. 1380.

  16. Florescu A., Florescu V. // Phys. Rev. A. 2000. V. 61. P. 033406.

  17. Lebed’ A.A., Roshchupkin S.P. // Phys. Rev. A. 2010. V. 81. P. 033413.

  18. Roshchupkin S.P., Lysenko O.B. // Laser Phys. 1999. V. 9. P. 494.

  19. Lebed’ A.A. // Laser Phys. Lett. 2016. V. 13. P. 045401.

  20. Lebed’ A.A., Padusenko E.A., Roshchupkin S.P., Du-bov V.V. // Phys. Rev. A. 2016. V. 94. P. 013424.

  21. Lebed’ A.A., Padusenko E.A., Roshchupkin S.P., Du-bov V.V. // Phys. Rev. A. 2018. V. 97. P. 043404.

  22. Krachkov P.A., Piazza A.Di., Milstein A.I. arXiv: 1904.05094. 2019.

  23. Roshchupkin S.P., Tsybul’nik V.A., Chmirev A.N. // Laser Phys. 2000. V. 10. P. 1256.

  24. Dubov A., Dubov V.V., Roshchupkin S.P. arXiv: 1907.10431. 2019.

  25. Volkov D.M. // Zeit. Phys. 1935. V. 94. P. 250.

  26. Berestetskii V.B., Lifshitz E.M., Pitaevskii L.P. / Quantum Electrodynamics. M., Nauka, 1980.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика плазмы

Архивы выпусков Информация о журнале Отправить рукопись в журнал