Физика плазмы, 2020, T. 46, № 3, стр. 213-218

1. ВВЕДЕНИЕ

В наземных условиях плазменный кристалл формируется заряженными пылевыми частицами, левитирующими в приэлектродной области газового разряда. Исследованию структуры и динамики плазменных кристаллов посвящена значительная часть физики пылевой плазмы, и обзор основных идей и достижений можно найти в монографиях [1–3].

Как для аналитической теории, так и для численного моделирования кристаллов нужны те или иные предположения о характере взаимодействия между отдельными частицами. Во многих работах предполагается, что пылинки взаимодействуют посредством изотропного или экранированного кулоновского потенциала (например, [4–9]). Предположение изотропности позволяет построить теорию колебаний и исследовать устойчивость одномерного или двумерного плазменного кристалла, левитирующего в горизонтальной плоскости. Существенно, что в приближении изотропного потенциала взаимодействия колебания частиц в вертикальном направлении и в горизонтальной плоскости оказываются независимыми.

Однако в области существования плазменного кристалла окружающая плазма сильно анизотропна и характеризуется наличием ионного потока в направлении электрода. Это приводит к тому, что потенциал электрического поля вокруг отдельного заряда оказывается несимметричным. Как следствие, силы, действующие между отдельными частицами, оказываются невзаимными, т.е. для них не выполняется третий закон Ньютона.

Простых аналитических выражений для потенциала заряда в плазме с ионными потоками не существует. Поэтому в теории часто используется так называемая модель ионного фокуса [10]. В этой модели с каждой отрицательно заряженной пылинкой связывается виртуальный заряд противоположного знака, расположенный на фиксированном расстоянии ниже по течению ионного потока. При этом считается, что поле виртуального заряда не действует на другие заряды, расположенные выше по течению, т.е. межчастичные силы оказываются невзаимными. В свою очередь, более сложный характер взаимодействия приводит к связи вертикальных и горизонтальных смещений частиц и развитию специфических неустойчивостей (например, [11–13]).

Изотропный дебаевский потенциал и модель ионного фокуса представляют собой достаточно грубое приближение реального взаимодействия. В работе [14] исследовалось стационарное состояние плазменного кристалла, и при этом потенциал взаимодействия рассчитывался численными методами в предположении, что окружающая плазма состоит из направленного потока холодных ионов и максвелловских электронов. В настоящей работе, являющейся продолжением [14], исследуется устойчивость линейной цепочки пылевых частиц. Подобная геометрия представляет опредленный методический интерес и, кроме того, может быть реализована в эксперименте (например, [15]).

Принимается следующая модель линейного кристалла. Предполагается, что в равновесии все частицы расположены на одной высоте во внешнем гармоническом потенциальном поле с характерной частотой колебаний ${{\Omega }_{0}}$. Частицы расположены вдоль оси x на расстоянии a друг от друга. В приближении ближайших соседей частоты колебаний определяются тремя силовыми константами. Эти константы в подходящих безразмерных переменных зависят от межчастичного расстояния и от дополнительного параметра M, который для квазинейтральной плазмы имеет смысл числа Маха ионного потока. Параметры ${{\Omega }_{0}}$, a и M считаются независимыми. Задача заключается в поиске области в трехмерном пространстве параметров, в которой колебания линейной цепочки устойчивы, и определения типа неустойчивости на границе области.

В следующем разделе приведено выражение для потенциала взаимодействия, а явные формулы для силовых констант, использованные в численных рассчетах, выписаны в Приложении 1. Далее в разделе 3 обсуждаются уравнения движения, в разделе 4 выписаны собственные частоты колебаний и определены условия, при которых колебания устойчивы.

2. ПОТЕНЦИАЛ ВЗАИМОДЕЙСТВИЯ

Потенциал электрического поля, создаваемый неподвижной частицей с зарядом Q, в однородном потоке плазмы дается выражением

где u – скорость потока. В дальнейшем предполагается, что поток плазмы направлен в сторону $z \to - \infty $.

Все пространственные переменные нормализованы на характерную длину $\lambda = u{\text{/}}{{\omega }_{{pi}}}$, где ${{\omega }_{{pi}}}$ – ионная плазменная частота, а межчастичные силы нормализованы на ${{F}_{0}} = {{Q}^{2}}{\text{/}}{{\lambda }^{2}}$. Естественный масштаб времени для частиц с массой ${{M}_{0}}$ равен $M_{0}^{{1/2}}{{\lambda }^{{3/2}}}{\text{/}}\left| Q \right|$.

В безразмерных переменных сила, действующая на другую частицу с тем же зарядом Q в точке r, равна ${\mathbf{F}}({\mathbf{r}}) = - \nabla U({\mathbf{r}})$. Потенциальная функция $U({\mathbf{r}}) = U(\rho ,z)$ получается из (1) интегрированием по полярному углу

Предполагается, что плазма состоит из холодного потока ионов и максвелловских электронов с температурой ${{T}_{e}}$. В этом случае диэлектрическая проницаемость плазмы в безразмерных переменных имеет вид

где ν – бесконечно малая частота столкновений ионов с нейтралами, учет которой необходим для правильного обхода полюсов в интеграле (2). В выражении (3) $M = ({{n}_{e}}{\text{/}}{{n}_{i}})u\sqrt {{{m}_{i}}{\text{/}}{{T}_{e}}} $, где ${{n}_{{e,i}}}$ – равновесные плотности электронов и ионов, а ${{m}_{i}}$ – масса ионов. В общем случае плазма в пристеночном слое не является нейтральной, т.е. ${{n}_{e}} \ne {{n}_{i}}$, однако при этом неоднородностью плазмы пренебрегается. Представляет интерес случай чисто ионного потока с $M = 0$, когда влиянием электронов можно пренебречь. Для квазинейтральной плазмы с ${{n}_{e}} = {{n}_{i}}$ параметр M совпадает с числом Маха потока, т.е. отношению скорости u к скорости ионного звука.

Для исследования устойчивости ансамбля частиц, левитирующих на одной высоте, нужны различные производные потенциала (2) при $z = 0$. В настоящей работе используется приближение ближайших соседей, т.е. учитывается взаимодействие выделенной частицы лишь с частицами, расположенными на фиксированном расстоянии a. Соответствующие силовые константы обозначаются как

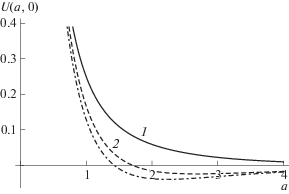
Использованные для численных расчетов формулы приведены в Приложении 1. На рис. 1 показано несколько примеров зависимости межчастичного потенциала от расстояния. Заметим, что при $M < 1$, т.е. в дозвуковом или чисто ионном потоке [16], потенциал взаимодействия является притягивающим в определенном интервале расстояний, тогда как при $M > 1$ частицы отталкиваются.

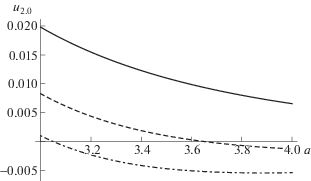
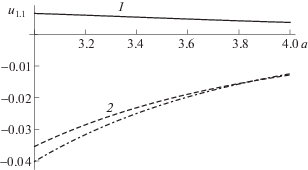
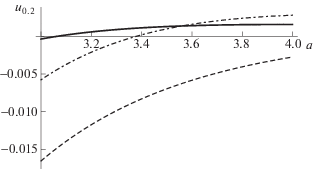
Для анализа устойчивости важны вторые производные (4). На рис. 2, 3 показаны зависимости силовых констант ${{u}_{{0,2}}}$ и ${{u}_{{2,0}}}$ от a. Как видно из рисунков, обе величины ${{u}_{{2,0}}}$, ${{u}_{{0,2}}}$ могут менять знак. Насколько можно судить по результатам численного анализа, смешанная производная ${{u}_{{1,1}}}$ (рис. 4), обусловленная невзаимным характером сил, всегда положительна при $M > 1$ и отрицательна при $M < 1$. Более существенно, что по абсолютной величине $\left| {{{u}_{{1,1}}}} \right|$ примерно на порядок больше, чем $\left| {{{u}_{{2,0}}}} \right|$ и $\left| {{{u}_{{0,2}}}} \right|$.

3. УРАВНЕНИЯ ДВИЖЕНИЯ

Предполагается, что в равновесии все частицы левитируют на одной высоте ${{z}^{0}}$, причем в вертикальном направлении на них действует внешняя удерживающая сила с потенциалом ${{U}^{{ext}}} = 1{\text{/}}2\Omega _{0}^{2}{{z}^{2}}$.

Рассмотрим линейную цепочку пылевых частиц, взаимодействующих посредством сил с потенциалом (2). Пусть в равновесии координаты частиц равны $x_{n}^{0} = an$, ${{y}_{n}} = 0$, $z_{n}^{0} = {{z}^{0}}$ ($n = 0$, ±1, ±2, ...). Предполагая, что движение вдоль оси $y$ каким-то образом заморожено и вводя малые отклонения от равновесия ${{x}_{n}} \to an + {{x}_{n}}$, ${{z}_{n}} \to {{z}^{0}} + {{z}_{n}}$, запишем общие уравнения движения в виде

Эти уравнения учитывают взаимодействие только между ближайшими соседями. Как отмечалось в [14], подобное приближение хорошо работает лишь при достаточно большом межчастичном расстоянии $a > 2$. В стационарном состоянии из уравнений (5) получается равновесная высота левитации ${{z}^{0}} = - 2{{u}_{{0,1}}}{\text{/}}\Omega _{0}^{2}$. В линейном приближении по малым отклонениям от равновесия уравнения (5) переписываются в виде

Введем двумерный вектор ${{{\mathbf{r}}}_{n}} = ({{x}_{n}},{{z}_{n}})$ и совершим дискретное преобразование Фурье

где волновой вектор k лежит в первой зоне Бриллюэна $ - \pi \leqslant k \leqslant \pi $. Уравнения (6) теперь переписываются в матричном виде где и

Заметим, что матрица (9) симметрична, но неэрмитова. По этой причине в литературе широко распространено утверждение, что даже в отсутствие диссипации невзаимные силы разрушают механические интегралы движения, и уравнения типа (8) не допускают гамильтонову форму записи. В действительности это не так. В явном виде подходящие переменные и гамильтониан для уравнений (8) выписаны в Приложении 2. Поэтому обсуждаемые в дальнейшем сценарии потери устойчивости вполне типичны для бифуркаций гамильтоновых систем (например [17]).

4. СОБСТВЕННЫЕ ЧАСТОТЫ

Собственные значения и векторы матрицы (9) определяют частоты и поляризации колебаний линейной цепочки. В явном виде квадраты частот равны

где $D(k) = {{(\Omega _{x}^{2}(k) - \Omega _{z}^{2}(k))}^{2}} - 4{{g}^{2}}(k)$.

В отсутствие невзаимных сил $g(k) = 0$, поэтому колебания разделяются на горизонтальные и вертикальные в зависимости от направления вектора поляризации e. Частота вертикальных колебаний равна ${{\Omega }_{z}}(k)$ (10) и ${{{\mathbf{e}}}_{z}} = (0,1)$. Линейная цепочка частиц может потерять устойчивость, если ${{u}_{{0,2}}} < 0$ и $\Omega _{0}^{2} + 4{{u}_{{0,2}}} < 0$. Эта неустойчивость, в литературе называемая изгибной (bending), носит апериодический характер и наступает при уменьшении частоты внешнего удерживающего потенциала ${{\Omega }_{0}}$. При достижении порога $\Omega _{0}^{2} + 4{{u}_{{0,2}}} = 0$ первой теряет устойчивость волна с $k = \pi $, и векторы смещения частиц можно записать как ${{r}_{n}} = {{( - 1)}^{n}}{{e}_{z}}$. Частота горизонтальных колебаний с ${{{\mathbf{e}}}_{x}} = (1,0)$ равна ${{\Omega }_{x}}(k)$ (10). При наличии притяжения между частицами коэффициент ${{u}_{{2,0}}}$ может менять знак в некоторой области параметров (см. рис. 3), и цепочка частиц становится неустойчивой. При этом максимум инкремента достигается на границе зоны Бриллюэна $k = \pi $, и векторы смещений частиц имеют вид ${{{\mathbf{r}}}_{n}} = {{( - 1)}^{n}}{{{\mathbf{e}}}_{x}}$.

При учете невзаимных сил дисперсионные кривые качественно меняются. Для достаточно больших значений частоты ${{\Omega }_{0}} > {{\Omega }_{{cr}}}$ дискриминант $D(k)$ в (11) положителен для любых волновых векторов. По мере уменьшения ${{\Omega }_{0}}$ функция $D(k)$ обращается в нуль для каких-то значений $k = {{k}_{0}}$ и ${{\Omega }_{0}} = {{\Omega }_{{cr}}}$, а при ${{\Omega }_{0}} < {{\Omega }_{{cr}}}$ становится отрицательной в некотором конечном интервале k. Явные выражения для ${{\Omega }_{{cr}}}$ и ${{k}_{0}}$ получаются из решения двух уравнений $D(k) = 0$, $\partial D(k){\text{/}}\partial k = 0$

При ${{\Omega }_{0}} = {{\Omega }_{{cr}}}$ и $k = {{k}_{0}}$ частоты (11) совпадают ${{\omega }_{0}} = {{\omega }_{{1,2}}}$. Собственные векторы матрицы (9) равны ${\mathbf{e}} = (1, - i)$, т.е. в конфигурационном пространстве частицы совершают круговое движение ${{x}_{n}} = cos({{k}_{0}}n - {{\omega }_{0}}t)$, ${{z}_{n}} = sin({{k}_{0}}n - {{\omega }_{0}}t)$.

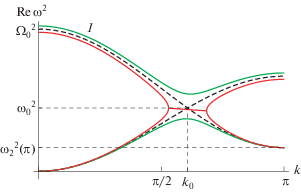
На рис. 5 показаны характерные примеры поведения дисперсионных кривых при ${{\Omega }_{0}} \approx {{\Omega }_{{cr}}}$. Входящие в (10) коэффициенты вычислялись при помощи потенциала (14). Пунктирной кривой изображены частоты (11) при ${{\Omega }_{0}} = {{\Omega }_{{cr}}}$, пересекающиеся в точке $({{k}_{0}},{{\omega }_{0}})$. В области устойчивости ${{\Omega }_{0}} > {{\Omega }_{{cr}}}$ при $k \approx {{k}_{0}}$ образуется щель (кривые 1, 2 на рис. 5). При ${{\Omega }_{0}} < {{\Omega }_{{cr}}}$ в окрестности точки $({{k}_{0}},{{\omega }_{0}})$ формируется область неустойчивости (кривая 3 на рис. 5). Подобное поведение кривых обычно называют неустойчивостью связанных мод.

При ${{\Omega }_{0}} > {{\Omega }_{{cr}}}$ возможен другой сценарий потери устойчивости, связанный с тем, что квадрат частоты $\omega _{2}^{2}(k)$ (11) может изменить знак при каком-то значении k. Из явных выражений (10, 11) легко получить, что это происходит при смене знака коэффициента ${{u}_{{2,0}}}$ и при этом волновой вектор лежит на границе зоны Бриллюэна $k = \pi $. Поскольку $g(\pi ) = 0$, поляризация колебаний при потере устойчивости соответствует горизонтальным смещениям с ${\mathbf{e}} = (1,0)$. Это соответствует структурному фазовому переходу, в результате которого период цепочки удваивается, и в каждой элементарной ячейке содержится две частицы. Судя по результатам численных расчетов, этот переход возможен только в дозвуковом режиме $M < 1$ (см. рис. 3).

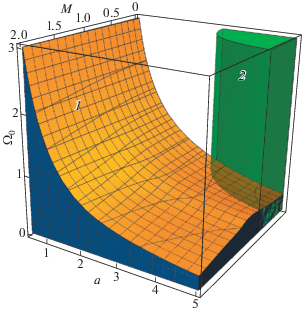
Входящие в выражения (10) силовые константы ${{u}_{{0,2}}}$, ${{u}_{{2,0}}}$, ${{u}_{{1,1}}}$ рассчитывались в области параметров $2 \leqslant a \leqslant 6$ и $0 \leqslant M \leqslant 2$. Общая диаграмма устойчивости цепочки в исследованной области параметров $a,\;M,\;{{\Omega }_{0}}$ показана на рис. 6, где области неустойчивости затенены. Поверхность 1 задается условием ${{\Omega }_{0}} = {{\Omega }_{{cr}}}(a,M)$, и при пересечении этой поверхности развивается неустойчивость связанных мод. Цилиндрическая поверхность 2 задается условием ${{u}_{{2,0}}}(a,M) = 0$, и при пересечении этой поверхности происходит структурный фазовый переход, приводящий к удвоению периода цепочки. Заметим, что, двигаясь из области устойчивости ${{\Omega }_{0}} > {{\Omega }_{{cr}}}(a,M)$, ${{u}_{{2,0}}}(a,M) > 0$, можно пересечь поверхность 1 при изменении любого параметра a, M, Ω₀, а условие структурного фазового перехода не зависит от частоты ${{\Omega }_{0}}$.

5. ЗАКЛЮЧЕНИЕ

В статье была построена диаграмма устойчивости линейного плазменного кристалла. В отличие от предыдущих работ, потенциал взаимодействия рассчитывался численными методами в предположении, что окружающая плазма состоит из направленного потока холодных ионов и максвелловских электронов. В использованной модели состояние плазменного кристалла определятся характерной частотой внешнего удерживающего потенциала ${{\Omega }_{0}}$, расстоянием между частицами a и числом Маха ионного потока M, которые считаются независимыми параметрами. Показано, что кристалл может терять устойчивость либо вследствие развития осцилляторной неустойчивости связанных волн, либо в результате развития апериодической неустойчивости, приводящей к удвоению периода кристалла. Обсуждавшаяся в литературе изгибная неустойчивость оказывается полностью подавленной.