Физика плазмы, 2020, T. 46, № 4, стр. 329-350

1. ВВЕДЕНИЕ

В плазменной оболочке Земли, которая состоит из тесно связанных между собой ионосферы и магнитосферы, а также в обтекающем магнитосферу солнечном ветре, идут взаимно согласованные сложные процессы в широком диапазоне пространственных и временных масштабов.

Глобальное распределение электромагнитного поля и плазмы в ионосфере и магнитосфере определяется магнитосферно-ионосферной токовой системой, которая формируется в результате относительно крупномасштабных и медленных безызлучательных процессов. С точки зрения моделирования магнитное поле в околоземном космическом пространстве можно разделить на две сопоставимые между собой части. Первая часть создается токовой системой внутри Земли, и в численных моделях ионосферы и магнитосферы считается заданной, например, дипольной в простейшем случае. Вторая часть магнитного поля создается магнитосферно-ионосферной токовой системой, важную часть которой составляют продольные токи, протекающие вдоль силовых линий магнитного поля, причем эти токи начинаются от внешней границы магнитосферы – магнитопаузы, пересекают магнитосферу, втекают в высокоширотную ионосферу, пересекают F-слой, затем “замыкаются” в E-слое ионосферы и вытекают обратно в магнитосферу.

На фоне этого глобального распределения электромагнитного поля и плазмы и в сильной зависимости от него протекает широкий набор более мелкомасштабных процессов, которые можно разделить на две группы. В первую группу входят достаточно медленные безызлучательные плазменные процессы, такие как развитие тиринг-неустойчивости, а также возбуждение и распространение различных магнитогидродинамических волн. Во вторую группу входят еще на порядки более мелкомасштабные процессы, в которых важны разделение заряда, а также генерация и распространение электромагнитных волн.

Описывающую плазму систему уравнений удобно разделять на две части: на систему уравнений переноса, которая описывает движение каждой компоненты плазмы, и на систему уравнений для полей. При кинетическом, гидродинамическом или гибридном подходе к описанию крупномасштабных относительно медленных процессов в плазме солнечного ветра, магнитосферы и ионосферы рассматривается эволюция распределений электромагнитного поля и гидродинамических параметров плазмы на пространственных масштабах, начиная с гирорадиуса тепловых протонов, который на два и более порядков больше теплового гирорадиуса замагниченных электронов и на три и более порядков больше их дебаевского расстояния. При этом рассматриваются временные масштабы, которые на несколько порядков больше характерных периодов циклотронного вращения и плазменных колебаний электронов. Указанные соотношения масштабов означают, что, во-первых, с высокой точностью выполняется условие квазинейтральности, и рассматриваются усредненные по циклотронному вращению и плазменным колебаниям электронов распределения электромагнитного поля и гидродинамических параметров плазмы, и, во-вторых, что электромагнитным излучением плазмы можно пренебречь.

Исключение излучения с учетом квазинейтральности равносильно отбрасыванию тока смещения, что означает переход в описании полей к мгновенному дальнодействию с бесконечной скоростью распространения взаимодействия. В этом приближении поля определяются текущим пространственным распределением гидродинамических параметров плазмы и граничными условиями из системы уравнений эллиптического типа, которые не должны содержать частных производных по времени.

Система уравнений для магнитного поля удовлетворяет этим условиям, поскольку состоит из уравнения Гаусса и уравнения Ампера, которые сводятся к векторному уравнению Пуассона, имеющему эллиптический тип.

Также известно, что в неоднородной плазме квазинейтральность равносильна усреднению по плазменным колебаниям электронов вдоль силовых линий магнитного поля и поддерживается продольным электрическим полем, которое определяется из условия продольного силового равновесия электронов. Это условие дает явное выражение продольного электрического поля через продольную составляющую дивергенции тензора давления электронов и их концентрацию. Таким образом, необходимо получить систему уравнений для определения электрического поля, в которой это условие, а также указанные выше условия эллиптичности и отсутствия частных производных по времени, должны точно выполняться.

В данной работе дается общее решение указанной проблемы при помощи подхода, предложенного в [1, 2]. В этом подходе электрическое поле разлагается на потенциальную и соленоидальную части, берется ротор от уравнения Фарадея, и частная производная по времени от ротора магнитной индукции выражается из уравнения Ампера через частную производную по времени от плотности тока. Последняя при помощи обобщенного закона Ома выражается через гидродинамические переменные каждой компоненты плазмы и их пространственные частные производные, а также через поля. Обобщенный закон Ома получается суммированием уравнений потока импульса каждой компоненты плазмы, записанных через плотность тока данной компоненты. Его форма зависит от наличия замагниченности компонент плазмы.

В результате для соленоидальной части электрического поля получено линейное уравнение эллиптического типа, которое в ходе итерационного процесса численного интегрирования описывающей плазму системы уравнений на каждой итерации сводится к уравнению Пуассона. Потенциальная часть электрического поля определяется из уравнения продольного силового равновесия электронов интегрированием этого уравнения вдоль силовых линий магнитного поля. При этом плотность тока и ее частная производная по времени, которые определяют правые части в системе уравнений для полей, находятся из системы уравнений переноса.

В работе рассматриваются три формы обобщенного закона Ома, соответствующие различным уровням замагниченности плазмы, которые, в зависимости от используемой системы уравнений переноса каждой компоненты плазмы, определяют пять вариантов описывающей плазму системы уравнений.

Первый вариант обобщенного закона Ома относится к общему случаю, когда все компоненты плазмы не замагничены, и в уравнениях присутствует тензор давлений электронов. Ему соответствует только один вариант системы уравнений переноса – уравнения Власова для каждой компоненты плазмы.

Второй вариант закона Ома относится к случаю, когда все ионные компоненты плазмы не замагничены, а замагничены только электроны. Тогда в уравнениях тензор давлений электронов выражается через их продольное и поперечное давление, а также магнитное поле. Для этого случая возможны два варианта системы уравнений переноса, причем в обоих ионы описываются уравнениями Власова. В первом варианте электроны описываются уравнением Власова в дрейфовом приближении (см. [3–5]). Во втором варианте они описываются системой уравнений магнитной газодинамики Чу–Гольдбергера–Лоу (далее используем сокращение ЧГЛ) с исходными уравнениями для давлений без использования адиабатических инвариантов (см. [6–8]). По сложившейся терминологии этот вариант называется гибридным описанием плазмы (см. [9, 10]).

Третий вариант закона Ома относится к случаю, когда все компоненты плазмы замагничены, и в уравнениях тензор давлений каждой компоненты заменяется его выражением через продольное и поперечное давление, а также магнитное поле. Для этого случая также возможны два варианта системы уравнений переноса. В первом варианте каждая компонента описывается уравнением Власова в дрейфовом приближении. Во втором варианте каждая компонента описывается системой уравнений магнитной газодинамики Чу–Гольдбергера–Лоу также с исходными уравнениями для давлений без использования адиабатических инвариантов.

Отметим, что на основе полученных в работе систем уравнений можно создавать численные модели для широкого круга актуальных задач физики космической плазмы. Результаты работы создают необходимый теоретический задел для разработки глобальной численной модели атмосферы-ионосферы-магнитосферы.

2. СИСТЕМА УРАВНЕНИЙ ДЛЯ ПОЛЕЙ НА БОЛЬШИХ МАСШТАБАХ

Рассмотрим схему вывода системы уравнений для полей. Для моделирования мелкомасштабных быстрых процессов с учетом разделения заряда в модели необходимо иметь пространственное разрешение меньшее дебаевского расстояния электронов, временное разрешение меньше их плазменного периода, и использовать систему уравнений Власова–Максвелла, в которой уравнения Власова замыкаются системой уравнений Максвелла в вакууме. Последняя система (в системе единиц СИ) имеет вид

Здесь и далее через $H{\kern 1pt} \left( {x,t} \right)$, $B\left( {x,t} \right)$ и $E{\kern 1pt} \left( {x,t} \right)$, $D\left( {x,t} \right)$ обозначены векторы напряженности и индукции магнитного поля, а также векторы напряженности и индукции электрического поля соответственно, через ${\rho }\left( {x,t} \right)$ и $j\left( {x,t} \right)$ – полные плотности заряда и тока, которые рассматриваются как функции, зависящие от пространственной координаты $x = {{\left( {{{x}_{1}},{{x}_{2}},{{x}_{3}}} \right)}^{T}} \in {{\mathbb{R}}^{3}}$ и времени t. Также здесь и далее через ${{{\varepsilon }}_{0}}$ и ${{{\mu }}_{0}}$ обозначены электрическая и магнитная постоянные, а через $c = {{\left( {{{{\varepsilon }}_{0}}{{{\mu }}_{0}}} \right)}^{{ - 1/2}}}$ – скорость света в вакууме.

Для дальнейшего изложения введем следующие обозначения. Будем обозначать через $\left( {u \cdot v} \right)$ и $\left[ {u \cdot v} \right]$ скалярное и векторное произведения векторов u и v в пространстве ${{\mathbb{R}}^{3}}$ соответственно. Также будем использовать единичный вектор вдоль магнитного поля $b\left( {x,t} \right)$ и скорость электрического дрейфа ${{v}_{E}}\left( {x,t} \right)$, которые определяются формулами

Для произвольного векторного поля $a\left( {x,t} \right)$ введем его продольную ${{a}_{\parallel }}\left( {x,t} \right)$, а также ортогональную ${{a}_{ \bot }}\left( {x,t} \right)$ части по отношению к магнитному полю, которые определяются формулами

При моделировании крупномасштабных медленных процессов в космической плазме с пространственным разрешением на 2–3 порядка больше дебаевского расстояния систему Власова–Максвелла использовать нельзя, поскольку она не позволяет воспроизвести реальные значения возникающей за счет относительно очень малого разделения заряда потенциальной части электрического поля. Этот вопрос детально рассматривается в [2]. В этом случае необходимо использовать систему уравнений, в которой уравнение Пуассона (2.3) и вектор электрической индукции $D\left( {x,t} \right)$ не рассматриваются, а вместо них для определения электрического поля учитываются условие квазинейтральности (см., например, [11])

и условие продольного силового равновесия электронов. Оно определяет продольную составляющую напряженности электрического поля через продольную составляющую дивергенции тензора давления электронов ${{{\mathbf{\hat {P}}}}_{e}}\left( {x,t} \right)$ и их концентрацию ${\kern 1pt} {{n}_{e}}\left( {x,t} \right)$ из уравнения где e – заряд протона. Формула (2.9) означает, что продольная компонента объемной плотности электрической силы, действующей на электроны, уравновешивается продольной компонентой дивергенции тензора давления электронов.

Рассмотрим систему уравнений для полей в приближении продольного силового равновесия электронов. Отбрасывание в уравнении Максвелла (2.4) тока смещения ${{\partial D} \mathord{\left/ {\vphantom {{\partial D} {\partial {\kern 1pt} t}}} \right. \kern-0em} {\partial {\kern 1pt} t}}$ в соответствии с приближением безызлучательности, а также учет второго материального уравнения в (2.5) приводит к уравнению Ампера

Учет известного векторного тождества

позволяет получить из последнего уравнения и уравнения Гаусса (2.1) следующие векторные уравнения Пуассона как для B: так и для векторного потенциала ${\mathbf{A}}{\kern 1pt} \left( {{\mathbf{x}},t} \right)$ в калибровке Кулона:

Использование уравнения (2.12) вместе с граничными условиями Дирихле или Неймана позволяет получить магнитное поле в области моделирования Ω, непрерывно переходящее в известное заданное вне области моделирования ${\Omega }$ магнитное поле ${{B}_{{{\text{ext}}}}}\left( {x,t} \right)$.

Взятие ротора от уравнения Фарадея (2.2) и учет продифференцированного по времени уравнения Ампера (2.10) приводит к уравнению

Это уравнение определяет только соленоидальную (вихревую) часть электрического поля, а его потенциальная часть определяется из условия продольного равновесия электронов (2.9).

Далее будем использовать разложение в ограниченной области Ω пространства ${{\mathbb{R}}^{3}}$ векторного поля $a{\kern 1pt} \left( {x,t} \right)$ на потенциальную ${{a}_{{p}}}\left( {x,t} \right) = - \nabla {{\Phi }_{a}}\left( {x,t} \right)$ и соленоидальную ${{a}_{v}}{\kern 1pt} \left( {x,t} \right)$ части

которые удовлетворяют в области ${\Omega }$ следующим уравнениям:

Это разложение определено с точностью до градиента гармонической в области Ω функции, и для его единственности необходимо использовать какое-либо граничное условие, например, условие Дирихле для нормальной к границе $\partial {\Omega }$ области моделирования компоненты поля.

Разлагая электрическое поле на потенциальную ${{E}_{p}}\left( {x,t} \right) = - \nabla {\varphi }{\kern 1pt} \left( {x,t} \right)$ и соленоидальную ${{E}_{v}}{\kern 1pt} \left( {x,t} \right)$ части

а также используя применительно к $E\left( {x,t} \right)$ то-ждество (2.11), можно получить равенство $ - \nabla \times \nabla \times E = \Delta {{E}_{v}}$, подстановка которого в (2.14) дает уравнение

Если считать в этом уравнении правую часть формально известной, то с математической точки зрения относительно поля ${{E}_{v}}\left( {x,t} \right)$ оно является векторным уравнением Пуассона, которое вместе с граничными условиями Дирихле однозначно определяет это поле в области моделирования. В качестве граничных условий удобно потребовать, чтобы на границе поле ${{E}_{v}}\left( {x,t} \right)$ совпадало с полным электрическим полем, которое должно быть задано:

Потенциальная часть электрического поля ${{E}_{p}}\left( {x,t} \right) = - \nabla \varphi \left( {x,t} \right)$ находится из условия продольного равновесия электронов (2.9), которое дает уравнение

Оно позволяет при уже найденных полях ${{E}_{v}}{\kern 1pt} \left( {x,t} \right)$ и ${{E}_{\parallel }}{\kern 1pt} \left( {{\mathbf{x}},t} \right)$ определить потенциал $\varphi \left( {{\mathbf{x}},t} \right)$ в области моделирования Ω интегрированием вдоль силовых линий магнитного поля из уравнения

причем на границе $\partial {\Omega }$ и вне области моделирования в соответствии с граничным условием (2.18) потенциал тождественно равен нулю

Отметим, что для каждой компоненты плазмы из системы уравнений переноса вытекает уравнение потока импульса. Оно, как это будет сделано ниже, может быть представлено в форме выражения частной производной по времени плотности тока данной компоненты плазмы ${{\partial {{j}_{\alpha }}} \mathord{\left/ {\vphantom {{\partial {{j}_{\alpha }}} {\partial t}}} \right. \kern-0em} {\partial t}}$ через поля, а также через гидродинамические переменные данной компоненты и их пространственные частные производные. В результате суммирования этих уравнений получается выражение для 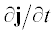через указанные выше параметры, которое принято называть обобщенным законом Ома. При этом поля входят в правую часть этого уравнения линейно. Подстановка обобщенного закона Ома в правую часть уравнения (2.17) и учет разложения (2.16) дают векторное линейное эллиптическое уравнение относительно ${{E}_{v}}{\kern 1pt} \left( {x,t} \right)$.

Таким образом, для определения полей получается система, состоящая из уравнений (2.1), (2.10), (2.16), уравнения (2.17) с учетом обобщенного закона Ома в правой части, и уравнения (2.19). Эта система уравнений имеет эллиптический тип, и не содержит частных производных по времени, т.е. реализует принцип мгновенного дальнодействия. В случае учета замагниченности электронов из дрейфовой теории вытекает выражение для их плотности тока ${{j}_{e}}$, а также выражение для вклада электронов 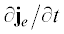в обобщенный закон Ома и выражение для дивергенции их тензора давлений, которое присутствует в правой части (2.19). В случае учета замагниченности ионных компонент аналогичным образом изменяется выражение для плотности тока ${{j}_{{\alpha }}}$ этой компоненты, а также выражение для ее вклада 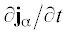в обобщенный закон Ома.

3. СИСТЕМА УРАВНЕНИЙ ВЛАСОВА В ПРИБЛИЖЕНИИ ПРОДОЛЬНОГО СИЛОВОГО РАВНОВЕСИЯ ЭЛЕКТРОНОВ

Рассмотрим систему уравнений Власова в приближении квазинейтральности и продольного силового равновесия электронов. Пусть плазма содержит K сортов ионов и электроны. Обозначим через ${{f}_{\alpha }}{\kern 1pt} \left( {t,x,v} \right)$ функцию распределения плазменной компоненты сорта α, где ${\alpha } = 1, \ldots ,K$ для ионных компонент и ${\alpha } = e$ для электронов, которая зависит от времени t, пространственной координаты $x = {{\left( {{{x}_{1}},{{x}_{2}},{{x}_{3}}} \right)}^{T}} \in {{\mathbb{R}}^{3}}$ и скорости $v = {{\left( {{{v}_{1}},{{v}_{2}},{{v}_{3}}} \right)}^{T}} \in {{\mathbb{R}}^{3}}$. Для частиц сорта α через ${{q}_{\alpha }}$ и ${{m}_{\alpha }}$ обозначим заряд и массу частиц, через ${{n}_{\alpha }}\left( {x,t} \right)$ и ${{j}_{\alpha }}\left( {x,t} \right)$ – их концентрацию и плотность тока. При этом заряд протона ${{q}_{1}}$ обозначим через e, т.е. для электронов ${{q}_{e}} = - e$.

В системе СИ систему уравнений Власова вместе с определениями концентрации и тока можно представить в следующем виде (3.1)–(3.3):

Здесь и далее через ${{\rho }_{i}}\left( {x,t} \right)$ и ${{j}_{{{\kern 1pt} i}}}\left( {x,t} \right)$ обозначены суммарные плотности заряда и тока ионов, а $\rho \left( {x,t} \right)$ и $j\left( {x,t} \right)$ – ранее введенные полные плотности заряда и тока.

Будем использовать для каждой компоненты плазмы $\alpha = 1, \ldots ,K,e$ гидродинамическую скорость ${{u}_{\alpha }}\left( {x,t} \right)$, а также тензор напряжений ${{\hat {\Pi }}_{\alpha }}\left( {x,t} \right)$ и тензор давления ${{{\mathbf{\hat {P}}}}_{\alpha }}\left( {x,t} \right)$, которые определяются следующими формулами:

Здесь и далее через $U \otimes {\kern 1pt} {\kern 1pt} {\kern 1pt} V$ будем обозначать диадный тензор, образованный векторами U и V в пространстве ${{\mathbb{R}}^{3}}$, декартовы компоненты которого определяются через соответствующие компоненты образующих его векторов по формуле ${{\left( {U \otimes V} \right)}_{{k,l}}} = {{U}_{k}}{{V}_{l}}$. Отметим, что верны формулы

Из уравнений Власова (3.1) для каждой компоненты плазмы $\alpha = 1, \ldots ,K,e$ вытекают следующие гидродинамические уравнения: уравнение непрерывности (потока массы)

а также уравнение потока импульса

Отметим, что суммирование умноженных на заряд ${{q}_{\alpha }}$ уравнений неразрывности (3.7) дает уравнение непрерывности заряда

Далее будем использовать традиционные обозначения для полных производных по времени от произвольной функции $\Phi {\kern 1pt} \left( {{\mathbf{x}},t} \right)$ вдоль линий тока каждой компоненты плазмы

С помощью этих обозначений и первой формулы в (3.4), а также уравнения непрерывности (3.7), можно получить следующее выражение для ${{\partial {{j}_{\alpha }}} \mathord{\left/ {\vphantom {{\partial {{j}_{\alpha }}} {\partial t}}} \right. \kern-0em} {\partial t}}$ через производные от ${{n}_{\alpha }}$ и ${{u}_{\alpha }}$:

Подстановка этого выражения в уравнение (3.8) после несложных выкладок приводит к уравнению

Суммирование уравнений потока импульса (3.8) по всем компонентам плазмы дает уравнение для полного тока, которое принято называть обобщенным законом Ома

Представим это уравнение в форме, наиболее удобной для учета условий квазинейтральности (2.8) и продольного силового равновесия электронов (2.9). Для этого введем для каждой компоненты плазмы гидродинамическую скорость ${{u}_{{\alpha {\text{0}}}}}$ за вычетом скорости электрического дрейфа ${{v}_{E}}$ (определяемой в (2.6)), а также соответствующую ей плотность тока ${{j}_{{\alpha {\text{0}}}}}$, и соответствующие суммарную плотность тока ионов ${{j}_{{{\kern 1pt} i{\text{0}}}}}$ и полную плотность тока ${{j}_{{{\kern 1pt} {\text{0}}}}}$ по формулам

Подстановка этих формул в слагаемое ${{j}_{\alpha }}{\kern 1pt} \otimes {{u}_{\alpha }}$ дает формулу

Из второй, третьей и четвертой формул в (2.16) вытекают формулы

Они получаются в результате суммирования по ионным компонентам плазмы второй формулы в (3.14), а также ее суммирования по всем компонентам плазмы, с учетом определений плотности заряда ионов ${{{\rho }}_{i}}$ и полной плотности заряда ρ в (3.2), а также с учетом определений плотности тока ионов ${{j}_{{{\kern 1pt} i}}}$ и полной плотности тока j в (3.3). Аналогичное суммирование по всем компонентам плазмы формулы (3.15) дает формулу

Условие квазинейтральности (2.8) с учетом обозначений в (3.2) дает равенство

Подстановка этого условия в формулы (3.16) и (3.17) приводит к равенствам

Также отметим, что подстановка первой формулы в (3.14) в выражение $E - \left[ {B \times {{u}_{\alpha }}} \right]$ с учетом равенства $\left[ {B \times {{v}_{E}}} \right] = E - b\left( {E \cdot b} \right)$ дает формулу

Подстановка этой формулы в обобщенный закон Ома (3.13) и учет первых двух формул в (3.14) приводят его к виду

Подстановка в первое слагаемое этого уравнения условия продольного равновесия электронов (2.9), и подстановка в последнее слагаемое формулы (3.18) приводит обобщенный закон Ома к форме

в которой учтены условие квазинейтральности (2.8) и условие продольного силового равновесия электронов (2.9), а также выделены слагаемые, формально содержащие электрическое поле.

Использование формы (3.20) обобщенного закона Ома необходимо для создания глобальной совместной численной модели ионосферы и магнитосферы, в которой самосогласованно рассчитывается поле магнитосферно-ионосферной токовой системы. При этом в данной модели для учета специфики каждой области в качестве системы уравнений переноса в Е-слое ионосферы следует использовать систему уравнений магнитной газовой динамики с замагниченными электронами и незамагниченными ионами, в F-слое ионосферы следует использовать систему уравнений магнитной газовой динамики с замагниченными электронами и ионами, в переходной зоне использовать кинетическую систему уравнений Больцмана–Власова с учетом замагниченности заряженных компонент, а далее в магнитосфере использовать систему уравнений Власова с замагниченными электронами.

Подстановка уравнения (3.20) в правую часть уравнения (2.17) дает уравнение

Отметим, что электрическое поле в правую часть этого уравнения входит линейно, причем, только в последние два слагаемых. Это означает, что относительно ${\kern 1pt} {{{\mathbf{E}}}_{v}}\left( {{\mathbf{x}},t} \right)$ это уравнение является линейным эллиптическим уравнением 2-го порядка.

Проведенные выкладки и рассуждения позволяют записать систему уравнений Власова в приближении продольного силового равновесия электронов с оптимальной точки зрения численного решения формой уравнений для электрического поля. Первая версия этой системы уравнений была впервые получена в [2].

Рассматриваемая система в качестве системы уравнений переноса включает в себя уравнения Власова (3.1) и определения гидродинамических переменных (3.2)–(3.4), (3.13) для каждой компоненты плазмы, а также условие квазинейтральности в форме (3.18). Система уравнений для полей включает в себя уравнения Гаусса (2.1) и Ампера (2.10) для магнитного поля, а также систему уравнений (2.16), (3.21), (2.19) для определения электрического поля.

Подчеркнем, что в уравнениях для полей отсутствуют частные производные по времени, и магнитное и электрическое поле определяются текущим распределением плазмы и граничными условиями из соответствующих систем уравнений эллиптического типа в приближении мгновенного дальнодействия.

Для рассматриваемой системы уравнений Власова в приближении продольного силового равновесия электронов нами разработана схема численного интегрирования по времени. В ходе каждого шага этой схемы выполняется итерационный процесс, на каждой итерации которого условия квазинейтральности (2.8) и условие продольного силового равновесия электронов (2.9) выполняются численно за счет специальной коррекции функции распределения электронов.

При выполнении текущей итерации сначала в уже известных полях предыдущей итерации на новом временном слое рассчитываются функции распределения и гидродинамические переменные всех компонент плазмы. При этом функция распределения электронов подвергается специальной процедуре коррекции, чтобы условия квазинейтральности (2.8) были выполнены численно. Эта процедура детально описана в [2]. Затем нужно найти магнитное поле в новой итерации из системы уравнений Гаусса (2.1) и Ампера (2.10). Далее, используя это поле и входящие в правую часть уравнения (3.21) гидродинамические переменные, можно организовать отдельный итерационный процесс для нахождения электрического поля в новой итерации шага численного интегрирования. В ходе итерации последнего процесса нужно сначала вычислить соленоидальную часть ${\kern 1pt} {{{\mathbf{E}}}_{v}}$ в результате решения краевой задачи Дирихле для уравнения Пуассона (3.21). Затем нужно найти потенциальную часть электрического поля в результате численного интегрирования уравнения (2.19) вдоль силовых линий магнитного поля. При этом условие продольного силового равновесия электронов (2.9) также будет выполнено численно на каждой итерации.

4 УСЛОВИЯ ЗАМАГНИЧЕННОСТИ, КВАЗИНЕЙТРАЛЬНОСТИ И ПРОДОЛЬНОГО СИЛОВОГО РАВНОВЕСИЯ ЭЛЕКТРОНОВ

Для каждой компоненты плазмы α тензор температур ${{{\mathbf{\hat {T}}}}_{\alpha }}\left( {{\mathbf{x}},t} \right)$ и средняя температура ${{T}_{\alpha }}\left( {x,t} \right)$ определяются в электрон-вольтах через тензор давления и концентрацию по формулам

где через ${\text{Tr}}{\mathbf{\hat {A}}}$ обозначен след (сумма диагональных элементов) матрицы ${\mathbf{\hat {A}}}$. Также для каждой компоненты будем обозначать через ${{V}_{{T\alpha }}}(x,t) = $ $ = \,{{\left( {{{e{{T}_{\alpha }}} \mathord{\left/ {\vphantom {{e{{T}_{\alpha }}} {{{m}_{\alpha }}}}} \right. \kern-0em} {{{m}_{\alpha }}}}} \right)}^{{1/2}}}$ – ее тепловую скорость, через ${{{\omega }}_{{p\alpha }}}\left( {x,t} \right) = \left| {{{q}_{\alpha }}} \right|{{\left( {{{{{n}_{\alpha }}} \mathord{\left/ {\vphantom {{{{n}_{\alpha }}} {\left( {{{{\varepsilon }}_{0}}{{m}_{\alpha }}} \right)}}} \right. \kern-0em} {\left( {{{{\varepsilon }}_{0}}{{m}_{\alpha }}} \right)}}} \right)}^{{1/2}}}$ и ${{\theta }_{{p\alpha }}}\left( {x,t} \right) = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {{{\omega }_{{p\alpha }}}}}} \right. \kern-0em} {{{\omega }_{{p\alpha }}}}}$ – плазменную частоту и плазменный период, через ${{{{\omega }_{{c\alpha }}}\left( {x,t} \right) = \left| {{{q}_{\alpha }}} \right|B} \mathord{\left/ {\vphantom {{{{\omega }_{{c\alpha }}}\left( {x,t} \right) = \left| {{{q}_{\alpha }}} \right|B} {{{m}_{\alpha }}}}} \right. \kern-0em} {{{m}_{\alpha }}}}$ и ${{\theta }_{{c\alpha }}}\left( {x,t} \right) = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {{{\omega }_{{c\alpha }}}}}} \right. \kern-0em} {{{\omega }_{{c\alpha }}}}}$ – гирочастоту и гиропериод, через ${{\lambda }_{{D\alpha }}}\left( {x,t} \right) = {{{{V}_{{T\alpha }}}} \mathord{\left/ {\vphantom {{{{V}_{{T\alpha }}}} {{{\omega }_{{p\alpha }}}}}} \right. \kern-0em} {{{\omega }_{{p\alpha }}}}}$ = = ${{\left[ {{{{{\varepsilon }_{0}}e{{T}_{\alpha }}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{0}}e{{T}_{\alpha }}} {\left( {q_{\alpha }^{2}{{n}_{\alpha }}} \right)}}} \right. \kern-0em} {\left( {q_{\alpha }^{2}{{n}_{\alpha }}} \right)}}} \right]}^{{1/2}}}$ – дебаевское расстояние, через ${{R}_{{c\alpha }}}\left( {x,t} \right) = {{{{V}_{{T\alpha }}}} \mathord{\left/ {\vphantom {{{{V}_{{T\alpha }}}} {{{{\omega }}_{{c\alpha }}}}}} \right. \kern-0em} {{{{\omega }}_{{c\alpha }}}}}$ – тепловой гирорадиус.

Отметим, что в бесстолкновительной плазме околоземного солнечного ветра и магнитосферы, а также в слабостолкновительной плазме верхнего F-слоя ионосферы максимальным пространственным кинетическим масштабом в такой плазме является гирорадиус тепловых протонов ${{R}_{{cp}}}$, а максимальным временным кинетическим масштабом является гиропериод протонов ${{\theta }_{{cp}}}$, поскольку имеют место следующие соотношения между пространственными и временными масштабами:

Условия замагниченности компоненты плазмы α состоят в том, что, во-первых, характерные пространственный ${{L}_{f}}$ и временной ${{\Theta }_{f}}$ масштабы изменения полей много больше соответственно теплового гирорадиуса ${{R}_{{c{\alpha }}}}$ и гиропериода ${{\theta }_{{c\alpha }}}$ этой компоненты:

и, во-вторых, компонента находится в поперечном силовом равновесии. Последнее означает, что в уравнении (3.12) ортогональная часть слева и справа равна нулю, т.е. выполнены уравнения

Из второго уравнения можно явно выразить ортогональную часть гидродинамической скорости ${{{\mathbf{u}}}_{\alpha }}$ через поля и тензор давления по формуле

Подстановка условия (4.3) в уравнение потока импульса в форме (3.12) дает уравнение

Также подстановка условия (4.3) в уравнение потока импульса в форме (3.11) приводит это уравнение для замагниченной компоненты α к следующей форме:

В околоземной плазме ионосферы, магнитосферы и солнечного ветра наименьшие гирорадиус и гиропериод всегда имеют электроны. Поэтому из замагниченности любой ионной компоненты α вытекает замагниченность электронов, т.е. выполнение условий

Эти условия означают, что в приближении замагниченности в околоземной плазме могут рассматриваться только достаточно медленные и крупномасштабные процессы.

Как известно, на пространственных масштабах, которые на 2 и более порядков больше характерного дебаевского расстояния ${{{\lambda }}_{{De}}}$, выполняется условие квазинейтральности (2.8) (см., например, [11]), которое означает осреднение по плазменным колебаниям электронов вдоль силовых линий магнитного поля и равносильно условию продольного силового равновесия электронов (2.9). Последнее условие состоит в том, что в уравнении (3.12) продольная компонента равна нулю слева и справа, т.е. выполнены уравнения

Из последнего уравнения можно явно выразить продольное электрическое поле ${{E}_{\parallel }}\left( {x,t} \right) = b\left( {E \cdot b} \right)$ через магнитное поле, концентрацию и тензор давления электронов по формуле

Таким образом, из замагниченности электронов вытекает, что они находятся в полном силовом равновесии

Подстановка этого условия в уравнение потока импульса для них в форме (3.11) с учетом ${{q}_{e}} = - e$ приводит к следующему уравнению для плотности тока электронов в дивергентном виде:

Отметим, что в случае изотропного электронного давления, когда ${{{\mathbf{\hat {P}}}}_{e}} = {{p}_{e}}{\mathbf{\hat {I}}}$ и $\nabla \cdot {{{\mathbf{\hat {P}}}}_{e}}\left( {x,t} \right) = $ $ = \nabla {{p}_{e}}\left( {x,t} \right)$, где ${\mathbf{\hat {I}}}$ – единичный тензор, условие силового равновесия электронов вдоль магнитного поля (4.8) традиционно и успешно используется в различных численных газодинамических моделях ионосферы (см., например, [12–17]).

Далее будут рассмотрены основные детали вывода системы уравнений для магнитного и электрического полей в двух наиболее важных для приложений случаях, когда система уравнений Власова в приближении продольного силового равновесия электронов существенно упрощается. В первом случае электроны замагничены, а ионы не замагничены. Во втором замагничены все компоненты плазмы. В этих случаях в обобщенном законе Ома сокращается часть слагаемых.

В первом случае суммирование уравнений (3.8) для ионов по $\alpha = 1, \ldots ,K$ с уравнением (4.11) для замагниченных электронов после выкладок, аналогичных таковым при выводе уравнения (3.20), дает обобщенный закон Ома в форме

которая отличается от (3.20) тем, что в первых трех суммах пропал вклад электронов ввиду их полного силового равновесия, и суммирование ведется только по ионным компонентам.

Во втором случае суммирование уравнений (4.6) для замагниченных ионов по $\alpha = 1, \ldots ,K$ с уравнением (4.11) для замагниченных электронов после соответствующих выкладок дают обобщенный закон Ома в форме

Таким образом, для замыкания системы уравнений для полей в этих двух случаях необходимо получить выражения для гидродинамической скорости и тензора давления каждой замагниченной компоненты плазмы через поля в рамках дрейфовой теории.

5. УРАВНЕНИЕ ВЛАСОВА В ДРЕЙФОВОМ ПРИБЛИЖЕНИИ

Рассмотрим необходимые для дальнейшего изложения сведения из дрейфовой теории. Для частицы сорта α с вектором скорости $v \in {{\mathbb{R}}^{3}}$ в точке x в момент времени t поля $B{\kern 1pt} \left( {x,t} \right)$ и $E{\kern 1pt} \left( {x,t} \right)$ определяют продольную компоненту скорости ${{v}_{\parallel }}\left( {t,x,v} \right)$ и ее продольную часть ${{v}_{\parallel }}{\kern 1pt} \left( {t,x,v} \right)$, ларморовскую компоненту скорости ${{v}_{L}}\left( {t,x,v} \right)$ и ее ларморовскую часть ${{v}_{L}}\left( {t,x,v} \right)$, а также гирорадиус ${{R}_{{c{\alpha }}}}\left( {t,x,v} \right)$ и положение ведущего центра ${{r}_{{c{\alpha }}}}\left( {t,x,v} \right)$ по формулам

где единичный вектор вдоль магнитного поля $b\left( {x,t} \right)$ и скорость электрического дрейфа ${{v}_{E}}{\kern 1pt} \left( {x,t} \right)$ определяются формулами (2.4).

Обозначим через $\left\{ {{{h}_{1}}\left( {x,t} \right),{{h}_{2}}\left( {x,t} \right),b\left( {x,t} \right)} \right\}$ какой-либо декартов базис связанной с магнитным полем системы координат в точке x в момент времени t, т.е. единичные векторы ${{h}_{1}}$ и ${{h}_{2}}$ ортогональны магнитному полю и вместе с b образуют правую тройку. Тогда в этом базисе вектор скорости $v \in {{\mathbb{R}}^{3}}$, а также его ларморовская часть ${{v}_{L}}\left( {t,x,v} \right)$ и гирорадиус ${{R}_{{с{\alpha }}}}\left( {t,x,v} \right)$ могут быть представлены в виде

т.е. при фиксированных $\left( {x,t} \right)$ переменные $\left( {{{v}_{L}},{{\phi }_{v}},{{v}_{\parallel }}} \right)$ являются цилиндрическими координатами вектора $v - {{v}_{E}}$в пространстве скоростей.

Для дальнейшего изложения нам потребуются ортонормированные векторы физического базиса $\left\{ {{{h}_{L}}\left( {t,x,v} \right),{{h}_{\phi }}\left( {t,x,v} \right),b\left( {x,t} \right)} \right\}$ этой системы координат, первые два из которых определяются формулами

Также будем использовать представление дивергенции по скорости векторного поля $A\left( {t,x,v} \right)$ в пространстве скоростей в этих координатах:

Вычисляя якобиан определяемой формулами (5.2) переменных замены $v \leftrightarrow \left( {{{v}_{L}},{{\phi }_{v}},{{v}_{\parallel }}} \right)$, получим равенство $\frac{{\partial \left( {{{v}_{1}},{{v}_{2}},{{v}_{3}}} \right)}}{{\partial \left( {{{v}_{L}},{{\phi }_{v}},{{v}_{\parallel }}} \right)}} = {{v}_{L}}$, из которого следует формальное соотношение ${{d}^{3}}v = {{v}_{L}}d{{v}_{L}}d{{v}_{\parallel }}{\kern 1pt} d{{\phi }_{v}}$ и формула для вычисления интеграла по пространству скоростей от функции $\Phi {\kern 1pt} \left( {t,x,v} \right)$:

В рассматриваемом здесь нерелятивистском случае для замагниченной частицы сорта α при помощи асимптотического метода осреднения из системы уравнений движения Ньютона–Лоренца

выводится система уравнений движения ведущего центра (см. [8, 18–20]), в которой исключена переменная ${{\phi }_{v}}$ – фаза циклотронного (ларморовского) вращения. Эту систему можно представить в виде где скорость ведущего центра ${{U}_{{c\alpha }}}\left( {t,r,{{v}_{\parallel }},{{v}_{L}}} \right)$, ускорение вдоль магнитного поля ${{a}_{{\alpha \parallel }}}\left( {t,r,{{v}_{\parallel }},{{v}_{L}}} \right)$ и модуль “ларморовского” ускорения ${{a}_{{L\alpha }}}\left( {t,r,{{v}_{\parallel }},{{v}_{L}}} \right)$ являются заданными функциями, причем от переменных $\left( {t,r} \right)$ они зависят не напрямую, а только через поля $B\left( {r,t} \right)$ и $E\left( {r,t} \right)$.

Конкретная форма системы уравнений движения ведущего центра (5.7) является тонким вопросом и зависит от специфики задачи, от характерной величины параметра

а также от того, какое приближение используется – нулевого или первого порядка. Функции в правых частях уравнений системы (5.7) содержат наибольшее число слагаемых для приближения первого порядка в наиболее общем случае “сильного электрического поля”, когда параметр ${{{\delta }}_{\alpha }}$ не является малым, т.е. когда

Для этого случая правильный и полный вид системы уравнений ведущего центра в форме (5.7) был получен в работе [18], и называется системой Морозова–Соловьева. В случае “слабого электрического поля”, когда параметр ${{\delta }_{\alpha }}$ является малым

ряд слагаемых, которые в случае (5.8) имеют первый порядок малости, становятся слагаемыми второго порядка малости, и поэтому отбрасываются, т.е. система (5.7) в первом приближении существенно упрощается. Для этого случая правильный вид системы уравнений (5.7) в первом приближении был независимо получен в работах [19, 20], и называется системой Брагинского–Сивухина.

Однако в нулевом приближении система (5.7) имеет один и тот же вид для обоих случаев (5.8) и (5.9), и была получена в работе [8]. В этой системе скорость ведущего центра не зависит от сорта частиц и ларморовской скорости, ${{U}_{{c\alpha }}}\left( {t,r,{{v}_{{\parallel {\kern 1pt} }}},{{v}_{L}}} \right) = $ $ = {{U}_{c}}\left( {t,r,{{v}_{\parallel }}} \right)$, модуль “ларморовского” ускорения также не зависит от сорта частиц, ${{a}_{{L{\alpha }}}}\left( {t,r,{{v}_{\parallel }},{{v}_{L}}} \right) = $ $ = {{a}_{L}}\left( {t,x,{{v}_{\parallel }},{{v}_{L}}} \right)$, и только ускорение вдоль магнитного поля ${{a}_{{\parallel {\kern 1pt} \alpha }}}\left( {t,r{\kern 1pt} ,{{v}_{\parallel }},{{v}_{L}}} \right)$ зависит от сорта частиц. Эти функции определяются формулами (см. [8]), которые можно представить в виде

если учитывать известные легко проверяемые тождества

Исходная система уравнений движения Ньютона–Лоренца (5.6) бездивергентна и является характеристической системой обыкновенных дифференциальных уравнений для уравнения Власова (2.1), что позволяет представить его в дивергентной форме

Представляя последнее слагаемое в этом уравнении $\nabla \cdot {{\;}_{v}}\left( {{{A}_{\alpha }}{{f}_{\alpha }}} \right)$ в цилиндрических координатах $\left( {{{v}_{L}},{{\phi }_{v}},{{v}_{\parallel }}} \right)$ в пространстве скоростей по формуле (5.4), получим уравнение Власова в форме

где векторы ${{h}_{{{\kern 1pt} L}}}\left( {t,x,v} \right)$ и ${{h}_{{{\kern 1pt} \phi }}}\left( {t,x,v} \right)$ определяются формулами (5.3).

Функция распределения ведущих центров ${{F}_{\alpha }}\left( {t,x,{{v}_{\parallel }},{{v}_{L}}} \right)$ определяется как осреднение функции распределения ${{f}_{\alpha }}\left( {t,x,v} \right)$ по фазе циклотронного вращения в пространстве скоростей:

где векторы ${{h}_{{{\kern 1pt} 1}}}\left( {x,t} \right)$ и ${{h}_{{{\kern 1pt} 2}}}\left( {x,t} \right)$ образуют ортонормированный базис в плоскости ортогональной магнитному полю. Функция ${{F}_{\alpha }}\left( {t,x,{{v}_{\parallel }},{{v}_{L}}} \right)$ зависит только от двух компонент скорости $\left( {{{v}_{\parallel }},{{v}_{L}}} \right)$ в связанной с местным магнитным полем $B{\kern 1pt} \left( {x,t} \right)$ цилиндрической системе координат. В дрейфовом приближении для замагниченной компоненты плазмы сорта α ее функция распределения ${{f}_{\alpha }}\left( {t,x,v} \right)$ представляется в виде (см. [4, 8, 21])

Рассмотрим определение гидродинамических переменных, начиная с концентрации. Подстановка в определение концентрации в (3.2) формулы для интеграла по пространству скоростей (5.5) и формулы (5.14) приводит к следующему выражению для концентрации ${{n}_{\alpha }}\left( {x,t} \right)$:

Рассмотрим плотность продольного тока и продольную гидродинамическую скорость. Из определения плотности тока и гидродинамической скорости по формулам в (3.3) и в (3.6), определения продольной компоненты в (2.7), а также формулы (5.5) и формулы (5.14) вытекает следующее выражение для продольных компонент плотности тока ${{j}_{{\alpha \parallel }}}{\kern 1pt} \left( {x,t} \right)$ и гидродинамической скорости ${{u}_{{\alpha \parallel }}}\left( {x,t} \right)$:

Рассмотрим продольное и ортогональное (поперечное) давления. Из определения тензора давления в (3.4), формулы (5.5) и формулы (5.14), а также формул (5.16) и (5.17) вытекает следующее выражение для продольного давления ${{p}_{{\alpha \parallel }}}{\kern 1pt} \left( {x,t} \right)$:

а для ортогонального (поперечного) давления ${{p}_{{\alpha \bot }}}\left( {{\mathbf{x}},t} \right)$ аналогичным образом с учетом предположения ${{u}_{{\alpha \bot }}} \approx {{v}_{E}}$ выводится приближенное выражение

Рассмотрим вывод уравнения Власова в дрейфовом приближении. Подстановка формулы (5.14) в уравнение Власова в дивергентной форме (5.13) и осреднение по циклотронным вращениям приводит к следующему уравнению Власова в дрейфовом приближении для функции распределения ведущих центров в дивергентной форме:

В дрейфовой теории доказывается, что система уравнений движения ведущего центра в каждом приближении также должна быть бездивергентна, т.е. удовлетворять уравнению (см. [8, 18–20])

Это условие является критерием правильности системы уравнений движения ведущего центра, и равносильно условию сохранения исходного фазового объема системы Ньютона–Лоренца (5.6) в 6-мерном фазовом пространстве $\mathbb{R}_{{\mathbf{x}}}^{3} \times \mathbb{R}_{{\mathbf{v}}}^{3}$ при осреднении по переменной ${{\phi }_{v}}$ – фазе циклотронного вращения, которая введена в (5.2). Полученная в [8] система уравнений движения ведущего центра в нулевом приближении с правыми частями (5.10), а также полученные в первом приближении в [18–20] системы Морозова–Соловьева и Брагинского–Сивухина удовлетворяют этому условию.

При помощи условия бездивергентности (5.21) уравнение Власова в дрейфовом приближении приводится к форме, аналогичной (3.1):

Отметим, что необходимость условия бездивергентности (5.21) была осознана не сразу. Асимптотический метод осреднения для получения приближенных решений (асимптотических разложений решения) систем обыкновенных дифференциальных уравнений был разработан Н.М. Крыловым и Н.Н. Боголюбовым в 1930-х гг. и успешно применен ими для ряда задач нелинейной механики. Дрейфовая теория движения заряженных частиц и первая версия системы уравнений движения ведущего центра была разработана в 1950-е гг. Н.Н. Боголюбовым и Д.Н. Зубаревым (см. [22, 23]). Однако в приведенной в работах [22, 23] системе уравнений движения ведущего центра были учтены не все слагаемые первого порядка малости, и поэтому она не является бездивергентной, т.е. не удовлетворяет условию (5.21). Отметим, что наиболее строгое и современное изложение метода осреднения содержится в монографии [24].

Рассмотрим выражение для плотности тока замагниченной компоненты. Тензор давления замагниченной компоненты плазмы сорта $\alpha $ определяется формулой

где ${\mathbf{\hat {I}}}$ – единичный тензор, из которой вытекают формулы для дивергенции

Подстановка в формулу (4.4) первой формулы в (5.24) дает следующее выражение для ортогональной части ${{u}_{{\alpha \bot }}}$ гидродинамической скорости:

Учитывая продольную часть этой скорости ${{u}_{{{\alpha }\parallel }}}\, = {{u}_{{{\alpha }\parallel }}}{\kern 1pt} {\kern 1pt} b{\kern 1pt} $, а также разложения (2.7) и (3.14), получим следующие выражения для плотности тока и гидродинамической скорости:

6. СИСТЕМА УРАВНЕНИЙ МАГНИТНОЙ ГАЗОВОЙ ДИНАМИКИ ДЛЯ ЗАМАГНИЧЕННОЙ КОМПОНЕНТЫ

Отметим, что при переходе к гидродинамическому описанию данной компоненты плазмы система уравнений переноса для нее выводится интегрированием по пространству скоростей соответствующего исходного кинетического уравнения.

Рассмотрим вывод системы уравнений магнитной газовой динамики для замагниченной компоненты плазмы, который можно выполнить двумя способами. Эта система состоит из четырех гидродинамических уравнений переноса, которые описывают эволюцию концентрации ${{n}_{\alpha }}\left( {x,t} \right)$, продольной гидродинамической скорости ${{u}_{{\alpha {\kern 1pt} \parallel }}}\left( {x,t} \right)$, поперечного давления ${{p}_{{\alpha \bot }}}\left( {x,t} \right)$ и продольного давления ${{p}_{{\alpha \parallel }}}\left( {x,t} \right)$.

В первом способе в уравнение Власова в дивергентной форме (5.12) подставляется локально бимаксвелловская функции распределения в форме

умноженная на соответствующие множители 1, ${{v}_{\parallel }}$, ${{m}_{\alpha }}v_{L}^{2}{\text{/}}2$ и ${{m}_{\alpha }}v_{\parallel }^{2}$. В этой функции, в отличие от обычной бимаксвелловской функции распределения, концентрация ${{n}_{\alpha }}\left( {x,t} \right)$, продольная скорость ${{u}_{{\alpha {\kern 1pt} \parallel }}}\left( {{\mathbf{x}},t} \right)$ и температуры ${{T}_{{\alpha \parallel }}}\left( {x,t} \right)$, ${{T}_{{\alpha \bot }}}\left( {x,t} \right)$ не остаются постоянными, а являются функциями координат и времени. При этом температуры и давления связаны между собой формулами

Затем выполняется интегрирование по пространству скоростей. При этом необходимо учитывать, что продольная скорость ${{v}_{\parallel }}$ не является независимой переменной как полная скорость v, а задается функцией координат и времени: ${{v}_{\parallel }} = {{v}_{\parallel }}\left( {t,x,v} \right) = $ $ = \left( {v \cdot b\left( {v,t} \right)} \right)$.

Во втором способе локально бимаксвелловская функции распределения ведущих центров в форме

умноженная на соответствующие множители 1, ${{v}_{\parallel }}$, ${{m}_{\alpha }}v_{L}^{2}{\text{/}}2$ и ${{m}_{\alpha }}v_{\parallel }^{2}$, подставляется в уравнение Власова в дрейфовом приближении в дивергентной форме (5.21), в котором скорость ведущего центра ${{U}_{{c\alpha }}}$, модуль “ларморовского” ускорения ${{a}_{{L\alpha }}}$, и ускорение вдоль магнитного поля ${{a}_{{\parallel \alpha }}}$определяются формулами (5.10). Далее аналогичным образом выполняется интегрирование по пространству скоростей. При этом продольная скорость ${{v}_{\parallel }}$ является независимой переменной, поэтому второй способ существенно проще и более формализован.

Отметим, что в работах [6, 7] (см. также [8] и [4, 21]) рассматриваемая ниже система уравнений переноса приводится без вывода. Мы тщательно проверили ее вывод и установили, что она является точной только для локально бимаксвелловской функции распределения (6.1). Таким образом, эта система уравнений является приближенной только для функций распределения, которые относительно мало отличаются от локально бимаксвелловской функции распределения (6.1).

Будем использовать аналогичные (3.10) традиционные обозначения для полных производных по времени от произвольной функции $\Phi {\kern 1pt} \left( {x,t} \right)$ вдоль линий тока каждой компоненты плазмы:

В результате вывода обоими описанными выше способами для замагниченной компоненты α бесстолкновительной плазмы получается система уравнений переноса, которая включает в себя

1) уравнение потока массы

2) уравнение для продольной гидродинамической скорости

3) уравнение для поперечного давления

4) уравнение для продольного давления

Эта система уравнений описывает эволюцию четырех гидродинамических переменных, определяемых функцией распределения ведущих центров по формулам (5.16)–(5.19), и используется при газодинамическом описании замагниченной ионной компоненты.

Отметим, что для электронов эта система уравнений переноса должна быть упрощена с учетом условий квазинейтральности (2.8). Для электронов используются только уравнения (6.6) и (6.7) для давлений. Концентрация электронов вместо уравнения (6.4) определяется из уравнения (3.18) по концентрациям ионов, которые находятся в результате численного решения системы уравнений переноса для каждой ионной компоненты. Продольная гидродинамическая скорость электронов определяется из последнего уравнения в (2.8) $\nabla \cdot {\mathbf{j}}({\mathbf{x}},t) \equiv 0$. Учет вытекающих из формул (5.25), (5.26), (3.19) равенств

дает уравнение в котором ионный ток ${{j}_{{i0}}}\left( {x,t} \right)$ определяется формулой (3.15). Последнее уравнение позволяет найти ${{j}_{{e\parallel }}}\left( {x,t} \right)$ при помощи специальной процедуры интегрирования вдоль силовых линий магнитного поля, и по нему найти ${{u}_{{e\parallel }}} = - {{{{j}_{{e\parallel }}}} \mathord{\left/ {\vphantom {{{{j}_{{e\parallel }}}} {{{{\rho }}_{i}}}}} \right. \kern-0em} {{{{\rho }}_{i}}}}$.

7. СЛУЧАЙ КИНЕТИЧЕСКОГО ОПИСАНИЯ ЗАМАГНИЧЕННЫХ ЭЛЕКТРОНОВ

Рассмотрим систему уравнений Власова в приближении продольного силового равновесия электронов в случае, когда электроны замагничены, а ионы не замагничены. Эта система также была получена в [2]. Здесь мы приведем для нее более удобную форму с точки зрения численного решения.

В рассматриваемом случае плотность тока электронов определяется формулами (5.25) при ${{q}_{e}} = - e$, а плотность полного тока определяется формулами

Подстановка выражения для дивергенции тензора давления электронов по формуле (5.24) в уравнение (4.9) приводит это уравнение к виду

Аналогичная подстановка выражения для дивергенции тензора давления электронов по формуле (5.24) в обобщенный закон Ома в форме (4.12), дает следующую форму этого уравнения:

Подстановка уравнения (7.3) в правую часть уравнения (2.17) дает уравнение

Также подстановка выражения для дивергенции тензора давления электронов по формуле (5.24) в уравнение (2.19) для потенциала дает следующую форму этого уравнения:

В результате получаем, что рассматриваемая система уравнений в качестве системы уравнений переноса включает в себя:

1) уравнения Власова (3.1) и определения гидродинамических переменных (3.2), (3.3), (3.4) для каждой компоненты ионов $\alpha = 1, \ldots ,K$, а также полных ионных плотности заряда и тока;

2) уравнение Власова в дрейфовом приближении для функции распределения ведущих центров электронов ${{F}_{e}}\left( {t,x,{{v}_{\parallel }},{{v}_{L}}} \right)$ при ${\alpha } = e$

в котором скорость ведущего центра ${{{\mathbf{U}}}_{c}}\left( {t,r,{{v}_{\parallel }}} \right)$, модуль “ларморовского” ускорения ${{a}_{L}}\left( {t,x,{{v}_{\parallel }},{{v}_{L}}} \right)$ и ускорение вдоль магнитного поля ${{a}_{{\parallel {\kern 1pt} e}}}\left( {t,r{\kern 1pt} ,{{v}_{\parallel }},{{v}_{L}}} \right)$ определяются формулами (5.10) при $\alpha = e$ и ${{q}_{e}} = - e$;

3) определения дрейфовых гидродинамических переменных электронов ${{n}_{e}}$, ${{j}_{{e\parallel }}}$, ${{u}_{{e\parallel }}}$,${{p}_{{e\parallel }}}$, ${{p}_{{e \bot }}}$ по формулам (5.16)–(5.19);

4) определения плотности тока ${{j}_{{e0}}}$, ${{j}_{e}}$и гидродинамической скорости ${{u}_{{e0}}}$, ${{u}_{e}}$ электронов по формулам (5.25), (5.26) (при ${{q}_{e}} = - e$);

5) определения полной плотности заряда в формуле (3.2) и плотности полного тока плазмы по формуле (7.1);

6) условие квазинейтральности (2.8).

Система уравнений для полей включает в себя:

7) уравнения Гаусса (2.1) и Ампера (2.10) для магнитного поля;

8) систему уравнений (2.16), (7.4), (7.5) для определения электрического поля.

Отметим, что учет замагниченности приводит к существенной экономии вычислительных ресурсов при численном моделировании, поскольку пространство скоростей замагниченной компоненты является двумерным вместо трехмерного в общем случае. При этом размер сетки в пространстве скоростей уменьшается в число раз, равное числу узлов на одно измерение, которое обычно составляет порядка 100.

8. ГИБРИДНОЕ ОПИСАНИЕ ПЛАЗМЫ

Подход, при котором незамагниченные ионные компоненты описываются уравнениями Власова, а замагниченные электроны описываются в рамках какой-либо упрощенной газовой динамики, называется гибридным описанием плазмы. Для получения правильного описания полей в этом случае в системе уравнений для плазмы из предыдущего раздела 7 нужно заменить уравнение Власова в дрейфовом приближении для электронов упрощенной системой уравнений ЧГЛ (3.18), (6.6)–(6.10), которая рассмотрена в разделе 6. При этом система уравнений для полей остается без изменений.

В результате получаем, что рассматриваемая система уравнений гибридного описания плазмы включает в себя:

1) уравнения Власова (3.1) и определения гидродинамических переменных (3.2), (3.3), (3.4) для каждой компоненты ионов $\alpha = 1, \ldots ,K$, а также полных ионных плотности заряда и тока;

2) упрощенную систему уравнений ЧГЛ (3.18), (6.6)–(6.10) для электронов;

3) определения плотности тока ${{j}_{{e0}}}$, ${{j}_{e}}$ и гидродинамической скорости ${{u}_{{e0}}}$, ${{u}_{e}}$ электронов по формулам (5.25), (5.26) (при ${{q}_{e}} = - e$);

4) определение плотности полного тока плазмы по формуле (7.1);

5) уравнения Гаусса (2.1) и Ампера (2.10) для магнитного поля;

6) систему уравнений (2.16), (7.4), (7.5) для определения электрического поля.

Отметим, что различные варианты гибридного описания бесстолкновительной плазмы рассматриваются в очень большом числе работ начиная с 1970-х годов (см., например, [9, 10] и [25–30]). Однако все существующие варианты имеют тот же принципиальный недостаток в определении магнитного поля, что и система уравнений одножидкостной магнитной газодинамики ЧГЛ, который будет рассмотрен ниже в разделе 12.

9. СЛУЧАЙ ПОЛНОСТЬЮ ЗАМАГНИЧЕННОЙ ПЛАЗМЫ

Рассмотрим систему уравнений Власова в приближении продольного силового равновесия электронов в случае, когда все компоненты плазмы замагничены и описываются уравнением Власова в дрейфовом приближении. Эта система уже была получена в [2]. Здесь мы также приведем для нее оптимальную с точки зрения численного решения форму системы уравнений для электрического поля.

Для дальнейшего изложения аналогично соответствующим плотностям заряда и тока в формулах (3.2) и (3.3) введем продольный ток ионов и полный продольный ток

а также продольное и поперечное давления ионов ${{p}_{{i\parallel }}}{\kern 1pt} \left( {x,t} \right)$ и ${{p}_{{i \bot }}}{\kern 1pt} \left( {x,t} \right)$, и аналогичные полные давления ${{p}_{{{\kern 1pt} \parallel }}}{\kern 1pt} \left( {x,t} \right)$ и ${{p}_{ \bot }}{\kern 1pt} \left( {x,t} \right)$:

Тогда суммирование формул (5.25) с учетом этих обозначений и определения (2.3), а также учет условия квазинейтральности (2.8) и формул (3.14), (3.16) и (3.19) дают следующее выражение для плотности ионного тока ${{j}_{{i0}}}\left( {x,t} \right)$ и полного тока в замагниченной плазме:

Подстановка выражения для дивергенции тензора давления по второй формуле в (5.24) для электронов и всех ионов в обобщенный закон Ома в форме (4.14) дает следующую форму этого уравнения:

Подстановка этого уравнения в правую часть уравнения (2.17) дает уравнение для соленоидальной части электрического поля

В результате получаем, что рассматриваемая система уравнений включает в себя:

1) уравнения Власова в дрейфовом приближении (5.22) для функций распределения ведущих центров каждой компоненты плазмы ${{F}_{\alpha }}(t,x,{{v}_{\parallel }},{{v}_{L}})$ при $\alpha = 1, \ldots ,K,e$, в котором скорость ведущего центра ${{U}_{c}}(t,r,{{v}_{\parallel }})$, модуль “ларморовского” ускорения ${{a}_{L}}(t,x,{{v}_{{\parallel {\kern 1pt} }}},{{v}_{L}})$ и ускорение вдоль магнитного поля ${{a}_{{\parallel {\kern 1pt} \alpha }}}(t,x,{{v}_{\parallel }},{{w}_{L}})$ определяются формулами (5.10);

2) определения дрейфовых гидродинамических переменных для каждой компоненты плазмы ${{n}_{\alpha }}$, ${{j}_{{\alpha \parallel }}}$, ${{u}_{{\alpha \parallel }}}$,${{p}_{{\alpha \parallel }}}$, ${{p}_{\alpha }}_{ \bot }{\kern 1pt} $ по формулам (5.16)–(5.19) и определения ионной плотности заряда ${{{\rho }}_{i}}$ по формулам в (3.2);

3) определения плотности тока ${{j}_{{\alpha 0}}}$ и гидродинамической скорости ${{u}_{{{\alpha }0}}}$ для каждой ионной компоненты плазмы по формулам (5.25), (5.26), а также определение плотности ионного тока ${{j}_{{i0}}}$ по формулам (9.1)–(9.3) и определение плотности электронного тока ${{j}_{{e0 \bot }}}$ по формуле (6.9);

4) условие квазинейтральности в форме (3.18);

5) уравнение (6.10) для определения плотности продольного электронного тока ${{j}_{{e\parallel }}}$;

6) определение плотности полного тока плазмы по формулам (9.1), (9.2), (9.4);

7) уравнения Гаусса (2.1) и Ампера (2.10) для магнитного поля;

8) систему уравнений (2.16), (9.6), (7.4) для определения электрического поля.

Отметим, что для этой системы уравнений нами также разработана схема численного интегрирования по времени, которая обеспечивает выполнение в численном виде условия квазинейтральности (2.8) и условия продольного силового равновесия электронов в форме (7.2).

10. СИСТЕМА УРАВНЕНИЙ МНОГОКОМПОНЕНТНОЙ МАГНИТНОЙ ГАЗОВОЙ ДИНАМИКИ ДЛЯ БЕССТОЛКНОВИТЕЛЬНОЙ ЗАМАГНИЧЕННОЙ ПЛАЗМЫ

Отметим, что при переходе к гидродинамическому описанию всех компонент плазмы система уравнений переноса для соответствующих компонент выводится интегрированием по пространству скоростей соответствующих исходных кинетических уравнений, а система уравнений для полей при этом не изменяется.

В рассматриваемом случае по сравнению с системой уравнений Власова в дрейфовом приближении происходят следующие изменения. Вместо уравнений Власова в дрейфовом приближении для описания движения каждой ионной компоненты используется система уравнений ЧГЛ (6.4)–(6.7), а для электронов используется скорректированная система (3.18), (6.6)–(6.10). Система уравнений для полей и определение полного тока не изменяются.

Таким образом, система уравнений многокомпонентной магнитной газовой динамики, которая описывает замагниченную бесстолкновительную плазму из K сортов ионов и электронов включает в себя:

1) систему уравнений переноса (6.4)–(6.7) для каждой ионной компоненты $\alpha = 1, \ldots ,K$;

2) определения плотности тока ${{j}_{{\alpha 0}}}$ и гидродинамической скорости ${{u}_{{\alpha 0}}}$ для каждой компоненты плазмы по формулам (5.25), (5.26);

3) определение ионной плотности заряда ${{{\rho }}_{i}}$ в формуле (3.2), а также определение плотности ионного тока ${{j}_{{i0}}}$ по формулам (9.1)–(9.3);

4) систему уравнений переноса для электронов (3.18), (6.6)–(6.10);

5) определение полного тока плазмы по формулам (9.1), (9.2), (9.4);

6) уравнения Гаусса (2.1) и Ампера (2.10) для магнитного поля;

7) систему уравнений (2.16), (7.5), (6.4) для определения электрического поля.

11. ОБЛАСТЬ ПРИМЕНИМОСТИ ОДНОЖИДКОСТНОЙ МГД

Рассмотрим известную систему уравнений Чу–Гольдбергера–Лоу (далее ЧГЛ) для протонно-электронной плазмы, которая была впервые представлена в [6] и [7], вывод которой также рассмотрен в [8], [4], [21] и [31]. Эта система в качестве неизвестных функций от переменных $\left( {x,t} \right)$ содержит концентрацию n, гидродинамическую скорость V, продольное и поперечное давления ${{p}_{\parallel }}$ и ${{p}_{ \bot }}$, а также магнитное поле B, т.е. 9 скалярных функций, и может быть представлена в виде

где использовано обозначение для производной вдоль линии тока, аналогичное (3.10):

Выражения $\left( {{{{{p}_{ \bot }}} \mathord{\left/ {\vphantom {{{{p}_{ \bot }}} {\left( {n{\kern 1pt} B} \right)}}} \right. \kern-0em} {\left( {n{\kern 1pt} B} \right)}}} \right)$ и $\left( {{{{{p}_{\parallel }}{{B}^{2}}} \mathord{\left/ {\vphantom {{{{p}_{\parallel }}{{B}^{2}}} {{{n}^{3}}}}} \right. \kern-0em} {{{n}^{3}}}}} \right)$ в уравнениях (11.3) являются постоянными вдоль линий тока и называются адиабатическими инвариантами.

Традиционный подход одножидкостной магнитной гидродинамики основан на двух следующих предположениях.

1. Считается, что гидродинамическая скорость плазмы $V\left( {x,t} \right)$ имеет вид

т.е. ортогональная к магнитному полю часть гидродинамической скорости каждой компоненты плазмы равна скорости электрического дрейфа.

Это предположение нарушается в околоземной плазме магнитосферы и солнечного ветра в областях с существенной пространственной неоднородностью. Гидродинамическая скорость замагниченной компоненты плазмы определяется формулами (5.25), (5.26). Оценки характерных значений по данным измерений на космических аппаратах показывают, что в средней и дальней магнитосфере Земли скорость электрического дрейфа по порядку величины составляет от единиц до сотен километров в секунду: ${{v}_{E}} \sim 1 - $ 100 км/с и имеет характерное значение ${{v}_{{E0}}} \sim $ ~ 10 км/с. Действительно, величина электрического поля в хвосте магнитосферы Земли лежит в пределах $E \sim {{10}^{{ - 5}}} - {{10}^{{ - 3}}}$ В/м, причем характерная величина ${{E}_{0}} \sim {{10}^{{ - 4}}}$ В/м. Характерная величина магнитного поля составляет $10\;{\text{нТл}} = {{10}^{{ - 8}}}\;{\text{Тл}}$. На основе этих данных получаются оценки

При этом имеющие одинаковый порядок третье и четвертое слагаемые в формуле (5.25) для протонов

в указанных выше областях неоднородности могут иметь тот же порядок, что и ${{v}_{E}}$, и даже могут быть на порядок больше. С учетом формул (6.2) имеют место следующие формулы и вытекающие из них оценки: где ${{L}_{f}}$ – характерный пространственный масштаб изменения полей.

В хвосте магнитосферы Земли типичная температура протонов бывает в пределах ${{T}_{p}} \sim 1{\kern 1pt} - {\kern 1pt} $ 10 КэВ, характерный пространственный масштаб изменения полей составляет ${{L}_{f}} \sim 1000$ км = 10⁶ м. Подставляя эти значения в оценку (11.9), получаем оценку

Сравнение этой оценки с оценкой (11.7) показывает, что введенные в (11.8) скорости ${{u}_{{p1}}}$ и ${{u}_{{p2}}}$ одного порядка или на порядок больше скорости электрического дрейфа.

2. Предполагается, что электрическое поле имеет вид

т.е. отбрасывается продольная часть электрического поля ${{E}_{\parallel }}{\kern 1pt} \left( {x,t} \right)$, которая обеспечивает квазинейтральность плазмы и определяется из условия продольного силового равновесия электронов через магнитное поле, концентрацию, а также продольное и ортогональное давления электронов формулой (7.2).

Предположение (11.11) также нарушается в околоземной плазме магнитосферы и солнечного ветра в областях с сильной пространственной неоднородностью.

Формула (7.2) означает, что продольное электрическое поле ${{E}_{\parallel }}{\kern 1pt} \left( {x,t} \right)$ возникает в любой области неоднородности плазмы вдоль магнитного поля. В плазме солнечного ветра и в ионосфере электроны и ионы имеют сравнимые температуры (обычно отличаются не более чем в два раза), а в различных областях магнитосферы температура электронов меньше температуры протонов примерно в 2–8 раз, т.е. электроны нельзя считать холодными по сравнению с протонами. Из этого условия, а также из условия квазинейтральности вытекает, что продольные градиенты ионного и электронного давления сонаправлены и одного порядка по величине.

Тензоры давления протонов и электронов будут качественно близки, а их дивергенции будут примерно сонаправлены. Поэтому продольное электрическое поле будет направлено против продольного градиента давления протонов, т.е. будет тормозить протоны вдоль силовых линий магнитного поля, и этим существенно влиять на их движение.

В хвосте магнитосферы Земли типичная температура электронов по порядку величины бывает в пределах ${{T}_{e}} \sim 100{\kern 1pt} - {\kern 1pt} 1000$ эВ. Подстановка в формулу (7.2) первых формул (6.2) и учет второй формулы в (11.9) для температур электронов

дает следующие оценки:

Эта оценка характерных значений по данным измерений на космических аппаратах показывает, что в магнитосфере Земли в областях неоднородности продольное электрическое поле ${{E}_{\parallel }}{\kern 1pt} \left( {x,t} \right)$ может иметь тот же порядок по величине, или быть на порядок больше, что и характерная величина его ортогональной части ${{E}_{ \bot }}{\kern 1pt} \left( {x,t} \right)$.

Подстановка предположения (11.11) в уравнение Фарадея (2.2) дает эволюционное уравнение индукции (уравнение вмороженности) для магнитного поля (11.4), которое содержит частную производную по времени, имеет гиперболический тип, и используется в магнитной гидродинамике для определения магнитного поля. Определение магнитного поля из уравнения вмороженности (11.4) физически означает, что уравнение Ампера не учитывается, т.е. текущие в плазме токи вообще никак не влияют на магнитное поле, поскольку из-за квазинейтральности вклад скорости электрического дрейфа в полный ток равен нулю. Кроме того, при таком подходе качественно меняется физическое описание магнитного поля – вместо мгновенного дальнодействия (обусловленного отбрасыванием тока смещения в уравнении Максвелла (2.4)) оно описывается эволюционным гиперболическим уравнением.

Нарушение уравнения вмороженности (11.4) приводит к нарушению полученных с его помощью уравнений для давлений в системе ЧГЛ в форме адиабатических инвариантов (11.3).

Поэтому приближение одножидкостной магнитной гидродинамики является адекватным и дает хорошее соответствие с данными измерений только для процессов в слабо неоднородной плазме, например, для распространения магнитогидродинамических волн.

12. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Одной из актуальных задач физики околоземной космической плазмы является создание корректной глобальной модели ионосферы и магнитосферы Земли, которые тесно связанны друг с другом.

С точки зрения моделирования магнитное поле в околоземном космическом пространстве можно разделить на две сопоставимые между собой части. Первая часть создается токовой системой внутри Земли, и в численных моделях ионосферы и магнитосферы считается заданной, например, дипольной в простейшем случае. Вторая часть магнитного поля создается магнитосферно-ионосферной токовой системой, важную часть которой составляют продольные токи, которые протекают вдоль силовых линий магнитного поля и пересекают высокоширотную ионосферу – так называемые токи зон 1, 2 и 3.

Эти токи в спокойных условиях начинаются от внешней границы магнитосферы – магнитопаузы, пересекают магнитосферу, втекают в ионосферу и пересекают F-слой, затем “замыкаются” в E-слое ионосферы и вытекают обратно вдоль силовых линий через F-слой в магнитосферу. Во время глобальных возмущений магнитосферы и ионосферы – магнитных бурь и суббурь эта токовая система испытывает очень существенные изменения по времени и пространству, причем как в ионосфере, так и в магнитосфере. В области протекания этих токов в E-слое ионосферы – в районе полярного овала, существенно изменяется магнитное поле, что отмечается в данных наземных измерений.

Изменения по времени магнитного поля создают, согласно уравнению Фарадея, соленоидальное электрическое поле. Это поле во время магнитных бурь и суббурь в полярной и среднеширотной ионосфере может быть достаточно сильным, так что на Земле оно регулярно вызывает сильные так называемые геоиндукционные токи в трубопроводах, в линиях электропередачи, на железных дорогах. Это достаточно сильное соленоидальное электрическое поле и вариации магнитного поля существенно воздействуют на движение заряженных частиц, изменяя пространственное распределение гидродинамических скоростей всех компонент ионосферного газа в области высоких и средних широт, а также потенциальную часть электрического поля. Таким образом, соленоидальное электрическое поле существенно влияет на глобальную динамику ионосферы в возмущенных условиях, и должно учитываться в численной модели ионосферы.

Для физически корректного моделирования этих процессов необходимо в рамках одной модели рассматривать всю магнитосферно-ионосферную токовую систему в целом. Кроме того, на движение ионосферной плазмы в Е-слое, в котором замыкаются продольные токи зон 1, 2 и 3, важное влияние оказывает взаимодействие с расположенной ниже атмосферой. Поэтому единственно возможным физически корректным подходом будет создание совместной глобальной самосогласованной численной модели атмосферы–ионосферы–магнитосферы.

Отметим, что для существующих сейчас численных моделей ионосферы в сферическом слое высотой в несколько сотен километров поведение системы в основном определяется граничными условиями снизу на атмосфере, и сверху при переходе к магнитосфере. Эти условия достоверно не известны, и задаются из гипотетических теоретических соображений. Поэтому уже на уровне постановки задачи существующие модели ионосферы не могут претендовать на достаточно точное описание реальных процессов.

Все существующие численные модели ионосферы в плане описания электрического и магнитного полей являются лишь в разной степени частично самосогласованными, и не учитывают соленоидальную часть электрического поля. В наиболее продвинутых последних моделях [14–17] пространственное распределение магнитного поля считается заданным входным параметром задачи, причем считается либо дипольным, либо задается по эмпирической модели IGRF. Потенциальная часть электрического поля рассчитывается по очень упрощенной методике, в которой потенциал считается двумерным (зависящим только от углов в сферических координатах) и проектируется вдоль силовых линий магнитного поля. Детальный анализ различных вариантов этой методики приведен в [32]. Такой подход без самосогласованного описания магнитного и электрического полей не учитывает важнейшие физические процессы, и в принципе не может дать описание реального поведения ионосферы, особенно ее неоднородности по вертикали.

Также отметим, что в настоящее время существуют три подхода к построению глобальных численных моделей магнитосферы, основанных на трех различных типах систем уравнений. Однако ни одна из этих систем уравнений не дает правильного описания указанных выше крупномасштабных процессов, и поэтому в принципе не позволяет построить глобальную модель магнитосферы, которая бы была корректна с физической и вычислительной точки зрения.

Первый подход основан на использовании системы уравнений Власова–Максвелла, которая корректно описывает только очень мелкомасштабные быстрые излучательные процессы. Поэтому для создания на основе этой системы уравнений корректной модели необходимо очень высокое пространственное и временное разрешение, которое в случае глобальной модели магнитосферы требует огромного объема вычислительных ресурсов, на порядки превосходящего доступный в ближайшей перспективе объем. Поэтому в глобальных численных моделях магнитосферы или в численных моделях пространственно крупномасштабных магнитосферных явлений используется ряд упрощающих модельных предположений, которые дают на много порядков завышенное относительное нарушение электронейтральности. Последнее приводит к завышенному на еще большее число порядков потенциальному электрическому полю за счет разделения заряда, поскольку уравнение Пуассона является мультипликатором погрешности при численном решении. В результате в численных моделях получается неправильная динамика плазмы за счет на порядки завышенной скорости электрического дрейфа, и, как следствие, неправильные токи и магнитное поле. Детально этот вопрос рассматривается в [1, 2].

Второй подход основан на использовании какой-либо версии системы уравнений магнитной газовой динамики (далее сокращенно МГД). Как показано в предыдущем разделе, предположения, на которых основан подход МГД, нарушаются в важнейших областях магнитосферы с сильной пространственной неоднородностью, а сам подход противоречит приближению мгновенного дальнодействия. Это приводит к физически неверному описанию электромагнитного поля и движения плазмы. Система уравнений МГД корректно описывает только процессы в плазме со слабой пространственной неоднородностью, например, различные магнитогидродинамические волны, для которых она дает хорошее согласие с данными измерений, но не описывает процессы со значительной пространственной неоднородностью. Эта система является аналогом приближения акустики в газовой динамике. Результаты развития глобальных МГД-моделей магнитосферы за последние четыре десятилетия показывают, что такой подход в принципе не позволяет воспроизвести важнейшие особенности системы хотя бы на минимальном качественном уровне.

Третий подход основан на использовании какой-либо версии системы уравнений гибридного описания бесстолкновительной плазмы, при котором ионные компоненты описываются уравнениями Власова, а электроны описываются в рамках какой-либо упрощенной версии системы уравнений газовой динамики, рассматриваются в очень большом числе работ, начиная с 1970-х гг. (см., например, [9, 10] и [25–30]). При этом для определения магнитного поля используется или тот же подход, что и в рассмотренной в предыдущем разделе одножидкостной системе уравнений магнитной газодинамики ЧГЛ (например, в [26]), или уравнение Фарадея (например, в [30]). В обоих подходах для расчета магнитного поля на новом временном слое используется конечно-разностная аппроксимация его частной производной по времени, что также противоречит приближению мгновенного дальнодействия, вытекающему из отбрасывания тока смещения. При этом в численных моделях из-за схем интегрирования появляется схемная вязкость, которая приводит к нефизической численной диссипации.

Из сказанного выше следует, что современные подходы к развитию глобальных численных моделей как ионосферы, так и магнитосферы находятся в теоретическом и методическом тупике, и в принципе не позволяют создать глобальную численную модель ионосферы и магнитосферы, корректную с физической и вычислительной точки зрения.

Отметим, что предложенный в работе подход позволяет вывести следующие системы уравнений.

1) Систему уравнений для корректного самосогласованного описания плазмы Е-слоя ионосферы, в которой учитывается замагниченность электронов, т.е. для них системой уравнений переноса является “модифицированная” система ЧГЛ с учетом трения о нейтральные компоненты и фотохимии. При этом системой уравнений переноса для не замагниченных ионных компонент является полная система уравнений газовой динамики с учетом трения о нейтральные компоненты и фотохимии.

2) Систему уравнений для корректного описания плазмы F-слоя ионосферы, в которой учитывается замагниченность электронов и ионов, т.е. для них системой уравнений переноса является “модифицированная” система ЧГЛ с учетом трения о нейтральные компоненты и фотохимии.

3) Систему уравнений для корректного описания слабостолкновительной замагниченной плазмы переходной области между F-слоем ионосферы и ближней магнитосферой.

13. ВЫВОДЫ

В работе предложено решение фундаментальной проблемы описания магнитного и электрического полей для достаточно крупномасштабных безызлучательных процессов в бесстолкновительной космической плазме с использованием условий квазинейтральности и продольного силового равновесия электронов. В рамках предложенного подхода реализуется концепция мгновенного дальнодействия при определении полей по текущим параметрам плазмы полностью аналогично тому, как это имеет место для системы уравнений Власова–Пуассона или системы Власова–Дарвина.

Уравнения, описывающие плазму, делятся на две части: систему уравнений переноса, которая описывает движение каждой компоненты плазмы, и систему уравнений для полей, которая не содержит производных по времени и имеет эллиптический тип. В последней системе магнитное поле определяется из уравнения Гаусса и уравнения Ампера. Для соленоидальной части электрического поля получено линейное уравнение эллиптического типа, которое в ходе итерационного процесса численного интегрирования описывающей плазму системы уравнений на каждой итерации, сводится к уравнению Пуассона. Потенциальная часть электрического поля определяется из уравнения продольного силового равновесия электронов интегрированием этого уравнения вдоль силовых линий магнитного поля. При этом плотность тока и ее частная производная по времени, которые определяют правые части в системе уравнений для полей, находятся из системы уравнений переноса.

В работе рассматриваются три формы обобщенного закона Ома, соответствующие различным уровням замагниченности плазмы, которые, в зависимости от используемой системы уравнений переноса каждой компоненты плазмы, определяют пять вариантов описывающей плазму системы уравнений.

Первый вариант обобщенного закона Ома относится к общему случаю, когда все компоненты плазмы не замагничены, и в уравнениях присутствует тензор давлений электронов. Ему соответствует только один вариант системы уравнений переноса – уравнения Власова для каждой компоненты плазмы.

Второй вариант закона Ома относится к случаю, когда все ионные компоненты плазмы не замагничены, а замагничены только электроны. Тогда в уравнениях тензор давлений электронов выражается через их продольное и поперечное давление, а также магнитное поле. Для этого случая возможны два варианта системы уравнений переноса, причем в обоих ионы описываются уравнениями Власова. В первом варианте электроны описываются уравнением Власова в дрейфовом приближении. Во втором варианте они описываются системой уравнений магнитной газодинамики Чу–Гольдбергера–Лоу с исходными уравнениями для давлений не в форме адиабатических инвариантов. По сложившейся терминологии этот вариант называется гибридным описанием плазмы.

Третий вариант закона Ома относится к случаю, когда все компоненты плазмы замагничены, и в уравнениях тензор давлений каждой компоненты заменяется его выражением через продольное и поперечное давление, а также магнитное поле. Для этого случая также возможны два варианта системы уравнений переноса. В первом варианте каждая компонента описывается уравнением Власова в дрейфовом приближении. Во втором варианте каждая компонента описываются системой уравнений магнитной газодинамики Чу–Гольдбергера–Лоу с уравнениями для давлений не в форме адиабатических инвариантов.

Результаты работы создают теоретические и методические предпосылки для построения на основе полученных систем уравнений адекватных численных моделей для широкого круга актуальных задач физики бесстолкновительной космической плазмы с максимально возможным учетом специфики конкретной задачи. Предложенный в работе подход допускает обобщение на случай слабостолкновительной плазмы, и может быть использован для вывода полностью самосогласованных систем уравнений для описания ионосферной плазмы F и E-слоев, которые должны учитывать, в том числе, и индукционную часть электрического поля, а также зависимость электрического поля от высоты. Таким образом, результаты работы создают необходимый теоретический задел для разработки глобальной численной модели системы атмосфера–ионосфера–магнитосфера.

Авторы выражают признательность А.В. Артемьеву и М.В. Клименко за плодотворные обсуждения. Работа О.В. Хабаровой поддержана грантом РФФИ 17-02-01328, работа Х.В. Маловой поддержана государственной программой Плазма.