Физика плазмы, 2020, T. 46, № 4, стр. 358-367

1. ВВЕДЕНИЕ

Заряженные пылевые частицы, левитирующие в приэлектродной области газового разряда, часто образуют различные структуры и, в частности, могут выстраиваться в плоскую гексагональную решетку. Изучению динамики ансамбля взаимодействующих частиц посвящена значительная часть физики пылевой плазмы. Обзор основных идей и достижений можно найти в монографиях [1–3].

Для развития теории плазменных кристаллов нужны те или иные предположения о характере взаимодействия между отдельными частицами. Во многих работах предполагается, что пылинки взаимодействуют посредством изотропного, например, экранированного кулоновского потенциала (например, [4–9]). Это предположение позволяет построить теорию колебаний и исследовать устойчивость двумерного плазменного кристалла, левитирующего в горизонтальной плоскости. Существенно, что в приближении изотропного потенциала взаимодействия колебания частиц в вертикальном направлении и в горизонтальной плоскости оказываются независимыми.

В области существования плазменного кристалла окружающая плазма сильно анизотропна и характеризуется наличием ионного потока в направлении электрода. Это приводит к тому, что потенциал электрического поля вокруг отдельного заряда оказывается несимметричным, а силы, действующие между отдельными частицами, оказываются невзаимными, т. е. для них не выполняется третий закон Ньютона. Простых аналитических выражений для потенциала заряда в плазме с ионными потоками не существует. Поэтому в теории часто используется так называемая модель ионного фокуса [10]. В этой модели с каждой отрицательно заряженной пылинкой связывается виртуальный заряд противоположного знака, расположенный на фиксированном расстоянии ниже по течению ионного потока. При этом считается, что поле виртуального заряда не действует на другие заряды, расположенные выше по течению, т. е. межчастичные силы оказываются невзаимными. Точность подобного приближения не известна, однако модель ионного фокуса позволяет на качественном уровне воспроизвести некоторые наблюдаемые явления. В частности, более сложный характер взаимодействия приводит к связи вертикальных и горизонтальных смещений частиц и развитию осциллирующей неустойчивости связанных мод, наблюдаемой в эксперименте (например, [11–14]).

Настоящая статья является продолжением работ [15, 16], в которых для описания стационарного состояния кристалла и колебаний линейной цепочки пылевых частиц использовалась более приближенная к реальности модель взаимодействия. Предполагается, что в равновесии все частицы расположены на одной высоте во внешнем гармоническом потенциальном поле с характерной частотой колебаний ${{\Omega }_{0}}$. Окружающая плазма считается состоящей из направленного вниз потока холодных ионов и распределенных по Больцману электронов.

Частицы расположены на расстоянии a друг от друга и в равновесии образуют правильную гексагональную решетку. В приближении ближайших соседей частоты колебаний определяются четырьмя силовыми константами, которые рассчитываются численными методами.Эти константы зависят от межчастичного расстояния и от дополнительного параметра M, который для квазинейтральной плазмы имеет смысл числа Маха ионного потока. Величины ${{\Omega }_{0}}$, a и M являются внешними управляющими параметрами и считаются независимыми. Задача заключается в поиске областей в трехмерном пространстве параметров, в которых колебания кристалла устойчивы, и определения типа неустойчивости на их границах.

Предполагается, что все пылевые частицы имеют одинаковый и постоянный заряд Q. Используются безразмерные переменные, в которых масштаб длины равен $\lambda = u{\text{/}}{{\omega }_{{pi}}}$, где ${{\omega }_{{pi}}}$ – ионная плазменная частота и u – направленная скорость ионов, межчастичные силы нормализованы на ${{F}_{0}} = {{Q}^{2}}{\text{/}}{{\lambda }^{2}}$, а естественный масштаб времени для частиц с массой ${{M}_{0}}$ равен $M_{0}^{{1/2}}{{\lambda }^{{3/2}}}{\text{/|}}Q{\text{|}}$.

Статья организована следующим образом. Для удобства ссылок и введения обозначений в разделе 2 выписаны общие уравнения движения двумерного кристалла. В разделе 3 приведено общее выражение для используемого потенциала взаимодействия и показаны графики зависимости силовых констант от a и M. Далее, в разделе 4 обсуждаются дисперсионные кривые колебаний кристалла для двух симметричных направлений. В разделе 5 приведены итоговые диаграммы областей устойчивости.

2. УРАВНЕНИЯ ДВИЖЕНИЯ

Пусть в равновесии все частицы расположены на одной высоте ${{z}_{{n,m}}} = {{z}_{0}}$ и в горизонтальной плоскости образуют правильную гексагональную решетку, т.е. горизонтальные координаты $\rho = (x,y)$ частиц равны ${{\rho }_{{m,n}}} = a(m{{{\mathbf{A}}}_{1}} + n{{{\mathbf{A}}}_{2}})$, где $n,\;m$ – целые числа и a – межчастичное расстояние. В качестве базисных выберем единичные векторы ${{{\mathbf{A}}}_{1}} = (1,0)$, ${{{\mathbf{A}}}_{2}} = (1,\sqrt 3 ){\text{/}}2$.

Сила взаимодействия между частицами считается потенциальной ${\mathbf{F}}({\mathbf{r}}) = - \nabla U({\mathbf{r}})$, где потенциал изотропен в горизонтальной плоскости, т.е. $U({\mathbf{r}}) = U(\rho ,z)$ ($\rho = \sqrt {{{x}^{2}} + {{y}^{2}}} $). Невзаимность межчастичных сил проявляется в том, что $U(\rho ,z) \ne U(\rho , - z)$ и смешанные производные $U(\rho ,z)$ не равны нулю при $z = 0$.

Уравнения движения для частицы с индексами $m,n$ имеют вид

Разложим уравнения движения (1) по малым отклонениям от равновесия (${{z}_{{m,n}}} \to {{z}_{0}} + {{z}_{{m,n}}}$, ${{\rho }_{{m,n}}} \to a(m{{{\mathbf{A}}}_{1}} + n{{{\mathbf{A}}}_{2}}) + {{\rho }_{{m,n}}}$) и совершим дискретное преобразование Фурье

Двумерный вектор ${\mathbf{k}} = ({{k}_{x}},{{k}_{y}})$ лежит в первой зоне Бриллюэна, представляющей собой правильный шестиугольник, одна из вершин которого лежит в точке ${{{\mathbf{b}}}_{1}} = \tfrac{{4\pi }}{3}(1,0)$, а остальные ${{{\mathbf{b}}}_{{2 \ldots 5}}}$ получаются последовательными поворотами на угол $\pi {\text{/}}3$.

Предполагая, что межчастичное расстояние достаточно велико $a > 2$ [15, 16], ограничимся учетом взаимодействия лишь между ближайшими соседями. После простых стандартных вычислений получаем уравнения движения ${\mathbf{\ddot {r}}}({\mathbf{k}}) = {\mathbf{M}}({\mathbf{k}}) \cdot {\mathbf{r}}({\mathbf{k}})$, где силовая матрица имеет компоненты

Силовая матрица M с матричными элементами (3) обладает очевидными свойствами симметрии, унаследованными от исходной гексагональной решетки кристалла. Это, во-первых, симметрия ${{C}_{6}}$ относительно поворотов ${\mathbf{M}}\left( {{{{\mathbf{R}}}_{{\pi /3}}} \cdot {\mathbf{k}}} \right) = $ $ = {{{\mathbf{R}}}_{{\pi /3}}} \cdot {\mathbf{M}}({\mathbf{k}}) \cdot {\mathbf{R}}_{{\pi /3}}^{{ - 1}}$, где ${{{\mathbf{R}}}_{{\pi /3}}}$ – матрица поворота на угол $\pi {\text{/}}3$ относительно оси z. Во-вторых, имеется 6 плоскостей зеркальной симметрии, ${\mathbf{M}}({{{\mathbf{R}}}_{\alpha }} \cdot {\mathbf{k}}) = $ $ = {{{\mathbf{R}}}_{\alpha }} \cdot {\mathbf{M}}({\mathbf{k}}) \cdot {\mathbf{R}}_{\alpha }^{{ - 1}}$ ($\alpha = 1 \ldots 6$), где ${{{\mathbf{R}}}_{\alpha }}$ – матрицы отражений в плоскостях xz и yz и любых им эквивалентных, получающихся поворотом на угол $\pi {\text{/}}3$ относительно оси z. По этой причине собственные значения матрицы M, определяющие собственные частоты кристалла ${{\omega }_{i}}({\mathbf{k}})$, инвариантны относительно тех же элементов симметрии. В частности, в выбранной системе координат собственные частоты являются четными функциями ${{k}_{x}}$ и ${{k}_{y}}$, т. е. ${{\omega }_{i}}({{k}_{x}},{{k}_{y}}) = {{\omega }_{i}}( - {{k}_{x}},{{k}_{y}}) = {{\omega }_{i}}({{k}_{x}}, - {{k}_{y}})$.

3. ПОТЕНЦИАЛ ВЗАИМОДЕЙСТВИЯ

Для приведенных ниже аналитических выражений явный вид $U(\rho ,z)$ не играет роли. Для анализа устойчивости и построения графиков используется потенциал [15, 16]

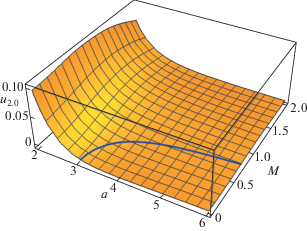
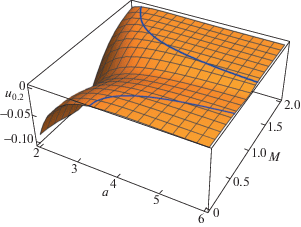
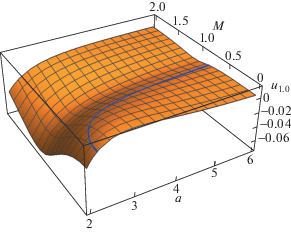
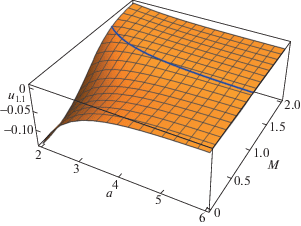
В настоящей статье исследована область параметров $2 \leqslant a \leqslant 6$, $0 \leqslant M \leqslant 2$. Удобные выражения для численных расчетов потенциала (5) и его производных приведены в [16]. Графики зависимости силовых констант от a и M приведены на рис. 1–4, где сплошными линиями показаны линии уровня, на которых соответствующий коэффициент обращается в нуль. Заметим, что все силовые константы могут менять знак при изменении параметров a и M. В общем случае смешанная производная ${{u}_{{1,1}}}$ того же порядка, что и все остальные коэффициенты, и поэтому невзаимность межчастичных сил нельзя считать малой.

Рис. 1.

Зависимость коэффициента ${{u}_{{2,0}}}$ от параметров a и M.

Рис. 2.

Зависимость коэффициента ${{u}_{{0,2}}}$ от параметров a и M.

Рис. 3.

Зависимость коэффициента ${{u}_{{1,0}}}$ от параметров a и M.

Рис. 4.

Зависимость коэффициента ${{u}_{{1,1}}}$ от параметров a и M.

4. СОБСТВЕННЫЕ ЧАСТОТЫ

Частоты и поляризации колебаний кристалла определяются собственными значениями и векторами матрицы (3). Помимо волнового вектора k эта матрица зависит от трех внешних параметров a, M и ${{\Omega }_{0}}$, которые считаются независимыми. Основная цель дальнейшего исследования заключается в поиске поверхностей в пространстве внешних параметров a, M, ${{\Omega }_{0}}$, на которых собственные частоты ω становятся комплексными для каких-то волновых векторов k, и исследовании характера возникающей неустойчивости.

Стратегия поиска границ области устойчивости кристалла заключается в следующем. Собственные частоты определяются корнями дисперсионного уравнения $P({{\omega }^{2}},{\mathbf{k}},a,M,{{\Omega }_{0}}) = 0$, которое представляет собой кубическое уравнение относительно ${{\omega }^{2}}$ с действительными коэффициентами. Условие действительности и положительности корней дисперсионного уравнения ${{\omega }^{2}}({\mathbf{k}})$ накладывает некоторые ограничения на коэффициенты дисперсионного уравнения. Эти ограничения можно записать в виде ${{f}_{i}}({\mathbf{k}},a,M,{{\Omega }_{0}}) > 0$, где функции ${{f}_{i}}$ алгебраически выражаются через матричные элементы (3), и которые должны выполняться для любых векторов k из первой зоны Бриллюэна. При изменении внешних параметров какое-либо из неравенств, например ${{f}_{1}}({\mathbf{k}},a,M,{{\Omega }_{0}}) > 0$, может нарушиться. Если точка $(a,M,{{\Omega }_{0}})$ лежит на границе области устойчивости, то в окрестности этой точки функция ${{f}_{1}}$ должна иметь минимум в некоторой точке ${\mathbf{k}} = {{{\mathbf{k}}}_{0}}$, причем ${{f}_{1}}({{{\mathbf{k}}}_{0}},a,M,{{\Omega }_{0}}) = 0$. Таким образом, границы областей устойчивости кристалла в пространстве параметров a, M, ${{\Omega }_{0}}$ и соответствующее значение ${{{\mathbf{k}}}_{0}}$ определяются из уравнений ${{f}_{i}}({\mathbf{k}},a,M,{{\Omega }_{0}}) = 0$, $\partial {{f}_{i}}({\mathbf{k}},a,M,{{\Omega }_{0}}){\text{/}}\partial {\mathbf{k}} = 0$. При этом необходимо следить, чтобы вторые производные ${{f}_{i}}$ по k образовывали положительно определенную квадратичную форму.

При изменении внешних параметров могут реализоваться два сценария. Во-первых, может произойти слияние двух действительных положительных корней дисперсионного уравнения для какого-либо вектора k, после чего они становятся комплексными. В этом случае мы имеем дело с осцилляционной неустойчивостью, которую называют неустойчивостью связанных волн. Во-вторых, действительный положительный корень $\omega {{({\mathbf{k}})}^{2}}$ может изменить знак, и в этом случае развивается апериодическая неустойчивость, которая указывает на возможный переход кристалла в другое фазовое состояние.

Учет симметрии решетки упрощает исследование поведения собственных частот. Как уже отмечалось, собственные частоты и коэффициенты дисперсионного уравнения являются четными функциями ${{k}_{x}}$ и ${{k}_{y}}$, т. е. их производные по ${{k}_{y}}$ при ${{k}_{y}} = 0$ и по ${{k}_{x}}$ при ${{k}_{x}} = 0$ тождественно обращаются в нуль. Поэтому для анализа устойчивости необходимо исследовать поведение собственных частот в диапазонах волновых векторов ${{k}_{y}} = 0$, ${\text{|}}{{k}_{x}}{\text{|}} \leqslant 4\pi {\text{/}}3$ и ${{k}_{x}} = 0$, ${\text{|}}{{k}_{y}}{\text{|}} \leqslant 2\pi {\text{/}}\sqrt 3 $, которые соответствуют первой зоне Бриллюэна. Для этих выделенных направлений поперечные колебания, в которых смещения частиц лежат в плоскости xy и перпендикулярны k, оказываются несвязанными с двумя другими ветвями спектра.

Прежде, чем обсуждать общий случай конечных волновых векторов, выпишем простые аналитические выражения для собственных частот в длинноволновом пределе.

4.2. Колебания с произвольным волновым вектором

Как уже отмечалось, для анализа устойчивости необходимо рассмотреть распространение колебаний вдоль двух симметричных направлений – вдоль оси x и вдоль оси y. Остальные симметричные направления получаются поворотом на угол $\pi {\text{/}}3$ вокруг оси z. Для этих направлений общее дисперсионное уравнение в явном виде разделяется на два сомножителя $P({{\omega }^{2}}) = ({{\omega }^{2}} - $ $ - \;{{\omega }_{t}}{{({\mathbf{k}})}^{2}}){{P}_{2}}({{\omega }^{2}}) = 0$, где ${{\omega }_{t}}({\mathbf{k}})$ – частота поперечных колебаний с вектором поляризации, лежащим в плоскости xy и перпендикулярным k, а ${{P}_{2}}({{\omega }^{2}})$ – квадратный полином ${{\omega }^{2}}$, определяющий дисперсию связанных продольно-вертикальных колебаний.

4.2.1. Поперечные колебания. Частота поперечных колебаний, распространяющихся вдоль оси x, равна

(9)

${{\omega }_{{t,x}}}{{({{k}_{x}})}^{2}}\, = {\kern 1pt} \,2si{{n}^{2}}({{\theta }_{1}}{\text{/}}2)\left( {3{{u}_{{2,0}}}\, + \frac{{{{u}_{{1,0}}}}}{a}\left( {4cos({{\theta }_{1}})\, + 5} \right)} \right),$

а частота колебаний, распространяющихся вдоль оси y, равна

(10)

${{\omega }_{{t,y}}}{{({{k}_{y}})}^{2}} = 2si{{n}^{2}}({{\theta }_{2}}{\text{/}}2)\left( {{{u}_{{2,0}}} + \frac{3}{a}{{u}_{{1,0}}}} \right),$

где ${{\theta }_{1}} = {{k}_{x}}{\text{/}}2$ (${\text{|}}{{\theta }_{1}}{\text{|}} \leqslant 2\pi {\text{/}}3$), ${{\theta }_{2}} = \sqrt 3 {{k}_{y}}{\text{/}}2$ (${\text{|}}{{\theta }_{2}}{\text{|}} \leqslant \pi $).

Величина (9) положительна для любых волновых векторов из первой зоны Бриллюэна (${\text{|}}{{k}_{x}}{\text{|}} \leqslant 3\pi {\text{/}}4$), если выполняются два неравенства

(11)

$3{{u}_{{1,0}}} + a{{u}_{{2,0}}} > 0,$

(12)

${{u}_{{1,0}}} + a{{u}_{{2,0}}} > 0,$

а для положительности же (10) при ${\text{|}}{{k}_{y}}{\text{|}} \leqslant 2\pi {\text{/}}\sqrt 3 $ достаточно выполнения лишь первого из них (11). Неравенство (11) обеспечивает положительность квадрата фазовой скорости длинноволновых поперечных колебаний (8). При нарушении второго неравенства (12) частота поперечных (9) колебаний, распространяющихся вдоль оси $x$, становится комплексной в вершине зоны Бриллюэна (${\text{|}}{{k}_{x}}{\text{|}} = 4\pi {\text{/}}3$).

На рис. 5 затенены области в плоскости параметров a и M, полученные при помощи потенциала (5), для которых нарушаются неравенства (11, 12). На рис. 6 показаны характерные примеры дисперсионных кривых (9) на границах облас-тей 1 и 2 на рис. 5.

Рис. 5.

Область 1 – плавление кристалла ($3{{u}_{{1,0}}} + a{{u}_{{2,0}}} < 0$), область 2 – апериодическая неустойчивость при ${{k}_{x}} = 4\pi {\text{/}}3$, ${{k}_{y}} = 0$, (${{u}_{{1,0}}} + a{{u}_{{2,0}}} < 0$), область 3 – апериодическая неустойчивость при ${{k}_{x}} = 0$, ${{k}_{y}} = 2\pi {\text{/}}\sqrt 3 $, (${{u}_{{1,0}}} + 3a{{u}_{{2,0}}} < 0$). Если $M > {{M}_{0}}(a)$, то ${{\Omega }_{{cr,y}}}(a,M) > {{\Omega }_{{cr,x}}}(a,M)$; ${{a}_{0}} \approx 3.14$.

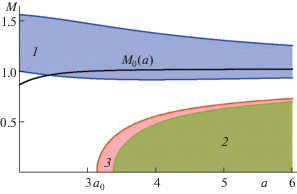
Рис. 6.

Дисперсия поперечных колебаний (9) для параметров a и M, лежащих на границах областей 1 и 2 на рис. 5. Кривая 1 – $a = 4$, $M \approx 1.377$, кривая 2 – $a = 4$, $M \approx 0.474$.

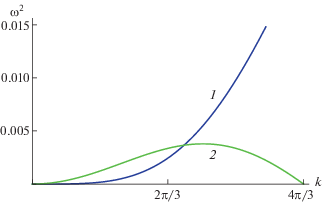
При переходе в область 1 на рис. 5 нарушается первое неравенство (11), т. е. фазовая скорость поперечных волн (8), а значит и модуль сдвига решетки обращаются в нуль (кривая 1 на рис. 6). При этом в исследованной области параметров квадрат фазовой скорости продольных звуковых волн (7) положителен. Такое поведение характерно для фазового перехода твердое тело–жидкость, поэтому эта неустойчивость в дальнейшем называется плавлением двумерного кристалла.

При переходе в область 2 на рис. 5 апериодическая неустойчивость поперечных колебаний развивается для волновых векторов, лежащих в вершинах зоны Бриллюэна (кривая 2 на рис. 6). Для волнового вектора ${\mathbf{k}} = {{{\mathbf{b}}}_{1}}$ смещения частиц направлены вдоль оси y и равны ${{y}_{{m,n}}} = $ $ = Acos(2(2m + n)\pi {\text{/}}3)$, где A – амплитуда волны, величина которой в рамках линейной теории остается неопределенной. Поскольку числа m, n целые, частицы кристалла разделяются на две группы. Для одной из них смещения равны A, а для другой смещения равны $ - A{\text{/}}2$, причем число частиц во второй группе вдвое больше, чем в первой. Возникающая при этом структура показана на рис. 7. Симметрия решетки понижается и возникает выделенное направление, совпадающее в данном случае с осью y. В качестве базисных векторов новой решетки можно выбрать, например, ${\mathbf{A}}_{1}^{'} = {{{\mathbf{A}}}_{1}} + {{{\mathbf{A}}}_{2}}$, ${\mathbf{A}}_{2}^{'} = 2{{{\mathbf{A}}}_{1}} - {{{\mathbf{A}}}_{2}}$, а в элементарной ячейке теперь содержатся три частицы.

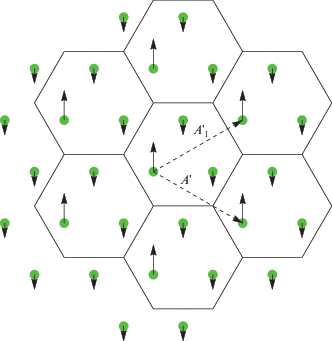
Рис. 7.

Структура, возникающая при переходе в область 2 на рис. 5. Кружками показаны исходные положения частиц, стрелками – векторы смещений. Штриховые стрелки – базис новой решетки, шестиугольники – элементарные ячейки.

4.2.2. Продольно-вертикальные колебания. Частоты смешанных продольно-вертикальных колебаний определяются корнями биквадратного уравнения ${{P}_{2}} = {{\omega }^{4}} + \alpha (k){{\omega }^{2}} + \beta (k) = 0$, явный вид коэффициентов которого зависит от направления распространения волны. Для волн, распространяющихся вдоль оси x, коэффициенты имеют вид

$\begin{gathered} \alpha ({{k}_{x}}) = - \Omega _{0}^{2} - 6{{u}_{{0,2}}} - 3{{u}_{{2,0}}} - \frac{{3{{u}_{{1,0}}}}}{a} + \\ \, + cos\left( {{{\theta }_{1}}} \right)\left( {\frac{{3{{u}_{{1,0}}}}}{a} + 4{{u}_{{0,2}}} + {{u}_{{2,0}}}} \right) + \\ \, + 2\left( {{{u}_{{0,2}}} + {{u}_{{2,0}}}} \right)cos\left( {2{{\theta }_{1}}} \right), \\ \end{gathered} $

(13)

$\begin{gathered} \beta ({{k}_{x}}) = 2si{{n}^{2}}({{\theta }_{1}}{\text{/}}2)\left[ {\frac{{3{{u}_{{1,0}}}\left( {6{{u}_{{0,2}}} + \Omega _{0}^{2}} \right)}}{a} + } \right. \\ \, + {{u}_{{2,0}}}\left( {22{{u}_{{0,2}}} + 5\Omega _{0}^{2}} \right) + 20u_{{1,1}}^{2} + \\ \end{gathered} $

$\begin{gathered} \, + 4cos\left( {{{\theta }_{1}}} \right)\left( { - \frac{{3{{u}_{{0,2}}}{{u}_{{1,0}}}}}{a} + \Omega _{0}^{2}{{u}_{{2,0}}} + 8u_{{1,1}}^{2}} \right) + \\ \, + cos\left( {2{{\theta }_{1}}} \right)\left( {16u_{{1,1}}^{2} - \frac{{6{{u}_{{0,2}}}\left( {3a{{u}_{{2,0}}} + {{u}_{{1,0}}}} \right)}}{a}} \right) + \\ \,\left. { + 4\left( {u_{{1,1}}^{2} - {{u}_{{0,2}}}{{u}_{{2,0}}}} \right)cos\left( {3{{\theta }_{1}}} \right)} \right]. \\ \end{gathered} $

Если же вектор k параллелен оси y, то

$\begin{gathered} \alpha ({{k}_{y}}) = - \Omega _{0}^{2} - \frac{{{{u}_{{1,0}}}}}{a} - 4{{u}_{{0,2}}} - 3{{u}_{{2,0}}} + \\ \, + cos\left( {{{\theta }_{2}}} \right)\left( {\frac{{{{u}_{{1,0}}}}}{a} + 4{{u}_{{0,2}}} + 3{{u}_{{2,0}}}} \right), \\ \end{gathered} $

(14)

$\beta ({{k}_{y}}) = 2si{{n}^{2}}({{\theta }_{2}}{\text{/}}2)\left[ {\Omega _{0}^{2}\left( {\frac{{{{u}_{{1,0}}}}}{a} + 3{{u}_{{2,0}}}} \right) + } \right.$

$\begin{gathered} \, + \frac{{4{{u}_{{0,2}}}{{u}_{{1,0}}}}}{a} + 12u_{{1,1}}^{2} + 12{{u}_{{0,2}}}{{u}_{{2,0}}} + \\ \,\left. { + 4cos({{\theta }_{2}})\left( { - \frac{{{{u}_{{0,2}}}{{u}_{{1,0}}}}}{a} + 3u_{{1,1}}^{2} - 3{{u}_{{0,2}}}{{u}_{{2,0}}}} \right)} \right]. \\ \end{gathered} $

Рассмотрим сначала волны, распространяющиеся вдоль оси x с коэффициентами дисперсионного уравнения (13). При достаточно большом значении частоты ${{\Omega }_{0}}$ дискриминант $D(k) = \alpha {{(k)}^{2}} - 4\beta (k)$ положителен для любых волновых векторов. По мере уменьшения ${{\Omega }_{0}}$ при фиксированных значениях a и M функция $D(k)$ обращается в нуль для какого-то значения $k = {{k}_{0}}$ и ${{\Omega }_{0}} = {{\Omega }_{{cr,x}}}(a,M)$, а при ${{\Omega }_{0}} < {{\Omega }_{{cr,x}}}(a,M)$ становится отрицательной в    некотором конечном интервале k. При ${{\Omega }_{0}} < {{\Omega }_{{cr,x}}}(a,M)$ частоты комплексны в некотором диапазоне волновых векторов и возникает неустойчивость связанных волн. Значения величин ${{\Omega }_{{cr,x}}}(a,M)$ и ${{k}_{0}}$ получаются из решения двух уравнений

(15)

$D(k) = 0,\quad \frac{{\partial D(k)}}{{\partial k}} = 0.$

Численное решение этих уравнений позволяет определить критическое значение частоты внешнего потенциала ${{\Omega }_{{cr,x}}}$ и волнового вектора ${{k}_{0}}$ как функции параметров a и M. Характерный пример поведения дисперсионных кривых при возникновении неустойчивости связанных волн показан на рис. 8. В критической точке ${{\Omega }_{0}} = {{\Omega }_{{cr,x}}}$, $\omega = {{\omega }_{0}}$, ${{k}_{x}} = {{k}_{0}}$ собственные значения матрицы (3) двукратно вырождены, а собственный вектор равен ${{{\mathbf{p}}}_{1}} = (1,0,i)$ и не зависит от внешних параметров. Это означает, что при развитии неустойчивости связанных волн частицы кристалла совершают круговые движения в плоскости xz.

Рис. 8.

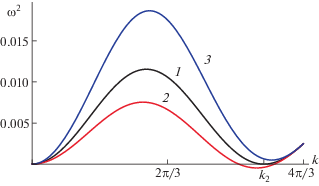
Неустойчивость связанных волн при $a = 3.5$, $M = 0.6$, ${{k}_{y}} = 0$. Кривые 1 – ${{\Omega }_{0}} = {{\Omega }_{{cr,x}}} \approx 0.45$, кривые 2 – ${{\Omega }_{0}} = {{\Omega }_{{cr,x}}} + 0.01$, кривые 3 – ${{\Omega }_{0}} = {{\Omega }_{{cr,x}}} - $ $ - {\kern 1pt} \,0.01$. Кривые 1 пересекаются в точке ${{k}_{0}} \approx 2.36$, ${{\omega }_{0}} \approx 0.08$.

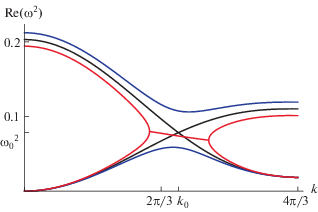
Другой тип неустойчивости связан с изменением знака одного из корней дисперсионного уравнения, причем второй корень должен быть положительным. Критические значения управляющих параметров и волнового вектора находятся из условий

(16)

$\beta (k) = 0,\quad \frac{{\partial \beta (k)}}{{\partial k}} = 0,\quad \alpha (k) < 0.$

Неустойчивость при этом носит апериодический характер. Численный анализ показывает, что апериодическая неустойчивость возникает при возрастании частоты ${{\Omega }_{0}}$, т. е. область устойчивости определяется неравенством ${{\Omega }_{0}} < {{\Omega }_{1}}(a,M)$. Пример дисперсионной зависимости низкочастотной ветви продольно-вертикальных волн показан на рис. 9. Заметим, что период возникающей при развитии этой неустойчивости структуры несоизмерим с периодом исходной гексагональной решетки, поэтому можно говорить о тенденции к формированию сверхрешетки. Соответствующий собственный вектор матрицы (3) имеет вид ${{{\mathbf{p}}}_{2}} = ({{p}_{2}},0,i)$, причем величина ${{p}_{2}}$ зависит от управляющих параметров и в исследованной области велика: ${{p}_{2}} = 10{\kern 1pt} - {\kern 1pt} 100$. Таким образом, частицы в этом случае смещаются примерно параллельно волновому вектору в плоскости xy, а смещение в вертикальном направлении не велико.

Рис. 9.

Апериодическая неустойчивость низкочастотных волн при $a = 3.5$, $M = 0.3$. Кривая 1 – ${{\Omega }_{0}} = {{\Omega }_{1}} \approx 0.64$, кривая 2 – ${{\Omega }_{0}} = {{\Omega }_{1}} + 0.1$, кривая 3 – ${{\Omega }_{0}} = {{\Omega }_{1}} - 0.1$. Кривая 1 касается оси абсцисс при ${{k}_{2}} \approx 3.58$.

Таким же образом исследуются волны, распространяющиеся вдоль оси y. Решение уравнений (15) с коэффициентами (14) определяет некоторую критическую частоту ${{\Omega }_{{cr,y}}}(a,M)$. При ${{\Omega }_{0}} < {{\Omega }_{{cr,y}}}$ развивается неустойчивость связанных волн, аналогичная показанной на рис. 8. Критические частоты для волн, распространяющихся в перпендикулярных направлениях, не равны друг другу. Однако для потенциала (5) численное отличие двух критических частот оказывается небольшим (меньше 10%), и ${{\Omega }_{{cr,y}}}(a,M) > {{\Omega }_{{cr,x}}}(a,M)$ при $M > {{M}_{0}}(a)$ (см. рис. 5).

Исследование уравнений (16) с коэффициентами (14) для продольно-вертикальных волн с ${{k}_{x}} = 0$ показывает, что апериодическая неустойчивость развивается только на границе зоны Бриллюэна (рис. 10). При ${{k}_{x}} = 0$, ${{k}_{y}} = 2\pi {\text{/}}\sqrt 3 $ минимальная частота равна ${{\omega }^{2}} = 6{{u}_{{2,0}}} + 2{{u}_{{1,0}}}{\text{/}}a$ и вектор поляризации равен $(0,1,0)$. Таким образом, для устойчивости кристалла помимо неравенств (11), (12) необходимо выполнение еще одного

(17)

${{u}_{{1,0}}} + 3a{{u}_{{2,0}}} > 0.$

Рис. 10.

Частоты колебаний при ${{k}_{x}} = 0$ на границе неустойчивости продольных волн при $3a{{u}_{{2,0}}} + {{u}_{{1,0}}} = 0$ (область 3 на рис. 5). Кривые 1, 2 – продольно-вертикальные волны, кривая 3 – поперечная волна (10); $a = 4$, $M \approx 0.553$, ${{\Omega }_{0}} = 0.325$.

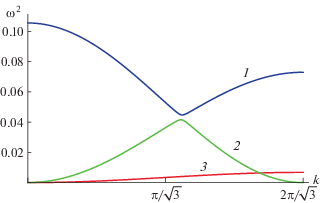
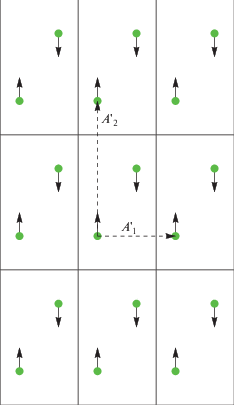
В области 3 на рис. 5 неравенство (17) нарушается. При переходе в область 3 смещение частицы с индексами $m,\;n$ направлено вдоль оси y и равно ${{y}_{{m,n}}} = A{{( - 1)}^{n}}$, где A – амплитуда волны. В результате симметрия исходной решетки понижается, и возникает кристаллическая структура, показанная на рис. 11. В качестве базиса решетки можно выбрать векторы ${\mathbf{A}}_{1}^{'} = (1,0)$, ${\mathbf{A}}_{2}^{'} = (0,\sqrt 3 )$. Элементарная ячейка Вигнера–Зейтца теперь представляет собой прямоугольник со сторонами ${{\Delta }_{x}} = 1$, ${{\Delta }_{y}} = \sqrt 3 $, в котором содержатся две частицы с противоположными направлениями смещений.

Рис. 11.

Структура, возникающая при переходе в область 3 на рис. 5. Кружками показаны исходные положения частиц, стрелками – векторы смещений. Штрихованные стрелки – базис новой решетки, прямоугольники – элементарные ячейки.

Заметим, что в отсутствие невзаимных сил (${{u}_{{1,1}}} = 0$) гибридизации продольных и вертикальных колебаний не происходит, и в этом случае может развиться обсуждавшаяся в литературе (например, [7]) изгибная неустойчивость двумерного кристалла. При этом общая картина дисперсионных кривых похожа на рис. 10, однако при потере устойчивости частицы смещаются в вертикальном направлении. Наличие невзаимных сил приводит к смене поляризации при потере устойчивости, и смещения частиц лежат в плоскости $xy$.

5. ОБЛАСТИ НЕУСТОЙЧИВОСТИ КРИСТАЛЛА

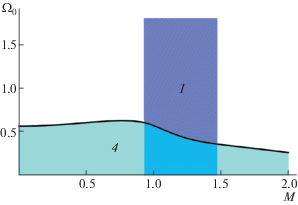
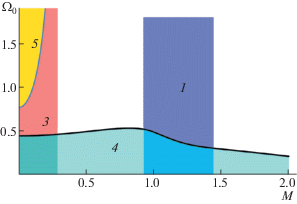
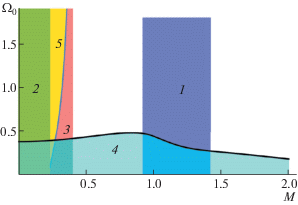
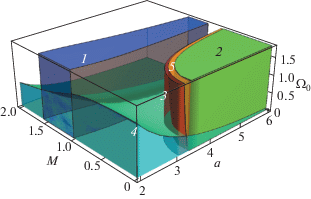
Различные области неустойчивости в переменных ${{\Omega }_{0}}$, M для некоторых характерных значений a показаны на рис. 12–14. Общее представление о расположении различных областей неустойчивости дает трехмерная диаграмма на рис. 15.

Рис. 12.

Области неустойчивости при $a = 3.0$.

Рис. 13.

Области неустойчивости при $a = 3.3$.

Рис. 14.

Области неустойчивости при $a = 3.5$.

Рис. 15.

Расположение областей неустойчивости в пространстве внешних параметров.

Кристалл устойчив в двух разделенных областях, одна из которых расположена в сверхзвуковой области ($M > 1$), а другая – преимущественно в дозвуковой ($M < 1$). Они отделяются друг от друга областью 1 на рис. 5, 12–14, на границах которой обращается в нуль фазовая скорость поперечных звуковых волн (8), и которая ассоциируется с плавлением кристалла.

В обеих областях устойчивости существует критическая частота внешнего потенциала ${{\Omega }_{{cr}}} = max({{\Omega }_{{cr,x}}},{{\Omega }_{{cr,y}}})$. Если ${{\Omega }_{0}} < {{\Omega }_{{cr}}}$ (область 4 на рис. 12–14), то развивается осцилляторная неустойчивость связанных волн. Для сверхзвукового потока с $M > 1$ неустойчивыми оказываются волны, распространяющиеся вдоль оси y, а при $M < 1$ – вдоль оси x.

В случае сверхзвукового потока ($M > 1$, $a{{u}_{{2,0}}} + 3{{u}_{{1,0}}} > 0$) и для достаточно большой частоты ${{\Omega }_{0}} > {{\Omega }_{{cr}}}$ кристалл устойчив при любых межчастичных расстояниях a, что обусловлено отталкивающим характером взаимодействия в этой области. При уменьшении скорости потока ($M < 1$, $a{{u}_{{2,0}}} + 3{{u}_{{1,0}}} > 0$) может возникнуть притяжение между частицами. Для достаточно малых межчастичных расстояний ($a < 3.141$) кристалл устойчив (см. рис. 12). По мере увеличения a при фиксированном значении M на границе области 3 на рис. 5, 13 становятся неустойчивыми продольные колебания на границе зоны Бриллюэна (рис. 10) и формируется структура, показанная на рис. 11. Одновременно возникает еще один канал неустойчивости (область 5 на рис. 13), указывающей на формирование сверхрешетки (см. рис. 9). Заметим, что границы областей 3 и 5 на рис. 13, 14 сливаются при ${{\Omega }_{0}} \gg 1$.

При дальнейшем увеличении межчастичного расстояния ($a > 3.38$) можно попасть в область 2 на рис. 5, 14, где неустойчивыми становятся продольные волны в вершинах зоны Бриллюэна (кривая 2 на рис. 6) и формируется структура, показанная на рис. 7.

6. ЗАКЛЮЧЕНИЕ

В статье определены границы устойчивости двумерного плазменного кристалла. Помимо известной неустойчивости связанных мод обнаружены четыре новых канала апериодических неустойчивостей, приводящих либо к плавлению кристалла, либо к формированию новых фаз с более сложной структурой.

Следует отметить, что фазы 2 и 5 на рис. 13–15 не имеют общей границы с областью устойчивости. Однако эти фазы отделены от устойчивой гексагональной решетки очень узкой полосой в пространстве внешних параметров, и при их адиабатическом изменении вполне достижимы. Кроме того, использованное в работе выражение для потенциала взаимодействия является приближенным и не учитывает, например, затухание ионно-звуковых волн, конечную температуру ионов и неоднородность плазмы в приэлектродной области. В то же время, детали поведения границ различных фаз весьма чувствительны к значениям силовых констант, поэтому при более точном описании могут измениться. Однако учет любых уточняющих факторов делает задачу слишком многопараметрической.

Выше обсуждались каналы потери устойчивости при распространении волн вдоль наиболее симметричных направлений. В принципе, это не исключает возможности появления экстремальных точек, не связанных с симметрией решетки. Однако в процессе длительных путешествий по пространству внешних параметров (рис. 15) какие-либо дополнительные неустойчивости обнаружены не были.