Физика плазмы, 2020, T. 46, № 4, стр. 351-357

1. ВВЕДЕНИЕ

Описание основных моделей солнечных вспышек можно найти в обзоре [1]. Согласно современным представлениям, наиболее вероятным источником энергии вспышек является магнитное пересоединение в нейтральном токовом слое. Во время вспышки первичная энергия поля превращается в тепловую энергию, происходит быстрый нагрев аркообразных магнитных трубок. Рассматривались и альтернативные подходы: концепция фракталов [2], “самоорганизованная критичность” [3].

Давно выделены вопросы, связанные с механизмом накопления энергии, ее высвобождением и вторичными эффектами [4]. Задача нестационарного нагрева магнитной трубки, основного элемента вспышки, в импульсной фазе неоднократно решалась путем численного расчета переходных процессов для стандартного гидродинамического отклика солнечной атмосферы [5–9]. Общая картина, в целом, хорошо описывает нагрев вспышечной области, однако имеются нерешенные вопросы, связанные, в частности, с наблюдениями локализованных высокотемпературных структур [10], уменьшением меры эмиссии [11].

В работе [11] по наблюдениям рентгеновского излучения было установлено, что на ранней стадии вспышки нагрев плазмы происходит в ускоренном режиме, возможно, в режиме с обострением. Это явилось основанием для разработки нового подхода к моделированию процесса тепловыделения во время вспышки.

Для описания процесса нагрева магнитной трубки мы использовали модель тепловых структур [12, 13], построенную в 1970–1980-х гг. и описывающую процесс термоядерного горения плазмы. Она основана на квазилинейном уравнении теплопроводности

где $q\left( T \right)\sim {{T}^{\beta }}$ – объемный источник нагрева, $\lambda \left( T \right)\sim {{T}^{\sigma }}$ – коэффициент теплопроводности. При определенных условиях уравнение (1) допускает решения в виде нестационарных диссипативных структур, локализованных в некоторой области пространства и существующих конечное время. Температура внутри области локализации растет в режиме с обострением. Типы получаемых структур зависят от соотношений между параметрами σ и β. Известно, что:

а) необходимым условием возникновения режима с обострением является степень нелинейности источника $\beta > 1$;

б) локализованные структуры возникают, когда источник “сильнее” теплопроводности, а именно, при $\beta \geqslant \sigma + 1$. При выполнении строгого неравенства полуширина структур сокращается с ростом температуры, что можно трактовать как явление “самофокусировки тепла” (LS-режим). При $\beta = \sigma + 1$ возникает структура типа “остановившийся фронт”(S-режим);

в) при $1 < \beta < \sigma + 1$ процесс также развивается в режиме с обострением, однако локализация отсутствует. В этом случае область горения расширяется с ростом температуры (HS-режим).

Нагрев плазмы на ранней стадии вспышки может быть описан уравнением вида (1) [14–17] с анизотропным коэффициентом теплопроводности и обобщенным объемным источником тепла, к которому сводится уравнение энергии для неподвижной вспышечной плазмы в магнитной трубке [18].

Необходимый для реализации режима с обострением объемный источник с $\beta > 1$ возникает, в частности, при механизме ускорения заряженных частиц Ферми 1 рода [19] в коллапсирующей магнитной ловушке, образованной сходящимися перетяжками магнитной трубки ($\beta = 1.5$ [20, 21]). Обобщенный источник также учитывает радиационное охлаждение, которое описывается известной полуэмпирической кусочно-степенной функцией лучистых потерь $L(T)$ [22].

Классическая теплопроводность плазмы с магнитным полем имеет анизотропный характер [18]: высокая вдоль магнитного поля, обусловленная столкновениями тепловых электронов с ионами (${{\sigma }_{{||}}} = 2.5$) и низкая поперек магнитного поля, обусловленная ионами (${{\sigma }_{ \bot }} = - 0.5$). Применение классического приближения обусловлено следующими факторами: длина свободного пробега электронов ${{l}_{{ei}}} = 1.8 \times {{10}^{4}}{{T}^{2}}{\text{/}}n$ при T = 7 MK, n = 10¹⁰ см^–3 составляет ~10³ км, что меньше размера наблюдаемых структур (~2 × 10³ км [10]) и допустимо считать плазму столкновительной. При T > 20 MK вспышечная плазма беcстолкновительная: длина свободного пробега электронов становится больше характерного размера структур. В этих условиях определяющую роль может играть плазменная турбулентность, столкновения электронов теперь определяются не частицами, а волнами, теплопроводность значительно снижается [23]. Однако для достаточного повышения частоты столкновений необходим слишком высокий уровень турбулентности (порядка тепловой энергии), вспышечная плазма беcстолкновительная.

Вопрос о структуризации магнитной трубки в поперечном сечении является новым для модели стандартного вспышечного отклика. Как следует из [24], установившиеся распределения температуры в поперечном сечении магнитной трубки могут иметь вид суперпозиции стоячих волн, масштаб которых (десятки метров) определяется коэффициентом поперечной теплопроводности. В работах [15, 16] численно показано, что при пониженной теплопроводности поперек магнитного поля (${{\sigma }_{ \bot }} = - 0.5$) происходит филаментация температурного поля в поперечном сечении трубки и формирование в режиме с обострением “горячих” микроструктур. Предполагается, что наблюдаемое на ранней стадии вспышки уменьшение интегральной меры эмиссии [11] может быть объяснено уменьшением фактора заполнения вспышечного объема горячей плазмой за счет сокращения поперечного размера структур, характерного для LS-режима с обострением.

В настоящей работе рассматривается полная двумерная модель, описывающая динамику нагрева плазмы в цилиндрически симметричной магнитной трубке (схематическое изображение типичной корональной петли приведено в [25]). В модели учитываются эмпирические степенные зависимости плотности плазмы и, соответственно, коэффициентов теплопроводности, источника нагрева и функции охлаждения от температуры. Параметры модели вычисляются в соответствии с реальными физическими данными.

2. ОПИСАНИЕ МОДЕЛИ

Уравнение энергии для неподвижной вспышечной плазмы в магнитной трубке с объемным источником нагрева и лучистым охлаждением может быть приведено к виду [4, 18]

где ε – внутренняя энергия, k_B – постоянная Больцмана; n – концентрация заряженных частиц в плазме; Q₀ обеспечивает баланс довспышечного нагрева и охлаждения, Q₁(T) – источник энергии вспышки. Считается, что плазма является квазинейтральной, n_i = n_e = n.

Учитывая, что $n\sim \sqrt {EM} $, где мера эмиссии EM определяется интегрированием по объему вспышечной области: $EM = \int {{{n}^{2}}} dV$, в случае однородного объема эмпирическая степенная связь концентрации и температуры в отдельных интервалах времени может быть взята из наблюдений в виде [11]

В качестве модельной будем рассматривать вспышку 05.07.2009 г. [11]. Для рассматриваемых условий $\chi \approx - 0.64$. В предельных случаях $\chi = 0$ (при постоянстве концентрации, $n = {\text{const}}$), и $\chi = - 1$ (при постоянстве газового давления, $nT = {\text{const}}$).

Лучистое охлаждение n²L(T) учитывается в приближении оптически прозрачной полностью ионизованной плазмы; L(T) – известная немонотонная функция с несколькими максимумами, обычно представляемая в кусочно-степенном виде [22]

Для фоновой (довспышечной) температуры плазмы вспышки 05.07.2009 г. [11] ${{T}_{0}} \approx 7$ MK, ${{n}_{0}} = {{10}^{{10}}}$ см^–3, $L({{T}_{0}}) \approx 7 \times {{10}^{{ - 23}}}$ эрг ⋅ см³ ⋅ с^–1, $n_{0}^{2}L({{T}_{0}}) \approx 7 \times {{10}^{{ - 3}}}$ эрг ⋅ см^–3 ⋅ с^–1, $\alpha \approx - 0.5$.

Как было сказано выше, быстрый нагрев в режиме с обострением может быть обусловлен объемным источником тепла, главный член разложения которого имеет степенной вид $Q(T)\sim {{T}^{\beta }}$ с показателем степени $\beta > 1$. В нашем случае $\beta = 1.5$ [20]. Нами подобрана следующая знакопеременная функция источника:

где ${{\beta }_{1}} + {{\beta }_{2}} = 1.5$.

Такая функция хорошо аппроксимирует наблюдаемые данные. Она имеет необходимую для развития режима с обострением асимптотику $Q(T) \cong {{q}_{0}}{{T}^{{1.5}}}$ и позволяет описать развитие вспышки на ненулевом температурном фоне при сверхкритических выделениях энергии. Возмущения фона ниже критического уровня затухают и релаксируют к фону. Значения параметров подобраны так, чтобы в отсутствие вспышки нагрев уравновешивал охлаждение, поддерживая температуру фона на уровне ${{T}_{0}}$.

Коэффициент теплопроводности плазмы поперек магнитного поля, обусловленной ионами, имеет вид [18]

где B – напряженность магнитного поля. Мы использовали оценочное значение $B = 100$ Гс, которое следует, в частности, из анализа радиоданных. С учетом (3)

Вдоль магнитного поля коэффициент теплопроводности плазмы обусловлен переносом тепла электронами [18]

где Λ – кулоновский логарифм; для рассматриваемого диапазона температур $\Lambda \approx 15$.

Размерности величин: [n] = cм^–3, [Т] = К, [B] = Гc.

Задача Неймана для уравнения (2) рассматривается в цилиндрической трубке длиной L и радиусом R. Размер трубки выбирается достаточно большим (больше размера формирующихся структур), так чтобы граничные условия не оказывали влияния на решение.

Уравнение (2) в цилиндрической системе координат для радиально-симметричного случая после ряда преобразований приводится к виду (см. Приложение)

где $\tilde {U}$ – нормированная температура, безразмерная переменная. До начала вспышки, когда температура равна фоновой, $\tilde {U}$ = 1. $\tilde {q}(\tilde {U})$ – степенное выражение со старшей степенью в разложении, равной ${{\tilde {U}}^{{\tilde {\beta }}}}$. Таким образом, уравнение (2) сводится к виду (1) с модифицированными показателями степеней

Вспышка в модели инициируется путем задания начального возмущения фона в небольшой области в центре трубки. При полученных значениях параметров (8) численно находятся решения задачи в зависимости от размера и формы начального возмущения.

3. РЕЗУЛЬТАТЫ РАСЧЕТОВ

Для численного решения поставленной двумерной задачи для уравнения (7) в цилиндрической трубке применялась разностная схема переменных направлений. Использовалась равномерная сетка по радиусу и по оси z с шагами ${{h}_{r}} = 0.01$ и ${{h}_{z}} = 0.5$, соответственно, и переменный шаг по времени. Полученные значения функции $\tilde {U}$ пересчитывались в значения исходной функции по формуле $T(t,r,z) = {{T}_{0}}\tilde {U}{{(t,r,z)}^{{{{{(1 + \chi )}}^{{ - 1}}}}}}$.

В рассматриваемом случае параметры связаны соотношениями

Выполнение условия $\tilde {\beta } > 1$ обеспечивает существование решений, развивающихся в режиме с обострением. При этом первое условие в (9) соответствует LS-режиму, при котором имеет место эффективная локализация области интенсивного горения и формирование нестационарных структур с сокращающейся полушириной. Это означает, что по радиальному направлению формирующаяся тепловая структура будет сжиматься с ростом температуры. Второе условие в (9), в свою очередь, соответствует HS-режиму, при котором процесс горения не локализован в пространстве, а эффективная полуширина структур растет. Это означает, что с ростом температуры вдоль оси цилиндра происходит расширение тепловой структуры.

Из наблюдений [10] следует, что при толщине магнитной трубки ~10³ км линейный размер горячих (>10 MK) вспышечных ядер составляет ~2 × 10³ км. В расчетах рассматривалась область протяженности $L = 4 \times {{10}^{3}}$ км в вершине трубки. Это характерный “масштаб теплопроводности” вдоль магнитного поля. В поперечном сечении рассматривался цилиндр радиуса $R = 1\,$ км при характерном “масштабе” теплопроводности ~100 м.

На рисунке приведены результаты расчетов, выполненных для значений параметров ${{\beta }_{1}} = {{\beta }_{2}} = $ $ = 0.75$, $\tilde {T}_{1}^{{{{\beta }_{1}}}} = 1.0006$, $\tilde {T}_{2}^{{{{\beta }_{2}}}} = 1.001$. На рис. 1а изображено температурное поле $T(t,0,z)$ в сечении трубки при $r = 0$ вдоль оси z. Горение среды было инициировано заданием сверхкритического начального возмущения вида (П7), где $\Delta r = 0.3$ км, $\Delta z = 75$ км, $\Delta \tilde {T} = 1$. Минимальное значение температуры (фон) отображается черным цветом, максимальное – белым, промежуточные значения – градацией серого цвета. Результаты приведены для трех последовательных моментов времени: ${{t}_{1}} = 0$, ${{t}_{2}} = 7.975 \times {{10}^{{ - 2}}}$ с, ${{t}_{3}} = 8.08 \times {{10}^{{ - 2}}}$ с. На рис. 1б, в показаны профили температуры по радиальному направлению и вдоль оси цилиндра соответственно для тех же моментов времени.

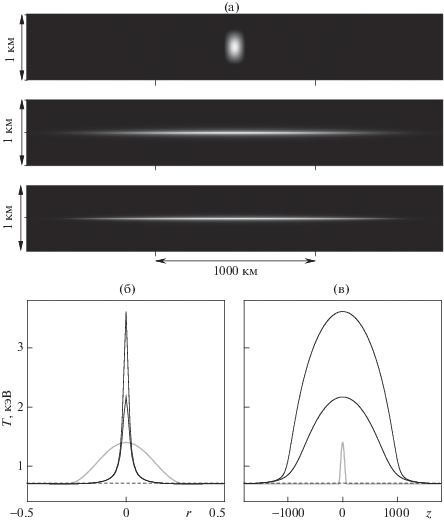
Таким образом, выполнение соотношений (9) приводит к реализации в данной задаче так называемого LS–HS-режима. В пространстве формируется область интенсивного горения, внутри которой происходит взрывной рост температуры. При этом область сжимается с течением времени по радиальному направлению и расширяется вдоль оси цилиндра. Тепловая структура представляет собой нить, вытянутую вдоль магнитного поля, температура которой быстро растет по сравнению с окружающим фоном. С течением времени нить “схлопывается” по толщине и вытягивается вдоль магнитной трубки. Непосредственно наблюдать отдельные “самофокусирующиеся” по толщине нити не представляется возможным из-за их чрезвычайно малых размеров (r < 100 м), однако наличие множества подобных нитей с сокращающейся толщиной в магнитной трубке приводит к упомянутому уменьшению фактора заполнения вспышечного объема горячей плазмой и может проявиться, как предполагается, в наблюдаемом на ранней фазе вспышки уменьшении интегральной меры эмиссии [11].

4. ЗАКЛЮЧЕНИЕ

Проведены исследования начальной стадии вспышечного нагрева в коллапсирующей магнитной ловушке, образованной сходящимися перетяжками трубки. Возникающий объемный источник обеспечивает рост температуры плазмы в режиме с обострением.

Проблема формирования тепловых структур в магнитной трубке во время вспышечного нагрева решается в рамках уравнения энергии для анизотропной плазмы с объемным источником нагрева, классической теплопроводностью и лучистым охлаждением. Показано, что оно может быть сведено к нелинейному уравнению теплопроводности со степенными зависимостями источника и коэффициентов диффузии от температуры. На основе этого уравнения построена математическая модель, которая описывает нагрев плазмы как процесс формирования на ненулевом температурном фоне вспышечных структур, развивающихся в режиме с обострением.

Построено двумерное решение, описывающее формирование вспышечной структуры в виде “схлопывающейся” тонкой горячей нити, погруженной в более холодную фоновую плазму. Решение такого вида позволяет объяснить наблюдаемый на ранней стадии вспышки эффект уменьшения меры эмиссии как результат уменьшения общего вспышечного объема за счет сжатия тепловых структур в поперечном направлении.

Полученные результаты представляют интерес для изучения режимов вспышечного нагрева, классификация которых позволяет по наблюдениям оценить относительную роль нелинейного источника и теплопроводности. Модель нагрева в диффузионном приближении является основой для построения полной модели вспышечного гидродинамического отклика солнечной атмосферы.

Дальнейшее обобщение может быть связано с расчетом нагрева, сопровождаемого формированием не только отдельного элемента – “горячей нити”, но и микроструктуры всего поперечного сечения магнитной трубки, состоящей из множества нитей.

Работа выполнена при поддержке РФФИ, проекты № 18-01-00436; 17-02-00308.