Физика плазмы, 2020, T. 46, № 6, стр. 551-563

1. ВВЕДЕНИЕ

В работах по исследованию антивещества сообщалось о наличии электрон-позитронной (e–p) плазмы в различных астрофизических средах, таких как атмосфера Солнца, верхние слои атмосферы Земли (область ионосферы), магнитосфера пульсаров и черные дыры, а также она наблюдалась в экспериментах с взрывами, происходящими под действием излучения лазеров высокой мощности, и других экспериментах [1–5]. Позднее, при исследовании астрофизических сред в уникальных условиях, существование ионов в электрон-позитронной (e–p) плазме было подтверждено данными спутника ASCA (AdvancedSatelliteforCosmologyandAstrophysics) [6]. Что касается оценки масс, то позитрон обладает гораздо меньшей массой по сравнению с массой тяжелых ионов. В связи с этим, присутствие позитронов в электрон-ионной (e–i) плазме приводит к результатам, не описываемым в рамках пространственно-временных скейлингов (e–i) плазмы [1].

За последние несколько десятилетий были проведены многочисленные исследования процессов формирования ионно-звуковых уединенных волн, ударных волн, двойных слоев и суперблуждающих волн в различных видах плазмы: релятивистской, нерелятивистской и квантовой e‒p–i [7–11]. Кроме того, в системах со сверхвысокой энергией для исследования структур с произвольной (большой) амплитудой в e–p–i плазме часто используют потенциал Сагдеева [12–14] и в рамках этого подхода находят область параметров, подходящую для формирования уединенных волн сжатия и разрежения. В работе [12] с использованием потенциала Сагдеева исследовалось формирование ионно-звуковых уединенных волн в нерелятивистской e–p–i плазме. Авторы установили, что волновые амплитуды ионно-звуковых уединенных волн уменьшаются из-за присутствия в системе значительного количества горячих позитронов. Однако если e–p–i плазма является релятивистской или слаборелятивистской, то, решая уравнение КдВ, можно получить решения в виде уединенных волн с малой амплитудой [9, 15–17]. В работе [9] с использованием уравнения КдВ изучались ионно-звуковые уединенные волны, формирующиеся в слаборелятивистской e–p–i плазме. Сообщалось об изменениях амплитуды и ширины уединенной волны, возникших из-за релятивистского эффекта. Кроме этого, в работе [18] с использованием кинетической теории исследовалось влияние позитронного и ионного пучков, распространяющихся в e–i и e–p плазмах. Была обнаружена дестабилизирующая тенденция к возрастанию электростатических возмущений в системе, которая возникает при увеличении плотности позитронов в плазме. Инжекция позитронного пучка в равновесную плазму является существенной частью исследования, поскольку благодаря инжекции пучка в системе появляется избыточная свободная энергия, которая делает плазму нестабильной.

Очевидное присутствие пыли в лабораторных и космических средах расширило область исследований ученых, занимающихся пылевой плазмой [19–21]. Исследования нелинейных пылевых ионно-звуковых (ПИЗ) волн продолжаются до сих пор. Например, присутствие частиц пыли в плазме рассматривается как некоторый массивный фон, или же процесс зарядки частиц пыли включается в теорию ограниченного орбитального движения (ООД) [22–25]. В работе [22] для различных видов пылевых частиц исследуются флуктуации заряда пылевых частиц, которые оказывают влияние на особенности нелинейного распространения ПИЗ волн в плазме. В работе [26] исследованы отчетливо проявляющиеся нелинейные особенности распространения уединенной ПИЗ волны малой амплитуды с учетом динамики флуктуаций заряда зерен пыли. В работе наблюдалось изменение фазовой скорости ПИЗ волны, возникающее из-за изменений заряда пылевого зерна. Таким образом, вплоть до настоящего времени проводятся многочисленные исследования четырехкомпонентной плазмы, состоящей из электронов, позитронов, ионов и частиц пыли – (e–p–i–d) плазмы [27–30]. Такой состав обычно имеет плазма в магнитосферах Земли и Юпитера, ионосферах Земли и Марса, плазма, образовавшаяся при взрыве сверхновых, а также в лабораторных условиях при взрывах вещества под действием мощных лазерных пучков. К настоящему времени, уже опубликованы результаты исследований e–p–i–d плазмы в рамках нерелятивистского подхода. В работе [31] с использованием модифицированного уравнения КдВ разработана модель e–p–i–d плазмы, в состав которой входят надтепловые электроны и позитроны. Было установлено, что в таких плазменных условиях в определенных областях расчетной области существуют как решения в виде уединенных волн, так и в виде двойных слоев, причем решения в виде уединенных волн существуют в более широких областях параметров, чем решения в виде двойных слоев. Кроме того, авторы утверждают, что в такой плазме наличие пылевой, позитронной, ионной и электронной компонент с различными температурами оказывает заметное влияние на амплитуды и ширины формирующихся нелинейных волновых структур. В работе [32] с использованием псевдопотенциала Сагдеева было показано, что в e–p–i–d плазме могут распространяться ПИЗ уединенные волны сжатия и разрежения большой амплитуды, а также формироваться двойные слои с отрицательным потенциалом. Наблюдалось увеличение амплитуды волны, возникающее в результате возрастания концентрации позитронов в плазме. Недавно в работе [33] сообщалось об исследованиях e–i плазмы в присутствии отрицательно заряженных частиц пыли. Авторы задавали начальные скорости потоков ионов и электронов, и наблюдали образование в рассматриваемой плазме ПИЗ уединенных волн сжатия и разрежения.

В работе [34] исследовалось влияние ионного пучка большой энергии на распространение ионно-звуковых уединенных волн в лабораторной пылевой плазме, содержащей электроны, положительные ионы и отрицательно заряженные пылевые зерна. Было установлено, что существует критическая скорость пучка, при превышении которой амплитуда быстрой уединенной волны начинает уменьшаться, а амплитуда медленной волны разрежения нарастает. Кроме того, был проведен эксперимент, показавший, что рост плотности пылевых частиц вызывает заметные изменения фазовой скорости медленной волны. В работе [35] также сообщалось о существовании двух критических значений отношения скорости пучка к ионно-звуковой скорости, вне интервала между которыми формирование ионно-звуковой уединенной волны малой, но конечной амплитуды становилось невозможным. В этой работе плазма состояла из больцмановских электронов, положительных ионов и неподвижных частиц пыли. В работе [36] с использованием нерелятивистской модели исследовалось распространение ионно-звуковой уединенной волны в плазме, содержащей холодный позитронный пучок, электроны с вихревым распределением и подвижные ионы. Большинство из упомянутых выше работ посвящено динамическому рассмотрению нерелятивистской плазмы. Однако, когда мы говорим о верхних слоях атмосферы Земли (области ионосферы), радиационных поясах Ван Аллена, солнечной короне и космической плазме и рассматриваем инжектирование высокоэнергичного пучка позитронов, электронов или ионов, то предпочтительным является использование релятивистской модели [37–39]. В недавней работе [40] рассматривалось распространение гиперзвуковых солитонов/уединенных волн в вырожденной магнитоплазме в присутствии ионного пучка. Было установлено, что при выбранных параметрах магнитного квантования и вырождения плазмы происходит генерация гиперзвуковой волны, а также распространение фоновых ионно-звуковых и медленных волн. В гиперзвуковом режиме как нелинейность, так и дисперсия распространяющихся волн оказались высокими.

Однако данные космических наблюдений и многочисленных исследований астрофизической плазмы дают основание полагать, что состояние термодинамического равновесия плазмы является неустойчивым из-за разницы плотностей ионов и электронов, а также их температур [41–44]. Кроме того, в условиях, когда на плазму оказывает влияние распространяющийся в ней пучок, трудно ожидать, что плазма будет находиться в термодинамическом равновесии, подчиняясь максвелловскому распределению. Таким образом, более реалистичной является модель плазмы с немаксвелловской функцией распределения. Такая плазма с немаксвелловской функцией распределения была обнаружена в различных областях магнитосфер различных планет, а также в солнечном ветре [45–47]. Каппа-распределение, неэкстенсивная q-функция распределения и функция распределения Кеирнса сильно отличаются от максвелловского распределения и прекрасно подходят для описания нетепловых состояний плазмы. В ряде работ уже проведено рассмотрение нетепловых и надтепловых электронов в таких плазменных средах [48–50]. Кроме того, при исследовании распространения ПИЗ уединенных волн малой амплитуды в условиях космической плазмы, часто используется редуцированная теория возмущений, в результате чего, с использованием модели слаборелятивистской плазмы, выводится нелинейное волновое уравнение КдВ [9, 51, 52].

В этой работе мы продолжили теоретическое исследование четырехкомпонентной релятивистской плазмы, состоящей из подвижных положительно заряженных ионов, позитронного пучка, фоновых отрицательно заряженных частиц пыли и нетепловых электронов. Было обнаружено, что позитронный пучок оказывает влияние на движение плазмы, приводя к ее неустойчивости. Развитие неустойчивостей оказывает большое влияние на распространение ПИЗ уединенных волн и при определенных плазменных условиях может привести к их затуханию и даже распаду. Насколько нам известно, до сих пор не исследовано распространение ионно-звуковых уединенных волн в таких плазменных условиях, когда учитываются релятивистские эффекты при описании положительных ионов и позитронного пучка и считается, что пылевая плазма характеризуется нетепловым распределением плотности электронов.

2. ОСНОВНЫЕ УРАВНЕНИЯ

Для изучения нелинейного распространения ПИЗ уединенных волн в релятивистской e–p–i пылевой плазме рассмотрим бесстолкновительную незамагниченную плазму, состоящую из подвижных положительных ионов, позитронного пучка, чрезвычайно массивных отрицательно заряженных зерен пыли и нетепловых электронов. Поскольку период волны сопоставим с периодом зарядки частиц пыли в пылевой плазме, флуктуации заряда зерен пыли являются важным фактором, влияющим на распространение ПИЗ волны в плазме. Основные математические уравнения, описывающие поведение системы (уравнение непрерывности и уравнения для импульса и давления), выглядят следующим образом:

Плотность нетепловых электронов ${{n}_{e}}$ может быть записана в виде

где ${{n}_{j}}$, ${{m}_{j}}$, ${{v}_{j}}$, ${{q}_{j}}$, ${{p}_{j}}$ $\left( {j = i,b} \right)$ – плотность, масса, скорость, заряд и давление положительных ионов; ${{z}_{d}}$ – число электронов, находящихся на пылевом зерне, ψ – скалярный электростатический потенциал; ${{\gamma }_{b}} = {{\left( {1 - v_{b}^{2}{\text{/}}{{c}^{2}}} \right)}^{{ - 1/2}}}$ – релятивистский фактор; ${{n}_{d}}$ – плотность пыли; и ${{\alpha }_{e}} = $ $ = 4{{\beta }_{e}}{\text{/}}\left( {1 + 3{{\beta }_{e}}} \right)$ – параметр, характеризующий нетепловые электроны. Известно, что при ${{\alpha }_{e}} = 0$ (т.е. ${{\beta }_{e}} = 0$) приведенная выше функция распределения плотности нетепловых электронов переходит в распределение Больцмана. Однако образование нелинейных структур (уединенных волн и двойных слоев) возможно при $0 \leqslant {{\alpha }_{e}} \leqslant \infty $, когда параметр ${{\beta }_{e}}$ находится в пределах ограниченной области $0 \leqslant {{\beta }_{e}} \leqslant 4{\text{/}}3$ [44].

Нормализованная система основных уравнений (1)–(5) выглядит следующим образом:

где ${{V}_{i}} + V_{i}^{3}{\text{/}}(2c_{1}^{2})$ и ${{\bar {V}}_{b}} = {{V}_{b}} + V_{b}^{3}{\text{/}}(2c_{1}^{2}{\text{)}}$. Здесь ${{N}_{j}}$, ${{V}_{j}}$, ${{P}_{j}}$ ($j = i,b$) обозначают плотность, скорость жидкости и давление соответственно. Величина ${{N}_{j}}$ нормирована на равновесное значение n_j0, величина ${{V}_{j}}$ на ${{c}_{s}} = {{({{\kappa }_{b}}{{T}_{e}}{\text{/}}{{m}_{i}})}^{{1/2}}}$ и величина ${{P}_{j}}$ на ${{n}_{{j0}}}{{\kappa }_{b}}{{T}_{j}}$, где индекс j принимает значения $j = i,b$ для положительных ионов и позитронов; ${{\kappa }_{b}}$– постоянная Больцмана и ${{c}_{1}} = c{\text{/}}{{c}_{s}}$, где c – скорость света. Волновой потенциал φ нормирован на ${{\kappa }_{b}}{{T}_{e}}\psi {\text{/}}e$, временная переменная T – на $\omega _{{pi}}^{{ - 1}} = {{({{m}_{i}}{\text{/}}4\pi {{n}_{0}}{{e}^{2}})}^{{1/2}}}$, пространственная переменная X – на ${{c}_{s}}{\text{/}}{{\omega }_{{pi}}}$ и ${{Z}_{d}}$ – на ${{Z}_{{d0}}}$. Здесь мы предположили, что ${{Z}_{{d0}}}$ не является постоянной величиной, а меняется при изменении масштабов пространства и времени. Напомним, что ${{\beta }_{1}} = {{m}_{e}}{\text{/}}{{m}_{i}}$ (${{\beta }_{2}} = {{m}_{b}}{\text{/}}{{m}_{i}}$) – отношение масс электрона и иона (позитрона и иона); ${{\mu }_{e}} = {{n}_{{e0}}}{\text{/}}{{n}_{{i0}}}$, ${{\mu }_{b}} = {{n}_{{b0}}}{\text{/}}{{n}_{{i0}}}$ и ${{\mu }_{d}} = {{Z}_{{d0}}}{{n}_{{d0}}}{\text{/}}{{n}_{{i0}}}$ – это отношения концентраций электронов, позитронов и пылевых частиц к концентрации ионов ${{n}_{{i0}}}$. Здесь ${{\sigma }_{i}} = {{T}_{i}}{\text{/}}{{T}_{e}}$, ${{\sigma }_{b}} = {{T}_{b}}{\text{/}}{{T}_{e}}$ – отношения температур, где ${{T}_{i}}$, ${{T}_{e}}$ и ${{T}_{b}}$ представляют собой температуры положительных ионов, электронов и позитронного пучка соответственно.

Общее условие нейтральности заряда в состоянии равновесия выглядит следующим образом: $1 + {{\mu }_{b}} - {{\mu }_{d}} = {{\mu }_{e}}$. С учетом флуктуаций пылевого заряда, уравнение для нормализованного пылевого заряда может быть записано в виде

где ${{I}_{e}}$, ${{I}_{i}}$ и ${{I}_{p}}$ – нормированные токи нетепловых электронов, тонов и позитронов, определяемые следующими выражениями: где $\theta = {{Z}_{{d0}}}{{e}^{2}}{\text{/}}({{r}_{d}}{{\kappa }_{b}}{{T}_{e}})$ и ${{\phi }_{d}} = - {{Z}_{d}}e{\text{/}}{{r}_{d}}$. Здесь считается, что равновесный заряд пылевого зерна равен ${{Z}_{{d0}}} = {{10}^{2}}$ и радиус пылевых частиц равен ${{r}_{d}} = 7$ мкм.

Уравнение (12) можно упростить и переписать в виде

где $a = {{n}_{{e0}}}r_{d}^{2}{{\lambda }_{D}}\sqrt {8\pi } {\text{/}}({{Z}_{{d0}}}\sqrt {{{\beta }_{1}}} )$, $b = {{n}_{{i0}}}r_{d}^{2}{{\lambda }_{D}}\sqrt {8\pi } {\text{/}}{{Z}_{{d0}}}$ и $c = {{n}_{{b0}}}r_{d}^{2}{{\lambda }_{D}}\sqrt {8\pi } {\text{/}}({{Z}_{{d0}}}\sqrt {{{\beta }_{2}}} )$ – постоянные члены, в которых ${{\lambda }_{D}} = \sqrt {{{\kappa }_{b}}{{T}_{e}}~{\text{/}}4\pi {{n}_{{i0}}}{{e}^{2}}} $.

3. ВЫВОД УРАВНЕНИЯ КДВ

Для изучения характеристик распространения ПИЗ уединенной волны малой амплитуды в настоящей модели была использована редуцированная теория возмущений, где использованы две независимые растянутые переменные: пространственная ξ и временная τ, которые могут быть записаны следующим образом:

где ε – малая ненулевая постоянная, характеризующая слабость дисперсии, также характеризует и возмущение среды, λ – число Маха (фазовая скорость) волны, нормированное на ионно-звуковую скорость ${{c}_{s}}$.

Зависимые переменные ${{N}_{j}}$, ${{V}_{j}}$, ${{P}_{j}}$ $\left( {j = i,b} \right)$, ψ и ${{Z}_{d}}$ могут быть разложены в ряды по степеням ξ следующим образом:

Подставляя уравнения (17)–(22) в систему нормализованных уравнений (6)–(11) и приравнивая коэффициенты при членах нижнего порядка по $\varepsilon $, получаем

а из уравнения (16) получаем

Используя уравнения (23) и (26), получаем выражение для фазовой скорости λ пылевой ионно-звуковой уединенной волны в виде

где и

Из уравнения (16) с использованием членов более высокого порядка по ε получим выражения

Приравнивая коэффициенты при членах следующего порядка по ε в уравнении Пуассона (11) и дифференцируя по ξ, получаем

Приравнивая коэффициенты при членах следующего порядка по $\varepsilon $ в уравнениях (6)–(11), (16), используя выражения $\partial N_{i}^{{\left( 2 \right)}}{\text{/}}\partial \xi $, $\partial N_{b}^{{\left( 2 \right)}}{\text{/}}\partial \xi $, $\partial Z_{d}^{{\left( 2 \right)}}{\text{/}}\partial \xi $ и исключая члены, соответствующие возмущениям второго порядка $N_{j}^{{\left( 2 \right)}}$, $V_{j}^{{\left( 2 \right)}}$, $P_{j}^{{\left( 2 \right)}}$ $\left( {j = i,b} \right)$ и ${{\varphi }^{2}}$, в итоге из уравнения (16) получаем уравнение КдВ, которое выглядит следующим образом:

где и где ${{V}_{{j0}}} = {{v}_{j}}{\text{/}}{{c}_{s}}$, и $j = i,b$ соответствует положительным ионам и позитронам пучка. Уравнение (30) представляет собой уравнение КдВ, описывающее распространение ПИЗ уединенных волн малой амплитуды в релятивистской e–p–i–d плазме. Уравнение (30) дает общее представление о том, что распространение уединенной волны зависит и от нелинейности среды (A), и от ее коэффициента дисперсии (B), который является функцией всех параметров плазмы, что видно из уравнений (31) и (32).

Теперь, используя граничные условия $\varphi \to 0$, $\partial \varphi {\text{/}}\partial \xi \to 0$ и ${{\partial }^{2}}\varphi {\text{/}}\partial {{\xi }^{2}} \to 0$ при $\xi \to \pm \infty $, получаем стационарное решение уравнения КдВ в виде

где ${{\psi }_{m}}$ и Δ – амплитуда и ширина уединенной волны, которые определяются выражениями

Здесь U – постоянная скорость уединенной волны. Для ${{\kappa }_{b}}{{T}_{e}} = 1.5~$ эВ, ${{n}_{{d0}}} = {{10}^{2}}$ см^–3, ${{z}_{{d0}}} = {{10}^{2}}$, и ${{r}_{d}} = 7~$ мкм, получаем следующие значения θ и ${{\lambda }_{D}}$: $\theta = 0.0137$ и ${{\lambda }_{D}} = 6.4345~$ см.

4. РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Число Маха $\lambda $ ионно-акустических уединенных волн в пылевой плазме зависит от различных параметров плазмы, а именно, отношений температур (${{\sigma }_{i}}$,$~{{\sigma }_{b}}$), релятивистских факторов (${{\gamma }_{{ir}}}$,$~{{\gamma }_{{br}}}$), отношений концентраций $({{\mu }_{{b,}}}~~{{\mu }_{d}})$, параметра нетепловых электронов ${{\alpha }_{e}}$, флуктуаций заряда зерен пыли $~{{Z}_{{d0}}}$ и радиуса пылевых зерен $~{{r}_{d}}$. Поэтому при анализе распространения нелинейной волны (уединенной волны) в пылевой плазме выбирались следующие диапазоны изменения этих параметров: $~{{\sigma }_{i}} = 0.1{\kern 1pt} - {\kern 1pt} 0.4$, ${{\sigma }_{b}} = 1.5{\kern 1pt} - {\kern 1pt} 6$, ${{\gamma }_{{ir}}} = $ 0.001–0.5, ${{\gamma }_{{br}}} = 0.1{\kern 1pt} - {\kern 1pt} 0.8$, ${{\mu }_{b}} = 0.05{\kern 1pt} - {\kern 1pt} 0.3$, ${{\mu }_{d}} = 0.1{\kern 1pt} - {\kern 1pt} 0.5$, и ${{\alpha }_{e}} = 0.1{\kern 1pt} - {\kern 1pt} 0.5$. Эти диапазоны изменения параметров соответствуют параметрам верхних слоев атмосферы Земли и параметрам космической плазмы. Из-за наличия большого количества положительных ионов водорода в большинстве видов космической плазмы и в верхних слоях атмосферы Земли, именно такая плазменная система будет предметом дальнейших исследований, представленных в этой статье. Процесс зарядки пылевого зерна будет рассмотрен в рамках теории ограниченного орбитального движения (ООД) [53]. Кроме того, предполагается, что в данной плазменной системе позитронный пучок, приходящий из космоса с начальной скоростью ${{V}_{{b0}}}\left( { = 5{{C}_{s}}} \right)$ и описываемый в терминах изменяющегося релятивистского фактора ${{\gamma }_{{br}}}$, оказывает влияние на распространение в ней ПИЗ уединенных волн. Также важно упомянуть, что при выбранных параметрах плазмы, в основном, благодаря учету скоростей позитронного пучка ${{V}_{{b0}}}$ (в терминах ${{\gamma }_{{br}}}$) и потока положительных ионов ${{V}_{{i0}}}$ (в терминах ${{\gamma }_{{ir}}}$) в плазме, нормализованные числа Маха оказались соответствующими практически гиперзвуковому режиму.

На рис. 1 показаны результаты компьютерного моделирования нормализованной фазовой скорости (числа Маха) λ и амплитуды волнового потенциала ${{\varphi }_{m}}$ в зависимости от величины γ_br, а также зависимости потенциала уединенной волны φ от пространственной координаты ξ, демонстрирующие переход от волн сжатия к волнам разрежения.

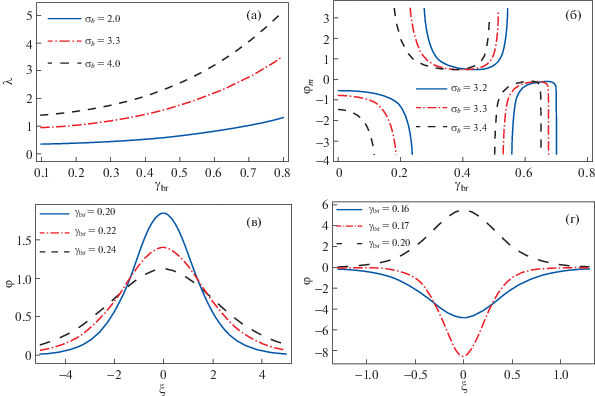
Изменение числа Маха λ при возрастании релятивистского фактора позитронного пучка ${{\gamma }_{{br}}}$ для различных значений ${{\sigma }_{b}}$ показано на рис. 1а. Видно, что для всех значений ${{\sigma }_{b}}$ с ростом ${{\gamma }_{{br}}}$ число Маха также возрастает. При ${{\sigma }_{b}} = 2$ с ростом ${{\gamma }_{{br}}}$ число Маха меняется в пределах, соответствующих сначала дозвуковому режиму, а потом околозвуковому режиму (т.е., λ меняется от 0.3 до 1). При больших значениях ${{\sigma }_{b}}$ (3.3 или 4) с ростом ${{\gamma }_{{br}}}$ число Маха уже меняется в пределах, соответствующих сначала околозвуковому режиму, а потом сверхзвуковому режиму (т.е., λ меняется от 1 до 5). Исходя из этих результатов, можно утверждать, что вследствие релятивистского эффекта позитронного пучка, распространяющегося в нетепловой пылевой плазме с выбранными параметрами, возрастание таких параметров, как ${{\gamma }_{{br}}}$ и ${{\sigma }_{b}}$ приводит к значительным изменениям числа Маха, вплоть до значений, соответствующих сверхзвуковому режиму.

Теперь, чтобы исследовать распространение ПИЗ уединенных волн в плазме, рассмотрим область чисел Маха от 1 до 3, когда сверхзвуковой режим еще не достигается. На рис. 1б для различных значений ${{\sigma }_{b}}$ показано изменение амплитуды потенциала ${{\varphi }_{m}}$ при изменении релятивистского фактора в диапазоне $~{{\gamma }_{{br}}} = 0.1{\kern 1pt} - {\kern 1pt} 0.8$. Видно, что для всех значений (${{\sigma }_{b}} = 3.2$, 3.3, 3.4) с ростом ${{\gamma }_{{br}}}$ амплитуда ${{\varphi }_{m}}$ сначала возрастает по величине (будучи отрицательной). Это продолжается до тех пор, пока ${{\gamma }_{{br}}}$ не достигнет определенной величины (0.22, 0.16 и 0.08). Таким образом, в этих условиях в плазме могут распространяться ПИЗ уединенные волны отрицательной полярности (волны разрежения). Затем вследствие наличия сингулярности в системе происходит возрастание величины ${{\varphi }_{m}}$ до бесконечности. Это связано с тем, что при этом значении ${{\gamma }_{{br}}}$ нелинейный коэффициент A обращается в ноль. Назовем это значение критической точкой $~{{\gamma }_{{bc}}}$. При значениях ${{\gamma }_{{br}}}$, превышающих критическое значение, полярность амплитуды волны меняется, и происходит формирование ПИЗ уединенные волны положительной полярности (волны сжатия). Как показано на рис. 1б, сначала амплитуда ${{\varphi }_{m}}$ уединенной волны положительной полярности уменьшается, пока релятивистский фактор не возрастет до величины $~{{\gamma }_{{br}}} = 0.4$. При дальнейшем возрастании ${{\gamma }_{{br}}}$ амплитуда вновь начинает возрастать. Таким образом, при выбранных параметрах в этой системе образуются две критические точки$~{{\gamma }_{{bc1}}}$ и $~{{\gamma }_{{bc2}}}$, в которых происходит смена полярности волны, что приводит к образованию ПИЗ уединенных волн как положительной, так и отрицательной полярности.

Основываясь на рис. 1б, рассмотрим формирование уединенных волн при различных значениях ${{\gamma }_{{br}}}$. На рис. 1в показаны потенциалы уединенной волны φ как функции пространственной переменной $\xi $, рассчитанные для ${{\sigma }_{b}} = 3.3$. Видно, что в области $~{{\gamma }_{{bc1}}} < {{\gamma }_{{br}}} < {{\gamma }_{{bc2}}}$ существует идеально сбалансированная потенциальная структура, приводящая к формированию положительной ПИЗ уединенной волны (волны сжатия). Также видно, что в области $~{{\gamma }_{{bc1}}} < {{\gamma }_{{br}}} < 0.4$ амплитуда потенциала уединенной волны сжатия φ уменьшается с ростом величины ${{\gamma }_{{br}}}$. С физической точки зрения это можно сформулировать так, что при фиксированных значениях отношений температур $({{\sigma }_{i}},{{\sigma }_{b}})$ и концентраций $({{\mu }_{{b,}}}~{{\mu }_{d}})$, увеличение ${{\gamma }_{{br}}}$ приводит к увеличению нелинейности системы, и возникает вероятность поступления большего количества энергии в волну из соседних волн. Поэтому при увеличении ${{\gamma }_{{br}}}$ можно наблюдать уменьшение амплитуды уединенной волны. Кроме того, с ростом ${{\gamma }_{{br}}}$ происходит уширение уединенной волны сжатия. На рис. 1г показано, как с ростом ${{\gamma }_{{br}}}$ происходит изменение структуры волнового потенциала: уединенная волна отрицательной полярности переходит в уединенную волну положительной полярности (расчеты выполнены для ${{\sigma }_{b}} = 3.3$).

На рис. 2 показаны результаты компьютерного моделирования зависимостей амплитуды волнового потенциала ${{\varphi }_{m}}$ от величины отношения температур ${{\sigma }_{b}} = {{{{T}_{b}}} \mathord{\left/ {\vphantom {{{{T}_{b}}} {{{T}_{e}}}}} \right. \kern-0em} {{{T}_{e}}}}$ (для различных значений нормализованной фазовой скорости λ) и зависимостей потенциала уединенной волны φ от пространственной переменной ξ. Кроме того, представлены зависимости потенциала уединенной волны φ от пространственной координаты ξ, демонстрирующие переход от волн сжатия к волнам разрежения.

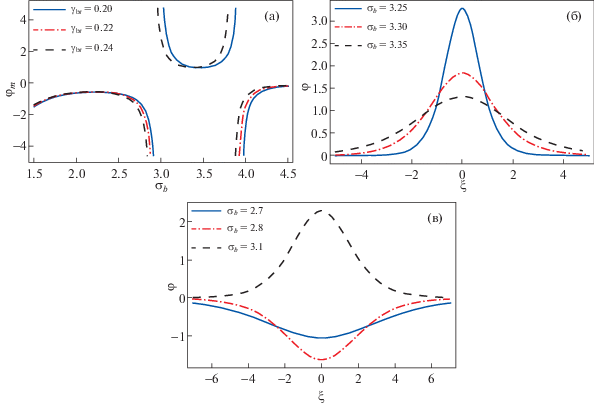
На рис. 2а показано изменение амплитуды ${{\varphi }_{m}}$ в широком диапазоне значений ${{\sigma }_{b}}$ для различных значений ${{\gamma }_{{br}}}$ (0.2, 0.22 и 0.24). Видно, что при ${{\sigma }_{b}} < 3.1$ в плазменной системе формируются уединенные волны разрежения. При более высоких отношениях температур ${{\sigma }_{b}} > 3.1$ формируются уединенные волны сжатия, и их амплитуда ${{\varphi }_{m}}$ уменьшается с ростом ${{\sigma }_{b}}$ до величины ${{\sigma }_{b}} = 3.5$. При дальнейшем увеличении ${{\sigma }_{b}}$ амплитуда начинает возрастать и становится бесконечно большой, что связано с наличием сингулярности в критической точке ${{\sigma }_{{bc2}}}$. После этого полярность амплитуды уединенной волны меняется, и в системе становится возможным распространение уединенной волны отрицательной полярности (волны разрежения). Как говорилось выше, сингулярность возникает тогда, когда нелинейный коэффициент A становится равным нулю, и при этом амплитуда ${{\varphi }_{m}}$ становится бесконечно большой.

На рис. 2б показано как меняется потенциал уединенной волны φ как функция пространственной координаты ξ при нескольких значениях отношения температур ${{\sigma }_{b}}$. Видно, что во всех случаях волны характеризуются идеально сбалансированной потенциальной структурой, соответствующей уединенной волне сжатия. На рис. 2 также видно, что с ростом ${{\sigma }_{b}}$ амплитуда потенциала φ уединенной волны сжатия уменьшается. Следовательно, можно утверждать, что при возрастании ${{\sigma }_{b}}$ усиливается нелинейность уединенной волны сжатия и происходит ее уширение. На рис. 2в видна точка перехода ${{\sigma }_{{bc1}}}$, демонстрирующая, что в области ${{\sigma }_{b}} < {{\sigma }_{{bc1}}}$ (${{\sigma }_{b}} < 3.1$) происходит формирование структур волнового потенциала, соответствующих уединенной волне отрицательной полярности (волне разрежения).

На рис. 3а показано изменение числа Маха λ при изменении ${{\gamma }_{{br}}}$ в широком диапазоне от 0.1 до 0.8. Расчеты выполнены для трех значений параметра нетепловых электронов ${{\alpha }_{e}}$. Приведенные зависимости отличаются от зависимостей, приведенных на рис. 1а. Видно, что при фиксированном значении ${{\gamma }_{{br}}}$ число Маха уменьшается при увеличении параметра нетепловых электронов ${{\alpha }_{e}}$ в системе. С физической точки зрения это означает, что с увеличением температуры горячих электронов фазовая скорость волны уменьшается.

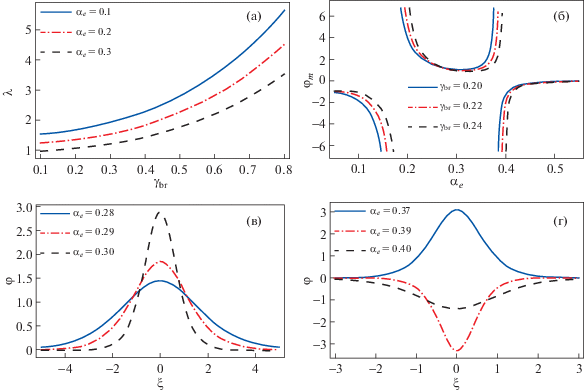
На рис. 3б для различных значений ${{\gamma }_{{br}}}$ показаны амплитуды волнового потенциала ${{\varphi }_{m}}$ как функции ${{\alpha }_{e}}$. Видно, что с увеличением ${{\alpha }_{e}}$, сначала (при ${{\alpha }_{e}} < 0.18$) амплитуда волнового потенциала ${{\varphi }_{m}}$ меняется, соответствуя волне отрицательной полярности. Затем наличие сингулярности в системе приводит к формированию критической точки ${{\alpha }_{{ec1}}}$, при переходе через которую в области ${{\alpha }_{e}} > {{\alpha }_{{ec1}}}$ полярность уединенной волны меняется, и она превращается в волну сжатия. Видно, что при увеличении ${{\gamma }_{{br}}}$ увеличивается значение критического параметра, соответствующего точке сингулярности. На рис. 3б видно, что волны разрежения формируются в системе в области ${{\alpha }_{e}} > 0.38$. Поэтому видно, что в рамках данной модели в системе могут распространяться волны разрежения (сжатия) в следующих областях параметра нетепловых электронов: ${{\alpha }_{e}} < 0.18$ и ${{\alpha }_{e}} > $ > 0.38 (волны разрежения) и $0.2 \leqslant {{\alpha }_{e}} < 0.38$ (волны сжатия).

На рис. 3в видно, что в области 0.18 < $ < {{\alpha }_{e}} < 0.38~$ зависимости потенциала уединенной волны φ от независимой пространственной координаты ξ соответствуют уединенным волнам сжатия. Рисунок показывает, что в этом диапазоне параметра нетепловых электронов ${{\alpha }_{e}}$ система поддерживает распространение только волн сжатия. Амплитуда волны растет с увеличением ${{\alpha }_{e}}$. Это связано с тем, что коэффициент нелинейности A уменьшается с ростом ${{\alpha }_{e}}$; ширина уединенной волны также уменьшается с ростом ${{\alpha }_{e}}$. С физической точки зрения это соответствует тому, что с ростом ${{\alpha }_{e}}$ возрастает энергия электронов в плазме. Поэтому давление электронов в плазме увеличивается, и это приводит к росту возвращающей силы для ионно-звуковых волн. При этом амплитуда уединенных волн сжатия возрастает из-за увеличения возвращающей силы в плазменной системе. На рис. 3г показан переход волнового потенциала уединенной волны сжатия в соответствующий потенциал волны разрежения, происходящий при изменении ${{\alpha }_{e}}$. Как и ожидалось, при постоянных значениях ${{\sigma }_{b}} = 3.3$ и ${{\gamma }_{{br}}} = 0.2$ происходит формирование уединенной волны отрицательной полярности (волны разрежения) в области ${{\alpha }_{e}} > 0.38$, а в области ${{\alpha }_{e}} < 0.38$ – формирование уединенной волны положительной полярности (волны сжатия).

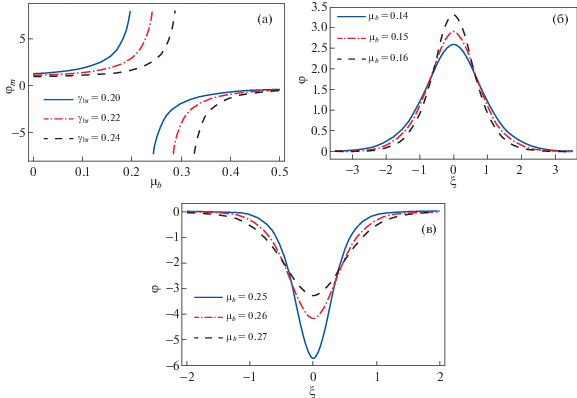
На рис. 4а показаны зависимости амплитуды ${{\varphi }_{m}}$ от ${{\mu }_{b}}$, рассчитанные при фиксированном значении ${{\sigma }_{b}} = 3.3$ для различных значений ${{\gamma }_{{br}}}$. Видно, что при ${{\mu }_{b}} \leqslant 0.204$ в плазменной системе формируются уединенные волны сжатия, что также видно на рис. 4б. Кроме того, на рис. 4б видно, что амплитуда уединенной волны сжатия растет при увеличении ${{\mu }_{b}}$. Это означает, что при увеличении концентрации позитронного пучка в плазме энергия ионов возрастает. Тем самым движущая сила, создаваемая ионами, вносит большой вклад в возрастание амплитуды ионно-звуковой уединенной волны, увеличивая ее энергию. При дальнейшем увеличении ${{\mu }_{b}}$ наличие сингулярности в критической точке приводит к увеличению амплитуды до бесконечности. Более того, при ${{\mu }_{b}} > 0.204$ полярность волновой амплитуды меняется при всех значениях релятивистского фактора, для которых проводились расчеты (${{\gamma }_{{br}}} = 0.2$, 0.22 и 0.24), и в этом диапазоне значений отношения концентраций система поддерживает распространение только уединенных волн сжатия, что подтверждается рис. 4в.

На рис. 5а показаны амплитуды потенциала ${{\varphi }_{m}}$ как функции величины ${{Z}_{{d0}}}$, рассчитанные для различных значений ${{\alpha }_{e}}$. На рисунке видно, что существуют две критические точки на оси ${{Z}_{{d0}}}$. Из-за наличия сингулярности в системе, при прохождении критических точек происходит смена полярности уединенной волны, поэтому в этой плазменной системе возможно распространение как уединенных волн сжатия, так и уединенных волн разрежения. Из рисунка также следует, что при увеличении параметра нетепловых электронов формирование критической точки происходит при меньших значениях ${{Z}_{{d0}}}$.

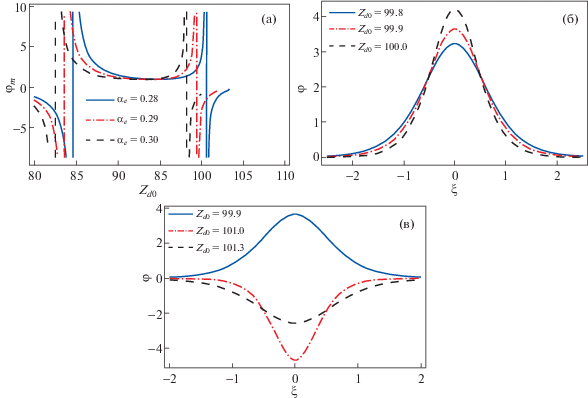
На рис. 5б показано, как меняется волновой потенциал φ уединенной волны сжатия при увеличении заряда пылевого зерна ${{Z}_{{d0}}}$. Видно, что при фиксированной плотности пылевых частиц ${{n}_{{d0}}}$ с ростом заряда пылевого зерна ${{Z}_{{d0}}}$ амплитуда уединенной волны возрастает. Это означает, что при увеличении заряда пылевого зерна ${{Z}_{{d0}}}$ в процессе зарядки происходит уменьшение плотности электронов в плазме, и это приводит к увеличению средней электронной температуры в плазменной системе [54]. На протяжении всего этого времени эффективная температура ионов также возрастает, тем самым увеличивая потенциал φ ПИЗ уединенной волны.

На рис. 5в показано, как при ${{\alpha }_{e}} = 0.28$ происходит изменение волнового потенциала φ, демонстрирующее переход от уединенной волны сжатия к уединенной волне разрежения. В соответствии с рис. 5а, при ${{Z}_{{d0}}} > 100$ в системе происходит формирование потенциала, соответствующего уединенной волне разрежения.

5. ВЫВОДЫ

При изучении распространения ПИЗ уединенных волн конечной амплитуды в релятивистской e–p–i пылевой плазме при наличии в ней позитронного пучка мы предположили, что положительные ионы и позитронный пучок являются подвижными, то есть имеющими начальные скорости течения. Кроме того, считается, что распределение электронов по энергии является нетепловым, и массивные неподвижные пылевые частицы присутствуют в фоновой плазме. В расчетах также учитывается зарядка пылевых частиц, происходящая из-за прилипания электронов к поверхности частиц. Было установлено, что при выбранных параметрах плазмы увеличение заряда пылевых частиц ${{Z}_{{d0}}}$ в плазме амплитуда уединенной волны сжатия возрастает из-за увеличения средней температуры электронов в процессе зарядки пылевых частиц. При инжекции позитронного пучка (${{V}_{{b0}}} = 5{{C}_{s}}$) в релятивистскую плазму происходит заметное увеличение числа Маха, при котором скорость потока может достигать гиперзвуковой. В этом исследовании, подбирая подходящие параметры задачи, мы нашли достоверную область параметров, при которых возможно формирование ПИЗ уединенных волн, а также их распространение в плазме. Кроме того, исследовались изменения структуры потенциала ПИЗ уединенных волн, происходящие при увеличении заряда пылевых зерен ${{Z}_{{d0}}}$, релятивистских факторов (${{\gamma }_{{br}}}$ и ${{\gamma }_{{ir}}}$), отношения температур (${{\sigma }_{b}}$), параметра нетепловых электронов ${{\alpha }_{e}}$ и отношений концентраций (${{\mu }_{b}}$ и ${{\mu }_{d}}$). Обнаружено, что для этих выбранных параметров плазмы на соответствующих зависимостях существуют критические точки ${{\gamma }_{b}}$, ${{\sigma }_{b}}$, ${{\alpha }_{e}}$,${{\mu }_{b}}$ и ${{Z}_{{d0}}}$ в которых существует сингулярность и коэффициент нелинейности A обращается в ноль, а волновая амплитуда ${{\varphi }_{m}}$ устремляется в бесконечность. Для выбранных параметров плазмы наблюдалось наличие двух критических точек, в которых происходит изменение полярности волн. В такой плазме возможно распространение как уединенных волн сжатия, так и уединенных волн разрежения в пределах их областей существования. Однако, с ростом ${{\gamma }_{{br}}}$ и ${{\sigma }_{b}}$, нелинейность системы возрастает, что приводит к уменьшению амплитуды потенциалов уединенных волн сжатия. Однако, при увеличении в плазме заряда пылевого зерна ${{Z}_{{d0}}},$ также как и параметра нетепловых электронов ${{\alpha }_{e}}$, число Маха уменьшается, что играет важную роль в увеличении амплитуды потенциала уединенной волны. Параметры, использованные в расчетах в данном исследовании, соответствуют параметрам плазмы верхних слоев атмосферы Земли (область ионосферы). Результаты данной работы могут быть полезны с точки зрения лучшего понимания процессов, происходящих в авроральной области ионосферы и в астрофизической плазме, где применима e–p–i–d модель плазмы.

Б. Боро выражает благодарность Совету по научным и промышленным исследованиям (CSIR, NewDelhi, India) за финансовую поддержку в рамках Программы поддержки исследований молодых ученых (CSIR JuniorResearchFellowship) (проект № 09/1221(0001)/2018-EMR-1).