1. На главную
  2. Электронные версии
  3. Физика плазмы
  4. T. 46, № 8, 2020

Физика плазмы, 2020, T. 46, № 8, стр. 675-684

Диагностические возможности диамагнитных измерений с двумя петлями в токамаках

В. Д. Пустовитов a, b, *

a Национальный исследовательский центр “Курчатовский институт”
Москва, Россия

b Национальный исследовательский ядерный университет МИФИ
Москва, Россия

* E-mail: Pustovitov_VD@nrcki.ru

Поступила в редакцию 26.04.2019
После доработки 05.03.2020
Принята к публикации 20.03.2020

Полный текст (PDF)

Аннотация

Магнитный поток через диамагнитную петлю состоит из двух частей: одна создается полоидальным током в плазме, а другая – внешними токами. Разделение этих частей является главным предметом этого полностью аналитического исследования. Система считается осесимметричной. Тогда “индуктивности” в соотношениях поток–ток выражаются через легко трактуемые интегралы. С такими точно определенными коэффициентами показана теоретическая возможность идеального разделения с использованием двух независимых одновременных измерений. Желаемый результат может быть получен из величин, измеренных либо методом двойной петли, либо с помощью одной диамагнитной петли и корректирующей катушки. Этот вывод более оптимистичен, чем в общепринятых концепциях. Предлагается дополнительный шаг для определения по тем же магнитным данным полоидального тока, индуцированного в стенке. Этот ток может быть полезен для оценки силы на стенку при срыве. Предложенные алгоритмы можно применять как в существующих токамаках с двумя петлями, так и в токамаке ИТЭР.

Ключевые слова: токамак, диамагнитные измерения, двойные петли, наведенные токи

1. ВВЕДЕНИЕ

Диамагнитные измерения являются частью широко применяемой диагностики в токамаках и стеллараторах [1–23]. Диамагнитная петля d, охватывающая тороидальную плазму, непосредственно измеряет напряжение из-за изменения магнитного потока $d{{\Phi }_{d}}{\text{/}}dt$, а конечной целью является определение тепловой энергии плазмы. На поток

(1)
${{\Phi }_{d}} \equiv \int\limits_d {{\mathbf{B}} \cdot d{{{\mathbf{S}}}_{d}}} $
с интегрированием по площади петли влияют изменения полного магнитного поля
(2)
${\mathbf{B}} = {{{\mathbf{B}}}^{{pl}}} + {{{\mathbf{B}}}^{{tc}}} + {{{\mathbf{B}}}^{w}} + {\mathbf{b}},$
где pl, tc и w обозначают соответственно плазму, тороидальные катушки и стенку вакуумной камеры, в то время как b включает в себя полоидальное поле и, возможно, поле ошибки. Для диагностических целей [1, 2, 24–26] необходим только вклад от плазмы. Чтобы извлечь его из ${{\Phi }_{d}}$, мы должны знать поток поля ${\mathbf{B}} - {{{\mathbf{B}}}^{{pl}}}$.

Два экспериментальных подхода были предложены для выделения этой части из ${{\Phi }_{d}}$, оба включали дополнительное измерение либо с аналогичной диамагнитной петлей d2, но с площадью иной, чем у d1 [2–10], либо с петлей cc, обходящей плазму стороной в вакуумном зазоре плазма–стенка и поэтому реагирующей только на поток поля ${{{\mathbf{B}}}^{{tc}}} + {{{\mathbf{B}}}^{w}}$ [2, 6, 12, 14, 16, 18, 22, 23, 27]. Построения, лежащие в основе этих методов, в целом описанные в превосходном обзоре Стрэйта и др. [2], а с конкретными подробностями в [2–10, 12, 14, 16, 18, 22, 23, 27], иллюстрируются рис. 1.

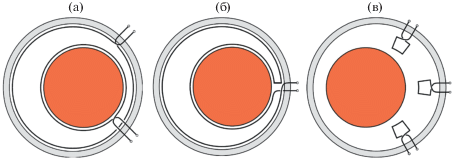
Рис. 1.

Схематическое изображение основных элементов в задаче. Внешняя оболочка – вакуумная камера (стенка), центральная часть – плазма. В вакуумном зазоре плазма–стенка показаны: а) две диамагнитные петли d1 и d2, образующие двухпетлевую конфигурацию; б) обходящая плазму корректирующая катушка в форме полумесяца; в) локальные петли малого размера. В идеале d1 и d2 и другие петли должны лежать в плоскости, перпендикулярной тороидальной оси.

Несмотря на долгую историю исследований, широкое использование этой диагностики и ее будущее применение в токамаке ИТЭР [27], некоторые неясности все еще остаются неразрешенными. Поэтому для ИТЭР был предложен набор так называемых компенсационных формул, в то время как соотношение, принятое в токамаке JET для вклада ${{{\mathbf{B}}}^{w}}$ в ${{\Phi }_{d}}$, было отвергнуто [27].

В стандартных постановках электромагнитной части задачи [2–13, 15–17, 20, 22, 23, 27] даже правила операций с основными неизвестными не были четко установлены [28]. Для конкретности, поля ${{{\mathbf{B}}}^{{tc}}}$ и ${{{\mathbf{B}}}^{w}}$ появляются в (2) в комбинации ${{{\mathbf{B}}}^{{tc}}} + {{{\mathbf{B}}}^{w}}$, но с их вкладами в ${{\Phi }_{d}}$ в (1) часто обращаются по-разному. Это порождает противоречивые мнения по основной проблеме: устранению фонового магнитного поля и влиянию вихревых токов на измерение относительно слабых диамагнитных сигналов. Например, в [3] утверждается, что двухпетлевой метод позволяет сделать это “в высокой степени”. В [2] эта точка зрения была поддержана, но с перестраховочной оговоркой, что двухпетлевая конфигурация может быть дополнена компенсационной катушкой, “чтобы получить более лучшее подавление вклада от тока в камере”. Такая промежуточная позиция была отчасти поддержана экспериментальными результатами на KSTAR [6]. С другой стороны, алгоритм и результаты для токамака Tore Supra показали [4] довольно плохую компенсацию с помощью этого метода. Это сильное и все еще неопровергнутое несогласие с [3], также подрывающее силу аргументации в [2], до сих пор остается необъясненным.

Здесь мы разрешаем эти противоречия. Получены выражения, готовые для использования и свободные от типичных неопределенностей существующей теории. В частности, “индуктивности” в соотношениях “поток–ток” явно заданы в удобной для работы форме, в то время как в [2, 4, 9, 11–13, 15, 16, 27] они рассматриваются как неопределенные константы. Последнее может служить лишь для иллюстрации общих линейных зависимостей. Здесь мы добавляем количественный аспект и приходим к выводам на основе строгой математики.

2. ПОСТАНОВКА ПРОБЛЕМЫ

Приведенный ниже анализ выполнен для осесимметричной тороидальной конфигурации с плазмой, отделенной от стенки камеры вакуумным зазором. Чаще всего [1–10, 12, 14, 16, 19, 22, 23, 27], хотя бывает и иначе [13, 15, 17, 20, 21], диамагнитные петли (одна или две, обозначенные ниже как d1 и d2) и так называемые компенсационные катушки (которые не охватывают плазму) помещают в этом промежутке, как показано на рис. 1. Здесь мы рассмотрим этот ИТЭР-подобный вариант [27]. Петли и зонды предполагаются перпендикулярными тороидальной оси, вклад b не учитывается. На практике это означает, что мы вычисляем ${{\Phi }_{d}}$ после компенсации (если она необходима) эффектов, связанных с возможными отклонениями от этого состояния.

Аксиально симметричное магнитное поле B, удовлетворяющее уравнению $\nabla \cdot {\mathbf{B}} = 0$, может быть задано в виде

(3)
$2\pi {\mathbf{B}} = \nabla \psi \times \nabla \zeta + {{\mu }_{0}}I\nabla \zeta ,$
где ζ – тороидальный угол, так что $\nabla \zeta = {{{\mathbf{e}}}_{\zeta }}{\text{/}}r$ и $\left| {{{{\mathbf{e}}}_{\zeta }}} \right| = 1$. Это представление и уравнение
(4)
$2\pi {\mathbf{j}} = \nabla I \times \nabla \zeta - {{r}^{2}}\nabla \zeta \left[ {\nabla \cdot \frac{{\nabla \psi }}{{{{\mu }_{0}}{{r}^{2}}}}} \right]$
для плотности тока
(5)
${\mathbf{j}} = \nabla \times {\mathbf{B}}{\text{/}}{{\mu }_{0}}$
подразумевают, что
(6)
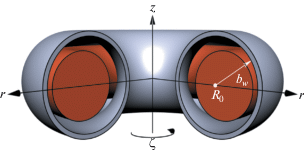
$I(r,z) \equiv \int {{\mathbf{j}} \cdot d{{{\mathbf{S}}}_{{pol}}}} = 2\pi \int\limits_0^r {{\mathbf{j}} \cdot {{{\mathbf{e}}}_{z}}rdr} $
– это полный (полоидальный) ток через мембрану, ограниченную кругом радиуса r в плоскости $z = {\text{const}}$. Здесь и далее $(r,\zeta ,z)$ – цилиндрические координаты, связанные с главной осью. Определения иллюстрируются рисунками 2 и 3.

Рис. 2.

Геометрия задачи и обозначения. Плазма отделена от резистивной стенки вакуумным зазором. ${{R}_{0}}$ – это большой радиус, а ${{b}_{w}}$ – малый радиус стенки; $(r,\zeta ,z)$ – цилиндрические координаты, связанные с главной осью симметрии тора.

Рис. 3.

Определения тороидального магнитного потока Φ и полоидального тока I.

Из (3) и (4) следует, что внутри вакуумной камеры

(7)
$2\pi ({{{\mathbf{B}}}^{{tc}}} + {{{\mathbf{B}}}^{w}}) \cdot {{{\mathbf{e}}}_{\zeta }} = {{\mu }_{0}}{{I}_{g}}{\text{/}}r,$
а ${{I}_{g}}$ – зависящая от времени константа
(8)
${{I}_{g}}(t) = {{I}_{{tc}}} + {{I}_{w}},$
равная сумме полного полоидального тока ${{I}_{{tc}}}$ в тороидальных катушках и тока ${{I}_{w}}$, индуцированного в стенке камеры. Следовательно, произведенная внешними полями часть ${{\Phi }_{d}}$ равна
(9)
$\Phi _{d}^{e} \equiv \int\limits_d {({{{\mathbf{B}}}^{{tc}}} + {{{\mathbf{B}}}^{w}}) \cdot d{{{\mathbf{S}}}_{d}}} = {{L}_{d}}({{I}_{{tc}}} + {{I}_{w}})$
для диамагнитных петель, размещенных внутри камеры (случай, представляющий основной интерес, как в [1–10, 12, 14, 16, 19, 22, 23, 27]) с $d{{{\mathbf{S}}}_{d}} = {{{\mathbf{e}}}_{\zeta }}d{{S}_{d}}$ и

(10)
${{L}_{d}} \equiv \frac{{{{\mu }_{0}}}}{{2\pi }}\int\limits_d {\frac{{d{{S}_{d}}}}{r}} .$

Соответственно соотношение

(11)
${{\Phi }_{d}} = \delta {{\Phi }_{{pl}}} + \Phi _{d}^{e},$
где
(12)
$\delta {{\Phi }_{{pl}}} \equiv \int\limits_{pl} {{{{\mathbf{B}}}^{{pl}}} \cdot d{{{\mathbf{S}}}_{{pl}}}} ,$
превращается в

(13)
${{\Phi }_{d}} = \delta {{\Phi }_{{pl}}} + {{L}_{d}}({{I}_{{tc}}} + {{I}_{w}}).$

Подробнее, особенно насчет $\delta {{\Phi }_{{pl}}}$ и связи ${{I}_{w}}$ с параметрами плазмы, см. [28, 29]. Часто ${{I}_{w}}$ называют вихревым током [1–4, 6, 7, 9, 11–17, 19, 22, 23, 27], а иногда [2, 8, 12, 13, 15, 17] – током изображения.

Будучи простым следствием (7) и (8) с $\nabla {{I}_{g}} = 0$ во всем объеме внутри камеры, соотношения (9) и (10) играют важную роль в предстоящем анализе. Они показывают, в частности, что ${{I}_{{tc}}}$ и ${{I}_{w}}$ входят в $\Phi _{d}^{e}$ и тем самым в ${{\Phi }_{d}}$ в (13) с одним и тем же множителем ${{L}_{d}}$, определенным формулой (10). Напротив, при обсуждениях диамагнитных измерений традиционно оперируют с выражениями

(14)
$\Phi _{d}^{e} = {{M}_{{tc}}}{{I}_{{tc}}} + {{M}_{w}}{{I}_{w}},$
где ${{M}_{{tc}}}$ и ${{M}_{w}}$ называются взаимными индуктивностями между петлей и, соответственно, тороидальными катушками и вакуумной камерой [2, 4, 13, 27]. Это прекрасно подходит, чтобы указать на линейную зависимость $\Phi _{d}^{e}$ от ${{I}_{{tc}}}$ и ${{I}_{w}}$, которая является универсальным следствием (5), но не раскрывает тот важный факт, что
(15)
${{M}_{{tc}}} = {{M}_{w}} = {{L}_{d}}$
для каждой петли внутри камеры.

Последнее, очевидно, возникает из уравнений (7)–(9), которые также приводят к строгому определению (10) величины ${{L}_{d}}$. Однако в [2, 4, 13, 27] эквиваленты ${{M}_{{tc}}}$ и ${{M}_{w}}$ в (14) описаны лишь словесно, без намека на свойство (15) или точные значения этих величин.

Соотношение (14), содержащее ${{I}_{{tc}}} + \alpha {{I}_{w}}$ с неопределенным $\alpha ({{{\mathbf{r}}}_{{d1}}},{{{\mathbf{r}}}_{{d2}}},t)$ и двумя неизвестными ${{I}_{{tc}}}(t)$ и ${{I}_{w}}(t)$, подразумевает, что (при $\alpha \ne 1$, пока обратное не доказано) для компенсации $\Phi _{d}^{e}$ в (11) нужны два дополнительных измерения, см. [2, 4, 13, 27], но уравнение (13) показывает, что и одного было бы достаточно, если бы оно дало нам ${{I}_{{tc}}} + {{I}_{w}}$. Ниже мы обсудим это и другие следствия использования (9) и (10) вместо единственного традиционного (14).

3. ДВУХПЕТЛЕВЫЕ ДИАМАГНИТНЫЕ ИЗМЕРЕНИЯ

Рассмотрим случай с двумя диамагнитными петлями d1 и d2 разной площади, как показано на рис. 1a. Такая компоновка реализована на токамаках Tore Supra [4], KSTAR [5, 6], HL-2A [7], J‑TEXT [9], WEST [10] и стеллараторах Heliotron J [3], U-2M и У-3М [8]. Термин “двойная петля” взят из [3], а также он используется в [2, 9]. Иногда эту конструкцию называют двумя концентрическими диамагнитными петлями [3–7, 10, 13]. Это не указывает на форму и расположение катушек, но служит для того, чтобы отличать их от “эксцентрических” катушек [16, 30], одна из которых (показанная как cc на рисунках 1a и 1б) не окружает плазму, а вторая - это d1.

Применяя (13) к каждой из “двойных” петель, получаем два равенства

(16)
${{\Phi }_{{d1}}} = \delta {{\Phi }_{{pl}}} + {{L}_{{d1}}}({{I}_{{tc}}} + {{I}_{w}})$
и
(17)
${{\Phi }_{{d2}}} = \delta {{\Phi }_{{pl}}} + {{L}_{{d2}}}({{I}_{{tc}}} + {{I}_{w}}),$
где ${{L}_{{d1}}}$ и ${{L}_{{d2}}}$ задаются формулой (10) с подстановкой d1 и d2 вместо d, соответственно. Эти две “индуктивности” заменяют четыре коэффициента, возникающие из (14) в аналогичных соотношениях для ${{\Phi }_{{d1}}}$ и ${{\Phi }_{{d2}}}$ в [4] (обозначенных там как ${{\Phi }_{{L1}}}$ и ${{\Phi }_{{L2}}}$) и в [2].

Из (16) и (17) следует, что

(18)
$\frac{{{{\Phi }_{{d1}}} - {{\Phi }_{{d2}}}}}{{{{L}_{{d1}}} - {{L}_{{d2}}}}} = {{I}_{{tc}}} + {{I}_{w}}$
и

(19)
$\frac{{{{L}_{{d1}}}{{\Phi }_{{d2}}} - {{L}_{{d2}}}{{\Phi }_{{d1}}}}}{{{{L}_{{d1}}} - {{L}_{{d2}}}}} = \delta {{\Phi }_{{pl}}}.$

Последнее равенство напрямую дает нам желаемую величину $\delta {{\Phi }_{{pl}}}$. Оно показывает, что теоретически полная компенсация $\Phi _{d}^{e}$ в (11) должна быть возможной с двумя неидентичными диамагнитными петлями, что оказывается даже более лучшим результатом, чем аналогичный, но полученный как приблизительный в [3].

Однако, когда $\Phi _{d}^{e}$ описывается формулой (14), а свойство (15) не учитывается, вычитание, подобное указанному в (19), формально позволяет исключить только один неизвестный ток, ${{I}_{{tc}}}$ [2] или же ${{I}_{w}}$ [4]. Тогда линейные комбинации ${{\Phi }_{{d1}}}$ и ${{\Phi }_{{d2}}}$ рассматриваются как производящие либо $\delta {{\Phi }_{{pl}}} + x{{I}_{w}}$ [2], либо $\delta {{\Phi }_{{pl}}} + y{{I}_{{tc}}}$ [4]. В [4] наличие остаточного члена $y{{I}_{{tc}}}$ обсуждалось как требующее нескольких дополнительных процедур для его нахождения. Уравнение (17) в [2] с $\delta {{\Phi }_{{pl}}} + x{{I}_{w}}$, подобное нашему (19), заставило сделать противоположный вывод, что двухпетливая схема позволяет компенсацию ${{I}_{w}}$, потому что $x$ может быть малым, хотя такой вывод был немедленно принижен комментарием о полезности дополнительной компенсационной катушки.

Утверждения и предлагаемые действия в [2] и [4] основаны на ожиданиях, что x и y должны быть ненулевыми, поскольку эти величины построены из математически неопределенных ${{M}_{{tc}}}$ и ${{M}_{w}}$ в равенстве (14), примененным к двум петлям.

Добавление (15) приводит к существенным упрощениям по сравнению с алгоритмами, описанными в [2] и [4]. При $x = y = 0$ задача сводится к вычислению левой части в (19). Это доказывает, что для нахождения $\delta {{\Phi }_{{pl}}}$ необходимы только два подобных измерения с использованием d1 и d2.

Переписав (19) в виде

(20)
$\delta {{\Phi }_{{pl}}} = \left( {1 - \frac{1}{k}} \right)\left( {{{\Phi }_{{d2}}} - \frac{{{{\Phi }_{{d1}}}}}{k}} \right),$
мы воспроизводим уравнение (2) из [5], где величина k оценивалась из измерения потока вакуумного поля. Наш анализ подтверждает правильность этого уравнения и методики эксперимента в [5]. Кроме того, мы даем точную формулу $k = {{L}_{{d2}}}{\text{/}}{{L}_{{d1}}}$, позволяющую наперед рассчитать k по (10).

Справедливость (19) существенно основана на том факте, что тороидальное поле в вакуумном зазоре плазма–стенка определяется суммой ${{I}_{{tc}}} + {{I}_{w}}$, см. (7) и (8), и та же самая константа определяет “нежелательную” часть ${{\Phi }_{d}}$ в (13). Это подразумевает, что $\delta {{\Phi }_{{pl}}}$ можно найти с помощью одной диамагнитной петли, если бы величина ${{I}_{{tc}}} + {{I}_{w}}$ была бы измерена независимо. Последнее может быть выполнено с помощью меньшей петли вне плазмы вместо использования второй диамагнитной петли для той же цели.

4. ОДНА ПЕТЛЯ ПЛЮС КАТУШКА КОМПЕНСАЦИИ

Это ИТЭР-подобный случай [27]. Хотя ИТЭР будет оснащаться тремя наборами основных диамагнитных петель внутри камеры, сценарий с двойной петлей не может быть реализован, поскольку ${{L}_{{di}}}$ будут практически идентичны. Однако тороидальное поле вне плазмы будет измеряться тремя парами “компенсационных катушек” (cc).

Однажды cc была описана как катушка, “чья активная область окружает, но не охватывает плазменное сечение” [30]. На самом деле окружение необязательно, cc может быть и локальным зондом [2, 27]. Варианты были представлены в [2, 6, 12–17, 20–23, 27]. Терминология cc была изобретена, чтобы подчеркнуть ценность производимого плазмой $\delta {{\Phi }_{{pl}}}$ в противовес (загрязняющему [27] или паразитному [3, 27]) вкладу $\Phi _{d}^{e}$ от внешних токов.

Поток через катушку cc, помещенную внутри вакуумной камеры перпендикулярно тороидальному направлению, равен

(21)
${{\Phi }_{{cc}}} = {{L}_{{cc}}}({{I}_{{tc}}} + {{I}_{w}}),$
где

(22)
${{L}_{{cc}}} \equiv \frac{{{{\mu }_{0}}}}{{2\pi }}\int\limits_{cc} {\frac{{d{{S}_{{cc}}}}}{r}} .$

Данное равенство естественно выглядит как (9) и (18), потому что эти три соотношения дают потоки одного и того же тороидального поля ${{\mu }_{0}}({{I}_{{tc}}} + {{I}_{w}}){\text{/}}(2\pi r)$. Следствием этого является то, что комбинация ${{I}_{{tc}}} + {{I}_{w}}$ или, скорее, ее вариация, необходимая в (16) или (17), может быть найдена из измерений только посредством cc:

(23)
${{I}_{{tc}}} + {{I}_{w}} = {{\Phi }_{{cc}}}{\text{/}}{{L}_{{cc}}}.$

С теоретической точки зрения, (18) и (23) формально отличаются лишь из-за различий областей, охватываемой cc или заключенной между петлями d1 и d2. На практике комбинации одной диамагнитной петли d и дополнительной cc предполагают гораздо более широкий выбор, чем система двух петель d1 и d2, поскольку cc может быть помещена в любую свободную зону камеры. Кроме того, cc может быть любой формы и размера, вплоть до локального зонда. Это верно в осесимметричной модели. В реальном токамаке оптимальное место и геометрию cc можно найти, сравнивая результаты расчетов по (18) и (23) при учете реальной геометрии стенки.

Отметим, что, как (9) и (14), соотношение поток–ток (21) отличается от уравнения (14) в [2], которое имеет вид

(24)
${{\Phi }_{{cc}}} = {{M}_{{cctc}}}{{I}_{{tc}}} + {{M}_{{ccw}}}{{I}_{w}}.$

Причина та же, что и упомянутая выше: мы явно используем свойство ${{M}_{{cctc}}} = {{M}_{{ccw}}} = {{L}_{{cc}}}$, которое выявляется после подстановки (7) в интегралы для потока. Также у нас есть соотношение (22) для ${{L}_{{cc}}}$.

5. ОСНОВНОЕ ПРИМЕНЕНИЕ ДАННЫХ

Уравнение (19) можно переписать в виде

(25)
$\delta {{\Phi }_{{pl}}} = {{\Phi }_{{d1}}} - \frac{{{{L}_{{d1}}}}}{{{{L}_{{d1}}} - {{L}_{{d2}}}}}({{\Phi }_{{d1}}} - {{\Phi }_{{d2}}}),$
близко напоминающем равенство
(26)
$\delta {{\Phi }_{{pl}}} = {{\Phi }_{{d1}}} - \frac{{{{L}_{{d1}}}}}{{{{L}_{{cc}}}}}{{\Phi }_{{cc}}},$
полученное объединением (16) и (23). Важно, что для нахождения $\delta {{\Phi }_{{pl}}}$ необходимы лишь два измеряемых сигнала. Практическое следствие состоит в том, что в обоих случаях для извлечения $\delta {{\Phi }_{{pl}}}$ можно использовать гораздо более простые процедуры, чем описанные в [2, 4].

Конечной целью диамагнитных измерений является оценка энергии плазмы, что может быть проиллюстрировано простейшей формулой [24–26] (см. также [6, 13, 15–18, 22, 23])

(27)
$2\frac{{\delta {{\Phi }_{{pl}}}}}{{{{\Phi }_{{pl}}}}} = \frac{{B_{J}^{2}}}{{B_{0}^{2}}} - \beta ,$
где ${{\Phi }_{{pl}}} = {{B}_{0}}{{S}_{{pl}}}$ с ${{S}_{{pl}}}$, обозначающим площадь поперечного сечения плазменного шнура, ${{B}_{0}} = $ $ = {{\mu }_{0}}{{I}_{{tc}}}{\text{/}}(2\pi R)$ – тороидальное поле, R – большой радиус, ${{B}_{J}}$ – полоидальное поле на границе плазмы (поле полного тока плазмы J), β – отношение усредненного по объему давления плазмы p к давлению магнитного поля $B_{0}^{2}{\text{/}}(2{{\mu }_{0}})$. В общем случае широко используемое цилиндрическое соотношение (27) следует заменить на
(28)
${{I}_{g}}\delta {{\Phi }_{{pl}}} = {{C}_{J}}{{J}^{2}} - {{C}_{p}}\int\limits_{pl} {pdV} ,$
где ${{C}_{J}}$ и ${{C}_{p}}$ – положительные геометрические константы, слабо зависящие от профилей тороидального тока и p. Для оценок можно взять ${{C}_{p}} \approx 1$ и
(29)
${{C}_{J}} \approx \frac{{{{\mu }_{0}}}}{2}R\frac{K}{{{{K}^{2}} + 1}},$
где K означает вертикальное удлинение плазмы. Выводы, приводящие к (28), и точные формулы для ${{C}_{J}}$ и ${{C}_{p}}$ представлены в разд. 6 в [29]. Оба коэффициента находятся из решения уравнения Грэда–Шафранова для интересующей конфигурации. Для круглой плазмы равенство (28) сводится к (27), для эллиптической плазмы с (29) оно воспроизводит уравнение (10) в [27], см. также [1, 2, 26].

Каждая из трех измеряемых величин ${{\Phi }_{{d1}}}$, ${{\Phi }_{{d2}}}$ и ${{\Phi }_{{cc}}}$ зависит от полоидального тока ${{I}_{w}}$, наведенного в стенке, и флуктуирующего тока ${{I}_{{tc}}}$ в тороидальных катушках, а результаты в (25) и (26) – нет. Это следствие подтверждает идеи [3], подкрепленные там приблизительными соотношениями для стелларатора, но опровергает модель, предложенную в [4]. Справедливость (25) и (26) может быть проверена экспериментально в разрядах без плазмы, иногда называемых холостыми [12, 15] или предназначенными для измерений вакуумного потока [5–7, 18]. В таких разрядах подстановка измеренных потоков в правые части (25) и (26) должна давать $\delta {{\Phi }_{{pl}}} = 0$ при любом $\partial {{I}_{{tc}}}{\text{/}}\partial t \ne 0$.

Полная компенсация в (25) и (26) имеет то привлекательное следствие, что мгновенные значения $\delta {{\Phi }_{{pl}}}$ могут быть найдены экспериментально без временных задержек, связанных с реакцией резистивной стенки. Это достигается из-за того, что ${{I}_{{tc}}} + {{I}_{w}}$ прямо выражается через измеряемые ${{\Phi }_{{d1}}} - {{\Phi }_{{d2}}}$ и ${{\Phi }_{{cc}}}$, см. (18) и (23).

Описанные процедуры дают два математических решения, $\delta {{\Phi }_{{pl}}}$ и ${{I}_{{tc}}} + {{I}_{w}}$, но только $\delta {{\Phi }_{{pl}}}$ всегда рассматривается как физически ценное. Далее мы предлагаем простой метод для извлечения ${{I}_{w}}$ из найденных таким образом величин $\delta {{\Phi }_{{pl}}}$ и ${{I}_{{tc}}} + {{I}_{w}}$. Будучи основанным на использовании уравнения для ${{I}_{w}}$ в резистивной стенке, оно не требует каких-либо других измерений. Мы также объясним, где знание ${{I}_{w}}$ может быть полезным.

6. ОПРЕДЕЛЕНИЕ ${{I}_{w}}$ ИЗ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

В диагностических задачах ток в стенке ${{I}_{w}}$ традиционно рассматривается как нежелательный источник ошибок [1–18, 22, 23, 27]. Метод двойных петель [2–10] и использование компенсационных катушек [2, 6, 12, 14, 16, 18, 22, 23, 27] направлены на подавление его вклада в ${{\Phi }_{d}}$. Побочный продукт этих подходов, ${{I}_{{tc}}} + {{I}_{w}}$, который дается уравнениями (18) и (23), никогда не был целью диагностики. Основная причина заключается в том, что при нормальной работе и медленной эволюции плазмы величина ${{I}_{w}}$ должна быть очень мала по сравнению с ${{I}_{{tc}}}$. Ничто не указывало на то, что этот ток может повлиять на работу токамака, но недавно было показано [31–33], а затем подтверждено в [34, 35], что во время срывов с ${{I}_{w}}$ может быть связана большая сила, действующая на стенку.

Уравнения (18) и (23) дают нам ${{I}_{{tc}}} + {{I}_{w}}$, где ток ${{I}_{w}}$ и флуктуирующую часть ${{I}_{{tc}}}$ следует рассматривать как сопоставимые величины. С этими двумя неизвестными нам нужно дополнительное соотношение для выделения ${{I}_{w}}$ в (18) или в (23). Найти этот ток можно было бы путем измерения потока тороидального поля ${{B}_{{tc}}} \equiv {{\mu }_{0}}{{I}_{{tc}}}{\text{/}}(2\pi r)$ за стенкой, как это делается в токамаках TCV [13, 17], STOR-M [15] и ASDEX Upgrade [20, 21] с использованием компенсационных петель вне вакуумной камеры. Такой вариант также предусмотрен в токамаке ИТЭР с тремя наборами локальных зондов [27].

Вместо этого или в качестве дополнительного инструмента мы предлагаем использовать уравнение [29]

(30)
${{L}_{w}}\frac{{d{{I}_{w}}}}{{dt}} + {{R}_{w}}{{I}_{w}} + \frac{d}{{dt}}\delta {{\Phi }_{{pl}}} + {{L}_{w}}\frac{{d{{I}_{{tc}}}}}{{dt}} = 0,$
описывающее эволюцию ${{I}_{w}}$, когда плазма оторвана от стенки. Здесь
(31)
${{L}_{w}} \equiv \frac{{{{\mu }_{0}}}}{{2\pi }}\int\limits_w {\frac{{d{{S}_{w}}}}{r}} $
и

(32)
${{R}_{w}} \equiv \oint\limits_w {\frac{{d{{\ell }_{w}}}}{{2\pi r{{d}_{w}}\sigma }}} .$

В (32) интегрирование выполняется по полоидальному контуру стенки, σ – проводимость стенки, ${{d}_{w}}$ – ее толщина (как правило, функции полоидальной координаты).

Уравнение (30) содержит величины $\delta {{\Phi }_{{pl}}}$ и ${{I}_{{tc}}} + {{I}_{w}}$, которые выражаются через ${{\Phi }_{{d1}}}$ и либо ${{\Phi }_{{d2}}}$, либо ${{\Phi }_{{cc}}}$ посредством (18), (19), (23), (25) и (26). Будучи переписанным как

(33)
${{I}_{w}} = - \frac{1}{{{{R}_{w}}}}\frac{d}{{dt}}[\delta {{\Phi }_{{pl}}} + {{L}_{w}}({{I}_{{tc}}} + {{I}_{w}})],$
оно явно дает нам ток в стенке ${{I}_{w}}$ в терминах измеряемых величин и четко определенных ${{L}_{w}}$ и ${{R}_{w}}$. Последнее определено формулой (32), справедливой для осесимметричной сплошной стенки. На самом деле стенка неоднородна, в ней есть разрезы и отверстия. Тогда ${{R}_{w}}$ или постоянная времени
(34)
${{\tau }_{1}} \equiv {{L}_{w}}{\text{/}}{{R}_{w}} \cong {{\mu }_{0}}\sigma {{d}_{w}}{{S}_{w}}{\text{/}}{{\ell }_{w}}$,
где ${{\ell }_{w}}$ – длина полоидального контура стенки, могут быть подобраны путем сравнения ${{I}_{w}}(t)$, экспериментально найденного из (33) при изменяющемся ${{I}_{{tc}}}(t)$ в холостых (неплазменных) разрядах, с решением (30)
(35)
${{I}_{w}} = - {{\tau }_{1}}\frac{d}{{dt}}({{I}_{{tc}}} + {{I}_{w}}) = - {{e}^{{ - t/{{\tau }_{1}}}}}\int\limits_0^t {{{e}^{{t/{{\tau }_{1}}}}}\frac{{d{{I}_{{tc}}}}}{{dt}}dt} $
для такого случая с ${{I}_{w}}(0) = 0$. Отметим, что
(36)
${{\tau }_{1}} = {{\tau }_{w}}{\text{/}}2,$
где ${{\tau }_{w}}$ – “резистивное время стенки”, используемое в описании винтовых мод с резистивной стенкой (RWM) [36, 37]. Для некоторых токамаков величины ${{\tau }_{w}}$ приведены в табл. 1 в [36]. Обычно это несколько миллисекунд. Для стенки ИТЭР оценка ${{\tau }_{w}}$ составляет от 0.34 с [38] до 0.5 с [39].

В токамаке ASDEX Upgrade сопротивление стенки вакуумной камеры было недавно оценено с использованием измерений напряжения внешней петлей и сигналов от пар магнитных зондов внутри и снаружи камеры [40]. Это, однако, было сделано для плотности тока стенки в тороидальном направлении. Можно ожидать, что сопротивление стенки для полоидального тока будет того же порядка, что и оценка по наклону кривой на рис. 8 в [40], но это требует подтверждения. Разброс на упомянутом рисунке и четырехкратное превышение измеренного удельного сопротивления по сравнению с ожидаемым значением могут быть связаны с тем, что времена затухания $m = 0$ и $m = 1$ полоидальных гармоник ${{j}_{\zeta }}$ должны различаться примерно в 2 раза [41].

Уравнения (30) или (33) показывают, что в пределе идеальной стенки, применимом к быстрым событиям, таким как TQ или импульсы ELM,

(37)
$\Delta {{I}_{w}} = - \Delta \delta {{\Phi }_{{pl}}}{\text{/}}{{L}_{w}},$
что можно рассматривать как верхнюю границу для ${{I}_{w}}$. С
(38)
${{L}_{w}} \approx \frac{{{{\mu }_{0}}{{S}_{w}}}}{{2\pi R}}$
и $\delta {{\Phi }_{{pl}}}$ из (27) уравнение (37) дает для “круглого” токамака (${{S}_{w}} = \pi b_{w}^{2}$)
(39)
$\Delta {{I}_{w}} = \frac{{\pi R{{B}_{0}}}}{{{{\mu }_{0}}}}\frac{{{{b}^{2}}}}{{b_{w}^{2}}}\Delta \left( {\beta - \frac{{B_{J}^{2}}}{{B_{0}^{2}}}} \right),$
где b и ${{b}_{w}}$ – соответственно малые радиусы плазмы и стенки. При падении β на 1% (TQ) это дает: $\Delta I_{w}^{{TQ}} = - 0.14$ MA для токамака JET с $R = {\text{ }}2.9$ м и ${{B}_{0}} = {\text{ }}3.45$ Tл, и $\Delta I_{w}^{{TQ}} = - {\text{0}}{\text{.47}}$ MA для токамака ITER с $R = {\text{ 6}}{\text{.2}}$ м и ${{B}_{0}} = {\text{ }}5.35$ Tл (параметры из табл. 5 в [39] и $b{\text{/}}{{b}_{w}} = 0.75$).

В приведенных примерах тороидальное поле в вакуумном зазоре плазма–стенка изменится менее чем на 0.3%. Это практически не скажется на положении и форме плазмы, но изменит магнитное давление на стенку на ≈0.6% от $B_{0}^{2}{\text{/}}(2{{\mu }_{0}})$. Последний эффект очевидно силен и заслуживает внимания [31–33, 42].

В рамках модели величина $B_{J}^{2}{\text{/}}B_{0}^{2}$ перед срывом может быть оценена как 3.7% при типичном $R{\text{/}}b = 3$ и запасе устойчивости на границе ${{q}_{b}} = b{{B}_{0}}{\text{/}}(R{{B}_{J}}) = 3$. Тогда для полного быстрого CQ мы получили бы из (39) $\Delta I_{w}^{{CQ}}$ около +0.5 MA для JET и +1.7 MA для токамака ИТЭР. Противоположные знаки $\Delta I_{w}^{{TQ}}$ и $\Delta I_{w}^{{CQ}}$ отражают известную конкуренцию диа- и парамагнитного откликов равновесной плазмы, содержащихся в (27) и перенесенных в (39).

Из (37) и (38) следует, что при одинаковых $\Delta \delta {{\Phi }_{{pl}}}$ и малом радиусе ${{b}_{w}}$ оценки сверху для $\Delta I_{w}^{{TQ}}$ и $\Delta I_{w}^{{CQ}}$ в стенке с вытянутостью ${{K}_{w}}$ должны быть в ${{K}_{w}}$ раз меньше. Вытянутость плазмы $K$ играет меньшую роль, она практически не влияет на ${{C}_{p}}$ в (28), в то время как ${{C}_{J}}$ уменьшается лишь на 20% при изменении K от 1 до 2, см. (29).

Эти оценки в пределе идеальной стенки дают шкалу того, что следует ожидать для скачкообразных переходов с характерным временем $\tau \ll {{\tau }_{1}}$. Для более медленных событий величина ${{I}_{w}} = I_{w}^{{TQ}} + I_{w}^{{CQ}}$, подчиняющаяся (30), будет меньше из-за резистивного затухания обоих вкладов, см. типичные решения в [43].

Объемная плотность электромагнитной силы на стенку, обусловленная взаимодействием полоидального тока, индуцированного в стенке, с тороидальным полем ${{{\mathbf{B}}}_{t}}$, составляет

(40)
${{{\mathbf{j}}}_{p}} \times {{{\mathbf{B}}}_{t}} = - \frac{{{{\mu }_{0}}\nabla {{I}^{2}}}}{{8{{\pi }^{2}}{{r}^{2}}}}.$

Ее интегрирование через стенку дает

(41)
$\begin{gathered} \int\limits_{wall} {{{{\mathbf{j}}}_{p}} \times {{{\mathbf{B}}}_{t}}d{{\ell }_{ \bot }}} = \\ \, = - \frac{{{{\mu }_{0}}}}{{8{{\pi }^{2}}{{r}^{2}}}}[I_{{tc}}^{2} - {{({{I}_{{tc}}} + {{I}_{w}})}^{2}}]{{{\mathbf{n}}}_{w}} \approx \frac{{{{B}_{0}}{{I}_{w}}}}{{2\pi }}\frac{R}{{{{r}^{2}}}}{{{\mathbf{n}}}_{w}}, \\ \end{gathered} $
где ${{{\mathbf{n}}}_{w}}$ – нормаль к стенке. Уравнения (33) и (41) показывают, что эту силу можно оценить, используя “основные” результаты (19) или (26) диамагнитных измерений и их кажущиеся бесполезными “побочные продукты” (18) или (23).

Предложенный алгоритм, основанный на этих соотношениях, открывает прямой способ проверки теоретических предсказаний [31–35, 42] или сильно от них отличающихся (по неустановленным причинам) суждений [44] о роли ${{I}_{w}}$ в проблеме сил при срывах. Традиционно такие нагрузки относят к срыву тока (CQ) [19, 31, 39, 45–48]. Более того, в ряде подходов даже во время CQ полоидальный ток в стенке полностью игнорируется, см. [19, 49–56] и обсуждения и ссылки в [31–33]. Однако общие уравнения (28) и (30) и упрощенная оценка (39) в пределе идеальной стенки доказывают, что ${{I}_{w}}$ могут генерировать как TQ, так и CQ.

С известным ${{I}_{w}}$ мы также можем найти ${{I}_{{tc}}}(t)$ из (18). Кроме того, можно использовать соотношение

(42)
$\frac{{d{{\Phi }_{w}}}}{{dt}} = - {{R}_{w}}{{I}_{w}}$
(см. (23) в [29] и обсуждение в [28]) для перекрестной проверки точности измерений диамагнитной петлей, помещенной на стенку, когда ${{\Phi }_{d}} = {{\Phi }_{w}}$. Это применимо к токамакам TCV [13, 17], JET [19], KSTAR [6], ASDEX Upgrade [20, 21], T-15MD [43] и ИТЭР [27].

7. ВЫВОДЫ

В осесимметричном токамаке внешнее тороидальное поле описывается формулой (7) с $\nabla {{I}_{g}} = 0$ внутри вакуумной камеры. Вклад $\Phi _{d}^{e}$ этого поля в поток ${{\Phi }_{d}}$ через диамагнитную петлю внутри камеры дается формулой (9). Полоидальные токи ${{I}_{{tc}}}$ и ${{I}_{w}}$ входят в задачу в виде суммы ${{I}_{g}} = {{I}_{{tc}}} + {{I}_{w}}$. Поэтому для извлечения произведенного плазмой $\delta {{\Phi }_{{pl}}}$ из ${{\Phi }_{d}}$ требуется только одно дополнительное измерение. Таким образом, $\delta {{\Phi }_{{pl}}}$ можно найти с использованием либо двух диамагнитных петель, покрывающих разные области, либо одной такой петли и “компенсационной катушки” внутри вакуумной камеры, см. (25) и (26). В противоположность [2, 4], где подобные соотношения содержат некоторые неопределенности, приводящие к усложнениям при обработке данных, здесь все величины строго определены. Уравнения (25) и (26) готовы к применению, требуемые процедуры намного проще, чем описанные в [2, 4] и реализованные в KSTAR [6].

Вместе с (18) или (23) они также дают ${{I}_{{tc}}} + {{I}_{w}}$, как бонус к $\delta {{\Phi }_{{pl}}}$. Эта пара полностью определяет ${{I}_{w}}$ через (33). С помощью ${{I}_{w}}$ можно оценить силу (41) на стенку, что стало бы экспериментальным тестом теорий [31–35, 42], утверждающих, что вызванный срывом полоидальный ток в стенке может создавать значительную силу.

Соотношения (25) и (26), на которых базируются выводы, являются прямыми следствиями уравнений Максвелла $\nabla \cdot {\mathbf{B}} = 0$ и ${{\mu }_{0}}{\mathbf{j}} = \nabla \times {\mathbf{B}}$ и того факта, что внутри вакуумной камеры $\nabla ({{I}_{{tc}}} + {{I}_{w}}) = 0$. Поэтому, будучи чисто электромагнитными, результаты могут применяться к любой плазме, она может быть анизотропной, вращающейся, неидеальной. Единственное предположение здесь состоит в том, что система является осесимметричной, но расширение на стеллараторы является несложным [57]. Связь с плазмой, описываемая традиционным балансом сил $\nabla p = {\mathbf{j}} \times {\mathbf{B}}$, использовалась только для получения (27), (28) и оценки (39).

Отметим, что “индуктивности” ${{L}_{\alpha }}$ могут изменяться во времени, если петли/катушки динамически деформируются или смещаются. Такие события и колебания петли были упомянуты в [2, 3, 7, 12, 13, 15–17, 22, 27, 30] как влияющие на измерения. Определения (10), (22) и (31) позволяют включить эти геометрические эффекты в модель и легко оценить их в (18), (19), (23), (25), (26) и (33).

Автор благодарен L. Giannone, J.G. Bak, G. Vayakis, В. Яновскому, С. Герасимову и команде COMPASS за полезные обсуждения и информацию о диагностических деталях, а также С.В. Коновалову за постоянную поддержку. Рисунки сделаны Д.И. Кирамовым.

Признателен анонимному рецензенту, который рекомендовал упомянуть, что диамагнитные измерения впервые были выполнены в 1965 г. на токамаке Т-5 в Институте атомной энергии [58].

Список литературы

  1. Strait E.J. // Rev. Sci. Instrum. 2006. V. 77. 023502.

  2. Strait E.J., Fredrickson E.D., Moret J.-M., Takechi M. // Fusion Sci. Technol. 2008. V. 53. P. 304.

  3. Besshou S., Aizawa K., Tomiyama K., Kondo K., Mizuuchi T., Nagasaki K., Obiki T., Okada H., Sano F. // Rev. Sci. Instrum. 2001. V. 72. P. 3859.

  4. Joffrin E. and Defrasne P. // Rev. Sci. Instrum. 2002. V. 73. P. 2266.

  5. Bak J.G., Lee S.G., Ka E.M. // Rev. Sci. Instrum. 2008. V. 79. 10F118.

  6. Bak J.G., Lee S.G., Kim H.S. // Rev. Sci. Instrum. 2011. V. 82. 063504.

  7. Ji X.Q., Yang Q.W., Xu Y., Sun T.F., Yuan B.S., Feng B.B., Liu Y., Cui Z.Y., Lu J. // Rev. Sci. Instrum. 2013. V. 84. 083507.

  8. Pashnev V.K., Petrushenya A.A., Sorokovoy E.L. // Problems of Atomic Science and Technology. 2013. V. 83. P. 276. http://vant.kipt.kharkov.ua/TABFRAME2.html

  9. Zhu L.Z., Chen Z.P., Li F.M., Liu H., Chen Z.Y., Zhuang G. // Rev. Sci. Instrum. 2016. V. 87. 11D420.

  10. Moreau P., Le-Luyer A., Spuig P., Malard P., Saint-Laurent F., Artaud J.F., Morales J., Faugeras B., Heumann H., Cantone B., Moreau M., Brun C., Nouaille-tas R., Nardon E., Santraine B., Berne A., Kumari P., Belsare S., WEST Team // Rev. Sci. Instrum. 2018. V. 89. 10J109.

  11. Tonetti G., Christiansen J.P., de Kock L. // Rev. Sci. I-nstrum. 1986. V. 57. P. 2087.

  12. Saha S.K., Kumar R., Hui A.K. // Rev. Sci. Instrum. 2001. V. 72. P. 4289.

  13. Moret J.-M., Buhlmann F., Tonetti G. // Rev. Sci. I-nstrum. 2003. V. 74. P. 4634.

  14. Shen B., Sun Y.W., Wan B.N., Qian J.P. // Rev. Sci. I-nstrum. 2007. V. 78. 093501.

  15. Trembach D., Xiao C., Dreval M., Hirose A. // Rev. Sci. Instrum. 2009. V. 80. 053502.

  16. Kumar S., Jha R., Lal P., Hansaliya Ch., Gopalkrishna M.V., Kulkarni S., Mishra K. // Rev. Sci. Instrum. 2010. V. 81. 123505.

  17. Sevillano M.G., Garrido I., Garrido A.J., Romero J., Paley J., Moret J.-M., Coda S., Felici F., Curchod L., the TCV team // Proc. 50th IEEE Conf. on Decision and Control and European Control Conf. (CDC-ECC), Orlando, FL, USA, 2011. P. 7536.

  18. Han H.S., Hahn S.H., Bak J.G., Hyatt A., Johnson R., Woo M.H., Kim J.S., Bae Y.S., KSTAR team // Fusion Eng. Des. 2015. V. 95. P. 44.

  19. Gerasimov S.N., Abreu P., Baruzzo M., Drozdov V., Dvornova A., Havlicek J., Hender T.C., Hronova O., Kruezi U., Li X., Markovič T., Pánek R., Rubinacci G., Tsalas M., Ventre S., Villone F., Zakharov L.E., JET Contributors // Nucl. Fusion. 2015. V. 55. 113006.

  20. Giannone L., Geiger B., Bilato R., Maraschek M., Odstrcily T., Fischer R., McCarthy P.J., Fuchs J.C., Mer-tens V., Schuhbeck K.H., ASDEX Upgrade Team // Rev. Sci. Instrum. 2016. V. 87. 053509.

  21. Giannone L., Fischer R., Fuchs J.C., Geiger B., Maraschek M., Rittich D., Sieglin B., Bock A., Hobirk J., Kallenbach A., Mertens V., Schuhbeck K.H., McCar-thy P.J. // Rev. Sci. Instrum. 2018. V. 89. 106101.

  22. Endler M., Brucker B., Bykov V., Cardella A., Carls A., Dobmeier F., Dudek A., Fellinger J., Geiger J., Gros-ser K., Grulke O., Hartmann D., Hathiramani D., Hö-chel K., Köppen M., Laube R., Neuner U., Peng X., Rahbarnia K., Rummel K., Sieber T., Thiel S., Vorköper A., Werner A., Windisch T., Ye M.Y. // Fusion Eng. Des. 2015. V. 100. P. 468.

  23. Rahbarnia K., Thomsen H., Neuner U., Schilling J., Geiger J., Fuchert G., Andreeva T., Endler M., Hathirama-ni D., Bluhm T., Zilker M., Carvalho B.B., Werner A., Wendelstein 7-X Team // Nucl. Fusion. 2018. V. 58. 096010.

  24. Брагинский С.И., Шафранов В.Д. // Физика плазмы и проблема управляемых термоядерных реакций. М.: Изд-во АН СССР, 1958. Т. 2. С. 26. [S.I. Bra-ginskii and V. D. Shafranov. Plasma Physics and Problem of Controlled Thermonuclear Reactions / Ed. M.A. Leontovich. New York: Pergamon, 1959. V. 2. P. 39.]

  25. Mukhovatov V.S., Shafranov V.D. // Nucl. Fusion. 1971. V. 11. P. 605.

  26. Lao L.L., St. John H.E., Stambaugh R.D., Pfeiffer W. // Nucl. Fusion. 1985. V. 25. P. 1421.

  27. Fresa R., Albanese R., Arshad S., Coccorese V., de Magistris M., Minucci S., Pironti A., Quercia A., Rubi-nacci G., Vayakis G., Villone F. // Fusion Eng. Des. 2015. V. 100. P. 133.

  28. Pustovitov V.D. // Fusion Eng. Des. 2019. V. 138. P. 53.

  29. Pustovitov V.D. // Fusion Eng. Des. 2017. V. 117. P. 1.

  30. Haegi M., Sand F. // Plasma Phys. 1975. V. 17. P. 997.

  31. Villone F., Ramogida G., Rubinacci G. // Fusion Eng. Des. 2015. V. 93. P. 57.

  32. Pustovitov V.D. // Plasma Phys. Control. Fusion. 2017. V. 59. 055008.

  33. Pustovitov V.D., Kiramov D.I. // Plasma Phys. Control. Fusion. 2018. V. 60. 045011.

  34. Yanovskiy V.V., Isernia N., Pustovitov V.D., Villone F., Abate D., Bettini P., Chen S.L., Havlicek J., Herr-mann A., Hromadka J., Hron M., Imrisek M., Komm M., Paccagnella R., Panek R., Pautasso G., Peruzzo S., Sestak D., Teschke M., Zammuto I., the COMPASS team // Fusion Eng. Des. 2019. V. 146. P. 2338.

  35. Isernia N., Pustovitov V.D., Villone F., Yanovskiy V. // Plasma Phys. Control. Fusion. 2019. V. 61. 115003.

  36. Chu M.S., Okabayashi M. // Plasma Phys. Control. Fusion. 2010. V. 52. 123001.

  37. Pustovitov V.D. // J. Plasma Phys. 2015. V. 81. 905810609.

  38. Gribov Y., Pustovitov V.D. // 19th IAEA Fusion Energy Conf., Lyon, 2002. IAEA-CN-94/CT/P-12. CD-ROM file CT/P-12 and http://www-pub.iaea.org/MTCD/publications/PDF/csp_019c/html/node174.htm

  39. Hender T.C., Wesley J.C., Bialek J., Bondeson A., Boo-zer A.H., Buttery R.J., Garofalo A., Goodman T.P., Granetz R.S., Gribov Y., Gruber O., Gryaznevich M., Giruzzi G., Guenter S., Hayashi N., Helander P., Heg-na C.C., Howell D.F., Humphreys D.A., Huys-mans G.T.A., Hyatt A.W., Isayama A., Jardin S.C., Kawano Y., Kellman A., Kessel C., Koslowski H.R., La Haye R.J., Lazzaro E., Liu Y.Q., Lukash V., Manickam J., Medvedev S., Mertens V., Mirnov S.V., Nakamura Y., Navratil G., Okabayashi M., Ozeki T., Paccagnella R., Pautasso G., Porcelli F., Pustovitov V.D., Riccardo V., Sato M., Sauter O.,Schaffer M.J., Shimada M., Sonato P., Strait E.J., Sugihara M., Takechi M., Turnbull A.D., Westerhof E.,Whyte D.G., Yoshino R., Zohm H. Progress in the ITER Physics Basis, Ch. 3 // Nucl. Fusion. 2007. V. 47. P. S128.

  40. Giannone L., Fischer R., McCarthy P.J., Odstrcil T., Zammuto I., Bock A., Conway G., Fuchs J.C., Gude A., Igochine V., Kallenbach A., Lackner K., Maraschek M., Rapson C., Ruan Q., Schuhbeck K.H., Suttrop W., Wenzel L., ASDEX Upgrade Team // Fusion Eng. Des. 2015. V. 100. P. 519.

  41. Pustovitov V.D. // Phys. Plasmas. 2018. V. 25. 062510.

  42. Пустовитов В.Д. // Физика плазмы. 2016. Т. 42. С. 957. [V.D. Pustovitov. Plasma Phys. Rep. 42, 1005 (2016).]

  43. Dubrov M.L., Pustovitov V.D. // Plasma Phys. Control. Fusion. 2019. V. 61. 065018.

  44. Дубров М.Л., Лукаш В.Э., Хайрутдинов Р.Р., Доку-ка В.Н. // ВАНТ. Серия: Термоядерный синтез. 2019. Т. 42. Вып. 1. С. 39. (https://doi.org/)https://doi.org/10.21517/0202-3822-2019-42-1-39-50

  45. Lehnen M., Arnoux G., Brezinsek S., Flanagan J., Gerasimov S.N., Hartmann N., Hender T.C., Huber A., Jachmich S., Kiptily V., Kruezi U., Matthews G.F., Morris J., Plyusnin V.V., Reux C., Riccardo V., Sieglin B., de Vries P.C., JET EFDA Contributors // Nucl. Fusion. 2013. V. 53. 093007.

  46. Campbell D.J. // Phys. Plasmas. 2015. V. 22. 021701.

  47. Hollmann E.M., Aleynikov P.B., Fulop T., Humphreys D.A., Izzo V.A., Lehnen M., Lukash V.E., Papp G., Pautasso G., Saint-Laurent F., Snipes J.A. // Phys. Plasmas. 2015. V. 22. 021802.

  48. Eidietis N.W., Gerhardt S.P., Granetz R.S., Kawano Y., Lehnen M., Lister J.B., Pautasso G., Riccardo V., Tan-na R.L., Thornton A.J. and The ITPA Disruption Database Participants // Nucl. Fusion. 2015. V. 55. 063030.

  49. Xu W., Liu X., Song Y., Li J., Lu M. // Fusion Eng. Des. 2013. V. 88. P. 1848.

  50. Albanese R., Carpentieri B., Cavinato M., Minucci S., Palmaccio R., Portone A., Rubinacci G., Testoni P., Ventre S., Villone F. // Fusion Eng. Des. 2015. V. 94. P. 7.

  51. Rozov V., Alekseev A. // Nucl. Fusion. 2015. V. 55. 083022.

  52. Roccella R., Roccella M., Riccardo V., Chiocchio S., JET Contributors // Nucl. Fusion. 2016. V. 56. 106010.

  53. Khayrutdinov R.R., Lukash V.E., Pustovitov V.D. // Plasma Phys. Control. Fusion. 2016. V. 58. 115012.

  54. Xu Weiwei, Liu Xufeng, Du Shuangsong, Song Yuntao // Fusion Eng. Des. 2017. V. 114. P. 131.

  55. Ma Xuebin, Li Min, Liu Songlin // Fusion Eng. Des. 2018. V. 131. P. 21.

  56. Chen S.L., Villone F., Sun Y.W., Xiao B.J. // Nucl. Fusion. 2018. V. 58. 076009.

  57. Pustovitov V.D. // Reviews of Plasma Physics. V. 21 / Ed. by B.B. Kadomtsev and V.D. Shafranov. New York: Consultants Bureau, 2000. P. 1.

  58. Разумова К.А. // Атомная энергия. 1966. Т. 20. Вып. 6. С. 459.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Физика плазмы

Архивы выпусков Информация о журнале Отправить рукопись в журнал