Физика плазмы, 2020, T. 46, № 8, стр. 721-729
Перераспределение стохастической кинетической энергии в ансамблях неидентичных заряженных частиц
О. С. Ваулина a, b, *, С.В. Кауфман a
a Московский физико-технический институт (государственный университет)
Московская обл., Долгопрудный, Россия
b Объединенный институт высоких температур РАН
Москва, Россия
* E-mail: olga.vaulina@bk.ru
Поступила в редакцию 16.01.2020
После доработки 25.02.2020
Принята к публикации 20.03.2020
Аннотация
Исследуются процессы энергетического обмена в системах неидентичных взаимодействующих частиц (имеющих различные размеры, массы и заряды) с пространственно-неоднородным распределением источников стохастической кинетической энергии. Рассмотрена теоретическая модель для анализа энергетического баланса в таких системах. Представлены аналитические соотношения, описывающие перераспределение стохастической кинетической энергии между двумя заряженными частицами. Предложенные соотношения проверены путем численного моделирования задачи для частиц c кулоновским взаимодействием. Выполнен численный анализ процессов перераспределения стохастической энергии в двумерных ансамблях с разделенными фракциями частиц разных размеров и температур. Результаты настоящей работы применимы для систем с любым типом попарных взаимодействий и могут быть полезны для анализа энергетического обмена в неоднородных системах, которые представляют интерес в физике плазмы, физике полимеров и коллоидных систем.
1. ВВЕДЕНИЕ
Исследования процессов энергетического обмена в неоднородных системах взаимодействующих частиц вызывает значительный интерес в различных областях науки и техники (физике плазмы, биологии, физике полимеров и т.д.) [1–5]. Ряд актуальных вопросов касается особенностей физических характеристик в ансамблях неидентичных частиц, имеющих различный характер парного взаимодействия, заряды, размеры, диэлектрическую проницаемость и т.д. [1–8].
Пылевая (комплексная) плазма представляет собой ионизованный газ, содержащий заряженные частицы вещества микронных размеров (пыль). Такая плазма широко распространена в природе и образуется в ряде технологических процессов [1–3]. Большинство теоретических и численных работ, посвященных исследованию свойств пылевой плазмы, имеют дело с идентичными пылевыми частицами, поскольку такие системы легче поддаются математическому описанию и более просты для понимания. Тем не менее, в реальных условиях пылевые структуры редко содержат идентичные частицы. Даже в случае лабораторных исследований монодисперсные пылевые частицы могут иметь различную величину заряда и/или стохастической кинетической энергии в зависимости от их пространственного положения [1, 2].
Большинство лабораторных исследований пылевой плазмы проводится в газовых разрядах различных типов [9–12]. Обычно, в центре газоразрядных камер наблюдается некоторое превышение концентрации ионов плазмы над концентрацией ее электронной компоненты [13]. Данное обстоятельство приводит к формированию эффективных ловушек для отрицательно заряженных частиц пыли [1, 2]. Стохастическая кинетическая энергия пылевых частиц (их “кинетическая температура”) в таких условиях может достигать ~0.2–5 эВ, что значительно выше температуры окружающего их газа. Механизмы такого “аномального разогрева” пылевых частиц обычно связывают с временными и/или пространственными изменениями их зарядов, или положения в объеме неоднородной плазмы [14–19]. Так как заряд пылевой частицы определяется локальными параметрами плазмы в ее окрестности, мощность источников подкачки энергии, а, соответственно, и “кинетическая температура” частицы могут существенно изменяться в пространстве [1, 2]. Источниками неравномерного нагрева системы частиц также могут являться неоднородное распределение температуры окружающего газа, лазерное излучение, используемое для диагностики и т.д.
Флуктуации зарядов пылевых частиц, вызванные случайной природой ионных и электронных токов, заряжающих эти частицы, присущи любым типам плазмы [1, 2]. В условиях лабораторной газоразрядной плазмы дополнительная стохастическая кинетическая энергия, ΔТf, для отдельной пылевой частицы, связанная с этими флуктуациями может быть записана в виде [1, 14‒16]
Здесь Q, М и ν – заряд, масса и коэффициент трения частицы, α ≈ 0.5 – параметр, отвечающий за амплитуду флуктуаций их зарядов, υ ∝ аd – характерная частота этих флуктуаций для частицы радиусом аd, а E – напряженность электрического поля в анализируемой системе, необходимая для равновесного положения пылевой частицы в поле действующих сил. В условиях микрогравитации величина ΔТf определяется флуктуациями зарядов окружающих частиц пылевого облака, E ≅ Eint ~ Q/d2, где d – среднее расстояние между пылевыми частицами. Для наземных лабораторных экспериментов, где основной внешней неэлектрической силой является сила тяжести: E ≅ Eint + Eext, где Eext ≅ gM/Q.
Отсутствие простых теоретических моделей для описания энергетического баланса в системах неидентичных заряженных частиц с неоднородным распределением тепловых источников (источников их стохастической кинетической энергии) затрудняет анализ процессов передачи тепла в реальных системах.
В настоящей работе речь пойдет о механизме переноса тепла, который не связан с процессами массопереноса, и возникает за счет передачи стохастических колебаний отдельных частиц вблизи их равновесного положения, что не возможно без взаимодействия между частицами системы. Особенности энергетического обмена в ансамблях неидентичных частиц рассматриваются для условий близких к условиям лабораторных экспериментов в газоразрядной плазме. Представлены аналитические соотношения для случая двух взаимодействующих частиц, которые могут быть полезны для анализа качественной картины энергетического обмена между частицами в протяженных системах.
Рассмотрены условия перераспределения стохастической кинетической энергии в двумерных ансамблях с двумя разделенными фракциями неидентичных частиц разных размеров и температур. Причины формирования раздельных фракций для частиц разных размеров обычно связывают с наличием термофоретических сил, ${{F}_{{\text{T}}}} = {{C}_{{\text{T}}}}a_{d}^{2}\nabla {{T}_{n}}$, или сил ионного увлечения, ${{F}_{{\text{I}}}} = {{C}_{{\text{I}}}}a_{d}^{2}{{u}_{i}}$. Здесь ad – радиус частицы, ∇Tn – градиент температуры нейтрального газа (который направлен в сторону уменьшения Tn), ui – дрейфовая скорость ионов (которая направлена по внешнему электрическому полю), а коэффициенты CT и CI зависят от внешних условий и параметров окружающей плазмы [1, 20–22]. Указанные силы (FI, FТ) зависят от размера частицы иным образом, чем сила электрического поля, FЕ ≈ QE ∝ ad, действующая на заряженную пылевую частицу. За счет направления электрических полей и градиентов температур газа в обычных условиях газоразрядных камер обе упомянутых силы (FI, FТ) будут давать дополнительный вклад в баланс сил, ослабляющий воздействие внешних электрических сил FЕ на пылевую частицу [13]. И этот вклад будет тем больше, чем больше размер пылевых частиц. Таким образом, в случае системы, состоящей из двух фракций частиц, более крупные частицы будут располагаться на оболочке пылевого облака.
В настоящей работе внешнее электрическое поле полагалось линейным. Для представленных здесь теоретических и численных расчетов мы полагали, что плотность материала, ρ, одинакова для различных фракций частиц, ρ1= ρ2, т.е. отношение их масс M1/M2 ∝ (ad1/ad2)3. Заряды частиц задавались согласно приближению ограниченных орбит (Orbit Motion Limited): Qi ∝ adi [1, 2]; а их коэффициенты трения согласно свободномолекулярному приближению: ${{\nu }_{i}} \propto a_{{di}}^{2}{\text{/}}{{M}_{i}}$ [23]. С учетом принятых приближений отношение величин дополнительной энергии (1) за счет флуктуаций зарядов пылевых частиц разного размера (ad1, ad2) можно оценить как: $\Delta Т_{f}^{1}{\text{/}}\Delta Т_{f}^{2}$ ~ (d2 /d1)4 для Eint ≫ Eext; или $\Delta Т_{f}^{1}{\text{/}}\Delta Т_{f}^{2}$ ~ (ad1/ad2)2 для Eint ≪ Eext, если основной действующей неэлектрической силой в системе является сила тяжести.
2. ДВЕ ЧАСТИЦЫ (ОСНОВНЫЕ СООТНОШЕНИЯ)
Рассмотрим систему линеаризованных уравнений движения, описывающих отклонения двух частиц (с зарядами Q1(2) , массой M1(2) и попарным взаимодействием) от их положения равновесия (ξ1, ξ2) в поле внешних сил под действием случайной силы Fb1(2), которая является источником стохастической (тепловой) энергии частиц:
(2a)
${{M}_{1}}\frac{{{{d}^{2}}{{\xi }_{1}}^{{}}}}{{d{{t}^{2}}}} = - v_{1}^{{}}{{M}_{1}}\frac{{d{{\xi }_{1}}}}{{dt}} + {{a}_{1}}{{\xi }_{1}}^{{}} + b{{\xi }_{2}} + F_{{b1}}^{{}},$(2б)
${{M}_{2}}\frac{{{{d}^{2}}{{\xi }_{2}}^{{}}}}{{d{{t}^{2}}}} = - {{v}_{2}}{{M}_{2}}\frac{{d{{\xi }_{2}}}}{{dt}} + {{a}_{2}}{{\xi }_{2}}^{{}} + b{{\xi }_{1}} + F_{{b2}}^{{}},$Остановимся на случае вертикальной конфигурации частиц, см. рис. 1. Тогда для их вертикальных смещений ξ1(2)= z1(2): коэффициент a1(2) = –(Q1(2)βz – F') и b = –F'. Для радиальных смещений ξ1(2)= r1(2): a1(2) = –(Q1(2)βr- F/d) и b = = F/d. Здесь βr и βz – величины градиентов электрического поля в радиальном и вертикальном направлении, соответственно, d – расстояние между частицами, F – сила взаимодействия между частицами, а F' ее производная в направлении z. Для кулоновского взаимодействия: F = Q1Q2/d2; F ' = –2Q1Q2/d3.
Рис. 1.
Вертикальная конфигурация двух взаимодействующих частиц в электрическом поле ловушки E = = E(z,r) с цилиндрической симметрией.
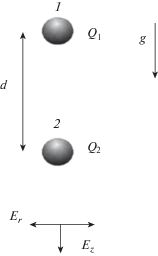
Задача об устойчивой конфигурации двух идентичных частиц, взаимодействующих с различными типами потенциалов, рассматривалась в работах [24–27]. Было показано, что устойчивость их вертикальной конфигурации определяется соотношением βr > βz, в обратном случае (βr < βz) – формируется горизонтальная конфигурация частиц. Для двух частиц с разной массой для условий наземных экспериментов (где нельзя пренебречь силой тяжести) условия баланса сил дают [8]
(3)
$g({{M}_{1}}{{Q}_{2}}--{{M}_{2}}{{Q}_{1}}) + {{Q}_{1}}{{Q}_{2}}{{b}_{z}}d = {\text{ }}({{Q}_{1}} + {{Q}_{2}})F.$При этом условие формирования неустойчивости в такой системе можно записать как [8]:
(4)
$\begin{gathered} {{Q}_{1}}{{Q}_{2}}{{\beta }_{r}} < ({{Q}_{1}} + {{Q}_{2}})F{\text{/}}d = \\ = {{Q}_{1}}{{Q}_{2}}{{\beta }_{z}} + g({{M}_{1}}{{Q}_{2}}--{{M}_{2}}{{Q}_{1}}){\text{/}}d. \\ \end{gathered} $Для M1(2) ≡ M и Q1(2) ≡ Q данное условие приобретает вид βr < βz , в соответствие с критерием, изложенным выше. Исследование условий развития неустойчивостей (4) для различных параметров задачи представлены в работе [8].
Для поиска корреляторов скоростей и смещений частиц в системе (2а)–(2б) отметим, что корреляторы случайной силы Fb1(2) подчиняются уравнениям: 〈Fb1〉 = 〈Fb2〉 ≡ 0, 〈Fb1Fb2〉 = 0, 〈Fb1V2〉 = = 〈Fb2V1〉 ≡ 0, 〈Fb1ξ2〉 = 〈Fb2ξ1〉 ≡ 0, 〈Fb1ξ1〉 = 〈Fb2ξ2〉 ≡ 0, 〈Fb1V2〉 = 〈Fb2V1〉 ≡0. Здесь и далее угловые скобки 〈 〉 обозначают усреднение по времени при t → ∞. При движении частиц по ограниченным траекториям: 〈ξ1V1〉 = 〈ξ2V2〉 ≡ 0, а 〈V1(2)Fb1(2)〉 = $\nu T_{{1\left( 2 \right)}}^{0}$ , где $T_{{1\left( 2 \right)}}^{0}$ – температура тепловых источников [28–31]. Тогда уравнения для корреляторов можно представить в виде [30, 31]
(5a)
${{a}_{{1\left( 2 \right)}}}\langle \xi _{{1(2)}}^{2}\rangle + b\left\langle {{{\xi }_{2}}{{\xi }_{1}}} \right\rangle + T_{{1\left( 2 \right)}}^{0} + \delta {{T}_{{1\left( 2 \right)}}} = 0,$(5б)
$\begin{gathered} - {{\nu }_{{1\left( 2 \right)}}}{{М}_{{1\left( 2 \right)}}}\langle {{\xi }_{{2\left( 1 \right)}}}{{V}_{{1\left( 2 \right)}}}\rangle + {{a}_{{1\left( 2 \right)}}}\langle {{\xi }_{2}}{{\xi }_{1}}\rangle + \\ + \;b\langle \xi _{{2\left( 1 \right)}}^{2}\rangle + {{М}_{{1\left( 2 \right)}}}\langle {{V}_{1}}{{V}_{2}}\rangle = {\text{ }}0, \\ \end{gathered} $(5в)
${{\nu }_{{1\left( 2 \right)}}}\delta {{T}_{{1\left( 2 \right)}}} = b\langle {{\xi }_{{2\left( 1 \right)}}}{{V}_{{1\left( 2 \right)}}}\rangle ,$(5г)
$\begin{gathered} - {{\nu }_{1}}{{М}_{1}}\langle {{V}_{1}}{{V}_{2}}\rangle - {{\nu }_{2}}{{М}_{2}}\langle {{V}_{1}}{{V}_{2}}\rangle + \\ + {\text{ }}{{a}_{1}}\langle {{\xi }_{1}}{{V}_{2}}\rangle + {{a}_{2}}\langle {{\xi }_{2}}{{V}_{1}}\rangle = 0, \\ \end{gathered} $Здесь ${{T}_{1}} = T_{1}^{0} + \delta {{T}_{1}}$, ${{T}_{2}} = T_{2}^{0} + \delta {{T}_{2}}$, где T1, T2– температура частиц для равновесного состояния системы, $T_{1}^{0}$, $T_{2}^{0}$ – энергия источников (которая при численном моделировании задачи соответствует их заданной/начальной температуре), а δT1, δT2– приращение температуры в процессе установления равновесия.
Обозначим $\Delta T = T_{2}^{0} - T_{1}^{0}$, тогда
где(7)
$\begin{gathered} С = {{\left( {{{a}_{2}}{{M}_{1}} - {\text{ }}{{a}_{1}}{{M}_{2}}} \right)}^{2}}{\text{/}}({{\nu }_{1}}{{М}_{1}}{{М}_{2}} + {{\nu }_{2}}{{М}_{2}}{{М}_{1}}){\text{ + }} \\ + \;{{b}^{2}}({{\nu }_{1}} + {{\nu }_{2}}){\text{/}}({{\nu }_{1}}{{\nu }_{2}}) - ({{a}_{2}}{{\nu }_{1}}{{М}_{1}} + {\text{ }}{{a}_{1}}{{\nu }_{2}}{{М}_{2}}). \\ \end{gathered} $Для двух идентичных частиц (Q1(2) = Q, M1(2)= = M, ν1(2) = ν, a1(2) = а) решение системы уравнений (5а)–(5д) для их вертикальной конфигурации можно записать как [8]
(8)
$\delta {{T}_{{1\left( 2 \right)}}} = \pm {{b}^{2}}\Delta T{\text{/}}(2\{ {{b}^{2}} - {{\nu }^{2}}Мa\} ).$В этом случае δT1 = –δT2, а при b2 ≫ –ν2Мa величина |δT1(2)| → |△T|/2, т.е. энергия равномерно распределяется между частицами системы, а при ν → ∞ величина |δT1(2)| → 0.
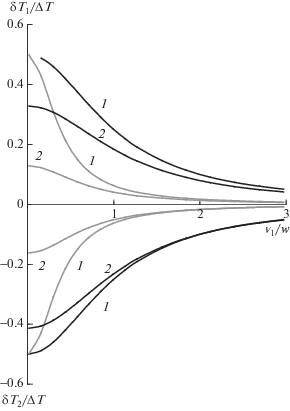
Иллюстрация зависимостей δT1/ΔT и δT2/ΔT от ν1/ω, где $\omega = {{(Q_{1}^{2}{\text{/}}{{d}^{3}}{{М}_{1}})}^{{1/2}}}$, описывающая перераспределение энергии в вертикальном и радиальном направлениях, для двух частиц с кулоновским взаимодействием при g = 0, βr/βz = 4, $T_{1}^{0} < T_{2}^{0}$ показана на рис. 2.
Рис. 2.
Зависимости δT1/ΔT и δT2/ΔT от ν1/ω в вертикальном (черные линии) и радиальном (серые линии) направлениях для двух частиц с кулоновским взаимодействием при βr/βz = 4, $T_{1}^{0} < T_{2}^{0}$ для: 1 – М1 = М2, d = 0.1 см; 2 – М2 = 2М1, d ≅ 0.105 см.
В заключение данного раздела рассмотрим два частных случая для частиц равной массы M1(2) = = M при $T_{2}^{0} \ne T_{1}^{0}$: (i) ν1(2) = ν, a1 ≠ a2; (ii) ν1 ≠ ν2, a1(2) = а.
В первом случае (ν1(2) = ν, a1 ≠ a2) получим следующее уравнение баланса:
(9)
$\begin{gathered} \delta {{T}_{{1\left( 2 \right)}}} = \pm {{b}^{2}}\Delta T{\text{/}}(2\{ {{b}^{2}} - {{\nu }^{2}}М({{a}_{1}} + {{a}_{2}}){\text{/}}2 + \\ + \;{{({{a}_{1}} - {{a}_{2}})}^{2}}{\text{/}}4\} ). \\ \end{gathered} $При этом общая энергия системы будет сохраняться, δT1 + δT2 = 0, а при b2 ≫ –ν2М(a1 + a2), величина |δT1(2)/△T| → (2 + (a1 – a2)2/2b2)–1.
Отметим, что случай a1 ≠ a2 может реализоваться для пылевых частиц в плазме даже в случае их попарного взаимодействия, например, за счет разницы в зарядах частиц, или отличия градиентов внешнего поля в точке их равновесного положения. Данные обстоятельства определяются возможными пространственными изменениями параметров окружающей их плазмы (например, концентраций и температур ионов/электронов).
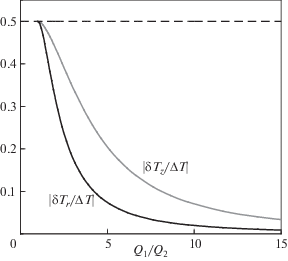
Учтем уравнение баланса сил (3) для двух частиц при Q1 ≠ Q2 и M1(2) = M (для g = 0). Тогда величина |δT1(2)/ΔT| → 0 при (Q1/Q2– Q2/Q1)2→ ∞. Это связано с уменьшением сил взаимодействия в рассматриваемой системе с увеличением разницы между Q1 и Q2, что является следствием условия баланса сил (3), необходимого для равновесного состояния системы. На рис. 3 показаны отношения δTz/ΔT и δTr/ΔT в зависимости от Q1/Q2, описывающие перераспределение энергии в вертикальном и радиальном направлениях, соответственно. Расчеты были выполнены при βr/βz = 4 для частиц с кулоновским взаимодействием, расположенными на расстоянии d ≈ 0.1 см.
Рис. 3.
Отношения |δTz/ΔT| и |δTr/ΔT| в зависимости от Q1/Q2 для частиц с кулоновским взаимодействием, расположенными на расстоянии d ≈ 0.1 см.
Рассмотрим второй случай: M1(2) = M, a1(2) = а, $T_{2}^{0} \ne T_{1}^{0}$, ν1 ≠ ν2. Неравная величина коэффициентов трения, ν1 ≠ ν2, в этом случае может возникать, например, за счет градиентов температур и/или давлений окружающего буферного газа. Тогда для частиц с равными зарядами Q1(2) ≡ Q получим уравнения баланса в виде
(10а)
$\delta {{T}_{1}} = {{b}^{2}}{{\nu }_{2}}\Delta T{\text{/}}({{\nu }_{1}} + {{\nu }_{2}})\{ {{b}^{2}} - {{\nu }_{1}}{{\nu }_{2}}Мa\} {\text{ }},$(10б)
$\delta {{T}_{2}} = - {{b}^{2}}{{\nu }_{1}}\Delta T{\text{/}}({{\nu }_{1}} + {{\nu }_{2}})\{ {{b}^{2}} - {{\nu }_{1}}{{\nu }_{2}}Мa\} {\text{ }}{\text{.}}$Общая энергия системы не сохраняется: δT1 + + δT2 ≠ 0. При b2 ≫ –ν1ν2 Мa: δT1 + δT2 → ΔT (ν2 – – ν1)/(ν1+ ν2). Поскольку $\Delta T = T_{2}^{0} - T_{1}^{0}$, это означает, что при $T_{2}^{0} > T_{1}^{0}$ и ν1> ν2 – система будет терять энергию, в случае $T_{2}^{0} < T_{1}^{0}$ и ν1> ν2 – будет приобретать ее. Это связано с тем, что при меньших коэффициентах трения одной из частиц в рассматриваемой системе, она менее активно обменивается энергией с другой частицей. Легко увидеть, что диапазон изменений кинетической температуры всей системы при любых ν1 и ν2 будет варьироваться в пределах от $T_{2}^{0}$ до $T_{1}^{0}$.
Зависимость |δT1/ΔT| и |δT2/ΔT| от ν1/ν2 при βr/βz = 4 для частиц с кулоновским взаимодействием, расположенными на расстоянии d ≈ ≈ 0.1 см, показана на рис. 4.
Рис. 4.
Зависимость |δT1/ΔT| и |δT2/ΔT| от ν1/ν2 в вертикальном направлении для частиц с кулоновским взаимодействием, расположенными на расстоянии d ≈ 0.1 см.
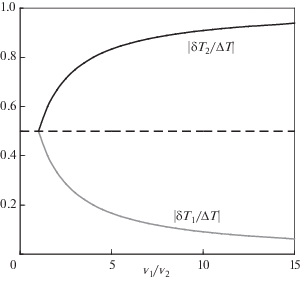
Предельные случаи для двух последних из рассмотренных задач (Q1/Q2 ≫ 1 и ν1/ν2 ≫ 1) не могут реализоваться в лабораторной практике. Тем не менее, иллюстрации, представленные на рис. 3, 4 качественно демонстрируют изменения величины перераспределяемой энергии в зависимости от параметров задачи.
3. РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ И ИХ ОБСУЖДЕНИЕ
Численное исследование процессов энергетического обмена выполнялось методом молекулярной динамики Ланжевена для частиц, взаимодействующих с кулоновским потенциалом, в анизотропном электрическом поле ловушки с цилиндрической симметрией. Техника моделирования подробно описана в работах [1, 2].
Моделирование проводилось для двух отдельных частиц и для двумерных ансамблей с разделенными фракциями частиц разных размеров и температур (при g = 0). Отношения масс, M2/M1, и отношения температур тепловых источников, $T_{2}^{0}{\text{/}}T_{1}^{0}$ (или $T_{2}^{0}{\text{/}}T_{1}^{0}$), для частиц различных фракций изменялись от одного до десяти. Заряды и коэффициенты трения задавались как Qi ∝ adi и ${{\nu }_{i}} \propto a_{{di}}^{{ - 1}}$, соответственно; i = 1, 2. Отношение ω1(2)/ν1(2) варьировалось от ~0.7 до ~7, где ${{\omega }_{{1\left( 2 \right)}}} = {\text{ }}$ $ = {\text{ }}{{(Q_{{1\left( 2 \right)}}^{2}{\text{/}}{{d}^{3}}{{М}_{{1\left( 2 \right)}}})}^{{1/2}}}$. Здесь для двумерных бинарных систем: d – среднее расстояние между частицами отдельной фракции. Число частиц в каждой из фракций (N1, N2) менялось от 50 до 400.
Температура тепловых источников $T_{{1\left( 2 \right)}}^{0}$ варьировалась в пределах от ~0.2 эВ до ~2 эВ и задавалась одинаковой по степеням свободы: $T_{z}^{0} = T_{x}^{0} = T_{y}^{0}$. В процессе моделирования начальная стохастическая кинетическая энергия (энергия источников) перераспределялась от более “горячих” частиц к менее “горячим”. Во всех случаях наблюдаемые распределения скоростей частиц были близки к Максвелловским функциям. При этом для случая двух частиц фиксировалось неравномерное перераспределение энергий по степеням свободы Tz ≠ Tx = Ty.
Иллюстрации отдельных результатов численных исследований для двух частиц при βr/βz = 4, ω1/ν1 ≈ 1.4 и d ≈ 0.1 см представлены на рис. 5–7 совместно с аналитическими решениями задачи. Так на рис. 5 показаны функции распределения скоростей для двух идентичных частиц f1(V1) и f2(V2) в вертикальном и в радиальном направлениях для при $T_{1}^{0}{\text{/}}T_{2}^{0}$ = 10. Согласно результатам, представленным в разд. 2, полная энергия моделируемой системы не менялась (T2 + T1) = = ($T_{2}^{0} + T_{1}^{0}$), (δT1 + δT2) = 0.
Рис. 5.
Функции распределения скоростей для двух частиц системы f1(V1) (а) и f2(V2) (б) в вертикальном и в радиальном направлениях при βr/βz = 4 и М1 = М2. Символами обозначены результат численного моделирования, сплошными линиями функции Максвелла с температурами: 1 – $T_{1}^{0}$ = 2.08 эВ; 2 – $T_{1}^{r}$ ≅ 1.87 эВ; 3 – $T_{1}^{z}$ ≅ 1.46 эВ; 4 – $T_{2}^{z}$ ≅ 0.83 эВ; 5 – $T_{2}^{r}$ ≅ 0.416 эВ; 6 – $T_{2}^{0}$ = 0.208 эВ.
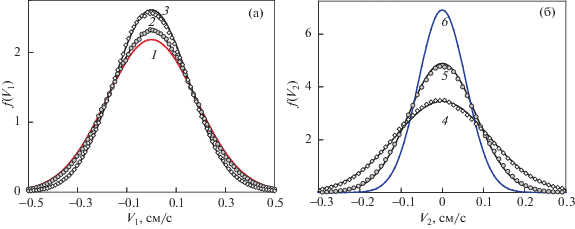
Рис. 6.
Функции f1(V1) (а) и f2(V2) (б) в вертикальном и в радиальном направлениях при βr/βz = 4 и М2 = 2М1. Символами обозначены результат численного моделирования, сплошными линиями функции Максвелла с температурами: 1 – $T_{1}^{0}$ =0.208 эВ; 2 – $T_{1}^{r}$ ≅ 0.33 эВ; 3 – $T_{1}^{z}$ ≅ 0.66 эВ; 4 – $T_{2}^{z}$ ≅ 1.53 эВ; 5 – $T_{2}^{r}$ ≅ 1.94 эВ; 6 – $T_{2}^{0}$ = 2.08 эВ.
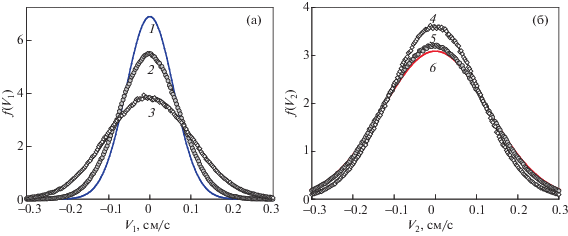
Рис. 7.
Функции f1(V1) (а) и f2(V2) (б) в вертикальном и в радиальном направлениях при βr/βz = 4 и М2 = 2М1. Символами обозначены результат численного моделирования, сплошными линиями функции Максвелла с температурами: 1 – $T_{1}^{0}$ = 2.08 эВ; 2 – $T_{1}^{r}$ ≅ 1.93 эВ; 3 – $T_{1}^{z}$ ≅ 1.6 эВ; 4 – $T_{2}^{z}$ ≅ 0.735 эВ; 5 – $T_{2}^{r}$ ≅ 0.38 эВ; 6 – $T_{2}^{0}$ = 0.208 эВ.
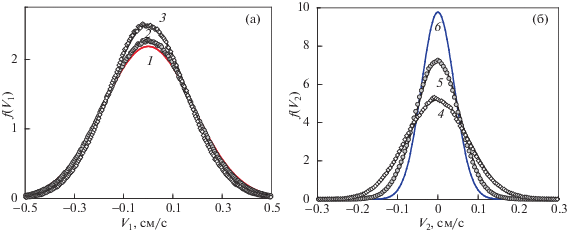
На рис. 6, 7 оказаны функции f1(V1) и f2(V2) для М2 = 2М1, Q2/Q1 = 21/3, ν1/ν2 = 21/3 при $T_{2}^{0}{\text{/}}T_{1}^{0}$ = 10 и $T_{1}^{0}{\text{/}}T_{2}^{0}$ = 10, соответственно. В обоих случаях (δT1 + δT2) ≠ 0. При этом для $T_{2}^{0}{\text{/}}T_{1}^{0}$ = 10, см. рис. 6, приращение энергии было отрицательным (δT1 + δT2) < 0, а (T2 + T1)/($T_{2}^{0} + T_{1}^{0}$) ≈ 0.97. Для случая $T_{1}^{0}{\text{/}}T_{2}^{0}$ = 10, см. рис. 7, приращение энергии было положительным (δT1 + δT2) > 0, а (T2 + T1)/($T_{2}^{0} + T_{1}^{0}$) ≈ 1.02. Величина |δT1/δT2| ≅ ≅ ν2/ν1, см. формулы (10а), (10б).
Таким образом, результаты численного моделирования для двух частиц согласуются выводами, представленными в разд. 2. Функции распределения скоростей f1(V1) и f2(V2) полностью соответствовали их температурам, найденным из аналитических соотношений.
Перейдем к двумерным ансамблям, состоящим из двух разделенных фракций частиц разного размера. Частицы в моделируемых системах находились под воздействием электрических сил ловушки, FЕ ∝ ad, и сторонних сил ${{F}_{{{\text{T(I)}}}}} \propto a_{d}^{2}$, направленных противоположно силе FЕ. Здесь мы рассматриваем упомянутые силы только в первом (линейном) приближении. Поскольку основным предметом исследований является баланс энергии, а подробный анализ природы сил, механизмов и условий разделения частиц по размерам выходит за рамки настоящей работы.
Расчеты проводились для различных отношений |FT(I)/FЕ|, которые варьировались от 5% до 25% для мелких частиц, и от 10% до ~30% для крупных частиц, соответственно, в зависимости от отношения размеров крупных и мелких частиц. При этом отношение градиентов ∇F1/∇F2 суммарных сил, F1(2), действующих на частицы изменялось от ~1.05 до ~1.2. Во всех случаях наблюдалось заметное разделение системы по фракциям и более крупные частицы находились на оболочке двумерного облака, см. рис. 8.
Рис. 8.
Иллюстрация положений частиц в двумерной системе при N = 600 (N1 = 200, N2 = 400). Белыми символами показаны частицы массой М1, серыми – массой М2 = 2М1.

На рис. 9, 10 показаны результаты численного моделирования для частиц с параметрами, близкими к параметрам экспериментов в условиях микрогравитации [21, 22]: М2/М1 = 8, Q2/Q1 = 2, ν1/ν2 = 2, $T_{1}^{0} + T_{2}^{0}$ = 4 при ∇F1/∇F2 ~ 1.1. Средние расстояния между частицами крупной фракции составляли d ≈ 0.07 см, между легкими частицами – d ≈ 0.035 см. Отношение ω1/ν1 ~ 6.8, ω2/ν2 ~ 3.4, где ω1(2) = ${{(Q_{{1\left( 2 \right)}}^{2}{\text{/}}{{d}^{3}}{{М}_{{1\left( 2 \right)}}})}^{{1/2}}}$. На рис. 9 показана вероятность, f(r), нахождения частиц различной массы М1(2) на расстояниях, r, от центра ловушки, а на рис. 10 представлена радиальная зависимость их кинетических температур, Т(r).
Рис. 9.
Вероятность нахождения частиц f(r) разной массы М1 (черная линия) и М2 (серая линия) на разных расстояниях, r, от центра ловушки (М2/М1 = 8, Т1/Т2 = 4).
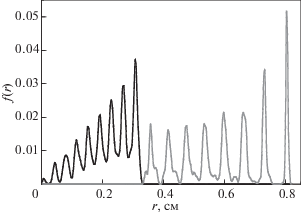
Рис. 10.
Зависимость отношения кинетических температур $T(r){\text{/}}T_{2}^{0}$ для частиц разной массы М1 (белые символы – ${{T}_{1}}(r){\text{/}}T_{2}^{0}$) и М2 (серые символы – ${{T}_{2}}(r){\text{/}}T_{2}^{0}$) от расстояния, r, до центра ловушки (М2/М1 = 8, $T_{1}^{0}{\text{/}}T_{2}^{0}$ = 4, ν1/ν2 = 2). Сплошная черная линия показывает заданные температуры частиц и границу раздела фракций.
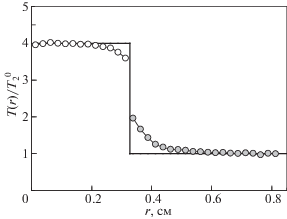
Результаты исследования баланса энергии в системе частиц, состоящей из двух фракций, представлены на рис. 11–14 для случая М2/М1 = 2, Q2/Q1 = 21/3, ∇F1/∇F2 ~ 1.1, ν1/ν2 = 21/3 при ν1 = 5 с–1 (ω1/ν1 ~ 5.6, ω2/ν2 ~ 4.5) и ν1 = 10 с–1 (ω1/ν1 ~ 2.8, ω2/ν2 ~ 2.25).
Рис. 11.
Функция f(r) для частиц разной массы М1 (черная линия) и М2 (серая линия) при М2/М1 = 2, Т1/Т2 = 10.
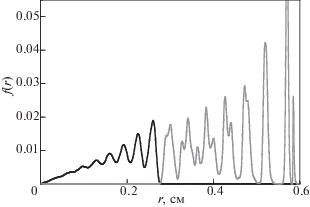
Рис. 12.
Функция $T(r){\text{/}}T_{2}^{0}$ для частиц разной массы при М2/М1 = 2, $T_{1}^{0}{\text{/}}T_{2}^{0}$ = 10, ν1/ν2 = 21/3: белые символы – ${{T}_{1}}(r){\text{/}}T_{2}^{0}$; серые символы – ${{T}_{2}}(r){\text{/}}T_{2}^{0}$. (Кружки – ν1 = 5 с–1; ромбы – ν1 = 10 с–1.) Сплошная черная линия показывает заданные температуры частиц и границу раздела фракций.
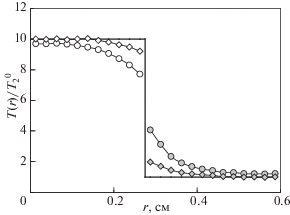
Рис. 13.
Функция f(r) для частиц разной массы М1 (черная линия) и М2 (серая линия) при М2/М1 = 2, Т2/Т1 = 10.
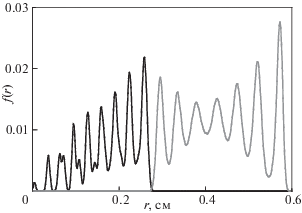
Рис.14.
Функция $T(r){\text{/}}T_{1}^{0}$ для частиц разной массы при М2/М1 = 2, $T_{2}^{0}{\text{/}}T_{1}^{0}$ = 10, ν1/ν2 = 21/3: белые символы – ${{T}_{1}}(r){\text{/}}T_{1}^{0}$; серые символы – ${{T}_{2}}(r){\text{/}}T_{1}^{0}$. (Кружки – ν1 = 5 с–1; ромбы – ν1 = 10 с–1.) Сплошная черная линия показывает заданные температуры частиц и границу раздела фракций.
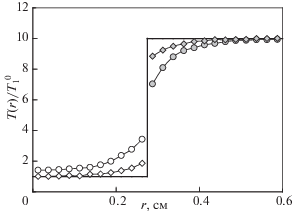
Так на рис. 11, 12 показана вероятность, f(r), нахождения частиц различной массы на разных расстояниях, r, от центра ловушки и радиальная зависимость их кинетических температур, Т(r), при $T_{1}^{0} - T_{2}^{0}$ = 10. А на рис. 13, 14 представлены функции f(r) и Т(r) для случая $T_{2}^{0} - T_{1}^{0}$ = 10.
Анализ результатов численного моделирования для двумерных ансамблей частиц показал, что вдоль линий раздела двух фракций, когда |δT1(2)/T1(2)| > 3% (т.е. ошибок численного эксперимента), величина отношения |δT1(r)/δT2(r)| = = ${\text{|}}({{T}_{1}}(r) - T_{1}^{0}){\text{/}}({{T}_{2}}(r) - T_{2}^{0}){\text{|}}$ ≈ ν2/ν1, см. рис. 10, 12, 14; где r – расстояние до центра ловушки. При этом дополнительная энергия δT1(2) ∝ ΔT = $T_{2}^{0} - T_{1}^{0}$, и уменьшалась с ростом ν1(2), см. рис. 12, 14.
4. ЗАКЛЮЧЕНИЕ
Выполнено исследование процессов энергетического обмена в диссипативных системах неидентичных взаимодействующих частиц (имеющих различные массы, размеры, заряды) с неоднородным распределением источников тепла и/или любых других источников стохастической кинетической энергии. Рассмотрены теоретическая модель для анализа энергетического баланса в таких системах и аналитические соотношения, описывающие перераспределение стохастической кинетической энергии между двумя неидентичными частицами. Предложенные соотношения проверены путем численного моделирования задачи для систем из двух частиц c кулоновским взаимодействием.
Выполнен численный анализ процессов перераспределения энергии в двумерных ансамблях неидентичных частиц, состоящих из двух раздельных фракций, формирующихся в электрических полях ловушки (FЕ ∝ ad) под воздействием дополнительных сил пропорциональных квадрату радиуса частиц (${{F}_{{{\text{T(I)}}}}} \propto a_{d}^{2}$), например, термофоретических сил, или сил ионного увлечения.
Результаты настоящей работы применимы для систем с любым типом попарных (взаимных) взаимодействий и могут быть полезны для анализа энергетического обмена в неоднородных системах, которые представляют интерес в физике плазмы, физике полимеров и коллоидных систем.
Данная работа частично поддержана Российским фондом фундаментальных исследований (грант № 18-38-20175), а также Программой Президиума РАН.
Список литературы
Ваулина О.С., Петров О.Ф., Фортов В.Е., Хра-пак А.Г., Храпак С.А. Пылевая плазма (эксперимент и теория). М.: Физматлит, 2009.
Complex and Dusty Plasmas / Ed. by Fortov V.E. and Morfill G.E., CRC Press (2010).
Ivlev A., Morfill G., Lowen H., Royall C.P. Complex Plasmas and Colloidal Dispersions: Particle-Resolved Studies of Classical Liquids and Solids. Singapore: World Scientific, 2012.
Photon Correlation and Light Beating Spectroscopy / Edited by H. Z. Cummins and E. R. Pike, Plenum, New York (1974).
Овчинников А.А., Тимашев С.Ф., Белый А.А. Кинетика диффузионно-контролируемых химических процессов. М.: Химия, 1986.
Филиппов А.В., Дербенев И.Н. // ЖЭТФ 2016. Т. 150. С. 1262.
Ваулина О.С. // ЖЭТФ 2016. Т. 149. С. 218.
Ваулина О.С. // ЖЭТФ 2017. Т. 151. С. 982.
Герасимов Ю.В., Нефедов А.П., Синельщиков В.А., Фортов В.Е. // Письма в ЖТФ. 1998. Т. 24. С. 62.
Fortov V.E., Nefedov E.A., Sinel’shchikov V.A., Usa-chev A.D., Zobnin A.V. // Phys. Lett. A. 2000. V. 267. P. 179.
Vaulina O.S., Vasilieva E.V., Petrov O.F., Fortov V.E. // Physica Scripta 2011. V. 84. P. 025503.
Aschinger A., Winter J. // New Journal of Physics 2012. V. 14. P. 093036.
Райзер Ю.П. Физика газового разряда. М.: Наука, 1987.
Vaulina O.S., Khrapak S.A., Petrov O.F., Nefedov A.P. // Phys. Rev. E. 1999. V. 60. P. 5959.
Quinn R.A. and Goree J. // Phys. Rev. E. 2000. V. 61. P. 3033.
Vaulina O.S., Khrapak S.A., Samarian A.A., Petrov O.F. // Phys. Scripta 2000. T84. P. 229.
Ваулина О.С., Нефедов А.П., Петров О.Ф., Фор-тов В.Е. // ЖЭТФ. 2000. Т. 118. С. 1319.
Ваулина О.С., Самарян А.А., Петров О.Ф., Джеймс Б., Mеландсо Ф. // Физика плазмы 2004. Т. 30. С. 698.
Vaulina O.S. // EPL 2016. V. 115. P. 10007.
Псахье С.Г., Зольников К.П. // Физическая мезомеханика 2008. Т. 11. С. 39.
Morfill G.E., Thomas H.M., Konopka U., Rothermel H., Zuzic M., Ivlev A., Goree J. // Phys. Rev. Lett. 1999. V. 83. P. 1598.
Thomas H.M. and Morfill G.E. // Contrib. Plasma Phys. 2001. V. 41. P. 255.
Лифшиц Е.М., Питаевский Л.П. Физическая кинетика. М.: Наука, 1979.
Ваулина О.С., Лисина И.И., Косс К.Г. // Физика плазмы 2013. Т. 39. С. 455.
Lisina I.I., Vaulina O.S. // EPL. 2003. V. 103. P. 55002.
Ваулина О.С., Адамович К.Г., Дранжевский И.Е. // Физика плазмы. 2005. Т. 31. С. 562.
Vaulina O.S., Adamovich X.G., Vladimirov S.V. // Phys. Scr. 2009. V. 79. P. 035501.
Саметов Э.А., Лисин Е.А., Ваулина О.С. // ЖЭТФ. 2020.
Саметов Э.А., Лисин Е.А., Ваулина О.С. // Вестник ОИВТ. 2019. Т. 2. С. 33.
Vaulina O.S. // Physics of Plasmas. 2017. V. 24. P. 023705.
Ваулина О.С. // ЖЭТФ. 2017. Т. 151. С. 982.
Дополнительные материалы отсутствуют.


